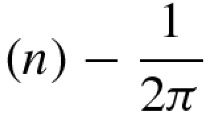Abstract
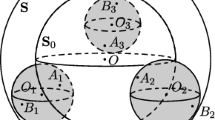
The results presented in this paper are generalizations of earlier work on the linear stability of non-rotating round gas balls in equilibrium, with respect to perturbations with zero angular momentum. Here we allow a more general barotropic equation of state for the gas, a non-zero angular momentum of the equilibrium state, and we are considering arbitrary numbers of gas balls, intending to use the result later to prove non-linear stability. The result requires an energy stability condition, which we verify for a single, slowly rotating gas ball, and the restricted class of equations of state used in earlier papers.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Friedman A.: Partial Differential Equations. Krieger Malabar, Florida (1983)
Gilbarg, D., Trudinger, N.: Elliptic partial differential equations of second order, second edition, Springer, Berlin (1983)
Günter N.M.: Potential Theory and its Applications to Basic Problems of Mathematical Physics. Frederick Ungar, New York (1967)
Guo Y., Tice I.: Decay of viscous surface waves without surface tension in horizontally infinite domains, Anal. PDE 6(6), 1429–1533 (2013)
Guo Y., Tice I.: Almost exponential decay of periodic viscous surface waves without surface tension. Arch. Ration. Mech. Anal. 207(2), 459–531 (2013)
Li D., Ströhmer G., Wang L.: Symmetry of integral equations on bounded domains. Proc. AMS 137, 3695–3702 (2009)
Padula M.: Asymptotic Stability of Steady Compressible Fluids. Springer, Heidelberg (2011)
Solonnikov, V. A.: On the stability of uniformly rotating viscous incompressible self-gravitating liquid. (English, Russian summary) Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 348 (2007), Kraevye Zadachi Matematicheskoi Fiziki i Smezhnye Voprosy Teorii Funktsii. 38, 165–208, 305 (translation in J. Math. Sci. (N. Y.) 152(5),713–740) (2008)
Ströhmer G., Zajązkowski W.: On the existence and properties of the rotationally symmetric equilibrium states of compressible barotropic self-gravitating fluids. Indiana Univ. Math. J. 46, 1181–1220 (1997)
Ströhmer G.: About the linear stability of the spherically symmetric solution for the equations of a barotropic viscous fluid under the influence of self-gravitation. J. Math. Fluid Mech. 8, 36–63 (2006)
Ströhmer G.: About the stability of gas balls. J. Math. Fluid Mech. 11, 572–608 (2009)
Ströhmer G.: Existence and structural stability for certain configurations of rotating barotropic fluids. J. Math. Fluid Mech. 16, 193–210 (2014)
Triebel, H.: Interpolation Theory, Function Spaces, Differential Operators. North Holland, Amsterdam (1978)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by H. Amann
Rights and permissions
About this article
Cite this article
Ströhmer, G. About Linear Stability for Multiple Gas Balls. J. Math. Fluid Mech. 18, 71–88 (2016). https://doi.org/10.1007/s00021-015-0231-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00021-015-0231-8