Skip to main content
SpringerLink
Log in

Fault Identification in Nonlinear Systems Based on Sliding Mode Observers with Weakened Existence Conditions

  • SYSTEMS THEORY AND GENERAL CONTROL THEORY
  • Published:
Journal of Computer and Systems Sciences International Aims and scope

Abstract

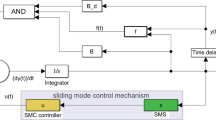
This paper considers the problem of fault identification in systems described by nonlinear dynamic equations with disturbances. Sliding mode observers are used for the solution. The proposed approach is based on constructing a reduced (lower-dimensional) model of the original system with selective sensitivity to defects and disturbances. This model is introduced mainly to weaken the existence conditions for sliding mode observers compared to the known works, particularly the minimum phase, detectability, and matching conditions. The weakening effect is achieved since the reduced model may not have the original system’s properties hindering the construction of sliding mode observers. This theory is illustrated by an example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. L. A. Mironovskii, Functional Diagnostics of Dynamic Systems (MGU-GRIF, Moscow, 1998) [in Russian].

    Google Scholar 

  2. V. I. Utkin, Sliding Modes and their Application in Systems with a Variable Structure (Nauka, Moscow, 1974) [in Russian].

    Google Scholar 

  3. A. N. Zhirabok, A. V. Zuev, and A. E. Shumskii, “Diagnosis of linear systems based on sliding mode observers,” J. Comput. Syst. Sci. Int. 58, 898 (2019).

    Article  Google Scholar 

  4. A. N. Zhirabok, A. V. Zuev, and A. E. Shumskii, “Method for fault identification in nonlinear systems based on sliding-mode observers,” J. Comput. Syst. Sci. Int. 60, 9 (2021).

    Article  MathSciNet  Google Scholar 

  5. C. Edwards and S. Spurgeon, “On the development of discontinuous observers,” Int. J. Control 59, 1211–1229 (1994).

    Article  MathSciNet  Google Scholar 

  6. T. Floquet, J. Barbot, W. Perruquetti, and M. Djemai, “On the robust fault detection via a sliding mode disturbance observer,” Int. J. Control 77, 622–629 (2004).

    Article  MathSciNet  Google Scholar 

  7. A. N. Zhirabok, A. V. Zuev, and A. E. Shumskii, “Diagnosis of linear dynamic systems: An approach based on sliding mode observers,” Autom. Remote Control 81, 211 (2020).

    Article  MathSciNet  Google Scholar 

  8. X. Yan and C. Edwards, “Nonlinear robust fault reconstruction and estimation using sliding mode observers,” Automatica 43, 1605–1614 (2007).

    Article  MathSciNet  Google Scholar 

  9. J. He and C. Zhang, “Fault reconstruction based on sliding mode observer for nonlinear systems,” Math. Probl. Eng. 2012, 451843-1–22 (2012).

    MathSciNet  MATH  Google Scholar 

  10. H. Alwi and C. Edwards, “Fault tolerant control using sliding modes with on-line control allocation,” Automatica 44, 1859–1866 (2008).

    Article  MathSciNet  Google Scholar 

  11. K. Chandra, H. Alwi, and C. Edwards, “Fault reconstruction for a quadrotor using an LPV sliding mode observer,” in Proceedings of the 9th IFAC Symposium on Safeprocess, France, Paris, 2015, pp. 374–379.

  12. K. Zhang, B. Jiang, X. Yan, and Z. Mao, “Sliding mode observer based incipient sensor fault detection with application to high-speed railway traction device,” ISA Trans. 63, 49–59 (2016).

    Article  Google Scholar 

  13. A. Zhirabok, A. Zuev, and V. Filaretov, “Fault identification in underwater vehicle thrusters via sliding mode observers,” Int. J. Appl. Math. Comput. Sci. 30, 679–688 (2020).

    MathSciNet  MATH  Google Scholar 

  14. T. Floquet, C. Edwards, and S. Spurgeon, “On sliding mode observers for systems with unknown inputs,” Int. J. Adapt. Contr. Signal Proc. 21, 638–656 (2017).

    Article  MathSciNet  Google Scholar 

  15. L. Fridman, A. Levant, and J. Davila, “Observation of linear systems with unknown inputs via high-order sliding-modes,” Int. J. Syst. Sci. 38, 773–791 (2007).

    Article  MathSciNet  Google Scholar 

  16. S. Tan and S. Edwards, “Robust fault reconstruction using multiple sliding mode observers in cascade: Development and design,” in Proceedings of the American Control Conference, St. Louis, USA, 2009, pp. 3411–3416.

  17. H. Alwi, C. Edwards, and C. Tan, “Sliding mode estimation schemes for incipient sensor faults,” Automatica 45, 1679–1685 (2009).

    Article  MathSciNet  Google Scholar 

  18. H. Rios, D. Efimov, J. Davila, T. Raissi, L. Fridman, and A. Zolghadri, “Nonminimum phase switched systems: HOSM based fault detection and fault identification via Volterra integral equation,” Int. J. Adapt. Contr. Signal Proc. 28, 1372–1397 (2014).

    Article  Google Scholar 

  19. R. Hmidi, A. Brahim, F. Hmida, and A. Sellami, “Robust fault tolerant control design for nonlinear systems not satisfying matching and minimum phase conditions,” Int. J. Contr., Autom. Syst. 18, 1–14 (2020).

    Article  Google Scholar 

  20. X. Wang, C. Tan, and D. Zhou, “A novel sliding mode observer for state and fault estimation in systems not satisfying matching and minimum phase conditions,” Automatica 79, 290–295 (2017).

    Article  MathSciNet  Google Scholar 

  21. A. N. Zhirabok, A. E. Shumskii, and S. V. Pavlov, “Diagnosis of linear dynamic systems by the nonparametric method,” Autom. Remote Control 78, 1173 (2017).

    Article  MathSciNet  Google Scholar 

Download references

Funding

This work was supported by the Russian Science Foundation, project nos. 22-19-00028 (the method to construct sliding mode observers) and 22-29-01303 (sliding mode observer design).

Author information

Authors and Affiliations

  1. Far Eastern Federal University, 690091, Vladivostok, Russia

    A. N. Zhirabok & A. E. Shumsky

  2. Institute of Marine Technology Problems, Far Eastern Branch, Russian Academy of Sciences, 690091, Vladivostok, Russia

    A. V. Zuev

  3. Institute of Automation and Control Processes, Far Eastern Branch, Russian Academy of Sciences, 690041, Vladivostok, Russia

    V. F. Filaretov

Authors
  1. A. N. Zhirabok
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Zuev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. F. Filaretov
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. E. Shumsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. N. Zhirabok.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

Translated by A. Mazurov

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhirabok, A.N., Zuev, A.V., Filaretov, V.F. et al. Fault Identification in Nonlinear Systems Based on Sliding Mode Observers with Weakened Existence Conditions. J. Comput. Syst. Sci. Int. 61, 313–321 (2022). https://doi.org/10.1134/S1064230722030169

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1064230722030169

Search

Navigation