Abstract
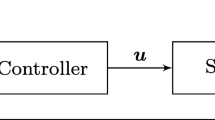
An optimization problem with the quality criterion that differs from the conventional one by some modifications is given. The state of the system is described by a second-order unobservable random sequence, while the observations are described by an optimizable noisy linear output. The fact that the unobservable state of the system is independent of the control is substantiated by interpreting the statement as the optimization problem for resource allocation for the system as opposed to the conventional statement that suggests controlling its state. A variant of the practical substantiation of the statement involved, i.e., optimizing operation of a software system, is proposed. A dynamic programming method is used to solve the problem. The optimal strategy is found as a linear combination of the output and predictions of the state up to the optimization horizon. Since the optimal strategy is computationally laborious, the possibility to simplify it and apply a locally optimal strategy is discussed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. J. Gitman and M. D. Joehnk, Fundamentals of Investing, 7th ed. (Addison-Wesley, Reading, MA, 1999).
GOST (State Standard) No. 7.70–2003, SIBID. Description of the data bases and machine-readable informa-tion resources. The composition and characteristic designation (Izd-vo standartov, Moscow, 2003).
GOST (State Standard) No. 28195–89. Evaluation of Software Quality. General provisions (Izd-vo standartov, Moscow, 2001).
A. S. Tanenbaum and A. S. Woodhull, Operating Systems Design and Implementation (Prentice Hall, Englewood Cliffs, NJ, 1997).
C. J. Date, An Introduction to Database Systems, 8th ed. (Pearson, Addison Wesley, Boston, 2003).
R. Elsässer, B. Monien, and R. Preis, “Diffusion schemes for load balancing on heterogeneous networks,” The-ory Comput. Syst. 35 (3), 305 (2002).
M. Welzl, Network Congestion Control (Wiley, New York, 2005).
S. H. Low, F. Paganini, and J. C. Doyle, “Internet congestion control,” IEEE Control Syst. Mag. 22 (1), 28–43 (2002).
A. V. Bosov and A. V. Ivanov, “Programmnaya infrastruktura Informatsionnogo web-portala RAN,” Informa-tika I Ee Primeneniya 1 (2), 39–53 (2007).
A. V. Borisov, A. V. Bosov, and A. I. Stefanovich, “Optimal estimates for the operating parameters of an infor-mation web portal,” Autom. Remote Control 71, 379 (2010).
A. V. Bosov, “Analysis and optimization problems for some users activity model. Part 2. Internal Resources opti-mization,” Inform. Primen. 6 (1), 18–25 (2012).
A. V. Bosov, “Analysis and optimization problems for some users activity model. Part 3. External Resources opti-mization,” Inform. Primen. 6 (2), 15–22 (2012).
A. V. Bosov, “The generalized problem of software systme resources distribution,” Inform. Primen. 8 (2), 39–47 (2014).
A. V. Bosov, “Analysis and optimization problems for some users activity model. Part 1. Analysis and predic-tion,” Inform. Primen. 5 (4), 40–52 (2011).
M. M. Kogan and Yu. I. Neimark, “Adaptive local-optimal control,” Avtom. Telemekh., No. 8, 126–136 (1987).
D. P. Bertsekas and S. E. Shreve, Stochastic Optimal Control: The Discrete-Time Case (Academic, New York, 1978; Nauka, Moscow, 1985).
A. Albert, Regression and the Moore-Penrose PseudoInverse (Academic Press, New York, 1972).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © A.V. Bosov, 2016, published in Izvestiya Akademii Nauk. Teoriya i Sistemy Upravleniya, 2016, No. 3, pp. 19–35.
Rights and permissions
About this article
Cite this article
Bosov, A.V. Discrete stochastic system linear output control with respect to a quadratic criterion. J. Comput. Syst. Sci. Int. 55, 349–364 (2016). https://doi.org/10.1134/S1064230716030060
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1064230716030060