1 INTRODUCTION

For the first time, coherent neutrino scattering on nuclei was discussed by Freedman in [1] and by Freedman and his coauthors in [2] on the basis of the general quantum-mechanical rule for the addition of the probability amplitudes for indistinguishable processes leading to the same final state. The application of this quantum-mechanical rule led to the result that, in the case of interaction between neutrinos of moderate energy and a nucleus consisting of a significant number of nucleons, the probability for such an interaction is several orders of magnitude higher than the analogous probability in the case of neutrino scattering on an individual nucleon. This is the phenomenon that Freedman called coherent neutrino scattering on nuclei. It became clear almost immediately that neutrinos may be scattered coherently not only on nucleons within nuclei [1–3] but also on atoms including orbital electrons [4–6]. In view of this, coherent neutrino scattering became rather fast an important potential source of new information about nuclei and neutrinos, as well as about physics beyond the Standard Model. However, a key problem here was that, in order to ensure the occurrence of the coherence effect, weak interaction should proceed in this case via the neutral-current channel. As a result, an extremely low recoil energy of the nucleus turns out to be the only observable here. For a long time, it remained beyond the reach of the most sensitive neutrino detectors.

From the practical point of view, the presence or absence of the coherent effect depends, according to [2], on the dimensionless product \(qR\), where \(q\) is the absolute value of the 3-momentum transfer from the neutrino to the target nucleus, whose characteristic size is specified by the radius \(R\). If \(qR\simeq 1\) (or \(qR\geqslant 1\)), then all \(A\) independent scattering centers (nucleons) are overly far from one another and have different relative phase factors. As a result, a substantial mutual cancellation of the contributions of different nucleons occurs, so that the total cross section turns out to be proportional only to the number of the scattering centers themselves. If, on the contrary, \(qR\leqslant 1\) (that is, \(q\) is much smaller than the inverse target size), the phase factors are immaterial (since they are nearly equal to one another), so that a coherent addition of the contributions of all scattering centers occurs. As a result, the total cross section turns out to be enhanced in proportion to the factor \(A^{2}\). Thus, we see that, according to [2], the quantum-mechanical condition of coherence has the form of the inequality

$$qR\ll 1.$$
(1)

The coherence condition holds well for neutrinos and antineutrinos from a significant number of available sources, including reactor antineutrinos, solar neutrinos, and (anti)neutrinos from supernova explosions, as well as neutrinos from accelerators [7]. At the neutrino energy of about 40 MeV, the recoil energy of nuclei, which is the only observable, as was mentioned above, is nevertheless in the keV region; it is very low and is inaccessible to direct detection. In 2017, however, the COHERENT experiment at the Spallation Neutron Source (SNS, Oak Ridge National Laboratory, USA) sidestepped the problem by employing a high-energy (anti)neutrino flux [8].

It turned out, however, that the data coming from the COHERENT experiment and underlying the statement that this experiment detected elastic coherent scattering of neutrinos on nuclei (CE\(\nu\)NS) do not meet the condition in (1) (see, for example, [9, 10]); therefore, it would be illegitimate to associate these data unambiguously with a pure CE\(\nu\)NS process. In these data, there is a substantial contribution of inelastic (anti)neutrino–nucleus interactions, which, in no way, could be discriminated from CE\(\nu\)NS, since only the recoil energy of the nucleus was recorded in the experiment [9, 10]. We can state that the experiment in question recorded events of neutrino interactions with nuclei in the channel of weak neutral currents at energies in the MeV region, and this is a highly important achievement in and of itself. The potential of the COHERENT experiment can be aimed at studying in detail a dynamical transition between elastic and inelastic neutrino–nucleus interactions in the kinematical region of this experiment. On this path, it seems possible to detect experimentally (perform estimations of respective cross sections) coherent and inelastic [9, 10] neutrino–nucleus interactions (CI\(\nu\)NS—abbreviation proposed by Yu. Efremenko) by measuring, for example, the flux of photons from the removal of nuclear excitations caused by this interaction. The present study is devoted to precisely this goal.

2 CROSS SECTION FOR (ANTI)NEUTRINO SCATTERING ON NUCLEI

As a rule, the interactions of neutrinos and antineutrinos that have energies not higher than several hundred MeV units can be described in terms of the effective interaction Lagrangian of the Standard Model in the four-fermion approximation; that is,

$$\mathcal{L}\left(x\right)=\frac{G_{\textrm{F}}}{\sqrt{2}}\bar{\psi}_{\nu}\left(x\right)\gamma_{\mu}\left({1-\gamma_{5}}\right)\psi_{\nu}\left(x\right)$$
(2)
$${}\times\sum\limits_{f=n,p}\bar{\psi}_{f}\left(x\right)\gamma^{\mu}\left({g_{V}^{f}-g_{A}^{f}\gamma_{5}}\right)\psi_{f}\left(x\right).$$

Here, the left- and right-handed nucleon chiral coupling constants are expressed in terms of the vector and axial-vector constants as

$$g_{L}^{p/n}=\frac{1}{2}\left({g_{V}^{p/n}+g_{A}^{p/n}}\right),$$
(3)
$$g_{R}^{p/n}=\frac{1}{2}\left({g_{V}^{p/n}-g_{A}^{p/n}}\right).$$

The total cross section for (anti)neutrino scattering on a nuclear target [9, 10] has the form of the sum of coherent and incoherent terms; that is,

$$\frac{d\sigma^{\nu/\bar{\nu}}}{dT_{A}}=\frac{d\sigma_{\textrm{inc}}^{\nu/\bar{\nu}}}{dT_{A}}+\frac{d\sigma_{\textrm{coh}}^{\nu/\bar{\nu}}}{dT_{A}},$$
(4)

where \(G_{\textrm{F}}\) is the Fermi constant and \(T_{A}\) is the kinetic recoil energy for a nucleus of mass \(m_{A}\). Hereafter, the left and right upper indices refer to neutrinos and antineutrinos, respectively. The coherent and incoherent terms in (4) have the form

$$\frac{d\sigma_{\textrm{inc}}^{\nu/\bar{\nu}}}{dT_{A}}=\frac{4G_{\textrm{F}}^{2}m_{A}}{\pi}\mathop{\sum}\limits_{f=p,n}\left({1-\left|{F_{f}\left({q^{2}}\right)}\right|^{2}}\right)$$
(5)
$${}\times\Biggl{[}\mathbf{A}_{\mp}^{f}\left({g_{R/L}^{f}}\right)^{2}\frac{s\left({1-y}\right)^{2}-m^{2}\left({1-y}\right)}{s-m^{2}}$$
$${}+\mathbf{A}_{\pm}^{f}\Biggl{\{}\left({g_{L/R}^{f}-g_{R/L}^{f}\frac{ym^{2}}{s-m^{2}}}\right)^{2}$$
$${}+\left({g_{R/L}^{f}}\right)^{2}\frac{ym^{2}\left[{s\left({1-y}\right)-m^{2}}\right]}{\left({s-m^{2}}\right)^{2}}\Biggl{\}}\Biggl{]},$$
$$\frac{d\sigma_{\textrm{coh}}^{\nu/\bar{\nu}}}{dT_{A}}=\frac{4G_{\textrm{F}}^{2}m_{A}}{\pi}\left({1-\frac{T_{A}}{T_{A}^{\max}}}\right)$$
(6)
$${}\times\Biggl{|}\sum\limits_{f=p,n}F_{f}\left({q^{2}}\right)\Biggl{\{}\mathbf{A}_{\pm}^{f}\left[{g_{L/R}^{f}+g_{R/L}^{f}\frac{my}{\sqrt{s}+m}}\right]$$
$${}+\mathbf{A}_{\mp}^{f}\left[{1-\frac{\sqrt{s}y}{\sqrt{s}+m}}\right]\Biggl{\}}\Biggl{|}^{2}.$$

Here, \(A_{\pm}^{p}\) and \(A_{\pm}^{n}\) are the numbers of respectively, protons and neutrons that have the spin projection of \({\pm 1}/2\) onto the direction of motion of the incident neutrino. Introducing the notation \(A^{f}=A_{+}^{f}+A_{-}^{f}\) and \(\Delta A^{f}=A_{+}^{f}-A_{-}^{f}\), we recast these terms into the form

$$\frac{d\sigma_{\textrm{inc}}^{\nu/\bar{\nu}}}{dT_{A}}=\frac{4G_{\textrm{F}}^{2}m_{A}}{\pi}\sum\limits_{f=p,n}\left({1-\left|{F_{f}\left({q^{2}}\right)}\right|^{2}}\right)$$
(7)
$${}\times\Biggl{\{}\mathbf{A}^{f}\biggl{[}\left({g_{L/R}^{f}}\right)^{2}+\left({g_{R/L}^{f}}\right)^{2}\left({1-y}\right)^{2}$$
$${}-g_{L}^{f}g_{R}^{f}\frac{2m^{2}y}{s-m^{2}}\biggl{]}+\left({\pm}\Delta{\mathbf{A}_{f}}\right)$$
$${}\times\left[{g_{L/R}^{f}-g_{R/L}^{f}\left({1-y}\right)}\right]$$
$${}\times\left[{g_{L/R}^{f}+g_{R/L}^{f}\left({1-y\frac{s+m^{2}}{s-m^{2}}}\right)}\right]\Biggl{\}},$$
$$\frac{d\sigma_{\textrm{coh}}^{\nu/\bar{\nu}}}{dT_{A}}=\frac{4G_{\textrm{F}}^{2}m_{A}}{\pi}\left({1-\frac{T_{A}}{T_{A}^{\max}}}\right)$$
(8)
$${}\times\left|{G_{V}^{\nu/\bar{\nu}}\left({q^{2}}\right)+G_{A}^{\nu/\bar{\nu}}\left({q^{2}}\right)}\right|^{2},$$

where

$$G_{V}^{\nu/\bar{\nu}}\left({q^{2}}\right)=\sum\limits_{f=p,n}F_{f}\left({q^{2}}\right)g_{V}^{f}$$
$${}\times\left\{{\mathbf{A}^{f}\left({1-\frac{y\tau}{2}}\right)+\frac{y}{2}\left({\pm\Delta\mathbf{A}^{f}}\right)}\right\},$$
$$G_{A}^{\nu/\bar{\nu}}\left({q^{2}}\right)=\sum\limits_{f=p,n}F_{f}\left({q^{2}}\right)\left({\pm g_{A}^{f}}\right)$$
$${}\times\left\{{\mathbf{A}^{f}\frac{y\tau}{2}+\left({1-\frac{y}{2}}\right)\left({\pm\Delta{\mathbf{A}}^{f}}\right)}\right\}.$$

Further, the kinematical variables are given by

$$q^{2}=\left({k-k^{\prime}}\right)^{2},\quad y=\frac{\left({p,q}\right)}{\left({p,k}\right)}\simeq\frac{s-m^{2}}{s}\frac{T_{A}}{T_{A}^{\max}},$$
$$E_{\nu}=\frac{s-m^{2}}{2\sqrt{s}},\quad\tau=\frac{\sqrt{s}-m}{\sqrt{s}+m}.$$

Here, \(s=\left({p+k}\right)^{2}\) is the square of the total energy of the neutrino and nucleon, where \(k\) is the initial-lepton 4-momentum and \(p\) is the effective scattering-nucleon 4-momentum obtained by solving the equation of energy–momentum conservation for the nucleus [9, 10].

The expressions for the coherent- and incoherent-scattering cross sections can be substantially simplified by discarding terms proportional to (a small value of the variable) \(y\approx 3{\%}E_{\nu}/\)(30 MeV) and terms proportional to \(\Delta A_{f}\Delta A_{f^{\prime}}\). The latter is quite justifiable for spinless nuclei or for heavy nuclei, where \(\Delta A\ll A\). As a result, the following simple expressions are obtained for the coherent and incoherent cross sections:

$$\frac{d\sigma_{\textrm{coh}}}{dT_{A}}=\frac{G_{\textrm{F}}^{2}m_{A}}{\pi}\left({1-\frac{T_{A}}{T_{A}^{\max}}}\right)$$
(9)
$${}\times\sum\limits_{f=p,n}A_{f}^{2}\left|{F_{f}}\right|^{2}\left({g_{V}^{f}}\right)^{2},$$
$$\frac{d\sigma_{\textrm{inc}}}{dT_{A}}=\frac{2G_{\textrm{F}}^{2}m_{A}}{\pi}\sum\limits_{f=p,n}A_{f}\left({1-\left|{F_{f}}\right|^{2}}\right)$$
$${}\times\left({\left({g_{L}^{f}}\right)^{2}+\left({g_{R}^{f}}\right)^{2}}\right).$$

From here, we can see that the cross sections for neutrino and antineutrino scattering on nuclei are hardly distinguishable.

In addition, it is legitimate to discard terms that are proportional to \(g_{V}^{p}\), since \(g_{V}^{p}\ll 1\) within the Standard Model, and this leads to the well-known result for the coherent neutrino–nucleus scattering cross section [1, 7, 11–20]. Specifically, it turns out to be proportional to the square of the number of neutrons in the target nucleus:

$$\frac{d\sigma_{\textrm{coh}}}{dT_{A}}\approx\frac{G_{\textrm{F}}^{2}m_{A}}{\pi}\left({1-\frac{T_{A}}{T_{A}^{\max}}}\right)\left|{F_{n}}\right|^{2}\left({g_{V}^{n}}\right)^{2}N^{2},$$
(10)

Expressions (4)–(8) demonstrate a ‘‘smooth’’ transition [9, 10] of the cross section for (anti)neutri- no–nucleus scattering from the coherent mode [Eq. (8)] to the incoherent mode [Eq. (7)]. Indeed, elastic (coherent according to the standard terminology) interactions, upon which the nucleus remains in its initial quantum state, lead to a quadratic (in the number of nucleons) enhancement (proportional to \(A_{f}^{2}\)) of the observed cross section and simultaneously to the dependence of this cross section on the square of the nuclear proton and neutron form factors \(\left|{F_{n/p}\left({\mathbf{q}}\right)}\right|^{2}\) normalized to unity.

On the other hand, the cross section for inelastic (or incoherent according to the standard terminology) processes, in which the quantum state of the target nucleus changes, exhibits a linear dependence on the number of nucleons (that is, it is proportional to \(A\)) and is simultaneously proportional to the expression \(\left({1-\left|{F_{n/p}\left({\mathbf{q}}\right)}\right|^{2}}\right)\). The terms in (7) and (8) of the total cross section in (4) depend on the same nuclear form factors \(F_{n/p}\left({\mathbf{q}}\right)\).

If \(\mathbf{q}\to 0\), then the form factors tend to unity, \(F_{n/p}\left({\mathbf{q}}\right)\to 1\), in which case the contribution of the incoherent term in (7) to the total cross section vanishes. At the same time, the coherent contribution in (8) determines completely the observed cross section in (4). In the opposite case of high values of the 3-momentum transfer \(\mathbf{q}\), the form factors tend to zero, \(F_{n/p}\left({\mathbf{q}}\right)\to 0\), with the result that the coherent cross section in (8) does not contribute, whereas the incoherent cross section in (7) determines completely the observed cross section in (4). Obviously, the coherent and incoherent contributions to the total cross section should be considered simultaneously in the intermediate region of values of the 3-momentum transfer \(\mathbf{q}\) to the nucleus.

From the practical point of view, it is convenient to deal with the quantity obtained by integrating the cross section for the process under study over the admissible interval of the recoil kinetic energy of the nucleus; that is,

$$\sigma\left({E_{\nu/\bar{\nu}},T_{A}^{\min}}\right)=\int\limits_{T_{A}^{\min}}^{T_{A}^{\max}}\frac{d\sigma^{\nu/\bar{\nu}}}{dT_{A}}dT_{A}.$$
(11)

This integrated cross section depends substantially on the threshold \(T_{A}^{\min}\) for the detection of the recoil kinetic energy of the nucleus (minimum detectable recoil energy) for each individual detector.

3 RESULTS

The claim of the COHERENT Collaboration to have observed CE\(\nu\)NS gave impetus to other collaborations. For example, the authors of [21] proposed employing the European Spallation Source (ESS, Lund, Sweden) to detect this process. They indicate the advantages of ESS and propose the use of a wider set of nuclei for investigations than that in the experiments performed at SNS. By considering the example of target nuclei used and proposed for use in low-threshold measurements—in particular, for detecting and studying coherent neutrino–nucleus scattering in the COHERENT experiment and at ESS—we will discuss, in the following, the theoretical results obtained above and will also estimate numerically the contributions of coherent and incoherent processes to the total cross section for (anti)neutrino scattering on these nuclei.

As the first test facility, we will consider a germanium detector usually used to record fluxes of electron antineutrinos from nuclear reactors. We assume that its working substance consists exclusively of the isotopes of natural germanium, \({}^{\mathrm{74}}\)Ge. For bolometric germanium detectors, the expected threshold for electron-energy detection is 200 eV [22], which, according to the estimation of the energy-transformation coefficient (quenching) in [23], corresponds to about 1 keV for the recoil kinetic energy of \({}^{\mathrm{74}}\)Ge nuclei. The \(\nu\)GEN experiment performed by a collaboration of physicists from Joint Institute for Nuclear Research (JINR, Dubna) and Institute for for Theoretical and Experimental Physics (ITEP, Moscow) at the Kalinin nuclear power plant [24] can be indicated as a specific example where a detector of this type is used. In our calculations, we set the threshold for the nuclear recoil energy to 0, 1, 3, and 5 keV. The differential cross sections for this detector are calculated at the (anti)neutrino energy of 50 MeV, while the total cross sections are calculated for the interval of possible (anti)neutrino-flux energies between 1 and 50 MeV. For the estimated energy of the lowest excited level of the \({}^{\mathrm{74}}\)Ge nucleus, we take the value of \(\Delta\varepsilon=900\) keV.

The CsI scintillation detector (calorimeter) used by the COHERENT Collaboration to detect neutrinos from the SNS Oak Ridge neutron source [8] is the second test facility. The total cross sections were estimated over the interval between 1 and 150 MeV. We assume that the excitation energy of the \({}^{\mathrm{133}}\)Cs nucleus is approximately \(\Delta\varepsilon=100\) keV, while the excitation energy of the \({}^{\mathrm{127}}\)I nucleus is close to \(\Delta\varepsilon=60\) keV. The threshold for the recoil energy of \({}^{\mathrm{133}}\)Cs and \({}^{\mathrm{127}}\)I nuclei is 5 keV, in just the same way as in the COHERENT experiment, and the neutrino-beam energy is 30 and 50 MeV, respectively.

The RED-100 two-phase emission detector that employs liquid xenon and which has the recoil-energy threshold of 4 keV for \({}^{\mathrm{132}}\)Xe nuclei [25] is the third test facility. The excitation energy of the nucleus is about \(\Delta\varepsilon=670\) keV. The total cross sections for this facility were obtained in the interval between 1 and 150 MeV at two energies of the (anti)neutrino beam—30 and 50 MeV.

The liquid-argon detector that has an unprecedentedly low detection threshold of 0.6 keV reached in the DarkSide experiment for the recoil energy of \({}^{\mathrm{40}}\)Ar nuclei [26] is yet another facility that can be used in experiments of the type being discussed. The differential and total cross sections for this facility were obtained, respectively, for the excitation energy and in the interval between 1 and 120 MeV. The excitation energy of the nucleus is about \(\Delta\varepsilon=2\) MeV, while the neutrino-beam energy is 30 and 50 MeV.

The remaining calculations were performed for nuclei proposed for detecting coherent neutrino scattering at ESS [21]: \({}^{\mathrm{28}}\)Si, \({}^{\mathrm{19}}\)F, \({}^{\mathrm{12}}\)C, and \({}^{\mathrm{16}}\)O. The neutrino-beam energy was 30 and 50 MeV in the calculation. The differential and total cross sections were obtained, respectively, for the excitation energies and in the interval between 1 and 150 MeV. The excitation energies of the nuclei were approximately 1780 keV for \({}^{\mathrm{28}}\)Si, 110 keV for \({}^{\mathrm{19}}\)F, 4439 keV for \({}^{\mathrm{12}}\)C, and 6048 keV for \({}^{\mathrm{16}}\)O. The thresholds for the recoil energy of the nuclei were taken to be 3.2, 3.3, 3.3, and 10 MeV, respectively.

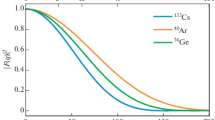
In order to obtain numerical results, we used two (for protons and neutrons) nuclear form factors \(F_{n/p}\left({\mathbf{q}}\right)\) and data on excited energy levels. We have considered the most popular parametrization of the nuclear form factors on the basis of the symmetrized Fermi distribution [27] and the Helm nuclear form factor [28]. For the chosen nuclei, Fig. 1 shows the behavior of the Helm form factor as a function of the 3-momentum transfer \(\left|{\mathbf{q}}\right|\) to the target nucleus. This figure demonstrates explicitly that, for \(\mathbf{q}\to 0\), the form factor tends to unity, \(F_{n/p}\left({\mathbf{q}}\right)\to 1\), with the result that the contribution of the incoherent cross section vanishes, so that the coherent term dominates completely. On the other hand, the coherent term disappears in the opposite case of high values of \(\mathbf{q}\), and the cross section for incoherent scattering then proves to be fully dominant.

Fig. 1
figure 1

Helm nuclear form factor as a function of the absolute value of the 3-momentum transfer \(\left|{\mathbf{q}}\right|\).

Full size image

Figures 2 and 3 and Figs. 4 and 5 show, respectively, the differential and the total integrated [in the sense of the definition in (11)] cross sections for coherent and incoherent (anti)neutrino–nucleus scattering for the chosen test facilities.

Fig. 2
figure 2

Differential cross sections \(\frac{d\sigma^{\nu}}{dT_{A}}\) for (solid curves) coherent and (dashed curves) incoherent neutrino scattering on (left-hand panels) \({}^{\mathrm{74}}\)Ge, \({}^{\mathrm{40}}\)Ar, and \({}^{\mathrm{28}}\)Si target nuclei and on (right-hand panels) \({}^{\mathrm{19}}\)F, \({}^{\mathrm{16}}\)O, and \({}^{\mathrm{12}}\)C target nuclei versus the nuclear recoil energy \(T_{A}\). The vertical lines correspond to the experimental energy thresholds for each target.

Full size image
Fig. 3
figure 3

Differential cross section \(\frac{d\sigma^{\nu/\bar{\nu}}}{dT_{A}}\) for (solid curves) coherent and (dashed curves) incoherent (left-hand panels) neutrino and (right-hand panels) antineutrino scattering on \({}^{\mathrm{133}}\)Cs, \({}^{\mathrm{132}}\)Xe, and \({}^{\mathrm{127}}\)I target nuclei versus the nuclear recoil energy \(T_{A}\) at the initial-(anti)neutrino energies of 30 and 50 MeV. The vertical lines correspond to the experimental energy thresholds for each target.

Full size image
Fig. 4
figure 4

Integrated cross sections \(\sigma^{\nu}\) for (solid curve) coherent and (dashed curve) incoherent neutrino scattering on (left-hand panels) \({}^{\mathrm{74}}\)Ge, \({}^{\mathrm{40}}\)Ar, and \({}^{\mathrm{28}}\)Si target nuclei and on (right-hand panels) \({}^{\mathrm{19}}\)F, \({}^{\mathrm{16}}\)O, and \({}^{\mathrm{12}}\)C target nuclei versus the incident-neutrino energy. The curves in blue and red stand for the cross sections calculated, respectively, for idealized experimental setups having zero energy threshold and for real setups having the best energy thresholds for them. For the \({}^{\mathrm{74}}\)Ge nucleus, the curves in red, blue, and green stand for the energy thresholds of 1, 3, and 5 keV, respectively, while the curve in black corresponds to zero energy threshold.

Full size image
Fig. 5
figure 5

Integrated cross sections \(\sigma^{\nu/\bar{\nu}}\) for (solid curve) coherent and (dashed curve) incoherent (left-hand panels) neutrino and (right-hand panels) antineutrino scattering on \({}^{\mathrm{133}}\)Cs, \({}^{\mathrm{132}}\)Xe, and \({}^{\mathrm{127}}\)I target nuclei versus the incident-(anti)neutrino energy. The curves in blue and red stand for the cross sections calculated, respectively, for idealized experimental setups having zero energy threshold and for real setups having the best energy thresholds for them.

Full size image

In what concerns the balance of the coherent and incoherent cross sections, there are some properties common to neutrino and antineutrino beams. If the recoil energy of the target nucleus tends to zero, then the coherent cross section is dominant, fully determining the cross sections in (4) for neutrino–nucleus (\(\nu A\)) and antineutrino–nucleus (\(\bar{\nu}A\)) scattering, since the incoherent contribution vanishes. For an individual nucleus, the differential coherent cross section is independent of the (anti)neutrino energy in this limit [apart from insignificant corrections according to (8)].

If the recoil energy of the nucleus tends to its kinematical limit, then the coherent cross section decreases quite fast, ultimately vanishing, but the incoherent cross section grows monotonically with increasing \(T_{A}\). It is noteworthy that, because of the possibility of spending the energy acquired by the target nucleus to excitation, the maximum possible kinetic energy of the nucleus in incoherent processes, \(T_{A}\), is systematically less than the maximum recoil energy reachable in the coherent case, \(T_{A}^{\max}\). This is the reason why, in Figs. 2 and 3, the dashed (‘‘incoherent’’) curves always terminate somewhat earlier as \(T_{A}\) grows than the solid (‘‘coherent’’) curves do.

At small values of the energy \(E_{\nu/\bar{\nu}}\), the coherent cross section always exceeds substantially its incoherent counterpart at each value of the kinetic recoil energy \(T_{A}\) of the nucleus. At higher \(E_{\nu/\bar{\nu}}\), the recoil energy \(T_{A}\) can already take values above which the incoherent cross section becomes larger than the coherent cross section, as can be seen from Fig. 3 for heavy nuclei and the (anti)neutrino-beam energy of 50 MeV and for \(E_{\nu/\bar{\nu}}\geqslant 30{-}35\) MeV. At small values of the beam energy \(E_{\nu/\bar{\nu}}\), the integrated coherent cross section (see Figs. 4 and 5) exceeds the incoherent cross section by several orders of magnitude, since the factors \(1-\left|{F_{n/p}\left({\mathbf{q}}\right)}\right|^{2}\) suppress strongly the incoherent contribution at low values of the 3-momentum transfer \(\mathbf{q}\). However, the coherent contribution gradually ceases to be overwhelmingly dominant as the (anti)neutrino energy grows, and the integrated incoherent cross section becomes quite sizable at some values of \(E_{\nu/\bar{\nu}}\).

The existence of a real experimental detection threshold \(T_{A}^{\min}>0\) reduces sizably the integrated cross sections, this reduction being somewhat weaker in the case of incoherent scattering. As a matter of fact, a nonzero threshold (vertical lines in Figs. 2 and 3) truncates a substantial part of the differential cross section, this occurring in the region where coherent scattering makes the maximum contribution to the cross section.

Figures 6 and 7 illustrate this statement quantitatively, showing the ratio \(\sigma_{\textrm{inc}}/\sigma_{\textrm{coh}}\) of the integrated cross sections calculated according to the definition in (11). One can see that, in the case of, for example, the \({}^{\mathrm{127}}\)I nucleus (see Fig. 7) on which the scattering of 30-MeV (50-MeV) neutrinos (left-hand panels) occurs, this ratio is about 5\({\%}\) (15\({\%}\)) at \(T_{A}^{\min}=0\) and reaches 10\({\%}\) (25\({\%}\)) for the real energy threshold of \(T_{A}^{\min}=5\) keV. In this case, the incoherent contribution becomes equal to the coherent contribution at the incident-neutrino energy of about 125 MeV. Obviously, the contribution of incoherent interactions grows substantially with increasing interaction energy.

Fig. 6
figure 6

Ratio \(\sigma_{\textrm{inc}}/\sigma_{\textrm{coh}}\) of the incoherent to the coherent cross section for neutrino scattering on (left-hand panels) \({}^{\mathrm{74}}\)Ge, \({}^{\mathrm{40}}\)Ar, and \({}^{\mathrm{28}}\)Si nuclei and on (right-hand panels) \({}^{\mathrm{19}}\)F, \({}^{\mathrm{16}}\)O, and \({}^{\mathrm{12}}\)C nuclei versus the neutrino energy \(E_{\nu}\). The curves in blue and red are plotted for, respectively, \(T_{A}^{\min}=0\) and real neutrino-detection thresholds indicated in the main body of the text. For \({}^{\mathrm{74}}\)Ge, the curves in red, blue, and green stand for the ratios in question at the thresholds of 1, 3, and 5 keV, respectively, while the curve in black corresponds to zero energy threshold.

Full size image
Fig. 7
figure 7

Ratio \(\sigma_{\textrm{inc}}/\sigma_{\textrm{coh}}\) of the incoherent to the coherent cross section for (left-hand panels) neutrino and (right-hand panels) antineutrino scattering on \({}^{\mathrm{133}}\)Cs, \({}^{\mathrm{132}}\)Xe, and \({}^{\mathrm{127}}\)I target nuclei versus the energy \(E_{\nu/\bar{\nu}}\). The curves in blue and red are plotted for, respectively, \(T_{A}^{\min}=0\) and real (anti)neutrino-detection thresholds.

Full size image

We have already indicated that, after undergoing interaction with neutrinos or antineutrinos, the nucleus involved has only two possibilities: either it remains in the same quantum state (elastic scattering), or its intrinsic quantum state changes (inelastic scattering). If, however, the experimental setup used is able to measure only the kinetic recoil energy of the nucleus, then it is next to impossible to find out whether the interacted nucleus remained in its initial state or whether it underwent a transition to an excited level.

If the transition of the nucleus to an excited state is allowed in energy, the inelastic interaction that occurred should be accompanied by the emission of photons removing the excitation, whereupon the nucleus returns to its original state. The energy of these photons is determined by the difference of the energy levels of the nucleus being considered [29]. For example, the time scale of the emission of such photons for the \({}^{\mathrm{133}}\)Cs nucleus ranges between several picoseconds and several nanoseconds, while their energies lie around several hundred keV units. These photons are expected to generate, in a scintillation calorimetric detector, quite a detectable signal that should be correlated with the time of target irradiation with a neutrino beam from an accelerator.

There are several lines along which one can perform precision studies of the CE\(\nu\)NS effect and its implications. The first consists in separating the ‘‘truly coherent and truly elastic’’ signal from an incoherent admixture on the basis of the aforementioned possibility of observing photons removing a nuclear excitation. This possibility was mentioned as far back as 1975 [29] and recently by the authors of [9, 10] in the context of coherent neutrino scattering. Indeed, incoherent (inelastic) processes provide, albeit being a moderate background to coherent interactions in the kinematical region under consideration, experimentalists with important information if it is possible to detect photons emitted by the nucleus excited in the interaction event. For each specific target nucleus, these photons are of importance in three aspects. First, their energy determined by the difference of the excitation energies of the nuclear levels involved is substantially greater, as a rule, than the recoil energy of the nucleus. Second, the emission of photons with energy determined by the difference of the excited energy levels of the nucleus is shifted in time with respect to the incident neutrino beam by deexcitation times for a given excitation energy that are peculiar to specific nuclei. The third aspect of importance is that, under conditions of a simultaneous (more precisely, correlated) detection of two signals in the form of the recoil energy of the nucleus and the energy of photons deexciting the nucleus, the counting rate for these photons provides the only way to separate the pure CE\(\nu\)NS effect from inelastic processes and, hence, to perform, on the basis of CE\(\nu\)NS, a precision study of the nuclear structure and searches for new physics beyond the Standard Model, as is discussed in [30–43].

The counting rate for such photons is given by

$$N_{\textrm{inc}}=\int\limits_{E_{\nu\textrm{th}}}^{\infty}dE_{\nu}\frac{d\Phi}{dE_{\nu}}\int\limits_{dT_{A}^{\min}}^{dT_{A}^{\max}}dT_{A}\frac{d\sigma_{\textrm{inc}}}{dT_{A}}\varepsilon\left({T_{A}}\right)N,$$
(12)

where \(\varepsilon\left({T_{A}}\right)\) is the detector efficiency and \(N\) is the number of atoms.

The number of such photons under conditions of the COHERENT experiment at SNS and the proposed experiment at ESS, as well as the \(\nu\)GEN experiment at the Kalinin nuclear power plant, was estimated (see Table 1).

Table 1 Data and results for calculating the number of photons emitted from target nuclei in inelastic processes
Full size table

For the COHERENT experiment at SNS (with a neutrino flux of \(9.2\times 10^{21}\nu\) per year and with a CsI detector characterized by a mass of 14.5 kg and a threshold of 5 keV and positioned at a distance of 22 m [8]), the estimation according to Eq. (12) reveals that the counting rate for such ‘‘incoherent’’ photons is \(7.1\times 10^{-3}\gamma\) per day. If a similar detector is installed at ESS (where the presumed neutrino flux is \(8.5\times 10^{22}\nu\) per year [24]), the counting rate will be one order of magnitude higher owing to a higher neutrino flux—that is, \(6.6\times 10^{-2}\gamma\) per day. In the case of enlarging the detector mass by a factor of two up to 29 kg, the counting rate for ‘‘incoherent’’ photons will grow to \(1.3\times 10^{-1}\gamma\) per day. For the germanium detector used in the \(\nu\)GEN experiment, characterized by a mass of 1 kg and a threshold of 1 keV, and positioned at a distance of 10 m from the reactor, a rough estimation according to Eq. (12) yields about \(1.6\times 10^{-3}\) photons per day at the antineutrino flux of \(5\times 10^{13}\nu\) per second. This estimate was obtained upon taking into account real data on the detector efficiency, the flux of antineutrinos from the reactor, and the isotopic composition of the detector material. In the \(\nu\)GEN experiment, it is planned to harness four detectors in which the total mass of active substance is 6 kg. Clearly, the number of detected photons will accordingly grow to \(9.6\times 10^{-3}\) events per day.

If one employs beams of neutrinos and antineutrinos that have energies substantially lower than those in the COHERENT experiment—for example, antineutrinos from nuclear reactors or solar neutrinos—there is a different way to study the CE\(\nu\)NS effect. This way was originally viewed as a unique one and was based on the aspiration to create and use (anti)neutrino detectors that would have extremely low thresholds for detecting recoil energies of nuclei (less than a few hundred eV units). It was assumed to collect data by means of them in those kinematical regions where incoherent (inelastic) interaction is almost impossible kinematically or is suppressed very strongly—that is, where the form factors \(\left|{F_{n/p}\left({\mathbf{q}}\right)}\right|^{2}\) are nearly indistinguishable from unity. Work along this line is currently being continued (see, for example, [35]). We believe that, owing to the extremely low energy thresholds already reached, the \(\nu\)GeN JINR–ITEP project [22, 24] at the Kalinin nuclear power plant and, probably in the near future, the DarkSide experiment [26] at Laboratori Nazionali del Gran Sasso seem the most promising in this respect.

We note that the cross section for incoherent (anti)neutrino scattering on nuclei was calculated without relying on a specific nuclear model via employing the completeness condition for nuclear-state wave functions. Also, some simplifying assumptions were made in deriving the above formulas. Correlations of interactions with different nucleons were taken to be negligible; it was also assumed that, for any initial orientation of the active-nucleon spin, all final spin orientations are equiprobably possible [9, 10]. Therefore, the estimates obtained above for the incoherent contribution to the cross section for (anti)neutrino scattering on nuclei are upper bounds, and this is especially clear for light nuclei (see, for example, the graphs in [13, 44, 45]).

4 CONCLUSIONS

Owing to their common nature associated with weak neutral currents, elastic and inelastic (anti)neu- trino processes are experimentally indistinguishable if the recoil energy of the target nucleus is the only observable. It follows that, in experiments aimed at studying coherent scattering of neutrinos at rather high energies by detecting the recoil energy alone, an incoherent background indistinguishable from the main signal may appear if photons removing nuclear excitations escape detection. In particular, the incoherent cross section may reach 10 to 25\({\%}\) of the coherent cross section for \({}^{\mathrm{133}}\)Cs cesium and \({}^{\mathrm{127}}\)I iodine nuclei at neutrino energies between 30 and 50 MeV. If ‘‘incoherent’’ photons removing the nuclear excitation are not detected in an experiment of the COHERENT type, the resulting CE\(\nu\)NS data are expected to contain inelastic-admixture events at a level of 10 to 25\({\%}\).

On the other hand, the coherent contribution can be measured (estimated) directly by detecting photons emitted by target nuclei excited in inelastic processes. These photons should be correlated in time with the neutrino beam and have energies substantially higher, as a rule, than the kinetic recoil energy of the nucleus, with the result that their detection is quite simple. Moreover, the number of such photons is determined by the ratio of the inelastic to the elastic cross section. A simultaneous detection of two signals in the form of the recoil energy of the nucleus involved and photons removing the nuclear excitation permits separating pure CE\(\nu\)NS contributions, whereby one can study in detail the nuclear structure and perform precision searches for new physics in neutrino processes of this type.

In the present study, we have demonstrated the possibility of performing a simultaneous experimental investigation of the elastic and inelastic contributions to the total neutrino–nucleus cross section and have shown that this possibility is implementable not only in experiments at accelerators, where the neutrino energy reaches several hundred MeV units, but also in reactor experiments, where antineutrino energies do not exceed 10 MeV. We have obtained upper bounds on the number of photons characterizing coherent inelastic interaction for a number of nuclei.