INTRODUCTION

In the process of loading aircraft structures made of composite materials (CMs), the effects of shock damage, overloads causing their stratification, and deterioration of strength and stiffness characteristics are investigated. The resulting defects can lead to sudden destruction of the carbon fiber material. The danger is represented even by relatively small impacts that do not leave visible marks on the surface of the composite structure but produce internal defects [1–3].

Monitoring and evaluating the development of defects due to impacts in the elements of aircraft structures made of carbon fiber requires both recording the collision process and the subsequent testing of the material in the impact area [4, 5].

Ultrasonic, X-ray, thermal imaging, optical, acoustic emission (AE), and other methods of nondestructive testing (NDT) are used to inspect composite material structures. The AE method has high sensitivity and allows one to determine defect hazardousness, localize destruction zone in real time, and assess the residual life of the structure.

When testing carbon fiber structures, it is necessary to take into account the effect of anisotropy on the propagation velocity of elastic waves from defects, which affects the accuracy of their location. The presence of noise from loading devices, difficulties in obtaining live data about the main informative parameters of AE signals that are related functionally to the processes of defect development and structural failure—all this requires further analysis and development of testing methods to improve accuracy.

In the results of AE studies by NASA, it was noted that when registering impacts in aerospace structures, the microstructure of the composite affects not only its strength and mechanical properties but also the structure of the AE signals themselves [6]. When solving problems of locating defects, this can degrade accuracy and complicate the decoding and processing of AE information. Informative parameters such as MARSE, structural coefficient, planar location, impact energy, and amplitude distribution are used [7–11] when developing testing methods for determining the coordinates, type, and hazardousness of a defect in composite structures.

It is known that AE systems mainly work with piezoelectric acoustic emission transducers (AET). However, at present, both in our country [8, 12–14] and abroad [15–20], research is being carried out in which fiber-optic sensors (FOS) are included in antennas used in AE testing. One of the main advantages of FOS sensors (compared to AET sensors) worth mentioning are small dimensions and weight, insensitivity to electromagnetic noise and interference, weak sensitivity to vibration, linearity of the amplitude-frequency response, the ability to use a single optical fiber for multipoint measurements, and the organization of various types of sensors on a single fiber designed not only to work with acoustic signals but also for measuring temperature and strain [12].

The aim of this work is to analyze the results of locating AE signals recorded in a carbon fiber sample from shock loads using an AE system operating with various antennas consisting of a combination of piezoelectric and fiber optic sensors.

RESEARCH PROCEDURE

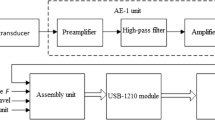
For the tests, we used a T700 carbon fiber sample with a size of \(800 \times 450 \times 1.2\) mm, where four piezoelectric sensors PC 01-07 and four Fabry–Perot FOS sensors were installed to form rectangular location antennas with dimensions of \(360 \times 280\) mm (Fig. 1). Four types of antennas were organized when recording AE information during shock loading of the sample. The first antenna consisted of four piezoelectric AET sensors. The second and third antennas consisted of two piezoelectric AET sensors and two FOS sensors. Four FOS sensors were included in the fourth antenna. Errors in locating AE signals during load discharge and rebound were determined in the tests.

Fig. 1.
figure 1

Appearance of location antenna with piezoelectric and fiber-optic sensors and marked impact sites on a carbon fiber sample.

Full size image

Prior to testing, 16 points spaced 80 mm from each other were marked in the working area of the sample (see Fig. 1). First, we used the first antenna, consisting of four piezoelectric AET sensors operating in the frequency range 100–700 kHz. Recording of AE information was carried out by an SCAD-16.10 AE system with “floating” selection thresholds (certificate of the Federal Agency for Technical Regulation and Metrology RU.C.27/ 007 A no. 40707, registration number in the State Register of Measuring Instruments 45154-10).

Errors in measuring the coordinates of defects in composite structures determined by the AE method depend on errors in measuring the arrival time of signals to antenna sensors and on errors in determining the sonic speed in the working area [4, 5]. To measure the speed of sound in T700 carbon fiber, automated calibration of the working location zone of the sample was carried out in which each AET sensor was alternately switched to the emission mode, with the remaining three antenna sensors operating in the reception mode.

According to calibration results, the sound velocity of the fast mode \(S0\) propagating in the direction of the \(X\)-axis between sensors AET4 and AET5 (see Fig. 1) was \({{V}_{x}}\) = 360 mm/72 μs = 5.0 mm/μs. The propagation velocity of the fast mode \(S0\) passing along the \(Y\)-axis from sensor AET4 to sensor AET3 was equal to \({{V}_{y}}\) = 280 mm/48 μs = 5.83 mm/μs and that in the \(XY\)-direction from sensor AET4 to sensor AET2, \({{V}_{{xy}}}\) = 456 mm/84 μs = 5.43 mm/μs. Thus, an appreciable anisotropy was observed for this sample in terms of the speed of sound. Based on the results of automated calibration, the coordinates of the AET sensors in the location zone were determined in units of time (μs) for the fast mode \(S0\): AET4 (0; 0), AET5 (72.7; 0); AET2 (72.7; 48.5); and AET3 (0; 48.5).

Before the start of impact tests, signals from a simulator were introduced at each of the 16 points marked on the sample (see Fig. 1). Two types of simulators were used. When working with the Su–Nielsen simulator, a 0.5 mm diameter pencil lead with a hardness of 2H was fractured at an angle of 45° at each point. When working with an electronic simulator, electrical signals with a voltage of 80 V and a duration of 150 μs were introduced at each point. The signal from the electronic simulator was transmitted to the piezoelectric AET sensor and switched the sensor into emission mode. After experiments with the simulators, errors in determining the coordinates of each point marked on the sample were calculated.

Then the impacts associated with dropping steel balls from a height of \({{h}_{1}} = 300\) mm and \({{h}_{2}} = 600\) mm into each point marked on the sample were performed. Balls with a diameter of d1 = 10 mm and a weight of 4.5 g and with a diameter of \({{d}_{2}} = 16\) mm and a weight of 18.5 g were used for testing. The precise discharge of the balls at each point on the sample was achieved through using a 600 mm long pipe. The ball with the diameter of \({{d}_{2}} = 16\) mm was dropped from a height of \({{h}_{1}} = 300\) mm and the ball with the diameter of \({{d}_{2}} = 10\) mm was dropped from a height of \({{h}_{2}} = 600\) mm.

The impact energy was determined as [10]

$$E = mgh,$$
(1)

where \(m\) is the load mass, kg, \(g\) is the acceleration due to gravity, m/s2, and \(h\) is the load drop height, m.

Thus, the energy of the ball with mass \({{m}_{1}} = 4.5\) g dropped from the height of \({{h}_{2}} = 600\) mm determined by formula (1) amounted to \({{E}_{{12}}} = 0.026\) J. The impact energy when dropping the ball with mass \({{m}_{2}} = 18.5\) g from the height of \({{h}_{1}} = 300\) mm was \({{E}_{{21}}} = 0.055\) J.

AE signals were recorded by the system both after the ball was dropped and during its repeated bounces. Then clusters of AE signals recorded during shock impacts at each point of the sample were formed [21]; 16 clusters were formed and for each of them the coordinates of the center were determined as the average value of the coordinates of all signals in the cluster. To determine the coordinates of the points marked on the sample, the location of the AE signals was carried out. The random component of the coordinate error was calculated from the root mean square deviations \(\left( {{{S}_{{xi}}},{{S}_{{yi}}}} \right)\) in each cluster [22].

In the calculation, the systematic component of the error in the \(X\)- and \(Y\)-coordinates of the cluster center was determined in units of the arrival time difference (ATD) in microseconds and multiplied by the speed of the fast mode \(S0\) along the \(X\) (5.0 mm/μs) and \(Y\) (5.83 mm/μs) axes. The coordinates of the location center were determined in millimeters as [22]

$${{X}_{i}} = {{x}_{{{\text{ATD}}}}}{{V}_{x}};\quad {{Y}_{i}} = {{y}_{{{\text{ATD}}}}}{{V}_{y}},$$

where \(i\) is the number of the impact point (cluster), \({{x}_{{{\text{ATD}}}}}\) and \({{y}_{{{\text{ATD}}}}}\) are the coordinates of the sensors in the time domain, μs; \({{X}_{i}}\) and \({{Y}_{i}}\) are the measured coordinates of the source along the \(X\)- and \(Y\)-axes, mm, and \({{V}_{x}}\) and \({{V}_{y}}\) are the propagation velocities of the fast mode \(S0\) along the \(X\)- and \(Y\)-axes, mm/μs.

Calculations were carried out using the threshold method, the root mean square deviation method, and the two-interval method [7, 10] to determine the errors in the arrival times of AE signals to AET sensors.

The arrival time according to the threshold method was calculated by the moment when an AE signal exceeds a certain level determined by noise in its past history. At the same time, automatic detection of the threshold level was introduced, where the threshold was set as [7]

$${{U}_{{{\text{thr}}}}} = {{U}_{{{\text{noise}}}}} + {{U}_{{{\text{add noise}}}}},$$

where \({{U}_{{{\text{noise}}}}}\) is the noise level calculated in the area of the signal past history and \({{U}_{{{\text{add noise}}}}}\) is an addition to the noise level.

When using the RMS deviation method, we used a time “window” of several microseconds superimposed on the digitization of the AE signal. In the “window,” we calculated a certain parameter responding to a local change in the signal structure. This algorithm considerably increases the degree of reliability of determining the arrival times of AE signals compared to the method based on threshold discrimination [7]. When moving the “window” on digitization, the RMS deviation parameter was chosen for the signal structure parameter characterizing the energy level [7, 9],

$${{\sigma }_{j}} = \sqrt {\frac{{\sum\limits_{i = {{T}_{1}}}^{i = {{T}_{2}}} {{{{\left( {{{x}_{i}} - {{x}_{{{\text{avg}}}}}} \right)}}^{2}}} }}{{{{T}_{2}} - {{T}_{1}} - 1}}} ,$$

where \({{T}_{1}}\) and \({{T}_{2}}\) are the numbers of the counts by the analog-to-digital converter corresponding to the moments of the beginning and end of the time “window,” \({{x}_{{{\text{avg}}}}}\) is the average value of the AE signal realization in the “window,” and \(i\) is the number of the point in the RMS array.

The advantage of this method is manifested in processing complex multimode signals, when several acoustic wave modes are present in the digitization. By selecting the threshold level, it is possible to tune in to determine the beginning of the signal in the selected mode [7].

The two-interval method allows one to determine the time of arrival of the AE signal, coinciding with the moment of a change in its power. The structure parameter \(A\left( t \right)\) of the AE signal is written as [7]

$$A\left( t \right) = \mathop \smallint \limits_t^{t + {{T}_{{{\text{window}}}}}} \left| {U\left( t \right)} \right|dt,$$

where \(U{\kern 1pt} \left( t \right)\) is the AE electrical signal and \({{T}_{{{\text{window}}}}}\) is the size of the “window” used for calculating the signal power.

The arrival time of the AE signal corresponds to the maximum value of the modified two-interval coefficient \(K{\kern 1pt} \left( t \right)\) defined [8] as

$$K\left( t \right) = \frac{{A\left( {t + {{T}_{{{\text{window}}}}}} \right) - A\left( {t - {{T}_{{{\text{window}}}}}} \right)}}{{A\left( {t - {{T}_{{{\text{window}}}}}} \right)}}.$$

The advantage of using the two-interval method is that summing the parameters of the AE signal structure in a time “window” practically eliminates random outliers. This makes it possible to more accurately determine the arrival time \({{t}_{0}}\) of the AE signal to the corresponding AET sensor, and, consequently, to reduce the spread of the defect coordinates and determine them automatically [8].

The design random error components for each impact point (see Fig. 1) were determined using the formulas [10, 22]

$${{S}_{{xi}}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{{\left( {{{x}_{i}} - {{x}_{{{\text{avg}}}}}} \right)}}^{2}}} }}{{\left( {n - 1} \right)}}} ;\quad {{S}_{{yi}}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{{\left( {{{y}_{i}} - {{y}_{{{\text{avg}}}}}} \right)}}^{2}}} }}{{\left( {n - 1} \right)}}} ,$$

where \(n\) is the number of counts, \({{x}_{i}}\) and \({{y}_{i}}\) are the measured values along the \(X\)- and \(Y\)-axes, and \({{x}_{{{\text{avg}}}}}\) and \({{y}_{{{\text{avg}}}}}\) are the average values along the \(X\)- and \(Y\)-axes.

The resulting random error \({{S}_{{xyi}}}\) for each point of the sample is [22]

$${{S}_{{xyi}}} = \sqrt {\left( {S_{{xi}}^{2} + S_{{yi}}^{2}} \right)} ,$$

where \({{S}_{{xi}}}\) and \({{S}_{{yi}}}\) are the calculated coordinates along the \(X\)- and \(Y\)-axes, mm.

The systematic component of the error for each coordinate was estimated as the modulus of the difference between the coordinates of the cluster center \(\left( {{{X}_{i}},{{Y}_{i}}} \right)\) and the coordinates \({{X}_{{i0}}}\) and \({{Y}_{{i0}}}\) measured by a gaged ruler,

$$\Delta {{X}_{i}} = \left| {{{X}_{i}}-{{X}_{{i0}}}} \right|;$$
$$\Delta {{Y}_{i}} = \left| {{{Y}_{i}}-{{Y}_{{i0}}}} \right|,$$

where \(i\) is the number of the impact point (cluster) and \({{X}_{i}}\) and \(~{{Y}_{i}}\) are the measured coordinates of the source, mm.

The total systematic error at each point of the sample was determined by the formula [22]

$$\Delta X{{Y}_{i}} = \sqrt {\left( {\Delta X_{i}^{2} + \Delta Y_{i}^{2}} \right)} ,$$

where \(\Delta {{X}_{i}}\) and \(\Delta {{Y}_{i}}\) are the calculated systematic components of the error along the \(X\)- and \(Y\)-axes, mm.

RESULTS AND DISCUSSION

The systematic and random components of the error in calculating the coordinates of the location of AE signals when using the antenna consisting of four AETs were averaged over all impact points. The calculation results are listed in Table 1, where \(S1\) and \(\Delta 1\) indicate random and systematic errors obtained when determining the coordinates of the location zone using electronic simulator; \(S2\) and \(\Delta 2\), when dropping the metal ball with diameter \(d = 10\) mm from height \(h = 600\) mm; and \(S3\) and \(\Delta 3\), when dropping the metal ball with diameter \(d = 16\) mm from height \(h = 300\) mm.

Table 1. Systematic and random location errors for various methods of calculating ATD when using antenna consisting of four AETs
Full size table

The arrival times of AE signals for the fast mode \(S0\) were determined by the RMSD method [7]. Then, the values of the coordinates of the signal source in ATD units were calculated using triangulation formulas.

For general estimation of the error of the \(X,Y\) coordinate measurement method, the average value of the systematic component of the error and the average value of the random error for two impact points were used (see Fig. 1). The summary values of the errors are given in Table 2, where \({{\Delta }_{X}}\) and \({{\Delta }_{Y}}\) are the average values of systematic errors in determining the \(X\)- and \(Y\)-coordinates.

Table 2. Averaged values of systematic and random errors in determining X- and Y-coordinates for various AE signal simulators
Full size table

As follows from Table 2, the systematic component of the error increases along with the random component. The minimum errors were obtained using an electronic simulator. Comparing the location errors of AE signals when using different calculation methods (see Table 1), it can be noted that the lowest average values of the systematic and random error components were obtained by the RMD method when dropping a ball with a diameter of \(d = 10\) mm from a height of \(h = 600\) mm. The greatest errors in determining the coordinates from the impact were obtained when a ball with a diameter of 16 mm was dropped onto the sample from a height of 300 mm.

The two-interval coefficient was used to estimate the measurement error of AE signal arrival time. For the planar location of AE signals when using the three-channel antenna, the channel with a minimum two-interval coefficient was selected, since it introduces the greatest error in the calculation of arrival times. The correlation of the average value of this coefficient at the impact points with the value of the random error of coordinates was calculated. This coefficient corresponds to the signal-to-noise ratio of the signal where the arrival time is determined in the time domain.

The shape of an AE signal produced by the simulator differs considerably from the shape of the signal obtained when dropping a metal ball. This is accompanied by a decrease in the amplitude of the fast mode \(S0\), whose time of arrival is considered to be the signal arrival time in all considered calculation algorithms. The main differences in all methods of impact on a composite sample are the change in the ratio of the amplitudes of the fast \(S0\) and slow \(A0\) modes. In addition, differences are observed in the spectrum of AE signals, since the energy in the spectrum is slightly shifted towards the low-frequency region due to shock effects (Table 3).

Table 3. Parameters of the shape and spectrum of AE signals received from sensor AET3 at point 6 (see Fig. 1) of sample for different types of impacts
Full size table

In Table 3, \(K{\kern 1pt} \left( t \right)\) denotes the average value of the two-interval coefficient for all signals at the start point of the signal of the fast \(S0\) mode. The signal-to-noise ratio is denoted by \(S{\text{/}}{{N}_{{s0}}}\) and \(S{\text{/}}{{N}_{{a0}}}\) and is determined by the ratio of the maximum signal span to the noise span in the past history for the fast \(S0\) and slow \(A0\) modes. The median frequency of the AE signal spectrum is denoted by \({{F}_{{{\text{med}}}}}\), and the ratio of the amplitude of the slow mode to the amplitude of the fast mode is designated as \({{P}_{{a/s}}}~\).

The main difference of these signals from those due to the impact with a steel ball is an increase in the ratio \({{P}_{{a/s}}}\) of the amplitudes of slow and fast modes (see Table 3) and a decrease in the average value of the two-interval coefficient \(K{\kern 1pt} \left( t \right)\).

The antenna consisting of four FOS sensors was used to estimate the error in determining the coordinates of the source. AE signals were recorded by the eight-channel module of the SCAD-16.10 AE system in which the piezoelectric AET sensors were connected to four channels and the FOS sensors to the other four channels (see Fig. 1). The process of auto-calibration of the location zone had a feature associated with the fact that the signal from the FOS sensors exceeded the selection threshold only from the nearest emitting AET sensor of the electronic simulator. At the same time, it was not possible to determine the speed of sound from the FOS signals during autocalibration using electronic simulator. The speed of sound was determined during calibration using a ball dropped at a point outside the location zone on the line between the pair of FOS sensors.

Figure 2a shows the shape of an AE signal due to the ball with diameter 10 mm dropped outside the location zone between piezoelectric sensors AET4 and AET5, and Fig. 2b shows the shape of an AE signal due to this ball dropped in the area between sensors FOS0 and FOS1. The distance between these sensors was 360 mm, and the speed of a sound wave of the fast mode \(S0\) according to the results of the measurement of the ATD of piezoelectric sensors AET4 and AET5 was \({{V}_{x}}\) = 360 mm/70 μs = 5.14 mm/μs.

Fig. 2.
figure 2

Signal shape during calibration of location zone by dropping a ball with diameter 10 mm: signal at the output of sensor AET4 (a), sensor AET5 (b); signal at the output of sensor FOS0 (c), sensor FOS1 (d).

Full size image

The time of arrival of the AE signal to the sensor FOS0 was reliably determined (Fig. 2c). The time of arrival at sensor FOS1 was visually determined as \({{T}_{1}}\) (Fig. 2d). For the arrival time \({{T}_{1}}\), the ATD is 62 μs and the velocity \({{V}_{x}}\) = 350 mm/62 μs = 5.64 mm/μs. Calibration with FOS sensors gives a large error in determining the velocity of the fast mode \(S0\), therefore, calibration results obtained by piezoelectric sensors AET4 and AET5 were used to calculate the coordinates.

The results of calculations of coordinates for the case of dropping the ball with diameter 10 mm from the height of 600 mm for location zones made up of combinations of AET and FOS sensors are shown in Table 4. In this table, location zone 1 is composed of four piezoelectric AET sensors (AET2, AET3, AET4, and AET5). Two FOS sensors and two piezoelectric AET sensors (FOS0, FOS1 and AET2, AET3) were included in location zone 2. Location zone 3 consisted of two FOS and two piezoelectric AET sensors (AET4, AET5 and FOS6, FOS7). Zone 4 consisted of four FOS sensors (FOS0, FOS1, FOS6, and FOS7). When arranging various antennas, the AET and FOS sensors on the sample did not move.

Table 4. Design values of systematic and random error in determining X- and Y-coordinates averaged over impact points for four location zones using AET and FOS sensors
Full size table

The location errors in zones 2 and 3 increase considerably when two FOS sensors are included in the antenna compared to zone 1 (see Table 4). The increase in the error in determining the coordinates is due to the low amplitude of the signals recorded by the FOS sensors caused by their low sensitivity and errors in determining the time of arrival of signals.

When using the antenna consisting of four AETs that form zone 1, all shock effects applied at 16 points were localized (Fig. 3a). The average location error for all points in this case was 4.2 mm on the \(X\)-axis and 8.6 mm on the \(Y\)-axis. At the same time, 98.8% of all recorded signals were localized (see Table 4).

Fig. 3.
figure 3

Location of AE signals when using piezoelectric antennas consisting of four AETs (a), two AETs and two FOS (b, c), four FOS (d).

Full size image

The replacement of two AET sensors with FOS sensors led to a substantial drop in the accuracy of determining the coordinates of localized AE signals. The results of determining the coordinates of AE signals for location zones 2 (Fig. 3b) and 3 (Fig. 3c) were analyzed.

The accuracy of locating AE signals in zone 2 was higher than in zone 3 (see Table 4). The systematic component of the \(X\)-axis error in zone 2 was four times smaller than in zone 3 and amounted to 9.7 mm. Along the \(Y\)-axis, the systematic error was equal to 32.3 mm, that is, it was two times smaller than in zone 3. In addition, 18% more signals were localized in zone 2 than in zone 3 (see Fig. 3b).

Figure 3c shows the results of location when using the antenna forming zone 3. In this case, the share of localized AE signals decreased to 61% of all recorded ones, and the errors began to be 36.6 mm along the \(X\)-axis and 62.3 mm along the \(Y\)-axis (see Table 4). The maximum total amplitude of signals localized in zone 1 was twice as high as in zone 3. Thus, the inclusion of various FOS sensors in the second and third antennas (see Figs. 3b–3c) had an impact on the accuracy of location results. This is determined by the low sensitivity and the spread of characteristics of FOS sensors.

When using the antenna consisting of four FOS sensors, no location of AE signals was obtained when the steel ball weighing 18.5 g was dropped on the sample. Therefore, in order to achieve stable location of AE signals, we used a shock effect produced by a blunt tip load weighing \(m = 530\) g [10]. The load was dropped from heights of \({{h}_{1}} = 200\) mm and \({{h}_{2}} = 400\) mm. The values of the energy of the dropped load weighing \(m = 530\) g calculated using formula (1) were \({{E}_{1}} = 1\) J for the drop height \({{h}_{1}} = 200\) mm and \({{E}_{2}} = 2\) J for the drop height \({{h}_{2}} = 400\) mm. At the same time, the maximum amplitude of localized AE signals (Fig. 3d) was equal to 0.6 V. Dropping the load weighing \(m = 530\) g at four points 5, 8, 10, and 11 marked on the sample (see Fig. 1) allowed obtaining the location shown in Fig. 3d.

When a shock damage was inflicted, the load was dropped from a height of \({{h}_{2}} = 400\) mm. During the test, 62 AE signals were registered, with 28 of them corresponding to impacts and the rest to load bounces and noises. Filtering was performed to estimate the errors and only useful signals were selected. Table 5 shows the results of calculating systematic and random errors for points 5, 8, 10, and 11 shown in Fig. 1. The largest values of the error in determining the coordinates were obtained in the location area for an impact at point 5. The total systematic component of the error was \({{\Delta }_{{XY}}} = 54.3\) mm, and the total random component was \({{S}_{{XY}}} = 23.2\) mm. The highest accuracy was observed for an impact at point 8. In this case, the systematic and random error components were equal to \({{\Delta }_{{XY}}} = 9.7\) mm and \({{S}_{{XY}}} = 10.6\) mm.

Table 5. Design values of systematic and random error in determining X- and Y-coordinates when applying shock damage at points 5, 8, 10, and 11 of the sample and using antenna consisting of four FOS sensors
Full size table

It was noted that when processing AE information recorded by FOS sensors, a decrease in location accuracy was associated with their low sensitivity and, as a consequence, with difficulties in determining the arrival times of AE signals.

CONCLUSIONS

1. Methods for determining the arrival times of AE signals to antenna sensors are analyzed. It is established that the smallest location errors from impacts with a steel ball with a diameter of 10 mm dropped from a height of 600 mm are achieved by using an antenna consisting of four AETs using the RMSD method when determining the arrival times of AE signals. At the same time, the average location error was 4.15 mm along the \(X\)-axis and 8.6 mm along the \(Y\)-axis (see Table 4). 98.8% of all recorded signals were localized. The largest errors (see Table 2) in determining the coordinates from the impact were obtained when a ball with a diameter of 16 mm was dropped onto the sample from a height of 300 mm.

2. During the tests, all sensors were installed on the sample once, after which, through their various combinations, four location antennas were considered. This made it possible to experimentally determine the location errors when applying shock damage for four types of antennas and analyze the possibilities of their practical usage.

3. The use of an antenna consisting of two AET and two FOS sensors led to a decrease in the accuracy of determining the coordinates of localized AE signals. In this case, strikes were delivered with a ball 10 mm diameter dropped from a height of 600 mm. The share of localized AE signals decreased to 61.0% of those registered, and the errors began to be 36.6 mm along the \(X\)-axis and 62.3 mm along the \(Y\)-axis.

4. In the case of using an antenna consisting of four FOS sensors, due to their low sensitivity, the impacts caused by the balls were not localized by the AE system. Therefore, to investigate the possibilities of location, the impact energy was increased and a load weighing 530 g dropped from a height of 400 mm was used. In this case, the minimum values of systematic and random error were \({{\Delta }_{{XY}}} = 9.7\) mm and \({{S}_{{XY}}} = 10.6\) mm.