INTRODUCTION

Type AISI 321 austenitic stainless steel has found wide application in various industrial fields such as shipbuilding and nuclear and chemical industries. The main areas of application of this steel are associated with its high strength properties, as well as good weldability. Heat-affected zones (HAZ’s) are formed during the manufacture of a welded joint. The structure of these zones differs significantly from the structure of the base material (BM). In the HAZ, there is an inhomogeneity of the phase composition and a gradient of physical and mechanical properties, and a complex stress-strain state is realized [1]. We also note that, in contrast to low-carbon steels, a welded joint made of AISI 321 steel can change magnetic properties both in the process of force [2–6] and thermal action [7–9]. As a rule, the HAZ is the weakest zone in the welded joint where structural failure often occurs. In this regard, the analysis of the state of the material must be carried out not only in the base material but also in the welded joint HAZ.

The acoustic echo method is convenient and effective to analyze the state of the material in volume due to its high penetrating power, safety, and ability to control with one-sided access to the product [10].

As a rule, changes in magnetic properties associated with phase transformations in steels of the austenitic class are evaluated using eddy current nondestructive testing [11–13]. It should be noted that the results of eddy current testing can be influenced by various exogenous factors. Moreover, on a real object, the structure of the HAZ will depend on the specifics of manufacturing the weld (welding speed, temperature, electrodes used, cooling rate, plate thickness, etc.). Taking into account the influence of these factors is especially important for stainless steels of the austenitic class. In [14], the effect of welding modes on the temperature gradient along and across the weld, as well as on the microstructure and properties of the HAZ of 12Kh18N10T stainless steel of the austenitic class was investigated. Due to the influence of exogenous factors in the manufacture of the weld, the amount of magnetic phase in the HAZ of chromium-nickel steels may vary. The volume fraction of this phase affects the magnetic [15, 16] and electrical [17] properties of austenitic stainless steel and, as a consequence, the readings of the eddy current instrument. This gives rise to the uncertainty of the original state of the material of welded joints of industrial facilities in operation. However, to reduce the likelihood of hot cracks and intergranular corrosion, welding of austenitic steels is carried out with heating, and residual welding stresses are removed by heat treatment [18, 19]. These operations can reduce the content of magnetic phase and neutralize the uncertainty in the initial structural state. The lack of information about the initial state of material is a significant limitation for the use of most structure-sensitive methods of nondestructive testing when assessing damage to material.

The inhomogeneity of the structural state in the HAZ leads to an uneven distribution of acoustic characteristics and magnetic properties of the welded joint material [20, 21]. It is shown that under uniaxial tension of a austenitic-steel welded joint, the intensities of changes in acoustic parameters and electromagnetic properties in the HAZ and the base material differ.

In contrast to plastic deformation, fatigue is a more frequent cause of structural failure. In the works devoted to the study of the process of fatigue fracture in steels of the austenitic class, it is shown that the cycle deformation amplitude affects the rate of change in the elastic and acoustic characteristics, as well as the phase composition. The combined use of ultrasonic and eddy-current testing [22] gives a more complete picture of the state of material, which can be used to predict the moment of destruction [23]. The problem of predicting the fatigue failure of a welded joint made of austenitic steel is a more complex problem.

In the present work, the process of fatigue fracture of welded joints made of AISI 321 stainless steel using ultrasonic and eddy-current types of testing was investigated. On the basis of the obtained regularities of changes in the characteristic parameters in the HAZ and the base material, we propose a method for assessing the fatigue damage to a welded joint.

EXPERIMENTAL

A. Test Material and Samples

Circular cross-section samples were made of stainless steel of the austenitic class AISI 321 to study the process of fatigue fracture in welded joints.

To manufacture welded samples, workpieces were divided in half. A double-sided butt weld with two symmetrical bevels of the edges was prepared by manual argon-arc welding.

The chemical composition is listed in Table 1.

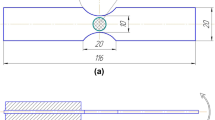
Table 1. Chemical composition of AISI 321 steel, %
Full size table

The working part of the samples was 28 mm, the diameter of the working section was 8 mm. Two plane-parallel platforms were cut out on the working part of each sample for ultrasonic and eddy current testing. The surface in the test section was divided into 6 zones (three zones to the left and right of the welded joint), with the width of each of 4 mm (Fig. 1). Ultrasonic and eddy-current testing was carried out in each zone. Marks were made with a permanent marker to improve the accuracy of positioning the sensors.

Fig. 1.
figure 1

Diagram of mounting sensors on the sample (dimensions in mm).

Full size image

Microstructure analysis in the base material and in the heat-affected zone was carried out by metallographic method using an Altami MET 3M optical microscope. Microsections were made, electrolytic etching was carried out using a 10% aqueous solution of oxalic acid under a voltage of 1 V at room temperature.

Cyclic deformation was carried out on a universal BISS Nano machine in the area of low-cycle fatigue. The samples were subjected to uniaxial tension–compression (symmetry coefficient \(R = -1\)) with a cycle deformation amplitude \({{\varepsilon }_{a}}\) (0.3, 0.4, and 0.5%) at a frequency of 2 Hz. Each sample was loaded in stages. Ultrasonic and eddy-current testing were performed before testing and after each stage of cyclic deformation up to the formation of a macrocrack.

B. Ultrasonic Testing

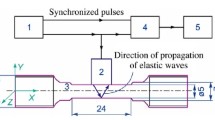
Acoustic studies of the material were carried out using the ultrasonic echo method. Figure 2a shows a block diagram of the acoustic experimental setup.

Fig. 2.
figure 2

Block diagram of installation for acoustic measurements (a) (1) ultrasonic flaw detector, (2) PET, (3) sample, (4) digital oscilloscope (5) PC; (b) amplitude–time diagram of shear wave echo pulses, zero crossing point between the minimum and maximum in the pulse.

Full size image

Signal generator 1 supplies electrical pulses to piezoelectric transducer 2 emitting ultrasonic signals into test sample 3. The signals reach the opposite side of the sample and are reflected and sent back to the piezoelectric transducer, which generates electrical signals. The electrical signals from the transducer and sync pulses from a generator are fed to the input of digital oscilloscope 4, and amplitude-time diagram array in digital form is fed to personal computer 5 from the oscilloscope.

In this work, a commercially available ultrasonic flaw detector (model A1212 MASTER manufactured by AKS LLC, Russia) was used to generate electrical pulses that excite the piezoelectric transducer. To obtain the time base of the signals from the piezoelectric transducer, we employed an LA-n1USB digital oscilloscope (Rudnev-Shilyaev LLC, Russia) and the ADCLab application. The sampling rate of the digital oscilloscope was 1 GHz, and the time sweep resolution was 1 ns. We used a broadband small-sized combined piezoelectric V157-RM shear wave transducer manufactured by Olympus with a central frequency of \(\sim ~5\) MHz and a piezoelectric element diameter of 3 mm. The acoustic path length between the plane-parallel areas in the sample was 14 mm. Epoxy resin without hardener was used as a couplant. The resulting time base was saved to a data file for analysis and processing in the MathCAD program. The propagation time of elastic waves was measured between the first \({{t}_{1}}\) and the third \({{t}_{3}}\) reflected pulses at the points of the zero transition between the minimum and maximum in the pulse (Fig. 2b). The time measurement error was no more than 2 ns.

As a rule, many materials demonstrate some anisotropy of elastic properties. In an orthotropic material (in our case, sheet metal), three body waves can propagate in one direction—one longitudinal and two transverse—polarized along and across the axes of elastic anisotropy [24].

The following expression was used to describe the anisotropy of elastic properties [25]

$$A = 2\frac{{{{t}_{{zy}}} - {{t}_{{zx}}}}}{{{{t}_{{zy}}} - {{t}_{{zx}}}}},$$
(1)

where \({{t}_{{zx}}}\) and \({{t}_{{zy}}}\) are the propagation times of transverse elastic waves polarized along and across the loading axis, respectively. The absolute error of measurement of the parameter \(A\) was \(4 \times {{10}^{{ - 4}}}\).

C. Eddy-Current Testing

It is well known that phase changes can occur in austenitic steels under load. From the austenite \(\gamma \)‑phase with the FCC lattice, \(\alpha '\)-martensite phase is formed, which, in the general case, has a tetragonal lattice. Due to the fact that the \(\alpha '\)-martensite phase is ferromagnetic, in contrast to paramagnetic austenite, eddy current testing is widely used to study changes in the magnetic properties of material during phase transformation [12–13, 20–23]. Eddy-current testing of the content of ferromagnetic phase is based on the analysis of the interaction between an external electromagnetic field and the electromagnetic field of eddy currents induced in austenitic steel by this field.

Structurally sensitive studies of changes in electromagnetic characteristics were carried out using a multifunctional MVP-2M eddy-current device manufactured by LLC NPTs Kropus, Russia. The device was developed, among other things, for determining the percentage of the ferritic phase \(\Phi \) in austenitic steels. The device was calibrated by the manufacturer using samples with a known ferrite content. The relative measurement error did not exceed 5%.

RESULTS AND DISCUSSION

The microstructure of the base material is typical of austenitic stainless steels. Austenite grains have a polyhedral shape with thin boundaries, annealing twins, and fine point precipitates of the second phase (Fig. 3a). The average grain diameter in the base material is 35 \({{\boldsymbol{\mu} \mathbf{m}}}\). Coarsening of austenite grains is observed in the heat-affected zone near the fusion area (Fig. 3b), the average grain diameter is 70 \({{\boldsymbol{\mu} \mathbf{m}}}\). The weld structure has a directed dendritic structure at the edges and a disoriented dendritic structure in the center. Cyclic deformation of the welded samples was carried out until the formation of the main crack, which propagated along the HAZ in the weld (Fig. 3c).

Fig. 3.
figure 3

Photographs of the microstructure of base material (a) and of HAZ and weld in initial state (b) and after destruction (c).

Full size image

As a result of ultrasonic studies, the propagation time of shear waves of different polarization in each zone of the samples was determined and the acoustic anisotropy parameter A was calculated using formula (1). The inhomogeneity of the distribution of the acoustic anisotropy parameter A along the sample is shown in Fig. 4. The value of parameter A in the base material zone differs significantly from the value in the HAZ; this can be used to determine the HAZ size. The inhomogeneity of the distribution of the acoustic anisotropy parameter A increases in the process of cyclic deformation.

Fig. 4.
figure 4

Distribution of parameter \(A\) along samples with deformation amplitudes \({{\varepsilon }_{{\text{a}}}} = 0.3\% \) (a), \({{\varepsilon }_{{\text{a}}}} = 0.4\% \) (b), \({{\varepsilon }_{{\text{a}}}}\) = 0.5% (c), with the number of cycles \(N = 0~\,\,\left( {a1,~b1,~c1} \right)\), \(N = 3500~\,\,\left( {{\text{a}}2} \right)\), \(N = 5900\,\,~\left( {{\text{a}}3} \right)\), \(N = 7500~\,\,\left( {{\text{a}}4} \right)\), \(N = 500\,\,~\left( {{\text{b}}2} \right)\), \(N = 2700\,\,~\left( {{\text{b}}3} \right)\), \(N = 3800~\,\,\left( {{\text{b}}4} \right)\), \(N = 300\,\,~\left( {{\text{c}}1} \right)\), \(N = 600~\,\,\left( {{\text{c}}2} \right)\), \(N = 1400\,\,~\left( {{\text{c}}3} \right)\).

Full size image

In the process of cyclic deformation, it was revealed that the change in the average values of the acoustic anisotropy parameter \(\Delta \bar{A}\) both in the base material and in the HAZ monotonically decrease for deformation amplitudes of 0.3 and 0.4 (Figs. 5a, 5b). For the cycle deformation amplitude of 0.5 at the initial stage of cyclic deformation, a slight increase in the parameter \(\bar {A}\) is observed (Fig. 5c). The intensity of the change in the parameter \(\bar{A}\) in the base material is greater than in the HAZ. The value of \(\bar{A}\) decreases with further deformation (\({N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}~ > 0.2\), where \({{N}_{{\text{f}}}}\) is the number of cycles to failure). The intensity of the change in the parameter \(\bar{A}\) in the HAZ is greater than in the base material. The increase in \(\bar{A}\) at the initial stage of deformation at \({{\varepsilon }_{{\text{a}}}} = 0.5\% \) can be explained by a more significant influence of the plastic component in the cycle on the crystallographic texture and on the anisotropy of elastic and acoustic properties, respectively. An increase in parameter \(A\) during plastic deformation of austenitic stainless steel has been demonstrated in [8, 21]. With further cyclic deformation, just as with plastic deformation, the material is hardened, the rotation of the grains is hindered, and the intensity of the change in texture decreases.

Fig. 5.
figure 5

Change in acoustic anisotropy parameter in base material (1) and in HAZ (2) for \({{\varepsilon }_{{\text{a}}}}\) = 0.3% (a), \({{\varepsilon }_{{\text{a}}}}\) = 0.4% (b), and \({{\varepsilon }_{{\text{a}}}}\) = 0.5% (c) in the process cyclic deformation.

Full size image

The change in the average value of the acoustic anisotropy parameter \(\Delta \bar{A}\) both in the base material and in the HAZ during cyclic deformation is sensitive to the amplitude of the cycle deformation (Fig. 6). In the base material, \(\Delta \bar{A}\) increases with an increase in the amplitude of the deformation cycle. In the HAZ, the opposite effect is observed: \(\Delta \bar{A}\) decreases with increasing \({{\varepsilon }_{{\text{a}}}}\).

Fig. 6.
figure 6

Change in parameter \(\Delta \bar{A}\) during cyclic deformation in base material (a) and HAZ (b) for \({{\varepsilon }_{{\text{a}}}}\)= 0.3% (1), \({{\varepsilon }_{{\text{a}}}}\) = 0.4% (2), and \({{\varepsilon }_{{\text{a}}}}\) = 0.5% (3).

Full size image

As a result of eddy-current inspection of changes in electromagnetic properties in the process of cyclic deformation, monotone dependences of the change in parameter \(\Phi \) on the number of cycles were obtained for three amplitudes of cycle deformation in the zone of the base metal and in the heat affected zone (Fig. 7).

Fig. 7.
figure 7

Change in parameter \(\Phi \) in base material (1) and in HAZ (2) for \({{\varepsilon }_{{\text{a}}}}\) = 0.3% (a), \({{\varepsilon }_{{\text{a}}}}\) = 0.4% (b), and \({{\varepsilon }_{{\text{a}}}}\) = 0.5% (c) in the process of cyclic deformation.

Full size image

With the smallest cycle deformation amplitude (\({{\varepsilon }_{{\text{a}}}} = 0.3\% \)), the dependences \(\Phi \left( N \right)\) in the base metal and HAZ differ insignificantly. It can be concluded that for low amplitudes, phase changes in the base material and HAZ occur with the same intensity. With an increase in the amplitude, the intensity of the change in the parameter \(\Phi \) in the base material becomes more substantial than in the HAZ.

The dependences \(\Phi \left( {{N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}~} \right)\) for the base material are sensitive to the deformation amplitude (Fig. 8a); this is consistent with the previous studies [5, 23, 26].

Fig. 8.
figure 8

Dependences of parameter \(\Phi \) on \({N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}\) for base material (a) and HAZ (b) for \({{\varepsilon }_{{\text{a}}}}\) = 0.3% (1), \({{\varepsilon }_{{\text{a}}}}\) = 0.4% (2), and \({{\varepsilon }_{{\text{a}}}}\) = 0.5% (3).

Full size image

In the area of low-cycle fatigue, the relationship between the critical value of parameter \(\Phi \) in the base material and the amplitude of the cycle deformation can be described by the linear relationship

$${{\Phi }_{{\text{f}}}} = 75{{\varepsilon }_{{\text{a}}}} - 4.$$
(2)

With a known cycle deformation amplitude in the area of the low-cycle fatigue in a regular loading mode, one can use formula (2) to predict the value of parameter \({{\Phi }_{{\text{f}}}}\) corresponding to material fracture. This fact can be used to predict the moment of fracture of welded joint.

In contrast to the base material, the intensity of change in parameter \(\Phi \) in the HAZ is practically the same for different amplitudes of deformations. This can be explained by the effect of the weld and the peculiar HAZ microstructure. The dependences \(\Phi \left( {{N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}} \right)\) in the low-cycle fatigue mode can be described by one curve (Fig. 8b).

Using the fact that the dependences \(\Phi \left( {{N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}} \right)\) are not sensitive to the cycle deformation amplitude, it is possible to determine the relative number of cycles based on the results of eddy-current testing in the HAZ using the formula

$$\frac{N}{{{{N}_{{\text{f}}}}}} = 0.24\sqrt {\Delta \Phi } .$$
(3)

The values of \({N \mathord{\left/ {\vphantom {N {{{N}_{{\text{f}}}}}}} \right. \kern-0em} {{{N}_{{\text{f}}}}}}~\) calculated by formula (3) are in good agreement with the experimental values (the correlation coefficient is 0.96) in Fig. 9.

Fig. 9.
figure 9

Correlation field with respect to relative number of cycles.

Full size image

Thus, by using formula (3), one can calculate the relative number of cycles and estimate the fatigue damage to the material of welded joints based on the results of eddy-current testing in the heat-affected zone. This approach has a number of limitations, for example, it is necessary to know the initial state of material in the HAZ and a training experiment is required for specific welded joints in order to determine the numerical value of the multiplier included in formula (2). Further research on this topic can be aimed at taking into account the influence of external factors, the initial structural state, as well as the amplitudes of deformations from a wider range.

CONCLUSIONS

As a result of ultrasonic and eddy-current testing, it has been established that the measured parameters are sensitive to differences in the structural state in the HAZ and the base material. The combined use of these types of testing allows one to increase the accuracy of determining the dimensions of the HAZ in the welded joint.

It has been found that the inhomogeneity of the distribution of acoustic anisotropy parameter in the heat-affected zone and in the base material increases in the process of cyclic deformation.

The intensity of the change in acoustic anisotropy parameter during cyclic deformation is sensitive to the amplitude of cycle deformation both in the base material and in the HAZ.

It has been found that with an increase in the cycle deformation amplitude, the intensity of phase changes in the base material becomes more significant than in the HAZ.

A method is proposed for assessing the fatigue damage to the material of welded joints in the heat-affected zone based on the results of eddy-current testing.