Abstract
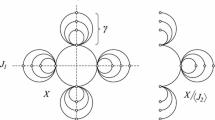
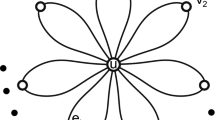
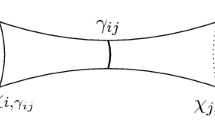
The present paper is devoted to the further development of the discrete theory of Riemann surfaces, which was started in the papers by M. Baker and S. Norine and their followers at the beginning of the century. This theory considers finite graphs as analogs of Riemann surfaces and branched coverings of graphs as holomorphic mappings. The genus of a graph is defined as the rank of its fundamental group. The main object of investigation in the paper is automorphism groups of a graph acting freely on the set of half-edges of the graph. These groups are discrete analogs of groups of conformal automorphisms of a Riemann surface. The celebrated Hurwitz theorem (1893) states that the order of the group of conformal automorphisms of a compact Riemann surface of genus g > 1 does not exceed 84(g — 1). Later, K. Oikawa and T. Arakawa refined this bound in the case of groups that fix several finite sets of prescribed cardinalities. This paper provides proofs of discrete versions of the mentioned theorems. In addition, a discrete analog of the E. Bujalance and G. Gromadzki theorem improving one of Arakawa’s results is obtained.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. Baker and S. Norine, “Harmonic morphisms and hyperelliptic graphs,” Int. Math. Res. Notes 15, 2914–2955 (2009). doi 10.1093/imrn/rnp037
S. Corry, “Genus bounds for harmonic group actions on finite graphs,” Int. Math. Res. Notes 19, 4515–4533 (2011). doi 10.1093/imrn/rnq261
A.D. Mednykh, “On the Riemann–Hurwitz formula for graph coverings” (2015). https://arxiv.org/pdf/1505.00321.pdf
A.D. Mednykh and R. Nedela, “Harmonic morphisms of graphs and the Riemann–Hurwitz theorem,” Dokl. Math. 93 (1), 23–26 (2016). doi 10.1134/S1064562416010105
A. Hurwitz, “Ueber algebraische Gebilde mit eindeutigen Transformationen in sich,” Math. Ann. 41, 403–442 (1892). doi 10.1007/BF01443420
I.A. Mednykh, “On the Farkas and Accola theorems for graphs,” Dokl. Math. 87 (1), 65–68 (2013). doi 10.1134/S1064562413010250
I.A. Mednykh, “Discrete analogs of Farkas and Accola’s theorems on hyperelliptic coverings of a Riemann surface of genus 2,” Math. Notes 96 (1–2), 84–94 (2014). doi 10.1134/S0001434614070074
M.P. Limonov, “Non-regular graph coverings and lifting the hyperelliptic involution,” Sib. Electron. Math. Rep. 12, 372–380 (2015). doi 10.17377/semi.2015.12.031
M.P. Limonov, “Accola theorem on hyperelliptic graphs,” Ars Math. Contemp. 11 (1), 91–99 (2016). doi 10.26493/1855–3974.790.202
A. Mednykh and I. Mednykh, “On Wiman’s theorem for graphs,” Discrete Math. 338, 1793–1800 (2015). doi 10.1016/j.disc.2015.03.003
K. Oikawa, “Notes on conformal mapping of a Riemann surface onto itself,” Kodai Math. Sem. Rep. 8, 23–30 (1956). doi 10.2996/kmj/1138843714
T. Arakawa, “Automorphism groups of compact Riemann surfaces with invariant subsets,” Osaka J. Math. 37, 823–846 (2000).
E. Bujalance and G. Gromadzki, “On automorphisms of Klein surfaces with invariant subsets,” Osaka J. Math. 50, 251–269 (2013).
A. D. Mednykh, I.A. Mednykh, and R. Nedela, “A generalization of Hurwitz’ theorem for groups acting on a graph” Dokl. Math. 91 (1), 87–90 (2015). doi 10.1134/S1064562415010275
A. Malnič, R. Nedela, and M. Škoviera, “Lifting graph automorphisms by voltage assignments,” Europ. J. Combin. 21 (7), 927–947 (2000). doi 10.1006/eujc.2000.0390
Author information
Authors and Affiliations
Corresponding authors
Additional information
Dedicated to the 70th birthday of our friend and colleague Academician S. V. Matveev
Russian Text © The Author(s), 2017, published in Trudy Instituta Matematiki i Mekhaniki UrO RAN, 2017, Vol. 23, No. 4, pp. 243–252.
Rights and permissions
About this article
Cite this article
Mednykh, A.D., Mednykh, I.A. & Nedela, R. On the Oikawa and Arakawa Theorems for Graphs. Proc. Steklov Inst. Math. 304 (Suppl 1), S133–S140 (2019). https://doi.org/10.1134/S0081543819020147
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0081543819020147