Skip to main content
SpringerLink
Log in

Stability of an Elastic Tube Conveying a Non-Newtonian Fluid and Having a Locally Weakened Section

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

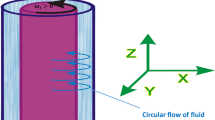
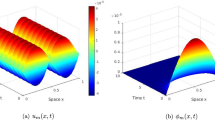
The work is devoted to the stability analysis of the flow of a non-Newtonian powerlaw fluid in an elastic tube. Integrating the equations of motion over the cross section, we obtain a one-dimensional equation that describes long-wave low-frequency motions of the system in which the rheology of the flowing fluid is taken into account. In the first part of the paper, we find a stability criterion for an infinite uniform tube and an absolute instability criterion. We show that instability under which the axial symmetry of motion of the tube is preserved is possible only for a power-law index of n < 0.611, and absolute instability is possible only for n < 1/3; thus, after the loss of stability of a linear viscous medium, the flow cannot preserve the axial symmetry, which agrees with the available results. In the second part of the paper, applying the WKB method, we analyze the stability of a tube whose stiffness varies slowly in space in such a way that there is a “weakened” region of finite length in which the “fluid–tube” system is locally unstable. We prove that the tube is globally unstable if the local instability is absolute; otherwise, the local instability is suppressed by the surrounding locally stable regions. Solving numerically the eigenvalue problem, we demonstrate the high accuracy of the result obtained by the WKB method even for a sufficiently fast variation of stiffness along the tube axis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. V. Abakumov, I. V. Ashmetkov, N. B. Esikova, V. B. Koshelev, S. I. Mukhin, N. V. Sosnin, V. F. Tishkin, A. P. Favorsky, and A. B. Khrulenko, “Strategy of mathematical cardiovascular system modeling,” Mat. Model. 12 (2), 106–117 (2000).

    MATH  Google Scholar 

  2. M. Anand and K. R. Rajagopal, “A shear-thinning viscoelastic fluid model for describing the flow of blood,” Int. J. Cardiovasc. Med. Sci. 4 (2), 59–68 (2004).

    Google Scholar 

  3. A. M. Barlukova, A. A. Cherevko, and A. P. Chupakhin, “Traveling waves in a one-dimensional model of hemodynamics,” Prikl. Mekh. Tekh. Fiz. 55 (6), 16–26 (2014) [J. Appl. Mech. Tech. Phys. 55, 917–926 (2014)].

    MATH  Google Scholar 

  4. A. Bers, “Space-time evolution of plasma instabilities—absolute and convective,” in Handbook of Plasma Physics, Ed. by A. A. Galeev and R. N. Sudan (North-Holland, Amsterdam, 1983), Vol. 1, pp. 451–517.

    Google Scholar 

  5. C. D. Bertram, C. J. Raymond, and T. J. Pedley, “Mapping of instabilities for flow through collapsed tubes of differing length,” J. Fluids Struct. 4 (2), 125–153 (1990).

    Article  Google Scholar 

  6. C. D. Bertram and J. Tscherry, “The onset of flow-rate limitation and flow-induced oscillations in collapsible tubes,” J. Fluids Struct. 22 (8), 1029–1045 (2006).

    Article  Google Scholar 

  7. R. J. Briggs, Electron-Stream Interaction with Plasmas (MIT Press, Cambridge, MA, 1964).

    Google Scholar 

  8. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System, Ed. by L. Formaggia, A. Quarteroni, and A. Veneziani (Springer, Milano, 2010), Model. Simul. Appl. 1.

    Google Scholar 

  9. J.-M. Chomaz, P. Huerre, and L. G. Redekopp, “A frequency selection criterion in spatially developing flows,” Stud. Appl. Math. 84 (2), 119–144 (1991).

    Article  MathSciNet  MATH  Google Scholar 

  10. P.-P. L. O. Coene, A. K. Groen, P. H. P. Davids, M. Hardeman, G. N. J. Tytgat, and K. Huibregtse, “Bile viscosity in patients with biliary drainage. Effect of co-trimoxazole and N-acetylcysteine and role in stent clogging,” Scand. J. Gastroenterol. 29 (8), 757–763 (1994).

    Article  Google Scholar 

  11. L. Formaggia, D. Lamponi, and A. Quarteroni, “One-dimensional models for blood flow in arteries,” J. Eng. Math. 47, 251–276 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  12. G. P. Galdi, R. Rannacher, A. M. Robertson, and S. Turek, Hemodynamical Flows: Modeling, Analysis and Simulation (Birkh¨auser, Basel, 2008).

    MATH  Google Scholar 

  13. F. J. H. Gijsen, F. N. van de Vosse, and J. D. Janssen, “The influence of the non-Newtonian properties of blood on the flow in large arteries: Steady flow in a carotid bifurcation model,” J. Biomech. 32 (6), 601–608 (1999).

    Article  Google Scholar 

  14. A. G. Gorshkov, V. I. Morozov, A. T. Ponomarev, and F. N. Shklyarchuk, Aerohydroelasticity of Designs (Fizmatlit, Moscow, 2000) [in Russian].

    Google Scholar 

  15. J. B. Grotberg and O. E. Jensen, “Biofluid mechanics in flexible tubes,” Annu. Rev. Fluid Mech. 36, 121–147 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  16. M. Heil and J. Boyle, “Self-excited oscillations in three-dimensional collapsible tubes: Simulating their onset and large-amplitude oscillations,” J. Fluid Mech. 652, 405–426 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  17. M. Heil and A. L. Hazel, “Fluid-structure interaction in internal physiological flows,” Annu. Rev. Fluid Mech. 43, 141–162 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  18. O. E. Jensen, “Instabilities of flow in a collapsed tube,” J. Fluid Mech. 220, 623–659 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  19. O. E. Jensen and T. J. Pedley, “The existence of steady flow in a collapsed tube,” J. Fluid Mech. 206, 339–374 (1989).

    Article  MathSciNet  MATH  Google Scholar 

  20. A. I. Katz, Y. Chen, and A. H. Moreno, “Flow through a collapsible tube: Experimental analysis and mathematical model,” Biophys. J. 9 (10), 1261–1279 (1969).

    Article  Google Scholar 

  21. D. N. Ku, “Blood flow in arteries,” Annu. Rev. Fluid Mech. 29, 399–434 (1997).

    Article  MathSciNet  Google Scholar 

  22. A. G. Kuchumov, V. Gilev, V. Popov, V. Samartsev, and V. Gavrilov, “Non-Newtonian flow of pathological bile in the biliary system: Experimental investigation and CFD simulations,” Korea–Aust. Rheol. J. 26 (1), 81–90 (2014).

    Article  Google Scholar 

  23. R. B. Kudenatti, N. M. Bujurke, and T. J. Pedley, “Stability of two-dimensional collapsible-channel flow at high Reynolds number,” J. Fluid Mech. 705, 371–386 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  24. S. Le Dizès, P. Huerre, J. M. Chomaz, and P. A. Monkewitz, “Linear global modes in spatially developing media,” Philos. Trans. R. Soc. London A 354 (1705), 169–212 (1996).

    Article  MATH  Google Scholar 

  25. H. F. Liu, X. Y. Luo, and Z. X. Cai, “Stability and energy budget of pressure-driven collapsible channel flows,” J. Fluid Mech. 705, 348–370 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  26. X. Y. Luo and T. J. Pedley, “Multiple solutions and flow limitation in collapsible channel flows,” J. Fluid Mech. 420, 301–324 (2000).

    Article  MATH  Google Scholar 

  27. A. Marzo, X. Y. Luo, and C. D. Bertram, “Three-dimensional collapse and steady flow in thick-walled flexible tubes,” J. Fluids Struct. 20 (6), 817–835 (2005).

    Article  Google Scholar 

  28. A. B. Metzner and J. C. Reed, “Flow of non-Newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions,” AIChE J. 1 (4), 434–440 (1955).

    Article  Google Scholar 

  29. J. E. Moore Jr., S. E. Maier, D. N. Ku, and P. Boesiger, “Hemodynamics in the abdominal aorta: A comparison of in vitro and in vivo measurements,” J. Appl. Physiol. 76 (4), 1520–1527 (1985).

    Article  Google Scholar 

  30. M. P. Päıdoussis, Fluid-Structure Interactions: Slender Structures and Axial Flow (Academic, San Diego, CA, 1998), Vol. 1.

    Google Scholar 

  31. T. J. Pedley, “Arterial and venous fluid dynamics,” in Cardiovascular Fluid Mechanics, Ed. by G. Pedrizzetti and K. Perktold (Springer, Wien, 2003), pp. 1–72.

    Google Scholar 

  32. T. J. Pedley, B. S. Brook, and R. S. Seymour, “Blood pressure and flow rate in the giraffe jugular vein,” Philos. Trans. R. Soc. London B: Biol. Sci. 351 (1342), 855–866 (1996).

    Article  Google Scholar 

  33. P. Reymond, F. Merenda, F. Perren, D. Rüfenacht, and N. Stergiopulos, “Validation of a one-dimensional model of the systemic arterial tree,” Am. J. Physiol. Heart Circ. Physiol. 297 (1), 208–222 (2009).

    Article  Google Scholar 

  34. A. H. Shapiro, “Physiological and medical aspects of flow in collapsible tubes,” in Proc. 6th Canadian Congress of Applied Mechanics (Univ. Br. Columbia, Vancouver, 1977), pp. 883–906.

    Google Scholar 

  35. S. S. Simakov, A. S. Kholodov, and A. V. Evdokimov, “Methods of calculation of global blood flow in a human body involving heterogeneous computation models,” in Medicine in the Mirror of Informatics (Nauka, Moscow, 2008), pp. 124–170 [in Russian].

    Google Scholar 

  36. N. P. Smith, A. J. Pullan, and P. J. Hunter, “An anatomically based model of transient coronary blood flow in the heart,” SIAM J. Appl. Math. 62 (3), 990–1018 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  37. Yu. Vassilevski, S. Simakov, V. Salamatova, Yu. Ivanov, and T. Dobroserdova, “Numerical issues of modelling blood flow in networks of vessels with pathologies,” Russ. J. Numer. Anal. Math. Model. 26 (6), 605–622 (2011).

    MathSciNet  MATH  Google Scholar 

  38. R. J. Whittaker, M. Heil, O. E. Jensen, and S. L. Waters, “Predicting the onset of high-frequency self-excited oscillations in elastic-walled tubes,” Proc. R. Soc. London A 466, 3635–3657 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  39. V. S. Yushutin, “Stability of flow of a nonlinear viscous power-law hardening medium in a deformable channel,” Vestn. Mosk. Univ., Ser. 1: Mat., Mekh., No. 4, 67–70 (2012) [Moscow Univ. Mech. Bull. 67 (4), 99–102 (2012)].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Steklov Mathematical Institute of Russian Academy of Sciences, ul. Gubkina 8, Moscow, 119991, Russia

    V. V. Vedeneev

  2. Institute of Mechanics, Moscow State University, Michurinskii pr. 1, Moscow, 119192, Russia

    A. B. Poroshina

Authors
  1. V. V. Vedeneev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. B. Poroshina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Vedeneev.

Additional information

Original Russian Text © V.V. Vedeneev, A.B. Poroshina, 2018, published in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2018, Vol. 300, pp. 42–64.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vedeneev, V.V., Poroshina, A.B. Stability of an Elastic Tube Conveying a Non-Newtonian Fluid and Having a Locally Weakened Section. Proc. Steklov Inst. Math. 300, 34–55 (2018). https://doi.org/10.1134/S0081543818010030

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543818010030

Search

Navigation