1 INTRODUCTION

Automotive suspension systems are important parts of vehicles and are vital for ride comfort, safety, and handling performance. The basic components of suspension are generally composed of suspension springs, shock absorbers, and guiding mechanisms [1, 2]. Currently, there are three main approaches for improving the performance of suspension, that is, nonlinear passive suspensions, active suspensions, and semi-active suspension [3, 4]. Active suspensions can be seen in premium passenger cars, but their high cost and energy consumption are unavoidable problems. Moreover, the application of magnetorheological dampers (MD) in semi-active suspension faces similar challenges to the active suspension, albeit with slightly lower energy consumption [5]. Suspensions that comprise traditional constant-stiffness springs and shock dampers with no regulating capacity are referred to as passive suspensions and the mass–spring–damper parameters cannot be changed once the suspension has been designed. Nevertheless, passive suspensions are still the type used most widely because of their lower cost, higher reliability, simple structure, and lack of energy consumption. The stiffness of traditional passive linear suspensions is about 20 N/mm because of the limited suspension working space. In order to improve the ride comfort of the vehicle, it is a good choice to reduce the suspension stiffness. Hence, various nonlinear passive vehicle suspensions have been widely developed, including the air spring suspension, the quasi-zero-stiffness (QZS) suspension [6–8], and the inerter-spring-damper (ISD) suspension [9, 10]. However, the air spring suspension faces the problem of lateral stability. The others possess the problem of complex structures, which limited their applications. Thus, the present study of a novel passive suspension is worthwhile, especially in combination with material technology.

Nanoscale porous materials are usually used in heterogeneous catalysis, gas absorption, and sewage treatment. As a member of this class of materials, hydrophobic aerogels are efficient absorbers of substances that are soluble and insoluble in water [11]. New research findings have suggested that mechanical energy can be stored or dissipated by the forced intrusion or extrusion of water into or from hydrophobic nanoporous materials [12, 13]. In vehicle suspensions, the authors of [14] studied its application in car shock-absorbers. However, their application research as a suspension spring is lacking. In particular, the application of ZIF-8 in vehicle suspension has not been reported. A nonlinear vehicle molecular spring suspension based on 2-methylimidazole zinc salt (ZIF-8) which is a kind of hydrophobic nanoporous material can achieve similar nonlinear characteristics to those of air spring suspension and avoid lateral buckling.

The natural frequency of suspension is directly related to its performance indices (body acceleration, suspension working space, dynamic tire load). Therefore, the design and test of natural frequency of vehicle suspension is the main goal of this paper.

First, this paper focuses on the design of a novel nonlinear vehicle molecular spring suspension (hereinafter referred to as VMSS) on the basis of a hydrophobic nanoporous material (ZIF-8). Then, static and dynamic testing of the VMSS is done.

2 STRUCTURAL DESIGN OF VMSS

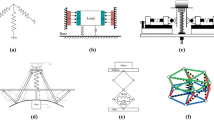
The cross section of VMSS shown in Fig. 1 mainly consists of four main components: a piston rod, a hydraulic fluid chamber, a rubber diaphragm, and a molecular spring chamber. The molecular spring chamber is full of the mixture of water and ZIF8. The hydraulic fluid chamber is filled with oil. The linear bearing is used to reduce friction on the bonding surface between the piston rod and the seal seat.

Fig. 1.
figure 1

A cross-sectional view of the VMSS.

Full size image

3 MECHANICAL MODEL OF VMSS

The VMSS works as follows: as the piston rod moves downwards, the pressure in the two chambers increases. The evolution of the stiffness of the VMSS contains three stages. At the first stage, oil and water are the compressed object. When the pressure is high enough, water molecules will be forced into the ZIF-8 nanopores. At the last stage, oil and water become the compressed object again because of all of the filled nanopores.

At the first stage, the amounts of compression of the two liquids are formulated as:

$$\Delta {{V}_{W}} = {{V}_{w}}{{\eta }_{W}}(P - {{P}_{0}}),$$
(1)
$$\Delta {{V}_{O}} = {{V}_{O}}{{\eta }_{O}}(P - {{P}_{0}}),$$
(2)

where ∆VW and ∆VO are the amounts of compression of the water and oil, respectively. The compressibilities of water and oil are ηW and ηO, respectively; P is the external pressure and P0 is the atmospheric pressure; in reality, P (greater than 20 MPa) is much larger than P0 (0.1 MPa) and thus the latter can be ignored.

Let the vertical displacement of the piston rod be x. Then, the compression can be written as:

$$\Delta {{V}_{W}} + \Delta {{V}_{O}}{\text{ = }}x\left( {\frac{1}{4}\pi {{D}^{2}}} \right),$$
(3)

i.e.,

$$P = x\left( {\frac{1}{4}\pi {{D}^{2}}} \right){\text{/}}({{V}_{w}}{{\eta }_{W}} + {{V}_{o}}{{\eta }_{O}}),$$
(4)

where D is the piston-rod diameter.

The force–displacement relationship (the force is denoted by F and the displacement by x) and its stiffness denoted by K1 in this stage can be written respectively as:

$$F = x{{\left( {\frac{1}{4}\pi {{D}^{2}}} \right)}^{2}}{\text{/}}({{V}_{w}}{{\eta }_{W}} + {{V}_{o}}{{\eta }_{O}}),$$
(5)
$${{K}_{1}} = {{\left( {\frac{1}{4}\pi {{D}^{2}}} \right)}^{2}}{\text{/}}({{V}_{w}}{{\eta }_{W}} + {{V}_{o}}{{\eta }_{O}}).$$
(6)

At the middle stage (namely, the working stage), based on the linearity assumption, the static stiffness (K2) of the VMSS is written as:

$${{K}_{2}} = \frac{F}{{\Delta x}} = \frac{{3.14{{D}^{2}}({{P}_{s}} - {{P}_{i}})}}{{{{V}_{m}}m}},$$
(7)

where the measured porous volume of ZIF-8 is Vm; Pi and Ps are the intrusion pressure (the lowest pressure required for water to invade the ZIF-8 micropores) and the saturation pressure (the pressure required for water to fill all the micropores of ZIF-8), respectively; m is the mass of ZIF-8; Δx is the piston rod displacement at the working stage.

The principle of the stiffness in the last stage is the same as that in the first stage, so its stiffness model is omitted.

Hence, the calculation formula of the stiffness in each stage, which can be used to design the stiffness, can be deduced by Section 3.

4 THE EXPERIMENTAL PLATFORM OF VMSS

The test system of the VMSS for quasi-static loading is shown in Fig. 2. Its mechanical characteristics were tested by an electrohydraulic servo fatigue machine. The force sensor is used to measure the force. The displacement is recorded by the actuator. The quasi-static test procedure is as follows. First, according to GB/T 15168-2013 (a Chinese national standard), the downward velocity of the actuator is set to 5 mm/min. Then, the VMSS are preloaded. Finally, the stable static force displacement relationship can be measured after reloading.

Fig. 2.
figure 2

Quasi-static loading test.

Full size image

As can be seen from Fig. 3, in contrast with the control group (shown as the red line), the VMSS exhibits obvious nonlinear force displacement characteristics. Meanwhile, the agreement between the experimental curves (the blue line under loading procedure as indicated by the green arrow) and the theoretical force-displacement curve (the black line) is clearly shown in this figure. Thus, the correctness of the theoretical model is proved. Point A and point B are the turning points which depend on the intrusion pressure Pi and the saturation pressure Ps, respectively. Point C indicates the payload of the VMSS.

Fig. 3.
figure 3

Comparison of experimental and theoretical force-displacement curves (the dotted lines are guides for the eyes). Point A and point B are the turning points which depend on the intrusion pressure Pi and the saturation pressure Ps, respectively. Point C indicates the payload of the VMSS.

Full size image

The intrusion pressure Pi of ZIF-8 can be deduced by the Laplace capillary principle [15]. Apparently, the loading curve indicated by the green arrow and the unloading curve indicated by the magenta arrow do not coincide. In other words, the VMSS system has hysteresis.

Researches show that if confined in a sufficiently narrow hydrophobic nanopore, water can spontaneously evaporate [16]. The energy absorption capacity of confined water-ZIF systems at elevated strain rates is reported [17]. The authors in [18] proposed two mechanisms for energy dissipation. One is that some of the liquid cannot escape the material micropores. The other is the difficulty in gas-phase nucleation. Chemical modifications of the structure of the host material are expected to be related with the amount of hysteresis present [19]. Besides, obvious electrification effects upon reversible cycle of forced water intrusion-extrusion in nanoporous hydrophobic materials is proved by experimental evidence [20]. Obviously, the hysteresis in this paper can be explained by above researches according to the test results. Since the hysteresis is caused by the energy converted into other forms rather than the loss of water during cyclic process, the suspension can return to its start position. Air springs can help to understand this process. Although hysteresis can be also found in its loading and unloading, air springs can return to its start position (because the dissipated energy is converted into the internal energy of the rubber of the air suspension rather than a leak of air).

Therefore, further experimental tests are necessary to get a more accurate restoring force. A dynamic restoring force can predict its natural frequency more accurately for a hysteresis system. The test method of the dynamic restoring force of the VMSS is introduced as follows. First, according to the above standard, the VMSS need to be pressed to the payload position (point C) shown in Fig. 3. Second, set the input of the actuator as a constant frequency (2 Hz) sine signal. Third, set the sine amplitude to 1 mm. Then, record the maximum value of the force. Finally, change the amplitude (the amplitude range of 1−6 mm, interval of 1 mm) and repeat. The force value collected at each amplitude is represented by a red circle as shown in Fig. 4. From the figure, the difference between the dynamic restoring force and the static restoring force is clearly revealed. Assume that the stiffness at this stage is linear (as the two dotted lines shown in Fig. 4). The natural frequency calculated by the static and dynamic restoring forces is about 3.11 and 2.3 Hz, respectively.

Fig. 4.
figure 4

The difference between the dynamic and static restoring forces (2 g ZIF-8).

Full size image

Experimental results show that the frequency less than 12 Hz makes little difference to the dynamic restoring force. Thus, the paper only exhibits the results at 2 Hz.

As a suspension spring, its natural frequency is an important index. The natural frequency of front suspension of passenger cars is usually less than 1.5 Hz.

For convenience, the paper just studied the natural frequency when the amplitude of the VMSS does not exceed the middle stage.

In order to obtain the natural frequency of the VMSS, a vibration isolation test system was built and tested. The experimental system consists of a vibration exciter, a payload, the VMSS, a power amplifier, and a dynamic signal analyzer HP35670A, as shown in Fig. 5.

Fig. 5.
figure 5

Dynamic test system.

Full size image

The natural frequency of the VMSS in the test is shown in Fig. 6. The red line is the frequency response curve of the control group whose molecular spring chamber is full of water. The rest are the frequency response curves of the VMSS with different masses of ZIF-8. In comparison with the control group, the natural frequency of the VMSS (12 g ZIF-8) decreased from 4.30 to 1.06 Hz. Besides, the natural frequency of the VMSS with 2 g ZIF-8 is closer to the value calculated by the dynamic restoring force whose molecular spring chamber is filled with the same mass of ZIF-8 shown in Fig. 4.

Fig. 6.
figure 6

The natural frequency of the control group and the VMSS with different masses of ZIF-8.

Full size image

In comparison with two kinds of linear vehicle suspensions shown in Fig. 7, advantages of the VMSS is obvious. The VMSS with 6g ZIF-8 is chosen to contrast with linear suspensions to show the difference more clearly. Compared to the linear suspension 1 (shown by the black line) under the same sprung mass, the VMSS’s stiffness in the middle stage is lower than the stiffness of the suspension 1 when static displacement (40 mm) of the linear suspension 1 is equal to the VMSS’s one. Their stiffnesses are indicated by the slope of the blue line in middle stage and the black line. The lower stiffness is conducive to improve ride comfort. Compared to the suspension 2 under the same sprung mass, static displacement (40 mm) of the VMSS is shorter than the latter’s (90 mm) when the VMSS’s stiffness in the middle stage is equal to the stiffness of the suspension 2. In the limited installation space, especially for a multi-link front suspension, the shorter static displacement means the VMSS will be a better choice. In conclusion, the VMSS, as a novel nonlinear suspension which can behave like an air spring suspension, has advantages over traditional linear suspensions.

Fig. 7.
figure 7

Comparison of force-displacement curves with linear suspensions.

Full size image

5 CONCLUSIONS AND OUTLOOK

This paper has reported a passive nonlinear vehicle suspension based on ZIF-8. Mechanical energy can be stored or dissipated by the forced intrusion or extrusion of water into or from ZIF-8. Force displacement curves were verified in a quasi-static loading test. Then, the natural frequency of the VMSS is obtained by a vibration isolation test system. The test results show that the stiffness and the natural frequency of the VMSS can be as low as 13 N/mm (linear suspension is generally 20 N/mm) and 1.06 Hz, respectively. Suspension working space of the VMSS is about 20 mm when the mass of ZIF-8 is 6 g. However, its suspension working space can be easily adjusted by changing the mass of ZIF-8. The increase of suspension working space is beneficial to the work of suspension. As a new type of suspension, the VMSS resolves the contradiction between vibration bandwidth and static deflection. As a passive nonlinear suspension, he VMSS has a range of advantages over existing technologies: (i) the VMSS resolves the contradiction between vibration bandwidth and static deflection, which cannot be solved by linear suspensions; (ii) compared to air springs and spiral springs, lateral stability of the VMSS is outstandingly excellent. Thus, the new idea of ZIF-8 used to vehicle suspension design is worth of further study.