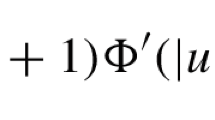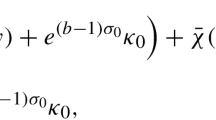Abstract
We consider a special boundary value problem for a nonlinear parabolic system proposed by J. Murray and used to describe population dynamics. The boundary conditions of the problem assume that the possible solutions have a zero front—a line on which the desired functions vanish and the parabolic type of the system degenerates. A particular case of such solutions to single degenerate equations is nonlinear heat (filtration, diffusion) waves considered by Ya.B. Zeldovich, G.I. Barenblatt, and A.A. Samarskii. In the present paper, we prove an existence and uniqueness theorem for a nontrivial analytical solution to the problem under study. In the course of the proof, a solution is constructed in the form of Taylor series, and recurrence coefficient formulas are written that can later be used to verify numerical calculations. Some exact solutions of the system with zero front are presented. Separately, examples are considered that illustrate the behavior of the solution when deviating from the conditions in the theorem. The first example shows the possibility of existence of solutions of the original system with two distinct zero fronts. The second example is an analog of the well-known counterexample by S.V. Kovalevskaya in the considered case.
Similar content being viewed by others
REFERENCES
Ladyzenskaja, O.A., Solonnikov, V.A., and Ural’ceva, N.N., Linear and Quasi-Linear Equations of Parabolic Type, vol. 23 of Translations of Mathematical Monographs, Providence: Am. Math. Soc., 1988.
Samarskii, A.A., Galaktionov, V.A., Kurdyumov, S.P., and Mikhailov, A.P., Blow-up in Quasilinear Parabolic Equations, Berlin–New-York: Walter de Gruyter, 1995.
Vazquez, J.L., The Porous Medium Equation: Mathematical Theory, Oxford: Clarendon, 2007.
Cuesta, C.M. and Pop, I.S., Numerical schemes for a pseudo-parabolic Burgers equation: discontinuous data and long-time behaviour, J. Comput. Appl. Math., 2009, vol. 224, pp. 269–283.
Perthame, B., Parabolic Equations in Biology. Growth, Reaction, Movement and Diffusion, New York: Springer, 2015.
Achouri, T., Ayadi, M., Habbal, A., and Yahyaoui, B., Numerical analysis for the two-dimensional Fisher–Kolmogorov–Petrovski–Piskunov equation with mixed boundary condition, J. Appl. Math. Comput., 2021, no. 1, pp. 1–26.
DiBenedetto, E., Degenerate Parabolic Equations, New York: Springer-Verlag, 1993.
Zel’dovich, Ya.B. and Raizer, Yu.P., Physics of Shock Waves and High Temperature Hydrodynamics Phenomena, New York: Dover, 2002.
Barenblatt, G.I., Entov, V.N., and Ryzhik, V.M., Dvizhenie zhidkostei i gazov v prirodnykh plastakh (Movement of Fluids and Gases in Natural Layers), Moscow: Nedra, 1984.
Polyanin, A.D. and Zaitsev, V.F., Handbook of Nonlinear Partial Differential Equations, Boca Raton–London–New York: Chapman & Hall/CRC Press, 2011.
Sidorov, A.F., Izbrannye trudy. Matematika. Mekhanika (Selected Works. Mathematics. Mechanics), Moscow: Fizmatlit, 2001.
Kazakov, A.L., Generalized Cauchy problem with data on two and three surfaces for a quasilinear system with singularities in the coefficients multiplying the derivatives, Differ. Equations, 2012, vol. 48, no. 4, pp. 538–551.
Filimonov, M.Yu., Korzunin, L.G., and Sidorov, A.F., Approximate methods for solving nonlinear initial boundary–value problems based on special construction of series, Russ. J. Numer. Anal. Math. Model., 1993, vol. 8. N.. 2, pp. 101–125.
Filimonov, M.Yu., Application of the special series method to the construction of new classes of solutions of nonlinear partial differential equations, Differ. Equations, 2003, vol. 39, no. 6, pp. 844–852.
Kazakov, A.L. and Lempert, A.A., Analytical and numerical study of a boundary value problem of nonlinear filtration with degeneration, Vychisl. Tekhnol., 2012, vol. 17, no. 1, pp. 57–68.
Kazakov, A.L., Kuznetsov, P.A., and Lempert, A.A., Analytical solutions to the singular problem for a system of nonlinear parabolic equations of the reaction–diffusion type, Symmetry, 2020, vol. 12, no. 6, p. 999.
Kazakov, A.L., Orlov, Sv.S., and Orlov, S.S., Construction and study of exact solutions to a nonlinear heat equation, Sib. Math. J., 2018, vol. 59, no. 3, pp. 427–441.
Kazakov, A.L., On exact solutions of the boundary value problem on the motion of a heat wave for the equation of nonlinear heat conduction, Sib. Elektron. Mat. Izv., 2019, vol. 16, pp. 1057–1068.
Kazakov, A.L., Kuznetsov, P.A., and Spevak, L.F., On a boundary value problem with degeneration for a nonlinear heat equation in spherical coordinates, Tr. Inst. Mat. Mekh. UrO RAN, 2014, vol. 20, no. 1, pp. 119–129.
Kazakov, A.L. and Kuznetsov, P.A., On the analytic solutions of a special boundary value problem for a nonlinear heat equation in polar coordinates, J. Appl. Ind. Math., 2018, vol. 21, no. 2, pp. 255–263.
Kudryashov, N.A. and Sinel’shchikov, D.I., Analytical solutions to the nonlinear convection–diffusion equation with nonlinear sources, Model. Anal. Inf. Sist., 2016, vol. 23, no. 3, pp. 309–316.
Polyanin, A.D. and Sorokin, V.G., Reductions and exact solutions of Lotka–Volterra and more complex reaction–diffusion systems with delays, Appl. Math. Lett., 2022, vol. 125, p. 107731.
Kazakov, A.L., Nefedova, O.A., and Spevak, L.F., Solution of the problem of initiating the heat wave for a nonlinear heat conduction equation using the boundary element method, Comput. Math. Math. Phys., 2019, vol. 59, no. 6, pp. 1015–1029.
Kazakov, A.L., Kuznetsov, P.A., and Spevak, L.F., Construction of solutions to a boundary value problem with singularity for a nonlinear parabolic system, J. Appl. Ind. Math., 2021, vol. 15, no. 4, pp. 616–626.
Kuznetsov, P.A., Analytical diffusion waves in a nonlinear parabolic “predator–prey” model, Tr. Inst. Mat. Mekh. UrO RAN, 2022, vol. 28, no. 2, pp. 158–167.
Murray, J.D., Mathematical Biology II: Spatial Models and Biomedical Applications. Interdisciplinary Applied Mathematics. Vol. 18 , New York: Springer, 2003.
Arnold, V.I., Ordinary Differential Equations, Berlin: Springer-Verlag, 1992.
Kozlov, V.V., Sofya Kovalevskaya: a mathematician and a person, Russ. Math. Surv., 2000, vol. 55, no. 6, pp. 1175–1192.
Funding
This work was financially supported by the Ministry of Science and Higher Education of the Russian Federation, project “Analytical and Numerical Methods of Mathematical Physics in Problems of Tomography, Quantum Field Theory, and Fluid and Gas Mechanics,” no. 121041300058-1.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by V. Potapchouck
Rights and permissions
About this article
Cite this article
Kazakov, A.L., Kuznetsov, P.A. Analytical Solutions with Zero Front to the Nonlinear Degenerate Parabolic System. Diff Equat 58, 1457–1467 (2022). https://doi.org/10.1134/S00122661220110039
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S00122661220110039