Skip to main content
SpringerLink
Log in

Various Manifestations of Wood Anomalies in Locally Distorted Quantum Waveguides

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

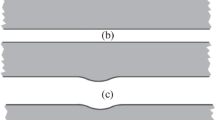
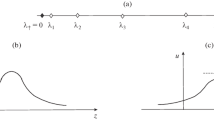
Anomalies of the diffraction pattern at near-threshold frequencies of the continuous spectrum of a cylindrical quantum waveguide with regular (smooth gentle) or singular (small cavities and bumps) perturbations of the boundary are studied. Wood anomalies are characterized by rapid variations in the scattering matrix near the thresholds. Conditions under which a Wood anomaly is absent, appears, and enhances are obtained by constructing asymptotics of solutions to the Dirichlet problem for the Helmholtz equation. The results are obtained by analyzing an artificial object—the augmented scattering matrix—and involve only operations with real values of the spectral parameter, but the relation between Wood anomalies and complex resonance points is also considered. Generated by almost standing waves, threshold resonances that cause near-threshold anomalies of other types are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. C. H. Wilcox, Scattering Theory for Diffraction Gratings (Springer, Singapore, 1997).

    MATH  Google Scholar 

  2. S. A. Nazarov and B. A. Plamenevsky, Elliptic Problems in Domains with Piecewise Smooth Boundaries (Walter de Gruyter, Berlin, 1994).

    Book  MATH  Google Scholar 

  3. R. Wood, “On the remarkable case of uneven distribution of light in a diffraction grating spectrum,” Proc. Phys. Soc. London 18, 269–275 (1902).

    Article  Google Scholar 

  4. I. V. Kamotskii and S. A. Nazarov, “The augmented scattering matrix and exponentially decaying solutions of an elliptic problem in a cylindrical domain,” J. Math. Sci. (New York) 111, 3657–3666 (2002).

    Article  MathSciNet  Google Scholar 

  5. S. A. Nazarov, “Asymptotic expansions of eigenvalues in the continuous spectrum of a regularly perturbed quantum waveguide,” Theor. Math. Phys. 167 (2), 606–627 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  6. L. A. Vainshtein, Diffraction Theory and Factorization Method (Sovetskoe Radio, Moscow, 1966) [in Russian].

    Google Scholar 

  7. S. A. Nazarov, “Scattering anomalies in a resonator above the thresholds of the continuous spectrum,” Sb. Math. 206 (6), 782–813 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  8. A. I. Korolkov, S. A. Nazarov, and A. V. Shanin, “Stabilizing solutions at thresholds of the continuous spectrum and anomalous transmission of waves,” Z. Angew. Math. Mech. 96 (10), 1245–1260 (2016).

    Article  MathSciNet  Google Scholar 

  9. W. Bulla, F. Gesztesy, W. Renrer, and B. Simon, “Weakly coupled bound states in quantum waveguides,” Proc. Am. Math. Soc. 125 (8), 1487–1495 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  10. R. R. Gadyl’shin, “Local perturbations of quantum waveguides,” Theor. Math. Phys. 145, 1678–1690 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  11. V. V. Grushin, “On the eigenvalues of finitely perturbed Laplace operators in infinite cylindrical domains,” Math. Notes 75, 331–340 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  12. S. A. Nazarov, “Variational and asymptotic methods for finding eigenvalues below the continuous spectrum threshold,” Sib. Math. J. 51 (5), 866–878 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  13. S. A. Nazarov, “Enforced stability of an eigenvalue in the continuous spectrum of a waveguide with an obstacle,” Comput. Math. Math. Phys. 52 (3), 448–464 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  14. S. A. Nazarov, “Enforced stability of a simple eigenvalue in the continuous spectrum of a waveguide,” J. Funct. Anal. 47, 195–209 (2013).

    Article  MATH  Google Scholar 

  15. S. A. Nazarov, “Localized elastic fields in periodic waveguides with defects,” J. Appl. Mech. Tech. Phys. 52, 311 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  16. S. A. Nazarov, “Nonreflection and trapping of elastic waves in a slightly curved isotropic strip,” Phys. Dokl. 59 (3), 139–143 (2014).

    Article  Google Scholar 

  17. S. A. Nazarov, “Near-threshold effects of the scattering of waves in a distorted elastic two-dimensional waveguide,” J. Appl. Math. Mech. 79 (4), 374–387 (2015).

    Article  MathSciNet  Google Scholar 

  18. L. I. Mandelstam, Lectures on Optics, Relativity Theory, and Quantum Mechanics (Akad. Nauk SSSR, Moscow, 1947), Vol. 2 [in Russian].

    Google Scholar 

  19. I. I. Vorovich and V. A. Babeshko, Mixed Dynamic Problems of Elasticity Theory for Nonclassical Domains (Nauka, Moscow, 1979) [in Russian].

    MATH  Google Scholar 

  20. S. A. Nazarov, “Umov–Mandelstam radiation conditions in elastic periodic waveguides,” Sb. Math. 205 (7), 953–982 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  21. N. A. Umov, Equations of Energy Transfer in Bodies (Tipogr. Ul’rikha i Shul’tse, Odessa, 1874) [in Russian].

    Google Scholar 

  22. J. H. Poynting, “On the transfer of energy in the electromagnetic field,” Phil. Trans. R. Soc. London 175, 343–361 (1884).

    Article  MATH  Google Scholar 

  23. V. A. Kozlov, S. A. Nazarov, and A. Orlof, “Trapped modes supported by localized potentials in the zigzag graphene ribbon,” C. R. Acad. Sci. Paris Ser. 1 354 (1), 63–67 (2016).

    Article  MATH  Google Scholar 

  24. M. D. Van Dyke, Perturbation Methods in Fluid Mechanics (Academic, New York, 1964).

    MATH  Google Scholar 

  25. A. M. Il’in, Matching of Asymptotic Expansions of Solutions of Boundary Value Problems (Nauka, Moscow, 1989; Am. Math. Soc., RI, Providence, 1992).

  26. M. I. Vishik and L. A. Ljusternik, “Regular degeneration and boundary layer for linear differential equations with small parameter,” Am. Math. Soc. Transl. 20 (2), 239–364 (1962).

    MathSciNet  Google Scholar 

  27. W. G. Mazja, S. A. Nasarow, and B. A. Plamenewski, Asymptotische Theorie elliptischer Randwertaufgaben in singulär gestörten Gebieten (Akademie-Verlag, Berlin, 1991), Vol. 1 (English translation: V. Maz’ya, S. Nazarov, and B. Plamenevsky, Asymptotic Theory of Elliptic Boundary Value Problems in Singularly Perturbed Domains (Birkhäuser, Basel, 2000), Vol. 1).

    Google Scholar 

  28. V. A. Kondrat’ev, “Boundary value problems for elliptic equations in domains with conical or corner points,” Tr. Mosk. Mat. O–va 16, 219–292 (1963).

    Google Scholar 

  29. V. G. Maz’ya and B. A. Plamenevskii, “On the coefficients in asymptotics of solutions of elliptic boundary value problems in domains with conical points,” Math. Nachr. 76, 29–60 (1977).

    Article  MathSciNet  Google Scholar 

  30. S. A. Nazarov, “Properties of spectra of boundary value problems in cylindrical and quasicylindrical domain,” in Sobolev Spaces in Mathematics, Vol. 2, Ed. by V. Maz’ya, International Mathematical Series (Springer, New York, 2008), Vol. 9, pp. 261–309.

    Google Scholar 

  31. T. Kato, Perturbation Theory for Linear Operators (Springer-Verlag, Berlin, 1966).

    Book  MATH  Google Scholar 

  32. G. Polya and G. Szego, Isoperimetric Inequalities in Mathematical Physics (Periodical Service, 1957).

    MATH  Google Scholar 

  33. L. Guilopé, “Théorie spctrale de quelques varietés à bouts,” Ann. Sci. Ecole Norm. Sup. 22 (4), 137–160 (1989).

    Article  Google Scholar 

  34. A. Aslanyan, L. Parnovski, and D. Vassiliev, “Complex resonances in acoustic waveguides,” Q. J. Mech. Appl. Math. 53, 429–447 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  35. S. Molchanov and B. Vainberg, “Scattering solutions in networks of thin fibers: Small diameter asymptotics,” Commun. Math. Phys. 273 (2), 533–559 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  36. D. Grieser, “Spectra of graph neighborhoods and scattering,” Proc. London Math. Soc. 97 (3), 718–752 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  37. K. Pankrashkin, “Eigenvalue inequalities and absence of threshold resonances for waveguide junctions,” J. Math. Anal. Appl. 449 (1), 907–925 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  38. S. A. Nazarov, “Almost standing waves in a periodic waveguide with a resonator and near-threshold eigenvalues,” St. Petersburg Math. J. 28 (3), 377–410 (2017).

    Article  MathSciNet  MATH  Google Scholar 

Download references

ACKNOWLEDGMENTS

This work was supported by the Russian Science Foundation, project no. 17-11-01003.

Author information

Authors and Affiliations

  1. St. Petersburg State University, 198504 , St. Petersburg, Russia

    S. A. Nazarov

  2. Institute of Problems of Mechanical Engineering, Russian Academy of Sciences, 199178, St. Petersburg, Russia

    S. A. Nazarov

Authors
  1. S. A. Nazarov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. Nazarov.

Additional information

Translated by I. Ruzanova

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nazarov, S.A. Various Manifestations of Wood Anomalies in Locally Distorted Quantum Waveguides. Comput. Math. and Math. Phys. 58, 1838–1855 (2018). https://doi.org/10.1134/S096554251811009X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S096554251811009X

Keywords:

Search

Navigation