Abstract
We study a central bank intervention (CBI) problem in the foreign exchange market when the exchange rate follows a jump-diffusion process and show that the optimal CBI policy is a control-band policy. Our main contribution is a rigorous proof of the existence and uniqueness of the optimal CBI policy.
Similar content being viewed by others
Notes
The number of domestic currency units per unit of foreign currency.
An impulse control is a double sequence
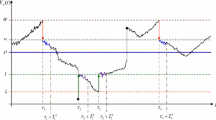
$$\nu = (\tau _{1},\tau _{2},\ldots ,\tau _{j},\ldots ;\zeta _{1},\zeta _{2},\ldots ,\zeta _{j},\ldots ),$$where \(\tau _{1}<\tau _{2}<\cdots \) are \({\mathcal {F}}_{t}\)-stopping times (the intervention times) and \(\zeta _{1},\zeta _{2},\ldots \) are the corresponding impulses at these times such that each \(\zeta _{j}\) is \({\mathcal {F}}_{\tau _{j}}\)-measurable.
For the sake of completeness, we have shown the optimality of \(\{\hat{x},\bar{x}\}\) -policy in this section. However, it should be noted that this result is clearly subsumed in the general framework of Øksendal and Sulem (2007).
References
Avesani R and Gallo G (1991). Jumping in the Band: Undeclared Intervention Thresholds in a Target Zone. Working paper, Economics Department, University of Torento.
Baccarin S (2009). Optimal impulse control for a multidimensional cash management system with generalized cost functions. European Journal of Operational Research 196:198–206.
Bekaert G and Gray S (1998). Target zones and exchange rates: An empirical investigation. Journal of International Economics 45:1–35.
Benkherouf L and Bensoussan A (2009). Optimality of an (s,S) policy with compound poisson and diffusion demands: A quasi-variational inequalities approach. SIAM Journal on Control and Optimization 48(2):756–762.
Bensoussan A and Lions JL (1984). Impulse Control and Quasi-Variational Inequalities. Gauhiers-Villars: Paris.
Bensoussan A, Long H, Perera S and Sethi S (2012). Impulse control with random reaction periods: A central bank intervention problem. Operations Research Letters 40(6):425–430.
Bertola G (1994). Continuous-time models of exchange rate and intervention. In: van der Ploeg F (ed). Handbook of International Macroeconomics. Basil Blackwell: London.
Bertola G and Caballero R (1992). Target zones and realignments. The American Economic Review 82(3):520–536.
Brekke KA and Øksendal B (1997). A verification theorem for combined stochastic control and impulse control. In: Decreasefond L et al (eds). Stochastic Analysis and Related Topics, Vol. 6, Springer Birkhauser: Geilo, Oslo.
Cadenillas A, Lakner P and Pinedo M (2010). Optimal control of a mean-reverting inventory. Operations Research 58(6):1697–1710.
Cadenillas A and Zapatero F (1999). Optimal central bank intervention in the foreign exchange market. Journal of Economic Theory 87(1):218–242.
Dominguez K and Frankel J (1993). Does Foreign Exchange Intervention Work? Institute for International Economics: Washington, DC.
Flood R and Garber P (1991). The linkage between speculative attack and target zone models of exchange rates. Quarterly Journal of Economics 106(4):1367–1372.
Froot KA and Obstfeld M (1991). Exchange rate dynamics under stochastic regime shifts: A unified approach. Journal of International Economics 31(3):203–230.
Garber PM and Svensson L (1996). The operation and collapse of fixed exchange rate regime. In: Rogoff K and Grossman G (eds). Handbook of International Economics. North-Holland: Amsterdam.
Jeanblanc-Picqué M (1993). Impulse control method and exchange rate. Mathematical Finance 3(2):161–177.
Jorion P (1988). On jump processes in the foreign exchange and stock markets. Review of Financial Studies 1(4):427–445.
Korn R (1997). Optimal impulse control when control actions have random consequences. Mathematics of Operations Research 22(3):639–667.
Korn R (1999). Some applications of impulse control in mathematical finance. Mathematical Methods of Operations Research 50(3):493–518.
Krugman P (1987). Trigger Strategies and Price Dynamics in Equity and Foreign Exchange Markets. NBER working paper # 2459.
Krugman P (1991). Target zones and exchange rate dynamics. Quarterly Journal of Economics 106(3):669–682.
Øksendal B and Sulem A (2007). Applied Stochastic Control of Jump Diffusions. Springer: Berlin.
Lumley R and Zervos M (2001). A model for investments in the natural resource industry with switching costs. Mathematics of Operations Research 26(4):637–653.
Miller M and Weller P (1991). Currency bands, target zones and price flexibility. IMF Economic Review 38(1):184–215.
Mundaca G and Øksendal B (1998). Optimal stochastic intervention control with application to the exchange rate. Journal Mathematical Economics 29(2):225–243.
Ohnishi M and Tsujimura M (2006). An impulse control of a geometric Brownian motion with quadratic costs. European Journal of Operational Research 168(2):311–321.
Perera S, Buckley W and Long H (2016). Market-reaction-adjusted optimal central bank intervention policy in a forex market with jumps. Annals of Operations Research. doi:10.1007/s10479-016-2297-y.
Presman E and Sethi SP (2006). Inventory models with continuous and poisson demands and discounted and average costs. Production and Operations Management 15(2):279–293.
Svensson L (1991). The term structure of interest rate differentials in a target zone. Journal of Monetary Economics 28(1):87–116.
Yao D, Yang H and Wang R (2011). Optimal dividend and capital injection problem in the dual model with proportional and fixed transaction costs. European Journal of Operational Research 211(3):568–576.
Acknowledgements
The authors thank the editors, Tom Archibald and Jonathan Crook, and the anonymous associate editor for their contribution. Moreover, we are grateful to the reviewer for his/her thoughtful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendix: Further generalization of the problem
Appendix: Further generalization of the problem
In our original problem in Section 2, we are only allowed to give impulses \(\zeta \) with values in \({\mathcal {Z}}:=(0,\infty )\). However, in some applications, we may also have to bring the exchange rate upward by applying impulses with negative values. Therefore, we now assume that we are allowed to give impulses \(\zeta \) with values in \({\mathcal {Z}}:=(-\infty ,\infty )\). Again, if we apply an impulse control \(\nu = (\tau _{1},\tau _{2},\ldots ,\tau _{j},\ldots ;\zeta _{1},\zeta _{2},\ldots ,\zeta _{j},\ldots )\) to \(X_{x}(t)\), the resulting intervened process \(X_{x}^{(\nu )}(t)\) can be defined by \(X_{x}^{(\nu )}(t)=X_{x}(t)+\sum _{\tau _{k} \le t} \zeta _{k}\). The cost of intervention in this case is defined by \(K(\zeta )=C+\lambda |\zeta |\). Then, the expected total discounted cost associated with the given impulse control is
We again seek \(\varPhi ^{*}(x)\) and \(\nu ^{*}= (\tau _{1}^{*},\ldots ,\tau _{j}^{*},\ldots ;\zeta _{1}^{*},\ldots ,\zeta _{j}^{*},\ldots )\) such that
Here, we assume that the corresponding Lévy measure \(\eta \) is symmetric, i.e., \(\eta (H)=\eta (-H)\) for all \(H\subset {\mathbb {R}}\setminus \{0\}\). By symmetry, we expect the continuation region to be of the form \({\mathbb {C}}=(-\bar{x},\bar{x})\), for some \(\bar{x}>0\) to be determined. As soon as \(X_{x}(t)\) reaches level \(\bar{x}\) (or \(-\bar{x}\)), there is an intervention and \(X_{x}(t)\) is brought down (or up) to a certain value \(\hat{x}\) (or \(-\hat{x}\)) where \(-\bar{x}<-\hat{x}<0<\hat{x}<\bar{x}\). We determine \(\bar{x}\) and \(\hat{x}\) in the following way.
In the continuation region \({\mathbb {C}}\), we have \(A\varPhi +f=0\). Therefore we have
Here, we try a solution of the form
where C is a constant (to be determined), \(b=\sigma ^{2}+\int _{{\mathbb {R}}}\theta ^{2} z^{2} \nu (\hbox {d}z)\), and \(\alpha >0\) is the positive solution of the equation \(F(\alpha )=-r+\mu r+\frac{\sigma ^{2}}{2}\alpha ^{2}+\int _{{\mathbb {R}}}\{\hbox {e}^{\alpha \theta z}-1-\alpha \theta z \}\nu (\hbox {d}z)\). Note that if we make no intervention at all, then the cost is
By the definition of \(\varPhi (x)\), we have \(0 \le \varPhi (x) \le \phi (x)\) for all \(-\bar{x}\le x \le \bar{x}\). Then, we get
for all \(-\bar{x}\le x\le \bar{x}\). From the right-hand side of the above inequality, we get \(C \cosh (\alpha x)\le 0\) for all \(-\bar{x}\le x\le \bar{x}\). Hence, \(C<0\). We now let \(C=-a\), where \(a>0\), and define
and let \(\varPhi (x):=\varPhi _{0} (x)\) for \(x\in {\mathbb {C}}\). The intervention operator in this case is
The first-order condition for a minimum \(\hat{\zeta }=\hat{\zeta }(x)\) of the function
is the following
Therefore, we look for points \(\hat{x}\) and \(\bar{x}\) such that \(0<-\bar{x}<-\hat{x}<0<\hat{x}<\bar{x}\), \(\varPhi '(-\hat{x})=-\lambda \) and \(\varPhi '(\hat{x})=\lambda \). Note that, since \(\hat{x}<\bar{x}\) and \(-\hat{x}>-\bar{x}\), \(\varPhi '(\hat{x})=\varPhi '_{0}(\hat{x})\) and \(\varPhi '(-\hat{x})=\varPhi '_{0}(-\hat{x})\). We also have that, if \(\zeta >0\), then \(x+\hat{\zeta }=-\hat{x}\) or \(\hat{\zeta }=-\hat{x}-x=-(\hat{x}+x)\) and if \(\zeta <0\), then \(x+\hat{\zeta }=\hat{x}\) or \(\hat{\zeta }=\hat{x}-x\).
For \(x > \bar{x}\) or \(x < -\bar{x}\), we have \(\varPhi (x)={\mathcal {M}}\varPhi (x)\) since \(x\notin {\mathbb {C}}\). Therefore, if \(\zeta >0\) (i.e., \(x<-\bar{x}\)), then
Equivalently, we have
Similarly, if \(\zeta <0\) (i.e., \(x>\bar{x}\)), then
Equivalently, we have
Consequently, we have
Differentiability at \(x=\bar{x}\) gives the equation \(\varPhi '_{0}(\bar{x})=\lambda \). Thus, we have
We also have that \(\varPhi '(\hat{x})=\lambda \). That is \(\varPhi '_{0}(\hat{x})=\lambda \). Equivalently, we have
Continuity at \(x=\bar{x}\) gives the equation
Substituting for \(\varPhi _{0}\) in the above equation, we get
Then, we have
Again, the solution to the CBI problem is uniquely determined by the system (15)–(17). We can prove the existence and uniqueness of the solution in this case by using a similar approach to Section 3.
Rights and permissions
About this article
Cite this article
Perera, S., Buckley, W. On the existence and uniqueness of the optimal central bank intervention policy in a forex market with jumps. J Oper Res Soc 68, 877–885 (2017). https://doi.org/10.1057/s41274-017-0208-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s41274-017-0208-5