1 Introduction

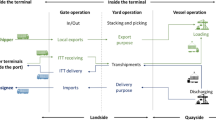
In general, intermodal freight transportation is referred to as moving goods or products by the usage of containers from shippers to consignees by different types of transportation modes, such as vessels, trains and trucks. In accordance with the International Standard Organization (ISO) specification, containers are classified into standard sizes in which 20- and 40-ft ones are the most commonly used and most truck chassis are designed to carry them. Cheung et al (2008) referred to the inland container transportation as the operation of moving loaded and empty containers amongst terminals, rail hubs, customers and depots, which is also called drayage as defined by Harrison et al (2008).

Under the influence of global integration, container transportation has grown impressively around the world during the last decades. As the major means used for last-mile delivery of containers, truck transportation as a result becomes more complex and difficult to manage. Although inland delivery covers very short distance in the entire container transportation, it is not as economical. Macharis and Bontekoning (2004) reported that about 25–40% of the total transportation cost is accumulated in drayage, which is then raised by Notteboom and Rodrigue (2005) to as high as 40–80%. This significant cost illustrates on the importance of optimizing the inland delivery routes, especially with a focus on reducing the unproductive routes to relocate empty containers. Inefficient usage of trucks not only yields higher delivery cost and emission, but also brings pressure on the operations of the port and introduces unnecessary traffic. In order to reduce unnecessary traffic flow, most works in the field attempt to combine pickup and delivery trips together to reduce empty movements of containers (Braekers et al, 2013). These studies are then extended to the cases that further merge the route with inland deliveries (Fazi, 2014) and/or consider the usage of dual-carriage trucks (Sterzik et al, 2015). No matter what specific context is considered, almost all previous studies base their discussions around the general mixed integer programming (MIP) model for the vehicle routing problem with simultaneous pickups and deliveries and time windows (VRP-SPDTW), which is originally designed in generic vehicle routing literature (Nossack and Pesch, 2013). The optimal decision tells which link should be travelled by which truck. This makes perfect sense in case that a number of individual trips are combinable to form a single delivery/pickup route, but not as necessary for container delivery since the latter normally just allows the combination of no more than two (import only) or four (import and export) trips in one return route due to the capacity of vehicle (dual carriage). On the other hand, as in the VRP-SPDTW model, one has to start from transforming the demand graph into one with a distinct node for every single task, and the number of nodes and links is largely increased which improves the difficulty of solving the problem and therefore makes the solution only available via heuristics.

In comparison, Vidović et al (2012) proposed an alternative way which formulates the trip combination problem as a multiple assignment model. This formula tries to merge customer requests (import and export) together to form full delivery routes, and the optimal decision directly shows which container should be paired with which other for transportation. Since the number of containers to combine is no more than two if the truck can carry only one container at a time or four if dual carriage, the decision variable is at most 4 dimensional in its index. Based on the observation of the authors, the multiple assignment model can be solved efficiently by commercial software for instances having 63 containers which is much larger than 19 with the VRP-SPDTW model. Our study furthers this idea by including more realistic restrictions on the general practice, such as the working restriction for drivers, the ready time of containers at and/or the expected departure from the port and, more importantly, containers with multiple customer locations as its receivers. Although the last case is infrequent in practice, the inclusion of it makes the model more adaptable. Later in this paper, we will show how to make use of the multi-destination container term to extend the initial, import-only model to solve import–inland and/or inland–export problems.

In this work, we firstly propose an optimization model for the pairing of containers in drayage transportation (PCDT). This model considers the joint delivery of import containers only, namely the container movements from the port to inland customers. This study is important in its own right as there are many countries, such as the UK, doing many more imports than exports so that the demands are not always balanceable to form round trips. In accordance with realistic situations, in the model we cover all major restrictions for the drayage service such as the empty leg transportation, the heterogeneous fleet size, the arrival time of vessels (containers), the time window restriction at customer locations and/or the port and the working time regulations. The aim of the model is to minimize total distance travelled by all vehicles used and the penalty paid for potential overtime works by the truck driver. Major contributions of this initial model are twofold: first it allows one container to have more than one receivers; second the model is more efficient to solve than the traditional models based on pickup and delivery in vehicle routing networks and therefore allow more accurate solution for large problems with more than 300 containers. Considering the usage of multi-destination containers, we then extend our parameter definitions to make the aforementioned optimization model also applicable to the combination of import (export) with inland trips and also to import–inland–export problems without using dual-carriage trucks. Taking use of our model the solution, difficulties for these three types of problems are similar, as there are no major modifications to the model itself but just to the interpretation of the input data.

This paper is structured as follows. A literature review is carried out in Section 2. In Section 3, the problem statement and the optimization model are described. A practical variant is demonstrated in Section 4, and numerical experiments are presented in Section 5. Section 6 is for the conclusions.

2 Literature review

In the pre-existing literature, some studies form their mathematical model around the movement of one individual container per truck, of the size 40 ft. Others focus upon the pairing of two 20-ft containers per truck. Ultimately, the objective of most papers already in existence is to minimize the cost of truck transportation through optimizing travelling times and/ or travelling distances. One paper which directly targets the costing of transportation is (Coslovich et al, 2006). This paper presents the problem of container transportation from the perspective of three types of costs: routing costs, resource costs and empty container delivery costs. A large amount of papers focuses on the transportation of one 40-ft container, such as Jula et al (2005). This paper proposed a multi-travelling salesman problem with time windows (M-TSPTW). If the problem became too large to handle with this method, a hybrid method was used, formed of dynamic programming techniques in conjunction with genetic algorithms. Other papers which expanded upon this idea by Jula et al (2005), with 40-ft containers, include Sterzik and Kopfer (2013) and Imai et al (2007). Each of these two papers adapts the initial M-TSPTW with a heuristic to improve the total operating time of all trucks. Sterzik and Kopfer (2013) impose hard constraints on the time windows of nodes, while Imai et al (2007) forms a first fit heuristic to solve the problem. Both of these two papers focus on the strip method of unloading containers; however, they vary in the amount of customers that can be served, 23 and up to 200, respectively.

Caris and Janssens (2009) extend Imai et al (2007) by imposing time windows at customers and depots. Within the grouping of 40-ft containers, it is becoming apparent, from existing works, that the strip method of emptying the truck, opposed to discharging the container from the truck, is a more popular idea to study. Zhang et al (2009, 2011) also follows this method of forming a mathematical model with the strip of a container at nodes. In this paper, meta-heuristics are used and solved by the reactive tabu search to create routes visited by trucks. Caris and Janssens (2009) also follow the strip method of unloading the trucks within their problem; however, they use a two-phase heuristic to solve the problem: combining the pickups and deliveries in truck routes; then using trucks with lowest costing first. Another paper which uses the strip method of container transportation is Smilowitz (2006) which introduces the multi-resource routing problem (MRRP). On the opposing side of the 40-ft container modelling, Zhang et al (2010) created a mathematical problem based upon discharging the container from the truck and returning to collect it later in the route. By forming a graph with repeated nodes for returning to a customer, this paper is based upon the M-TSPTW problem which is then developed into a window partition-based problem and compared to the reactive tabu search of Zhang et al (2009). Other papers look into the transportation of multiple containers in an effort to reduce travelling distances further. Some trucks are able to transport two 20-ft containers at a time, allowing the combination of two import or two export movements at a time. Before 2012, only two papers had looked into this: Chung et al (2007) who worked on a one-to-one pickup and delivery problem, and Vidović et al (2011) who determined routes from the matching of pickup and delivery nodes with empty and loaded containers. Like the majority of the 40-ft container focused papers, the majority of 20-ft container combinations focus upon the strip method of unloading containers. This saves time in the long run; reducing the distance the trucks travel in their route. These papers more commonly have a later dating than the 40-ft container papers as they are extending the pre-existing transportation problems by combining more container shipments together in a route. Lai et al (2013) applies a meta-heuristic to the Clarke and Wright method and its graph to reduce the length of routes. This paper does this by inter-switching nodes and the routes the trucks take. Later, Lai (2013) adapts the previous paper for heterogeneous and homogeneous fleet size, separately. By splitting and merging import and export routes and forming 7 tabu search heuristics within the paper, upon conclusion, the optimal is picked. In the paper, Caballini et al (2015) combine import, export and inland transportation trips, three by three. This paper also introduced time windows at each of the nodes which is considered within the mathematical method where it considers all combinations of nodes with the optimal being chosen. Few papers consider both the transportation of two 20-ft containers and one 40-ft container, something this paper does.

Zhang et al (2015) investigates the multi-size containers including one 40-ft or two 20-ft containers. They used a multiple travelling salesman model consisting of three tree search and an improved reactive tabu search algorithm. In addition, Schönberger et al (2013) and Funke and Kopfer (2016) consider the transportation of these two sized containers, with trucks being able to transport up to two 20-ft containers or one 40-ft container. Then, the authors improved a neighbourhood search (NS) technique to solve the container routing and scheduling (Funke and Kopfer, 2015). Schönberger et al (2013) focus upon a container pickup and delivery problem, while (Funke and Kopfer, 2016) duplicate nodes within the graphical representation to show customers that need visiting more than once. They then use a multi-commodity flow model with the multiple travelling salesperson problem to ensure that each container movement is covered and minimizes the distance and time travelled by trucks on their routes. Another paper which considers empty and loaded containers of size 20 and 40 ft is (Popović et al, 2014). This paper demonstrates the variable neighbourhood search (VNS) heuristic to solve container drayage problems considering time windows (CDPTW). Xue et al (2015) investigate the problem where containers are discharged from the truck and formulated in a mathematical model as well as a CBC method. Having looked at other papers, and progressing on their shortfalls, the aim of this paper is to propose a mathematical model to combine multiple container transportation requests using 20-ft containers, which allows the combination of containers in three following ways: import (export) and inland; import and export; and import–inland–export. By not involving a graphical model helps reduce working in the problem while also allowing the mathematical model to involve more constraints such as time windows and the working time of driver conditions which are unable to be shown on an individual graph. This significantly reduces the empty movements of the trucks on their routes while respecting time windows and laws which must be abided by.

3 Problem statement and optimization model

We start the description of the problem by defining some terms that will be used later. The term order in this paper is referred to as a customer request of delivering the content of a loaded container from its origin to destination (examples for import, inland and export orders are given in Table 5). Only 20-ft containers are used for transportation, since the delivery of 40-ft container can only be carried out by 40-ft trucks; therefore, we can simply assume all of them go without pairing to reduce the problem size. Note that in this study, when we are talking about the delivery (pickup) of container, we mean the delivery (pickup) of the cargo inside the container rather than the container itself. After striping the container at customer locations (for import case for example), it should be transported to a final empty storage which is normally the port or an inland depot, unless it has been assigned to a specific final destination. Similarly, an empty container has to be collected from an empty storage in order to start an inland or export trip, if the trip is not performed right after an import delivery (so that we have an empty container to use on the truck). One order comes with an origin (where the cargo departs), one (single-) or two (multi-) destinations (where the receiver locates), the time window constraints at all relevant locations (when the branches open), the available time of the container (when it is ready to be collected), the payload weight (weight of cargo) and probably an assigned final destination (where the empty goes to). For multi-destination orders, we follow the full-twin assumption that is introduced by Zhang et al (2015), i.e. a truck that has begun to handle the first customer’s location of the container has to handle the second customer’s location before the truck starts to carry out a new order. We assume all information is determined beforehand, including the visiting sequences of customer locations for multi-destination orders. Note further that the order is defined in a single container basis, for example, if there is a customer request consisting multiple containers, we have to split it into multiple orders with the same data and allow the customer to be visited by more than one truck.

The model is developed in the perspective of haulage companies who own a certain heterogeneous fleet of trucks and chassis, collect orders from shipping lines and other customers and commit to make the delivery of containers in time to their destinations. Decision is made on whether containers should be assigned to an individual trip that is executed by a truck that is able to transport one 20-ft container, or whether two containers should be paired in a specific order and served by a truck that is able to transport two 20-ft containers, as well as where to place the empty container after delivery. The aim is to minimize the total travelling costs of the whole fleet and the penalty costs for potential overtimes of trips. Note that we consider the working time regulation for drivers and penalty cost only in a daily basis. We assume there are adequate number of drivers employed so that no one will work overtime for more than once during a week.

3.1 Parameters and definitions

In following sections, we will formulate an assignment model whose results will inform how to serve every order. We will be starting from considering the import orders only (loaded containers starting from the port) and then extend the data definition to cover the import–inland and the import–inland–export cases. Parameters for the initial (import only) model are defined in the following Table. In more detail, we assume that the fleet consists of H 1 20-ft trucks and H 2 40-ft trucks. For the sake of simplicity and clarity in modelling, we assume that 40-ft truck is not allowed to perform single container transportation although in practice it might be possible. We assume all containers/orders considered, denoted by \({\mathcal {N}}\), are allowed to be paired with another in transportation. We denote by \({\mathcal {P}}_1\) and \({\mathcal {P}}_2\) the sets of orders having single destination and multiple (dual) destinations, respectively. Containers in subset \(D_p\) are the ones with final empty destinations determined, whereas \(D_0\) are the ones without. An import order (loaded container) \(i \in {\mathcal {N}}\) is picked up from the port (\(L_0\)) after its available time (\(A_i\)), delivered to its receivers (\(L_i\) if single destination, \(L_i^1\) and \(L_i^2\) in the determined sequence if multiple destinations) individually or paired within predetermined time window (\([T_i^s, T_i^e]\) if single destination, \([T_i^{s1}, T_i^{e1}]\) and \([T_i^{s2}, T_i^{e2}]\) if multiple destinations) and dropped off at the agreed final empty destination \(D_i\) if there is one or at a nearby empty storage that is chosen from \({\mathcal {M}}_0\). The handling time at the port (h i ) refers to the time of loading the container on the truck, whereas the turnaround time at receivers (\(O_i\)) is the time taken to strip the cargo from container i. We denote by \(W_i\) the container i’s payload weight (weight of cargo) and by V the weight of truck, chassis and the empty container. The gross weight limit, \(V_1^m\) for 20-ft truck and \(V_2^m\) for 40-ft truck, is applied to all delivery routes.

In the case of haulage companies to do the work, costs are normally determined based on banded rates, increasing in a roughly linear fashion relative to distance. In this study, for a known list of locations to visit, the cost is captured by a linear function to the total travel distance including both the loaded legs and empty leg, which is denoted by \((f({\mathbf{.}},\ldots , {\mathbf{.}} ))\). In addition to the mileage cost, we also consider the potential penalty that the haulage company may have to pay for overtime workings. According to the EU regulation, if a driver works more than T = 9 h, then a penalty of C should be paid for any extra time working. However, working longer than \(T_{\rm max} = 11\,{\rm h}\) in a day is strictly inadmissible.

Parameters

H 1::

total number of lorries available for single container delivery

H 2::

total number of lorries available for paired containers delivery

\({\mathcal {M}}_0\)::

set of port/depots/exporters as empty leg destinations

\({\mathcal {N}} = {\mathcal {P}}_1 \cup {\mathcal {P}}_2 = {\mathcal {D}}_0 \cup {\mathcal {D}}_p\)::

set of containers, in which:

\({\mathcal {P}}_1\)::

set of containers with single destination

\({\mathcal {P}}_2\)::

set of containers with multi-destination

\({\mathcal {D}}_0\)::

set of containers for which an empty leg destination is not yet determined

\({\mathcal {D}}_p\)::

set of containers for which the empty leg destination is a known port or depot or exporter

\(A_i, i \in {\mathcal {N}}\)::

available time of container (order) i for departure from the port

\(h_i, i \in {\mathcal {N}}\)::

handling time of container i at the port

\(O_i, i \in {\mathcal {N}}\)::

turnaround time at order i’s customer location

T::

regular working hours (9 h)

\(T_{\rm max}\)::

the maximum possible working time for one shift that is allocated by the regulation

C::

penalty cost for extra working hours

\(L_0\)::

the port

\(L_i, i \in {\mathcal {P}}_1\)::

customer location for single destination container i

\(L_i^1, L_i^2, i \in {\mathcal {P}}_2\)::

two consequence customer locations for multi-destination container i

\([T_i^s, T_i^e], i \in {\mathcal {P}}_1\)::

the time window during which the container i (single destination) is meant to arrive

\([T_i^{s1}, T_i^{e1}], i \in {\mathcal {P}}_2\)::

time window in which the container i is meant to arrive at the first location

\([T_i^{s2}, T_i^{e2}], i \in {\mathcal {P}}_2\)::

time window in which the container i is meant to arrive at the second location

\(D_i, i \in {\mathcal {D}}_p\)::

the empty leg destination that has been determined for orders in \({\mathcal {D}}_p\)

\(W_i, i \in {\mathcal {N}}\)::

the weight of container i, which contains both the cargo and the container weight

V::

weight of the lorry and chassis and the empty container

\(V_1^m\)::

weight limit for individual delivery

\(V_2^m\)::

weight limit for paired delivery

\(f({\mathbf{.}} ,\ldots , {\mathbf{.}})\)::

travelling cost for a sequence of locations. We rescale the straightline distance by a constant factor to approximate the road distance between each pair of locations

\(t({\mathbf{.}},\ldots , {\mathbf{.}})\)::

travel time for a sequence of locations

M::

large number

3.2 Decision variables

In order to capture the entire features of the model, two types of decision variables are introduced as below. Binary variables \(x_{ijd}\) and \(y_{id}\) are the decision on how the container should be transported, paired or individually and following what sequence; binary variables \(z_{ijd}\) and \(u_{id}\) are introduced to identify whether penalty cost should be paid for extra working time; continuous variables \(s_i, v_i, v_i^1, v_i^2, T_{id}, T_{ijd}\) are used to calculate the departure time of containers from the port, the arrival times at customer locations and the total working time of the paired and individual trips of the working plan.

Binary variables

  • \(\begin{aligned} &x_{ijd} = \left\{ \begin{array}{ll} 1, &\quad \text{ if } \text{ containers }\,{ i}\,\text{ and }\,{ j}\,\text{ are } \text{ delivered } \text{ paired } \text{ to } \text{ their } \text{ destinations\,(single } \text{ or } \text{ multi) }\\ &\quad \text{ on } \text{ a } \text{ same } \text{ lorry } \text{ and } \text{ end } \text{ at } \text{ empty } \text{ leg } \text{ destination } { d}.\\ 0, &\quad \text{ otherwise } \end{array}\right. \\ &\quad \forall i \ne j \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0.\end{aligned}\)

  • \(\begin{aligned} &y_{id} = \left\{ \begin{array}{ll} 1, &\quad \text{ if } \text{ container } { i} \text{ is } \text{ delivered } \text{ individually } \text{ to } \text{ its } \text{ destination(single } \text{ or } \text{ multi) }\\ &\quad \text{ and } \text{ end } \text{ at } \text{ empty } \text{ leg } \text{ destination } { d}.\\ 0, &\quad \text{ otherwise } \end{array}\right. \\ &\quad \forall i \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0.\end{aligned}\)

  • \(\begin{aligned} &z_{ijd} = \left\{ \begin{array}{ll} 1, &\quad \text{ if } \text{ working } \text{ hours } \text{ for } \text{ paired } \text{ trip } \text{ is } \text{ higher } \text{ than } \text{ the } \text{ regular } \text{ working } \text{ time }\\ 0, &\quad \text{ otherwise } \end{array}\right. \\ &\quad \forall i \ne j \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0.\end{aligned}\)

  • \(\begin{aligned} & u_{id} = \left\{ \begin{array}{ll} 1, &\quad \text{ if } \text{ working } \text{ hours } \text{ for } \text{ individual } \text{ trip } \text{ is } \text{ higher } \text{ than } \text{ the } \text{ regular } \text{ working } \text{ time } \\ 0, &\quad \text{ otherwise } \end{array}\right. \\ &\quad \forall i \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0.\end{aligned}\)

Continuous variables

  • \(s_i, \forall i \in {\mathcal {N}}\): departure time of container i from the port.

  • \(v_i, \forall i \in {\mathcal {P}}_1\): arrival time of one-destination container i.

  • \(v_i^1, v_i^2, \forall i \in {\mathcal {P}}_2\): arrival times of multi-destination container i at its two customer locations.

  • \(T_{id}, \forall i \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0\): total working time of the individual trip of servicing container i.

  • \(T_{ijd}, \forall i \ne j \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0\): total working time of the paired trip of servicing containers i and j.

3.3 Mathematical model

An assignment mixed integer linear programming (MILP) model for the paired/individual delivery on 40/20-ft chassis of import orders can be described as below. Note that this model is constructed for import orders only; in next section, we will discuss how this model can be implementable as well on import–inland and/or import–inland–export cases.

$$\begin{aligned} \min&\sum \limits _{i \in {\mathcal {P}}_1} \sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d \in {\mathcal {M}}_0} x_{ijd} \left[ f\left( L_0, L_i, L_j, d\right) \right] + \sum \limits _{i \in {\mathcal {P}}_2} \sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d \in {\mathcal {M}}_0} x_{ijd} \left[ f\left( L_0, L_i^1, L_i^2, L_j,d\right) \right] \\&+\sum \limits _{i \in {\mathcal {P}}_1} \sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d \in {\mathcal {M}}_0} x_{ijd} \left[ f\left( L_0, L_i, L_j^1, L_j^2, d\right) \right] + \sum \limits _{i \in {\mathcal {P}}_2} \sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d \in {\mathcal {M}}_0} x_{ijd} \left[ f\left( L_0, L_i^1, L_i^2, L_j^1,L_j^2,d\right) \right] \\&+\sum \limits _{i \in {\mathcal {P}}_1}\sum \limits _{d \in {\mathcal {M}}_0} y_{id} \left[ f\left( L_0, L_i, d\right) \right] + \sum \limits _{i \in {\mathcal {P}}_2}\sum \limits _{d \in {\mathcal {M}}_0} y_{id} \left[ f\left( L_0, L_i^1, L_i^2,d\right) \right] \\&+\sum \limits _{i \in {\mathcal {N}}} \sum \limits _{j \in {\mathcal {N}}} \sum \limits _{d \in {\mathcal {M}}_0} C z_{ijd} + \sum \limits _{i \in {\mathcal {N}}}\sum \limits _{d \in {\mathcal {M}}_0} C u_{id} \end{aligned}$$
(3.1)
$$\begin{aligned} s.t.& \\&\sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d \in {\mathcal {M}}_0} \left( x_{ijd} + x_{jid}\right) + \sum \limits _{d \in {\mathcal {M}}_0} y_{id} = 1, \forall i \in {\mathcal {N}}; \end{aligned}$$
(3.2)
$$s_i \ge A_i + h_i, \forall i \in {\mathcal {N}};$$
(3.3)
$$s_i \ge \left( A_j + h_j\right) \sum \limits _{d \in {\mathcal {M}}_0} \left( x_{ijd} + x_{jid}\right) , \forall i \ne j \in {\mathcal {N}}; $$
(3.4)
$$s_i - s_j \le M*\left( 1-\sum \limits _{d \in {\mathcal {M}}_0}\left( x_{ijd} + x_{jid}\right) \right) , \forall i \ne j \in {\mathcal {N}}; $$
(3.5)
$$V + W_i \sum \limits _{d \in {\mathcal {M}}_0} y_{id} \le V_1^m, \forall i \in {\mathcal {N}};$$
(3.6)
$$V + \left( W_i + W_j\right) \sum \limits _{d \in {\mathcal {M}}_0} \left( x_{ijd} + x_{jid}\right) \le V_2^m, \forall i \ne j \in {\mathcal {N}}; $$
(3.7)
$$\begin{aligned}&v_i = s_i + \sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j, L_i\right) + O_j\right] + \sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j^1, L_j^2, L_i\right) + 2O_j\right] \\&\qquad + \left( \sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d} x_{ijd} + \sum \limits _{d} y_{id}\right) t\left( L_0, L_i\right) , \forall i \in {\mathcal {P}}_1; \end{aligned}$$
(3.8)
$$\begin{aligned}&v_i^1 = s_i + \sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j, L_i^1\right) + O_j\right] + \sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j^1, L_j^2, L_i^1\right) + 2O_j\right] \\&\qquad + \left( \sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d} x_{ijd} + \sum \limits _{d} y_{id}\right) t\left( L_0, L_i^1\right) , \forall i \in {\mathcal {P}}_2; \end{aligned}$$
(3.9)
$$\begin{aligned}&v_i^2 = s_i + \sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j, L_i^1, L_i^2\right) + 2O_j\right] + \sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d} x_{jid} \left[ t\left( L_0, L_j^1, L_j^2, L_i^1, L_i^2\right) + 3O_j\right] \\&\qquad + \left( \sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d} x_{ijd} + \sum \limits _{d} y_{id}\right) \left[ t\left( L_0, L_i^1, L_i^2\right) + O_i\right] , \forall i \in {\mathcal {P}}_2; \end{aligned}$$
(3.10)
$$T_i^s \le v_i \le T_i^e, \forall i \in {\mathcal {P}}_1; $$
(3.11)
$$T_i^{s1} \le v_i^1\le T_i^{e1}, \forall i \in {\mathcal {P}}_2; $$
(3.12)
$$T_i^{s2} \le v_i^2 \le T_i^{e2}, \forall i \in {\mathcal {P}}_2; $$
(3.13)
$$T_{id} \ge v_i + \left[ O_i + t\left( L_i,d\right) \right] - s_i - M\left( 1-\sum \limits _{d} y_{id}\right) , \forall i \in {\mathcal {P}}_1; $$
(3.14)
$$T_{id} \ge v_i^2 + \left[ O_i + t\left( L_i^2,d\right) \right] - s_i - M\left( 1-\sum \limits _{d} y_{id}\right) , \forall i \in {\mathcal {P}}_2; $$
(3.15)
$$T_{ijd} \ge v_j + \left[ O_j + t\left( L_j,d\right) \right] - s_j - M\left( 1-\sum \limits _{d} x_{ijd}\right) , \forall i \in {\mathcal {N}}, j \in {\mathcal {P}}_1;$$
(3.16)
$$T_{ijd} \ge v_j^2 + \left[ O_j + t\left( L_j^2,d\right) \right] - s_j - M\left( 1-\sum \limits _{d} x_{ijd}\right) , \forall i \in {\mathcal {N}}, j \in {\mathcal {P}}_2;$$
(3.17)
$$T_{id} \le T + M \left( u_{id}\right) , \forall i \in {\mathcal {N}};$$
(3.18)
$$T_{ijd} \le T + M \left( z_{ijd}\right) , \forall i,j \in {\mathcal {N}};$$
(3.19)
$$T_{id} \le T_\mathrm{max}, \forall i \in {\mathcal {N}}; $$
(3.20)
$$T_{ijd} \le T_\mathrm{max}, \forall i,j \in {\mathcal {N}}; $$
(3.21)
$$y_{iD_i} + \sum \limits _{j \in {\mathcal {N}}} \left( x_{ijD_i} + x_{jiD_i}\right) = 1, \forall i \in {\mathcal {D}}_p; $$
(3.22)
$$\sum \limits _{i \in {\mathcal {N}}}\sum \limits _{d} y_{id} \le H_1; $$
(3.23)
$$\sum \limits _{i \in {\mathcal {N}}}\sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d} x_{ijd} \le H_2; $$
(3.24)
$$s_i, v_i, v_i^1, v_i^2, T_{id}, T_{ijd} \ge 0, \forall i,j \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0; $$
(3.25)
$$x_{ijd}, y_{id}, u_{id}, z_{ijd} \in \{0,1\}, \forall i,j \in {\mathcal {N}}, \forall d \in {\mathcal {M}}_0. $$
(3.26)

Objective function (3.1) is to minimize the total travelling cost as well as the total penalty cost for extra driving hours incurred from making the delivery for all collected orders from the port \((L_0)\) to the final destinations. Constraint (3.2) is to ensure that all containers are delivered paired or individually. Constraint (3.3) forces containers to depart after it is ready to collect from the port, while constraint (3.4) means that all containers which are paired with another must depart after both are ready. Constraint (3.5) ensures that all containers that are paired depart at the same time. Constraints (3.6) and (3.7) guarantee that the gross weight of the whole vehicle which includes weights of the vehicle, chassis, containers and cargo does not exceed the maximum allowance. Constraints (3.8), (3.9) and (3.10) calculate the arrival times at containers’ destinations, while constraints (3.11), (3.12) and (3.13) impose the time window restriction at the customer location. Constraints (3.14), (3.15), (3.16) and (3.17) calculate the total working time of the vehicle, by subtracting from the final arrival time at the empty leg destination the departure time from the port. Constraints (3.18) and (3.19) ensure that penalty is paid for extra working hours, while constraints (3.20) and (3.21) restrict the model from planning routes that exceed the maximum working hours for one shift. Constraint (3.22) emphasizes on the fact that all orders with predetermined empty leg destination must be delivered to the allocated location. Constraints (3.23) and (3.24) are there to ensure the total number of trucks used is no more than the corresponding fleet size. Finally, constraints (3.25) and (3.26) define the domain of variables.

4 Practical variant

Although the MILP model that is proposed in Section 3 is built to solve the pairing problem for import trips of containers only, the variant of it, however, can be applied onto a numerous of situations including both import, inland and/or export trips. Of course, the coverage of different situations is subject to necessary small modifications and appropriate interpretations of parameters/data used. In this section, we will discuss some major applications and how to adapt the model to achieve our aims.

4.1 Import (export) of containers only

The scale of container business is different from one country to another, and very rarely, a country has balanced import and export demands. In most developed countries like the UK, import is dominant, whereas in most developing countries such as China, export plays a far more important role than import. Although in general the pairing of import and export orders benefits, the imbalance in demands gives rise to potential decompositions of the entire delivery problem into subproblems having only import/export orders in it. Therefore, in the first part, we discuss around the original application for the combination of import orders only. To make this model more realistic, after all containers are served we consider an empty leg trip to some inland depots where the empty containers are temporarily stored or directly to an exporter that may have short-term demands (but we do not consider the export trip explicitly). This makes a connection between the import and export trips which is normally used in practice. The model also allows customer-specified empty leg destination, which covers the case if a full container has already been allocated for an empty destination after it is delivered. Note that in our model we also allow a single container to be delivered to multiple (two) customer locations. This is seen in situations where customers are running relatively small business and when customers are sharing the cargo of a single container. Examples of combined routes are shown in Figure 1.

Figure 1
figure 1

Graphical illustration of application on the import of containers

Full size image

Based on the optimal decision of the model, there are four types of possible delivery routes as shown in Figure 1:

  1. 1.

    Deliver a container individually and then drop the empty container at an empty destination (port/inland depot/exporter).

  2. 2.

    Deliver two containers jointly, which both have single destination and then drop the empty at an empty destination (port/inland depot/exporter).

  3. 3.

    Deliver two containers jointly, in which one has multiple destinations and then drop the empty at an empty destination (port/inland depot/exporter).

  4. 4.

    Deliver two containers jointly, which both have multiple destinations and then drop the empty at an empty destination (port/inland depot/exporter).

In opposite to import, the model can also be applied for the export-only case where empty containers should be picked up either from a depot/port or from an importer, travel for the pickup service and eventually deliver the loaded containers to the port.

4.2 Import (export) and inland containers transportation

In addition to the original problem setting, the MIP model can also be applied to the case where import trips are combined with inland trips. Container, as a means of safety delivery, is not only used in marine freight, but also in inland transportation of bulk commodities. As traditionally the last-mile delivery of containers is carried out by haulage companies who also serve inland orders, the combination of import and inland trips is therefore vital in reducing unproductive travels. Note that in Sections 4.2 and 4.3, unless stated in detail, we follow the problem statements and parameter descriptions proposed in Section 3.

Here we consider two types of orders, each is associated with one type of container transportation requests, say the import orders and inland orders. An import order, like before, is a customer request of transporting a loaded container from the port to a customer location; an inland order, on the other hand, refers to the customer request of transporting one container’s cargo from one inland location to another. Note that for the inland order, we assume that the customer does not own the container so that an empty container should be transported to the origin to do the loading, before visiting the destination for discharging. This defines the sequence following which the customer nodes should be visited for inland orders, which is in line with the full-twin assumption of multi-destination orders as mentioned before. So in this second scenario, we make use of the multi-destinations order set \({\mathcal {P}}_2\) to assemble inland orders, and all decision variables relating to multi-destination orders are then interpreted as “whether the inland order should be served by an individual trip or by a paired trip with another order”. In detail, \(x_{ijd} = 1, i\ne j \in {\mathcal {P}}_2\) means the inland order i should be combined with inland order j, so a 20-ft truck collects an empty container from the port/inland depot, picks up order i’s cargo from \(L_i^1\), delivers it to \(L_i^2\), then uses the same empty container to collect order j’s cargo at \(L_j^1\), delivers it to \(L_j^2\) and finally drops the empty container to a nearby depot; \(x_{ijd} = 1, i \in {\mathcal {P}}_1, j \in {\mathcal {P}}_2\) means the import order i should be combined with inland order j, so a 20-ft truck picks up the loaded container i (an import order) from the port, delivers it to \(L_i\), then uses the same empty container to collect order j’s cargo at \(L_j^1\), delivers it to \(L_j^2\) and then drops the empty container to a nearby depot; \(x_{ijd} = 1, i \ne j \in {\mathcal {P}}_1\) means the import order i is paired with another import order j, whereas \(y_{id} = 1, i \in {\mathcal {P}}_2\) (\(y_{id} = 1, i \in {\mathcal {P}}_1\)) mean the inland (import) order i is served individually.

Note that there is no longer import orders with multiple destinations as all orders in \({\mathcal {P}}_2\) are now interpreted as inland orders; therefore, the usage of 40-ft trucks in this case is only needed when two import orders are paired (\(x_{ijd} = 1, i\ne j \in {\mathcal {P}}_1\)). Constraints (3.23) and (3.24) are modified to:

$$\begin{aligned} \sum \limits _{i \in {\mathcal {N}}}\sum \limits _{d} y_{id} + \sum \limits _{i \in {\mathcal {N}}}\sum \limits _{j \in {\mathcal {P}}_2}\sum \limits _{d} x_{ijd}\le &\,\, H_1,\\ \sum \limits _{i \in {\mathcal {P}}_1}\sum \limits _{j \in {\mathcal {P}}_1}\sum \limits _{d} x_{ijd}\le &\,\, H_2 \end{aligned}$$

Weight constraints (3.6) and (3.7) should be modified accordingly as not in all paired cases we have two containers on the truck simultaneously.

$$\begin{aligned} V + W_i \sum \limits _{d \in {\mathcal {M}}_0} (y_{id} + x_{ijd})\le &\,\, V_1^m, \forall i \in {\mathcal {N}}, j \in {\mathcal {P}}_2\\ V + (W_i + W_j) \sum \limits _{d \in {\mathcal {M}}_0} x_{ijd}\le &\,\,V_2^m, \forall i \ne j \in {\mathcal {P}}_1 \end{aligned}$$

Also for inland orders, we need to set their “available time from the port”, \(A_i\), as zero (start of the day) so that it would not affect the departure time of the other container if it is paired, and use the time window to reflect its earliest available time at its pickup location. All other constraints stay the same as in the initial model.

Figure 2
figure 2

Graphical illustration for the import–inland transportation

Full size image

Figure 2 shows graphically the possible delivery routes in optimal solution. In detail, they are:

  1. 1.

    An import order which is followed by an inland order.

  2. 2.

    An import order which is followed by an inland journey starting directly from the importer.

  3. 3.

    A single import order delivered individually.

  4. 4.

    Two import orders are paired on a 40-ft truck and delivered one after another.

  5. 5.

    A single inland order delivered individually.

  6. 6.

    Two inland orders are paired and served one after another.

The same structure can also be used for the inland–export case, in which loaded containers are delivered from exporters to the port.

4.3 Import, inland and export containers transportation

Finally, we show that with small adaptations, our model can also be applied to the combination of import, inland and export trips. This is the most widely studied variant in the existing literature which is believed very useful in reducing empty travels of containers by constructing a closed tour starting and ending at the port. Like the variant above, for this case we just need to adjust some interpretations of the model parameters, but a major improvement can be seen in the size of problems that can be solved exactly.

As proposed in Section 4.2, we keep using the “multi-destination” subgroup \({\mathcal {P}}_2\) to capture inland orders. An export order, however, is defined as a customer request of transporting one container’s cargo from a customer location to the port. As the destination for an export order is fixed at the port, we only need to know the origin, which can be any customer location, plus the standard parameters such as time windows and the weight of cargo to complete the definition. So an export order can be represented by a container d with single “destination” (which should be interpreted as origin here), \(d \in {\mathcal {P}}_1\). Numerical examples of export orders are given in Table 5 as containers 6, 7 and 8. In this section, we consider all orders types, say import, inland and export orders, each is associated with the transportation of a single container’s cargo. Containers, which can be reused, are bound with chassis and are to be filled in/stripped at customer locations. Empty containers are generated after the delivery of import/inland orders and are demanded before the pickup of inland/export orders. The problem is to find out how to make the transportation of all orders, individually or pairwisely, to achieve a minimum cost delivery plan satisfying the time, weight and working hours restrictions. Note that we do not consider the usage of 40-ft trucks but only the combination of different types of trips on 20-ft ones, because we define the variable only in a way that the empty container can be reused.

Observe that if we construct a complete return route with an import, an inland and an export order, the empty container is kept reused for the next task so that the empty leg destination is no longer needed. Therefore, in the model, we are going to use the previous “empty destination” d as the index for export orders, namely from \(L_d\) we load an empty container with cargoes to be delivered to the port. \(x_{ijd} = 1, i \ne d \in {\mathcal {P}}_1, j \in {\mathcal {P}}_2\) is then interpreted as a 20-ft truck collects a loaded container i from the port, delivers its cargo to \(L_i\), then reuses the empty container to serve an inland order from \(L_j^1\) to \(L_j^2\), after which the same container is used to pickup cargo from \(L_d\) and delivers to the port. Note that in this case the number of variables actually reduces, since the round trip is only allowed in one way: import then inland then export. While to tackle with imbalances in these three types of demands, we also allow individual trips for every type of request and the combined trips for every two types of requests. So the decision variables are \(x_{ijd}, i \ne d \in {\mathcal {P}}_1, j \in {\mathcal {P}}_2\) for combined trips with import, inland and export orders, \(x_{ijd}, i \in {\mathcal {P}}_1, j \in {\mathcal {P}}_2, d \in {\mathcal {M}}_0\) for combined trips with import and inland orders, \(x_{ijd}, i \ne j \in {\mathcal {P}}_1, d = \hbox {port}\) for combined trips with import and export orders, \(y_{id}, i \in {\mathcal {P}}_2, d \in {\mathcal {P}}_1\) for combined trips with inland and export orders, \(y_{id}, i \in {\mathcal {P}}_1, d \in {\mathcal {M}}_0\) for import trips, \(y_{id}, i \in {\mathcal {P}}_2, d \in {\mathcal {M}}_0\) for inland trips and \(y_{id}, i \in {\mathcal {P}}_1, d = \hbox {port}\) for export trips. Note that when d is not taken from \({\mathcal {M}}_0\), an additional term (\(L_0\)) should be added to the travel distance and travel time function to include the travelling from \(L_d\) to the port. Also the fleet size constraint (3.23) and (3.24) should be combined into one as H 2 (40-ft trucks) no longer exists:

$$ \sum \limits _{i \in {\mathcal {N}}}\sum \limits _{j \in {\mathcal {N}}}\sum \limits _{d} x_{ijd} + \sum \limits _{i \in {\mathcal {N}}}\sum \limits _{d} y_{id} \le H_1, $$

as well as the weight constraints (3.6) and (3.7):

$$ V + W_i \sum \limits _{d} (y_{id} + x_{ijd} + x_{jid}) \le V_1^m, \forall i \in {\mathcal {N}} $$
Figure 3
figure 3

Graph explains the import–inland–export transportation

Full size image

As shown in Figure 3 and as we explained above, there will be different possibilities for this case which are:

  1. 1.

    A loaded order as import, followed by an inland order, and finally, the export order is delivered to the port.

  2. 2.

    A loaded order as import, followed by an inland order, and the empty container is delivered to an empty storage (port/inland depot/exporter).

  3. 3.

    A loaded order as import followed by an export tour.

  4. 4.

    A single import order served individually.

  5. 5.

    A single export order served individually.

  6. 6.

    A single inland order served individually.

  7. 7.

    Empty container is picked up from a nearby empty storage (port/inland depot/exporter) to start a single inland tour, which is then followed by an export trip.

5 Numerical results

In this section, we construct small examples according to the three applications as discussed in Section 4 and test our model against them to show the performance. The MIP model is coded in MPL and solved by Cplex.

5.1 Example 1: import only

In this example, five containers are to be delivered from a single port to a subgroup of ten customer locations, (1,...,7), where (0, 8, 9, 10) are defined as port/depot/exporter. Data are summarized in Table 1. For instance, container 1, whose cargo weights 8900 (kg), is available to pick up from the port at time 6.30 a.m. and should be delivered to customer location 1 between 8 a.m. and 2 p.m.

Table 1 Data for import-only example
Full size table
Figure 4
figure 4

Solution for example 1 (import of containers)

Full size image

Containers 1, 2 and 3 are for single destination, while containers 4 and 5 are allocated to two destinations each. In addition, there are eight lorries available for the import service, with four for paired delivery and four for single delivery. For all trucks, a gross weight limitation of 44,000 kg is applied, which includes the truck (7500 kg), the chassis (4800 kg), the empty container (2300 kg) and the cargo (given in the table as \(W_i\)). Maximum working time of truck driver is set to 9 h (according to UK regulation), and a penalty of 30 pounds should be paid for any extra hours driven. Average service time at all customer locations is 2 h. The empty containers should be delivered to the depot/port/exporter which minimizes the total travelling distance. Solution to this example is displayed in Figure 4. In the solution, there are four trips, one travelled by a 40-ft-long lorry to carry containers 2 and 4 pairwisely, three travelled by 20-ft-long lorries to deliver containers 1, 3 and 5 individually. Dashed lines represent the empty container movement.

Table 2 Solution for example 1 (import of containers)
Full size table

Table 2 gives more detailed information about the departure and arrival times at all customer locations. The result makes perfect sense. First, container 3 cannot be delivered pairwisely as its weight is too high to combine with any other container. Second, it is impossible to combine containers 4 and 5 (both for multi-destination) due to the time window constraints. Thirdly, although we need to pay for the overdue in working time for the paired delivery route, the total distance travelled is largely reduced than delivering containers 2 and 4 individually. Given these observations, the solution displayed in Figure 4 is optimal.

5.2 Example 2: import–inland transportation

Now we implemented the MIP for the import–inland transportation. As given in Table 3, there are six shipping requests of containers under consideration and two of them (container 4 and 6) are inland requests. Here we assume that the time window applies to the origin and destination nodes, and the time window for the port already exists in the model as the available time to pickup containers. The weight of containers is also specified.

Table 3 Data for import–inland example
Full size table
Figure 5
figure 5

Solution for example 2 (import and inland delivery)

Full size image
Table 4 Solution for example 2 (import–inland transportation)
Full size table

Solving this example by the MIP model, it creates paired delivery routes for all containers as shown in Table 4 and Figure 5. Specifically, two import orders, containers 1 and 2, are paired to form a trip that departs from the port at 10 a.m. and finishes at depot 8; import container 3 and inland container 4 are paired to form a trip that departs from the port at 11 a.m. and finishes at depot 8; import container 5 and inland container 6 are paired to form a trip that departs from the port at 10.50 a.m. and finishes at depot 9.

5.3 Example 3: import–inland–export transportation

In this example, we tested the model for combining the import, inland and export orders together.

Table 5 Data for import–inland–export example
Full size table
Figure 6
figure 6

Solution for example 3 (import–inland–export transportation)

Full size image
Table 6 Solution for example 3 (import–inland–export transportation)
Full size table

As seen in Table 5, eight orders are considered to deliver from their origins to final destinations, as well as the time windows and weight of each request of containers. Looking at the results given in Table 6 and Figure 6, we can see, in this case, the code has paired orders 1, 3 and 6, so the 20-ft-long lorry carries a single loaded container (container 1) and departs from the port at 11.00 a.m. to visit its allocated importer, location 1, at which the inland trip is started towards location 3 and then picks up an export loaded container from location 3 to deliver to the port. On the other hand, import order 2 is combined with inland order 4 and export order 7. This means a 20-ft-long lorry leaves from the port at 10.00 a.m. carrying container 2 and discharges it at location \(L_2\) at 12.50 p.m., and the empty truck is then moved to location 4 to start the inland tour from \(L_4\) to \(L_5\). The export tour starts at 19.11 p.m. from location 5 to the port. Similarly, orders 5 and 8 are paired on a 20-ft-long lorry travelling from the port at 12.27 p.m. and ending its return trip at the port after picking up the export order from \(L_7\) at 19.00 p.m. Penalty cost is charged on route (2, 4, 7), which violates the maximum working time regulation.

5.4 Real implementations

To test the performance of the MIP model for real-life instance, geographical information of the Port of Felixstowe, which is one of the major ports in the UK, and its major service areas is considered. Orders are represented by the number of 20-ft containers that should be distributed from the port to inland customer locations, between a pair of inland locations and from exporters/inland depots to the port. As for the convenience and diversity of tests, apart from the geographical location all other data are randomly generated. Instance sizes ranging from 10 to 300 orders per day are considered, which meets the basic service level of a medium-sized haulage company. Distances are calculated based on the straight-line distance which is rescaled by 1.3 as an approximation to the road distance. The average speed for lorries is randomly picked within [35, 40] mile/h, and the penalty cost is 200 pounds/h for extra working hours. Loading containers at the port take no time (h=0) as it has been considered in the container available time, while at customer locations it takes about 2 h. As mentioned above, the model is coded with MPL solved by Cplex, on a CPU with an Intel(R)Core(TM)i7-4790 processor. In what follows, we will show the numerical results of testing the model against three types of applications.

Table 7 Results for large size instances drawn from real geographical data—import only
Full size table
Table 8 Results for different real instances of the import–inland transportation
Full size table
Table 9 Results for different real instances of the import–inland–export transportation
Full size table

As it can be seen in Table 7, it explains the result for the import of containers. In each instance, we consider different number of loaded orders (containers), and some have single destination, while some others have dual destinations. More than 300 locations distributed around the south-east England are considered as the number of customers (importers) where the loaded containers should be delivered to. We also consider different number of inland depots (where empty containers should be delivered to) across examples. A number of 20- and 40-ft-long trucks are available to use, which can carry one or two 20-ft containers, respectively. It is clear from the result that in some cases a penalty should be paid for extra working hours for some planned routes. Looking at the result, we can see it is not always economical to use up the entire 40-ft fleets. There are three main reasons for this observation: first, some containers are not able to be paired with others due to the weight restriction; second, the penalty paid for extra working hours of a paired trip might be higher than the extra distance travelled by sending two individual trucks, especially when lots of containers are nominated for multiple destinations; thirdly, the existence of inland depots makes the individual delivery less costly than doubling the total travel distance of the paired trip, as empty containers can be easily dropped at a nearby depot. A major notice should be put on the solution time of the model, as in all existing literature that are known by the authors, no one can solve this type of problem with 350 orders within about half hour, not to mention after the inclusion of multi-destination orders which is introduced for the first time in this work. Based on the result, we have the reason to believe the assignment model as proposed does solve more efficiently than the VRP-SPDTW on the same type of container pairing problems.

On the other hand, the result of the import–inland delivery is shown in Table 8, where a number of import orders should be delivered from the port to their destinations and a number of inland orders should be delivered from one inland location (origin) to another (destination). In order to see by how much the combined delivery can reduce transportation costs, the solution of the MILP is compared with a trivial solution where all orders are served individually by 20-ft trucks. The result for this benchmark solution is given under “Without pairing” columns, whereas the solution of the MILP is displayed under “With pairing”. Note that the “With pairing” case also allows individual delivery—the optimal decision is simply picked up by the MILP model minimizing the total working cost (transportation plus penalty). The result shows that the minimum cost (O.F) for the paired case is 10–39% less than the cost (O.F) for the individual delivery across all cases that we have tested. In general, when the inland orders take a high proportion in the overall orders pool, the improvement of pairing is less significant over individual delivery. This is due to the fact that, with existences of inland depots, finding a nearby depot to start/end the inland trip is not difficult. So the necessity of combining the trip with an import or another inland order is diluted. On the other hand, as there is only one port which is normally far away from customer locations, the combination of orders for import delivery is more vital in reducing transportation cost. This also justifies our initial argument that emphasis should be made to the pairwise delivery import/export orders only. Table 9 shows the result for the combination of import–inland–export orders. Similar as the import–inland case, allowing combination of tours saves at most 44% of the total delivery cost. Notice that Table 9 gives the detailed number of tours that combined 1, 2 or 3 containers, these in turn represent the number of import/inland/export tours that are served individually, the number of import–inland/import–export/inland–export tours that are served pairwisely and the number of import–inland–export tours. The individual tour in this case is largely reduced with combination, which justifies the preference of using combined delivery as well.

6 Conclusions

In this paper, the delivery of 20-ft orders (containers) from their origins to destinations is investigated, and an assignment MILP optimization model is formulated for the PCDT with the aim of minimizing the travelling cost and penalty paid for over time working. A great number of realistic restrictions are considered in the model such as time windows at customer locations, and working time regulations, ready time of containers at the port and the usage of inland depots to reduce empty travels. In addition, this work also allows containers to be delivered to multi-destinations for discharging, which is economically convenient for customers running relatively small business.

The model can be implemented for different types of transportation such as the import (delivery) of containers, import–inland as well as the import–inland–export. The decision of delivering orders paired or individually can be made efficiently by solving the MILP model using commercial software like Cplex. Even under a dense inland depot setting, a 23% operations cost reduction is achievable in average across all testing examples. Testing on numerical examples drawn from realistic geographical data shows that up to 350 orders can be solved using the MILP model within reasonable time (about 30 min), which outperforms traditional models that are based on the VRP-SPDTW which normally solves instances up to 75 (Vidović et al, 2011). Without needing any heuristics, more accurate and reliable solution can be achieved efficiently by the proposed model.