Directional marginal productivity: a foundation of meta-data envelopment analysis

Abstract

Differential characteristics of the production function represent elasticity measures and marginal rates of production technologies; in particular, marginal productivity (MP) plays an important role in economic theory and applications. This study provides a theoretical foundation of directional marginal productivity (DMP) supporting the meta-data envelopment analysis (meta-DEA) which measures the efficiency via marginal-profit-maximized orientation. In addition, the segmented marginal rate of technical substitution is developed based on DMP. In fact, DMP is developed to address finding the improving direction of the efficient firm on the frontier towards the marginal profit maximization. This approach, which emphasizes “planning” over “efficiency evaluation”, forms the basis for transforming a typical “ex-post” DEA into an “ex-ante” DEA study. Two case studies show that the DMP provides an explicit span of directions for productivity improvement via a trade-off between these distinct directions.

1 Introduction

This study provides a theoretical foundation of directional marginal productivity (DMP) supporting the meta-data envelopment analysis (meta-DEA) which measures efficiency via marginal-profit-maximized orientation (Lee, 2014). We illustrate the derivation of the DMP and propose the segmented marginal rate of technical substitution (MRTS).

Differential characteristics of the production function generally can be calculated by the partial derivatives of the production function, given a smooth efficient frontier. However, the partial derivative usually presents one-to-one mapping, i.e. how a change in single input contributes to single output. In practice, one-to-many mapping, or how a change in single input contributes to multiple outputs simultaneously, is more meaningful. In fact, the microeconomic theory supports a substitution between multiple products and a multi-objective decision-making process is common. An expectable trade-off between multiple products refers to multi-output marginal productivity (MP) estimation. This study, a foundation of the meta-DEA, uses directional distance function (DDF) to develop the DMP theoretically.

Marginal rate plays an important role in economic theory and applications. The primary purpose of the estimation of a production function is to obtain estimates of the regression coefficients. These coefficients refer to MPs, which characterize how the dependent variable will be affected by changing one extra unit of independent variables. In a DEA framework, the dual multiplier linear program to the primal envelopment model represents the MP and it also refers to shadow price. Economists use the term “elasticity” to measure the percentage of how changing one variable affects the others.¹ Applications of MP or elasticity in the literature include Banker and Thrall (1992) and Førsund and Hjalmarsson (2004), who developed a range of scale elasticity to explicitly support the decision-maker since DEA may not have a unique shadow price. Cooper et al (2000) addressed marginal rates and elasticities of substitution using the slacks in an additive DEA model. The optimal slack values can be positive or negative to achieve the efficient frontier. Moreover, Lee et al (2002) and Mekaroonreung and Johnson (2012) estimated the shadow prices of SO₂ and NO_x, i.e. the undesirable outputs (pollution) generated from the production process via DEA and convex nonparametric least squares (CNLS) (Kuosmanen, 2008; Kuosmanen and Johnson, 2010; Lee et al, 2013).

From an engineering perspective, the estimation of MP also contributes to capacity planning and resource allocation. Capacity is the maximal output level of a production process. The output is a result of the total productive capability of a firm’s resources including workforce, machinery, and utilities. Capacity adjustment is the ability to adjust output levels to response uncertainty by controlling variable resources in the short run. In production theory, capacity adjustment can be interpreted as the MP of the production function, i.e. the extra output generated by one more unit of an input. Johansen’s (1968) definition of physical capacity is the maximum amount that can be produced with existing fixed inputs (e.g. plant and equipment), given an unlimited availability of variable factors. Johansen’s definition distinguishes between a short-run production function describing the production possibilities keeping capacity variables (e.g. capital equipment) fixed, and a long-run production function characterizing all inputs is variable inputs contributing to capacity measures. Färe et al (1989b) employed a nonparametric approach to obtain the capacity measure with a cross-sectional data set. Lee and Johnson (2014) proposed an “effectiveness” measure and “proactive DEA” approach, which benefit capacity adjustment under demand fluctuation via MP estimation.

The developments of MP estimation are limited due to the estimation difficulty at the edges of the frontier and anchor points (see Krivonozhko et al, 2004; Hadjicostas and Soteriou, 2006; Bougnol and Dulá, 2009). Identifying anchor points which define the transition from the Pareto–Koopmans efficient frontier to the free disposability of the boundary is extremely complicated. Thus, optimal solutions of dual multipliers in DEA are used to investigate the anchor points. However, using nonparametric techniques of DEA results in nonunique solutions, most of which present zero values. In addition, because the production function cannot be observed easily in practice, a piece-wise linear production function can be estimated using DEA based on collected observations (Banker et al, 1984; Fried et al, 2008). However, a piece-wise linear frontier forms a polyhedral set representing production technologies and thus is not differentiable. To overcome the problem of nondifferentiability, Podinovski and Førsund (2010) gave an explicit definition of differential characteristics on a nondifferentiable efficient frontier and proposed a directional-derivative approach to calculate elasticity measures without any simplifying assumptions. They applied differential characteristics to the DEA frontier and addressed elasticity measures and marginal rates of substitution (Asmild et al, 2006).

Several studies have addressed the performance evaluation or productivity improvement of an inefficient firm based on input-oriented measure, output-oriented measure, hyperbolic measure (Färe et al, 2002; Kuosmanen, 2005), or directional distance function (Chambers et al, 1996, 1998; Chung et al, 1997), yet only a few have discussed the productivity improvement of an efficient firm on the frontier. Zofio and Prieto (2006) suggested choosing the direction in the DDF to move towards the allocatively efficient benchmarks. Extending their work, to the case of efficient firms, Lee (2014) suggests that firms should select the direction via DMP to move towards the direction of marginal profit maximization.

This study provides a theoretical foundation of meta-DEA. An analytical expression of MP measures of multiple outputs (i.e. DMP) is obtained by solving the dual multipliers of DDF; in particular, one-to-many mapping is developed. This study also alternatively addresses the most general class of measures, including the mixed input and output bundles such as MRTS and any types of elasticity measure. We also consider the undesirable-output case.

This study is organized as follows. Section 2 introduces the estimation of single-output MP. Section 3 introduces the DDF. Section 4 develops the DMP estimation by DDF from one specific input to multiple outputs and illustrates the segmented MRTS. Section 5 presents a meta-DEA model. Section 6 introduces DMP for undesirable outputs. Section 7 gives two numerical examples, and Section 8 concludes the study and suggests future research.

2 Single-output marginal productivity

We first assess the single-output MP of a nondifferential efficient frontier constructed by the DEA estimator based on a directional-derivative technique proposed by Podinovski and Førsund (2010). Let set I represent the inputs and index i ∊ I. Set J represents outputs and index j ∊ J. Set K represents firm and index k ∊ K. Index r ∊ K is used for one specific firm and is an alias of k. Let observations X _ik be the ith input level and Y _jk be the jth output level of firm k. Let λ _k be the decision variable referring to the intensity weights representing the convex combination between firms, and let y _j be the decision variable representing the maximum absolute level of output j. When estimating DMP, based on the microeconomic theory, some of the inputs are not controllable and considered as the nondiscretionary inputs at their current values (Banker and Morey, 1986). Thus, we estimate possible change in the discretionary inputs and keep exogenously fixed inputs constant. Model (1) determines the maximum absolute level of one specific output $j^{*}$, given the level of one specific (discretionary) input $i^{*}$ of one specific firm r.

$$ \begin{array}{*{20}l} {\text{Max}} \hfill & {y_{{j^{*} }} } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{{i^{*} k}} \le X_{{i^{*} r}} } } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{ik} \le X_{ir} } ,\quad \forall i \ne i^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{{j^{*} k}} \ge y_{{j^{*} }} } } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{jk} \ge Y_{jr} } ,\quad \forall j \ne j^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} = 1} } \hfill \\ {} \hfill & {\lambda_{k} \ge 0,\quad y_{{j^{*} }} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(1)

Let v _i , u _j , and u ₀ be the decision variables representing the dual multipliers of input constraint, output constraint, and convex-combination constraint in model (1), respectively. We can now construct the dual model of model (1) as model (2).

$$ \begin{aligned} {\text{Min}} & \sum\limits_{i \in I} v_{i} X_{ir} - \mathop{\mathop{\sum}\limits_{j \in J}}\limits_{j \ne j^{*}} u_{j} Y_{jr} + u_{0} \hfill \\ {{\text{s}} . {\text{t}} . { }} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ik}} - \sum\limits_{j \in J} {u_{j} Y_{jk} + u_{0} \ge 0} ,\quad \forall k} \hfill \\ {} \hfill & {u_{{j^{*} }} = 1} \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{aligned} $$

(2)

Recalling that MP is a characteristic of the frontier, for one specific efficient firm r, the following revised formulation calculates the marginal rate $\beta_{{i^{*} j^{*} r}}^{{ + {\text{DEA}}}}$ approaching from the right side with respect to one particular input, $i^{*}$ and one output $j^{*}$. Since MP is defined on the efficient frontier, i.e. firm r is on the frontier and $y_{{j^{*} }} = Y_{{j^{*} r}}$ in model (1), we can derive the objective function $\sum\nolimits_{i} {v_{i} X_{ir} } - \sum\nolimits_{{j \ne j^{*} }} {u_{j} Y_{jr} + u_{0} = Y_{{j^{*} r}} }$ in model (2), and the model (3) estimates the $\beta_{{i^{*} j^{*} r}}^{{ + {\text{DEA}}}}$ (Podinovski and Førsund, 2010).

$$ \begin{aligned} \beta_{{i^{*} j^{*} r}}^{{ + {\text{DEA}}}} = {\text{Min}}\;v_{{i^{*} }} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ir}} - \sum\limits_{j \in J} {u_{j} Y_{jr} + u_{0} = 0} } \hfill \\ {} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ik}} - \sum\limits_{j \in J} {u_{j} Y_{jk} + u_{0} = 0} + u_{0} \ge 0,\quad \forall k} \hfill \\ {} \hfill & {u_{{j^{*} }} = 1} \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

(3)

To measure the marginal rate approaching from the left side, we simply replace the objective function by the following equation.

$$ \beta_{{i^{*} j^{*} r}}^{{ - {\text{DEA}}}} = {\text{Max}}\;v_{{i^{*} }} $$

(4)

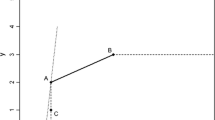
Therefore, Figure 1 illustrates the single-input single-output MP, $\beta_{{i^{*} j^{*} r}}^{{ + {\text{DEA}}}}$ or $\beta_{{i^{*} j^{*} r}}^{{ - {\text{DEA}}}}$, in terms of output expansion or contraction. ² Note that we do not define the MP for inefficient firms operating inside of the production frontier.

Figure 1

MP regarding output expansion or contraction

3 Directional distance function

The directional distance function (DDF) estimates efficiency by expanding outputs and reducing inputs at the same time (Luenberger, 1992; Chambers et al, 1996, 1998; Chung et al, 1997). Let $\varvec{g} = \left( {\varvec{g}^{\varvec{X}} ,\varvec{g}^{\varvec{Y}} } \right)$ be the predetermined directional vector for inputs and outputs, where $\varvec{g}^{\varvec{X}} \in {\Re }_{ + }^{\left| I \right|}$ and $\varvec{g}^{\varvec{Y}} \in {\Re }_{ + }^{\left| J \right|}$. Given direction vector $\left( {\varvec{g}^{\varvec{X}} ,\varvec{g}^{\varvec{Y}} } \right)$, we define the directional distance function as shown in model (5), where η is the decision variable for efficiency estimate. If η = 0, then a firm r is efficient; otherwise η > 0 represents the inefficient case.

$$ \begin{array}{*{20}l} {\text{Max}} \hfill & \eta \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{{i^{*} k}} \le X_{ir} - \eta g^{{X_{i} }} ,\quad \forall i} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{{j^{*} k}} \ge Y_{jr} + \eta g^{{Y_{j} }} } ,\quad \forall j} \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} = 1} } \hfill \\ {} \hfill & {\lambda_{k} \ge 0,\quad \eta \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(5)

To estimate the MP by DDF we develop model (6) to estimate the maximum absolute level of one specific output. Let $g^{{X_{{i^{*} }} }}$ and $g^{{Y_{{j^{*} }} }}$ be the given elements in directional vector $\varvec{g}$ of one specific input $i^{*}$ and one specific output $j^{*}$. Model (6) determines the maximum absolute level. Note that it is a variant of model (5), where $Y_{{j^{*} r}}$ is a constant describing output level of $j^{*}$ for a firm r and won’t affect the optimization result but for solely calculating the absolute level in objective function.

$$ \begin{array}{*{20}l} {\text{Max}} \hfill & { Y_{{j^{*} r}} + \eta g^{{Y_{{j^{*} }} }} } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{{i^{*} k}} \le X_{{i^{*} r}} - \eta g^{{X_{{i^{*} }} }} } } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{ik} \le X_{ir} ,} \quad \forall i \ne i^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{{j^{*} k}} \ge Y_{{j^{*} r}} + \eta g^{{Y_{{j^{*} }} }} } } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{jk} \ge Y_{jr} ,} \quad \forall j \ne j^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} = 1} } \hfill \\ {} \hfill & {\lambda_{k} \ge 0,\quad \eta \; {\text{is free}}} \hfill \\ \end{array} $$

(6)

We derive model (7) as the dual model of model (6) using dual variables mentioned above.

$$ \begin{array}{*{20}l} {\text{Min }} \hfill & { Y_{{j^{*} r}} + \sum\limits_{i \in I} {v_{i} X_{ir}} - \sum\limits_{j \in J} {u_{j} Y_{jr} + u_{0} } } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ik}} - \sum\limits_{j \in J} {u_{j} Y_{jk} + u_{0} } \ge 0,\quad \forall k} \hfill \\ {} \hfill & {v_{{i^{*} }} g^{{X_{{i^{*} }} }} + u_{{j^{*} }} g^{{Y_{{j^{*} }} }} = g^{{Y_{{j^{*} }} }} } \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(7)

Proposition 1

Given $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{{j^{*} }} }} } \right) = \left( {0,1} \right)$ if firm r is on the efficient frontier, then the objection function value of model (1) is equivalent to that of model (6), and the objection function value of model (2) is equivalent to that of model (7).

Proof

See Appendices 1 and 2.

Proposition 1 is important and shows that DDF is a generalized estimator, since it not only estimates efficiency by either one-input orientation or one-output orientation, but also achieves frontier by multi-orientation simultaneously. That is, DDF provides a hint to develop the DMP estimation of multi-product orientation by fine-tuning the given direction in DDF.

4 Directional marginal productivity via directional distance function

This section describes a proposed multi-output MP model (i.e. DMP). Based on the DDF, we develop a model to describe how the change of single input $X_{{i^{*} }}$ affects the multiple outputs. Let set $j^{*}$ ⊂ J be the outputs set whose MP will be investigated. We estimate DMP by model (8) given the direction vector $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{j} }} } \right)$ as parameters, where $g^{{X_{{i^{*} }} }} = 0$ and $\sum\nolimits_{{j \in J^{*} }} {g^{{Y_{j} }} = 1}$ for unit simplex (Färe et al, 2013).³ We then define the DDF as follows.

$$ \begin{array}{*{20}l} {\text{Max}} \hfill & \eta \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{{i^{*} k}} \le X_{{i^{*} r}} } } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} X_{ik} \le X_{ir} ,} \quad \forall i \ne i^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{jk} \ge Y_{jr} + \eta g^{{Y_{j} }} ,} \quad \forall j \ne J^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} Y_{jk} \ge Y_{jr} ,} \quad \forall j \in J \backslash J^{*} } \hfill \\ {} \hfill & {\sum\limits_{k \in K} {\lambda_{k} = 1} } \hfill \\ {} \hfill & {\lambda_{k} \ge 0,\quad \eta \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(8)

The firm r is on the frontier since MP is one of the differential characteristics on the frontier, i.e. $\eta = 0 = \sum\nolimits_{i \in I} {v_{i} X_{ir}} - \sum\nolimits_{j \in J} {u_{j} Y_{jr} + u_{0} .}$ Thus, we use a variant of dual model (9) to estimate the DMP of Y _j , j ∊ $j^{*}$, with respect to $X_{{i^{*} }}$ (Shapiro, 1979).

$$ \begin{array}{*{20}l} {\text{Min }} \hfill & {v_{{i^{*} }} } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ir}} - \sum\limits_{j \in J} {u_{j} Y_{jr} + u_{0} = 0} } \hfill \\ {} \hfill & {\sum\limits_{i \in I} {v_{i} X_{ik}} - \sum\limits_{j \in J} {u_{j} Y_{jk} + u_{0} \ge 0,} \quad \forall k} \hfill \\ {} \hfill & {\sum\limits_{{j \in J^{*} }} {u_{j} g^{{Y_{j} }} = 1} } \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(9)

Note that the direction $g^{{Y_{j} }}$ can be regarded as the “weightings” between investigated outputs. The larger the weight, the closer the DMP towards the output with the higher weight. For example, if $\left( {g^{{Y_{{j_{1} }} }} , g^{{Y_{{j_{2} }} }} } \right) = \left( {0,1} \right)$, then the DMP estimated by model (9) is the same as the single-output MP estimated by model (3) with respect to the second output.

To illustrate the “weights” (i.e. direction) among multi-output substitutability, we eliminate the unit of each factor for normalization. Let $X_{i}^{\text{Max}} = \hbox{max} \left\{ {X_{ik} } \right\}$ and $Y_{j}^{\text{Max}} = { \hbox{max} }\left\{ {Y_{jk} } \right\}$ and propose model (10).

$$ \begin{array}{*{20}l} {\alpha} = \hfill & {{\text{Min}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }}} \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i} {v_{i} \frac{{X_{ir} }}{{X_{i}^{\text{Max}} }}} - \sum\limits_{j} {u_{j} \frac{{Y_{jr} }}{{Y_{j}^{\text{Max}} }} + u_{0} = 0} } \hfill \\ {} \hfill & {\sum\limits_{i} {v_{i} \frac{{X_{ik} }}{{X_{i}^{\text{Max}} }}} - \sum\limits_{j} {u_{j} \frac{{Y_{jk} }}{{Y_{j}^{\text{Max}} }} + u_{0} \ge 0,} \quad \forall k} \hfill \\ {} \hfill & {\sum\limits_{{j \in J^{*} }} {u_{j} g^{{Y_{j} }} = 1} } \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad u_{0} \; {\text{is free}}} \hfill \\ \end{array} $$

(10)

The reason for introducing unit simplex and eliminating the measurement units of inputs and outputs is to normalize the weight which presents a trade-off among outputs. Take an example of two outputs. If we would like to estimate the MP passing the middle of two outputs, the weight $\left( {g^{{Y_{{j_{1} }} }} , g^{{Y_{{j_{2} }} }} } \right) = \left( {0.5,0.5} \right)$ should be assigned intuitively for calculating DMP since eliminating the measurement units makes units-invariant, i.e. the results are independent of the units of the inputs and outputs. Therefore, increasing one extra unit of $X_{{i^{*} }}$ of firm r means that the vector of the DMP with respect to output Y _j is $\frac{{\partial Y_{jr} }}{{\partial X_{{i^{*} r}} }} = \alpha \times \left( {g^{{Y_{j} }} Y_{j}^{\text{Max}} } \right),\forall j \in J^{*}$.

In addition, it is invalid to estimate the MP on the portion of free disposability with respect to the inputs. First, intuitively, the free disposable portion shows the direction that can reduce its input level while still maintaining the same outputs, i.e. this direction cannot truly reflect marginal productivity. Second, based on Proposition 2 below, MP estimates on the portion of free disposability with respect to inputs are equal to zero by model (10), even though MP in fact may not be zero.

Definition 1

Directional marginal productivity (DMP) is the MP characterizing how one extra unit of an input affects multiple outputs, i.e. $\frac{{\partial Y_{jr} }}{{\partial X_{{i^{*} r}} }} = \alpha \times \left( {g^{{Y_{j} }} Y_{j}^{\text{Max}} } \right),\forall j \in J^{*}$, generated from model (10).

Proposition 2

If the direction for MP estimation used in model (10) projects to the portion of free disposability with respect to inputs, then the MP estimate will be equal to 0.

Proof

See Appendices 1 and 2.

We also provide an alternative way to calculate the marginal rate of technical substitution (MRTS) of outputs based on DMP. The frontier in DEA is not smoothing; thus, in most cases, the estimation of the MP for a specific firm r is not a fixed value, but a range with minimal value and maximal value, i.e. [min, max], though it is possible that in some cases, i.e., the minimal value (min) is equal to the maximal value (max). To address the issue, we need to consider two-sided MP. Let DMP ⁺ be the DMP approaching from the right side which we obtain from model (10) with objective function $\alpha = {\text{Min}}\frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }}$; DMP⁻ be the DMP approaching from the left side we obtain from model (10) with objective function $\alpha = {\text{Max}}\frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }}$. Thus, DMP⁺ and DMP⁻ may form a range [min, max]. On the nonsmooth DEA frontier, MRTS should be calculated from both sides (see Podinovski and Førsund, 2010). For simplicity, we only illustrate MRTS⁺, which is generated by DMP⁺. The other case MRTS⁻ can be derived similarly.

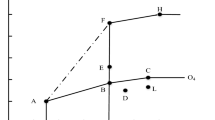
For a two-output case, we define a typical MRTS⁺ which can be calculated by two single-output MPs on a frontier hyperplane, where all inputs are fixed at some levels and all other output than $Y_{{j_{1} }}$ and $Y_{{j_{2} }}$ are fixed at some levels. That is, MRTS⁺ with the arbitrary two outputs $Y_{{j_{1} }}$ and $Y_{{j_{2} }}$ is calculated by ${\text{MRTS}}^{ + } = \frac{{ - {\text{MP}}_{{j_{1} }}^{ + } }}{{{\text{MP}}_{{j_{2} }}^{ + } }} = \frac{{ - \alpha_{1} Y_{{j_{1} }}^{\text{Max}} }}{{\alpha_{2} Y_{{j_{2} }}^{\text{Max}} }}$, where $j_{1} , j_{2} \in J^{*} ,\alpha_{1}$ is calculated by model (10), given the direction $\left( {g^{{Y_{{j_{1} }} }} , g^{{Y_{{j_{2} }} }} } \right) = \left( {1,0} \right)$, and α ₂ is calculated by $\left( {g^{{Y_{{j_{1} }} }} , g^{{Y_{{j_{2} }} }} } \right) = \left( {0,1} \right)$, which indicates a single-output MP (SOMP), respectively. Note, however, that because an estimated DEA piece-wise frontier in high dimensions forms a polyhedral set with multiple facets, a simple calculation of MRTS often provides a lower resolution. Figure 2 shows that each line segment (solid line) on the DEA frontier presents a different MRTS; the dashed line shows a rough but typical MRTS estimation by two single-output MPs. To resolve this issue, we develop a definition of “segmented MRTS (s-MRTS)” between any two DMPs by calculating the marginal difference of each output as follows (Section 7.1 describes an example illustration). For other approach to estimate s-MRTS, see Olesen and Petersen (1996, 2003).

Figure 2

MRTS and segmented MRTS: a two single-output MPs are used to calculate MRTS as dash line; b two DMPs are used to calculate s-MRTS as one piece-wise line segment on frontier

Definition 2

Segmented marginal rate of technical substitution (s-MRTS) can be calculated by investigating two specific outputs and defined as ${\hbox{s-MRTS}}^{ + } = \frac{{\Delta {\text{MP}}_{{j_{1} }} }}{{\Delta {\text{MP}}_{{j_{2} }} }} = \frac{{\left( {\alpha_{1} g_{1}^{{Y_{{j_{1} }} }} Y_{{j_{1} }}^{\text{Max}} - \alpha_{2} g_{2}^{{Y_{{j_{1} }} }} Y_{{j_{1} }}^{\text{Max}} } \right)}}{{\left( {\alpha_{1} g_{1}^{{Y_{{j_{2} }} }} Y_{{j_{2} }}^{\text{Max}} - \alpha_{2} g_{2}^{{Y_{{j_{2} }} }} Y_{{j_{2} }}^{\text{Max}} } \right)}}$, in particular, ${\text{DMP}}_{1}^{ + } = \left( {\alpha_{1} g_{1}^{{Y_{{j_{1} }} }} Y_{{j_{1} }}^{\text{Max}} ,\alpha_{1} g_{1}^{{Y_{{j_{2} }} }} Y_{{j_{2} }}^{\text{Max}} } \right)$ and ${\text{DMP}}_{2}^{ + } = \left( {\alpha_{2} g_{2}^{{Y_{{j_{1} }} }} Y_{{j_{1} }}^{\text{Max}} ,\alpha_{2} g_{2}^{{Y_{{j_{2} }} }} Y_{{j_{2} }}^{\text{Max}} } \right)$ are the two DMPs used for s-MRTS estimation.

In fact, the one-sided MRTS⁺ of transformation of output j ₁ with respect to output j ₂ can be calculated by model (9) with the objective function Max $- u_{{j_{2} }}$ and the given direction $\left( {g^{{Y_{{j_{1} }} }} , g^{{Y_{{j_{2} }} }} } \right) = \left( {1,0} \right)$.

5 Meta-DEA: direction towards marginal profit maximization

This section introduces meta-DEA to find a direction for an efficient firm to move towards its allocatively efficient benchmark based on maximization of the firm’s marginal profits (Lee, 2014). We know that different directions (i.e. weighting vector) may generate different DMPs, i.e. these DMPs can make a span like a frontier. However, this frontier is associated with MP rather than the levels of inputs or outputs. We term this a “meta-frontier”, i.e. frontier-about-frontier, because the DMPs are generated by DEA technique. Figure 3 gives an illustration, where P(x) is an output space referring to the production possibility set, given the level of one specific input. Note that DEA forms a “production possibility set” in the level of x, whereas meta-DEA forms a “marginal production possibility set” towards the level of x + Δx based on estimated MPs. Therefore, given input price and output price, we can find the direction for marginal profit maximization with one extra unit of input.

Figure 3

DEA frontier and meta-DEA frontier with two outputs

Given an input and output price vector (P _i , P _j ), there is a way to find the marginal-profit-maximized direction. We can generate the DMPs manually, given random-picked directions, and then calculate the allocative efficiency with respect to the meta-DEA frontier based on these discrete directions (i.e. vectors of DMPs). Let $g_{\psi }^{{Y_{j} }}$ be a “decision variable” representing ψth direction satisfying $\sum_{{j \in J^{*} }} {g_{\psi }^{{Y_{j} }} = 1}$ and $0 \le g_{\psi }^{{Y_{j} }} \le 1$, $\forall j \in J^{*}$. A direction vector $g_{\psi }^{{Y_{j} }}$ identified for marginal profit maximization is defined in mathematical formulation as the following equation.

$$ g_{\psi }^{{Y_{j} *}} = \arg \hbox{max} \left\{ {\sum\limits_{{j \in J^{*} }} {P_{j} \alpha_{\psi } g_{\psi }^{{Y_{j} }} Y_{j}^{\text{Max}} - P_{{i^{*} }} }\,|\, {\text{model}} \; \left( {10} \right) \; {\text{with price vector}} \; \left( {P_{i} ,P_{j} } \right), \forall \psi } \right\} $$

(11)

Note that, for changing one specific input, the marginal profit maximization is equivalent to the marginal revenue maximization due to a fixed marginal cost representing one extra unit of single input. See Lee (2014) for the benefits of meta-DEA and how it complements the profit-efficiency analysis (Nerlove, 1965).

So far, we have discussed a capacity expansion case. In estimating the marginal rate approaching from the right side, all of the elements $g^{{Y_{j} }}$ in a given direction are nonnegative. However, since some cases show capacity contraction towards marginal profit maximization, e.g. undesirable outputs such as pollution or waste, it is also helpful to estimate the marginal rate approaching from the left side via a negative direction. The next section discusses undesirable outputs in detail.

6 Directional marginal productivity for desirable and undesirable outputs

To estimate the marginal rate approaching from the left side, intuitively we can use a negative direction of $g^{{Y_{j} }}$. For a single-output case, we use models (3) and (4) to estimate $\beta_{{i^{*} j^{*} r}}^{{ + {\text{DEA}}}}$ and $\beta_{{i^{*} j^{*} r}}^{{ - {\text{DEA}}}}$; similarly, we can use model (10) with the objective function ${\text{Min}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha$ to estimate α for a DMP approaching from the right side and model (10) with the objective function ${\text{Max}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha$ for a DMP approaching from the left side. This gives rise to Proposition 3.

Proposition 3

The MP estimated by model (10) with the objective function ${\text{Max}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha$ is equivalent to the MP estimated, given a negative direction.

Proof

See Appendices 1 and 2.

Recall that the DEA estimator, in particular BCC model (Banker et al, 1984), assumes free disposability of undesirable outputs, which implies that a finite amount of input can produce an infinite amount of undesirable output. The assumption is physically unreasonable (Färe et al, 1989a; Färe and Grosskopf, 2003; Kuosmanen and Podinovski, 2009). Intuitively, we can reduce the level of the good output which in turn will result in a proportionate reduction of the undesirable outputs. This property is termed weak disposability (Shephard, 1974). The relationship between good output and undesirable output is nulljoint, and the undesirable output is a by-product of good output (Färe et al, 2007).

We introduce the weak disposability by Kuosmanen’s convex technology with undesirable outputs (Kuosmanen, 2005). Let Q be the set of undesirable output, Q ^* ⊂ Q be the subset of undesirable output investigated for DMP, and $g^{{B_{q} }}$ the direction of undesirable output q. For unit simplex $\sum\nolimits_{{j \in J^{*} }} {g^{{Y_{j} }}} + \sum\nolimits_{{q \in Q^{*} }} {g^{{B_{q} }} = 1}$, the direction is a vector $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{j} }} , g^{{B_{q} }} } \right)$, where $g^{{X_{{i^{*} }} }} = 0$, $g^{{Y_{j} }} \ge 0$, and $g^{{B_{q} }} \ge 0$. Model (12) defines the DDF with undesirable outputs as follows.

$$ \begin{array}{*{20}l} {\text{Max}} \hfill & \eta \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{k} {\left( {\lambda_{k} + \mu_{k} } \right)X_{{i^{*} k}} \le X_{{i^{*} r}} } } \hfill \\ {} \hfill & {\sum\limits_{k} {\left( {\lambda_{k} + \mu_{k} } \right)X_{ik} \le X_{ir} ,} \quad \forall i \ne i^{*} } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} Y_{jk} \ge Y_{jr} + \eta g^{{Y_{j} }} ,} \quad \forall j \in J^{*} } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} Y_{jk} \ge Y_{jr} ,} \quad \forall j \in J \backslash J^{*} } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} B_{qk} = B_{qr} - \eta g^{{B_{q} }} ,} \quad \forall q \in Q^{*} } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} B_{qk} = B_{qr} ,} \quad \forall q \in Q \backslash Q^{*} } \hfill \\ {} \hfill & {\sum\limits_{k} {\left( {\lambda_{k} + \mu_{k} } \right) = 1} } \hfill \\ {} \hfill & {\lambda_{k} , \mu_{k} \ge 0,\quad \eta \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} $$

(12)

Since the firm r is on the frontier, $\sum _{i} v_{i} X_{ir} - \sum _{j} u_{j} Y_{jr} + \sum _{q} w_{q} B_{qr} + u_{0} = 0$. Thus, let $B_{q}^{\text{Max}} = \hbox{max} \left\{ {B_{qk} } \right\}$, the dual model of model (12) estimates the DMP of $Y_{j} ,j \in J^{*}$ and $B_{q} ,q \in Q^{*}$ with respect to $X_{{i^{*} }}$ by eliminating the unit of factors.

$$ \begin{aligned} \alpha = {\text{Min}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i} {v_{i} } \frac{{X_{ir} }}{{X_{i}^{\text{Max}} }} - \sum\limits_{j} {u_{j} } \frac{{Y_{jr} }}{{Y_{j}^{\text{Max}} }} + \sum\limits_{q} {w_{q} } \frac{{B_{qr} }}{{B_{q}^{\text{Max}} }} + u_{0} = 0} \hfill \\ {} \hfill & {\sum\limits_{i} {v_{i} } \frac{{X_{ik} }}{{X_{i}^{\text{Max}} }} - \sum\limits_{j} {u_{j} \frac{{Y_{jk} }}{{Y_{j}^{\text{Max}} }}} + \sum\limits_{q} {w_{q} } \frac{{B_{qr} }}{{B_{q}^{\text{Max}} }} + u_{0} \ge 0,\quad \forall k} \hfill \\ {} \hfill & {\sum\limits_{i} {v_{i} \frac{{X_{ik} }}{{X_{i}^{\text{Max}} }} + u_{0} \ge 0,} \quad \forall k} \hfill \\ {} \hfill & {\sum\limits_{{j \in J^{*} }} {u_{j} g^{{Y_{j} }}} + \sum\nolimits_{{q \in Q^{*} }} {w_{q} g^{{B_{q} }} = 1} } \hfill \\ {} \hfill & {v_{i} , u_{j} \ge 0,\quad w_{q} ,u_{0} \; {\text{are}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

(13)

Therefore, we calculate the DMP with undesirable outputs by $\frac{{\partial \left( {Y_{jr} ,B_{qr} } \right)}}{{\partial X_{{i^{*} r}} }} = \alpha \times \left( {g^{{Y_{j} }} Y_{j}^{\text{Max}} , - g^{{B_{q} }} B_{q}^{\text{Max}} } \right)$, $\forall j \in J^{*} ,\forall q \in Q^{*}$. In this case, the firm would like to increase desirable outputs and decrease undesirable outputs simultaneously by controlling input level. The DMP provides a good insight into the best direction for effective resource allocation, i.e. “Generate more energy, but less pollution”. Note that to estimate MP on the portion of free disposability with respect to one investigated input is invalid, which is similar to the issue discussed in Section 4.

7 Numerical illustrations

Section 7.1 explains how to estimate a two-output MP case by using the proposed model (10) described in Section 4. Section 7.2 explains how to estimate a DMP case considering one-undesirable output by using the model (13) described in Section 6.

7.1 Two-output case

We return to the example in Podinovski and Førsund (2010), which includes one input, two outputs, and three observations. However, we change the scale of the second output to illustrate the benefit of unit elimination as model (10) (Table 1).

Table 1 Data set for a two-output MP case

For one specific unit A, given $g^{{Y_{1} }} + g^{{Y_{2} }} = 1$ for normalization, we use the direction $\left( {g^{{X_{1} }} ,g^{{Y_{2} }} , g^{{Y_{2} }} } \right)$ to generate model (14), where $g^{{X_{1} }} = 0$.

$$ \alpha = {\text{Min}} \frac{{v_{1} }}{4} $$

$$ \begin{aligned} \alpha = {\text{Min}} \frac{{v_{1} }}{4} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {v_{1} \frac{2}{4} - u_{1} \frac{1}{4} - u_{2} \frac{200}{300} + u_{0} = 0} \hfill \\ {} \hfill & {v_{1} \frac{4}{4} - u_{1} \frac{2}{4} - u_{2} \frac{300}{300} + u_{0} \ge 0} \hfill \\ {} \hfill & {v_{1} \frac{1}{4} - u_{1} \frac{4}{4} - u_{2} \frac{100}{300} + u_{0} \ge 0} \hfill \\ {} \hfill & {u_{1} g^{{Y_{1} }} + u_{2} g^{{Y_{2} }} = 1} \hfill \\ {} \hfill & {v_{1} , u_{1} , u_{2} \ge 0,\quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

(14)

When increasing one extra unit of X ₁ in unit A, the DMP of Y ₁ and Y ₂ is $\frac{{\partial \left( {Y_{1A} ,Y_{2A} } \right)}}{{\partial X_{1A} }} = \alpha \times \left( {4g^{{Y_{1} }} ,300g^{{Y_{2} }} } \right)$. Given the output price vector (P ₁, P ₂),⁴ where P ₁ > 0 and P ₂ > 0, we observe that the meta-DEA can identify the direction for marginal profit maximization. Due to our two-output case, the optimal direction is associated with output price ratio, i.e. P ₁/P ₂. We investigate a resolution of 10 intervals (11 cases) between $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {1,0} \right)$ and $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {0,1} \right)$ as shown in Table 2 and Figure 4.

Table 2 DMP and meta-DEA of Y ₁ and Y ₂ in unit A

Figure 4

DMP and meta-DEA of Y ₁ and Y ₂ in unit A (revised from Podinovski and Førsund, 2010)

Table 2 shows that the single-output MP of unit A is consistent with the result shown in Podinovski and Førsund (2010), i.e. the MP of Y ₁ is 4 using the direction $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {1,0} \right)$, and the MP of Y ₂ is 50 using the given direction $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {0,1} \right)$, respectively. Keeping in mind that the DEA frontier includes a free disposable portion with respect to outputs, and given that the same MP of Y ₂ is equal to 50, we can increase the MP of Y ₁ to obtain 0.44 by shifting the direction from $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {0,1} \right)$ to (0.4, 0.6). When we increase one extra unit of input, we prefer to choose the direction $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {0.4,0.6} \right)$, rather than (0, 1) to generate more.

In addition, given the output price vector, the meta-DEA shows the marginal profit maximization of the two outputs and points out the direction for productivity improvement. For instance, if the output price ratio is between 14.24 and $14.26-$, the meta-DEA suggests a direction $\left( {g^{{Y_{1} }} ,g^{{Y_{2} }} } \right) = \left( {0.6,0.4} \right)$. In fact, it points out the allocatively efficient benchmarks on MP frontier. We can also calculate the s-MRTS for unit A as shown in Table 2. For example, we use the DMPs in case 1 and case 2 to calculate ${\hbox{s-MRTS}} = \frac{{\Delta {\text{MP}}_{{j_{1} }} }}{{\Delta {\text{MP}}_{{j_{2} }} }} = \frac{{\left( {4 - 2.53} \right)}}{{\left( {0 - 21.05} \right)}} = - 0.07$. N/A represents s-MRTS which cannot be calculated due to a portion of free disposability of output Y ₁. Note that a typical MRTS is ${\text{MRTS}} = \frac{{ - {\text{MP}}_{1} }}{{{\text{MP}}_{2} }} = \frac{{\alpha_{1} Y_{1}^{\text{Max}} }}{{\alpha_{2} Y_{2}^{\text{Max}} }} = \frac{ - 1 \times 4}{0.167 \times 300} = - 0.08$, where α ₁ and α ₂ are calculated by $\left( {g^{{Y_{1} }} , g^{{Y_{2} }} } \right) = \left( {1,0} \right)$ and (0, 1), respectively. However, this MRTS across a boundary (edge) between two facets gives imprecise estimate of MRTS.

7.2 One-desirable-output and one-undesirable-output case

Returning again to Kuosmanen and Podinovski (2009), we consider two observations (units D and E in Table 3) and change the scale of the undesirable output.

Table 3 Data set for an undesirable-output MP case

We investigate a resolution of 10 intervals (11 cases) between $\left( {g^{{Y_{1} }} ,g^{{B_{1} }} } \right) = \left( {1,0} \right)$ and $\left( {g^{{Y_{1} }} ,g^{{B_{1} }} } \right) = \left( {0,1} \right)$ as shown in Table 4. The result shows that the MPs generated by cases 8, 9, and 10 will benefit unit D by decreasing its undesirable output and slightly increasing its good output by moving forward to unit E along the frontier. However, MPs estimated from case 1 to case 7 are equal to zeros based on Proposition 2, since the directions we assign project to the portion of free disposability with respect to input. MP equal to zero does not provide any useful information for productivity improvement when adjusting the input level. In fact, the MP estimate of unit D is not zero, given the direction projecting to the free disposability portion of the input.

Table 4 The DMP of Y ₁ and B ₁ in unit D

8 Conclusion

This study provides a theoretical foundation of DMP supporting the meta-DEA which measures efficiency via marginal-profit-maximized orientation. DMP investigates the differential characteristics of nonsmooth piece-wise linear frontier estimate by DEA, and we explicitly derived the DMP by DDF. Since increasing one extra unit of input can simultaneously contribute to multiple outputs, this study fills the gap in the literatures and extends the Podinovski and Førsund’s (2010) work to the DMP given the predetermined directional vector. In practice, the DMP can be used to build the span of MP frontier supporting the productivity improvement via resource reallocation, e.g. a capacity adjustment matching demand fluctuation. The managerial implication of DMP enhances the decision quality on marginal effects.

In addition, DMP can be also applied to the computation of MRTS and we develop an alternative measure of s-MRTS to compensate the typical MRTS measure via a segmentation technique and calculation of each output’s marginal difference. Typically, the MRTS can be estimated by the ratio of two derivatives of DDF with respect to different outputs (Grosskopf et al, 1995). However, these derivatives usually come from the dual variables of output constraints in DEA formulation, and thus, the nonunique dual solutions are common. The proposed s-MRTS addresses the issue and also complements the approach shown in Olesen and Petersen (2003).

For the future works, the synergistic effects of multiple inputs and multiple outputs can be considered. Noting that the estimation of the increase in output is conservative if two or more inputs are expanded simultaneously, we suggest separately estimating the marginal production of each inputs and then taking the dot product of the marginal product vector. However, doing so will not capture any synergistic effects between the different inputs. In addition, the DMP estimation can support capacity adjustment, but moving along the efficient frontier too far may be out of production possibility set. To maintain feasibility, meaning that a firm remains within its original production possibility set after taking adjustment, we suggest a limited range of the resource adjustments and recalculating the MP in each iterative short-distance move to ensure that the firm remains within the production possibility set due to the law of diminishing marginal returns (Lee and Johnson, 2014).

Appendices

Appendix 1: DEA as sign-constrained convex nonparametric least squares

The convex nonparametric least squares (CNLS) technique (Hildreth, 1954; Kuosmanen, 2008) describes the average behaviour of observations. CNLS avoid the prior assumptions regarding function form while maintaining the standard regularity conditions for production functions, namely continuity, monotonicity, and concavity. Later, Kuosmanen and Johnson (2010) demonstrated that inefficiency estimated by the sign-constrained CNLS is equivalent to that estimated by the additive output-oriented DEA. The coefficients associated with the independent factors intuitively provide estimates of the MP in a regression-based approach.

Now, we describe how to prove that β ^+DEA _ik is consistent with the β ^+CNLS _ik estimated by the sign-constrained CNLS. Let ɛ _r be the inefficiency term of specific firm r. We obtain the nonradial DEA inefficiency estimate ɛ ^DEA _r by solving the following linear programming formulation. Note that the DEA formulation (15) differs from the standard radial output-oriented variable-return-to-scale (VRS) DEA.

$$ \begin{aligned} \varepsilon_{r}^{\text{DEA}} = {\text{argmin}} \; \varepsilon_{r} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & { \sum\limits_{k} {\lambda_{k} Y_{k} + \varepsilon_{r} = Y_{r} } } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} X_{ik} \le X_{ir} ,\forall i} } \hfill \\ {} \hfill & {\sum\limits_{k} {\lambda_{k} = 1} } \hfill \\ {} \hfill & {\lambda_{k} \ge 0,\quad \forall k} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

(15)

Next, we obtain the inefficiency estimate ɛ ^CNLS _k of firm k by solving the following sign-constrained CNLS. Let index h be an alias of index k, α _k be the intercept coefficient, and β _ik be the slope coefficient of the ith input of kth firm.

$$ \begin{aligned} \varepsilon_{k}^{\text{CNLS}} = {\text{argmin}}\sum\limits_{k} {\varepsilon_{k}^{2} } \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {\varepsilon_{k} \le 0,\quad \forall k} \hfill \\ {} \hfill & {Y_{k} = \alpha_{k} + \sum _{i} \beta_{ik} X_{ik} + \varepsilon_{k} ,\quad \forall k} \hfill \\ {} \hfill & {\alpha_{k} + \sum\limits_{i} {\beta_{ik} X_{ik} \le \alpha_{h}} + \sum\limits_{i} {\beta_{ih} X_{ik} } ,\quad \forall k, \forall h} \hfill \\ {} \hfill & {\beta_{ik} \ge 0,\quad \forall i, k} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

(16)

Both models (15) and (16) measure inefficiency relative to the same DEA frontier; recall that Kuosmanen and Johnson proved $\varepsilon_{k}^{\text{DEA}} = \varepsilon_{k}^{\text{CNLS}}$. The firm is efficient if and only if its inefficiency estimate equals zero; otherwise, values smaller than zero represent measures of inefficiency. The result also shows that the estimates β _ik can be interpreted as MP. Since model (16) generates multiple solutions, the objective function could be replaced by $M \sum _{k} \varepsilon_{k}^{2} + \sum _{i,k} \beta_{ik}$ to acquire unique solution, where M is a large enough number. This expansion to estimate a unique solution keeps an identical piece-wise linear frontier and obtains the right-side MP $\frac{{\partial Y_{k} }}{{\partial X_{ik} }} = \beta_{ik}^{{ + {\text{CNLS}}}} = \beta_{ik}$. Vice versa, replacing the objective function with $M \sum\nolimits_{k} \varepsilon_{k}^{2} - \sum _{i,k} \beta_{ik}$ obtains the left-side MP $\frac{{\partial Y_{k} }}{{\partial X_{ik} }} = \beta_{ik}^{{ - {\text{CNLS}}}} = \beta_{ik}$ as Figure 1.

Since models (15) and (16) generate the same DEA frontier, based on Theorem 3.1 in Kuosmanen and Johnson’s (2010) we extend the proof with respect to MP by developing Proposition 4.

Proposition 4

For all real-valued data, the MP estimated by sign-constrained convex nonparametric least squares model (16) with objective function $M \sum\nolimits_{k} {\varepsilon_{k}^{2} } + \sum\nolimits_{i,k} {\beta_{ik} }$ is equivalent to the MP estimated by DEA model (3); that is, $\beta_{ik}^{{ + {\text{DEA}}}} = \beta_{ik}^{{ + {\text{CNLS}}}}$; the similar result can be applied to $\beta_{ik}^{{ - {\text{DEA}}}} = \beta_{ik}^{{ - {\text{CNLS}}}}$.

Proposition 4 is interesting. It explicitly illustrates the MP generated by DEA model (3) as the MP directly shown as the coefficient of independent factors in the regression-based CNLS model. Thus, it reveals that the MP can be generated by the DDF as an implicit formulation of model (15). This also gives rise to Proposition 5.

Proposition 5

The single-output MP estimation by additive DEA, sign-constrained CNLS, and DDF with direction vector $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{{j^{*} }} }} } \right) = \left( {0,1} \right)$ shows a consistent result.

Appendix 2: Proof of theorems

Proposition 1

Given $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{{j^{*} }} }} } \right) = \left( {0,1} \right)$ if firm r is on the efficient frontier, then the objection function value of model (1) is equivalent to that of model (6), and the objection function value of model (2) is equivalent to that of model (7).

Proof

Since firm r is on the efficient frontier, model (6) generates η = 0. In fact, $\sum\nolimits_{k} {\lambda_{k} Y_{{j^{*} k}} } \ge Y_{{j^{*} r}} + \eta g^{{Y_{{j^{*} }} }}$ and $\sum\nolimits_{k} {\lambda_{k} Y_{{j^{*} k}} \ge y_{j*} }$ are equivalent. Let $y_{j*} = Y_{{j^{*} r}} + \eta g^{{Y_{{j^{*} }} }}$, i.e. $\eta g^{{Y_{{j^{*} }} }} = y_{j*} - Y_{{j^{*} r}}$, if $g^{{X_{{i^{*} }} }} = 0$ and $g^{{Y_{{j^{*} }} }} = 1$, then $\eta = y_{j*} - Y_{{j^{*} r}}$. The model is exactly the same as model (1) when $\eta = 0$. Thus, λ _k are the same in model (1) and model (6). In addition, given $\left( {g^{{X_{{i^{*} }} }} , g^{{Y_{{j^{*} }} }} } \right) = \left( {0,1} \right)$ in model (7), then $u_{{j^{*} }} = 1$ and $Y_{{j^{*} r}}$ is a constant, which allows us to remove the terms $Y_{{j^{*} r}}$ and $u_{{j^{*} }} Y_{{j^{*} r}}$ from the objective function of model (7). The objective function of model (7) is the same as that of model (2). Thus, optimal solutions v _i and u _j are the same. Model (2) is equivalent to model (7).

Proposition 2

If the direction for MP estimation used in model (10) projects to the portion of free disposability with respect to inputs, then the MP estimate will be equal to 0.

Proof

To prove this proposition by model (10) is equivalent to proving it by model (9), since model (10) is a normalized version of model (9). If λ ₀, λ _k , and η are dual variables of each constraint in model (9), respectively, the dual model of model (9) with $\sum\nolimits_{{j \in J^{*} }} {g^{{Y_{j} }} = 1}$ is as follows.

$$ \begin{array}{*{20}l} {{\text{Max}}\;\eta } \hfill \\ {\sum\nolimits_{k} {\lambda_{k} X_{{i^{*} k}} \le 1 - \lambda_{0} X_{{i^{*} r}} } } \hfill \\ {\sum\nolimits_{k} {\lambda_{k} X_{ik} \le - \lambda_{0} X_{ir} ,} \quad \forall i \ne i^{*} } \hfill \\ {\sum\nolimits_{k} {\lambda_{k} Y_{jk} \ge - \lambda_{0} Y_{jr} + \eta g^{{Y_{j} }} ,} \quad \forall j \in J^{*} } \hfill \\ {\sum\nolimits_{k} {\lambda_{k} Y_{jk} \ge - \lambda_{0} Y_{jr} ,} \quad \forall j \in J \backslash J^{*} } \hfill \\ {\sum\nolimits_{k} {\lambda_{k} = - \lambda_{0} } } \hfill \\ {\lambda_{k} \ge 0,\eta ,\quad \lambda_{0} \; {\text{are}}\;{\text{free}}} \hfill \\ \end{array} $$

Note that in the above model, if −λ ₀ = 1, then the model is almost equivalent to model (8) except that first constraint $\sum\nolimits_{k} {\lambda_{k} X_{{i^{*} k}} \le 1 - \lambda_{0} X_{{i^{*} r}} }$. When model (9) estimates the MP projecting to the portion of free disposability with respect to one specific input, the slack in input constraints $\sum\nolimits_{k} {\lambda_{k} X_{{i^{*} k}} \le 1 - \lambda_{0} X_{{i^{*} r}} }$ is positive. That is, its dual variables $v_{{i^{*} }} = 0$ in model (9). Thus, the objective function in model (10) is $\frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha = 0$ and $\frac{{\partial Y_{jr} }}{{\partial X_{{i^{*} r}} }} = \alpha \times \left( {g^{{Y_{j} }} Y_{j}^{\text{Max}} } \right)$ will be a zero vector.

Proposition 3

The MP estimated by model (10) with the objective function ${\text{Max}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha$ is equivalent to the MP estimated, given a negative direction.

Proof

Given $g^{{Y_{j} }}$ is negative, let $\sum_{{j \in J^{*} }} {g^{{Y_{j} }} = - 1}$ for normalization. The objective function of model (8) will be ${\text{Max}} \eta \left( {\sum\nolimits_{{j \in J^{*} }} {g^{{Y_{j} }} } } \right) = {\text{Max}} - \eta$. To obtain the same optimal solution, we replace the objective function of model (8) by ${\text{Min }}\eta$. Thus, the first constraint of model (9) will be ∑  _i v _i X _ir  − ∑  _j u _j Y _jr  + u ₀ = 0 and the objective function of model (9) will be ${\text{Max}} v_{{i^{*} }}$. Finally, the objective function will be ${\text{Max}} \frac{{v_{{i^{*} }} }}{{X_{{i^{*} }}^{\text{Max}} }} = \alpha$ in model (10).

Proposition 4

For all real-valued data, the MP estimated by sign-constrained convex nonparametric least squares model (16) with objective function $M\sum\nolimits_{k} {\varepsilon_{k}^{2} } + \sum\nolimits_{i,k} {\beta_{ik} }$ is equivalent to the MP estimated by DEA model (3); that is, $\beta_{ik}^{{ + {\text{DEA}}}} = \beta_{ik}^{{ + {\text{CNLS}}}}$; the similar result can be applied to $\beta_{ik}^{{ - {\text{DEA}}}} = \beta_{ik}^{{ - {\text{CNLS}}}}$.

Proof

For the single-output case, we calculate MP using model (3).

$$ \begin{aligned} \beta_{ir}^{{ + {\text{DEA}}}} = {\text{Min}}\;v_{i} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i} {v_{i} X_{ir} - uY_{r} + u_{0} = 0} } \hfill \\ {} \hfill & {\sum\limits_{i} {v_{i} X_{ik} - uY_{k} + u_{0} \ge 0,\quad \forall k} } \hfill \\ {} \hfill & {u = 1} \hfill \\ {} \hfill & {v_{i} , u \ge 0, \quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

Then, for one specific firm r, we need to solve the following model k times.

$$ \begin{aligned} \beta_{ir}^{{ + {\text{DEA}}}} = {\text{Min}}\;v_{i} \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {Y_{r} = \sum\limits_{i} {v_{i} X_{ir} + u_{0} } } \hfill \\ {} \hfill & {Y_{k} \le \sum\limits_{i} {v_{i} X_{ik} + u_{0} ,} \quad \forall k} \hfill \\ {} \hfill & {v_{i} \ge 0, \quad u_{0} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

However, for all firm k, we only need to solve one time (i.e. one-shot solution) by using the following formation.

$$ \begin{aligned} \beta_{ik}^{{ + {\text{DEA}}}} = {\text{argmin}}_{{u_{0} ,v}} \sum\limits_{i,k} {v_{ik} } \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {Y_{h} = \sum _{i} v_{ih} X_{ih} + u_{0h} ,\quad \forall h} \hfill \\ {} \hfill & {Y_{k} \le \sum\limits_{i} {v_{ih} X_{ik} + u_{0h} ,} \quad \forall k, \forall h} \hfill \\ {} \hfill & {v_{ik} \ge 0, \quad u_{0k} \; {\text{is}}\;{\text{free}}} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

Let u _0k  = α _k  + ɛ _k , where α _k represents the intercept and ɛ _k represents the deviation of inefficiency. We know ɛ _k  = 0 since all firms k are on the efficient frontier. Therefore, we harmlessly impose the sign-constraint as an additional constraint. Clearly, the inefficient firms (for which ɛ _h  < 0) do not influence the shape of the DEA frontier, and thus, we add the inefficiency components into the constraint and write the formulation equivalently as follows.

$$ \begin{aligned} \beta_{ik}^{{ + {\text{DEA}}}} = {\text{argmin}}_{{u_{0} ,v}} \sum\limits_{i,k} {v_{ik} } \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & {Y_{h} = \sum\limits_{i} {v_{ih} X_{ih} + \alpha_{h} + \varepsilon_{h} } ,\quad \forall h} \hfill \\ {} \hfill & {\sum\limits_{i} {v_{ik} X_{ik} + \alpha_{k} + \varepsilon_{k} \le } \sum\limits_{i} {v_{ih} X_{ik} + \alpha_{h} + \varepsilon_{h} ,} \quad \forall k, \forall h} \hfill \\ {} \hfill & {v_{ik} \ge 0, \quad \alpha_{k} \; {\text{is}}\;{\text{free}},\quad \varepsilon_{k} = 0} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

The model is the same as the CNLS frontier characterized by all efficient firms with ɛ _k  = 0. We replace v _ik by β _ik . Finally, we derive the sign-constrained CNLS formulation to estimate the MP as follows.

$$ \begin{aligned} \beta_{ik}^{{ + {\text{CNLS}}}} = {\text{argmin}}_{\varepsilon ,\alpha ,\beta } M\sum\limits_{k} {\varepsilon_{k}^{2}} + \sum\limits_{i,k} {\beta_{ik}} = {\text{argmin}}_{\varepsilon ,\alpha ,\beta } \sum\limits_{i,k} {\beta_{ik} } \hfill \\ \begin{array}{*{20}l} {{\text{s}} . {\text{t}} . } \hfill & {\varepsilon_{k} = 0,\quad \forall k} \hfill \\ {} \hfill & {Y_{k} = \alpha_{k} + \sum\limits_{i} {\beta_{ik} X_{ik} + \varepsilon_{k} ,} \quad \forall k} \hfill \\ {} \hfill & {\alpha_{k} + \sum\limits_{i} {\beta_{ik} X_{ik} \le \alpha_{h}} + \sum\limits_{i} {\beta_{ih} X_{ik} ,} \quad \forall k, \forall h} \hfill \\ {} \hfill & {\beta_{ik} \ge 0,\quad \forall i, k} \hfill \\ {\text{Thus,}} \hfill & {\beta_{ik}^{{ + {\text{DEA}}}} = \beta_{ik}^{{ + {\text{CNLS}}}} .} \hfill \\ \end{array} \hfill \\ \end{aligned} $$

Proposition 5

The single-output MP estimation by additive DEA, sign-constrained CNLS, and DDF with direction vector $\left( {g^{{X_{{i^{*} }} }} ,g^{{Y_{{j^{*} }} }} } \right) = \left( {0,1} \right)$ shows a consistent result.

Proof

We can obtain the proof directly from Propositions 1 and 4.