1 Introduction

The effect of state dependent service rates in healthcare has been well studied in isolated hospitals. In Batt and Terwiesch (2012), an empirical study is undertaken and service rate slow down is identified. Furthermore, it is shown that modelling whilst ignoring these state dependent rates leads to errors. This effect is further identified in Chan et al (2014), Kc and Terwiesch (2012) where for example the negative effect on patient outcome is revealed. In Kim et al (2013), Shmueli et al (2003), this is expanded to consider a variety of admission policies in two CCUs; in particular the effect of rejection (due to too high occupancy) is measured. These policies are studied in the setting of a single hospital, and thus, from a game theoretic point of view correspond to rational behaviour (a good game theory reference text is Maschler et al (2013)). In practice, a simplification of rational strategies is managed by policy makers by setting utilisation targets that ensure that hospitals do not run at a level likely to have a high rejection rate (example of these can be seen in Bevan and Hood (2006), Kesavan (2013)).

The aim of this paper is to further investigate the effect of rational policies employed by Hospitals. In particular, the goal is to place this in a game theoretic setting so as to identify whether or not target policies result in uncoordinated behaviour that is damaging for patients.

A critical care unit (CCU), also sometimes referred to as an Intensive Therapy Unit or Intensive Therapy Department, is a special ward that is found in most acute hospitals. It provides intensive care (treatment and monitoring) for people who are critically ill or are in an unstable condition. CCUs face major challenges, on average, 8% of patients are refused admission to a CCU because the Unit is full (Audit Commission, 1999). The CCU occupancy rates for some hospitals are reportedly very high (Mitchell and Grounds, 1995; Smith et al, 1995) and a shortage of beds has been identified throughout the United Kingdom.

Many previous researchers have developed queueing models to help manage bed capacities in hospitals: Cooper and Corcoran (1974), Dumas (1984), Gallivan and Utley (2011), Gorunescu et al (2002), Griffiths et al (2013), Harper and Shahani (2002). Also, a vast amount of literature has been devoted to the simulation of CCUs; Cahill and Render (1999), Costa et al (2003), Griffiths et al (2005), Kim et al (1999), Litvak et al (2008), Shahani et al (2008).

This paper describes part of a project undertaken with managers from the Aneurin Bevan University Health Board (ABUHB), which is an NHS Wales organisation in South Wales, that serves 21% of the total population of Wales (Board, 2014). Critical care is delivered on two sites, at the Nevill Hall hospital in Abergavenny and at the Royal Gwent hospital in Newport. For the remainder of this paper, the Nevill Hall hospital will be referred to as NH and the Royal Gwent hospital as RG.

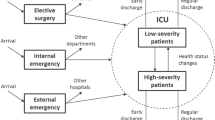
The main proposition of the work requested by the ABUHB was to develop a mathematical model of bed occupancies at the CCUs at RG and NH. After an initial analysis of the data, behavioural aspects became apparent; for example, delaying patients discharge if there was no pressure on CCU beds, or admitting fewer patients if bed occupancy levels were high. As a result of this, a state-dependent queueing model has been developed, which includes the dependency of admission rate on actual occupancy (Williams et al 2015). This state dependent model was applied to both NH and RG separately. It is however obvious that the actions of one CCU impact on the other CCU, as diversion of patients from one CCU to the other sometimes occurs. A pictorial representation of the situation is given in Figure 1.

Figure 1
figure 1

Diagrammatic representation of CCU interaction through patient diversion

Full size image

Most research where game theory is applied in healthcare has mainly concentrated on emergency departments (EDs) and how to deal with diversions of patients and ambulances. In Hagtvedt and Ferguson (2009), cooperative strategies for hospitals are considered, in order to reduce occurrences when ambulances are turned away due to the ED being full. In Deo and Gurvich (2011), a queueing network model of two EDs is proposed to study the network effect of ambulance diversion. Each ED aims to minimise the expected waiting time of its patients (walk-ins and ambulances) and chooses its diversion threshold based on the number of patients at its location. Decentralised decision making in the network is modelled as a non-cooperative game.

Some other work that has not concentrated on EDs, but has been applied to healthcare includes: Knight and Harper (2013), where results concerning the congestion related implications of decisions made by patients when choosing between healthcare facilities were presented. In Howard (2002), a model of the accept/reject decision for transplant organs is developed.

In the wider intersection of game theory and queueing theory (where this work lies), papers that consider price and/or capacity include Allon and Federgruen (2007), Cachon and Harker (2002), Cachon and Zhang (2007), Kalai et al (1992), Levhari and Luski (1978). In these models, the choice of price/or capacity determines the arrival rate for each firm; this is similar to the approach taken in this paper.

The work presented in this paper contributes to the growing body of literature by applying state-dependent queueing models in a game theoretical context to CCU interaction. In particular, this consideration allows for the investigation of targets imposed by central control (Bevan and Hood, 2006). The findings of this work justify and identify a choice of targets that align the interests of the individual hospitals with social welfare.

The data used for the work presented in this paper were provided by the Intensive Care National Audit and Research Centre (ICNARC) and refer to patients admitted to CCUs in NH and RG, and cover a period of three years, from the 1st January 2009 till the 31st December 2011. The dataset contains information about a patient’s source of admission, date and time of admission, date and time of discharge, CCU outcome and delay to discharge. The parameters obtained from the data used in this work are shown in Table 1.

Table 1 Parameter values used in the model
Full size table

Note that, the inter-arrival and service rates are not state dependent. These will serve as a base level for the state dependent rates used throughout the game theoretic models.

The paper is organised as follows: Section 2 presents the general methodology as well as a theoretical existence condition for Nash Equilibrium. Section 3 presents the findings from two models. Finally, conclusions and further ideas for progression are given in Section 4.

2 Queueing and game theoretic models

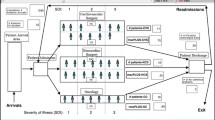
Throughout this paper, it is assumed that both CCUs (NH and RG) act selfishly and rationally. The strategies of each CCU are capacity thresholds at which they declare being in “diversion.” When in “diversion” the arrival rates of patients are modified. Given the proximity of the two CCUs, one CCU could for example divert their patients to the other. Figure 2 shows a diagrammatic representation of this where \(\lambda _H^{r}\) for \(H\in \{\text {NH}, \text {RG}\}\) and \(r\in \{(l,l), (l,h), (h,l), (h,h)\}\) simply denote arrival rates that will be defined for both models considered in Section 3, where r denotes regions with boundaries defined by the capacity thresholds. For example (l, h) denotes a region for which \(\text {NH}\) experiences low demand and \(\text {RG}\) experiences high demand. It is also assumed that diverted patients will be treated under the length of stay profile of the CCU they are admitted to. The capacity thresholds are denoted as \(K_{H}\in \mathbb {Z}\) for \(H\in \{\text {NH},\text {RG}\}\). Note that \(0\le K_H\le c_H\).

Figure 2
figure 2

General arrival rates for each CCU at each region, where \(H\in \{\text {NH}, \text {RG}\}\)

Full size image

To formally investigate the impact of decentralised decision making, the interaction between two CCUs is placed within a non-cooperative game framework. The interaction will be modelled through a two dimensional continuous Markov chain that will now be described.

2.1 Queueing model

The state space for the Markov chain is given by (1).

$$\begin{aligned} S=S(c_{\text {NH}}, c_{\text {RG}})= \{(u,v)\in \mathbb {Z}^2\ |\ 0\le u\le c_{\text {NH}},\ 0\le v\le c_{\text {RG}}\} \end{aligned}$$
(1)

For given \(K_{\text {NH}}, K_{\text {RG}}\) and using the notation of Figure 2, the generic Markov chain used to model the interactive queueing system in this paper is shown in Figure 3.

Figure 3
figure 3

Generic Markov chain underpinning the queueing model of this paper

Full size image

In total there are \((c_{\text {NH}}+1)\times (c_{\text {RG}}+1)\) states and they are indexed lexicographically: \((0,0), (0,1), (0,2), \dots\).

The stochastic transition rate matrix \(Q=Q(c_{NH},c_{RG})\) of the continuous-time Markov chain (Stewart 2009) has entries \(q_{ij}=q_{(u_i,v_i),(u_j,v_j)}\) which is the rate at which a transition from state i to state j occurs. The transition rates are given by (2) and are illustrated diagrammatically in Figure 3.

$$\begin{aligned} q_{(u_i,v_i),(u_j,v_j)}={\left\{ \begin{array}{ll} u\mu _{\text {NH}} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(1,0),\\ v\mu _{\text {RG}} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,1),\\ \lambda _{NH}^{(l,l)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(-1,0) \,\text{ and } \, u_i< K_{\text {NH}} \, \text { and } \, v_i< K_{\text {RG}},\\ \lambda _{RG}^{(l,l)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i< K_{\text {NH}} \, \text { and } \, v_i< K_{\text {RG}},\\ \lambda _{NH}^{(l,h)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i< K_{\text {NH}} \, \text { and } \, v_i \ge K_{\text {RG}},\\ \lambda _{RG}^{(l,h)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i< K_{\text {NH}} \, \text { and } \, v_i \ge K_{\text {RG}},\\ \lambda _{NH}^{(h,l)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i \ge K_{\text {NH}} \, \text { and } \, v_i< K_{\text {RG}},\\ \lambda _{RG}^{(h,l)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i \ge K_{\text {NH}} \, \text { and } \, v_i < K_{\text {RG}},\\ \lambda _{NH}^{(h,h)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i \ge K_{\text {NH}} \, \text { and } \, v_i \ge K_{\text {RG}},\\ \lambda _{RG}^{(h,h)} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i \ge K_{\text {NH}} \, \text { and } \, v_i \ge K_{\text {RG}},\\ 0 &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$
(2)

Utilities will be of interest when this queueing theoretical model will be inserted in the game theoretical model. Throughput of patients is a natural choice of utility given that most hospitals are financially rewarded per served patient (Pate, 2009). For each threshold pair \((K_{\text {NH}},K_{\text {RG}})\), the utilisation rate \(U_H\) and throughput \(T_H\) can easily be obtained for each CCU: \(H\in \{\text {NH},\text {RG}\}\), using the following formulas:

$$\begin{aligned} U_{H}={{\sum _{n=0}^{c_H} nP^{(H)}(n)}\over {c_{H}}} \end{aligned}$$
$$\begin{aligned} T_{H}=\mu _H \sum _{n=0}^{c_H} nP^{(H)}(n) \end{aligned}$$

where \(P^{(H)}=P^{(H)}(K_{\text {NH}},K_{\text {RG}})\) is the steady-state probability distribution function (obtained from the corresponding transition matrix \(Q=Q(K_{\text {NH}},K_{\text {RG}})\)) for \(H\in \{\text {NH},\text {RG}\}\).

For \(c_{\text {NH}}=8\), \(c_{\text {RG}}=16\), \(\lambda _{\text {NH}}=(\lambda _{\text {NH}}^{(l,l)},\lambda _{\text {NH}}^{(l,h)},\lambda _{\text {NH}}^{(h,l)},\lambda _{\text {NH}}^{(h,h)})=(1.5,3.74,0,0)\), \(\lambda _{\text {RG}}=(\lambda _{\text {RG}}^{(l,l)},\lambda _{\text {RG}}^{(l,h)},\lambda _{\text {RG}}^{(h,l)},\lambda _{\text {RG}}^{(h,h)})=(2.24,0,3.74,0)\) and \((K_{\text {NH}},K_{\text {RG}})=(6,12)\), the steady-state probabilities for each CCU are given in Figure 4.

Figure 4
figure 4

Steady-state probabilities for each hospital (\(H\in \{\text {NH},\text {RG}\}\)) with different threshold pairs (\((K_{\text {NH}}, K_{\text {RG}})=(6,12)\))

Full size image

For the parameters of Figure 4, the utilisation rates are 59% at NH and 62% at RG and a throughput of 1.23 at NH and 1.98 at RG (patients per day).

For a different threshold pair of \((K_{\text {NH}},K_{\text {RG}})=(1,12)\) the steady-state probabilities are given in Figure 5. The utilisation rates are 11% at NH and 67% at RG and throughput of 0.23 at NH and 2.13 at RG. We see that the RG is now busier as a result of NH having a lower diversion threshold. A model of this interaction will be given in the next section.

Figure 5
figure 5

Steady-state probabilities for each hospital (\(H\in \{\text {NH},\text {RG}\}\)) with different threshold pairs (\((K_{\text {NH}}, K_{\text {RG}})=(1,12)\))

Full size image

2.2 Game theoretic model

Based on the discussion above, the game theoretic model is presented as a synchronous optimisation problem shown in the following optimisation problem.

Optimisation problem.

For all \(H\in \{\text {NH}, \text {RG}\}\) minimise

$$\begin{aligned} \left( U_{H}-t\right) ^2 \end{aligned}$$

Subject to

$$\begin{aligned} 0\le&\; K_H \le c_{H}\\&K_H \in \mathbb {Z}\nonumber. \end{aligned}$$
(3)

This game is equivalent to a bimatrix game with restriction to pure strategies where both players aim to get their utilisation as close as possible to a certain target. Such a Nash Equilibrium is not guaranteed by traditional game theoretical results (Nash, 1950), which guarantee the existence of equilibria in mixed strategies. Based on discussions with ABUHB, long-term threshold policies are a realistic consideration and so a pure strategy space is used.

The following result is a sufficient condition for the existence of an equilibrium:

Theorem

Let \(f_{H}(k):[1,c_{\bar{H}}]\rightarrow [1,c_H]\) be the best response of player \(H\in \{\text {NH}, \text {RG}\}\) to the diversion threshold of \(\bar{H}\ne H\) (\(\bar{H}\in \{\text {NH}, \text {RG}\}\)).

If \(f_{H}(k)\) is a non-decreasing function in k then the game of (3) has at least one Nash Equilibrium.

Proof

The function \(f_H\) is well defined as it maximises a continuous function over a finite discrete set. In case of multiple values that minimise \(U_H\), it is assumed that \(f_H\) returns the lowest such value, this is consistent with the Price of Anarchy (PoA) being a theoretical upper bound of the effect of uncoordinated behaviour (Roughgarden, 2005).

As such if \(f_H\) is non-decreasing, then it is in fact a stepwise non-decreasing function. If we consider \(f_{\text {NH}}\) and \(f_{\text {RG}}\) plotted on the same axis (so that the domain of \(f_{\text {NH}}\) is the x-axis and the domain of \(f_{\text {RG}}\) is the y-axis), it is obvious to see that the functions must intersect at some point as shown in Figure 6.

Figure 6
figure 6

Plots of best response functions: \(f_{\text {NH}}(K_{\text {RG}})\) (crosses) and \(f_{\text {RG}}(K_{\text {NH}})\) (diamonds)

Full size image

This point of intersection corresponds to a Nash Equilibrium of (3). \(\square\)

This Theorem is in itself not that useful as the properties of \(f_{H}\) are difficult to ascertain. Although the methodology alluded to is how the equilibria are found for the work presented here (exhaustive investigation of best response functions). The following Lemma will however be of more use in Section 3.

Lemma

Using the convention of Figure 2:

  • If \(\lambda _{\text {NH}}^{(h,l)}\le \lambda _{\text {NH}}^{(h,h)},\lambda _{\text {NH}}^{(l,l)}\le \lambda _{\text {NH}}^{(l,h)}\) then \(f_{\text {NH}}(k)\) is a non-decreasing function in k.

  • If \(\lambda _{\text {RG}}^{(l,h)}\le \lambda _{\text {RG}}^{(h,h)},\lambda _{\text {RG}}^{(l,l)}\le \lambda _{\text {RG}}^{(h,l)}\) then \(f_{\text {RG}}(k)\) is a non-decreasing function in k.

Observation

The utilisation \(U_H=U_H(\lambda )\) is an increasing function in \(\lambda\). As the traffic intensity at H increases: H gets busier.

Proof

A proof for the first part of the Lemma is given (the proof for the second part is analogous).

Let \(\bar{\lambda }_{\text {NH}} = \bar{\lambda }_{\text {NH}}(K_{\text {RG}})\) be the effective arrival rate at NH. If \(\lambda _{\text {NH}}^{(h,l)}\le \lambda _{\text {NH}}^{(h,h)},\lambda _{\text {NH}}^{(l,l)}\le \lambda _{\text {NH}}^{(l,h)}\) then this implies that \(\bar{\lambda }_{\text {NH}}(K_{\text {RG}}) \ge \bar{\lambda }_{\text {NH}}(K_{\text {RG}} + 1)\) as shown in Figure 7.

Based on the previous observation this in turn implies: \(U_{\text {NH}}(K_{\text {RG}}) = U_{\text {NH}}(\bar{\lambda }_{\text {RG}}(K_{\text {RG}}) \ge U_{\text {NH}}(\bar{\lambda }_{\text {RG}}(K_{\text {RG}}+1)) = U_{\text {NH}}(K_{\text {RG}}+1)\) giving:

$$\begin{aligned} U_{\text {NH}}(K_{\text {RG}}) \ge U_{\text {NH}}(K_{\text {RG}}+1) \end{aligned}$$
(4)

In the same way (illustrated by Figure 8), this gives: \(U_{\text {NH}}(K_{\text {NH}}) = U_{\text {NH}}(\bar{\lambda }_{\text {NH}}(K_{\text {NH}})) \le U_{\text {NH}}(\bar{\lambda }_{\text {NH}}(K_{\text {NH}}+1)) = U_{\text {NH}}(K_{\text {NH}}+1)\) giving:

$$\begin{aligned} U_{\text {NH}}(K_{\text {NH}}) \le U_{\text {NH}}(K_{\text {NH}}+1) \end{aligned}$$
(5)

Using (4) and (5), the general inequalities associated with \(U_{\text {NH}}(K_{\text {NH}}, K_{\text {RG}})\) are summarised in Figure 9.

As \(U_{\text {NH}}\) increases from the lowest value (top left in Figure 9) to the highest (bottom right in Figure 9), the value of \(U_{\text {NH}}-t\) will change sign (from negative to positive). Let

$$\begin{aligned} f^+(K_{\text {RG}})={{\mathrm{arg\!min}}}_{\{0\le k \le C_{\text {NH}}|U_{\text {NH}}(k, K_{\text {RG}})\ge t\}}(U_{\text {NH}}(k, K_{\text {RG}})) \end{aligned}$$
(6)

and

$$\begin{aligned} f^-(K_{\text {RG}})={{\mathrm{arg\!max}}}_{\{0\le k \le C_{\text {NH}}|U_{\text {NH}}(k, K_{\text {RG}})\le t\}}(U_{\text {NH}}(k, K_{\text {RG}})). \end{aligned}$$
(7)

Thus, \(f^{\pm }({K_{\text {RG}}})\) is the value of \(K_{\text {NH}}\) that gives the value of \(U_{\text {NH}}(K_{\text {NH}}, K_{\text {RG}})\) that is closest to \(t\) such that

$$\begin{aligned} U_{\text {NH}}(f^-(K_{\text {RG}}),K_{\text {RG}})\le t \le U_{\text {NH}}(f^+(K_{\text {RG}}),K_{\text {RG}}). \end{aligned}$$
(8)

This immediately (from Figure 9) gives

$$\begin{aligned} f^{\pm }(K_{\text {RG}}) \le f^{\pm }(K_{\text {RG}} + 1). \end{aligned}$$
(9)

Let

$$\begin{aligned} S(K_{\text {RG}}) = \{f^{-}(K_{\text {RG}})\}\cup \{f^{+}(K_{\text {RG}})\}. \end{aligned}$$
(10)

Thus, \(f(K_{\text {RG}})\in S(K_{\text {RG}})\). Note that from (5) \(\max (S(K_{\text {RG}}))=f^{+}(K_{\text {RG}})\) and \(\min S(K_{\text {RG}})=f^{+}(K_{\text {RG}})\). In essence \(S(K_{\text {RG}})\) corresponds to the set of two values of \(K_{\text {NH}}\) that give a utilisation just below and just above \(t\).

There are two possibilities that will now be considered:

  1. 1.

    \(S(K_{\text {RG}})\ne S(K_{\text {RG}}+1)\)

  2. 2.

    \(S(K_{\text {RG}})= S(K_{\text {RG}}+1)\)

    If \(S(K_{\text {RG}})\ne S(K_{\text {RG}})\) this implies that \(f^{+}(K_{\text {RG}})\le f^{-}(K_{\text {RG}}+1)\) which gives

    $$\begin{aligned} f(K_{\text {RG}}) \le f^{+}(K_{\text {RG}}) \le f^{-}(K_{\text {RG}}+1) \le f(K_{\text {RG}}+1) \end{aligned}$$
    (11)

    which is the required result.

To finish the proof consider \(S(K_{\text {RG}})=S(K_{\text {RG}})\) which is equivalent to \(f^{\pm }(K_{\text {RG}})=f^{\pm }(K_{\text {RG}}+1)\) and assume

$$\begin{aligned} f(K_{\text {RG}})=f^{+}(K_{\text {RG}}) \text { but } \, f(K_{\text {RG}}+1)=f^{-}(K_{\text {RG}}+1) \end{aligned}$$
(12)

which, because it has been assumed that \(f^{-}(K_{\text {RG}}+1)=f^{-}(K_{\text {RG}})\), contradicts the required result (as this would imply that \(f(K_{\text {RG}})< f(K_{\text {RG}}+1)\)).

For simplicity of notation let

$$\begin{aligned} a^{\pm }=(f^{\pm }(K_{\text {RG}}), K_{\text {RG}})\,\, \text { and } \,\, b^{\pm }=(f^{\pm }(K_{\text {RG}}+1), K_{\text {RG}}+1))=(f^{\pm }(K_{\text {RG}}), K_{\text {RG}}+1)). \end{aligned}$$

Recalling equations (4–5) and Figure 9 gives

$$\begin{aligned} U_{\text {NH}}(b^-)&\le U_{\text {NH}}(a^-)\end{aligned}$$
(13)
$$\begin{aligned} U_{\text {NH}}(b^+)&\le U_{\text {NH}}(a^+) \end{aligned}$$
(14)

which implies

$$\begin{aligned} U_{\text {NH}}(b^-) + U_{\text {NH}}(b^+) \le U_{\text {NH}}(a^-) + U_{\text {NH}}(a^-). \end{aligned}$$
(15)

As \(f(K_{\text {RG}})=f^{+}(K_{\text {RG}})\) (this is the assumption made):

$$\begin{aligned} |U_{\text {NH}}(a^+)-t|<|U_{\text {NH}}(a^-)-t| \end{aligned}$$
(16)

which implies

$$\begin{aligned} U_{\text {NH}}(a^+)+U_{\text {NH}}(a^-)<2t. \end{aligned}$$
(17)

Similarly as \(f(K_{\text {RG}}+1)=f^{-}(K_{\text {RG}}+1)\) (this is the assumption made):

$$\begin{aligned} |U_{\text {NH}}(b^+)-t|>|U_{\text {NH}}(b^-)-t| \end{aligned}$$
(18)

which implies

$$\begin{aligned} U_{\text {NH}}(b^+)+U_{\text {NH}}(b^-)>2t. \end{aligned}$$
(19)

Combining (17) and (19) contradicts (15) implying that the original assumption was incorrect thus proving the required result. \(\square\)

Figure 7
figure 7

The effect of the threshold (\(K_{\text {RG}}\)) on the effective arrival rate (\(\bar{\lambda }\)). The same behaviour is exhibited for \(\lambda _{\text {NH}}^{(l,l)}\) and \(\lambda _{\text {NH}}^{(l, h)}\)

Full size image
Figure 8
figure 8

The effect of the threshold (\(K_{\text {NH}}\)) on the effective arrival rate (\(\bar{\lambda }\)). The same behaviour is exhibited for \(\lambda _{\text {NH}}^{(l,l)}\) and \(\lambda _{\text {NH}}^{(l, h)}\)

Full size image
Figure 9
figure 9

Values of utilisation (\(U_{\text {NH}}\)) and the corresponding inequalities for varying cutoff thresholds

Full size image

The aim of the work presented is to measure the inefficiency created by the removal of central control between CCUs.

We let \(\widetilde{T}\) denote the sum of throughputs at the Nash Equilibrium obtained by solving the game of (3) (in case of multiple equilibria we take \(\widetilde{T}\) to be the lowest throughput) and let \(T^*=\max _{K_{\text {NH}}, K_{\text {RG}}}\left( T_{\text {NH}}+T_{\text {RG}}\right)\). This optimal throughput \(T^*\) is independent of \(t\).

Note that intuitively it could be thought that \(T^*\) is obtained when \(K_{\text {NH}}=c_{\text {NH}}\) and \(K_{\text {RG}}=c_{\text {RG}};\) however, this is not always the case (numerical experiments have been carried out to verify this).

The measure used to quantify inefficiency is the Price of Anarchy (PoA) (Koutsoupias and Papadimitriou, 1999; Roughgarden, 2005), which is the ratio of the social optimum welfare to the welfare of the worst Nash Equilibrium. That is, the ratio of the largest social welfare, \(T^*\) , to the smallest social welfare, \(\widetilde{T}\), achieved at any Nash Equilibrium. Thus,

$$\begin{aligned} \text {PoA}={{T^*}\over {\widetilde{T}}}. \end{aligned}$$

Note that the classic definition of PoA has been modified here to allow for a maximisation problem. Social welfare is here considered to be a maximisation of throughput. An immediate alignment of interests can be obtained by setting \(t=1\). This however would not be in the interest of the hospital (nor necessarily in the interests of patients) as it would imply aiming to run at 100% utilisation which imply a large quantity of patients being rejected. A sensible value of t is the lowest value of t that ensures a low PoA.

3 Results

The game theoretic model of (3) is solved using exhaustive consideration of best responses whilst taking advantage of the structure identified by the Lemma of Section 2. For any given pair of threshold strategies, the matrix equation \(\pi Q=0\) is solved by obtaining a basis for the kernel of Q. For the purpose of this paper, this is implemented in Sagemath (Stein et al, 2013).

3.1 Model 1: Strict diversion

This model assumes that if the bed occupancy level at both CCUs exceeds a predetermined threshold, then the admission to the CCU is cancelled. This cancellation could correspond to sending the patient to a completely different CCUs (outside of the model), moving one of the current CCU patients (ready to be discharged) to another ward and/or using the post-anaesthesia care unit as a temporary overflow measure. This model corresponds to the first possibility: the patient is lost (from the point of view of this model).

Recalling Figure 2 this implies

$$\begin{aligned} \lambda _{\text {NH}}^{(r)}={\left\{ \begin{array}{ll} \lambda _{\text {NH}}, &{}\text {if }r=(l,l)\\ \lambda _{\text {NH}}+\lambda _{\text {RG}}, &{}\text {if }r=(l,h)\\ 0, &{}\text {if }r\in \{(h,l),(h,h)\}\\ \end{array}\right. } \qquad \qquad \lambda _{\text {RG}}^{(r)}={\left\{ \begin{array}{ll} \lambda _{\text {RG}}, &{}\text {if }r=(l,l)\\ \lambda _{\text {NH}}+\lambda _{\text {RG}}, &{}\text {if }r=(h,l)\\ 0, &{}\text {if }r\in \{(l,h),(h,h)\}\\ \end{array}\right. } \end{aligned}$$

We immediately see that the Lemma of Section 2 holds and so a Nash Equilibrium for our model exists.

If either CCU chooses their threshold at zero, patients are not admitted at all, and, consequently both Units are closed.

Therefore, the matrix Q has entries \(q_{ij}\) as follows:

$$\begin{aligned} q_{(u_i,v_i),(u_j,v_j)}={\left\{ \begin{array}{ll} u_i\mu _{NH} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(1,0),\\ v_i\mu _{RG} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,1),\\ \lambda _{\text {NH}} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i<K_{\text {NH}} \, \text { and } \, v_i<K_{\text {RG}},\\ \lambda _{\text {RG}} &{} \text { if } (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i<K_{\text {NH}} \, \text { and } \, v_i< K_{\text {RG}},\\ \lambda _{\text {NH}}+\lambda _{\text {RG}} &{} \text { if } \left\{ \begin{array}{l} (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i<K_{\text {NH}} \, \text { and } \, v_i \ge K_{\text {RG}} \text { or}\\ (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i \ge K_{\text {NH}} \, \text { and } \, v_i < K_{\text {RG}},\\ \end{array}\right. \\ 0 &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$
(20)

For the parameters of Table 1, the best responses are shown in Figure 10. For example, in Figure 10a if RG chooses \(K_{\text {RG}}=6\), NH has best response \(K_{\text {NH}}=8\) . Similarly, if \(K_{\text {NH}}=2\), RG has best response \(K_{\text {RG}}=15\). A Nash Equilibrium for our game is a pair of points that intersect.

Figure 10
figure 10

Best responses for each hospital (a: \(t=0.8\); b: \(t=0.6\)). The point of intersection is circled

Full size image

For this model, the Nash Equilibrium is at (8, 16), which gives \(\widetilde{T}=3.65\) and we obtain \(T^*=3.65\). Importantly, a PoA of 1 is not guaranteed for this problem. For example in Figure 10b similar best response behaviour is shown for \(t=0.6\) for which the \(\text {PoA}=1.18\) (the optimal throughput is again at (8, 16)).

Whilst removing central control, a certain influence can be exerted by a choice of t. Figure 11 (note: the non linear scale) and Table 2 show the effect of t and overall demand. We modify the demand rate from Table 1 by taking \(\lambda _H \leftarrow \lambda _H(1+x)\) for \(-0.9\le x\le 2\).

Figure 11
figure 11

PoA for different target and demand rates

Full size image
Table 2 Numerical values of PoA for different target and demand rates
Full size table

We see that an extremely large PoA is obtained for \(t<0.2\). For values of \(t>0.5\) the PoA is still high: a PoA of 2 corresponds to 100% less throughput of patients. These findings seem to give some backing to the targets implemented throughout the NHS (Bevan and Hood, 2006).

In particular, it can be seen that a value of \(t>0.8\) becomes imperative for high demand. The lowest value of t which gives PoA \(=1\) for the actual demand levels (\(x=0\)) is in fact \(t=0.72\). It is also noted that as demand increases the effect of uncoordinated behaviour increases (and the recommended target also increases) as shown in Figure 12. This is potentially due to the fact that as demand increases there is the scope for larger discrepancy between optimal and suboptimal behaviours.

Figure 12
figure 12

Lowest value of t ensuring PoA\(=1\)

Full size image

In this model, there is the potential for both CCUs to divert patients at the same time, and so patients are lost to the entire system. The model of the next section will investigate the effect of not allowing total rejections.

3.2 Model 2: Soft diversion

Recalling Figure 2, this model assumes

$$\begin{aligned} \lambda _{NH}^{(r)}={\left\{ \begin{array}{ll} \lambda _{NH}, &{}\text {if }r\in \{(l,l),(h,h)\}\\ \lambda _{NH}+\lambda _{RG}, &{}\text {if }r=(l,h)\\ 0, &{}\text {if }r=(h,l)\\ \end{array}\right. } \end{aligned}$$
$$\begin{aligned} \lambda _{RG}^{(r)}={\left\{ \begin{array}{ll} \lambda _{RG}, &{}\text {if }r\in \{(l,l), (h,h)\}\\ \lambda _{NH}+\lambda _{RG}, &{}\text {if }r=(h,l)\\ 0, &{}\text {if }r=(l,h)\\ \end{array}\right. } \end{aligned}$$

We immediately see that the Lemma of Section 2 holds and so a Nash Equilibrium for our model exists.

This means that if bed occupancy levels at both Units exceed a pre-determined threshold, then diversions do not occur and each CCU has to accommodate their own patients. In effect we are modelling a certain level of cooperation in this case where CCUs only divert if the other CCU is not busy.

Therefore, the transition matrix Q is obtained from the following transition rates \(q_{ij}\):

$$\begin{aligned} q_{(u_i,v_i), (u_j, v_j)}={\left\{ \begin{array}{ll} u_i\mu _{NH} &{} \text { if } \, (u_i,v_i)-(u_j,v_j)=(1,0),\\ v_i\mu _{RG} &{} \text { if } \, (u_i,v_i)-(u_j,v_j)=(0,1),\\ \lambda _{NH} &{} \text { if } \, (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, \left\{ \begin{array}{l} u_i<K_{NH} \, \text { and } \, v_i<K_{RG} \text { or } \\ u_i \ge K_{NH} \, \text { and } \, v_i \ge K_{RG},\end{array}\right. \\ \lambda _{RG} &{} \text { if } \, (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, \left\{ \begin{array}{l}u_i< K_{NH} \, \text { and } \, v_i<K_{RG}\text { or }\\ u_i\ge K_{NH} \, \text { and } \, v_i\ge K_{RG}, \\ \end{array}\right. \\ \\ \lambda _{NH}+\lambda _{RG} &{} \text { if } \, \left\{ \begin{array}{l} (u_i,v_i)-(u_j,v_j)=(-1,0) \, \text { and } \, u_i<K_{NH} \, \text { and } \, v_i \ge K_{RG} \text { or }\\ (u_i,v_i)-(u_j,v_j)=(0,-1) \, \text { and } \, u_i \ge K_{NH} \, \text { and } \, v_i < K_{RG}, \\ \end{array}\right. \\ 0 &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$
(21)

As before, Figure 13 and Table 3 present the PoA for different target values and demand rate changes.

Figure 13
figure 13

PoA for different target and demand rates for soft diversion

Full size image
Table 3 Numerical values of PoA for different target and demand rates
Full size table

We immediately note that the underlying cooperation that is now being forced on our players (divert only if the other player can accommodate the patients) has reduced the PoA. Note that PoA \(=1.02\) still implies a reduced throughput of 2% which has very large cost implications for a national health service. A tipping point is now visible as demand increases; this is similar to the profiles shown in Knight and Harper (2013) and can be explained as follows:

Also, for very low values of demand, cooperation can be obtained with no target. When the demand is low, there is no scope for uncoordinated behaviour to be damaging. When the demand is very high, the system is saturated and once again uncoordinated behaviour has no negative effect in comparison to optimal behaviour. There is however a region of demand for which there is a high PoA.

For example, for \(t=0.8\) the PoA starts to rapidly increase for demand changes higher than 0.1, and starts to decrease for a demand change of 0.6; this region will be investigated closely. Table 4 presents results for \(t=0.8\) and a demand change from 0.1 to 0.6. For a 50% increase in demand, without a matching increase in capacity, rational behaviour of CCUs would incur 6% less patient throughput.

Table 4 Soft diversion results for \(t=0.8\)
Full size table

Clearly, as the demand change increases, the Nash Equilibrium thresholds decrease. This is due to the fact that both CCUs are attempting to divert their patients in less busy states as these states become rarer. If one CCU diverts early, the other will follow suit (both CCUs incrementally reacting to each other). As a result the Nash Equilibrium for \(x=0.6\) is at (0, 0), meaning that each CCU takes care of their own patients. As the demand increases even further the Nash Equilibrium remains at (0, 0) and the PoA decreases.

Figure 14 shows the lowest values of t which gives a PoA of 1. We see that as demand increases this value also increases. Also, for very low values of demand, cooperation can be obtained with no target. For the actual demand (\(x=0\)) a target value of \(t=0.72\) is once again recommended.

Figure 14
figure 14

Lowest value of t ensuring PoA \(=1\)

Full size image

4 Conclusions

In this work, a generic game theoretical model has been presented that accounts for the rational actions of two CCUs. This game theoretic model is underpinned by a queueing model that takes into account the stochastic nature of queueing systems. This work extends the application of game theoretic models already present in the literature to healthcare (Li et al, 2002; Xie and Ai, 2006).

A result is proved that allows for the assertion of existence of a Nash Equilibrium. This result is then applied to two particular models that are influenced by discussions with a local health board. Strict diversion: patients can be lost to the system if both CCUs declare being in diversion. Soft diversion: if both CCUs are in diversion then they cannot divert their own patients.

An analysis of the effect of rational behaviour is given for both of these models in the form of PoA calculations. The PoA is calculated so as to measure the effect of rational behaviour on overall patient throughput. The PoA represents a theoretical lower bound for the potential damages caused by uncoordinated behaviour. High PoAs are found in the case of strict diversion which is to be expected as soft diversion implies a certain level of cooperation. Importantly, a non-negligible effect of rational behaviour is calculated for certain policy target values. A recommendation of setting \(t=0.72\) is found across both models. This gives some evidence to a particular target value of maximal utilisation in a two CCU ward setting.

This value of t is investigated against increasing demand and is shown to be increasing in overall demand across the system. Investigating demand is akin to investigating the capacity of the CCUs and as shown in Figure 15: if capacity is not sufficient, rational behaviour can have a very damaging effect on overall patient throughput.

Figure 15
figure 15

The effect of capacity on the PoA

Full size image

It is vital to acknowledge the limitations of the work presented:

  • The assumptions as to the strategy space of our players is restrictive: a single threshold policy might not be optimal (although it is present in various pieces of literature on optimal control of queueing systems: Naor, 1969, Shone et al, 2013). Indeed, in reality critical care managers could have far more complex boundaries for their heuristic decision making;

  • This model only assumes the presence of two players; however in reality the system has a variety of stakeholders. Multiplayer systems could be worth considering. This would reflect health boards/hospitals in a concentrated area so that interactions are not just between two hospitals but between many.

  • The restriction to pure strategies is influenced by discussions with ABUHB and also does not detract from the results presented thanks to the Theorem and Lemma of Section 2. However, allowing for mixed strategies could also be of interest, corresponding to decision making that is not constant over time. Managers could alternate between a variety of behaviours: at time accepting patient despite being busy and at other times not;

  • Patient length of stay is assumed to be dependent on the CCU at which they receive service. A further extension of the work would be to use the service rate from original CCU (prior to diversion). This would require a Markov chain with a higher dimensional state space. In practice this corresponds to patient morbidity corresponding to the original CCU.

Despite these mathematical limitations, the work presented here gives a strong analytical evidence as to the use of policies in a decentralised healthcare environment.

As discussed above, reducing the decision making of critical care managers to rational reactions to capacity targets is not without limitations. However, this quantitative model of behaviour was described as insightful and informative by ABUHB. In practice, stakeholders describe a target of 80% capacity. Whilst this is not only at times impossible, it is also not evidence based and in particular does not take in to account interactions between CCUs. This is a common theme in practice and the literature which this manuscript aims to address.

Finally, congestion and throughput are not the only concern of a healthcare system. Further work could involve the investigation of patient survival instead of throughput as utility. This would be similar to work such as Erkut et al (2008), Knight et al (2012).

The code used in this work can be found here: https://gist.github.com/anonymous/81effc06eea70a9e4e2f. The graphics for this paper were obtained using software described in Hunter (2007), Stein et al (2013); a worksheet with the data and code used for the plots can be found here: https://cloud.sagemath.com/projects/c293aefd-1fdf-4b9c-95f4-75bb77035e42/files/MeasuringThePriceOfAnarchyInCCUInteractions.sagews.