Introduction

In recent years, mechanical resonators have been used to excite high frequency phonons at low temperatures for investigating the quantum regime. For instance, O’Connell et al.1 realized single mechanical quantum excitation (phonon) control coupled to a qubit. Besides, the elaborate mechanical resonators can be also applied in the opto-mechanical system2,3, quantum motion4, gravitational wave detection5 and other fundamental physics6. However, the low quality factor (Q) still limits the coherence time of these quantum systems and therefore, it is crucial to manufacture high-Q resonators for the application7. In particular, Goryachev et al.8 adopted a kind of cavity resonators manufactured from the highest quality alpha-synthetic quartz and achieved high-Q at frequencies from hundreds of megahertz to near 1 GHz. Therefore, these bulk acoustic wave (BAW) cavities bring a prospect to achieve operation in the equilibrium ground state of hybrid mechanical systems with longer coherence time. More interestingly, the measurement results exhibit that Q obeys the Q × f 3 = const law and tends to decrease with T reducing, with f and T denoting respectively the resonant frequency and the temperature. These new features manifest that there is another source limiting the quality factor of the BAW resonators made of piezo-crystals at low-temperature.

The understanding of dissipative mechanisms is of great importance for measuring, analyzing and designing mechanical resonators9. At high temperature that ħω ≪ kBT, where ω ≡ 2πf is the angular frequency of the resonant phonons, the limitation of Q-factor is caused mainly by the interaction of acoustic waves with thermal phonons, i.e., the anharmonic effect. At high temperature that the thermal phonon lifetime τ is in the ωτ ≪ 1 regime and even ωτ ~ 1 regime, the Boltzmann equation method, or Akheiser theory, can be used to calculate the dissipation from this thermal effect10,11. If τ is long enough at sufficiently low-temperature such that ωτ ≫ 1 but the thermal effect still dominates (i.e., in the ħω ≪ kBT regime), this anharmonic interaction can be described by phonon-phonon coupling which is regarded as a perturbation of the harmonic vibration (Landau-Rumer method)10,12,13. On the other hand, as temperature keeps dropping, this thermal perturbation becomes negligible and the phonon scattering by defects plays a dominant role in the dissipation. Klemens came up with a model where phonons are scattered by static-point defects (SPDs)14 and exhibited that the dissipation α is proportional to the forth power of frequency (i.e. Q × f 3 = const from the relation Q = f/2α) and independent of temperature. Except the static-point defects, the disordered parts of solids contain the ensemble of so-called two-level systems (TLSs)15,16,17, which has been verified experimentally18,19 and theoretically20. Similar with the photon-TLS interaction21, the TLSs in solids should be coupled to the phonon as the excitation of mechanical vibration. This kind of dynamic defect, as well as the static one mentioned above, disturbs the resonant phonons via phonon-defect coupling to cause the dissipation of mechanical resonators22,23. Instead of the resonant absorption, the phonon elastic scattering by TLSs results in a main dissipation in resonators if the energy of scattered phonons is sufficiently lower than the energy splittings of most TLSs24. Actually, this kind of phonon-defect scattering has been proposed before25, but not derived from a specific perturbation term until recent work in ref. 24. Derived from the specific phonon-TLS interaction in the condition of elastic scattering, not only does Q obey the Q × f 3 = const law, but also drops with the reduction of temperature. The model calculation is in agreement with the recent measurement result8.

In this paper, we further discuss the phonon-TLS scattering mechanism under consideration of the PSD scattering mentioned above and obtain some quantitative results in comparison with the recent experiment8. In other words, this work is beyond the theoretical framework mentioned in ref. 24 that just discussed the effect from TLS without the static-point defeat and relates with experiments that should be influenced by both effects. First, we show that the distribution of energy splitting of TLSs influences the Q dependence on temperature. It provides a method to infer the distribution of energy splitting of TLS ensemble via measuring the Q-factor at various temperature. Besides, now that the PSD contribution is taken into account, we also estimate the relative contribution from phonon-TLS scattering at several temperature after determining the distribution of energy splitting of TLSs. In the end, two parameters, including the coupling coefficient of phonon-SPD scattering and the constant P0 of the TLS distribution, that are crucial for yielding phonon dissipation also need to be estimated and discussed. Our results are available for improving and testing the phonon dissipation mechanism and are helpful to improve the performance of mechanical resonators, apply the desired defects, or reveal the atom configuration in lattice structure of disordered crystals.

Results

The models

For sound wave propagating in crystals, the mechanical harmonic vibration breaks since the microscopic impurities randomly distribute in crystals26. The details for quantizing mechanical waves are given in Methods. These static-point defects lead to phonon elastic scattering for two reasons, including (a) the different mass between lattice atoms and impurities and (b) the different binding to neighbors between of lattice atoms and of impurities. This perturbation Hamiltonian Hi is described as27

where akj () is the annihilation (creation) operator of the mechanical mode with wave-vector k and polarization j, corresponding to the normal-mode frequency ωkj. The polarizations contain j = l, t for a longitudinal and two transverse branches, depending on whether the polarization vector e(kj) is parallel or perpendicular to the wave-vector k. In the case of long-wavelength phonons with the linear dispersive relation, the coefficient Ckj,k′j′ for mode (k, j) scattered elastically to (k′, j′) is given by14

where M describes the change or the binding-force changes at impurity position r in crystals.

According to the previous works28,29,30, two-level systems (TLSs) have been suggested to exist in disordered part of crystals. Two parameters are needed to describe a TLS: the asymmetry Δ and the tunneling Λ between the two bound states (see Fig. 1(a)). The effective Hamiltonian of a TLS can be written as

Figure 1
figure 1

(a) A TLS including two stable states. Δ and Λ denote the separation and the tunneling between the upper state |u〉 and the lower one |d〉, respectively. (b) Four elastic scattering processes due to the TLSs. Each dashed arrow with kj indicates incident or released phonon with wave vector k and polarization j.

Full size image

This is equivalent to a TLS with an energy splitting (the angular transition frequency Ω = 2πν) between the eigen ground state |g〉 and exited state |e〉. On the other hand, the coupling between strain field and a TLS happens mainly through the change of the asymmetry δ31,32. Therefore, the perturbation Hamiltonian for the coupling is given by

Here, δ is linear in the strain tensor field, δ = 2γijSij, where Sij = (∂iuj + ∂jui)/2 expresses the strain tensor with the displacement field (16) and γij indicates the linear coefficient. Once the Hamiltonian (3) is diagonalized17,33, we can obtain this phonon-TLS coupling in terms of phonon creation and annihilation operators,

with the coefficient and the rasing and lowing operators for TLSs, i.e., b +  and b. Here, ρ and V denote respectively the mass density and volume. In the phonon-TLS interaction (5), we only consider the longitudinal and transverse values of γij, denoted as γj with polarization j = l or t.

The phonon-TLS interaction leads to phonon elastic scattering and four processes make contributions to the scattering amplitude Ak′j′,kj from mode (k, j) into mode (k′, j′) (schematic diagram can be seen in Fig. 1(b) and calculation details in Methods). On the basis of second-order perturbation theory34, the amplitude Akj,k′j′ is equivalent to an effective Hamiltonian as

with coefficient

For the small value of ωkj/Ω, this coefficient can be written approximately as

The Q ~ ω−3 law. Applying fermi’s golden rule with equation (1), we can derive the dissipation of a phonon with frequency ω undergoing elastic scattering by static-point defects,

where we have considered the sum of factors Ki of various impurity contributions, denoted by factor . Nevertheless, the temperature independence of equation (9) means that this mechanism can not explain fully the measured results in ref. 8.

On the other hand, the dynamic defeats, i.e., TLS, should be taken into account. We obtain this dissipation of a longitudinal phonon (since the shear modes have larger dissipations and thus are difficult to couple to higher frequencies) scattered elastically by TLSs based on the Hamiltonian (6),

with parameter u = Λ/ε. We have introduced the function VP(ε, u) as the distribution density of parameters ε and u and thus the total dissipation α is expressed by an integration if these parameters of the TLS ensemble are regarded as a continuous distribution. In standard tunneling model35,36, the distribution function has the form , with the constant P0. Hence, the formula (10) becomes

with the coefficient and the lower and bounds Ωi,j = 2πνi,j. If Ωi is much larger than the resonant frequency ω, the attenuation becomes

It means that, if TLSs with high energy splitting dominate in crystals, most of excited phonons undergo elastic scattering by TLS ensemble and their dissipation formula (12) derived from phonon-TLS interaction (5) is proportional approximately to the fourth power of frequency. But unlike the static scattering mechanism, the dissipation resulted from TLSs drops with temperature rising. The physical interpretation for this anomalous T-dependence is that, at lower temperature, more TLSs are in their ground states to absorb resonant phonons and re-emit them in a random direction, leading to phonon dissipation. However, this anomalous temperature trend can not last at a higher temperature where phonon-phonon scattering prevails over the elastic scattering.

Finally, both independent dissipative mechanisms should be considered together and then based on equations (9) and (11) the total quality factor Q is expressed as

According to equations (8) or (12) in the condition ω ≪ Ωi, the above formula becomes

Obviously, equation (14) follows the Q × f 3 = const law at a given temperature and due to the second term in curly braces, quality factor rises as temperature increases. This result is in agreement with the recent experiment8. Just as shown in Fig. 2, the measurement data obey the f−3 law, with const = 2.2 × 1016 (4.2 × 1015) [MHz]3 at 3.8 K (15 mK).

Figure 2
figure 2

The comparison between our formula (13) and the experimental data8, which are denoted by solid lines and points, respectively.

Full size image

Temperature dependence influenced by the distribution of TLSs

As shown in Fig. 2, the constant of the product Q ⋅ f 3  changes with temperature. Back the formula (13), the term that is responsible for the influence of temperature also depends on the distribution of energy splitting of TLSs. However, this distribution has not been obtained from experiments yet and we can therefore analyze how the range of energy splitting of the TLS ensemble affects the scattering rate so far.

It is necessary to take the parameters for formula (14), including both longitudinal and transverse coupling parameters γl = 0.6 eV and γt = 0.4 eV, both longitudinal and transverse sound speeds cl ≈ 7 × 103 m/s and ct ≈ 4 × 103 m/s7 and the mass density of quartz ρ = 2.6 × 103 kg/m3 37. In addition, the undetermined constant of the u-distribution P0 is discussed below. In Fig. 3, we display the product constant of Q ⋅ f 3  as a function of temperature from 0.01 to 10 K with different ranges of transition frequency of the TLS ensemble. We take νi = 3 GHz, 10 GHz and 20 GHz corresponding respectively to the upper panels (a–c). The lower panels (i–iii) are chosen by the lines in panels (a–c), respectively. Besides, the curves in three lower panels are fixed partly by two measured points exhibited in Fig. 2. All panels in this figure show that the constant and thus the quality factor turn higher with temperature rising, in the situation where thermal-induced dissipation is still restricted at such low temperature.

Figure 3
figure 3

The dependence of the constant for the product Q · f 3  on temperature, influenced by the range of frequency splitting.

The upper panels (a–c) indicate the situations for the lower bound νi = 2 GHz, 10 GHz and 20 GHz, respectively. The lower panels (i)–(iii) respectively correspond to the upper panels (a–c) and each of them contains two lines for displaying the temperature dependences at two kinds of upper bound νf indicated via two lines in each of upper panels (a–c). Besides, the circle points in the lower panels are fixed due to the experiment8, i.e., const = 4.2 × 1015 at 15 mK and 2.2 × 1016 at 3.8 K in Fig. 2.

Full size image

For low νi [at least νi ≤ 10 GHz, see Fig. 3(a,b)], the constant with highly narrow-ν range increases with temperature and maintains larger than the one with relatively wide-ν range. Nevertheless, whether the ν range is narrow or wide, the temperature trend stops rising and the magnitude of the constant turns to a same value at several Kevin [see Fig. 3(i,ii)]. Besides, as the νf is up to high enough, the temperature trend nearly exhibits same behaviour even if the ν range is wider. In other words, the magnitude of νi plays a decisive role in the constant for the wide ν range. On the other hand, in high νi regime [see Fig. 3(c)], the constant with highly narrow-ν range still rises with temperature and keeps larger than the one with relatively wide-ν range in the temperature region of near 1 K, whereas the the latter exceeds the former at several Kelvin [see Fig. 3(iii)]. It seems that the TLS ensemble with wider transition frequency spectrum leads to more rapid increase of the constant with temperature rising at several Kelvin. In the relatively low temperature region of 10−2 −10−1 K, the lines of panels (ii) and (iii) in Fig. 3 hardly change with keeping a stable value. Compared with these cases of high νi, the panel (i) displays that the constant starts rising in this low temperature region. Apart from this, the comparison between panels (ii) and (iii) also shows this feature that the stable situation is in a wider range in low temperature region for higher νi situation.

The above analysis provides a clue for future experiments to reveal the distribution of energy splittings of TLS ensemble in crystals. In future measurements for Q-factor, if the line of the frequency behaviour of Q at T > 3.8 K is higher than the one at T = 3.8 K in Fig. 2, it will mean that the energy splittings of most TLSs lie in higher energy range. When the difference between these two lines is larger, the transition frequencies have a wider range from lower limit νi to upper limit νf. On the contrary, if the line at higher temperature is close to the one at 3.8 K, it is reasonable to infer that there are considerable TLSs with low energy splittings. In this situation, the Q-factor at medium temperature should be measured to determine the energy splitting range of the TLS ensemble, based on the temperature behaviour in Fig. 3(a,b) and (i,ii). However, once the range is wide enough, the νf can not be determined by this means, but the only decisive value νi.

The contribution from phonon-TLS scattering RTLS

Now that both TLSs and PSDs participate in the phonon elastic scattering, it is necessary to analyze and discuss their proportion to the phonon dissipation. Even though the parameters and P0 are unknown, the relative contribution of phonon-TLS elastic scattering can be estimated via comparing the formula (14) with the experiment in ref. 8. In this paper, we take the ratio of the inverse of Q ⋅ f 3  product only considering the TLS contribution to the total one including the both contributions of these scattering mechanisms mentioned above, denoted by RTLS, as the relative contribution of phonon-TLS scattering.

As illustrated in Fig. 4, its panels (a) and (b) depict the situation for fixing νi = 3 GHz and 10 GHz, respectively. Whether the TLS ensemble lies in low- or high-transition frequency region, the relative contribution RTLS is higher at lower temperature. Especially at dozens of milli-kelvin, the phonon-TLS elastic scattering is the dominative dissipation mechanism. Just because of the different ratios at various temperature, the experiment in ref. 8 displays the temperature dependence of elastic scattering rate which results from phonon-TLS scattering. Additionally, all lines at different temperature rises with νf increasing. The line at 0.1 K is close to the one at 0.01 K in the Fig. 4(b), in comparison with the two lines in the Fig. 4(a). At several Kelvin, while it seems that the TLS ensemble hardly takes part in the dissipation processes in the Fig. 4(a), the Fig. 4(b) shows that the contribution from the TLS ensemble is considerable. This difference of these two panels manifests that the TLSs with high transition frequency lead to the major contribution of phonon-TLS scattering at a given temperature.

Figure 4
figure 4

The relative contribution from phonon-TLS scattering, RTLS, for various ranges of transition frequency ν of TLS ensemble.

(a,b) Depict the situation for νi = 3 GHz and 10 GHz, respectively. In each figure, the lines from upper to lower indicate the various trends at T = 0.01, 0.1, 0.2, 0.3, 0.5 and 1 K, respectively. In particular, the lines for T = 0.01 and 0.1 K nearly overlap each other in panel (b).

Full size image

The coupling strength of phonon-SPD scattering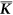

The above analysis reveals that quality factor at a given temperature is determined by the distribution of energy splitting of TLSs. Apart from the TLS scattering which is responsible for the temperature dependence, the static-point defects also make a contribution to the phonon elastic scattering. The coupling strength of this kind scattering can be determined at fixed lower bound νi and range Δν = νf − νi, according to formula (13) and the parameters given above, as shown in Fig. 5.

Figure 5
figure 5

The phonon-PSD coupling coefficient as a function of the lower bound νi and the range Δν = νf − νi.

The unit of is 10−17 MHz−3, while the units of νi and Δν are both GHz. The color indicates the magnitude of . There is an unallowed region of the νi − Δν plane, otherwise the coefficient enters the negative region.

Full size image

In Fig. 5, the elastic scattering can not occur in the colorless region, otherwise the coefficient enters the unallowed negative region. As a consequence, it manifests that, at a specific range Δν, the lower bound νi has a maximum magnitude that decreases with Δν increasing. Besides, if the lowest transition frequency νi is about several gigahertz, the coefficient is nearly unchanged no matter if the range Δν is extremely narrow or wide as dozens of gigahertz. However, the stable state of can not last as long as νi exceeds the several gigahertz region, which makes an obvious difference between the narrow and wide ranges Δν at a given high νi. On the other hand, the coefficient turns out to be more sensitive to νi and decreases to zero more rapidly if the range Δν is wider, also leading to the obvious difference of for various Δν in high-νi regime. In a conclusion, the distribution of the transition frequencies that responds to the largest concentrates narrowly on low νi region. In other words, the TLSs with higher transition frequency result more possibly in their scattering with phonons and thus the contribution from SPD scattering becomes less as well as coupling coefficient .

The distribution constant P0

Just as the coupling coefficient mentioned in above section, the constant P0 is also crucial for obtaining the model results and can be determined on the basis of the experiment in ref. 8 once νi and Δν are measured.

The Fig. 6 plots the magnitude of constant P0 and its dependence on both νi and Δν. If νi is low with narrow or wide range Δν, P0 is turned out to be suppressed highly, especially in wide range case. Despite all this, P0 still gets large with νi rising and this increase is highly rapid for extremely narrow spectrums of transition frequency ν. On the other hand, as the density of the transition frequency, the constant P0 also tends to be larger in the case that the spectrum of transition frequency ν is narrower at a given νi and this parameter increases more steeply as νi enter higher region. In general, the magnitude of P0 increases rapidly as the transition frequencies of the TLS ensemble turn to highly concentrate in high regime.

Figure 6
figure 6

The distribution constant P0 as a function of νi and Δν.

The unit of P0 is 1050 J−1 m−3, while the units of νi and Δν are both GHz. The color indicates the magnitude of P0.

Full size image

Discussion

In this paper, we first combine both the mechanisms of phonon dissipation, including the elastic scattering with two-level systems (TLSs) and point-static defects (PSDs), to obtain the quality factor (Q) formula (13) at low temperature. We then find that Q follows the Q ⋅ f 3 = const law, expressed by equation (14), in bulk mechanical resonators made of piezoelectric quartz. The phonon-TLS scattering reveals that the Q-factor rises with T increasing until, at a higher temperature, the anharmonic effect plays a considerable role in the mechanical dissipation. These frequency and temperature features of quality factor conform to the recent cryogenic measurement in ref. 8 (see Fig. 2). In conclusion, this work improves the theoretical framework in ref. 24 with full consideration (containing both static and dynamic defeats) and provides direct comparison with experiment and more quantitative analysis.

The detail of this paper is our quantitative results on the basis of the theoretical model. First of all, the distribution of energy splitting of the TLS ensemble should be considered to obtain the explicit T-dependency (see Fig. 3). These results are obtained via combining our formula equation (14) with the measurement in ref. 8. If there are considerable TLSs having low transition frequency ν (i.e. several gigahertz), the constant of Q ⋅ f 3  product, as well as Q, rises from low to high temperature with larger magnitude for the narrower ν spectrum. When the temperature is up to several Kelvin, the constant stops increasing and keeps a stable value. On the contrary, if transition frequencies of the TLS ensemble concentrate in higher regime (i.e. dozens of gigahertz), the temperature curve goes up more steeply and keeps this increase at several Kelvin. This situation becomes more obvious as the quartz crystal contains more TLSs with higher ν. This behaviour can be applied to infer the distribution of the transition frequency of the TLS ensemble. Once the distribution of the transition frequency is determined via experiments, the relative contribution of the phonon-TLS scattering to the total scattering rate can be estimated (see Fig. 4). As the temperature is lower, this relative contribution RTLS is larger and thus the phonon-TLS scattering is more dominant for the phonon dissipation. At a given temperature, the higher νi leads to larger proportion of the phonon-TLS scattering which still continues rising with νf increasing. It manifests that the TLSs with high transition frequency lead to the major contribution of phonon-TLS scattering at a given temperature. Furthermore, now that we have included the phonon elastic scattering induced by static-point defects, its effective coupling coefficient can be estimated from the Q formulas (13) and (14) via comparing with the experimental results (see Fig. 5). The distribution of the transition frequencies that responds to the largest concentrates narrowly on low νi region. At last, it is also important to estimate the contribution constant P0 for the final dissipation and the Fig. 6 illustrates the magnitude of constant P0 and its dependence on both νi and Δν. In general, the value of P0 increases rapidly as the transition frequencies of the TLS ensemble turn to highly concentrate in high regime.

The model describes the phonon dissipation, as well as Q, at low temperature due to the existence of various defects in crystals. Based on our results, further quantum experiments which are coupled with the mechanical systems with TLS defects1,18,38 can test whether our theory fits the physical facts. Moreover, we believe that our results give some clues to improve the performance of mechanical resonators7,8,39,40, apply the desired defects41, or reveal the atom configuration in lattice structure of disordered crystals.

Methods

The quantized method for mechanical waves

Our calculations are on basis of the quantization of the sound wave propagating in crystals. The quantized noninteracting phonon Hamiltonian of an ideal harmonic crystal can be expressed as

where akj () is the annihilation (creation) operator of the mechanical mode with wave-vector k and polarization j, corresponding to the normal-mode frequency ωkj. The theory is quantized via the standard commutation relation . The quantized displacement field at position r is then written as a sum of traveling waves,

where ei(kj) is the i-component of the unit polarization vector e(kj) for given k and j and ρ and V indicate respectively the mass density and the volume of crystals. For long-wavelength acoustic wave, the dispersion relation can be expressed linearly as ωkj = cjk, where cj is the sound velocity with polarization j in solids and k = |k|.

The perturbation method for obtaining equation (6)

Let Akj,k′j′ denote the total amplitude of phonon elastic scattering by a TLS with energy splitting ε ≡ ħΩ. On the basis of the perturbation term (5) and the second-order perturbation theory34, the contributions of processes (i)–(iv) in Fig. 1(b) to the total amplitude Akj,k′j′ are respectively as following:

where nkj denotes the phonon population of mode (k, j) and the factors fg and fe are as the probability for TLSs in ground and excited states, respectively. Obviously, The sum of above four formulae is the total amplitude

Take fg − fe = tan h(βħΩ/2) for thermal equilibrium atoms in solid.

Fermi’s golden rule of perturbation method

According to Fermi’s golden rule of perturbation theory14, the attenuation for mode (k, j) is written as

where H′ is the perturbation term of Hamiltonian, i.e., the equations (1) and (6) in this paper and both and indicate the matrix elements and 〈nkj + 1, nk′j′ − 1|H′|nkj, nk′j′〉 respectively. Besides, n is defined as deviation from equilibrium for mode (k, j) in the above equation, i.e., with the Bose-Einstein distribution . Then taking the perturbation terms (1) and (6), the attenuation formulae (9) and (10) can be obtained respectively.

Additional Information

How to cite this article: Li, G. et al. Dissipation induced by phonon elastic scattering in crystals. Sci. Rep. 6, 34148; doi: 10.1038/srep34148 (2016).