Introduction

Control of polarization, a fundamental physical property of electromagnetic (EM) waves, is manifested for a wide range of optical applications, using polarizers, half- and quarter-wave plates in different frequency regimes. Conventional methods for the polarization state control are based on birefringent materials, which support different phase delays along the two orthogonal axes. The main disadvantages of such methods include narrow-band of operating frequencies, bulky size and limited choice of materials. The situation is even worse in terahertz (THz) frequency regime (0.3 THz–3 THz), as THz wave interacts weakly with available materials in nature. For instance, the birefringence index Δn of quartz at 1 THz is around 0.048, which means that the thickness of quartz based THz quarter-wave plate needs to be at least a few millimeters1. Such a device is difficult to be integrated into ultra-compact THz optical systems. Expanding the working frequency of the birefringent materials based devices relies on multilayered designs, which further contributes to the device bulky2.

Metasurfaces, which are two-dimensional artificially engineered media, have enabled new approaches to manipulate the wavefront of EM waves. Composed of thin optical resonators of different materials and geometries, metasurfaces can control both the amplitude and phase of EM waves3. As demonstrated recently4, metasurfaces present unique properties, such as extremely short effective wavelength, abrupt phase change and strong chromatic dispersion, leading to many surprising phenomena. An intriguing property of metasurface is its ability to manipulate EM waves in a thin film of only nanoscale thickness, which promises potential for integration into ultra-compact optical systems. So far, researchers have demonstrated several extraordinary properties of metasurfaces, such as polarization conversion5,6,7,8,9,10, perfect absorption11,12, amplitude and phase modulation13,14,15,16,17,18,19,20,21,22,23,24,25. Particularly, flat lenses based on metasurfaces have become a milestone of the third-generation imaging devices4,25,26. Recently, metasurfaces-based birefringence has been demonstrated in THz range by using microscale resonators27,28. Due to the static response of the resonators, these metasurfaces work in a narrow frequency band. On the other hand, by stacking different layers of metasurfaces, the working frequency can be extended to a broadband29,30,31. However, this multilayer scheme needs an increased thickness and a more complicated fabrication process. To overcome this issue, Luo et al. established a theory for polarization controlling metasurface and presented the metasurface-assisted Fresnel’s equation4. Following this design principle, the chromatic dispersion of reflective metasurface was successfully utilized to achieve ultra-broadband polarization conversion9,10, demonstrating unprecedented performance compared with traditional devices. Luo has also unified the bandwidth-thickness limit9 of the perfect absorber and waveplate. It was shown that the thickness of broadband waveplates could be suppressed below the classic limit set by Max Planck almost a century ago4.

Metasurfaces integrated with active media enable the dynamic modulation of the optical properties without compromising the device thickness. Several active tuning media have been investigated, such as semiconductors32, phase change materials33,34,35 and MEMS36,37. In this work, we demonstrate a switchable ultrathin THz quarter-wave plate (QWP) by inserting vanadium dioxide (VO2) into metasurfaces. Through the phase transition, the conductivity of VO2 varies as much as almost four orders of magnitude, which makes VO2 a good platform for optical switching38. In our design, VO2 changes the effective length of resonators via the phase transition and the operating frequency of the QWP becomes switchable. At the working frequencies, the calculated ellipticities indicate a good polarization conversion. A Lorentz oscillator model is employed to analytically describe the performance of the THz QWP, which is in good agreement with the measurement and simulation. This switchable ultrathin THz QWP is applicable in compact tunable THz optical systems and this VO2 metasurface promises a new route for active micro/nano-photonic devices. Furthermore, this work could be extended to adaptive conformal polarization controlling metasurfaces, as inspired by the concept originally proposed in the work of Luo et al.4.

Results and Discussion

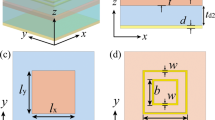
Figure 1a shows a schematic of the switchable QWP, which is composed of ultrathin asymmetric cross-shaped resonator arrays with VO2 pads inserted at the end of the cross-shaped resonators. The complementary metasurfaces present high transmission coefficients at the resonance frequencies due to the extraordinary optical transmission effect with specific phase delays39,40. It only allows the resonant EM wave to pass through, which eliminates the interference of the non-resonant EM wave. In our design, two slots in the QWP are perpendicular to each other with a slight difference in length. The fundamental resonance in each slot is able to present a maximum phase shift of 180° between the transmitted and the incident light. Therefore, birefringence can be introduced by controlling the length of the slots in the asymmetric cross-shaped resonators. The switching property of the QWP is controlled by a resistive heater as a proof of concept to manipulate the VO2 phase transition at different temperatures, which can also be realized by optical pumping41. When VO2 pads act as a semiconductor at 300 K, phase difference between two orthogonal slots can reach 90° at f1 = 0.468 THz, while the transmission coefficients in these two slots are the same. At this frequency, when the incident THz wave is polarized at θ = 45° to the two slots, the device operates as a QWP. Through the phase transition, free carriers in the VO2 pads increase, resulting in the rise of the electrical conductivity. The VO2 pads behave like a metal at 400 K. This leads to a shortened effective length of cross-shaped resonators and the QWP operates at f2 = 0.502 THz. Therefore, this THz QWP can switch its operating frequency between two states through the VO2 phase transition. The top right inset is the simulated ellipticities of the output THz wave at 300 and 400 K. It is observed that the ellipticites at f1 = 0.468 and f2 = 0.502 THz are close to 1, indicating a circular polarization of the output THz waves. The top left inset in Fig. 1a shows a microscope image of one unit cell in the fabricated metasurfaces.

Figure 1
figure 1

Switchable THz QWP design and fabrication results.

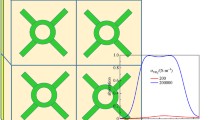
(a) Experimental switching schematic of the THz QWP. A linear normal incident THz wave polarized at θ = 45° to the two slots is converted into a circularly polarized light. Through the VO2 phase transition controlled by a resistive heater, the operating frequency of the QWP can be switched between f1 = 0.468 THz and f2 = 0.502 THz. The top left inset is a microscope image of one unit cell in the fabricated samples. The scale bar is 50 μm. The following are the geometrical parameters: P = 150, Lx = 90, Ly = 124, lx = 9, ly = 5 and w = 9 μm, respectively. The top right inset is the simulated ellipticities of the output THz waves, indicating that at both f1 and f2 the output THz waves are circularly polarized. (b) Schematic backside view of the resistive heater with a square aperture (6 × 6 mm2) milled at the center to allow THz to pass through. (c) Measured electrical conductivity of fabricated VO2 films at different temperatures during the heating and the cooling cycles. The fabricated films exhibit stable electrical conductivity switching between 300 and 400 K during either the heating or the cooling cycles.

Full size image

The VO2 pads were fabricated by pulsed laser deposition (PLD) on a c-cut sapphire substrate using a metallic vanadium target in an oxidizing background42. The asymmetric cross-shaped resonators were patterned by photolithography and ion milling (see the methods). To ensure a full coverage between the metal film and VO2 pads, the dimensions of VO2 pads are slightly larger than the designed parameters. The total size of the fabricated sample is 1 × 1 cm2. Figure 1b shows a schematic backside view of the resistive heater with a square aperture (6 × 6 mm2) milled at the center. The curved wires are tungsten resistors used for heating, which are controlled by an external voltage source. The electrical conductivity of the deposited VO2 film was measured in van der Pauw geometry using Quantum design PPMS42. The VO2 film shows a sharp insulator-metal transition as shown in Fig. 1c. In the insulating state, the electrical conductivity reaches σ = 140 S/m at 300 K. In the high temperature metal phase, the electrical conductivity is relatively temperature-independent at σ = 5 × 105 S/m at 400 K. The transition temperature during the heating cycle is about 353 K while it shifts to 342 K during cooling cycle with a hysteresis of 11 K.

A THz time domain spectroscope was used to perform the characterization (see the methods)43. The input and output polarizations of THz wave were controlled by two THz wire-grid polarizers. The QWP was measured with a normal incident THz wave polarized at θ = 45° to the two slots. The transmitted electric fields of THz wave were characterized along x- and y-axes, which were noted as Ēx and Ēy. A sapphire substrate with transmitted electric fields Ēx(ref) and Ēy(ref) was tested as a reference. The transmission coefficients of the QWP were calculated as  = |Ēx/Ēx(ref)| and  = |Ēy/Ēy(ref)|. The phase information of the THz wave along x- and y-axes were extracted by a fast Fourier transform, which were denoted as φx and φy. The phase delay between y- and x-axes was φ = φy − φx = arg() − arg(). At temperatures above the VO2 phase transition (controlled by the heater), the transmission coefficients and phase delays were measured by the same approach described above.

Figure 2a,b show the measured transmission coefficients and phase delays of THz QWP before and after the VO2 phase transition. At 300 K, the QWP presents a transmission coefficient of 0.59 at 0.468 THz and a phase delay of 80° between y- and x-axes. This means the incident linearly polarized THz wave is converted into a circularly polarized wave. When the QWP is heated to 400 K, the VO2 phase transition changes the performance of the QWP. As it can be seen, a transmission coefficient of 0.28 at 0.502 THz and a phase delay of 75° between y- and x-axes are obtained. Therefore, the THz QWP is able to switch its operating frequency with a switching range of 34 GHz. The numerical simulation and analytical model fitting results are shown in Fig. 2c–f, which will be discussed in the simulation and analytical modeling sections. The experimental phase delays at both 300 and 400 K are smaller than 90°, indicating that the output THz wave is not a perfect circularly polarized light. This is due to the size fluctuation in the fabrication process and the damping effect in the fabricated samples. To experimentally compensate the phase difference and obtain a perfect circularly polarized output THz wave, the optimized phase delay in the simulation should be larger than 90°.

Figure 2
figure 2

Performance of the switchable THz QWP.

(a) Measured transmission spectra along two slots at 300 K (solid line) and 400 K (dot line). (b) Measured phase difference between y- and x-axes at 300 K (solid line) and 400 K (dot line). The inserted triangle indicates at 300 K, the transmission coefficients along two axes are the same, while their phase difference is close to 90°. The marked cross presents similar results at 400 K. (c) Numerically simulated transmission spectra with the corresponding phase delay (d) based on different measured VO2 electrical conductivities. (e) Analytical fitted transmission spectra and (f) the corresponding phase delays.

Full size image

In order to further investigate the polarization state of output THz wave and its relation to the VO2 phase transition, the transmission coefficients and phase delays of the THz QWP at different temperatures were measured by the THz-TDS system and the Stokes parameters were calculated using the following equations6,29:

Figure 3a shows the measured S0 parameters at different temperatures, which indicate the power of the output THz wave. It is observed that when the temperature increases from 300 to 400 K, the output power decreases. This is attributed to loss in the VO2 pads. At 300 K, the VO2 pads behave as a semiconductor and the corresponding loss is low. When the temperature increases, free carries in the VO2 pads increase, leading to a high damping loss and small output power. From Fig. 2a and 3a, we can observe asymmetric transmitted peak amplitudes of and . When the conductivity of VO2 increases, the resonance frequency of shifts to a higher frequency, which is closer to the wood’s anomaly at 0.59 THz. The peak amplitude of becomes smaller, which is shown in Fig. 2a. Another contribution to this asymmetric peak transmission is the different sizes of VO2 pads. As shown in Fig. 1a, the size of VO2 pads along the x-axis is much larger than that along y-axis. 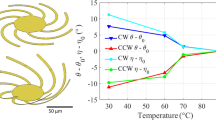This leads to different VO2 damping losses for and . The polarization state of the output THz wave can be described by ellipticity, which is defined as χ = S3/S0. When χ equals to either 1 or −1, the output THz wave is circularly polarized. Figure 3b shows the ellipticity of the output THz wave at different temperatures. At 300 K, the ellipticity of the output THz wave is around 0.98 at 0.468 THz. At 400 K, the ellipticity is around 0.97 at 0.502 THz. Between 300 and 400 K, the ellipticity is close to 1 with the operating frequency switching from 0.468 to 0.502 THz. This indicates that the output THz wave is circularly polarized at different temperatures. The numerical simulation results are shown in Fig. 3c,d, which will be discussed in the following section.

Figure 3
figure 3

Performance of the THz QWP at different temperatures.

(a) Calculated Stokes parameter S0 with respect to different temperatures based on THz-TDS measured results, indicating that the output power decreases when the temperature increases. (b) Measured ellipticities of the output THz wave at different temperatures, indicating the operation frequencies switching of the output circularly polarized THz wave. (c) Numerically simulated Stokes parameter S0 with respect to different conductivities of VO2 and (d) the corresponding ellipticities of the output THz wave.

Full size image

To confirm the performance of our designed THz QWP, numerical simulation was carried out by using commercial software CST Microwave Studio. In the simulation, a frequency-domain solver with a unit cell boundary condition was used to calculate the transmission coefficients and phase delays. The sapphire substrate was modeled as a lossless dielectric with a dielectric constant of εsub = 11.5 and the copper film was simulated as a lossy metal with a conductivity of σ = 5.8 × 107 S/m. A variable conductivity of VO2 was assumed to simulate the phase transition effect in the VO2 pads. The optical constant of VO2 in THz range was described by Drude Model as follows44,45:

where εm was the dielectric function, εi was the dielectric constant as 9, ωp was the plasma frequency, σ was the measured dc conductivity and τ was the relaxation time as 2.27 fs. The simulated transmission spectra and phase delays are shown in Fig. 2c,d. When the conductivity of VO2 is at σ = 140 S/m at 300 K, the QWP presents a transmission coefficient of 0.49 at 0.471 THz with a phase difference of 100° between y- and x-axes. When the conductivity of VO2 is at σ = 5 × 105 S/m at 400 K, the transmission coefficient is 0.30 at 0.508 THz and the phase difference is 88°. This means that the output THz waves at both 300 and 400 K are circularly polarized. At 0.59 THz, the wood’s anomaly in the simulation occur, which can be calculated as , where P is the periodicity of the resonators and εsub is the dielectric constant of sapphire substrate46. The performance of the QWP at different temperatures is simulated, which is shown in Fig. 3c and d. When the conductivity of VO2 increases from 140 to 5 × 105 S/m, the output power S0 decreases and the ellipticity is around 1 with a shift of the operating frequency. This is consistent with our THz-TDS measured results. The slight difference between the experimental and simulation results may be due to inadvertent dimensional variation during the fabrication. Experimentally, the resonance peaks are broader than those in the simulation. Another reason for the broadening of the resonance peaks might be the temperature gradient on the sample surface during heating in the THz-TDS system. This confirms that the experimental phase delay is smaller than the simulated results, which can be further optimized to achieve a perfect linear-to-circular polarization conversion.

To further elucidate the physics behind the designed QWP, a Lorentz oscillator model was introduced to analyze the performance of the THz QWP and the phase transition effect in the VO2 pads, following the dispersion model for anisotropic metasurface given by Luo et al.9. The incident electromagnetic wave can excite resonance modes inside the slots in the QWP, which is similar to rod antennas based on Babinet’s principle39,40,47. When the incident THz wave is polarized along x-axis, the corresponding transmitted electric field can be depicted as:

Similarly, for y-axis polarized incident THz wave, the transmitted electric field is modeled as:

tx, ty, γxand γy are transmitted electric fields and damping rates of two orthogonal resonance modes in the cross-shaped resonators. ωx and ωy are the corresponding resonance frequencies of two modes. gx and gy are geometric factors in the cross-shaped resonators. E0exp(iωt) is the electric field of the incident THz wave. By solving Equations (8) and (9), the analytical solutions for transmission coefficients tx and tywith the corresponding phase distributions φx and φy can be obtained.

With a proper parameter fitting based on the experimental results, the transmission spectra and phase delays of the THz QWP are plotted in Fig. 2e,f, which is in good agreement with the measurement and simulation. The fitted geometric factor g and damping rate γ at different temperatures are plotted in Fig. 4a,b. It is observed that when the VO2 pads go through the phase transition, the geometric factors decrease dramatically, indicating a weak coupling between the incident THz wave and the VO2 metasurfaces. When the conductivity of VO2 further increases to its maximum point, the geometric factor slightly increases. The difference of gx and gy indicates different losses for and , which are consistent with the measured and simulated results. The damping rates plotted in Fig. 4b show that both γxand γy increase with temperature. To illustrate the correlation of the fitting parameters and the performance of QWP, the fitted transmission coefficients and phase distributions at 300 and 400 K along y-axis are plotted in Fig. 4c,d. It is observed that the decrease of geometric factors correlate with the decrease of transmission coefficients. The increase of damping rates leads to a large resonance bandwidth as the spectral phase dispersion tends to be flat.

Figure 4
figure 4

Temperature dependent behaviors of the fitting parameters and the flowchart for QWP design.

(a) Analytical fitted geometric factors and (b) damping rates at different temperatures. (c) Fitted transmission spectra along y-axis at 300 and 400 K. (d) Fitted phase distributions along y-axis at 300 and 400 K. (e) A QWP design flowchart to optimize the parameters of the phase-change metasurfaces.

Full size image

Based on these observations, a flowchart for optimization of parameters in such VO2 metasurface-based QWP is presented in Fig. 4e. For simplicity, the periodicity P and the width w remain unchanged and we focus on optimizing the length of copper resonators and VO2 pads. For the 300 K case, we define the length difference between y- and x-axes as ΔL1 = (Ly + 2ly) − (Lx + 2lx). With any initial parameter of Lx, Ly, lx and ly, we can calculate the transmission spectra and phase delays. If at tx = ty, the phase difference φ1 = φy − φx equals to 90°, the operating frequency of the QWP at f1 is obtained. Otherwise, ΔL1 needs to be increased or decreased according to the flowchart. Similarly, for the case at 400 K, we define the length difference between y- and x-axes as ΔL2 = Ly − Lx and optimize the parameters to obtain the operating frequency of f2. Based on the variation trend of the geometric factors, the transmission coefficients of QWP at f2 are smaller than those at f1. Due to the increase of damping rates, the resonances tend to be broad and ΔL2should be larger than ΔL1 to maintain a phase delay of 90°. Therefore, the flowchart in Fig. 4e presents the optimization process for the VO2 metasurface-based QWP. A similar approach can be applied to other phase-change metasurfaces for both amplitude and phase manipulation.

Conclusion

In summary, by hybridizing metasurfaces with VO2, we have experimentally demonstrated an ultrathin switchable THz QWP with a switching range of 34 GHz. The inserted VO2 is able to change the effective length of the metal resonators in the metasurface through the phase transition. At 300 K, VO2 behaves like a semiconductor and the THz QWP operates at 0.468 THz. While at 400 K, VO2 acts as a metal and the operating frequency of the QWP is switched to 0.502 THz. The Stokes parameters of the output THz wave calculated at different temperatures indicate that the output wave is circularly polarized. The damping loss in VO2 and the wood’s anomaly lead to the decrease of the transmission coefficients at a high temperature. The simulation and analytical fitted results are in good agreement with the measured results. The fitted geometric factors and damping rates analytically illustrate the correlation of VO2 phase transition and the performance of the THz QWP. This switchable phase-change metasurface promises a new route for active THz polarization manipulation devices and can be applied to other ultrathin tunable meta-devices.

Methods

Fabrication

The THz QWP was fabricated on a 1 × 1 cm2 c-cut sapphire single crystal substrate. A commercial vanadium single crystal (100) oriented metal target with 5N purity (from Goodfellow) was used for the VO2 thin film growth. A 248 nm KrF excimer laser (pulse duration 20 ns) at a rate of 5 Hz and a laser fluence of 2 J/cm2 was used at the target. The deposition conditions were optimized (substrate temperature of 500 °C at a background oxygen pressure of 1 mTorr) to get a sharp metal-insulator transition. After 40,000 pulses deposition, the oxygen pressure was immediately increased to 5 mTorr and the VO2 film was annealed under this pressure for one hour at 500 °C. Then the sample was cooled down at a rate of 10 °C/min to room temperature. A step surface profiler was used to measure the thickness of the VO2 film, which was around 200 nm. The designed VO2 pads were patterned by photolithography. The VO2 area without protection from photoresist was etched away by ion milling. After a second photolithography, a 10 nm thick chromium film was coated on the sapphire substrate as an adhesion layer and a 200 nm thick copper film was deposited on the samples by a thermal evaporator (Edwards Auto 306), followed by a lift-off process to obtain the designed patterns.

Characterization

The performance of the QWP was tested in a THz time domain spectroscope. In this system, a femtosecond laser (10 fs, center wavelength 800 nm, repetition rate 80 MHz) was used to pump low-temperature-grown GaAs-based photoconductive antennas in the THz emitter and detector for THz wave generation and detection. Two wire-grid THz polarizers mounted on the rotation stages were positioned in front of the THz emitter and detector to control the polarization of the input and output THz waves. The system was sealed in a box with pure N2 gas to minimize the THz wave loss. A resistive heater with a square aperture (6 × 6 mm2) milled at the center was used to heat the samples and control the insulator-metal phase transition temperature of VO2. The temperature of the samples was monitored in real time by an infrared camera (FLIR Systems i60) to monitor the VO2 phase transition.

Additional Information

How to cite this article: Wang, D. et al. Switchable Ultrathin Quarter-wave Plate in Terahertz Using Active Phase-change Metasurface. Sci. Rep. 5, 15020; doi: 10.1038/srep15020 (2015).