Introduction

The capability of manipulating electromagnetic (EM) waves is of critical importance to many EM-based devices and systems in both fundamental and applied sciences. However, the typical EM devices relying on the gradually accumulated phase during wave propagation are suffering from curved or spatially-distributed shapes and bulky configurations, which limit their potential applications in EM integration for the ever-increasing demands on data-storage capacity and information processing speed. Additionally, EM devices that possess multiple diversified functionalities yet with miniaturized configurations are greatly desired. In recent years, metasurfaces, the two-dimensional analogues of metasurfaces that consist of planar arrays of nanostructures, have become an emerging research area due to their unprecedented control over scattered EM fields within the compact and ultrathin geometries, thereby releasing the nano-fabrication and decreasing the loss to some extent1,2,3,4. By designing artificial meta-atoms and positioning them properly in a periodic or aperiodic manner, arbitrary optical responses with different local amplitudes, phases, and polarizations can be achieved. Therefore, a variety of novel physics phenomena and attractive EM devices have been demonstrated with metasurfaces, such as generalized Snell’s law5,6,7,8,9,10,11,12,13,14, surface waves coupling15,16,17,18, focusing lenses19,20,21,22, holograms23,24,25, absorbers26,27, as well as polarization generation and detection28,29,30,31,32,33,34. Besides the surface-confined configurations, compact footprints and arbitrary wavefront control, metasurfaces are capable of effectively integrating multiple distinct functionalities into one single device35,36,37,38,39,40,41,42,43,44, superior to the aforementioned metasurfaces with single functionality.

However, in most of these approaches, the metasurfaces possess fixed functionalities once been fabricated, lacking the switchable ability and thus hindering practical applications. As such, it is highly desired to achieve switchable metasurfaces that are capable of integrating two or more diversified functionalities together and actively tuning different functionalities at the same time. To realize switchable metasurfaces, an effective way is to incorporate standard metasurfaces with phase-change materials (PCMs), such as chalcogenide GeSbTe(GST) alloys45,46,47,48,49,50,51,52,53,54, vanadium dioxide (VO2)55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71. In spite of the significant achievements in PCMs integrated metasurfaces with dynamic responses, switchable metasurfaces exhibiting totally different functionalities that can be actively switched over a wide frequency range are still largely unexplored.

In this paper, we propose a type of switchable metasurfaces by employing the insulator-to-metal transition in VO2, which possess tunable and diversified functionalities in the terahertz (THz) frequencies. The designed homogeneous metasurface can be dynamically tuned from a broadband absorber to a reflecting surface by thermally stimulus. At room temperature, VO2 is an insulator and the metasurface can efficiently absorb the incident THz wave at normal incidence in the frequency range of 0.535–1.3 THz with the average absorption as high as ~97.2%. If VO2 is heated up and switched to its fully metallic state, the metasurface could reflect the incident wave efficiently and the reflectivity is above 80% in the frequency spectrum ranging from 0.5 to 1.3 THz. Furthermore, we introduce phase-gradients by varying the topmost VO2 antennas of the metasurface when VO2 is in its fully metallic state and consequently realize beam-steering functionalities. Meanwhile, the metasurface can work as an efficient absorber when VO2 is in its insulating state.

Design of the Switchable Multifunctional THz Metasurfaces

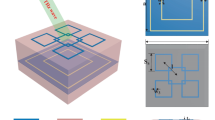
Figure 1 illustrates the basic unit cell of the VO2 integrated THz metasurfaces, which is composed of six different functional layers. Specifically, the functional layers from top to bottom are periodic VO2 brick-shaped antennas, a polyimide spacer layer, double chrome (Cr) square ring resonators (SRRs), a continuous VO2 layer, a second polyimide layer and a bottom Cr substrate (Fig. 1(b)). At room temperature, VO2 is an insulator with a low conductivity of σ = 200 S/m56. In this regard, the unit cell is equivalent to a dielectric-covered metal-insulator-metal (MIM) resonator that consists of Cr SRRs, the second polyimide spacer, and the bottom Cr substrate. Therefore, the incident THz wave can transmit through the topmost VO2 brick array and interact with Cr SRRs, resulting in highly-efficient absorption. On the other hand, once the temperature is increased above the phase-change temperature of Tc = ~340 K, VO2 undergoes an insulator-to-metal transition and gains a high conductivity56. When VO2 is in its fully metallic state, the conductivity σ can reach as high as 2 × 105 S/m59,61. In this case, the VO2 brick-shaped antennas interact strongly with the THz wave and the continuous VO2 film can block all the transmission, thereby forming another MIM cavity composed of VO2 brick array, the polyimide spacer and the VO2 continuous film. By tailoring the dimensions of such MIM cavity in which VO2 functions as metal, one can realize reflecting surface and consequently manipulate the reflected wave at will.

Figure 1
figure 1

(a) 3D schematic of the unit cell of proposed switchable multifunctional THz metasurfaces employing VO2. (b) Side view of the unit cell composed of six functional layers. (c,d) Top view of the unit cell in different cross-sections. The geometrical dimensions are p = 90 μm, lx = ly = 30 μm, t = 1 μm, td1 = 30 μm, td2 = 34 μm, a = 55 μm, b = 36 μm, w = 1 μm, and d = 0.3 μm, respectively.

Full size image

To begin with, we analyze a three-dimensional (3D) homogeneous metasurface composed of periodic meta-atoms shown in Fig. 1(a) by using the commercially available software Comsol Multiphysics (ver. 5.3) based on finite element method (FEM) to determine the reflection coefficients. Periodic boundaries are applied in both the x- and y-directions, and the medium above the unit cell is chosen to be air and truncated using a perfectly matched layer (PML) to minimize reflection. An x- or y-polarized plane wave is normally incident on the top surface as the excitation source along the -z-direction. In our simulations, the relative permittivity of VO2 is described by Drude model \(\varepsilon (\omega )={\varepsilon }_{\infty }-\frac{{\omega }_{p}^{2}\frac{\sigma }{{\sigma }_{0}}}{{\omega }^{2}+i\cdot \omega \cdot {\omega }_{d}}\) with epsilon infinity ε∞ = 12, the plasma frequency ωp = 1.4 × 1015 s−1, the damping frequency ωd = 5.75 × 1013 s−1, and σ0 = 3 × 105 S/m59,61. The conductivity σ of VO2 is 200 S/m and 2 × 105 S/m in insulating and fully metallic states corresponding to the temperature of ~298 K (room temperature) and ~358 K, respectively59,61. The thickness of VO2 structures is t = 1 μm. The thickness of Cr SRRs is d = 0.3 μm and the conductivity of Cr is set to be 2.2 × 105 S/m72. The polyimide spacer layer is considered to be a lossy dielectric with a constant relative permittivity of ε = 2.4 + 0.005i. The other geometrical dimensions are p = 90 μm, lx = ly = 30 μm, td1 = 30 μm, td2 = 34 μm, a = 55 μm, b = 36 μm, and w = 1 μm, respectively.

Figure 2 shows the simulated absorption and reflection spectra when VO2 is in different states. From Fig. 2(a), it is clearly observed that this VO2 incorporated metasurface can efficiently absorb the normally incident THz wave over an ultra-broadband spectrum when VO2 is in its insulating state at room temperature. In particular, the calculated absorption is exceeding 90% in the frequency range of 0.535–1.3 THz with the average absorption reaching ~97.2%. Such broadband and efficient absorption is ascribed to the bottom MIM cavity formed by the Cr SRRs, the continuous VO2 film, the second polyimide spacer and the bottom continuous Cr film, which can interact effectively with the incident wave. It is worth noticing that such MIM cavity can also be regarded as an asymmetric Fabry–Perot resonator73. When the THz wave impinges on the structure, the interface between Cr SRRs and the continuous VO2 film induces significant reflection/transmission phase. Thus, the conventional Fabry–Perot resonance condition will be modified as the propagation phase within the dielectric layer is no longer dominating.

Figure 2
figure 2

(a) Simulated absorption and reflection of the homogeneous metasurface at normal incidence when VO2 is in its insulating state with σ = 200 S/m. (b) Simulated absorption and reflection of the homogeneous metasurface at normal incidence when VO2 is in its fully metallic state with σ = 2 × 105 S/m.

Full size image

To verify the underlying mechanism for wideband absorption, we plot the field distributions of the two absorption peaks at f = 0.757 and 1.212 THz, respectively (Fig. 3(a)). When the THz wave impinges on the metasurface, it can firstly transmit through the topmost VO2 brick array which is transparent when VO2 is an insulator at room temperature (Fig. 3(b)). After that, the incident wave interacts strongly with the MIM cavity, especially the Cr SRRs, resulting in electric dipole resonances. Similar to the previous work61, the induced dipole resonances at certain frequencies are related to the SRRs’ arms that are parallel to the electric field of incident wave. Therefore, the two absorption peaks correspond to the resonances of the outer and inner SRRs, respectively. For instance, at f = 0.757 THz, the incident wave is mainly confined around the outer SRR with bigger size while the electromagnetic field near the inner SRR is weak. Once the inner or outer SRR is removed, the absorption becomes narrower with only one main peak. However, due to the coupling between inner and out SRRs, the resonance peak supported by single-sized SRR is not totally matched with the corresponding peak of double-sized SRRs, as shown in Fig. 3(b). Additionally, since Cr has more loss than other noble metals, such as gold and silver, these resonances have rather low quality-factor and they can merge together easily, thereby broadening the absorption bandwidth72.

Figure 3
figure 3

Mechanism of the broadband absorption when VO2 is in its insulating state with σ = 200 S/m. (a) Normalized Ez distributions of the two absorption peaks at f = 0.757 and 1.212 THz in the x-y plane. (b) Simulated absorption spectra of different configurations.

Full size image

Once the temperature increases gradually, the conductivity of VO2 increases and the absorption decreases. If the temperature is kept above 358 K, VO2 is switched to its fully metallic state and the designed unit cell transits to another MIM cavity consisting of topmost VO2 brick array, the polyimide spacer, and the VO2 continuous film, thus allowing for high reflection instead of absorption (Fig. 2(b)). As shown in Fig. 2(b), broadband and efficient reflection (>80%) is sustained in the frequency range from 0.5 to 1.3 THz when VO2 becomes fully metallic, distinct from the case of broadband absorption when VO2 is in the insulating state. Therefore, the designed VO2 integrated THz metasurface possesses switchable multiple functionalities, which can be switched from a broadband absorber to an efficient reflector by exploiting the temperature-controlled phase transition in VO2.

Switchable Multifunctional THz Metasurfaces with Phase-gradients

In addition to the switchable functionalities between broadband absorption and highly-efficient reflection with a homogeneous metasurface utilizing single meta-atom, the proposed metasurface can be further engineered with phase-gradients, thereby allowing for arbitrary beam-steering of the reflected THz wave when VO2 is in its fully metallic state while maintaining wideband absorption with insulating VO2. To achieve phase-gradients, we have calculated the reflection coefficients of each meta-atom at the design frequency of f = 0.8 THz by varying the lateral dimensions of the meta-atom (lx and ly) while the other parameters are kept fixed. As shown in Fig. 4(a), when VO2 is in its insulating state, the reflectivity is sufficiently low (less than 2%) regardless of the varied topmost VO2 bricks with different dimensions, which is consistent with the previous discussion that the absorption is mainly determined by the SRRs-polymer-Cr cavity. In contrast to the ultra-low and nearly-constant reflectivity when VO2 is in the insulating state at room temperature, the reflectivity and phase response of each unit cell can be engineered by changing the dimensions of VO2 bricks at f = 0.8 THz when VO2 is in its fully metallic state (Fig. 4(b)). For example, the reflectivity can be greatly modulated by lx while ly has little effect on x-polarized THz wave at f = 0.8 THz, which is ascribed to the strong absorption induced by the gap-surface plasmon (GSP) resonance within the VO2-polyimide-VO2 cavity. Meanwhile, the two degrees of freedom (dimensions lx and ly) allow us to vary the phases of reflected polarizations approximately within the whole phase space of ~2π12,44. Close to the GSP resonance, the reflection phase varies rapidly over the range of π. Away from the resonance, the reflection phase is affected by the retardation of the incident wave when being reflected by the bottom reflected or by the process of coupling into GSPs. Here it should be mentioned that for larger lx the reflection phase of x-polarized wave does depend on the value of ly, which is ascribed to the coupling between neighboring elements. Therefore, one should consider this dependence when designing phase-gradients.

Figure 4
figure 4

Calculated reflection as a function of the VO2 brick dimensions at the design frequency of f = 0.8 THz under x-polarization when VO2 is (a) in the insulating state with σ = 200 S/m and (b) in its fully metallic state with σ = 2 × 105 S/m. The reflectivity map is for x-polarization, while the lines are contours of the reflection phases for both x-polarization (solid lines) and y-polarization (dashed lines). Note that the reflectivity for y-polarization can be obtained by mirroring the map for x-polarization along the line lx = ly.

Full size image

In order to extend the functionalities, we first integrate several isotropic VO2 bricks in a supercell to create identical linear phase-gradients for both x- and y-polarizations along the x-direction when VO2 is in its metallic state. In this case, we can achieve polarization-insensitive anomalous reflection while maintaining broadband efficient absorption when VO2 is in its insulting state. Figure 5(a) illustrates the schematic of the supercell consisting of eight elements with a center-to-center distance of p = 90 μm, where four different square-shaped meta-atoms are selected from the intersection points between the solid and dashed lines in Fig. 4(b). In this regard, every meta-atom is arranged in pairs and the constructed supercell has a lateral period of 720 μm along x-direction, which is large enough to avoid generating driven surface waves15. When VO2 is an insulator at room temperature, the selected four meta-atoms have rather low reflectivity and the reflection phase plays little effect on the reflected field. Therefore, the resulting supercell can efficiently absorb the incident THz wave at the design frequency of f = 0.8 THz for x-polarization with the absorption reaching as high as 98.7% (Fig. 5(b)). Additionally, the high-performance absorption is sustained over a wide frequency band. For instance, the calculated absorption is exceeding 83% from 0.5 THz to 1.3 THz, and the average absorption is ~97.1%, as shown in Fig. 5(c). Furthermore, the supercell exhibits polarization-insensitive absorption due to the selected isotropic meta-atoms that have identical responses for two linear polarizations (Fig. 5(d,e)).

Figure 5
figure 5

(a) Supercell of the polarization-insensitive switchable multifunctional THz metasurface that functions as a broadband absorber. The dimensions are lx1 = 20 μm, lx2 = 64 μm, lx3 = 73.5 μm and lx4 = 88 μm. (b,c) Theoretical performance of the metasurface for x-polarization, displaying b) the x-component of the reflected electric field (Erx) at the design frequency of f = 0.8 THz, and (c) reflection and absorption spectra as a function of the frequency. (d,e) Theoretical performance of the metasurface for y-polarization, displaying d) the y-component of the reflected electric field (Ery) at the design frequency of f = 0.8 THz, and (e) reflection and absorption spectra as a function of the frequency. VO2 is in its insulating state with σ = 200 S/m.

Full size image

Distinct from the insulating state, the selected four meta-atoms have considerably high reflectivity and the reflection phase can be utilized to mold the reflected fields when VO2 is in its fully metallic state, according to the generalized Snell’s law5. In particular, the supercell with eight elements provides a polarization-insensitive 2π phase span with a phase step of π/2 for two incident linear polarizations along the x-direction, thus enabling polarization-independent beam-steering for the reflected THz wave with the anomalous reflection peak appearing at an angle of ~31.4°. In order to verify the polarization-insensitive beam-steering, 3D full-wave simulations were conducted by modeling the periodic supercell shown in Fig. 6(a). Figure 6(b) displays the reflected electric filed Exr at f = 0.8 THz for x-polarization when VO2 is in its fully metallic state, indicating the well-defined wavefront of a plane wave. In addition, the +1 diffraction order is dominating while other diffraction orders are greatly suppressed (Fig. 6(c)). Specifically, over 91.1% of the reflected light is routed to the +1 diffraction order and the absolute reflectivity reaches 67.0%. Given that around 26.5% of the incident THz light is absorbed when VO2 is in fully metallic state, the achieved diffraction efficiency in the desired direction is moderately high74,75,76. Here it is worth noting that though the 0 diffraction order is almost totally suppressed, the unwanted −1 diffraction order shows up at the design frequency, which may be ascribed to the variations in reflectivity produced by different elements comprising the supercell and the near-field coupling between different meta-atoms77.

Figure 6
figure 6

(a) Supercell of the polarization-insensitive switchable multifunctional THz metasurface that functions as a broadband beam-steerer. The dimensions are lx1 = 20 μm, lx2 = 64 μm, lx3 = 73.5 μm, and lx4 = 88 μm. The reflection phases of the meta-atoms 1–4 are −14.5°, 75.7°, 165.3°, and 254.9°, respectively, for both x- and y-polarizations. (b,c) Theoretical performance of the metasurface for x-polarization, displaying (b) the x-component of the reflected electric field (Erx) at the design frequency of f = 0.8 THz, and (c) amount of incident THz wave reflected into the different diffraction orders as a function of the frequency. (d,e) Theoretical performance of the metasurface for y-polarization, displaying (d) the y-component of the reflected electric field (Ery) at the design frequency of f = 0.8 THz, and (e) amount of incident THz wave reflected into the different diffraction orders as a function of the frequency. VO2 is in its fully metallic state with σ = 2 × 105 S/m.

Full size image

As expected, the y-polarized THz wave is also reflected to the +1-diffraction order (Fig. 6(d,e)). Compared to the performance of beam-steering for x-polarization, the reflected wave of y-polarization shows fewer distortions, assembling a better wavefront closer to a plane wave, as shown in Fig. 6(d). What’s more, ~96.5% of the reflected light is contained within the +1-diffraction order at the design frequency of f = 0.8 THz under y-polarized excitation, while the other diffraction orders are greatly suppressed with the intensities approaching 0. This slightly improved performance for y-polarization is related to the designed supercell that is periodically arranged in the y-direction with the period of 90 μm, perfectly mimicking the periodic boundary condition used to calculate the reflection coefficients of the meta-atoms shown in Fig. 1(a).

Besides polarization-insensitive beam-steering for reflected THz waves, a more desired functionality in practical applications is to achieve polarization-splitting that can anomalously reflected x-polarized and y-polarized waves into different directions. Therefore, we propose a polarization beam splitter by designing opposite linear phase-gradients for the two incident polarizations since the angle of anomalous reflection is mainly determined by the introduced phase-gradient5. Similar to the polarization-insensitive design, here we discretize the reflection phases with a step of π/2, and the contour lines for the x- and y-polarizations are displayed with solid and dashed black curves in Fig. 4(b). By properly selecting the meta-atoms from the intersection points, four anisotropic VO2 bricks are used to construct a supercell with eight meta-atoms, shown in Fig. 7(a). When VO2 is in its insulating state at room temperature, all the elements comprising the supercell have sufficiently high absorption, therefore making the metasurface functions as a broadband absorber with high-performance (Fig. 7(b–e)). More importantly, the absorption is independent of the incident polarization since the top VO2 antennas have negligible effect in the absorption process. From Fig. 7(c,e), one can clearly see the identical absorption efficiencies, which are consistent with the values in Fig. 5.

Figure 7
figure 7

(a) Supercell of the polarization-sensitive switchable multifunctional THz metasurface that functions as a polarization-independent broadband absorber. The dimensions are lx1 = 17 μm, ly1 = 17 μm, lx2 = 60.5 μm, ly2 = 88.4 μm, lx3 = 73.5 μm, ly3 = 73.5 μm, lx4 = 88.4 μm, and ly4 = 60.5 μm. (b,c) Theoretical performance of the metasurface for x-polarization, displaying b) the x-component of the reflected electric field (Erx) at the design frequency of f = 0.8 THz, and (c) reflection and absorption spectra as a function of the frequency. (d,e) Theoretical performance of the metasurface for y-polarization, displaying d) the y-component of the reflected electric field (Ery) at the design frequency of f = 0.8 THz, and (e) reflection and absorption spectra as a function of the frequency. VO2 is in its insulating state with σ = 200 S/m.

Full size image

When VO2 is in its fully metallic state, the supercell composed of eight elements supplies a 2π phase span with a constant phase step of ±π/2 for x- and y-polarizations at f = 0.8 THz, resulting in efficient diffractions into ±1 orders with angles of ±31.4°, respectively (Fig. 8). As shown in Fig. 8(b,d), the two orthogonal linear polarizations are reflected at the opposite sides of the surface normal with identical angles, indicating the good performance of polarization-splitting at f = 0.8 THz. To further investigate the performance quantitively, we calculate the amount of the reflected THz wave into different orders as a function of the frequency. At the design frequency of f = 0.8 THz, ~92.1% and ~96.7% of the reflected THz waves go to the ±1 diffraction orders with the absolute reflectivities reaching 66.4% and 65.6% for x- and y-polarizations, respectively. When the frequency moves away from the designed value, the capability of polarization-splitting is still good, manifesting the broad operation bandwidth.

Figure 8
figure 8

(a) Supercell of the polarization-sensitive switchable multifunctional THz metasurface that functions as a broadband polarization-splitter. The dimensions are lx1 = 17 μm, ly1 = 17 μm, lx2 = 60.5 μm, ly2 = 88.4 μm, lx3 = 73.5 μm, ly3 = 73.5 μm, lx4 = 88.4 μm, and ly4 = 60.5 μm. The reflection phases of the meta-atoms 1–4 are −15.1° (−15.1°), 74.8° (255.1°), 165.4° (165.4°) and 255.1° (74.8°), respectively, for x-polarization (y-polarization). (b,c) Theoretical performance of the metasurface for x-polarization, displaying b) the x-component of the reflected electric field (Erx) at the design frequency of f = 0.8 THz, and (c) amount of incident THz wave reflected into the different diffraction orders as a function of the frequency. (d,e) Theoretical performance of the metasurface for y-polarization, displaying (d) the y-component of the reflected electric field (Ery) at the design frequency of f = 0.8 THz, and (e) amount of incident THz wave reflected into the different diffraction orders as a function of the frequency. VO2 is in its fully metallic state with σ = 2 × 105 S/m.

Full size image

Potential Fabrication Process of the Proposed Structure

Regarding the potential fabrication pross of the proposed structure, we could combine the standard ultraviolet lithography with thin-film deposition techniques29,72. The fabrication process begins with a double-side-polished silicon (Si) wafer, and the process is presented as Fig. 9: (a) 300-nm-thick Cr layer is deposited on Si substrate using e-beam evaporation; (b) 30-μm-thick polyimide layer is spin coated and cured at ~300 °C; (c) 1-μm-thick VO2 layer is magneton sputtered and annealed at ~450 °C; (d) photoresist is spin coated and optical lithography; (e) 300-nm-thick Cr is deposed using e-beam evaporation; (f) the photoresist is dissolved by a lift-off process to form the Cr SRRs; (g) 34-μm-thick polyimide layer is spin coated and cured at ~300 °C; (h) photoresist is spin coated and optical lithography; (i) 1-μm-thick VO2 layer is magneton sputtered; (j) the photoresist is dissolved by a lift-off process to form the VO2 bricks and the remaining VO2 is then annealed at ~450 °C. As a final comment, it should be noted that our device would be insensitive to the proper multi-layer alignment errors during the fabrication since the proposed structure can be regarded as two independent devices isolated by the continuous VO2 film when VO2 is in different states (Fig. 10).

Figure 9
figure 9

Potential fabrication process of the processed structure: (a) 300-nm-thick Cr layer is deposited on double-side-polished Si substrate; (b) 30-μm-thick polyimide layer is spin coated and cured at high temperature (~300 °C) (c) 1-μm-thick VO2 layer is magneton sputtered and annealed at ~450 °C; (d) Photoresist is spin coated and optical lithography; (e) Cr is deposed. (f) Lift-off process; (g) 34-μm-thick polyimide layer is spin coated and cured at high temperature (~300 °C). (h) Photoresist is spin coated and optical lithography; (i) 1-μm-thick VO2 layer is magneton sputtered. (j) Lift-off process and the remaining VO2 is annealed at ~450 °C. The polyimide can survive at high temperature up to 450 °C.

Full size image
Figure 10
figure 10

Tolerance analysis when there is multi-layer alignment error. (a) Simulated absorption of the homogeneous metasurface at normal incidence when VO2 is in its insulating state with σ = 200 S/m. (b) Simulated reflection of the homogeneous metasurface at normal incidence when VO2 is in its fully metallic state with σ = 2 × 105 S/m. The inset in (a) shows the schematic of the mis-aligned structure. The geometrical parameters are the same as those in Fig. 1.

Full size image

Conclusions

In conclusion, we have proposed a type of switchable THz metasurfaces with tunable and diversified functionalities by utilizing the insulator-to-metal transition in VO2.

The designed homogeneous metasurface can be dynamically switched from a broadband absorber to an efficient reflector by altering the working temperature. When VO2 is in insulating state at room temperature, the metasurface is capable of absorbing the normally incident THz wave in the frequency range of 0.535–1.3 THz with the average absorption of ~97.2%. If the VO2 is switched to fully metallic state at high temperature, the designed metasurface exhibits broadband and efficient reflection (>80%) in the frequency range from 0.5 to 1.3 THz. Based on the meta-atom design, we further extend the functionalities by introducing phase-gradients when VO2 is in its fully metallic state and consequently achieve polarization-insensitive beam-steering and polarization-splitting, while maintaining broadband absorption in insulating state. It should be emphasized that the achieved two functionalities exhibit comparable and even superior performance once compared with the existing metasurface-based absorbers72 and beam-steerers74,75,76, in terms of efficiencies and operating bandwidth. Additionally, the fully insulator-to-metal transition makes VO2 an excellent candidate to bridge two isolated devices together, which is hard to achieve with other phase-change materials possessing limited tunability. Although VO2 only exhibits volatile switching, it is easier to realize reversible tuning between insulating and metallic states with lower power consumption, superior to GST alloys which need high power density and protective layer. The proposed switchable THz metasurfaces can enable advanced applications in THz society, such as temperature sensor and imaging.