Abstract
We study the nonlocality of arbitrary dimensional bipartite quantum states. By computing the maximal violation of a set of multi-setting Bell inequalities, an analytical and computable lower bound has been derived for general two-qubit states. This bound gives the necessary condition that a two-qubit state admits no local hidden variable models. The lower bound is shown to be better than that from the CHSH inequality in judging the nonlocality of some quantum states. The results are generalized to the case of high dimensional quantum states and a sufficient condition for detecting the non-locality has been presented.
Similar content being viewed by others
Introduction
Quantum mechanics is inherently nonlocal, as revealed by the violation of Bell inequality1. A bipartite quantum state may violates some Bell inequalities such that the local measurement outcomes can not be modeled by classical random distributions over probability spaces. Namely, the state admits no local hidden variable (LHV) model.
The nonlocality and quantum entanglement play important roles in our fundamental understandings of physical world as well as in various novel quantum informational tasks2,3. A quantum state without entanglement must admit LHV models4,5,6,7,8,9. However, not all the entangled quantum states are of nonlocality10,11,12,14. To show that a quantum state admits a LHV model, it is sufficient to construct such LHV model explicitly10,12. To show that a quantum state admits no LHV models, it is sufficient to show that it violates a Bell inequality15,16. Quantum states that violate Bell inequalities are also useful in building quantum protocols to decrease communication complexity17 and provide secure quantum communication18,19. Moreover, since the nonlocality is detected by the violation of Bell inequalities, quanum nonlocality could be quantified in terms of the maximal violation value for all Bell inequalities. However, it is a formidable task either to show that a state admits an LHV model, or to show that a state violates a Bell inequality.
Let Ai and Bi, i = 1,2, …, n, be observables with respect to the two subsystems of a bipartite state, with eigenvalues ±1. Let M be a real matrix with entries Mij such that  . Denote
. Denote  the corresponding Bell operator. Define
the corresponding Bell operator. Define

where 〈I〉ρ = tr(Iρ) stands for the mean value of the Bell operator associated to state  . Obviously a quantum state ρ can never be described by a LHV model if and only if Q is strictly larger than 1.
. Obviously a quantum state ρ can never be described by a LHV model if and only if Q is strictly larger than 1.
In10,11,12,13,14, the authors have investigated the nonlocality of Werner states. For two-qubit Werner state  ,
,  , the quantity Q is proved to be
, the quantity Q is proved to be  in12, where KG(3) is the Grothendieck’s constant of order three. However, since up to now one does not kown the exact value of the Grothendieck’s constant KG(3), Q is still is not known. The upper and lower bounds of the threshold value of this parameter Q have been refined by constructing better LHV models10,11,12 or by finding better Bell inequalities13,14.
in12, where KG(3) is the Grothendieck’s constant of order three. However, since up to now one does not kown the exact value of the Grothendieck’s constant KG(3), Q is still is not known. The upper and lower bounds of the threshold value of this parameter Q have been refined by constructing better LHV models10,11,12 or by finding better Bell inequalities13,14.
In the paper we study the nonlocality of arbitrary two-qubit states and present an analytical and computable lower bound of the quantity Q by computing the maximal violation of a set of multi-setting Bell inequalities. The lower bound is shown to be better than that derived in terms of the CHSH inequality for some quantum states. We also present a sufficient condition that a high dimensional quantum state admits LHV models.
Results
Lower bound of Q for two-qubit quantum states
A two-qubit quantum state ρ can be always expressed in terms of Pauli matrices  , i = 1, 2, 3,
, i = 1, 2, 3,

where  ,
,  and
and  . We denote T the matrix with entries tij.
. We denote T the matrix with entries tij.
The key point in computing Q is to find  over all M under the condition
over all M under the condition  . In14 a Bell operator has been introduced,
. In14 a Bell operator has been introduced,

where Ai, Bj, Cij and Dij are observables of the form  with
with  the unit vectors.
the unit vectors.
To find an analytical lower bound of  , we consider infinite many measurements settings, n → ∞. Then the discrete summation in (3) is transformed into an integral of the spherical coordinate over the sphere S2 ⊂ R3. We denote the spherical coordinate of S2 by (ϕ1, ϕ2). A unit vector
, we consider infinite many measurements settings, n → ∞. Then the discrete summation in (3) is transformed into an integral of the spherical coordinate over the sphere S2 ⊂ R3. We denote the spherical coordinate of S2 by (ϕ1, ϕ2). A unit vector  can parameterized by x1 = sin ϕ1 sin ϕ2, x2 = sin ϕ1 cos ϕ2, x3 = cos ϕ1. For any
can parameterized by x1 = sin ϕ1 sin ϕ2, x2 = sin ϕ1 cos ϕ2, x3 = cos ϕ1. For any  we denote
we denote 
Theorem 1: For arbitrary two-qubit quantum state ρ given by (2), we have

where Tt stands for the transposition of T and  . The maximum on the right side of the inequality goes over all the integral area
. The maximum on the right side of the inequality goes over all the integral area  with
with  and
and  .
.
See Methods for the proof of theorem 1.
The bound (4) can be calculated by parameterizing the integral in terms of the sphere coordinates. Once a two-qubit is given, the corresponding matrix T is given. And the bound is solely determined by T. This is similar to the CHSH inequality, where the maximal violation is given by the two larger singular values of T.
As an example, consider T = diag(p1, p2, p3), we have

 in (4) are similarly given. The first two terms in
in (4) are similarly given. The first two terms in  (4) are given by
(4) are given by


where

The last term in (4) is similarly to the second term, with T being replaced by Tt.
Thus for any given two-qubit quantum state, by substituting T into the integral, we have the lower bound of Q. The maximum taken over  can be searched by varying the integral ranges. The Werner state considered in10,11,12,13,14 is a special case that p1 = p2 = p3 = p. From our Theorem 1, we have that for 0.7054 < x ≤ 1, the lower bound of Q is always larger than that is derived from the maximal violation of the CHSH inequality, see Fig. 1.
can be searched by varying the integral ranges. The Werner state considered in10,11,12,13,14 is a special case that p1 = p2 = p3 = p. From our Theorem 1, we have that for 0.7054 < x ≤ 1, the lower bound of Q is always larger than that is derived from the maximal violation of the CHSH inequality, see Fig. 1.
Let us now consider the generalized Bell diagonal two-qubit states in detail,

The positivity property requires that the parameters {p1, p2, p3} must be inside a regular tetrahedron with vertexes {−1, −1, 1}, {1, −1, −1}, {1, 1, 1}, {−1, 1, −1}. By computing the lower bound of Q according to Theorem 1, we detect the regions where the quantum states can never be described by LHV models, see Fig. 2.
By setting p1 = 0.9, p2 = 0.9 and p3 = 0.9, one has the the cross-sectional view, see Fig. 3.
The same cross-sectional view of Fig. 2 for all p1 = 0.9, p2 = 0.9 and p3 = 0.9.
High dimensional case
Generalizing our approach to high dimensional case, now we study the nonlocality of general d × d bipartite quantum states. To detect the nonlocality of a quantum state, the important thing is to find a ‘good’ Bell operator. For even d, we set Γ1, Γ2 and Γ3 to be block-diagonal matrices, with each block an ordinary Pauli matrix,  ,
,  and
and  respectively, as described in5 for Γ1 and Γ3. When d is odd, we set the elements of the k th row and the
respectively, as described in5 for Γ1 and Γ3. When d is odd, we set the elements of the k th row and the  th column in Γ1, Γ2 and Γ3 to be zero, with the rest elements of Γ1, Γ2 and Γ3 being the block-diagonal matrices like the case of even d. Let Γ0 be a d × d matrix whose only nonvanishing entry is (Γ0)mm = 1 for m ∈ 1, 2, …, d, for odd d and be a null matrix for even d. We define observables
th column in Γ1, Γ2 and Γ3 to be zero, with the rest elements of Γ1, Γ2 and Γ3 being the block-diagonal matrices like the case of even d. Let Γ0 be a d × d matrix whose only nonvanishing entry is (Γ0)mm = 1 for m ∈ 1, 2, …, d, for odd d and be a null matrix for even d. We define observables  and
and  , where
, where  ,
,  and
and  are vectors with norm
are vectors with norm  . It is easy to check that the eigenvalues of the observables A and B are either 1 or −1.
. It is easy to check that the eigenvalues of the observables A and B are either 1 or −1.
We define the Bell operator to be

where Ai, Bj, Cij and Dij are observables of the form  and
and  respectively;
respectively;  and
and  are vectors with norm
are vectors with norm  .
.
The Bell operator (9) has the same structure as that in (3), but fits for d×d quantum system. For a d × d quantum state ρ, we set γ to be a matrix with elements γij = tr(ρΓi ⊗ Γj), i, j = 0, 1, 2, 3. A lower bound of  defined in (1) for d×d quantum system can be readily obtained as the follows.
defined in (1) for d×d quantum system can be readily obtained as the follows.
Theorem 2: For any quantum state ρ in d×d quantum system  , we have that
, we have that

where γt stands for the transposition of γ and  . The maximum on the right side of the inequality is taken over all the selection of integral area
. The maximum on the right side of the inequality is taken over all the selection of integral area  with
with  and
and  .
.
See Methods for the proof of theorem 2.
According to the definition of  in (1), we have that if the lower bound for Q in theorem 2 is larger than one, then a quantum state in d × d bipartite quantum system can never be described by an LHV model. The bound can readily calculated, similar to the two-qubit case, once the matrix γ for state is given.
in (1), we have that if the lower bound for Q in theorem 2 is larger than one, then a quantum state in d × d bipartite quantum system can never be described by an LHV model. The bound can readily calculated, similar to the two-qubit case, once the matrix γ for state is given.
Let us consider the isotropic state ρI20,21, a mixture of the singlet state  and the white noise:
and the white noise:  , 0 ≤ x ≤ 1. ρI is entangled for
, 0 ≤ x ≤ 1. ρI is entangled for  . For d = 3, ρI is entangled for x > 1/4. From Theorem 2, ρI is nonlocal for x > 0.7653.
. For d = 3, ρI is entangled for x > 1/4. From Theorem 2, ρI is nonlocal for x > 0.7653.
As another example we consider the state ρ from mixing the singlet state  with
with  ,
,  . One can list by Theorem 2 the points that admit no LHV model, see Fig. 4.
. One can list by Theorem 2 the points that admit no LHV model, see Fig. 4.
Discussions
Nowadays, quantum nonlocality is a fundamental subject in quantum information theory such as quantum cryptography, complexity theory, communication complexity, estimates for the dimension of the underlying Hilbert space, entangled games, etc.22. Thus it is a basic question to check and to qualify the nonlocality of a quantum state. We have derived an analytical and computable lower bound of the quantum violation by using a Bell inequality with infinitely many measurement settings. The bound is shown to be better than that is obtained from the CHSH inequality and the discrete models. Sufficient conditions for the LHV description of high dimensional quantum states have also derived. Apart from the computation of maximal violations for bipartite Bell inequalities, our methods can also contribute to the analysis of the nonlocality of multipartite quantum systems.
Methods
Proof of Theorem 1
For any two-qubit quantum state ρ given in (2), we have


Under the limit n → ∞, we have

which proves (4). ■
Proof of Theorem 2
With the special selected observables of the form  for
for  quantum systems, we have that
quantum systems, we have that

where in the last step, we have taken the limit n → ∞. ■
Additional Information
How to cite this article: Li, M. et al. Quantum Nonlocality of Arbitrary Dimensional Bipartite States. Sci. Rep. 5, 13358; doi: 10.1038/srep13358 (2015).
References
Bell, J. S. On the Einstein Podolsky Rosen Paradox. Physics 1, 195–200 (1964).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, England, 2000).
Di Vincenzo, D. P. Quantum Computation. Science 270, 255–261 (1995).
Gisin, N. Bell’s inequality holds for all non-product states. Phys. Lett. A 154, 201–202 (1991).
Gisin, N. & Peres, A. Maximal violation of Bells inequality for arbitrarily large spin. Phys. Lett. A 162, 15–17 (1992).
Popescu, S. & Rohrlich, D. Generic quantum nonlocality. Phys. Lett. A 166, 293–297 (1992).
Chen, J. L., Wu, C. F., Kwek, L. C., & Oh, C. H. Gisin’s Theorem for Three Qubits. Phys. Rev. Lett. 93, 140407 (2004).
Li, M. & Fei, S. M. Gisins Theorem for Arbitrary Dimensional Multipartite States. Phys. Rev. Lett. 104, 240502 (2010).
Yu, S. X., Chen, Q., Zhang, C. J., Lai, C. H. & Oh, C. H. All entangled pure states violate a single Bell’s inequality. Phys. Rev. Lett. 109, 120402 (2012).
Werner, R. F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277 (1989).
Barrett, J. Nonsequential positive-operator-valued measurements on entangled mixed states do not always violate a Bell inequality. Phys. Rev. A 65, 042302 (2002).
Acin, A., Gisin, N., & Toner, B. Grothendiecks constant and local models for noisy entangled quantum states. Phys. Rev. A 73, 062105 (2006).
Hua, B. B., Zhou, C. Q., Li, M., Zhang, T. G., Li-Jost, X. Q. & Fei, S. M. Towards Grothendieck constants and LHV models in quantum mechanics. J. Phys. A: Math. Theor. 48, 065302 (2015).
Vertesi, T. More efficient Bell inequalities for Werner states. Phys. Rev. A 78, 032112 (2008).
Li, M., Fei, S. M. & LI-Jost, X. Q. Bell Inequality, Separability and Entanglement Distillation. Chin. Sci. Bull. 56, 945–954 (2011).
Qi, J. X., Zha, X. W. & Sun, X. M. Testing the nonlocality of entangled states by a new Bell-like inequality. Sci. China-Phys. Mech. Astron. 56, 2236–2238 (2013).
Brukner, C., Zukowski, M. & Zeilinger, A. Quantum Communication Complexity Protocol with Two Entangled Qutrits. Phys. Rev. Lett. 89, 197901 (2002).
Scarani, V. & Gisin, N. Quantum Communication between N Partners and Bell’s Inequalities. Phys. Rev. Lett. 87, 117901 (2001).
Acín, A., Gisin, N. & Scarani, V. Security bounds in Quantum Cryptography using d-level systems. Quantum Inf. Comput. 3, 563–580 (2003).
Horodecki, M. & Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 59, 4206 (1999).
Vollbrecht, K. G. H. & Werner, R. F. Entanglement measures under symmetry. Phys. Rev. A 64, 062307 (2001).
Junge, M. & Palazuelos, C. Large violation of Bell inequalities with low entanglement. Commun. Math. Phys. 306, 695–746 (2011).
Acknowledgements
This work is supported by the NSFC 11105226, 11275131, 11401106; the Fundamental Research Funds for the Central Universities No. 15CX08011A, No. 24720122013 and the Project-sponsored by SRF for ROCS, SEM.
Author information
Authors and Affiliations
Contributions
M.Li and S.-M. Fei wrote the main manuscript text. T. Zhang, B. Hua and X.Q. Li-Jost computed the examples. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, M., Zhang, T., Hua, B. et al. Quantum Nonlocality of Arbitrary Dimensional Bipartite States. Sci Rep 5, 13358 (2015). https://doi.org/10.1038/srep13358
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep13358
- Springer Nature Limited
This article is cited by
-
Trade-Off Relations of CHSH Violations Based on Norms of Bloch Vectors
International Journal of Theoretical Physics (2019)
-
The norms of Bloch vectors and a trade-off relation of Svetlichny inequalities
Quantum Information Processing (2018)
-
Maximal violation of Bell inequalities under local filtering
Scientific Reports (2017)




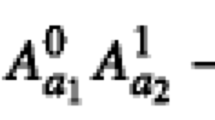


 that admits no LHV models are listed by the points parameterized by (p1, p2, p3).
that admits no LHV models are listed by the points parameterized by (p1, p2, p3).

 parameterized by
parameterized by  that admit no LHV model (blue regions).
that admit no LHV model (blue regions).