Introduction

Throughout much of the tropics and mid-latitudes, tropical cyclones (TCs) are the cause of extensive societal and scientific attention due to the destructive threat to life, property, and crops they pose1,2,3,4. Most of these threats are caused by the TC’s strong winds, either directly or indirectly through waves, storm surge, or moisture convergence driving extreme rain2,13,14. Thus, knowing the current state of the wind field of a storm and forecasting it well in advance is essential for effective preparation, evacuation, and mitigation2,9.

Complete reconstructions of hurricanes’ wind fields have numerous practical applications, including storm surge modeling, risk assessment for various wind strengths in hurricane-prone areas, and especially for forecasting the evolution of these wind fields. TC forecasting is typically performed using dynamical models2, which directly integrate the physical equations that govern fluid dynamics. While National Hurricane Center (NHC) forecasts have generally improved over time9,10, intensity errors had stagnated for decades9,15,16, with only some progress made in recent years10. Numerous studies highlight that accurate initial conditions for dynamical models are essential for accurate forecasts5,6,7, especially for obtaining reliable intensity forecasts7,8,9. In fact, much recent progress in dynamical forecast models is attributed to increased observational data and better data assimilation (DA) schemes for reconstructing the complete dynamical fields of storms10. Nonetheless, dynamical models still struggle, especially in forecasting intensity17, and particularly for storms which undergo rapid intensification (RI)15,18. Given that the most intense hurricanes (category 4 or greater), which are responsible for the majority of damage4, all undergo RI at some point in their lifetime19, predicting these intensity changes is extremely important. Due to anthropogenic climate change, the frequency with which TCs undergo RI just prior to landfall is expected to increase20,21,22. Thus, improved forecasting and accurate wind field reconstructions is essential as we adapt to our warming climate.

A major obstacle for reconstructing the flow field of a storm is that the full wind and thermodynamic fields are never observed at any given time and exhibit rich variability on a number of scales. Early schemes were pioneered by the works of Kurihara et al. in the 1990s5,8,23,24,25 in their efforts to reconstruct accurate initial conditions for hurricane forecast models at the Geophysical Fluid Dynamics Laboratory (GFDL). More recent methodologies have built on their work—the Hurricane Weather Research and Forecasting (HWRF) model’s scheme is one example, and it starts with the previous 6-h forecast’s vortex and performs dynamically consistent size and intensity corrections to better match current observations17,26. Modern initialization techniques also assimilate vast amounts of high-density observations when creating the initial vortex. Some of these DA techniques include Ensemble Kalman filters27,28 and most recently 4D Ensemble Variational (4DEnVar) algorithms29. Generally, these schemes consist of a Vortex Initialization phase in which a preliminary vortex is created or modified from a global model, and an assimilation phase in which high-density observations are used to push the initial vortex to a new one which matches the observations better.

These existing methods have allowed for great strides in hurricane forecasting, but they still have limitations. The ensemble nature of many of these methods is computationally expensive - they rely on running ensembles of the model in order to generate the initial conditions (independent of the ensemble used for the actual forecast after the initial conditions are obtained). Also, only linear adjustments of the governing equations can be performed in each iterative step of the variational algorithms, which can cause problems given the highly non-linear nature of the equations. Finally, despite their advances, these methods still have documented errors and biases10, which warrants exploration of alternative methods. Given the increasing availability of high-density observational data - e.g., hurricane hunter flights26,30, dropsondes31, satellites32,33, and radars27,34—we wish to develop a new framework to accurately and efficiently assimilate observational data into the vortex reconstruction, which could ultimately either complement or replace existing DA methods.

In light of recent advances in the field of deep learning, here we develop a physics-informed machine learning (ML) framework for vortex initialization and DA, with potential application for forecast model initial conditions, among other uses. The model of choice is a Physics-Informed Neural Network (PINN)11,12. To evaluate its efficacy, we use forecast data of Hurricane Ida (2021) from GFDL’s forecast model T-SHiELD35, in line with other Observing System Simulation Experiments (OSSE)36. Using forecast model data affords us a ground truth against which we can validate our results. Various studies have validated the quality of T-SHiELD37,38, including a study39 which directly compares it against the popular Hurricane Analysis and Forecast System (HAFS) model used by NOAA, so we assume the representation of storms in T-SHiELD is accurate and realistic. We sample data from model output to obtain synthetic observations (i.e., training data), and use those observations to reconstruct the full wind and pressure fields. First, we use PINNs to model the 2D and 3D wind and pressure fields of Hurricane Ida as they are represented in the SHiELD forecast. We also reconstruct the real (not simulated) Hurricane Ida using observational data collected in real-time by the hurricane hunter plane and dropsondes to assess the PINN’s applicability for real-world observations. Throughout, we describe the methodological details of the PINN that improved model performance.

The overarching objective of this paper is twofold: first, to demonstrate the power of PINNs and generally physics-informed ML to motivate more cross-disciplinary research, and second to offer an alternative or complement to existing DA schemes for hurricane flow field reconstruction. Through our experiments and analysis, we find our model is fast, accurate, and flexible, highlighting the potential of physics-informed ML paradigms40,41 to recover large-scale geophysical fluid flows.

Physics-informed neural networks

Physics-Informed Neural Networks (PINNs)11 are a powerful tool which combine the universal function-approximating power of neural networks42 with physics via encoded partial differential equations (PDEs). PINNs have been used for a variety of problems, such as numerically solving PDEs11,43 and equation discovery given sparse observations44. They are especially useful for inverse problems, which makes them aptly suited for DA12. PINNs have been applied to reconstruct wind fields in an idealized setting45 - Zhang and Zao (2021) reconstruct the 2D45 and 3D46 wind field in front of a wind turbine. They found very promising results with root mean square erros (RMSE) that were within 10% of the wind speeds observed. However, the flow field was idealized in nature and drawn purely from simulation data. To the best of our knowledge, no other papers to date have applied PINNs to large-scale (large enough such that the Coriolis force becomes important) wind fields or for the task of TC wind and pressure field reconstruction using real-world observations.

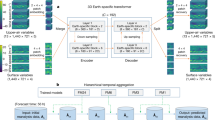
Figure 1 illustrates the general setup and structure of our PINN model. As seen in panel d, the input layer consists of the spatial coordinates—x, y, and p (we use pressure as the vertical coordinate instead of z) - and the temporal coordinate (t). The output layer of our PINN consists of the three components of the wind vector (u, v, w) and the geopotential (Φ). Example target output fields from SHiELD in the 2D case are shown in panel a. During training, any PINN requires two types of inputs: data points and collocation points (panel c). The data points are recorded observations of the flow field; collocation points are the points at which we evaluate our chosen set of PDEs and obtain equation residuals to measure how closely the PDEs are satisfied. The PINN is trained using these input points to produce a flow which both matches the observations and satisfies the provided equations. We found that the model performs better when fewer collocation points are used in the inner core of the storm (within 100 km of storm center) compared to outside the inner core. This is likely because the density of data points is higher near the center in all our examples so we don’t need to rely on the physics as much, and the complex dynamics of the eyewall are not fully captured by our simplified set of equations. This is discussed more in the 3D Case section.

Fig. 1: Illustration of the general PINN structure and training data.
figure 1

a The target output from SHiELD for the 2D case, showing the u and v components of the wind field and the geopotential field. b The loss function used to train the PINN, which consists of a data loss component and an equation loss component. Note that each data point in the data loss equation is weighted by the wind speed of the data point. n is the number of data points we sum over and m is the number of collocation points we sum over. c The collocation and data points used as inputs. The collocation points are randomly generated with the density of points in the inner core 5x lower than the density outside. Note these points will also have a time value, and in 3D reconstructions, they will have random pressure values, too. The data points shown are the example cross and plus patterns used in the 2D Case. d Illustration of the fully connected deep neural network structure, showing the inputs and outputs.

Full size image

The loss function the PINN iteratively optimizes, shown in panel b, is a weighted sum of the mean square errors of the PINN’s prediction at the data points (data loss \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{Data}}}}}}}}}\)) and the PINN’s mean square equation residual error at the collocation points (equation loss \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{Equation}}}}}}}}}\)). In the \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{Data}}}}}}}}}\) equation, each data point is weighted by the wind speed magnitude—since the higher wind speed magnitudes are important but sparse in the flow field, this weighting greatly improved the model performance and allowed it to learn the eyewall structure much better. While the PINN still slightly underestimates the maximum winds, this approach increased the max winds produced by the PINN by 10–20%—much closer to the true max wind values in the target storm. The data and equation losses are weighted by γ which ranges between 0 and 1, with a value closer to 1 prioritizing the equation loss more47. Our equations are the horizontal Navier–Stokes equations for inviscid fluids on a rotating planet and the continuity equation, assuming the hydrostatic approximation and non-divergent flows48. Refer to the methods section for a full description and brief derivation of the equations. The equations are non-dimensionalized and all variables are scaled so they have similar magnitudes49. Specifically, we non-dimensionalize all the input variables (spatial and time coordinates) and all the dynamical fields by constants that ensure all values are roughly between 0 and 1. The exact normalization is arbitrary, but re-scaling to similar magnitudes makes the PINN training easier, and ensures that the different PDEs and variables have similar magnitudes in the loss function.

In all of the following cases, we reconstruct the flow over a 12-h period (which we define as hours −6 to 6), using SHiELD data points from hours −3, 0, and 3. Results in figures are from hour 0. The SHiELD forecast used is a forecast for Hurricane Ida (2021) initialized at 0z Aug 27, 2021. Note that all SHiELD and PINN winds are the winds along a constant pressure surface. Loss curves for the PINN trained in each of the following three sections are in Supplementary Fig. 1. See Methods for full details on PINN implementation and training.

Results

2-Dimensional case

Figure 2a shows the PINN reconstruction of the 850hPa wind field of SHiELD’s 60-h forecast of hurricane Ida at Aug. 29, 12z, along with the target storm as represented in the SHiELD forecast (Fig. 2b). Supplementary Fig. 2 shows all PINN reconstructed fields. The data points used were sampled from the SHiELD output at hours −3, 0, and 3, and are shown in Fig. 2c (points were sampled along the lines shown). A cross pattern is used for the data points at hours −3 and +3 and at hour 0 a plus pattern is used, with the transects through the center of the storm mimicking the flight paths used for recon missions. Alternating between the cross and plus patterns increases the spatial extent of the data points while still using the same number of data points at each time point. The PINN performed better with this setup than if we just used the same pattern at each time point. Two transects were used because that was the minimum number with which the PINN could successfully reconstruct the field.

Fig. 2: 2-dimensional PINN wind speed prediction trained with SHiELD simulation data.
figure 2

a PINN 2-dimensional reconstruction of the SHiELD forecast of Ida at 850 hPa. b The SHiELD forecast of Ida (ground truth data) which the PINN is trying to reconstruct. c The data points used for PINN training sampled from the SHiELD forecast fields. At hours −3 and +3, a cross pattern is used and at hour 0 a plus pattern is used. The transects at each time point cross through the center of the storm, which is moving northwest with time. Along each transect, u, v, and the geopotential are sampled from the SHiELD output and used as data points for the PINN. d The solid blue line shows the PINN RMSE across the full grid as a function of radius from storm center. The dashed red (black) lines show the PINN (SHiELD) azimuthally averaged radial wind profile. e PINN wind speed error against SHiELD (simply (a) minus (c)). f Log PINN equation loss, as defined by the base 10 logarithm of \({{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Equation}}}}\) from Fig. 1b. For reference, the magnitudes of the terms in the PDEs are shown in Supplementary Figs. 4 and 5.

Full size image

Figure 2e shows the error between the PINN reconstruction and the SHiELD-modeled wind speeds. Using just two transects through the center of the storm every 3 h, the PINN is able to accurately capture the large-scale structure and features of the storm, including the location of the maximum winds and the overall radial wind profile (Fig. 2d). However, the PINN does struggle to capture the strongest winds of the storm, recording a maximum of 62 ms−1, compared to 69 ms−1 in the target SHiELD. This primarly occurs since the PINN struggles with high-gradient regions, especially in the eyewall. Note, however, these maximum winds only occupy a few gridpoints in the output. Nonetheless, it still achieves RMSE around 2–5 ms−1 in the eyewall (Fig. 2d, e). Equation losses are order 10−6 outside the eyewall and around 10−3 in the eyewall (Fig. 2f, Supplementary Fig. 3), orders of magnitudes smaller than the term magnitudes in the governing equation, which have magnitudes of 1-10 (Supplementary Figs. 4, 5 for the 3D case), indicating that our provided governing equations are accurately satisfied and have very small residuals. Term magnitudes are higher near the center of the storm, so the higher equation loss there is expected.

20,000 collocation points were used in this case—this high amount was necessary due to the sparseness of the data points. Near the center of the storm, the data points are closer together, so it was found that using a lower density of collocation points near the center of the storm yielded better results. A γ value of 0.99 was used—the model needed to rely heavily on physics to fill in the gaps between the sparse transects. A lower γ value would cause the PINN to overfit the data, while a higher γ value would cause it to struggle to obtain the full structure and max winds of the storm (Supplementary Fig. 6). Note that the optimal choice of γ will depend on how the input features are normalized. Between the two transects and the boundary points and the three time points, a total of 4498 data points were used, representing roughly 2.4% of the total points available from the SHiELD field. We use a network structure with 8 hidden layers, each with a size of 100 nodes for this case.

The key takeaway from these results is that the 2D large-scale characteristics of the storm can accurately be reconstructed by the PINN using just 2 transects through the storm center every 3 h.

3-Dimensional case

In this section, we reconstruct the full 3D flow of the same storm from SHiELD as the previous section. The data points consist of 0.05% of the gridpoints in the SHiELD output at each time point, for the time points t = −3, 0, and 3 h. This amounts to 4158 total data points. The data points are randomly sampled from SHiELD such that the density of points in the inner core (inner 100 km) of the storm is 5x higher than the density of points outside the inner core (shown in Fig. 3b). 10,000 collocation points are used and randomly generated such that the inner core density is 5x lower than the outer density (shown in Fig. 3c). The motivation for this setup is that more data points are needed near the center of the storm to learn the sharper gradients and most complex dynamics and fewer collocation points was necessary to give the model more freedom to fit these data points. So, in the inner core, the PINN relies more on the dense observations, while outside the core, it relies on physics to fill in the gaps between the sparser observations. Results from various trained models shown in Supplementary Table 1 show this effect. While the random sampling and uniformity in the vertical direction are unrealistic, a higher density of observations near the center is expected since that region is the focus of most observing campaigns.

Fig. 3: 3-dimensional PINN wind speed prediction trained with SHiELD simulation data.
figure 3

a PINN 3-dimensional reconstruction of the SHiELD forecast of Ida between 850 and 200 hPa. b The data points used for PINN training, with color indicating the pressure level of the sampled data point (0.05% of the SHiELD output data with a 5x higher density in the inner 100 km). c Like (b), but collocation points (10,000 points with a 5x lower density in the inner 100 km). d PINN-predicted wind speed along a vertical cross section at y = 0. e SHiELD wind speed along a vertical cross section at y = 0. f PINN RMSE for wind speed by radius from storm center. The vertical white dashed line indicates the radius of maximum winds.

Full size image

The full reconstructed wind field is shown in Fig. 3a, a vertical cross section in Fig. 3d, and a cross section of the SHiELD target wind field in Fig. 3e. The full 3D component fields from the PINN and the target SHiELD output are shown in Supplementary Fig. 7. Similar to the 2D case, the PINN is able to recover the key large-scale characteristic of the dynamical fields despite using so few data points. It is able to capture not just the horizontal patterns, but the vertical patterns in the wind, too. The PINN reaches a maximum wind speed of 58 ms−1—this is lower than in the 2D case since the model is trying to reconstruct flow over a much larger and more variable domain. The RMSE of the PINN output compared to SHiELD is shown in Fig. 3f. We see RMSE of 5–7 ms−1 in the eyewall and 1–3 ms−1 everywhere else. Equation errors (Supplementary Fig. 3) are orders of magnitude lower than the term magnitudes (Supplementary Figs. 4 and 5), indicating that the generated field satisfies our physical equations well. We can also see from the term magnitudes the transition from cyclostrophic balance (between the pressure and advection terms in the Navier–Stokes equations) to geostrophic balance (between the pressure and Coriolis terms) as we move from the storm core to the perimeter (Supplementary Fig. 8). A γ value of 0.5 was used in this case - the model was able to rely less on the physics as a regularizer since the large domain size already provided a constraint on the PINN output.

The total training time for this model was approximately 50 min. Only O(103) data points were used to train this model, but the training time scales well through about O(105) data points, and only increases around O(106) data points, as shown in the performance table in Supplementary Table 2. This is because the PINN is trained on a GPU which handles matrix multiplications very well, but is bottlenecked by memory capacities. We used a network with 4 hidden layers, each with 100 nodes for this case.

Real case

Finally, we use a combination of data from the SHiELD 12-h forecast output and real observations recorded in Hurricane Ida (2021) by the Hurricane Hunter plane centered around 12z August 27, 2021 (Fig. 4d) to reconstruct the wind and pressure field of Hurricane Ida at this time. Officially, Ida is recorded as having maximum sustained winds of 28 ms−1 (55 knots), but some dropsonde observations recorded winds up to 40 ms−1 (possibly with some observation errors). The sparse observational data (Fig. 4d, from the flight level data and dropsondes dropped near the core) alone is not enough to accurately reconstruct a realistic vortex, so we use the 12-h SHiELD forecast at this time to fill in the gaps, much like current DA schemes used in modern forecast models17,26. The sparse, but evenly distributed SHiELD forecast data gives the PINN general information about the shape and extent of Ida’s winds. Meanwhile, the dense areas of observations (especially near the storm center) allows the PINN to adjust the vortex to a physically realizable solution consistent with real observations. The forecast data also provides information about the field above flight level. Similar to the 3D case, we sample 0.5% of the SHiELD output data as training data points along with the real observations (Fig. 4d). The SHiELD data and the observations are treated equally as data points in the model, but the observations are weighted twice as high as the SHiELD points for a given wind speed magnitude. Between the SHiELD data and the observations, there are 54,663 total data points. Note that the SHiELD points and the observations were all sampled in storm-centered coordinates to avoid any negative impacts of the storm location in SHiELD not matching its actual observed location.

Fig. 4: PINN output trained with a combination of real hurricane hunter observations and SHiELD forecast data.
figure 4

a PINN 3D reconstruction of Hurricane Ida on August 27th, 12z. b PINN reconstruction at 850 hPa. Stars indicate locations of dropsonde observations, with the color indicating the wind speed measurement. c Same as (b), but for SHiELD reconstruction. d The locations and magnitudes of Ida flight level and dropsonde wind speed observations recorded roughly between 10z and 12z, Aug. 27. e Same as (b) but for HAFS reconstruction. f Observations from the Tail Doppler Radar (not used in PINN training) of the hurricane hunter plane around 12z Aug 27 at 1.5 km (roughly the altitude of the 850 hPa pressure level). Note this grid only extends out 150 km from the storm center. The correlations of the SHiELD, PINN, and HAFS fields in panels (b), (c), and (e) with these TDR observations are also printed on this panel.

Full size image

The full 3D PINN reconstruction (Fig. 4a) illustrates the complete and rich 3D structure. The 2D slices at 850 hPa of the PINN (Fig. 4b) and the SHiELD forecast (Fig. 4c) have very similar large-scale structures. We can see how the PINN compromises between the dropsonde observations and the SHiELD data: in the eastern eyewall, the dropsonde shows strong winds and SHiELD shows weak winds, so the PINN prioritizes the dropsonde observations which are weighted higher and produces a strong block of winds. In the northeast region of the storm, the dropsonde observations suggest a stronger region of winds, and SHiELD shows a very large region of strong winds—the PINN compromises with a broad region of moderately strong winds. Tail doppler radar50 (TDR) observations (not seen by the PINN during training) recorded by the hurricane hunter plane (Fig. 4f) offer a detailed view of what the inner core looks like, and validates the strong winds east of the eye that the PINN is able to recognize and develop. For reference, the reconstructed vortex generated by the HAFS model DA scheme is shown in Fig. 4e, which incorporates much more data than the PINN, including TDR and satellite data. Correlations between the TDR data and the 3 models (the two DA schemes - PINN and HAFS - and the 12hr forecast from SHiELD) are printed on Fig. 4f using the Pearson correlation coefficient. Despite the fact that the PINN isn’t a fully formed DA system yet, it still produces a better correlation with the ground-truth TDR data than HAFS. Additionally, the RMSE of the SHiELD, HAFS, and PINN fields against the TDR data are 4.5, 4.1, and 2.2 ms−1, respectively. We stress this is only one case, but it nonetheless offers a very encouraging result: the PINN can accurately and efficiently assimilate observational data to reproduce a realistic TC vortex using minimal data. It doesn’t record the fine-scale features or the exact maximum winds, but it produces a qualitatively accurate vortex based on observations. The training time for this model was 50 min, compared with the approximate 40 min it took to generate the HAFS reconstruction. Further modifications can be made to improve PINN performance, including finding more effective PINN structures and training on more GPUs. Currently, the PINN uses a single GPU core, while the HAFS analysis uses 128 CPU cores.

Discussion and summary

This idealized study provides a proof-of-concept that PINNs can be used to reconstruct TC vortices using sparse observations and a simplified set of governing equations. This study is also, to our knowledge, the first to demonstrate that PINNs can be used for the reconstruction of large-scale wind flows from real-world observations. We demonstrate that 2D and 3D TC vortices can be reconstructed using realistic and minimal observations, and we also show that a combination of artificially sampled model output combined with real-time observations can be used by a PINN to reconstruct the full 3D structure of a real TC. We describe implementation details critical to improved PINN performance, such as using fewer collocation points and more data points near the strongest winds, and weighting the data points in the cost function by their wind speed magnitude. The PINN outputs we produce lack the fine-scale structure and features of a real TC, but they recover the key large-scale characteristics of the storm well, including the radial wind profile and the location of maximum winds. The PINN does, however, struggle to recover the highest winds present in the storm. Nonetheless, generally, a more accurate reconstruction of the large-scale flow of the storm could improve both forecast model track and intensity errors, and an important next step is testing the PINN reconstructions as initial conditions in a forecast model, such as T-SHiELD, and assessing how it impacts track and intensity forecasts. The PINN can also be used for storm surge forecasting, risk assessment, or other applications.

The PINNs in this study use orders of magnitude fewer computational resources (1 GPU core vs. 128 CPU cores) than established DA methods for forecast models (such as the HAFS model). This is in part because the PINN does not rely on ensemble methods to generate the initial conditions. The PINN training time scales well with the number of observations used (Supplementary Table 2), and is robust to the locations and numbers of these data points. Unlike traditional methods, the PINN does not rely on an initial best-guess vortex from which it asimilates the observations. While we do make use of an initial vortex from the T-SHIELD output, with sufficient observations (such as from TDR or satellite data), no initial vortex would be necessary. Additionally, the PINN is essentially a continuous and differentiable function, so the output could be arbitrarily generated at any points in space or time within the training domain.

We emphasize that as a DA system, the PINN presented here needs more work to become a functional system in a forecast model. First, other field variables such as moisture and temperature need to be incorporated into the PINN output. This will also require updating/modifying the system of physical equations used by the model during training. It’s worth noting that the PINN equations can and should be tailored specifically to the forecast model it is being paired with, so the physics of the PINN reconstruction matches the physics of the forecast model. More work also needs to be done to better understand optimal network structures and numbers of data and collocation points for reconstructing the full 3D fields.

PINNs are an exciting branch of physics-informed ML that have been demonstrated in numerous studies as powerful tools for reconstructing fluid flows. This paper contributes to the growing list of their potential applications, and provides a promising alternative or complement to existing DA methods which could improve forecasting and other applications for decades to come.

Methods

SHiELD data

For the 2D and 3D cases, we use the GFDL forecast model SHiELD (System for High-resolution prediction on Earth-to-Local Domains, an overview of which can be found in ref. 35) for our TCs. SHiELD runs using the GFDL Finite-Volume Cube-Sphere (FV3) Dynamical Core51 and uses similar physical parameterizations as those used in the NCEP GFS model. We specifically use data from the T-SHiELD nest, which is an approximately 3.2 km resolution nest placed over the tropical North Atlantic which is coupled with the 13 km resolution SHiELD model to produce high-resolution forecasts and modeling of TCs and tropical convection in this basin (hereafter, we will refer to SHiELD and T-SHiELD collectively as SHiELD). It has been found to make accurate forecasts and capture many of the fine structural details found in hurricanes37,38.

In this paper, we focus on forecasts made by SHiELD for Hurricane Ida (2021), a storm which rapidly intensified from a category 1 hurricane to category 4 (with sustained winds of 150 mph) over one day while in the Gulf of Mexico, prior to making landfall in Louisiana. The forecast run we use is initialized at 00z August 27th, and runs for 72 h beyond that initialization (taking it through landfall on August 29th). Two-dimensional data is available at a temporal resolution of 1 h and a spatial resolution of 3.2 km, while 3-dimensional data is available at a resolution of 3 h and a vertical resolution of about 15 hPa (44 pressure levels between 150 and 900 hPa). We use the horizontal components of the wind field vector (u for the zonal component and v for the meridional component) and the geopotential (Φ). Vertical wind velocities are available, but we leave them out in this study as it is very difficult to get accurate vertical wind measurements in practice. We choose to focus on the 850 hPA level for the 2D case because this level is high enough from the ground that we can largely ignore the effects of friction, and it is a height around which hurricane hunters might fly through the TC eye. We focus on this storm at various points along the forecast and use our PINN to reconstruct the flow fields of Ida at these different forecast points. We created PINN reconstructions at forecast hours 11, 24, 36, 48, and 60, but in this work we focus on hour 60 (the strongest point) and hour 11 (a time at which we have plentiful observational data, about three days out from landfall before it underwent RI). Between hours 24 and 60, the storm undergoes RI and strengthens from a category 1 to a category 4 storm with maximum winds of 62.1 ms−1 (139 mph).

Real Ida observations

Processed real-time flight level and dropsonde observations are available through the NOAA website at https://www.aoml.noaa.gov/2021-hurricane-field-program-data/. We make use of just the Dropsonde and Flight Level Data from 20210827I1 Ida mission, when a hurricane hunter plane flew four transects through the eye of a developing Ida in a 6-h span around 12z Aug 27th with numerous dropsondes in the inner core. This data is very dense (collected every second), so 20 (3) second averages were taken for the flight level (dropsonde) data, resulting in horizontal (vertical) resolutions of 3 km (1 hPa) for the flight level (dropsonde) data.

For the Tail Doppler Radar data50, we use the Level 3 data available again through the NOAA AOML website from the link https://www.aoml.noaa.gov/ftp/pub/hrd/data/radar/level3/. We use the merged swaths dataset.

Physical equations to constrain PINN

Fluid flow must satisfy a governing set of physical equations—two important equations are the conservation of momentum and mass equations. The general conservation of momentum equations, known as the Navier–Stokes equations48, in a rotating reference frame are shown in equation (1). Bold terms indicate vectors, and \({{{{{{{\boldsymbol{v}}}}}}}}=u{{{\hat{{{{{\boldsymbol{x}}}}}}}}}+v{{{\hat{{{{{\boldsymbol{y}}}}}}}}}+w{{{\hat{{{{{\boldsymbol{z}}}}}}}}}\) indicates the velocity vector, p is the pressure field, ρ is the density field, τ is the deviatoric stress tensor of order 2, and Ω is the rotation vector for the earth, which can be represented by the vector \({{{{{{{\boldsymbol{\Omega }}}}}}}}=f/2{{{\hat{{{{{\boldsymbol{z}}}}}}}}}\). The Coriolis parameter f has value \(f=2{{\Omega }}\sin \phi\) where Ω = 7.2921e − 5 s−1 is the rotation rate of Earth and ϕ is the latitude. The conservation of mass equation is expressed in Equation (2).

$$\frac{\partial {{{{{{{\boldsymbol{v}}}}}}}}}{\partial t}+{{{{{{{\boldsymbol{v}}}}}}}}\cdot \nabla {{{{{{{\boldsymbol{v}}}}}}}}+2{{{{{{{\boldsymbol{\Omega }}}}}}}}\times {{{{{{{\boldsymbol{v}}}}}}}}=-\frac{1}{\rho }\nabla p+\nabla \cdot {{{{{{{\boldsymbol{\tau }}}}}}}}$$
(1)
$$\frac{\partial \rho }{\partial t}+{{{{{{{\boldsymbol{v}}}}}}}}\cdot \nabla \rho =0$$
(2)

We make some assumptions and simplifications to these equations because simpler equations are easier for the PINN to manage and are more computationally efficient. We also transform the equations to our specific domain and set of coordinates. First, we ignore the friction term in our equations and assume its magnitude is small, which is especially true at high altitudes away from land and the boundary layer. We also rewrite our equations using pressure as the vertical coordinate instead of z, so that our expression for vertical velocity becomes ω = dp/dt instead of w = dz/dt. Finally, we use the hydrostatic approximation (shown in Equation (6))—the hydrostatic approximation doesn’t exactly apply for a TC where in some regions of the storm there are strong vertical motions, but the approximation is close and greatly simplifies our task. Finally, we only use the horizontal NS equations since the hydrostatic assumption provides enough information to get good results.

These modifications and approximations yield the horizontal NS equations using pressure as the vertical coordinate, with each horizontal component shown separately in equations (3) and (4), and the continuity equation for incompressible flow shown in equation (5). Now, the pressure term is written in terms of the geopotential, Φ = gz. The hydrostatic approximation and pressure coordinates cause density to drop out of our equations, which means there is one fewer field variable we need to predict and include in our equations. We also use the beta-plane approximation for the Coriolis term (the last term on the left hand side of equations (3) and (4)) where fo is the Coriolis parameter at the latitude of the storm center at time t = 0 and β is the constant β = ∂f/∂y.

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\omega \frac{\partial u}{\partial p}-({f}_{o}+\beta y)v=-\frac{\partial {{\Phi }}}{\partial x}$$
(3)
$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\omega \frac{\partial v}{\partial p}+({f}_{o}+\beta y)u=-\frac{\partial {{\Phi }}}{\partial y}$$
(4)
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial \omega }{\partial p}=0$$
(5)
$$\frac{\partial p}{\partial z}=-\rho g$$
(6)

We use these same equations for the 2D and 3D cases—these equations provide three-dimensional information through the hydrostatic approximation. In the 2D case where we don’t have 3D data for training, the PINN essentially learns what vertical fields make sense and are compatible with the inputs it receives during training.

Data points for training

The data points are “observed” values measured in the flow domain. There are infinite possible flow fields that satisfy the NS and continuity equations alone, and the data points help constrain the PINN to find the solution which best matches the flow field of interest. For the 2D and 3D case we sample sparse points from the model output. There are 4 main data patterns (DP) which we evaluate for the 2D case—we call these 4 patterns All, Star, Cross, and Switch (the Switch DP consists of Cross and Plus DPs alternating at each time step of data observations). The ALL data pattern consists of all the data in the 800 × 800 km grid around the storm center. The cross DP consists of two diagonal transects through the storm’s eye from the corners of the 800 × 800 km storm-centered grid. The Plus DP is similar to the Cross DP, but with vertical and horiztonal transects through the eye instead of diagonal transects. And finally, the Star DP which consists of 4 transects through the eye (the Cross and Plus DPs combined). For the Star, Cross, and Plus DPs, we also include the boundary points, which in practice should be easy to approximate since they have low magnitudes and are influenced more by the large-scale environmental dynamics. The Switch DP allows us to see if gaining more spatial information about the storms (even if at different time steps) while using the same amount of information (two transects) improves the performance. These DPs can be thought of as synthetic flight patterns, simulating data that might be collected by the hurricane hunter plane flying transects through the center of storms.

In the 3D case, we sample points randomly from the SHiELD output. The sampling we do ensures the density of points in the inner 100 km of the storm is 5 times higher than the density of points outside the inner 100 km. This is intended to mimic how observing campaigns emphasize getting high density inner core observations. Figure 3b shows the horizontal distribution of these points. The pressure levels of these data points are chosen uniformly at random. We use 0.05% of the possible SHiELD points in the 3D case, which amounts to 4158 points. In the Real Case, we use 0.5% of the possible SHiELD points.

Data from the SHiELD model output has a 1 h resolution. We provide data points to the PINN at 3-h intervals, mimicking the typical time intervals between flight missions and NHC advisories (every 3–6 h). For example, if we are modeling the PINN in the interval t = [ − 6, 6] (where the units are hours), we would provide data points using the prescribed DP at times t = { − 3, 0, 3}. For the Switch DP in the 2D case, this would consist of the Cross DP at t = { − 3, 3} and the Plus DP at t = 0.

Collocation points for training

The collocation points are randomly sampled, with the density of points in the 100km inner core 5 times lower than the density of points outside 100km from the storm center. This configuration allows the PINN to prioritize fitting the high-density observations near the center of the storm over our PDEs, whose assumptions might break down in the complex dynamical environment of the eyewall. Outside the center where our data points are sparser, the high density of collocation points allows the PINN to prioritize fitting the large-scale environmental field. For the 3D and Real Cases, the collocation points are assigned uniformly at random a pressure value between 150 and 900 hPa. For all cases, the time of each collocation point is uniformly at random chosen from the time domain we’re interested in.

PINN structure

A general overview of the PINN structure can be seen in Fig. 1. It is structurally identical to a normal fully connected neural network—the only difference is the implementation of the loss function, described in the next section. The 4 inputs include the 3 spatial coordinates (x, y, and p) and the time coordinate (t). The outputs are the 3 components of the wind vector (u, v, and ω) and the geopotential height (Φ). The PINN then has a series of hidden layers of certain sizes. Each successive layer represents an affine transformation from one layer to the next, and each transformation matrix is comprised entirely of learnable parameters. Each layer beyond the input layer also has a bias vector of the same size as the layer. We experimented with numerous structures in the different sections. In the 2D case, the model has 8 hidden layers of size 100. In the 3D case the model has 4 hidden layers of size 100. In the real case the model has 4 hidden layers of size 50. For the 4 hidden layers of size 100 model, the biases combined with the matrices used to map each layer to the next result in a total of 31,204 learnable parameters for the entire PINN. We use a hyperbolic tangent activation function after each hidden layer.

PINN loss function

For model training, there will be two components to our loss function: the data loss (\({{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Data}}}}\)) on the data points and the equation loss (\({{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Equation}}}}\)) on the collocation points. In the following equations, items with the subscript “true” indicates the synthetic or real observation, and items with no subscript indicate outputs from the PINN. The data loss is defined in equation (7). This component of the loss is simply the MSE of the PINN output at the data points compared to the “true" values. Note that each point’s contribution to the loss is weighted by the magnitude wind speed of the observation at that point. This is done to force the model to prioritize getting the high wind speed points accurately since they are harder to predict there are fewer of these points than the lower wind speed points. Since we don’t have measurements at the collocation points, their contribution to the loss function, shown in equation (8), consists of the sum of the MSE of the equation residuals. Note that in the code, the equations are non-dimensionalized such that each variable roughly ranges between −1 and 1—this removes effects from different units and allows each equation to be weighted similarly in the loss function. It also allows for the data and equation losses to be weighted more equally since all terms of all the equations will be roughly on the same scale.

$${{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Data}}}}= \frac{1}{n}\sum \sqrt{{u}_{{{\mbox{true}}}}^{2}+{v}_{{{\mbox{true}}}\,}^{2}}\left[{(u-{u}_{{{\mbox{true}}}})}^{2}\right. \\ \left.+{(v-{v}_{{{\mbox{true}}}})}^{2}+{({{\Phi }}-{{{\Phi }}}_{{{\mbox{true}}}})}^{2}\right]$$
(7)
$${{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Equation}}}}= \frac{1}{m}\sum \left[{\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\omega \frac{\partial u}{\partial p}-({f}_{o}+\beta y)v+\frac{\partial {{\Phi }}}{\partial x}\right)}^{2}\right.\\ +{\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\omega \frac{\partial v}{\partial p}+({f}_{o}+\beta y)u+\frac{\partial {{\Phi }}}{\partial y}\right)}^{2}\\ \left.+{\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial \omega }{\partial p}\right)}^{2}\right]$$
(8)

Recall that since a PINN is a differentiable function, the partial derivatives in equation (8) can readily be calculated from the outputs. The total loss function is defined in equation (9) where γ is a hyperparameter which controls how the equation loss is weighted relative to the data loss. Higher (lower) γ values indicate the PINN will prioritize the equation loss more (less). Generally, the sparser your data points are, the higher γ value you will need to allow the model to use physics to fill in the gaps.

$${{{{{{{\mathcal{L}}}}}}}}=(1-\gamma ){{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Data}}}}+\gamma {{{{{{{{\mathcal{L}}}}}}}}}_{{{\mbox{Equation}}}}$$
(9)

PINN training

The PINNs are built in Python52 and trained using TensorFlow53 2.0 using code adapted from Raissi et al.11 which was written in TensorFlow 1.0. The models are trained using a single NVIDIA A100 GPU. Following Markidis54 our PINNs are first trained by the Adam optimizer55 for 20,000 iterations, followed by the L-BFGS optimizer56 for 180,000 iterations, for a total of 200,000 iterations. 10,000 collocations points were used for the 2D case and 20,000 for the 3D and Real cases. There is randomness in the PINN’s prediction, and occasionally the model solution would fail or blow up in certain regions. Consequently, we would train an ensemble of five models and choose the one whose results were the best, although they were all normally similar.