Introduction

In the last decade, machine learning (ML) techniques have become essential to find patterns in big data and to mine valuable information. Over the past half-century, the rapid progression of computing power has allowed the spawn of novel ML methods from simple linear algebraic data analysis techniques to sophisticated deep learning neural networks with billions of synaptic weights. Today, many state-of-the-art models require a significant amount of computational capacity to be trained and processed, with artificial intelligence and deep learning solutions at the top. Groundbreaking neural network models, such as GPT-31 and AlphaFold2, require a massive amount of resources. Still, the computational power demand and the need for new approaches to process and undermine information faster from ever more extensive datasets are rapidly increasing.

In such a framework, applying quantum computing to ML3,4,5,6,7 is a promising approach to train and exploit models, potentially in a fraction of the time and cost, without the need for power-consuming high-performance computing and data centers. However, the advantage offered by quantum computers can be quantified differently, depending on whether the focus is on increasing some ML metrics, such as either the classification score, or the precision, or the accuracy—by addressing classically intractable systems, or by reducing the training and query times, respectively. Indeed, quantum computers promise to accelerate ML algorithms from physics to chemistry8,9,10,11, biology12,13, finance14,15, and material science16, allowing unprecedented opportunities in almost any industry.

Although many algorithms have proven a theoretical advantage over classical computation17,18,19,20,21,22,23,24,25,26, quantum computers are currently in an early stage of technological development, limited by hardware engineering constraints.

Several quantum computer technologies and computational architecture paradigms exist, each characterized by different trade-offs in terms of the number of qubits, fidelity, and speed of quantum operations. The lack of sufficient resources to implement error-correction techniques implies noisy gates and de-cohering qubits, which in turn strongly affect the capability of such devices to provide an edge in real-world applications. Indeed, it is unclear which applications could provide a true advantage over classical computers, given the current noisy quantum devices.

Considering the current development of quantum computer hardware, adiabatic quantum annealers (AQAs)—suitable to physically implement quantum annealing—offer a viable path to demonstrate a quantum speed-up in today’s ML applications. In fact, AQA currently provides a higher number of qubits compared to any other gate-model quantum architectures, being able to address much larger datasets and problems. Although AQA is not a general-purpose quantum computer, it has many applications designed to solve combinatorial optimization problems, including chemistry and materials27,28,29, scheduling3,30,31, ML32,33,34, and finance14,15,35. Among all the quantum ML models that could exhibit a speed-up, restricted Boltzmann machines36 (RBMs), generative models based on neural networks, are widely investigated. Indeed, they can be efficiently trained on quantum annealers31,37,38 and be employed for several ML tasks from data reduction39 and feature extraction36, to classification40,41 and collaborative filtering42. Despite the high potential of the representative power, the adoption of RBMs is limited since they require a demanding computational training process, such as contrastive divergence (CD) and persistent contrastive divergence (PCD)43. In fact, the classical algorithm requires performing a thermalization cycle to sample states from an RBM, with a computational complexity that scales as O(k ⋅ N), where k is the number of thermalization steps and N are the number of RBM units38. Moreover, the classical procedure only approximates the correct model distribution, therefore intrinsically affecting the overall performance. On the other hand, the advent of commercial AQAs promises to address those problems, avoiding long thermalization cycles and sampling correctly distributed states by querying the QPU in principle once. If the computational cost of initializing the quantum computer is neglected, the quantum algorithm computational complexity to obtain a single sample scales as O(1).

Although AQAs offer a fundamentally different way to train and query the model, providing an asymptotically faster way to sample states and perform better than conventional methods, we are currently limited by the dimension of problems that can be embedded in the quantum device. In particular, D-Wave quantum annealers, the only commercial quantum annealers available today, are physical devices restrained by technological and engineering constraints. Sampling from a D-Wave quantum machine has a computational complexity that depends on the number of the involved physical qubits and the number of samples extracted, making it non-trivial to forecast the advantage the quantum computer would offer in the future. Today, the quantitative answer to the question of what scaling edge and which range of problem RBMs can provide on realistic, noisy finite-size quantum devices still lacks.

In this work, we address those questions by separately comparing the time to sample states during the training (training time) and querying the model after the training phase (exploitation time) and the performance of both classical and quantum-RBMs (QRBMs) on standardized cybersecurity datasets. In particular, we trained an RBM as a network intrusion detection system44,45,46,47 (NIDS) on two real-world cybersecurity datasets (NSL-KDD and CSE-CIC-IDS2018, respectively) to detect a quantum speed-up of today’s hardware by employing a quantum annealer and an equivalent model trained using the CD on classical hardware. Specifically, we compare a single-core CPU, a 128-core processor, and a quantum chip with a single copy of the model. RBM on classical computers48,49,50,51 and QRBM on an AQA have already been trained on cybersecurity data52, providing a proof of concept that a QA-based RBM can be trained on a 64-bit binary dataset.

Data from the cybersecurity world have previously been used for RBM training. Specifically, Aldwairi et al.50 conducted a study where they trained an RBM using CD and PCD on the ISCX 2012 dataset. The results showed an accuracy rate of over 88%. Dixit et al.53 trained an RBM on the D-Wave 2000Q employing it as both a classifier and a generative model, showing a proof of concept that a QA-based RBM can be trained on a 64-bit binary dataset. Hybrid approaches were also employed by Li et al.54, who trained 10% of the KDD-99 dataset by first reducing its dimensionality using an autoencoder and then employing a deep belief network for classification. Similarly, Salama et al.55 used a hybrid approach, employing a deep belief network for dimensionality reduction and a support vector machine for classification.

Previously, one of us has already shown the training of a fully connected QRBM by embedding techniques37, also including reverse annealing38, and quantum supervised learning in gate-model quantum computers by both variational methods56, quantum neural networks21, and quantum adversarial networks57. Here we find that sampling from the D-Wave Advantage quantum annealer returns a computational complexity that scales linearly with the number of QRBM units and the number of samples extracted, comparable with the classical algorithm. Still, the computational advantage of the quantum device could result in a reduction by orders of magnitude of the computational times. Such a speed-up is problem dependent since the computational time depends on the number of units, the number of Gibbs steps performed, and the number of quantum samples extracted from the quantum machine. The reduction in the computational times could be prominent today in all applications where datasets are massive, with many features, or alternatively, the models need to be re-trained to adapt to continuous changes, such as within the context of cybersecurity applications and intrusion detection systems.

We observed, by comparing the RBMs and QRBMs, that for the real-world cybersecurity datasets like NSL-KDD and CSE-CIC-IDS2018, sampling states for the negative phase are handled up to 64 times faster by the AQA during the training than the single-core times and 41 times faster than the 128 threads CPU. Therefore, we detected a quantum speed-up in existing hardware on real-world data, although it highly depends on the problem’s characteristics.

Results

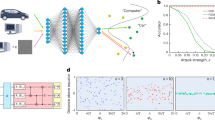
RBMs form a class of neural networks composed of units that can assume binary values, forming a bipartite system coupled by real weighted connections. The visible units represent the model input/output, while the hidden units raise the RBM’s ability to mimic the dataset’s structure. RBMs can be trained by both a supervised58 or unsupervised learning algorithm36, depending on the specific task. The training procedure consists of carefully modifying the model weights to learn how to generate and reconstruct the essential information encoded in the dataset. Several training procedures exist, including the use of quantum annealers, as shown in Fig. 1. The advantage of employing the D-Wave adiabatic quantum machine to exploit RBMs could emerge as an increase of performance metrics or as a reduction in the computational times, such as the training time and the query time. Reducing the training time is essential in all the applications where the model needs to be re-trained periodically to adapt to constantly changing environments59,60,61,62,63, while reducing the query time is crucial for all applications that benefit from the faster response possible, such as in some anomaly detection tasks64.

Fig. 1: Overview of the quantum and classical loop to train a restricted Boltzmann machine.
figure 1

a The purple shade shows the structure of the datasets used in this work. The NSL-KDD and CSE-CIC-IDS2018 datasets contain MR records of NR miscellaneous data type features. The processed NSL-KDD and CSE-CIC-IDS2018 dataset contain M = 125972 and M = 3040074 records, respectively, and N binary value column features. The last three bits of each record are reserved for encoding the label. b The blue arrows show the quantum training loop, while the red arrows show the classical training loop. In the former, the restricted Boltzmann machine (RBM) weights Θ are encoded in the quantum processor unit (QPU) and next, the s quantum samples are sampled from the QPU to estimate the negative phase statistic. In the latter, the RBM weights are used to perform k Gibbs sampling steps. The samples are subsequently used to estimate the negative phase. The positive phase statistic is calculated by loading a batch of elements sampled from the dataset in the visible units (red dots) and updating the Nh hidden units (blue dots) accordingly. Once the positive and negative phases have been evaluated, the RBM weights are updated, and the training loop continues until a maximum number of epochs is reached.

Full size image

Evaluation of the computational times

To quantify the potential advantage of the D-Wave quantum annealer in reducing computational time, we independently compared the times required to estimate the negative phase by a classical RBM and a QRBM implemented on the D-Wave quantum annealer. In such analysis, we are neglecting the performances of the models on a specific task, focusing on the computational times to estimate the negative phase only, which depends on the size of the models, the number of CD steps k, or the number of samples extracted by the QPU only.

The only difference between the quantum and classical approaches consists of the different methods to sample states with the correct Boltzmann distribution from the model. Since the computational time depends on the size of the model, we selected 676 different RBMs by varying the number of visible (N) and hidden (Nh) units. We measured the time required to perform k CD steps to benchmark the classical RBM. Figure 2 displays the classical times it takes to execute k steps by using either one thread or 128 threads of an AMD Ryzen Threadripper 3990X processor. The classical times highly depend on the size of the model, growing linearly by increasing the number of involved nodes and the number of CD steps.

Fig. 2: Time to compute k contrastive divergence steps as a function of the restricted Boltzmann machine size.
figure 2

Each contour plot has been obtained by measuring 676 different restricted Boltzmann machines (RBMs) arranged evenly on a square lattice as a function of the number of visible and hidden units. Each RBM has been evaluated 40,000/k times to reduce the variance. a Single-core times. The time to perform increases linearly with the number of contrastive divergence steps performed. b Multi-core times on a 64c/128t machine. The high number of threads available decreases the dependency between the time and hidden units.

Full size image

To measure the sampling times from the QPU, we embedded the same RBMs models on the D-Wave Advantage 4.1 machine by running the minorminer65 algorithm, commonly employed to map virtual qubits21 to physical qubits on the hardware. Differently from refs. 34,66, we run minorminer three times per machine to reduce the number of qubits involved and the qubit chain lengths, as described in the Method section. As the graph representing the hardware has limited qubits and connections, we therefore could embed just a fraction of the RBMs used to benchmark the classical approach. For each QRBM, we sampled 10, 100, and 1000 samples from the quantum processor, respectively. For a fair comparison, since we access the QPU by cloud, we discarded the network latency time by recording the QPU access time instead, corresponding to the execution time during which the QPU is unavailable to any other quantum machine job. Figure 3 shows the time required to sample states from the D-Wave Advantage 4.1 QPU as the model size increases. It shows the QPU access time measured to sample 10, 100, and 1000 states from the QPU. The QPU access time has a mild dependency on the number of visible and hidden units, while it strongly depends on the number of samples, so its value corresponds to 1.6 ⋅ 10−2 s, 3 ⋅ 10−2 s and 2 ⋅ 10−1 s, respectively. Therefore, the quantum hardware may reduce the computational time only in tasks that require both a high number of CD steps and a limited number of quantum samples to be extracted. It is worth noticing that if one wants to compare the speed-up of the classical and quantum models on a specific task, we must choose and fix the above quantities so that their performance metrics are comparable, as empirically done in the following subsection.

Fig. 3: D-Wave quantum processor units access time for different numbers of samples extracted as a function of the number of the restricted Boltzmann machine (RBM) size.
figure 3

The quantum processor unit (QPU) access time consists of a one-time initialization step to program the QPU and multiple sampling times for the actual execution of the QPU. The QPU access time depends on the number of qubits involved and the number of samples required. The contour plots highlight the region of visible and hidden units of currently embeddable RBMs on the D-Wave Advantage architecture.

Full size image

Figure 4 shows a linear relation between the number of QRBM units N and the QPU access time. The three data points, corresponding to sample 10, 100, and 1000 states from the QPU, were fitted by linear functions ys = msx + qs. We found angular coefficients m10 = 5.15 ⋅ 10−6 ± 1.3 ⋅ 10−7, m100 = 5.14 ⋅ 10−5 ± 1.3 ⋅ 10−6, and m1000 = 5.14 ⋅ 10−4 ± 1.3 ⋅ 10−5. Therefore, the computational complexity to sample states from the quantum device scales as O(N ⋅ s), where s is the number of samples extracted, which is comparable with the O(N ⋅ k) trend of the classical algorithm. Although we are currently limited by the size of the model that can be embedded in the QPU, we can forecast the QPU access time to be 0.514 ± 0.013 μs per unit per sample.

Fig. 4: D-Wave quantum processor units access as a function of the quantum-restricted Boltzmann machine (QRBM) size.
figure 4

The figure shows in green, blue, and orange color the quantum processor unit (QPU) access time measured to sample 10, 100, and 1000 samples, respectively, from the D-Wave Advantage 4.1 quantum annealer as a function of the number of QRBM units (hidden + visible units). The data points show a linear trend between times and QRBM units, as shown by the straight dashed lines. All the data points were fitted by a linear function (dashed gray line) with R2 = 0.979 and root mean square error (RMSE) of 7.1 ⋅ 10−5, 7.1 ⋅ 10−4, and 7.1 ⋅ 10−3, respectively.

Full size image

Speed-up on real-world cybersecurity datasets

Let us now search for the signature of a speed-up on real-world datasets. To detect a quantum potential advantage on today’s hardware for real-world tasks, we trained both an RBM and a QRBM as NIDSs. The goal is to detect an anomaly, i.e., an attack, from a benign instance. Like other classification and clustering problems, NIDS algorithms process training datasets. In the following, we consider the NSL-KDD67 and the CSE-CIC-IDS201868 datasets. The former represents one of the most widespread datasets in the NIDS domain, while the latter is a modern cyber-defense dataset.

Since the QRBM units require binary input values, we binarized the records of the two datasets to 85 binary features for the NSL-KDD dataset and 156 for the CSE-CIC-IDS2018 dataset (see the Methods). The former dataset comes with training and testing datasets with a ratio of roughly 80%:20%. The latter has been split into training and testing datasets with the same ratio. The two training datasets have been balanced by under-sampling the most common class.

Despite being a generative model, RBMs can be used effectively as classifiers encoding the label as part of the input state during the training and reconstructing the label during the exploitation phase. Here we reserved the last three bits for encoding the label. A majority vote rule was performed to obtain a final result from the model during reconstruction. For instance, if the last three bits are 101, it indicates a benign instance, while if they are 001, it reveals an attack.

To measure the classical RBM’s performance in the two datasets, we investigate the optimal number of hidden units and the number of Gibbs sampling during the training and once the model has been trained. First, let us compare the performance of classical RBMs by setting the number of CD steps to 1000 and increasing the number of hidden units until no further improvement in performance is detected. Therefore, in all the following experiments, the number of hidden units for the RBM and the QRBM are set to 30 for the NSL-KDD dataset and 90 for the CSE-CIC-IDS2018 dataset, respectively. Then the training performance of the RBMs is compared by varying the number of CD steps k during the training. The number of Gibbs sampling steps does not affect the performance of the model trained on the NSL-KDD dataset, while it has a mild effect on the CSE-CIC-IDS2018 dataset as shown in Fig. 5. Comparing the performance of the model by varying the number k during the exploitation phase, then in both datasets the performance of the RBMs depends on the number of CD steps, as shown in Table 1. In particular, it emerges a 13% increase in accuracy by employing 1000 CD steps compared to a single CD step in the CSE-CIC-IDS2018 dataset.

Fig. 5: Restricted Boltzmann machine (RBM) performance during classical training as a function of the number of Gibbs steps (k).
figure 5

The figure shows the F1 score (a, b) and the accuracy (c, d) achieved by training an RBM using different Gibbs step values for the NSL-KDD and the CSE-CIC-IDS2018 datasets during 2000 training epochs. F1 score and accuracy were chosen as performance metrics since computing the log-likelihood evaluation is impractical for RBMs of moderate size. In addition, these metrics allow for comparing RBM and QRBM models with existing literature on anomaly detection. The performance was measured using the testing dataset and averaged over 10 identical runs showing the 95% confidence interval as colored shadows. The number of Gibbs sampling steps does not affect the performance of the model trained on the NSL-KDD dataset, while it has a minor effect on the model performance trained on the CSE-CIC-IDS2018 dataset.

Full size image
Table 1 Performance of restricted Boltzmann machine (RBM) as a function of the number of Gibbs steps (k).
Full size table

Finally, the performance of the QRBM in the two datasets is measured by setting the same hyperparameters in common with the classical RBMs. More details on the hyperparameters employed during the training are given in Supplementary Table 1. The number of quantum samples required to train the QRBM is reasonably limited. In particular, it is possible to train the QRBM by extracting ten samples only from the QPU. In addition, the QRBM performance is comparable to the classical RBM, although less effective on the CSE-CIC-IDS2018 dataset, as shown in Table 2 and in Supplementary Fig. 1. Since we have not further optimized the hyperparameters in this work, the difference in the performance could be due to sub-optimal values and could be leveled by carefully choosing the optimal parameters. It is worth noting that the quantum model requires less training epochs to achieve a target accuracy (η) for the NSL-KDD dataset, while for the CSE-CIC-2018 dataset it is the opposite, as shown in Supplementary Table 3.

Table 2 Performance of quantum-restricted Boltzmann machine.
Full size table

By comparing the classical and quantum computational time, we detect a speed-up in the computational time by employing the QRBM as NIDS trained on the two real-world cybersecurity datasets. In fact, to maximize the performance of the classical machine during the exploitation phase, it is required to perform more than 10 and 100 CD steps for the NSL-KDD and CIC-IDS2018 datasets, respectively. At the same time, it is necessary to sample 10 samples only from the QPU. Table 3 summarizes the speed-up measured on the two datasets.

Table 3 Quantum speed-up for the NSL-KDD and CIC-IDS2018 datasets.
Full size table

Discussion

We now turn our attention to the computational time, the computational complexity, and the performance achieved by the model at the end of the training process on today’s classical and quantum hardware.

The time required to train and query the classical RBM depends on both the size of the model and the number of CD steps, respectively. The latter affects the performance achieved by RBMs and it should be chosen carefully depending on the particular problem to balance the times and model accuracy. Increasing the number of thermalization cycles comes at the cost of higher computational time, which can increase by orders of magnitude. Although it is possible to use a single CD step during the training phase, significantly reducing the time while still achieving excellent performance49,50,52, such choice is not possible in the exploitation phase, where one wants to maximize the performance of the model, as shown in Table 1.

Although in principle quantum annealing offers a different way of training machines by avoiding long thermalization cycles with the complexity of a single quantum operation in theory, in practice, sampling states from D-Wave is an operation that depends on the number of involved qubits and the number of samples extracted. In particular, Fig. 4 shows that the computational complexity scales linearly with the number of units and the number of samples extracted, comparable with the classical computer, where the dependence on the number of Gibbs steps and the model size is linear.

The quantum speed-up offered by quantum annealers is problem dependent. It could emerge only for a sufficiently large RBM or for tasks that require long thermalization cycles and, therefore, a high number of Gibbs steps. We observed an advantage in terms of the computational time by employing a QRBM as an NIDS trained on two real-world cybersecurity datasets up to 64x compared to a single-core trained RBM, as summarized in Table 3.

It is worth highlighting that modern CPUs can process batches of data thanks to parallel computing, while for large RBMs, the QPU is limited to processing a single data point at each cycle, hugely increasing the computational time of the quantum model during the exploitation phase. Such limitation could be mitigated by embedding multiple QRBM replicas on the QPU at the cost of increasing the number of physical qubits involved.

The advantage carried by a quantum annealer may increase in the following years through quantum hardware improvements. Increasing the number of physical qubits will make it possible to embed larger models and multiple replicas. However, improving the number of connections per qubit could provide a more significant advantage by reducing the number of physical qubits involved and, consequently, the computational complexity of quantum annealers.

Methods

Restricted Boltzmann machine

RBMs are probabilistic neural network models that consist of a layer of visible binary units v = (v1, v2, ⋯  , vN) connected to a layer of hidden binary units h = (h1, h2, ⋯  , hM). Although each unit is connected to all the units in the opposite layer, no intraconnection is allowed, forming a bipartite system. They belong to the class of generative models and they can learn the underlying probability distributions of the dataset inputs once properly trained. The RBM is an energy-based model where every “state”, i.e., specific configuration of v and h, is associated with an energy:

$$E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})=-\mathop{\sum}\limits_{i}{a}_{i}{v}_{i}-\mathop{\sum}\limits_{j}{b}_{j}{h}_{j}-\mathop{\sum}\limits_{i,j}{v}_{i}{W}_{ij}{h}_{j}$$
(1)

where a, b are biases and W are the weights that represent the connection strength between units. The joint probability of a state is given by the Boltzmann distribution is:

$$P({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})=\frac{\exp (-E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}}))}{{\sum }_{{{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}}}\exp (-E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}}))}$$
(2)

while the probability of finding an individual visible unit vi = 1 given the hidden units h is:

$$P({v}_{i}=1| {{{{{{{\bf{h}}}}}}}})=\frac{\exp ({a}_{i}+{W}_{ij}{b}_{j})}{1+\exp ({a}_{i}+{W}_{ij}{b}_{j})}=\sigma ({a}_{i}+{W}_{ij}{b}_{j})$$
(3)

where σ is the logistic function. In the same fashion, the probability of finding an individual visible unit hj = 1 given the visible units v is:

$$P({h}_{j}=1| {{{{{{{\bf{v}}}}}}}})=\sigma ({b}_{j}+{W}_{ij}{a}_{i})$$
(4)

The goal of the training is to learn the best parameters θ = (a, b, W) that maximize the data log-likelihood. One strategy to achieve that is to perform gradient ascent steps of the log-likelihood function ll(θ):

$${\theta }^{new}={\theta }^{old}+\epsilon \frac{\partial ll(\theta )}{\partial \theta }$$
(5)

where ϵ corresponds to the learning rate.

It can be proven that

$$\frac{\partial ll(\theta )}{\partial \theta }=\mathop{\sum }\limits_{t=1}^{N}{\left\langle \frac{\partial (-E({{{{{{{{\bf{v}}}}}}}}}_{t},{{{{{{{{\bf{h}}}}}}}}}_{t}))}{\partial \theta }\right\rangle }_{P({{{{{{{{\bf{h}}}}}}}}}_{t}| {{{{{{{{\bf{v}}}}}}}}}_{t})}-N\cdot {\left\langle \frac{\partial (-E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}}))}{\partial \theta }\right\rangle }_{P({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})}$$
(6)

where 〈⋅〉P(⋅) denotes the expectation values with respect a distribution P( ⋅ ), ht is sampled from vt by using Eq. (4), and the sum is over a dataset with N records. The first term in Eq. (6) is called “positive phase” and can be estimated by using the data. However, the second term, called “negative phase”, is model dependent and requires a sum over all the states, which is intractable except for very small RBMs. Although an exact computation is unfeasible, there exist several methods that can be employed to approximate the expectation, such as CD, PCD, and Fast PCD.

Contrastive divergence

The CD procedure is a technique to approximate the negative phase by running a Monte Carlo Markov chain until a near-to-equilibrium distribution is reached. Ideally, the number of iterations should be high enough to get almost unbiased samples of the distribution modeled by the RBM (Gibbs sampling). Since the computational time required to get unbiased samples is considerable, the procedure is usually stopped after k iterations (CD-k).

The basic training idea of CD-k is to start the learning procedure by randomly setting the parameters θ. Then k sequences of Gibbs sampling steps are performed by starting from a vector v(0) sampled from the dataset to reach state v(k) and h(k). More precisely, during each step l < k of the Gibbs sampling, we sequentially sample h(l) starting from v(l) using Eq. (4) followed by sampling v(l + 1) from h(l) using Eq. (3). The state v(k), h(k) are then used to estimate the negative phase and, therefore, the log-likelihood derivatives. Finally, θ is updated by a single gradient ascent step using Eq. (5).

It is worth noticing that the CD procedure does not approximate the correct model distribution P(v, h), returning a biased estimate of the desired update direction69. Nevertheless, it has proven to be successful in training challenging applications.

Quantum training

Quantum annealers can be used to estimate the negative phase by extracting samples from the distribution associated with the RBM. The basic idea is to embed the RBM weights and biases on the QPU and then perform an annealing cycle. While in principle the machine is expected to obtain samples representing the system’s ground state, in practice Dumoulin et al.70 observed that the AQA generates configurations with higher energy levels, as if they were extracted from a Boltzmann distribution. Specifically, a quantum annealer at very long annealing times returns a final population that is close to such a distribution, up to a point where the dynamics freeze and the system deviates from the equilibrium71. If the dynamics slow down and freeze out within a short period of time, then an AQA with a linear annealing schedule will provide samples from the Boltzmann distribution22. However, in such a region, the actual probability distribution sampled by the AQA52,70,72 deviates slightly from Eq. (2). In fact, at each annealing cycle, samples are extracted with probability:

$$P({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})=\frac{\exp (-E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})/{T}_{eff})}{{\sum }_{{{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}}}\exp (-E({{{{{{{\bf{v}}}}}}}},{{{{{{{\bf{h}}}}}}}})/{T}_{eff})}$$
(7)

where Teff is an effective temperature determined by thermal noise inside the chip73,74. To compensate for this problem, the energy is rescaled by a factor α so that we sample with an effective temperature Teff = 1. The optimal hyperparameter α should be set periodically since it changes over time, and its time evolution is challenging to forecast38,52. The mismatch between α and Teff might lead to sub-optimal RBM training. Supplementary Table 1 reports the value for the annealing time and α employed during the QRBM training for the two cybersecurity datasets.

Embedding

To sample states from a QRBM directly on a D-Wave system, or in general, to solve a QUBO problem directly on a D-Wave system, it is required to map the model onto the QPU topology. Such a procedure, called embedding, consists of identifying groups of physical qubits in the QPU (chains) so that they form the topology of the problem under investigation by behaving as individual units. The connectivity of each group can be enhanced by creating strong ferromagnetic couplings between the qubits (Jchain), which forces coupled qubits to stay in the same state. Achieving the optimal chain strength involves finding a balance where setting it too low increases the likelihood of encountering broken chains in the output, while setting it too high may result in weights that are not sufficiently distinguished by the analog control system73. Finding the best embedding is generally an NP-hard problem65. Although it is possible to get the optimal embedding of a QRBM manually by exploiting the specific topology of the QPU37,52,53, we exploited the minorminer algorithm65 provided by D-Wave to find the embedding for the QRBMs investigated in this work. Since the minorminer algorithm is heuristic and finds an embedding with some probability, we run the algorithm three times per QRBM to reduce the number of physical qubits involved in the mapping and the length of the chains. Supplementary Table 2 provides information on the lengths of the chains and the corresponding Jchain values used in the embedding for representing the QRBM utilized in the NSL-KDD and CSE-CIC-IDS2018 datasets.

The datasets

We selected two datasets for training RBMs on quantum and on classical computers. The first one, the NSL-KDD dataset, comes from the effort to partially solve the problems of the KDD-99 cup dataset67, such as duplicate data and a large number of records. Its wide diffusion makes it suitable for training ML models in the field of NIDS since it is essential to compare and relate the different performances of the proposed models. However, it suffers from some problems, as pointed out by McHugh75. For example, it is not representative of real networks because it lacks public datasets for network-based IDS and is not representative of low-footprint attacks. For this reason, we selected a second dataset, the CSE-CIC-IDS2018 dataset representing a modern, realistic dataset. The CSE-CIC-IDS2018 is one of the most recent intrusion detection datasets publicly available, with an extensive range of attack classes.

Feature extraction

The NSL-KDD dataset contains 41 variables (NR), excluding labels. The training dataset has 125,972 observations (M), while the testing dataset has 22,543 records. The training dataset includes 21 types of attacks, while the testing dataset contains 37 kinds of attacks. These attacks are classified into Denial Of Service, Probe, User to Root, and Root to Local. In this work, we perform a binary classification, i.e., we do not consider the different classes of attacks.

The CSE-CIC-IDS2018 dataset cannot be employed as it is, since it contains millions of records, with more than 80 network traffic features (NR), duplicate data, and missing values. Moreover, it is impossible to encode all the dataset features in the current D-Wave Advantage QPU due to their number and the limited number of physical qubits available. Therefore, after removing all the duplicated records and missing data, we selected a subset of features by applying hierarchical clustering on the Spearman rank-order correlation and keeping a single feature from each cluster76. As a result, we discarded the following features: “Fwd Seg Size Avg”, “TotLen Fwd Pkts”, “Bwd IAT Tot”, “Bwd Pkt Len Max”, “Subflow Fwd Byts”,"Pkt Size Avg”, “Bwd Seg Size Avg”, “Subflow Fwd Pkts”, “Bwd IAT Max”, “Subflow Bwd Pkts”, “Flow Pkts_over_s”, “Flow IAT Mean”, “Idle Max”, “Active Min”, “Active Max”, and “Pkt Len Min”.

QRBM models require binary value numbers for the input units. The two datasets were processed to fulfill this requirement. We used a one-hot encoding for nominal features with a limited number of distinct values, while we used a binary encoding for those with many different values. All the real-valued records have been digitized, i.e., we computed the histogram of the record, and we substituted the value with the indices of the bins to which the input belongs. We associated normal data with +1, and we used 0 for attacked records. For the sake of redundancy, the labels have been encoded three times, i.e., attacks are labeled as (0, 0, 0) and normal data as (1, 1, 1). At the end of the processing the NSL-KDD dataset in compressed by 85 bits (N) while the CSE-CIC-IDS2018 dataset 156 (N). Finally, we balance the datasets by under-sampling the most common class.

Performance metrics

During this evaluation process, we measured six metrics to test the performance of the models: accuracy, F1 score, true positive (TP), false negative (FN), false positive (FP), and true negative (TN).

True positive: the number of TP indicates the number of attacks correctly classified by the model.

True negative: the number of TN indicates the number of normal events correctly classified by the model.

False negative: the number of FN indicates the number of attacks classified as normal events by the model.

False positive: the number of FP indicates the number of normal events classified as attacks by the model.

Accuracy: represents the proportion of total predictions that have been classified correctly.

$${{{{{\rm{Accuracy}}}}}}=\frac{TP+TN}{TP+TN+FN+FP}$$

F1 score: represents a harmonic mean of precision and recall, where 1 represents the best score and 0 represents the worst score.

$$F1=\frac{2TP}{2TP+FP+FN}$$