Size and profile of skyrmions in skyrmion crystals

Abstract

Size is a fundamental quantity of magnetic skyrmions. A magnetic skyrmion can be a local circular object and in an isolated form. A skyrmion can also coexist with a group of its siblings in a condensed phase. Each skyrmion in a condensed phase takes a stripe shape at low skyrmion density and a circular shape at high skyrmion density. Skyrmions at high density form a skyrmion crystal (SkX). So far, skyrmion size in an SkX has not been seriously studied. Here, by using a generic chiral magnetic film, it is found that skyrmion size in an SkX has a different parameter dependence as those for isolated skyrmions and stripes. A size formula and a good spin profile for skyrmions in SkXs are proposed. These findings have important implications in searching for stable smaller skyrmions at the room temperature.

Introduction

Magnetic skyrmions, topological spin structures that have non-zero skyrmion number of $Q=\frac{1}{4\pi }\iint {{{{{\bf{m}}}}}}\cdot ({\partial }_{{{{\rm{x}}}}}{{{{{\bf{m}}}}}}\times {\partial }_{{{{\rm{y}}}}}{{{{{\bf{m}}}}}})\ {{{{{\rm{d}}}}}}x{{{{{\rm{d}}}}}}y$, where m is the unit vector of magnetization, have received intensive and extensive studies in magnetics for their academic interest and promising applications in information technology^1,2,3,4,5. These studies include skyrmion formation and creation^{6,7,8,9,10,11,12,13,14,15}, skyrmion imaging^{16,17,18,19,20}, skyrmion manipulation^{13,14,15,21,22,23,24,25,26,27}, and skyrmion dynamics^{28,29,30,31,32,33,34,35}. Our knowledge about magnetic skyrmions has been greatly advanced in recent years^4,36,37. It is known³⁴ that the size of isolated skyrmions increases with the Dzyaloshinskii–Moriya interaction (DMI) strength, and decreases with the exchange stiffness coefficient and magnetic anisotropy^27,34. Recently, we unambiguously showed that various stripes observed in helical phase in chiral magnetic films are spin textures of skyrmion number 1³⁶. The stripe width³⁶ increases with exchange stiffness coefficient and decreases with the DMI strength. Many fundamental properties of skyrmions are inadequately known despite of all those advances⁴. The underlying physics of isolated skyrmions and skyrmion crystals (SkXs) is different, but people do not distinguish the size of an isolated skyrmion from the ones in an SkX to date. How skyrmion size in SkXs depends on material parameters is an unsolved problem.

In this paper, a generic chiral magnetic film with exchange stiffness constant A, the DMI strength D, and perpendicular magnetic anisotropy K is used to show that κ ≡ π²D²/(16AK) = 1 separates isolated skyrmions (κ < 1) from condensed skyrmion states (κ > 1). In contrast to isolated skyrmions whose size increases with D/K and is insensitive to κ ≪ 1 and stripes whose width increases with A/D and is insensitive to κ ≫ 1, the skyrmion size in SkXs is inversely proportional to the square root of skyrmion number density and decreases with A/D. This finding provides general guidance for skyrmion size manipulation.

Results

Model

A two-dimensional (2D) chiral magnetic film of thickness d in the xy-plane is modelled by the following energy

$$E= d\iint \left\{A| \nabla {{{{{\bf{m}}}}}}{| }^{2}+D[({{{{{\bf{m}}}}}}\cdot \nabla ){m}_{{{{\rm{z}}}}}-{m}_{{{{\rm{z}}}}}\nabla \cdot {{{{{\bf{m}}}}}}]\right.\\ \left.+{K}_{{{{{{\rm{u}}}}}}}(1-{m}_{{{{\rm{z}}}}}^{2})-{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}{{{{{\bf{m}}}}}}\cdot {{{{{{\bf{H}}}}}}}_{{{{{{\bf{d}}}}}}}\right\}{{{{{\rm{d}}}}}}S,$$

(1)

where K_u, M_s, μ₀, and H_d are perpendicular uniaxial crystalline anisotropy constant, the saturation magnetization, the vacuum permeability and demagnetization field, respectively. The energy is set to zero, E = 0, for ferromagnetic state of ∣m_z∣ = 1. In a theoretical analysis, the demagnetization effect can be included through the effective perpendicular anisotropy constant $K={K}_{{{{{{\rm{u}}}}}}}-{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}/2$. This is a good approximation when the film thickness d is much smaller than the exchange length³⁴. Films with κ ≡ π²D²/(16AK) < 1 support isolated skyrmions that are metastable spin textures of energy $8\pi {{{\rm{Ad}}}}\sqrt{1-\kappa }$³⁴.

Demagnetization field as an effective anisotropy

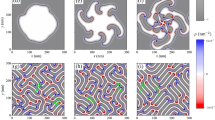
In order to prove that demagnetization field can accurately be included in the effective anisotropy $K={K}_{{{{{{\rm{u}}}}}}}-{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}/2$ even for highly inhomogeneous spin structures, we consider a 300 nm × 300 nm × 0.4 nm film with A = 10 pJ m⁻¹, D = 6 mJ m⁻², $K={K}_{{{{{{\rm{u}}}}}}}-{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}/2=0.7\ {{{{{\rm{MJ}}}}}}\ {{{{{{\rm{m}}}}}}}^{-3}$, M_s = 0.58 MA m⁻¹. Starting from a nucleation domain of 10 nm in diameter and under the dynamics of the LLG equation, a stable ramified stripe has the same skyrmion number as an isolated skyrmion or a skyrmion in an SkX, (see “Methods” section). The stable ramified stripe from MuMax3 is presented in Fig. 1a. In MuMax3³⁸ simulations, the unit-cell size is 1 nm × 1 nm × 0.4 nm. The black and red dots (90,000 in total) in Fig. 1b denote the crystalline anisotropy energy E_a and the sum of the anisotropy and demagnetization energies E_a + E_d for each cell from an MuMax3 simulation, respectively. Data are sorted by m_z. The blue curve is the effective anisotropy energy ${E}_{{{{{{\rm{a,eff}}}}}}}=V\left({K}_{{{{{{\rm{u}}}}}}}-\frac{1}{2}{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}\right)(1-{m}_{{{{\rm{z}}}}}^{2})+\frac{1}{2}V{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}^{2}$, where V is the volume of each cell. The red dots are almost on the blue curve, demonstrating the excellence of the approximation.

Fig. 1: Confirmation of demagnetization approximation.

a Structure of a ramified skyrmion. b Energies of 90,000 cells from spin texture shown in sub-figure (a). Cells are sorted by z-component of magnetization m_z.

Phase diagram of an isolated skyrmion and a ramified stripe

Figure 2 a plots the energy of one skyrmion in chiral magnets as a function of κ. The squares and diamonds, circles and stars, up-triangles and pentagons, are respectively from three groups of model parameters listed in “Methods” section. E is plotted in ${{{{{\rm{arcsinh}}}}}}(E)$ scale because E covers a huge range of values on both sides of zero, and κ is in ${{{{\mathrm{log}}}}}\,(\kappa )$ scale. Clearly, κ = 1 separates metastable isolated skyrmions from ramified stripes³⁶.

Fig. 2: Phase diagram and spin profiles of an isolated skyrmion and a ramified stripe.

a Energy (in ${{{{{\rm{arcsinh}}}}}}(E)$ scale) as a function of κ ≡ π²D²/(16AK) (in ${{{{\mathrm{log}}}}}\,(\kappa )$ scale) for various model parameters with very different exchange stiffness constant A, the Dzyaloshinskii–Moriya interaction coefficient D, and the effective perpendicular magnetic anisotropy constant K. E changes sign at κ = 1 that separate an isolated skyrmion from stripes and skyrmion crystals. b m_z(r) is the z-component of magnetization at position r measured from the centre of an isolated skyrmion shown in the inset. Symbols are simulation data and the solid curve are theoretical fit with skyrmion size R = 4.513 nm and skyrmion wall width w = 1.356 nm. c Spin profile m_z(x) of a stripe. Symbols are simulation data for stripes ①–④ in the inset and the solid curve is the theoretical fit with stripe width L = 8.95 nm and stripe wall width w = 1.82 nm. x is measured across the stripes and x = 0 is at the stripe centres.

For a better comparison, earlier results on spin profile of isolated skyrmions and stripes are summarized first. The spin profile of isolated skyrmions can be approximated by ${{\Theta }}(r)=2\arctan \left[\frac{\sinh (r/w)}{\sinh (R/w)}\right]$³⁴. Θ is the polar angle of the magnetization at position r measured from the center of a skyrmion where m_z = 1. R and w measure respectively the skyrmion size and skyrmion wall thickness. Figure 2b shows the excellent agreement between the theoretical spin profile (the solid curve) with R = 4.513 nm and w = 1.356 nm with numerical simulations from MuMax3 (the symbols) for an isolated skyrmion. Model parameters are A = 0.4 pJ m⁻¹, D = 0.15 mJ m⁻², K_u = 0.214 MJ m⁻³ (K = 0.2 MJ m⁻³), M_s = 0.15 MA m⁻¹. The inset shows the skyrmion structure. This profile leads to the skyrmion size formula of $R=w/\sqrt{1-\kappa }$ and w = πD/(4K)³⁴.

The spin profile of stripes can be approximated by ${{\Theta }}(x)=2\arctan \left[\frac{\sinh (L/2w)}{\sinh (| x| /w)}\right]$ for m_z < 0 and ${{\Theta }}(x)=2\arctan \left[\frac{\sinh (| x| /w)}{\sinh (L/2w)}\right]$ for m_z > 0³⁶. x is measured across a stripe and x = 0 is at the stripe centre (m_z = 1). L is the stripe width that is the distance between two parallel contour lines of m_z = 0. w measures skyrmion wall thickness. Figure 2c is spin profile of stripes with model parameters of A = 0.3 pJ m⁻¹, D = 0.24 mJ m⁻², K_u = 0.110 MJ m⁻³ (K = 0.096 MJ m⁻³), M_s = 0.15 MA m⁻¹. The symbols are the numerical data from various locations of stripes shown in the inset and the solid curve is the theoretical fit with L = 8.95 nm and w = 1.82 nm. The excellent agreements between the numerical data and the approximate profiles demonstrate that one can use this theoretical profile to extract the skyrmion size accurately. Data from different stripes, falling on the same curve, demonstrate that stripes, building blocks of irregular spin textures of skyrmion number 1, are identical. The stripe profile leads to the stripe width formula of L = g(κ)A/D, where g(κ) is about 2π for κ ≫ 1³⁶, opposite dependence on D as that for an isolated skyrmion.

From an earlier study³⁶, it is known that skyrmion–skyrmion interaction is important in SkX formation unlike isolated skyrmions and stripes that do not rely on the interaction. Thus, one should expect a different spin profile and parameter dependence of skyrmion size for an SkX. This is the main issue in this study.

SkX and spin profile

In order to study skyrmions in SkXs, we consider model parameters satisfying κ > 1 below. All initial configurations have sufficient number of nucleation domains in triangular lattices. Each domain of m_z = 1 is a disk of 10 nm in diameter. Each initial configuration leads to an SkX in a triangular lattice as shown in Fig. 3a–c respectively with 324, 400, and 484 skyrmions in a film of 400 nm × 346 nm × 1 nm. The model parameters are A = 5 pJ m⁻¹, D = 3 mJ m⁻², K_u = 30 kJ m⁻³ (K = 4.88 kJ m⁻³), M_s = 0.2 MA m⁻¹. Figure 3a–c show that the areas of m_z > 0 and m_z < 0 are different, and have different spin distribution. Lattice constant and skyrmion size are two obvious length scales. A new spin profile of ${{\Theta }}(r)=2\arctan \left\{\frac{\tan \left[\frac{\pi }{2}\cos (\frac{\pi R}{L})\right]}{\tan \left[\frac{\pi }{2}\cos (\frac{\pi r}{L})\right]}\right\}$ along three triangular lattice directions, (1,0), (1/2, $\sqrt{3}/2$), and (1/2, $-\sqrt{3}/2$), is proposed, where r labels the points on the yellow lines in Fig. 3a–c with r = 0 being the centre of a chosen skyrmion. R and L are respectively the skyrmion size (the radius of m_z = 0 contour) and the lattice constant. L relates to skyrmion number density n of an SkX in a triangular lattice as $L\approx 1.07/\sqrt{n}=22.11\$ nm for Fig. 3a, 19.90 nm for Fig. 3b, and 18.09 nm for Fig. 3c, where n is defined as the total skyrmion number divided by the total film area. Figure 3d–f are m_z(r) along the yellow lines in Fig. 3a–c, respectively. Symbols are numerical data from MuMax3 simulations while the curves are ${m}_{{{{\rm{z}}}}}(r)=\cos {{\Theta }}$ with fitting parameter R = 7.042 nm for Fig. 3d, 6.144 nm for Fig. 3e, 5.399 nm for Fig. 3f. R depends only on n, A/D, and κ. Numerical evidences of this claim is given in Supplementary Note 1.

Fig. 3: Skyrmion crystals and skyrmion spin profiles at various skyrmion number density.

a–c Spin configurations of skyrmion crystals with skyrmion density n = 2.34 × 10⁻³ nm⁻² (a), 2.89 × 10⁻³nm⁻² (b), and 3.50 × 10⁻³nm⁻² (c). m_z is the z-component of magnetization. d–f Spin profiles m_z(r) along the yellow lines in (a–c), respectively. The symbols are numerical data and the solid lines are the theoretical fits with skyrmion size R = 7.042 nm (d), 6.144 nm (e), and 5.399 nm (f).

Skyrmion size in SkXs

If energy per skyrmion in an SkX is from a skyrmion whose spin texture is described by Θ(r) for 0 ≤ r ≤ L/2, then energy per skyrmion can be expressed as a function of variable R,

$$E(R)=2\pi d[A{f}_{1}(\varepsilon )-DL{f}_{2}(\varepsilon )+K{L}^{2}{f}_{3}(\varepsilon )],$$

(2)

where $\varepsilon =\frac{2R}{L}$, f_i(x) (i = 1, 2, 3) are defined in the “Methods” section. The skyrmion size is then the solution of $\frac{{{{{{\rm{d}}}}}}E}{{{{{{\rm{d}}}}}}R}=0$. Under certain reasonable assumptions (see Supplementary Note 2), one has

$$R(n,A/D,\kappa )=\frac{0.54}{\sqrt{n}}-\sqrt{\frac{0.51}{\sqrt{n}\frac{A}{D}+0.56n\frac{{A}^{2}}{{D}^{2}}-0.02\frac{1}{\kappa }}}\frac{A}{D}.$$

(3)

Unlike stripe width that does not depend on n and increases with A/D, Eq. (3) says that R is almost inversely proportional to $\sqrt{n}$ and decreases with A/D. The interesting dependences agree with the underlying physics of SkXs that result from the balance of skyrmion–skyrmion repulsion and intrinsic stripe nature of skyrmions. R should then be proportional to the lattice constant of an SkX that is the skyrmion–skyrmion distance and, in turn, is inversely proportional to $\sqrt{n}$. Since skyrmions in an SkX come from the squeeze of stripe skyrmions, the amount of width deduction from the squeeze should be proportional to the original stripe width proportional to A/D. Thus, R should not only be smaller than the natural stripe width, but also decreases with A/D as what Eq. (3) says. Of course, one should not expect coefficients of $1/\sqrt{n}$ and A/D to be very accurate because the obvious approximations involved. For example, it is impossible to fill a plane by disks of radius L/2. Eq. (2) completely neglects energy from unfilled regions although their contributions are very small (because of m_z ≃ −1 there).

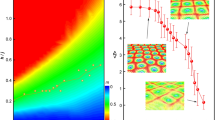
We carried out MuMax3 simulations with very different n, A, D, K in three different parameter regions. For each fixed parameters, skyrmion size R in the corresponding SkX can be obtained either from the size of m_z = 0 contour or through fitting of numerical spin profile to the new spin profile. The difference between two extracted values is negligible (see Supplementary Fig. 1), and all data shown below is from contour measurement. One can test our theoretical predictions of Eq. (3) against numerical simulations. As mentioned above, simulations show that R depends only on n, A/D, and κ. Figure 4a plots R vs. $1/\sqrt{n}$ for various fixed A/D and κ from three groups of model parameters. Simulation results (the symbols) are well described by our formula (the solid curves) of Eq. (3) without any fitting parameter. R is almost linear in $1/\sqrt{n}$. The A/D dependence and κ dependence of R can also be well captured by Eq. (3) as shown by good agreement between simulation data (the symbols) and theoretical formula of Eq. (3) (the solid curve) in Fig. 4b (A/D) and Fig. 4c (κ), respectively. Equation (3) says that R does not depend on anisotropy K for κ ≫ 1. Our new spin profile captures successfully the skyrmion–skyrmion repulsion effect that requires R to be proportional to the lattice constant, the inverse of the skyrmion number density n.

Fig. 4: Parameter dependences of skyrmion size.

Skyrmion size in skyrmion crystals as a function of skyrmion number density n for various A/D and fixed κ (a); as a function of A/D for various fixed n and κ (b), and as a function of κ for various n and A/D (c). A is exchange stiffness constant, D is the Dzyaloshinskii–Moriya interaction coefficient D, and κ ≡ π²D²/(16AK), where K is the effective perpendicular magnetic anisotropy. The symbols are numerical data from MuMax3 simulations. The solid curves are the formula of Eq. (3).

Discussion

Although most previous studies^39,40,41 investigate the lattice constant of SkXs rather than skyrmion size in an SkX, ref. ⁴² measured experimentally the skyrmion size of FeGe film. Parameters of FeGe are A ~ 18 pJ m⁻¹, D ~ 2.8 mJ m⁻², K ~ 0.01 MJ m⁻³⁴³, skyrmion number density in ref. ⁴² is around 209 μm⁻² [estimated from Fig. 2h in ref. ⁴²]. Thus, according to our theory, the skyrmion size should be around 22.7 nm that agrees well with the measured value of ~21 nm [estimated from Fig. 2h in ref. ⁴²]. One should also note that the presence of magnetic field can also affect the size of skyrmions that explains the small discrepancy.

According to the current results, magnetic skyrmions can be isolated, or condensed regular or irregular stripes distributed randomly or arranged as helical states of one-dimensional stripe lattices, or condensed circular skyrmions in crystal forms. The irregular stripes can even be in ramified, or in dendrite or maze forms³⁶. The underlying physics of skyrmion size are different for isolated skyrmions, stripes in different morphologies and structures, and skyrmions in an SkX. It is known that skyrmion formation energies are positive for isolated skyrmions and negative (with respect to the energy of a ferromagentic state) for stripes and SkXs. Positive formation energy results in an extra energy for skyrmion surfaces, similar to the surface tension of a liquid droplet, that favours a circular shape. Negative skyrmion formation energy is similar to a negative surface tension of a liquid droplet that prefers to wet its contacts and to spread out. From this viewpoint, it may not be surprising to see different parameter dependences of skyrmion size for isolated skyrmions and skyrmions in SkXs or stripes, each with skyrmion number 1. It is also not surprising that spin profile of skyrmions in SkXs has little similarity to those of isolated skyrmions and stripes because their shape comes from the balance of the skyrmion squeeze and their stripe nature. Two nearby skyrmions start to repel each other when their distance is order of L ≈ 13A/D. Thus, the critical skyrmion number density for SkX formation is about n_c ≈ D²/(169A²). For n > n_c, skyrmions tend to form a closely packed triangular lattice of lattice constant $1.07/\sqrt{n}$. The skyrmion squeeze leads to Eq. (3) in which skyrmion size decreases with A/D, opposite to the parameter dependence of the width of stripe skyrmions. There is a maximal skyrmion number density beyond which an SkX is not stable any more. The physics around the maximal skyrmion number density surely deserves a study, but it is not an issue in this work.

In applications, creating stable skyrmions of smaller size at the room temperature is a goal. According to current results, one needs to distinguish an isolated skyrmion (κ < 1) from a skyrmion in a condensed skyrmion phase (κ > 1). In the case of κ < 1, materials with large A and smaller D are preferred since larger A and smaller D imply a higher T_c and smaller skyrmion size. On the other hand, in the case of κ > 1, materials with larger A and larger D are required so that one may have both higher T_c and smaller skyrmion size. Interestingly, the same critical value of κ = 1 was also obtained by many people from comparing energy difference between a one-dimensional magnetic domain wall and the ferromagnetic state^8,28,44,45.

In conclusion, material parameter dependences of skyrmion size are very different for circular isolated skyrmions, stripes, and circular skyrmions in SkXs. Unlike an isolated skyrmion whose size increases with D/K and κ < 1, or a stripe whose size increases with A/D and decreases with κ > 1, the size of a circular skyrmion in SkXs is inversely proportional to the square root of skyrmion number density and decreases with A/D. Skyrmion size is a very important quantity, and high-density data storage requires, in general, smaller skyrmions. The findings here provide a practical guidance for searching proper materials in different applications.

Methods

Numerical simulations

The dynamics of m is governed by the Landau–Lifshitz–Gilbert (LLG) equation,

$$\frac{\partial {{{{{\bf{m}}}}}}}{\partial t}=-\gamma {{{{{\bf{m}}}}}}\times {{{{{{\bf{H}}}}}}}_{{{{{{\rm{eff}}}}}}}+\alpha {{{{{\bf{m}}}}}}\times \frac{\partial {{{{{\bf{m}}}}}}}{\partial t},$$

(4)

where γ and α are respectively gyromagnetic ratio and the Gilbert damping constant. The effective magnetic field ${{{{{{\bf{H}}}}}}}_{{{{{{\rm{eff}}}}}}}=\frac{2A}{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}}{\nabla }^{2}{{{{{\bf{m}}}}}}+\frac{2{K}_{{{{{{\rm{u}}}}}}}}{{\mu }_{0}{M}_{{{{{{\rm{s}}}}}}}}{m}_{{{{\rm{z}}}}}\hat{z}+{{{{{{\bf{H}}}}}}}_{{{{{{\rm{d}}}}}}}+{{{{{{\bf{H}}}}}}}_{{{{{{\rm{DM}}}}}}}$ includes the exchange field, the crystalline magnetic anisotropy field, the demagnetization field H_d, and the DMI field H_DM respectively.

Previous studies^36,37 demonstrate that a small nucleation domain of m_z = 1 in the background of ferromagnetic phase of m_z = − 1 can develop into a skyrmion in a chiral magnetic film. In the absence of energy source such as an electric current and at zero temperature, the LLG equation describes a dissipative system whose energy can only decrease^46,47. Thus, the long-time solution of the LLG equation with any initial configuration must be a stable steady spin texture of Hamiltonian Eq. (1). α does not change the stable steady spin structures of the LLG equation. However, α can change spin dynamics and which stable spin texture to pick because the evolution path and energy dissipation rate depend on damping. This is similar to the sensitiveness of attractor basins to the damping in a macro spin system⁴⁸. In this work, we use a large α = 0.25 to speed up our simulations.

In this study, we choose three groups of model parameters to simulate those chiral magnets of MnSi with A = 0.27–0.4 pJ m⁻¹, D = 0.15–0.33 mJ m⁻², K_u = 0.02–0.2 MJ m⁻³, M_s = 0.15–0.5 MA m⁻¹²¹; Co–Zn–Mn with A = 5–11 pJ m⁻¹, D = 0.5–2 mJ m⁻², K_u = 20–80 kJ m⁻³, M_s = 0.15–0.35 MA m⁻¹²⁹; and PdFe/Ir and W/Co₂₀Fe₆₀B₂₀/MgO^{1,2,13,15,22,23,25} with A = 2–10 pJ m⁻¹, D = 0.68–4 mJ m⁻², K_u = 228–2500 kJ m⁻³, M_s = 650–1160 kA m⁻¹. Periodic boundary conditions are used to eliminate boundary effects and the MuMax3 package³⁸ is employed to numerically solve the LLG equation with mesh size of 1 nm × 1 nm × 1 nm.

To obtain the energy of one static isolated skyrmion or one static ramified stripe, we start with one small domain of m_z = 1 of 10 nm in diameter. After a few nanoseconds, one can obtain a stable steady spin structure as well as quantities like Q and E from MuMax3 simulator.

In order to obtain an SkX, many small domains of m_z = 1 of 10 nm in diameter each are initially arranged in a triangular lattice in the background of m_z = −1. Under the dynamics of the LLG equation, each small domain of zero skyrmion number becomes a skyrmion of Q = 1. For each giving n > n_c, an SkX in triangular lattice is obtained. We can obtain SkXs with different density n by varying the number of domains in a film of a fixed-size.

Derivation of energy expressions

Substituting new spin profile Θ(r) into Eq. (1) and in the absence of an external field, energy per skyrmion E(R) consists of exchange E_ex, DMI E_DM, and anisotropy E_an energies

$${E}_{{{{{{\rm{ex}}}}}}} =2\pi Ad\int\nolimits_{0}^{\frac{L}{2}}\left[{\left(\frac{{{{{{\rm{d}}}}}}{{\Theta }}}{{{{{{\rm{d}}}}}}r}\right)}^{2}+\frac{{\sin }^{2}{{\Theta }}}{{r}^{2}}\right]r{{{{{\rm{d}}}}}}r\\ =8\pi Ad{f}^{2}(\varepsilon )\int\nolimits_{0}^{1}\frac{\left[{\xi }^{2}f{^{\prime} }^{2}(\varepsilon )+{f}^{2}(\xi )\right]}{\xi {\left[{f}^{2}(\xi )+{f}^{2}(\varepsilon )\right]}^{2}}{{{{{\rm{d}}}}}}\xi \\ =2\pi dA{f}_{1}\left(\varepsilon \right),$$

(5)

$${E}_{{{{{{\rm{DM}}}}}}}= -2\pi Dd\int\nolimits_{0}^{\frac{L}{2}}\left(\frac{{{{{{\rm{d}}}}}}{{\Theta }}}{{{{{{\rm{d}}}}}}r}+\frac{\sin 2{{\Theta }}}{2r}\right)r{{{{{\rm{d}}}}}}r\\ = -2\pi Ddf(\varepsilon )\\ \int\nolimits_{0}^{1}\left\{\frac{\xi f^{\prime} (\xi )}{{f}^{2}(\xi )+{f}^{2}(\varepsilon )}+\frac{f(\xi )\left[{f}^{2}(\varepsilon )-{f}^{2}(\xi )\right]}{{\left[{f}^{2}(\xi )+{f}^{2}(\varepsilon )\right]}^{2}}\right\}{{{{{\rm{d}}}}}}\xi \\ = -2\pi dDL{f}_{2}\left(\varepsilon \right),$$

(6)

$${E}_{{{{{{\rm{an}}}}}}} =2\pi Kd\int\nolimits_{0}^{\frac{L}{2}}{\sin }^{2}{{\Theta }}r{{{{{\rm{d}}}}}}r\\ =2\pi dK{L}^{2}\int\nolimits_{0}^{1}{\left[\frac{f(\xi )f(\varepsilon )}{{f}^{2}(\xi )+{f}^{2}(\varepsilon )}\right]}^{2}{{{{{\rm{d}}}}}}\xi \\ =2\pi dK{L}^{2}{f}_{3}\left(\varepsilon \right),$$

(7)

where ξ = 2r/L, $\varepsilon =\frac{2R}{L}$, $f(\varepsilon )=\tan \left[\frac{\pi }{2}\cos (\frac{\pi }{2}\varepsilon )\right]$. One can obtain Eq. (2) by suming up the three energies. Skyrmion size R is the solution of $\frac{{{{{{\rm{d}}}}}}E(R)}{{{{{{\rm{d}}}}}}R}=0$, or

$$2\pi d[A{f}_{1}^{\prime}(\varepsilon )-DL{f}_{2}^{\prime}(\varepsilon )+K{L}^{2}{f}_{3}^{\prime}(\varepsilon )]=0,$$

(8)

where ${f}_{{{{\rm{i}}}}}^{\prime}(\varepsilon )$ denotes derivatives of f_i(ε) (i = 1, 2, 3) with respect to ε. Since ${f}_{2}^{\prime}(\varepsilon )$ are non-zero in ε ∈ (0, 1), one can divide Eq. (8) by $D{f}_{2}^{\prime}(\varepsilon )$ to have

$$\frac{A}{D}{p}_{1}(\varepsilon )+\frac{K{L}^{2}}{D}{p}_{2}(\varepsilon )-L=0,$$

(9)

where ${p}_{1}(\varepsilon )={f}_{1}^{\prime}(\varepsilon )/{f}_{2}^{\prime}(\varepsilon )$ and ${p}_{2}(\varepsilon )={f}_{3}^{\prime}(\varepsilon )/{f}_{2}^{\prime}(\varepsilon )$. p₁ and p₂ can be approximated by two analytical functions.

$${p}_{1}(\varepsilon )\approx -0.615+\frac{1.883}{{(1-\varepsilon )}^{2}},$$

(10)

and

$${p}_{2}(\varepsilon )\approx 0.611\sqrt{1-\varepsilon }-0.404.$$

(11)

Thus one has

$$R=\frac{L}{2}-\frac{L}{2}\sqrt{\frac{1.883}{1+0.615\frac{A}{DL}-\frac{{\pi }^{2}DL}{16A}{p}_{2}(\varepsilon )\frac{1}{\kappa }}\frac{A}{DL}}.$$

(12)

$\frac{{\pi }^{2}DL}{16A}{p}_{2}(\varepsilon )\frac{1}{\kappa }$ in the denominator is very small for ε > 0.5. Replacing p₂(ε) by p₂(0.5), skyrmion size R, is then Eq.(3).