Introduction

Nilotinib hydrochloride monohydrate (NHM) lacks a chiral center, making it incapable of tautomerism. NHM is a chemical compound with the following name: 4-methyl-N-[3-(4-methyl-1H-imidazol1-yl)-5-(trifluoromethyl) phenyl]-3-[(4-pyridin-3-ylpyrimidin-2-yl) amino] benzamide hydrochloride monohydrate. It is a white powder with a slight yellowish or greenish-yellowish shade. At 25 °C, the aqueous solubility of NHM markedly decreases with pH. Moreover, it is almost insoluble in buffer solutions with pH values higher than 4.5. NHM shows slight solubility in ethanol and methanol. Further information can be found in Supplementary information.

According to scientific studies, a genetic mutation with unclear reasons in bone marrow hematopoietic (myeloid) cells leads to the formation of a malfunctioning chromosome known as the Philadelphia chromosome1. This defective chromosome is present in over 90% of individuals diagnosed with chronic myeloid leukemia (CML). The mentioned genetic abnormality sets in a chain of activities that eventually triggers the growth and reproduction of these cells and their carcinomic progression2.

The solubility rate is a critical factor affecting the bioavailability of the active components in orally administered drugs. The poor bioavailability of NHM can be due to its low water solubility, which influences its efficiency in the body. Chemotherapy is a conservative treatment in medical science which involves the use of low doses of drug due to its potential harm to the tumor-adjacent organs. Solubility enhancement avoids the long-term side effects of the drug while considerably reducing the required dosage. Bioavailability increment generally improves the efficacy of the drug in the body3. To this end, various techniques such as the utilization of amorphous solid dispersions and RESS can be employed to enhance the bioavailability of the drug. Among these strategies, the reduction of particle size is a prevalent and pragmatic approach.

Particle size reduction is a unique technique in the enhancement of drug solubility. Conventional processes such as sublimation and crystallization have been utilized in the pharmaceutical industry for this purpose. SC-CO2 technology is also a promising approach for producing nano-sized and micro-sized particles4,5,6. The use of SC-CO2 solvent in industrial plants has been increasing due to its non-toxicity and high effectiveness in extracting compounds. Additionally, it exhibits greater stability in various process and requires lower temperatures compared to alternative solvents. Supercritical fluids (SCFs) are similar to liquids in dissolving power and resemble gases in transfer characteristics (high permeability and low viscosity). The supercritical extraction also enjoys other advantages such as shorter processing time, high selectivity, sensitivity to temperature and pressure variations, and concentration of the solvent to achieve the ideal degrees of freedom for sorting or monitoring the strength of solubility, the sensitivity of the solvent to reach the desired degrees of freedom, better output quality, lower solvent usage, and temperature tolerance for components sensitive to high temperatures7,8,9. SCFs are characterized by their temperature and pressure exceeding the critical temperature (Tc) and critical pressure (Pc), respectively, enabling them to exhibit the properties of both a liquid and a gas. In the proximity of critical temperatures, SCFs demonstrate substantial compressibility, which facilitates moderate variations in pressure density and mass transport features that significantly influence their solvent capacity. Furthermore, the environmental concerns of toxic solvents can be resolved by the use of CO2 gas as a solvent in supercritical procedures due to its neutrality. As an example, organic solvents, particularly chlorinated solvents, are highly hazardous to the environment. Chlorinated solvents and several other industrial solvents, such as chlorofluorocarbons, have been shown to be harmful for the ozone layer. The substitution of chlorofluorocarbon with CO2 is an instance of resolving the issue of toxic and polluting solvents through the use of CO2 solvent. Other advantages of SC-CO2 process include its cost-effectiveness and availability at high purity and low critical pressure and temperature (PC = 73.8 bar and TC = 304.18 K), chemical neutrality desirable for use in food and pharmaceutical industries, suitability in critical conditions, and non-toxicity and non-flammability10. The researchers select the temperature and pressure based on previous studies and the constraints of the laboratory equipment8,11,12.

The solubility data presented in this study are valuable for evaluating the applicability of SCFs in a specific industrial process. Additionally, these data can aid in identifying the optimal conditions, in terms of temperature, pressure, and experimental measurement technique, for effective use of these fluids. Knowledge regarding the solubility of medicinal substances and their correlation with thermodynamic models in SC-CO2 can help in the development of pharmaceutical processes. This is due to the fact that the determination of solubility under various temperature conditions and high pressures can be monetarily costly and time-intensive.

As mentioned before, the experimental measurement of solubility in SC-CO2 is a valuable but time-consuming, complex, and costly task. Therefore, there is a need for alternative approaches, such as computational techniques, to replace experimental assessments. To this end, several theoretical methods have been proposed and developed for predicting the solubility of drugs in SC-CO2. Several situations influence molecular characteristics in liquid systems, which are connected to all nearby molecules in motion. Describing these specifications needs an efficient experiment and thermodynamic modeling of all potential solvent and soluble molecule configurations7,13. Empirical and semi-empirical, equations of state (EoSs), solid–liquid equilibrium models, and machine learning algorithms are the four most popular forms of thermodynamic models, each with a unique variety of ranges and notable scopes. Modeling with experimental and semi-empirical approaches requires no definition of the critical characteristics. These models rely on the SCF temperature, pressure, and volumetric mass. Models with three to six adjustable parameters, such as Bian14, Chrastil15, Jafari-Nejad16, Jouyban17, Sparks18, Sodeifian12, Mendez-Santiago and Teja19, Garlapati-Madras20, Bartle21, and Gordillo22 offer proper analysis for evaluating the reliability of experimental data. Different mixing rules are also employed in EoS models which enjoy applicability across a wide range of temperatures and pressures for fluids with various densities, from low-density gases to dense liquids. These equations are also applicable to gases, liquids, and SCFs. In addition, activity coefficient models, such as ELT, are commonly used to model solubility in SCFs. This approach assumes that the fugacity of the solid phase is equivalent to the SCF23.

Machine learning refers to a constantly developing group of computing instructions to simulate intelligence by learning from the surroundings. This strategy is now regarded as a means of communication with big data in the modern era. Machine learning-based algorithms have been successful in diverse fields, including pattern recognition, biomedical and medical applications, spacecraft engineering, computational biology, financial sectors, and entertainment24. Ionizing radiation (radiotherapy) is used to treat more than half of cancer cases; it is also the primary method in the treatment of advanced stages of localized diseases. Radiation therapy involves a variety of steps that extend not just from consultation through treatment but even beyond. Machine learning should be used to guarantee that patients receive the appropriate quantity of radiation and respond properly to the therapy. These instructions are easily programmable as they naturally modify their structure via repetitions (i.e., experience) for better production of the desired output. An effective approach presents two primary benefits: the ability to supplant laborious and repetitive human duties, and more importantly, capability of detecting complex patterns of incoming data which exceeds the ability of an average human observer. The significance of these benefits is particularly in radiation therapy. However, given the limitations of this approach, the final results are prone to uncertainty and observer variability. An imaging guide can identify microscopic features of an organ, immediately synthesizing information from several sources, or combining the knowledge of multiple observers to achieve low imaging error.

This research presents the first reports on the solubility of NHM in SC-CO2 within the temperature and pressure ranges of 308–338 K and 120–270 bar, respectively. Besides, four types of models were used to evaluate the correlation of the empirical findings of NHM: (1) ten empirical and semi-empirical density-based models (Chrastil, Bartle, Sparks, Sodeifian, MST, Bian, Jouyban, Garlapati-Madras, Gordillo, and Jafari-Nejad), (2) PR EoS model with vdW mixing rule, (3) ELT model (modified-Wilson model) for correlating fugacity, (4) ML algorithms (RF, DTs, MLP, and DNN) with 17 solubility datasets available in the previously published papers. The validity assessment of multiple models involved the evaluation of deviations of computed outcomes from empirical solubility data, utilizing three actual measures: average absolute relative deviation (AARD%), adjusted correlation coefficient (Radj), and F-value.

Experimental

Materials

NHM was supplied from Parsian Pharmaceutical Company with a guaranteed purity of 99% (Tehran-Iran) while CO2 (purity > 99.99%) was provided by Fadak Company (Kashan, Iran). Analytical grade dimethyl sulfoxide (DMSO) was also purchased from Merck (Darmstadt, Germany). Table 1 lists the physical and chemical characteristics of NHM.

Table 1 Molecular structure and physicochemical specifications of NHM.
Full size table

Experimental apparatus

This work aimed to determine the equilibrium solubility of NHM using a static approach. To this end, a UV–Vis spectrophotometer was utilized along with the equipment described in our previous research13,25,26,27. The experimental setup comprised various components, including gas cylinders, filters, sampler, refrigeration, heating elements, flow meter, 6-way valve, and a micrometer valve. All valves, connections, and piping were 1/8″ in size. The process is fully described in the previous work of the authors; however, a quick review is also provided here. Figure 1 depicts the experimental setup.

Figure 1
figure 1

Schematic of the used laboratory equipment for measuring solubility.

Full size image

The operation began with liquefying CO2 (the required temperature for CO2 liquefication ranges between − 15 to – 20 °C), which is an important section in CO2 preparation for pumping. A pressure gauge was employed to monitor pressure with an accuracy of ± 1 bar (EN 837-1, WIKA, Germany), while an oven was used to maintain the temperature of CO2 around the desired temperature within a tolerance of ± 0.1 K. Then, NHM (1 g) was placed inside a 70-mL equilibrium tube with 2 mm glass beads and sintering filters (1 µm, keeps undissolved drugs in the container) on both surfaces. The glass beads were used to homogeneously mix the drug and reduce channeling to enhance the interaction areas between the sample and SCF, following this, the container was exposed to SC-CO2. Based on previous publications, the present study achieved the equilibrium state within 60 min of equilibration11,13,25,28. Afterward, 600 µL of SC-CO2 (at saturation level) was introduced to the injection cycle through a 6-port, 2-position valve. Upon releasing the injection valve, the aforementioned substance moved toward the gathering vial, which had been already filled with a specific quantity of DMSO. Subsequently, the gathered DMSO (1 mL) in the vial was employed to clean the cycle. The total volume of the solution was 5 mL. The solubility of NHM in SC-CO2 was determined through maximum absorption observations, using a double-beam UV–Vis spectrophotometer (Unico, SQ-4802, USA) and 1-cm route silica cells. The solid pharmaceutical was dissolved in DMSO to achieve a final concentration of 100 μg L−1. Various dilutions were obtained by utilizing the standard solution within acceptable limits. The condensation of the drug in the collecting vial was determined using a standard curve with a regression ratio of 0.99. The UV spectral data were collected at 270 nm on a UV–Vis spectrophotometer to investigate NHM29. The equilibrium values of mole fraction (y2) and solubility (S (g/L)) in SC-CO2 were computed for various pressures and temperatures, using the following equations:

$${y}_{2}=\frac{{n}_{solute}}{{n}_{solute}+{n}_{C{O}_{2}}},$$
(1)

where:

$${n}_{solute}=\frac{{C}_{s}(\frac{g}{L}){V}_{s}(L)}{{M}_{s}(\frac{g}{mol})},$$
(2)
$${n}_{C{O}_{2}}=\frac{{V}_{l}\left(L\right)\rho \left(\frac{g}{mol}\right)}{{M}_{C{O}_{2}}\left(\frac{g}{mol}\right)}.$$
(3)

In which, \({n}_{solute}\) and \({n}_{C{O}_{2}}\) show the moles of solute (NHM) and CO2 in the measurement cycle, respectively. \({C}_{s}\) is the solute content (g/L) in the gathering vial according to the standard curve; while \({V}_{s}(L)\) = 5 × 10–3 and \({V}_{l}\left(L\right)\) = 600 × 10–6 denote the volume of the gathering vial and measuring cycle, respectively. \({M}_{s}\) and \({M}_{C{O}_{2}}\) also represent the molecular weights of the solute and CO2. Equation (4) was used to estimate the equilibrium solubility of the solute, S (g/L), in SC-CO230.

$$S\left(\frac{g}{L}\right)=\frac{{C}_{s}(\frac{ g}{L}){V}_{s}(L)}{{V}_{l}(L)}.$$
(4)

Theoretical background

In this work, the solubility of NHM was correlated with four types of models: (1) Empirical and semi-empirical models such as Chrastil, Bian, Sodeifian, etc. with 3–6 adjustable parameters; (2) EoS based model like Peng-Robinson with vdW mixing rule; (3) ELT (modified Wilson model) and (4) ML algorithms such as random forests, decision trees, MLP, and DNN. Details of the mentioned models can be found in the continue.

EoS-based model

The solubility of a solid solute in a SC-CO2 can be expressed as follows:

$${y}_{2}=\frac{{P}_{2}^{s}{\phi }_{2}^{s}}{P{\phi }_{2}^{f}}\mathrm{exp}\left[\frac{\left(P-{P}_{2}^{s}\right){\upsilon }_{2}}{RT}\right],$$
(5)

where P shows the pressure at the system temperature, \({P}_{2}^{s}\) denotes the pressure required for the sublimation of the pure solute. The molar volume of the solute is also represented by \({\upsilon }_{2}\), while the universal gas constant is denoted by R. Furthermore, the pure solute fugacity coefficient, denoted by \({\phi }_{2}^{s}\), is assumed to be 1.

In the present research, PR-EoS13,25,28,31 can be described as follows32,33:

$$P=\frac{RT}{\upsilon -b}-\frac{a\left(T\right)}{\upsilon \left(\upsilon +b\right)+b\left(\upsilon -b\right)}.$$
(6)

vdW2 is represented as:

$$a={y}_{1}^{2}{a}_{11}+{y}_{2}^{2}{a}_{22}+2{y}_{1}{y}_{2}{a}_{12},$$
(7)
$$b={y}_{1}^{2}{b}_{11}+{y}_{2}^{2}{b}_{22}+2{y}_{1}{y}_{2}{b}_{12}.$$
(8)

In addition, Table 1S (supplementary information) presents a summary of the EoS-based model.

$${a}_{12}=\left(1-{k}_{12}\right)\sqrt{{a}_{11}{a}_{22}},$$
(9)
$${b}_{12}=\left(1-{l}_{12}\right)\frac{\left({b}_{11}+{b}_{22}\right)}{2}.$$
(10)

\({k}_{12}\) and \({l}_{12}\) are interaction parameters whose values were determined by an objective function (OF) aimed at minimizing the resulting output. Thus, \({k}_{12}\) and \({l}_{12}\) can be obtained through the minimization of the mentioned objective function.

$$OF=\sum_{i=1}^{N}\frac{\left|{y}_{2,i}^{exp}-{y}_{2,i}^{calc}\right|}{{y}_{2,i}^{exp}}.$$
(11)

ELT model

The ELT takes SCFs as expanded liquids since their density is closer to that of a liquid rather than a gas. Therefore, this theory establishes thermodynamic phase equilibrium between solute and SCF as the solid–liquid equilibrium relevance and contractual activity coefficients. Accurate estimation of solid solubility in the supercritical (SC) phase relies on proper knowledge on these activity coefficients, which can be determined by understanding the fugacity of the composites. When the equilibrium and the fugacity are equivalent in two steps, the coefficients can be obtained by34:

$${f}_{2}^{s}={f}_{2}^{L}.$$
(12)

Here, the Modified Wilson model was employed to determine the activity coefficient of the solid solute.

Furthermore, the dimensionless energies of interaction can be determined by:

$$\lambda^{\prime}_{12} = \frac{{\lambda_{12} }}{{RT_{c} }},$$
(13)
$$\lambda^{\prime}_{21} = \frac{{\lambda_{21} }}{{RT_{c} }}.$$
(14)

An empirical expression was introduced to modify the Wilson model, considering the impact of high pressures. The modified model facilitates the prediction by establishing a linear correlation between the molar volume and density reduction.

$${\upsilon }_{2}=\alpha {\rho }_{r}+\beta .$$
(15)

The regressed parameters of the model are given by α, β, \(\lambda^{\prime}_{12} ,\) and \(\lambda^{\prime}_{21}\). Detailed information is available in supplementary information. Genetic algorithm (GA), nonlinear regression35 and simulated annealing (SA) algorithms were utilized to obtain optimum double interaction and regressed parameters of the ELT.

Semi-empirical models

The solubility data of NHM in SC-CO2 were compared with ten semi-empirical models. Researchers such as Garlapati-Madras, Chrastil, Bartle, MST, Sparks, Jouyban, Bian, and Sodeifian worked in this field and presented different models, as listed in Table 2.

Table 2 Summary of empirical models applied in present work.
Full size table

The discussion is focused on evaluating several models based on their AARD%, Radj, and F-value to identify the models with acceptable accuracy. The least squares method (LSM) was utilized for calculating curve-fitting variables. AARD% was utilized as a criterion to ensure comparable analyses, since the number of curve-fitting parameters is closely related to correlation precision. The value of AARD% was determined by the following equation, where Z represents the number of curve-fitting variables for the given model36,37:

$$AARD\%=\frac{100}{{N}_{i}-Z}\sum_{i=1}^{{N}_{i}}\frac{\left|{y}_{2}^{calc}-{y}_{2}^{exp}\right|}{{y}_{2}^{exp}}.$$
(16)

The models were further evaluated by a criterion known as Radj with the following definition:

$${R}_{adj}=\sqrt{\left|{R}^{2}-\left(Q\left(1-{R}^{2}\right)/\left(N-Q-1\right)\right)\right|}.$$
(17)

In the above equation, "N" denotes the number of sample points within each set. "Q" refers to the number of self-determining changeable elements in each equation and "R2" represents the correlation analysis36,38. F-value is another criterion in the assessment of the capacity of the models to match solubility data, which can be described as follows39.

$$F{\text{-}}value=\frac{\frac{{SS}_{R}}{Q}}{\frac{{SS}_{E}}{\left(N-Q-1\right)}}=\frac{{MS}_{R}}{{MS}_{E}}.$$
(18)

As seen, SST indicates the total of square summation, SSR represents the sum of squares of the regression, while MSR pertains to the average square of regression. Furthermore, MSE concerns with the average square of residuals. The F-value operates similar to the distribution and is characterized by Q and N-Q-1 grades of independence.

ML algorithms

Four ML algorithms were employed in this work to examine and evaluate the solubility of NHM. To this end, 432 data samples were used including data of 17 other drugs (published in the literature). These 17 drugs are described in Table 3.

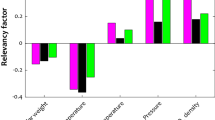
Table 3 Solubility data sets used in this work.
Full size table

Seventy-five percent of the samples were used for training (324), while 25% of them (108) were used for testing. Six basic parameters, including operating temperature and pressure, CO2 density, fusion enthalpy, fusion temperature, and sublimation pressure, were taken as effective factors of solubility. Drug solubility is influenced by various factors, among which, temperature, pressure, and CO2 density have been identified as key factors in numerous experimental and semi-experimental relationships. Solubility decreases by enhancing molecular weight due to the higher fusion enthalpy and temperature. Additionally, an increase in sublimation pressure results in greater solubility. This data set was evaluated by four algorithms: random forest, decision trees, multilayer perceptron, and deep neural networks. A summary of the applied algorithms can be found below:

Decision trees (DTs)

Data mining refers to a vast field of research dealing with pattern identification and categorization of massive and unclear data, in various formats such as text, audio, and video. Sometimes the presented data are insufficient, noisy, or destroyed. One strategy for dealing with this sort of data is classification. Decision trees are employed in data discovery and machine learning to provide an approximate answer. The DT algorithm is a highly effective and powerful tool for data mining capable of handling diverse input data, including nominal, numerical, and alphabetical which is one of the strengths of this algorithm.

This method is capable of processing incomplete data which encompass errors through various platforms and available data packages. DTs extract data from a huge deal of accessible information using decision rules. A DT merely categorizes data to be readily saved and classed again46,47.

Random forest (RF)

The RF algorithm is a sort of ensemble learning that can be utilized for both assortment and regression test. RF was first developed by Breiman to combine his bagged sampling methodology with the random selection of features48 originally described by Ho49, Amit and Garden50. This approach results in a set of decision trees with controlled variance. Bagging is used to randomly select training data with replacement to construct each tree. Studies have shown that approximately 64% of all occurrences will be represented within this selection. The residual samples (near 36%) are considered out-of-bag samples. In the RF model, each tree operates as a classification algorithm and specifies the class tag of an untagged sample using majority verdict51. Each classifier generates a model of its vote for the class tag it expects, and the tag with the maximum votes will be chosen as the category of the sample. Further information is available in supplementary section.

Multilayer perceptron (MLP)

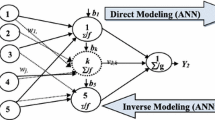
The MLP can be classified as a feedforward and fully connected artificial neural network (ANN). It commonly refers to any feedforward ANN and sometimes a network consisting of multiple perceptron layers which may raise the confusion. In cases with only one hidden layer, the multilayer perceptron is often referred to as a "vanilla" neural network. The MLP includes at least three node substrates: entry, undercover, and output substrates. Apart from the input nodes, each node represents a neuron with a nonlinear activation duty. A supervised learning approach labeled as backpropagation is utilized to train the MLP. The MLP differs from the linear perceptron in its use of multiple layers and nonlinear activation, enabling the identification of data which cannot be separated linearly52.

If all neurons in a MLP utilize a linear activation function to connect the weighted inputs to the output of every neuron, any number of layers can be reduced to a two-layer input–output model using linear algebra. However, some neurons in MLPs utilize a nonlinear activation function that imitates the modulation of action possibilities or firing in actual neurons53.

Deep neural network (DNN)

The deep neural network (DNN) is a neural network with a significant number of layers, known as "deep" layers. Utilizing advanced algorithms and structures, the DNN model can be considered a variant of the multilayer perceptron neural network (MLP). Comprising many layers of nodes, DNN is arranged using algorithms to extract deputations from datasets with no need for manual design of feature extractors. As its name implies, deep learning has a larger or deeper number of processing layers compared to the shallow learning with less units. The transition from surface to deep learning enables the planning of more complicated and nonlinear functions, which could not be efficiently mapped using external architectures. Various designs have addressed the difficulties in multiple fields or applied cases54,55.

Results and discussion

Experimental data

The reliability and validity of the solubility system and experimental outcomes were assessed in a recent article which evaluated the solubility of Riluzole in SC-CO256,57,58. Examination of the methods and equipment utilized in the experiments requires evaluation of the solubility of a "prototype solute"59. Our prior research involved measuring the solubility of naphthalene and α-tocopherol, which was then compared to previously reported data to confirm the dependability of both the apparatus and experimental findings31,57,60. Furthermore, the apparatus underwent a secondary validation process utilizing α-tocopherol in a CO2 environment prior to drug solubility measurements whose validation outcomes are illustrated in Fig. 2. The current investigation exhibits a satisfactory consistency with other references61,62. In this work, the equilibrium solubility S (g/L) and related mole fraction values of NHM were calculated at several pressures and temperatures (120–270 bar and 308–338 K, respectively) as summarized in Table 4.

Figure 2
figure 2

Solubility S (g/kg) of α-tocopherol in CO2: Our setup, Pereira et al.62 and Johannsen and Brunner61 all are shown by symbols.

Full size image
Table 4 Solubility of NHM in SC-CO2 at different temperatures and pressures. The experimental standard deviation was calculated by \({u}_{combined}/{y}=\sqrt{\sum_{i=1}^{N}{\left({P}_{i}u\left({x}_{i}\right)/{x}_{i}\right)}^{2}}\).Expanded uncertainty (U) and the relative combined standard uncertainty (ucombined/y) are determined, respectively, as follows: (U) = k*ucombined(k = 2) and \(u_{combined}/y=\sqrt{\sum_{i=1}^{N}{\left({P}_{i}u\left({x}_{i}\right)/{x}_{i}\right)}^{2}}\). In this work, u(xi) was considered as standard uncertainties of temperature, pressure, mole fraction, volumes and absorption. Pi, sensitivity coefficients, are equivalent to the partial derivatives of y equation (Eq. 1) with respect to the xi.
Full size table

Noteworthy, the data points were measured three times to ensure the reliability and maintain the relative standard uncertainties below 5%. Further information on the mole fractions uncertainties can be found in Table 5. The Span-Wagner equation (a CO2-specific EoS) was also employed to define the density of SC-CO263. The mole fraction (y) and solubility (S (g/L)) values of NHM ranged from 0.1 × 10–5 to 0.59 × 10–5 and 0.016–0.094, respectively. The highest and lowest values for the solubility of the solid medicine were detected at 338 and 338 K and pressures of 270 and 120 bar, respectively. The fundamental mechanism of drug solubility entails the disruption of intermolecular or inters ionic bonds among solute molecules. This provides enough room for solvent molecules to penetrate the solute molecules and facilitates particle wetting, which enables the required solvent–solute interactions for dissolution. As illustrated by the isotherms in Fig. 3, the solubility of NHM increased by enhancing the pressure at fixed temperatures. At a specific temperature, an increase in pressure leads to greater gas dissolution in a solvent, whereas a decrease in pressure reduces the gas solubility in a liquid. For example, when producing carbonated drinks, additional pressure is applied to the solute to enhance the solubility of CO2 in the liquid. The pressure enhancement compresses gas molecules within the solute, which creates more space for extra gas molecules, increasing the solubility of CO2 in the liquid. Therefore, the solubility of gases in liquids increases with pressure increment. From another point of view, when a gas molecule in the vapor phase makes contact with a liquid surface, it can either be repelled back into the gas or dissolved into the liquid to become a solute particle. Upon reaching the liquid surface, dissolved molecules will gain enough kinetic energy to escape into the gas phase. Therefore, there will be a constant exchange of particles across the gas–liquid boundary. Equilibrium is achieved at equal entry and exit rates of the gas phase, resulting in constant concentrations in each phase. Solubility is a measure of the concentration of dissolved gas particles in the liquid and is dependent on gas pressure. An increase in pressure leads to an increment in the collision frequency, increasing the solubility. Conversely, a decrease in pressure decrements the solubility. Such an increase in solubility can be assigned to the enhanced density and improved solvating power of SC-CO2 at higher pressures. The temperature has a dual impact on the solubility in SC-CO2 depending on the variations of vapor pressure of the solute and solvent density. The effect of temperature on solubility is contingent upon the characteristics of both the solute and solvent, including their interactions; while the behavior of solid and gaseous solutes differs. Solid solutes show solubility increment with raising the temperature, whereas gas solutes tend to become less soluble. This effect can be attributed to the heightened kinetic energy that is accompanied by an increase in temperature. Specifically, gas molecules possess greater kinetic energy at higher temperatures, which promotes the dissociation of intermolecular bonds between the gas solute and solvent. An increment in the solution temperature can augment the vapor pressure of the solute, further enhancing the solvation ability of SCF60,64,65.

Table 5 AARD% and correlation parameters of empirical and semi-empirical models for NHM solubility in SC-CO2.
Full size table
Figure 3
figure 3

NHM solubility in SC-CO2 vs. pressure.

Full size image

Conversely, elevated temperatures may decrease the density of SC-CO2, reducing its overall solvating capacity. Based on Fig. 3, the pressure range of 120–150 bar corresponds to the crossover pressure zone for NHM. Density and solute vapor pressure are the dominant variables at pressures above and below the crossover pressure. At pressures under (beyond) the crossover pressure area, solubility drops (rises) with temperature. Other individuals have also reported similar findings regarding the dual effect of temperature on SC-CO2 solubility60.

Regarding the challenges in fully guaranteeing the accuracy of experimental data, their agreement with specific thermodynamic relationships can be checked to confirm their thermodynamic consistency or inconsistency. The MST model is a commonly employed thermodynamic relationship for analyzing the consistency of experimental phase equilibrium data. In addition to its correlational capacity, the potential for extrapolation is a crucial advantage of any model or correlation. As such, the Mendez-Santiago and Teja model (MST), also known as the self-consistency test (Fig. 4), was conducted to assess the extrapolative capabilities of the models under examination. The findings indicated the linear behavior of all the isotherms and isobars in this study, thus enabling the solubility results to be estimated beyond their currently calculated range66,67. Therefore, NHM solubility can be predicted in temperatures and pressures beyond the current range due to their simple linear behavior. The experimental data, represented by a solid line for all temperatures, were internally consistent when considering solubility.

Figure 4
figure 4

Self-consistency trend obtained by MST model, dotted line presents prediction made by MST model and symbols refer to solubility data of NHM.

Full size image

Figure 4 demonstrates the stability of the experimental data obtained via the MST model.

Solubility correlation

Four commonly utilized models were applied to define the correlation between the solubility data of NHM in SC-CO2. These models include EoS-based, modified Wilson (ELT), and density-based semi-empirical models as well as machine learning algorithms. The results were compared based on AARD%, Radj, and F-value.

Empirical and semi-empirical models

Table 5 lists the outputs of the semi-empirical models used in this research. As shown, the mean values of AARD% for Chrastil, Gordillo, Sparks, Garlapati-Madras, Jafari-Nejad, Bian, Bartle, MST, Jouyban, and Sodeifian models were 12.29%, 11.67%, 12.28%, 8.11%, 12.57%, 11.38%, 14.70%, 20.92%, 11.60%, and 14.38%, respectively. Consequently, MST (Radj = 0.9608, F-value = 150.25) and Bian (Radj = 0.9763, F-value = 235.17) models are the best in characterizing the solubility data of NHM (some of results are summarized below in Fig. 5 at 338 K).

Figure 5
figure 5

NHM solubility in SC-CO2. Symbols are experimental points in one temperature (338 K); various types of line are calculated with empirical and semi-empirical models.

Full size image

The models with six adjustable parameters had the lowest correlation with the experimental data, while the models with 3, 4, and 5 parameters exhibited almost the same performance in terms of correlation with the solubility data. In addition, all the models in this study demonstrated satisfactory accuracy in fitting the solubility data. Further information is available in supplementary section (Figs. 1S–10).

PR EoS vdW2 model

The PR EoS was utilized along with the vdW mixing rule to evaluate the correlation of solubility data at four distinct temperatures of 308, 318, 328, and 338 K. Additionally, the sublimation pressure corresponding to each temperature was modified to facilitate the comparison. For modeling the solubility data, the use of equations of state requires an initial determination of the thermodynamic characteristics of the solid substance via various methods. These characteristics entail sublimation pressure, volume at critical temperature, acentric factor, and boiling temperature. The solubility of drugs is under the direct or indirect influence of various properties. As an illustration, the solubility of a drug can be increased by elevating the sublimation pressure, which in turn raises the vapor pressure. The sublimation pressure is contingent upon the acentric factor; on the other hand, the acentric factor is highly dependent on the boiling temperature. All these factors are interdependent with a remarkable impact on the drug solubility. The Marrero-Gani and Stein Brown methods were employed to estimate the boiling temperature, while Fedors method was utilized to assess volume at critical temperature. The Ambrose-Walton method was also applied for estimation of the sublimation pressure as listed in Table 6.

Table 6 Evaluated critical values and physicochemical properties of NHM.
Full size table

According to the results in Table 7 and Fig. 6 (F-value = 119.41, Radj = 0.9896), the best performance was achieved at 308 K. The correlation with the solubility data decrements with temperature enhancement and changes in the sublimation pressure. Therefore, the PR model had the lowest correlation with NHM solubility data at 338 K.

Table 7 Correlation outcomes for solubility of NHM in SC-CO2 by PR-EoS -vdW model.
Full size table
Figure 6
figure 6

NHM solubility vs. SC-CO2 density. Solid lines are calculated solubilities with PR EoS model, symbols are experimental data.

Full size image

The thermodynamic properties of NHM were estimated using both the Chrastil and Bartle models and the Chrastil and EoS. In this regard, vaporization (ΔHvap), total (ΔHtotal), and solvation (ΔHsol) enthalpies were calculated through the following method:

The Chrastil model (a1 = ΔHtotal/R = − 6296.2307) results in ΔHtotal of 52.35 kJ/mol (endothermic) while Bartle model (a1 = ΔHvap/R = − 8839.0557) leads to ΔHvap of 73.49 kJ/mol (endothermic). These computations can be expanded to estimate the solvation heat as ΔHsol =|ΔHtotal − ΔHvap|= 21.14 kJ/mol. Thereupon, the combination of Bartle and Chrastil models, results in the solvation enthalpy of (ΔHsol) − 21.14 kJ mol−1. Also, Table 2S (supplementary section) reports the enthalpies obtained in this work.

ELT model (modified Wilson model)

The correlation of modified Wilson-predicted solid–liquid equilibrium was compared with the solubility data of NHM. The results indicated that the ELT model outperformed the empirical and semi-empirical models of this work (see Table 8 and Fig. 7).

Table 8 Correlation outcomes for solubility of NHM in SC-CO2, by ELT, Modified Wilson model.
Full size table
Figure 7
figure 7

NHM solubility vs. SC-CO2 density. Solid lines are calculated solubilities with ELT model, symbols are experimental data.

Full size image

Machine learning algorithms

In the present investigation, the solubility of NHM was studied and evaluated via different models, for the first time. Four machine-learning algorithms were also used to compare the experimental data of various drugs including 17 previously published drugs. Among these algorithms, the RF algorithm showed the highest correlation with the solubility data. According to the initial results in Table 9, the RF algorithm provided the best performance (R2 = 0.9933) among all tested algorithms. Figure 8 and 9 also offer more perspectives about RF model results. Figure 10 also presents the results of all models in one figure. It should be noted that supplementary figures on some algorithms can be found in supplementary section (Figs. 11S–16S).

Table 9 Initial results of machine learning algorithms used in this work.
Full size table
Figure 8
figure 8

Regression line of NHM solubility (with 17 other drugs shown by symbols) vs. RF outputs.

Full size image
Figure 9
figure 9

NHM solubility (with 17 other drugs shown as a solid line) vs. RF outputs shown as dots.

Full size image
Figure 10
figure 10

All models in one frame, lines and dots are results of models.

Full size image

To ensure the validity of the machine learning algorithms, two non-parametric tests were employed by Eviews13 software: (1) Augmented Dickey–Fuller (ADF) and (2) Phillips–Perron. The results indicate that the probe value is less than 1%, thereby, confirming the reliability of the models. Furthermore, as the absolute static value is higher than 1%, 5%, and 10%, the models with an error coefficient of 1% provide a sufficient degree of accuracy and precision.

  1. 1.

    In statistics, the ADF test is employed to evaluate the presence of unit root in a given statistical sample. The null hypothesis is tested against alternative explanations, which can include stationarity or trend-stationarity depending on the applied specific test. This test has been developed as an advanced prescription of the Dickey–Fuller test, allowing the analysis of a wider range of time-series models. The ADF statistic produced by this test is negative, and the strength of rejection for the unit root hypothesis increases as the value becomes more negative with a certain level of confidence72.

  2. 2.

    Similar to the enhanced Dickey–Fuller test, the Phillips–Perron test addresses the concern that the data producing process for a variable may exhibit a greater level of autocorrelation than that of the test equation, leading to increased endogeneity and rejection of the Dickey–Fuller t-test. The ADF test resolves this issue through including lagged variables as regressors in the test equation. In contrast, the Phillips–Perron test introduces a non-parametric alteration to the t-test statistic. This approach has shown proper robustness against nonspecific autocorrelation and heteroscedasticity within the disorder process of the test equation. Davidson and MacKinnon demonstrated that the Phillips-Perron test outperformed the augmented Dickey–Fuller test in the case of finite samples73,74. The ADF and Philips–Perron results are shown in Table 10.

Table 10 Non-parametric tests results.
Full size table

Conclusion

Enhancing the solubility of poorly water-soluble pharmaceuticals has long been an efficient approach for producing more effective nanoparticles. Information on the solubility of drugs in supercritical conditions is highly essential to achieve this goal. This study thus explored the solubility of nilotinib hydrochloride monohydrate (NHM) in SC-CO2 at 308–338 K and pressure range of 120–270 bar, for the first time. The mole fraction of the drug dissolved in SC-CO2 ranges from 0.1 × 10–5 to 0.59 × 10–5 corresponding to the solubility range of 0.016–0.094 g/L. The maximum solubility of NHM (0.59 × 10–5) was achieved at 338 K and a pressure of 270 bar. The experimental data were correlated by four groups of models: (1) empirical and semi-empirical models, including Bartle (12.57%), Sodeifian (14.38%), Chrastil (12.29%), Sparks (11.67%), Galapati-Madras (12.28%), Bian (best among others with an AARD% of 8.11), Jouyban (14.70%), Jafari-Nejad (11.60%), MST (11.38%), and Gordillo (20.92%); (2) Peng-Robinson EoS model with vdW mixing rule (best AARD% in temperature of 308 K with the value of 3.39); (3) ELT (Modified Wilson model, with an AARD% of 10.73); and (4) machine learning techniques such as RF, DTs, MLP, and DNN (RF showed the best performance with the R2 value of 0.9933). The Bian and modified Wilson models exhibited the highest correlation with the experimental data. The MST model was also utilized to evaluate the self-consistency of the experimental results. Based on the correlation results proposed by Chrastil and Bartle, the NHM-CO2 solvation and vaporization enthalpies were estimated to be − 21.14 and 73.49 kJ/mol, respectively, that allows us to determine the thermodynamic characteristics of NHM.