Determination of the parameters of rock viscoelastic creep model and analysis of parameter degradation

Abstract

Different stress creep tests are conducted on the sandstone in this study to better describe the creep properties of rocks under different stress states. A model that describes the rock creep process is established. The various stages of creep can be described by combining the creep properties of the creep elements of the model. A new method for determining creep parameters is proposed by using the special point on the creep curve and the definition of creep deformation. The relationship between the creep parameters, stress, and time is analyzed. An improved creep model that considers the effects of stress state and time on the creep parameters is developed. This model is verified using experimental data and calculation results. Results shows that the improved creep model better describes the creep properties of rocks and provides a new method for determining future model parameters. The shear modulus of elastic model controls the instantaneous deformation. The shear modulus of viscoelastic model governs the limit of viscoelastic deformation. The shear viscoelastic coefficient of viscoelastic model increases with the increase in stress. The coefficient of viscoplastic model controls the viscoplastic creep rate. The coefficient of a nonlinear Newtonian dashpot mainly controls the accelerated creep deformation of rock. The calculation results of the proposed model agree well with the experimental data under the action of different stress levels. This model accurately reflects the creep characteristics of the primary and steady-state creep stages, and overcomes the shortcomings of the traditional Nishihara model in describing accelerated creep.

Introduction

The engineering rock mass exhibits short-term elastoplastic mechanical properties under geological and human disturbance and displays time-effect-related deformation and failure properties under certain stress and strain conditions^1,2. This time-dependent property of rock is referred to as the rheological behavior of the rock mass^3,4. Under the influence of geological actions, natural environment change, and engineering disturbance, the rock mass gradually deteriorates over time^5,6,7. This condition leads to the creation of new cracks and the expansion and development of existing cracks until they penetrate the rock. The deformation gradually increases until the rock mass loses its bearing capacity, ultimately resulting in the overall instability of the engineering rock mass^8,9. Microscopically, the internal mineral structure of the rock mass changes and reorganizes over time under the coupling of external loads, leading to a weakening of its physical and mechanical properties^10,11,12. The deformation of rock initially undergoes large and dynamic changes, then transforms into a quasi-static process of small deformation^13,14. With the development of time and external loads, the deformation of the rock becomes a dynamic process of large deformation^15,16. The rock exhibits a variety of macroscopic and localized phenomena.

The deterioration law of creep model parameters with time and stress was mainly obtained by fitting the established model with experimental data. The law of the change in parameters was then analyzed. Liu et al.¹⁷ developed a new model that describes accelerated creep in rock by replacing the viscous elements in the traditional Nishihara model with fractional elements that consider the changes in time and stress. The validity of the model was verified by fitting it to experimental data. Wang et al.¹⁸ studied the unloading creep characteristics of layered rock samples from Jinping II Hydropower Station and obtained the creep deformation curves under different confining pressures. They established a constitutive equation for a nonlinear creep model under 3D stress and identified the creep parameters using an optimization algorithm. The creep parameters showed a nonlinear decline with the decrease in confining pressure. Singh et al.¹⁹ proposed a combined creep model based on the Maxwell and Hooke models that was established using acoustic emission technology and calculated the elastic and viscous parameters of the model. The model can accurately predict the stress–strain response of rock salt under loading and unloading conditions. Hou et al.²⁰ presented a new nonlinear nonlinear creep damage model that considers the influence of initial damage on the creep properties of rock. The parameters of this model were obtained through fitting method, and the creep characteristics of sandstone under different initial damage conditions were verified. Wang et al.²¹ described sandstone creep test results using a nonlinear and nonstationary plastic viscosity (NNPV) creep model. The creep parameters of the rock at three osmotic pressure levels were determined, and the theoretical curves using the NNPV model agreed well with the experimental data. However, the fitting of the creep parameters by fitting did not have obvious physical meaning.

This study presented a model that describes the rock creep process. The creep properties of each component in the model corresponded to the various stages of the classic creep curve. On the basis of the above research on the rheological properties of rock and considering the influence of stress level and time on the deterioration of creep parameters, a method for determining creep parameters was proposed by combining the deformation characteristics of creep curves. A creep model that considers the effects of stress and time on the creep parameters was established. A 1D creep model was developed by using the proposed method to promote the 3D state. The relationship between the creep parameters, stress, and time in 3D state was analyzed. The equations for each creep parameter, stress, and time were substituted into the creep model, and the model curve was compared with the test curve. The validity of the model and the rationality of the new method for determining the creep parameters were verified by calculating the high similarity between the curve and the variation of the test curve. The creep parameter model was calculated to clarify the physical meaning of the creep parameters under different stresses and different times.

Parameter determination method for one-dimensional creep model

Creep process characteristics and creep model establishment

The creep property indicates that a rock gradually deteriorates over time due to constant external force. A large number of experimental studies have shown that the creep of rock has obvious stages. The rock creep process can be divided into three stages: primary creep, steady-state creep, and accelerated creep. The schematic of the rock creep process is shown in Fig. 1²².

Figure 1

Typical creep curve.

The instantaneous deformation in the 1D state can be expressed as

$$\varepsilon_{e} = \frac{\sigma }{{E_{1} }},$$

(1)

where E₁ is the modulus of elasticity, ε_e is the instantaneous strain value, and σ is the applied creep stress.

The variation law of primary creep deformation can be described by Kelvin.

$$\varepsilon_{K} = \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right],$$

(2)

where E₂ is the viscoelastic modulus, η₁ is the viscous coefficient, and t is the creep time.

The variation law of steady-state creep deformation can be described by using a viscoplastic model²³.

When σ < σ_s,

$$\varepsilon_{N} = 0,$$

(3)

when σ ≥ σ_s,

$$\varepsilon_{N} = \frac{{\sigma - \sigma_{s} }}{{\eta_{2} }}t,$$

(4)

where η₂ is the viscous coefficient of the viscoplastic model, and σ_s is the long-term strength of the rock.

The whole process of creep deformation is the process of progressive fracture and damage accumulation in rock until crack propagation and failure. Therefore, a parameter can be introduced to characterize the irreversible deformation of rock materials. Considering the nonlinear characteristics of rock, its stress–strain response often loses one-to-one correspondence. The deformation of rock is irreversible. The strain parameter can be selected to characterize whether the rock enters the accelerated creep stage. A nonlinear Newtonian pot is introduced to describe the deformation of rock in the accelerated creep stage. Therefore,The variation of the accelerated creep deformation can be described by using an nonlinear Newtonian dashpot as shown in Fig. 2.

Figure 2

NonlinearNewtonian dashpot.

The model can better reflect the accelerated creep characteristics of rock, and its creep constitutive equation is

$$\varepsilon_{3} = \frac{\sigma }{{2\eta_{3} }}\left( {t - t_{2} } \right)^{2} ,$$

(5)

where t₂ is the time to enter the accelerated creep, which can be directly obtained through experiments, and η₃ is the viscosity coefficient of the nonlinear Newtonian dashpot. The unit of viscosity coefficient of the nonlinear Newtonian dashpot η₃ is GPa·h².

The creep deformation constitutive equation of rock in 1D state is

$$\left\{ {\begin{array}{*{20}c} \begin{gathered} \varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right],\,\sigma < \sigma_{s} \hfill \\ \varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right] + \frac{{\sigma - \sigma_{s} }}{{\eta_{2} }}t,\,\sigma \ge \sigma_{s} ,t < t_{2} \hfill \\ \end{gathered} \\ {\varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right] + \frac{{\sigma - \sigma_{s} }}{{\eta_{2} }}t + \frac{\sigma }{{2\eta_{3} }}\left( {t - t_{2} } \right)^{2} ,\,\sigma \ge \sigma_{s} ,t \ge t_{2} } \\ \end{array} } \right..$$

(6)

Creep model and division of creep stage

A schematic corresponding to the model and the creep curve is drawn to more vividly represent the correspondence between the components of the creep model and the deformation of each stage of the creep, as shown in Fig. 3^24,25.

Figure 3

Corresponds to the model of the creep curve.

Determination of elastic modulus E₁

As shown in Fig. 3, the rock has a certain instantaneous strain ε_e at the initial moment of the creep curve under the action of stress. The instantaneous strain of the rock includes elastic and plastic strains. This part of the instantaneous strain is assumed to be elastic strain, and the elastic modulus E₁ of the rock can be determined by using Eq. (1)²⁶.

$$E_{1} = \frac{\sigma }{{\varepsilon_{e} }}.$$

(7)

Determination of the viscosity coefficient η₂ of viscoplastic model

Before the accelerated creep stage, rock can be called linear rheological process. Its deformation is mainly viscoelastic deformation. After rock unloading, the strain can be basically recovered. At this time, the permanent deformation is small or negligible. The accelerated creep stage can be called a nonlinear rheological process. After the accelerated creep begins, the viscoelastic deformation is stable. The permanent deformation is increasing, accounting for most of the total deformation. Therefore, rock creep is regarded as the superposition of linear creep and nonlinear creep. When the rock enters the steady-state creep stage, its primary creep strain reaches a steady state. With the progress of the creep time, the creep strain of the rock in the steady-state creep stage is the sum of the stable creep primary value and the steady-state creep strain value. The Kelvin model can better reflect the viscoelastic creep properties of the rock. Specifically, Eq. (2) can show the variation law of steady-state creep curve. At the same time, when the rock enters the accelerated creep stage, the viscoelastic deformation is basically stable. The strain increasing with time is only permanent deformation²⁷. When creep time t tended to ∞, the creep stability value of rock primary is obtained.

$$\varepsilon_{K,t \to \infty } = \mathop {\lim }\limits_{t \leftarrow \infty } \left\{ {\frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right]} \right\} = \frac{\sigma }{{E_{2\infty } }},$$

(8)

where E_2∞ is the viscoelastic modulus when the time is ∞.

The creep deformation values of t_i and t_j at the time point are obtained by randomly taking two time points t_i and t_j on the steady-state creep curve.

$$\left\{ \begin{gathered} \varepsilon_{i} = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2\infty } }} + \frac{{\sigma - \sigma_{s} }}{{\eta_{2i} }}t_{i} \hfill \\ \varepsilon_{j} = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2\infty } }} + \frac{{\sigma - \sigma_{s} }}{{\eta_{2i} }}t_{j} \hfill \\ \end{gathered} \right..$$

(9)

The above two equations are subtracted to obtain the difference in creep deformation of the rock at different times.

$$\varepsilon_{i} - \varepsilon_{j} = \frac{{\sigma - \sigma_{s} }}{{\eta_{2i} }}\left( {t_{i} - t_{j} } \right).$$

(10)

The viscosity coefficient η₂ of the viscoplastic model is obtained in accordance with Eq. (10).

$$\eta_{2i} = \frac{{\sigma - \sigma_{s} }}{{\varepsilon_{i} - \varepsilon_{j} }}\left( {t_{i} - t_{j} } \right).$$

(11)

Determination of viscoelastic modulus E₂ and viscosity coefficient η₁

When the applied stress is less than the long-term strength of the rock and the creep time t ≤ t₁, the creep constitutive model of the rock is

$$\varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right].$$

(12)

The primary creepcurve can take n time points t_i, and a creep strain value ε_i corresponds to each time point t_i. The elastic modulus E₁ is unaffected by the creep time but degrades under different stresses. The creep equation at any time t_i can be expressed as

$$\varepsilon_{i} = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2i} }}\left[ {1 - \exp \left( { - \frac{{E_{2i} }}{{\eta_{1i} }}t_{i} } \right)} \right].$$

(13)

The first-order derivation of time t is given to Eq. (12), and the creep rate of the rock is obtained.

$$\varepsilon^{\prime} = \frac{\sigma }{{\eta_{1} }}\exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right),$$

(14)

where έ is the creep rate.

The primary creep rate curve can take n time points t_i, and a creep rate value έ_i corresponds to each time point t_i.

$$\varepsilon^{\prime}_{i} = \frac{\sigma }{{\eta_{1i} }}\exp \left( { - \frac{{E_{2i} }}{{\eta_{1i} }}t_{i} } \right).$$

(15)

Equations (13) and (15) give the viscoelastic modulus E_2i and the viscosity coefficient η_1i, respectively.

$$\left\{ \begin{gathered} \varepsilon_{i} - \frac{\sigma }{{E_{1} }} = - \frac{{\sigma t_{i} }}{{\eta_{1i} \ln \left( {\frac{{\varepsilon^{\prime}\eta_{1i} }}{\sigma }} \right)}}\left[ {1 - \frac{{\varepsilon^{\prime}_{i} \eta_{1i} }}{\sigma }} \right] \hfill \\ E_{2i} = - \ln \left( {\frac{{\varepsilon^{\prime}\eta_{1i} }}{\sigma }} \right)\frac{{\eta_{1i} }}{{t_{i} }} \hfill \\ \end{gathered} \right..$$

(16)

The η_1i term is expanded by Taylor series, and equation for calculating η_1i is

$$\frac{{\varepsilon_{i} E_{1} - \sigma }}{{t_{i} E_{1} }}\eta_{1i}^{3} + \frac{{\varepsilon_{i} E_{1} - \sigma }}{{t_{i} E_{1} }}\left[ {{\text{ln}}\left( {\frac{{\varepsilon^{\prime}_{i} }}{\sigma }} \right) - 1} \right]\eta_{1i}^{2} - \sigma \eta_{1i} + \varepsilon^{\prime}_{i} = 0.$$

(17)

Equation (17) can be transformed into a unary cubic polynomial, and the specific value of η_1i can be determined in accordance with a root finding equation. The specific value of η_1i is obtained and substituted into Eq. (16) to obtain the creep parameter E_2i.

Determination of the viscosity coefficient η₃ of nonlinear Newtonian dashpot

When σ ≥ σ_s and t > t₂, the creep constitutive model of rock is

$$\varepsilon = \frac{\sigma }{{E_{1} }} + \frac{\sigma }{{E_{2} }}\left[ {1 - \exp \left( { - \frac{{E_{2} }}{{\eta_{1} }}t} \right)} \right] + \frac{{\sigma - \sigma_{s} }}{{\eta_{2} }}t + \frac{\sigma }{{2\eta_{3} }}\left( {t - t_{2} } \right)^{2} .$$

(18)

The elastic moduli E_1i and E_2i and the viscous coefficients η_1i and η_2i corresponding to each time point t_i are determined. The accelerated creep curve can take n time points t_i, and a creep strain value ε_i is found at each time point t_i.

$$\varepsilon_{i} = \frac{\sigma }{{E_{1i} }} + \frac{\sigma }{{E_{2i} }}\left[ {1 - \exp \left( { - \frac{{E_{2i} }}{{\eta_{1i} }}t_{i} } \right)} \right] + \frac{{\sigma - \sigma_{s} }}{{\eta_{2i} }}t_{i} + \frac{\sigma }{{2\eta_{3i} }}\left( {t_{i} - t_{2} } \right)^{2} .$$

(19)

The viscous coefficient η_3i of the nonlinear Newtonian dashpot of the rock is determined in accordance with Eq. (19).

$$\eta_{3i} = \frac{{\sigma \left( {t_{i} - t_{2} } \right)^{2} }}{{2\left\{ {\varepsilon_{i} - \frac{\sigma }{{E_{1i} }} - \frac{\sigma }{{E_{2i} }}\left[ {1 - \exp \left( { - \frac{{E_{2i} }}{{\eta_{1i} }}t_{i} } \right)} \right] - \frac{{\sigma - \sigma_{s} }}{{\eta_{2i} }}t_{i} } \right\}}}.$$

(20)

Equations (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19) and (20) are used to determine the parameters for the 1D viscoelastic-plastic creep model of rock.

Promotion of 3D creep model parameter determination

Establishment of 3D model

Under normal circumstances, the engineering rock mass in underground structures subjected to complex 3D stress. A triaxial compression rheological test is often conducted during the rock’s rheological experiment to better understand its stress state. This test provides information on the rocks’ mechanical properties²⁸ and allows for the establishment of a suitable rheological constitutive model and the determination of rheological parameters for numerical analysis of the rock’s rheology. Therefore, a creep constitutive equation of rock under 3D stress must be established.

The 1D creep model of rock is transformed into a 3D model, and creep deformation can be transformed by analogy. The viscoplastic model involves the yield function F and the plastic potential function Q. The stress tensor S_ij cannot be used to replace the stress σ in the original 1D model, so it must be derived from the yield function. The yield function takes the following form during creep^29,30.

$$F = \sqrt {J_{2} } - \sigma_{s} /\sqrt 3 ,$$

(21)

where J₂ is the stress partial tensor second invariant.

The 3D equation of the viscoplastic model is expressed as

$$\varepsilon_{ij}^{vp} = \frac{1}{{\eta_{2} }}\left\langle {\frac{F}{{F_{0} }}} \right\rangle^{n} \frac{\partial Q}{{\partial \sigma_{ij} }}t,$$

(22)

where F is the yield function, F₀ is the initial yield function value (generally taking F₀ = 1), n is a constant (generally taking n = 1), and Q is the plastic potential function.

The abovementioned viscoelastic-plastic constitutive model based on statistical damage theory and 1D state is extended to 3D state as follows:

When σ < σ_s,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} }}\left( {1 - \exp ( - \frac{{G_{2} }}{{\eta^{\prime}_{1} }})t} \right),$$

(23)

when σ ≥ σ_s and t < t₂,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} }}\left( {1 - \exp ( - \frac{{G_{2} }}{{\eta^{\prime}_{1} }})t} \right) + \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\eta^{\prime}_{2} }}t,$$

(24)

when σ ≥ σ_s and t > t₂,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} }}\left( {1 - \exp ( - \frac{{G_{2} }}{{\eta^{\prime}_{1} }})t} \right) + \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\eta^{\prime}_{2} }}t + \frac{{\sigma {}_{1} - \sigma_{3} }}{{6\eta^{\prime}_{3} }}\left( {t - t_{2} } \right)^{2} ,$$

(25)

where G₁ and G₂ are the shear moduli, K is the bulk modulus, and η'₁, η'₂, and η'₃ are the viscous coefficients in a 3D state.

Determination of 3D model parameters

When t → 0 +, the instantaneous strain of the rock in a 3D state is expressed as

$$\varepsilon_{11}^{e} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K}.$$

(26)

The test results show that the instantaneous deformation includes elastic and plastic deformation. However, the instantaneous deformation is assumed to be elastic. The bulk modulus K at each stress state is determined by the instantaneous volumetric strain value of the test curve, which can be expressed as

$$K = \frac{{\sigma_{m} }}{{3\varepsilon_{m} }} = \frac{{\sigma_{m} }}{{3\varepsilon_{V} }} = \frac{{\sigma {}_{1} + 2\sigma_{3} }}{{9\varepsilon_{V} }},$$

(27)

where σ_m is the stress sphere tensor.

In accordance with the analogy method, the viscous coefficient η'₁ and the viscoelastic modulus G_2i are obtained by combining Eqs. (16) and (17).

$$\varepsilon_{11}^{i} - \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} - \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} = \frac{{\left( {\sigma {}_{1} - \sigma_{3} } \right)t_{i} }}{{ - \left[ {{\text{ln}}\left( {\frac{{3\varepsilon^{\prime}_{i} }}{{\sigma {}_{1} - \sigma_{3} }}} \right) - {2}\eta_{1i} + 1} \right]3\eta_{1i} }}\left[ {1 - \frac{{3\eta^{\prime}_{1i} \varepsilon^{\prime}_{11i} }}{{\sigma {}_{1} - \sigma_{3} }}} \right].$$

(28)

$$G_{2i} = - \ln \left[ {\frac{{3\eta^{\prime}_{1i} \varepsilon^{\prime}_{11} }}{{\sigma {}_{1} - \sigma_{3} }}} \right]\frac{{\eta^{\prime}_{1i} }}{{t_{i} }}.$$

(29)

The viscosity coefficient η'_2i is obtained as

$$\eta^{\prime}_{2i} = \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\left( {\varepsilon_{11}^{i} - \varepsilon_{11}^{j} } \right)}}\left( {t_{i} - t_{j} } \right).$$

(30)

The viscous coefficient η'_3i corresponding to ti at any time point is determined as

$$\eta^{\prime}_{3i} = \frac{{\left( {\sigma {}_{1} - \sigma_{3} } \right)\left( {t_{i} - t_{2} } \right)^{2} }}{{6\left[ {\varepsilon_{11}^{i} - \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }} - \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} - \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2i} }}\left( {1 - \exp ( - \frac{{G_{{2_{i} }} }}{{\eta^{\prime}_{1i} }})t_{i} } \right) - \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\eta^{\prime}_{2i} }}t_{i} } \right]}}.$$

(31)

Indoor triaxial creep test of sandstone

Test equipment and sandstone sample

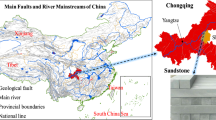
All the tests are conducted on a TAW-2000 triaxial testing machine (Fig. 4a). The test system consists of a loading part, a test part, and a control part. The sandstone samples used in the test are shown in Fig. 4b. The rock samples were collected from Hengda Coal Mine in Fuxin, Liaoning Province. The selected sandstone samples were buried at depths of 800 m to 850 m. The samples are dark gray in color, with a relatively uniform structure and a relatively hard texture. No visible microcracks and bedding are observed in the samples. Standard cylindrical specimens with a height of 100 mm and a diameter of 50 mm were processed in the laboratory. In accordance with the rock test rules of water conservancy and hydropower engineering, the density, water content, and natural water absorption of the sandstone were tested. The water content of the sandstone is determined to be 0.171% by the drying test. The natural water absorption of the sandstone is determined to be 2.349% by the free water absorption test. The density of the sandstone is determined to be 2.355 g/cm³ by the volumetric method. X-ray diffraction (XRD) analysis was conducted on the sandstone specimens in this test to better analyze the influence of the internal chemical composition and physical structure characteristics of the rock on its properties. The XRD results are shown in Fig. 4c.

Figure 4

Rock mechanics test system and sandstone rock sample.

As shown in Fig. 4c, the quartz content is 30.1%, the albite content is 33.8%, the dolomite content is 9.3%, the biotite content is 19.3%, and the kaolinite content is 7.5%.

Conventional triaxial compression test

The specific test steps are as follows.

• (1) The triaxial conventional compression test of sandstone is conducted the conditions of 10 and 15 MPa.

• (2) Lateral stress is applied at a predetermined value with a loading rate of 500 N/s.

• (3) The test piece is subjected to hydrostatic stress, and the lateral stress is kept constant during the experiment.

• (4) The axial load is applied with a loading rate of 0.002 mm/s by using displacement control.

• (5) The testing machine automatically collects the test data and converts them corresponding strain and stress outputs for the data acquisition system.

The sandstone stress–strain curve is drawn in accordance with the experimental data, as shown in Fig. 5.

Figure 5

Deviatoric stress–strain relationship of conventional triaxial compression.

As shown in Fig. 5, the peak strength of the sandstone and the elastic modulus increase with the increase in the confining stress. This condition results in the sandstone being more resistant to deformation and better able to withstand loads, making it less prone to damage.

Creep test plan and analysis of creep results

The specific test steps are as follows.

• (1) The initial load for the sample with a confining pressure of 10 MPa is set to 40 MPa, and the initial load for the sample with a confining pressure of 15 MPa is set 50 MPa.

• (2) The load is increased in increments of 10 MPa, with a loading rate of 500 N/s.

• (3) The duration of each loading stage is determined in accordance with the strain deformation. When the axial deformation of the test piece measured within 2 h is less than 0.001 mm, the deformation is considered to be relatively stable.

• (4) The next loading stage is applied, and the process is repeated until the sample becomes unstable.

The experimental data are superimposed by using Chen’s superposition principle, and the corrected axial deformation duration curve is obtained, as shown in Fig. 6.

Figure 6

Creep of axial under different axial stress states.

As shown in Fig. 6, the axial strain of the test piece is generated instantaneously at the axial stress level. The magnitude of the instantaneous strain is related to the stress level, with higher stress levels resulting in larger instantaneous strain values. However, the ratio of instantaneous strain to total strain increases first and then decreases. This behavior is probably caused by the extrusion closure of internal voids in the initial loading stage and subsequent crack propagation in later stages.

The creep rate is the slope of the creep test curve at each data point. However, due to the non-uniformity, anisotropy and micro-defects of the sample during the experiment, the test data oscillated. The determination of creep rate from the original test data is bound to cause the development trend of creep rate to fluctuate greatly. It is not conducive to analyze the creep rate and difficult to reflect the creep deformation law. The axial-radial and volume creep curves under different levels of stress under various confining pressure conditions are nonlinearly fitted by Origin software. It can fully reflect the creep development trend. Then the derivative operation is performed on each empirical equation. The more regular creep rate development trend can also be obtained. It also avoids data oscillation and beating. The creep rate is treated by the method in Reference^31,32.

In accordance with the basic concept of creep, the creep speed can be defined as the slope of the creep test curve at each data point. The test data may exhibit oscillations due to the nonuniformity, anisotropy, and microdefects of the sample during the experiment. A creep rate curve with a confining pressure of 15 MPa is shown in Fig. 7.

Figure 7

Creep strain rate when σ₃ = 15 MPa.

As shown in Fig. 7, the creep rate under each stage of stress decreases initially and gradually stabilizes over time. However, the creep rate begins to increase with time when the rock enters the accelerated creep phase.

An isochronous stress–strain curve represents the relationship between stress and strain at the same time and is depicted as a cluster of divergent polyline segments. The long-term strength of the rock can be determined by the stress value corresponding to the inflection point of the isochronous stress–strain curve. This curve is drawn in accordance with the creep-duration curve, as shown in Fig. 8.

Figure 8

Isochronous stress–strain curves.

As shown in Fig. 8, the isochronous stress–strain curve is a cluster of divergent broken line segments. The strain value of the isochronous stress–strain curve increases with the increase in stress. Until the stress value reaches 80 MPa, the curve appears as a coincident line, and the stress–strain relationship can be considered linear. Beyond 80 MPa, the curve becomes divergent, and the degree of divergence increases continuously with the increase in stress over time. In this case, the stress–strain relationship can be considered nonlinear. The stress value of 80 MPa marks the transition from linear deformation to nonlinear deformation. Therefore, the stress value corresponding to this point can be regarded as the long-term strength value of the rock.

Analysis of the variation law of creep parameters

Creep parameter determination

In practical engineering, the physical and mechanical parameters of rock under complex geological conditions obviously changes with stress and time. Parameters, such as the modulus of elasticity, strength, and viscosity, decrease over time. Therefore, the creep parameter is expressed as a functional expression of stress versus time better reflects the essential properties of rock materials. Under constant stress, the creep parameters are considered to be time-dependent. The shear modulus G₁ is constant and not affected by time under constant stress. The bulk modulus K can be obtained from the test data and Eq. (27). For other creep parameters under various stress conditions, the values at t = 0, 5, 10, 15, 20 and 25 h under the previous load and under the last stage load are determined by combining the test curves and the duration of the load. The creep parameters of rock under different stress levels and at different times are calculated by combining the results of triaxial indoor creep test and using the method for determining the parameters of the 3D viscoelastic-plastic creep model of rock from Eqs. (28), (29), (30) and (31).

Analysis of the variation law of shear modulus G₁

The instantaneous shear modulus has the following relationship with the instantaneous stress tensor S_ij and the instantaneous strain tensor e_ij.

$$S_{ij} = 2G_{1} e_{ij} .$$

(32)

The relationship between these variables is plotted in Fig. 9. Equation (33) represents the linear relationship between the instantaneous shear modulus of the rock and the stress tensor.

$$G_{1} = 10^{3} \times \,\left( {a_{1} - b_{1} S_{11} } \right),$$

(33)

where a₁and b₁ are fitting parameters.

Figure 9

Data fitting of G₁ when σ₃ = 15 MPa.

As shown in Fig. 9, the shear modulus G₁ of the rock decreases with the increase in the applied bias stress tensor S_ij. This condition embodies the nonlinear damage effect of rock loading through progressive loading. With the increase in the bias stress tensor S_ij, the strain tensor e_ij = S_ij/2G₁ gradually increases, indicating that the greater the stress tensor, the greater the change in rock shape.

Analysis of the variation law of bulk modulus K

In accordance with Table 4, the bulk modulus of the rock has a negative value between the stress level of 60 MPa and the creep time of 5 h to 10 h. The volume modulus K at each moment under the action of the stress level of 60 MPa is obtained by using Eq. (27). The relationship between the bulk modulus K and time under the load of each stage is shown in Fig. 10.

Figure 10

Duration of creep and bulk modulus.

As shown in Fig. 10, the change in the bulk modulus K value with time reflects the shrinkage and expansion of the rock volume from the side. When the axial stress is 50 MPa, K is positive and increased with time. The rate of increase gradually decreases and eventually stabilizes, indicating that the volume of the sample is in a compressed state relative to its original size, and the volume deformation is continuously reducing. Under the axial stress of 60 MPa, the volume strain is approximately zero and slowly decreases, suggesting a gradual transition from compression to expansion in the volume deformation. At the creep time of 24.17 h, the bulk modulus changes from positive infinity to negative infinity, reflecting a transition from a positive volumetric strain to a negative one, and a change from compression to expansion in the volume change. When t is less than 24.17 h, the bulk modulus K is positive and gradually increases from 113.56 GPa to positive infinity over time. When t is greater than 24.17 h, the bulk modulus K is negative and gradually increases from negative infinity to − 63.89 GPa over time. The bulk modulus K is negative under axial stresses of 70, 80 and 90 MPa. With the increase in the stress level, the absolute value decreases continuously. The rate of increase in K value increases with time, indicating that the sample is in the stage of expansion, and the expansion effect becomes increasingly obvious with the improvement of the stress level and the development of time.

In accordance with the distribution characteristics of K/σ_m with time, the variation of creep parameters under a stress level of 60 MPa is fitted in accordance with Eq. (34), and the bulk modulus under other loads is fitted in accordance with Eq. (35).

The variation law of the volume modulus K with time t is shown in Fig. 11. The fitting parameters for each load condition are shown in Table 1.

$$\frac{K}{{\sigma_{{\text{m}}} }} = a_{2} {\text{exp}}\left( { - t/b_{2} } \right) + c_{2} ,$$

(34)

where a₂, b₂, c₂, a₃, b₃, and c₃ are fitting parameters.

Figure 11

Bulk modulus.

Table 1 Fitting parameters under loads.

Analysis of the variation law of viscoelastic shear modulus G₂

The relationship between the viscoelastic shear modulus G₂ and the time t under each stage of loading is shown in Fig. 12.

Figure 12

Duration of G₁ when σ₃ = 15 MPa.

As shown in Fig. 12, G₂, which controls the limit viscoelastic deformation of the rock sample, gradually decreases with time. The absolute value of the slope of the curve gradually decreases, indicating that the viscoelastic deformation gradually increases with time and tends to a stable value. At the initial stage of loading, the viscoelastic shear modulus G₂ increases with increasing stress level. In the later stage of loading, the higher the stress level, the smaller the value of G₂. The higher the stress level, the larger the magnitude of the change in G₂. In accordance with the distribution characteristics of S₁₁/G₁ over time, the creep parameters under different stress levels are fitted by Eq. (36).

The variation law is shown in Fig. 13. The fitting parameters under each load are shown in Table 2.

$$\frac{{S_{11} }}{{G_{2} }} = a_{4} {\text{exp}}\left( { - t/b_{4} } \right) + c_{4} ),$$

(35)

where a₄, b₄, and c₄ are fitting parameters.

Figure 13

Fitting of S₁₁/G₂ contrast experiment curves when σ₃ = 15 MPa.

Table 2 Calculation result of S₁₁/G₁.

The value of S₁₁/G₂ represents the trend of the axial viscoelastic strain of the sample. As shown in Fig. 13, the longer the time and the higher the stress level, the greater the final viscoelastic strain.

Analysis of the variation law of viscous coefficient η'₁

The relationship between the shear viscoelastic coefficient η'₁ and time at different loads is shown in Fig. 14.

Figure 14

Duration of η₁ when σ₃ = 15 MPa.

As shown in Fig. 14, the shear viscoplastic coefficient η'₁ decreases with time under the same load, indicating that the creep rate gradually decreases with time and tends to a stable value. The creep of the sample enters the steady-state creep stage. The higher the stress level, the larger the magnitude of the change in η'₁.

In accordance with the distribution characteristics of S₁₁/η'₁ with time, the creep parameters under different stress levels are fitted by Eq. (37). The variation law is shown in Fig. 15. The fitting parameters under each load are shown in Table 3.

$$\frac{{S_{11} }}{{\eta^{\prime}_{1} }} = a_{5} {\text{exp}}\left( { - t/b_{5} } \right) + c_{5} ,$$

(36)

where a₅, b₅, and c₅ are fitting parameters.

Figure 15

Data fitting of S₁₁/η^’₁ when σ₃ = 15 MPa.

Table 3 Calculation result of S₁₁/η₁.

Analysis of the variation law of viscous coefficient η'₂

The plastic element only operates when σ₁ − σ₃ ≥ σ_s. The relationship between the shear viscoplastic coefficient η'₂ and time t at each moment under different loads is shown in Fig. 16.

Figure 16

Duration of η^’₂ when σ₃ = 15 MPa.

As shown in Fig. 16, η'₂ increases gradually with time under the same load, and the rate of viscoplastic creep decreases with time. When the axial stress is 80 MPa, the shear viscoplastic coefficient η^’₂ is higher than when under the action of 90 MPa. It shows that the rate of the strain-steady-state creep stage of the rock under action of 80 MPa is much less than 90 MPa. At the initial stage of loading, the shear viscoplastic coefficient η^’₂ increases with the increase in stress level. At the end of loading, η^’₂ decreases with increasing stress level. This condition is due to the greater internal reorganization of the rock’s viscosity as the stress level increases in the primary creepstage. As time progresses into a steady-state creep phase, the internal structure damage is more severe, and the load causes the viscosity to decrease.

In accordance with the distribution characteristics of S₁₁/η^’₂ with time, the creep parameters under the stress levels of 80 and 90 MPa are fitted by Eq. (37). The variation law is shown in Fig. 17. The fitting parameters under each load are shown in Table 4.

$$\frac{{S_{11} }}{{\eta^{\prime}_{2} }} = a_{6} {\text{exp}}\left( { - t/b_{6} } \right) + c_{6} ,$$

(37)

where a₆, b₆, and c₆ are fitting parameters.

Figure 17

Data fitting of S₁₁/η^’₂ when σ₃ = 15 MPa.

Table 4 Calculation result of S₁₁/η^’₂.

The value of S₁₁/η^’₂ mainly controls the rate of axially strained viscoplastic deformation of the specimen. As shown in Fig. 17, the higher the stress level, the greater the rate of viscoplastic deformation creep. The rate of viscoplastic deformation of the rock samples decreases with time and gradually stabilizes, and the rock creep enters a steady-state creep stage.

Analysis of the variation law of viscous coefficient η'₃

Only when t ≥ t₂, the nonlinear Newtonian dashpot starts to generate creep deformation. Therefore, the acceleration creep stage appears only when the stress level is 90 MPa. The relationship between the shear viscoplastic coefficient η'₃ at each moment and the time t is plotted in Fig. 18.

Figure 18

Duration of η^’₃ when σ₃ = 15 MPa.

In accordance with the distribution characteristics of S₁₁/η^’₃ with time, the creep parameters under the stress levels of 90 MPa is fitted by Eq. (39). The variation law is shown in Fig. 19.

$$\frac{{S_{11} }}{{\eta^{\prime}_{3} }} = a_{7} {\text{exp}}\left( { - t/b_{7} } \right) + c_{7} ,$$

(38)

where a₇, b_7, and c₇ are fitting parameters.

Figure 19

Data fitting of S₁₁/η^’₃ when σ₃ = 15 MPa.

The viscous coefficient η^’₃ mainly affects the accelerated creep stage. As shown in Fig. 19, S₁₁/η^’₃ gradually decreases with time.

Determination and verification of creep model

Determination of creep model under the influence of stress state and time

In this research, the creep parameters of the transient creep, primary creepphase, steady-state creep phase, and accelerated creep phase are analyzed with the stress level and time. A mathematical model is derived to describe the relationship between the creep parameters, stress, and time. This creep parameter model is substituted into Eqs. (23), (24) and (25) to obtain a creep 3D model that considers the stress state and time.

When σ < σ_s,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} \left( {S_{ij} } \right)}} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{{9K\left( {\sigma_{{\text{m}}} ,t} \right)}} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} \left( {S_{ij} ,t} \right)}}\left( {1 - \exp \left( - \frac{{G_{2} \left( {S_{ij} ,t} \right)}}{{\eta^{\prime}\left( {S_{ij} ,t} \right)_{1} }}\right)t} \right),$$

(39)

when σ ≥ σ_s and t < t₂,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} \left( {S_{ij} } \right)}} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{{9K\left( {\sigma_{{\text{m}}} ,t} \right)}} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} \left( {S_{ij} ,t} \right)}}\left( {1 - \exp\left ( - \frac{{G_{2} \left( {S_{ij} ,t} \right)}}{{\eta^{\prime}_{1} \left( {S_{ij} ,t} \right)}}\right)t} \right) + \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\eta^{\prime}_{2} \left( {S_{ij} ,t} \right)}}t,$$

(40)

when σ ≥ σ_s and t > t₂,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} \left( {S_{ij} } \right)}} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{{9K\left( {\sigma_{{\text{m}}} ,t} \right)}} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{2} \left( {S_{ij} ,t} \right)}}\left( {1 - \exp \left( - \frac{{G_{2} \left( {S_{ij} ,t} \right)}}{{\eta^{\prime}\left( {S_{ij} ,t} \right)_{1} }}\right)t} \right) + \frac{{\sigma {}_{1} - \sigma_{3} - \sigma_{s} }}{{3\eta^{\prime}_{2} \left( {S_{ij} ,t} \right)}}t + \frac{{\sigma {}_{1} - \sigma_{3} }}{{6\eta^{\prime}_{3} \left( {S_{ij} ,t} \right)}}\left( {t - t_{2} } \right)^{2} .$$

(41)

Verification of creep model

The curves of different stress levels and creep models at various times are plotted in Eqs. (39), (40) and (41) and compared with the experimental data, as shown in Fig. 20.

Figure 20

Experimental results compared with the calculated values.

As shown in Fig. 20, the model curve conforms to the variation curve of the creep test at confining pressures of 10 and 15 MPa. The high consistency between the model curve and the test curve indicates that substituting the method of calculating the creep parameters into the creep model is suitable and feasible to reflect the deformation process of rock creep. The model accurately reflects the creep characteristics of the primary and steady-state creep stages, and overcomes the shortcomings of traditional creep models, which are difficult to describe the accelerated creep. The model has a good predictive analysis of triaxial creep test data.

Verification and analysis of theoretical models for other types of rocks

The above analysis and verification results are based on sandstone. This study selects the surrounding rock of the No. 2 tunnel of Dali No. 1 section as the test object to verify the correctness and rationality of the proposed theoretical model. The rock is preliminarily determined as chlorite schist. The rock samples mainly contain quartz, kaolinite, illite, dolomite, and calcite. The XRD pattern of the rock sample is shown in Fig. 21.

Figure 21

XRD pattern of the rock sample.

In accordance with the above steps and the creep test data of the rock, the model parameters under different times and stresses are calculated. The model parameters are substituted into Eqs. (39), (40) and (41) to obtain the rock model curve. The model curve is drawn and compared with the experimental curve, as shown in Fig. 22.

Figure 22

Comparison of creep model and test curve.

As shown in Fig. 22, the creep model curve of the rock is highly fitted with the test curve, describing the whole process of decay creep, constant creep, and accelerated creep. This condition makes up for the shortcomings of traditional models in describing accelerated creep. The method of determining creep parameters and the new creep model proposed in this study can be applied to different types of rocks.

Conclusions

A method for determining creep parameters by creep curves is proposed. Various creep parameter models under different stresses and different times are established by assuming certain conditions. A creep model that can correspond to each creep stage is established. The model of creep parameters with respect to time and stress is substituted into the traditional creep model to create a time-dependent creep model that considers the stress state. The model curve conforms to the variation curve of the creep test at confining pressures of 10 and 15 MPa. The high consistency of the model curve and the test curve indicates that substituting the method of calculating the creep parameters into the creep model is suitable and feasible to reflect the deformation process of rock creep. Overall, the model has a good predictive analysis of triaxial creep test data.

The relationship between creep parameters and stress levels is unclear. The change in creep parameters with time reflects the deterioration of the rock structure to some extent. The shear modulus G₁ of the rock decreases with the increase in the applied bias stress tensor S_ij. Under the axial stress of 60 MPa, the relationship between bulk modulus and time is divided into two parts. The bulk modulus is positive, and its relationship with time shows a trend of steady increase first and then rapid increase. The bulk modulus is negative, and its relationship with time shows a trend of increasing first and then stabilizing. The shear viscoplastic coefficient η'₁ decreases with time under the same load. The value of S₁₁/G₂ represents the development trend of the axial viscoelastic strain of the sample. The longer the time and the higher the stress level, the greater the final viscoelastic strain. The η'₂ gradually increases with time under the same load. The slope of the curve gradually increases. The value of S₁₁/η^’₂ mainly controls the rate of axially strained viscoplastic deformation of the specimen. The viscous coefficient η^’₃ mainly affects the accelerated creep stage, and the S₁₁/η^’₃ gradually decreases with time.