Introduction

Tropospheric ozone (O3) pollution affects large areas of the world1,2. Ozone is strongly phytotoxic and is considered as a serious issue for the health and productivity of forests3. Ozone risk assessment may use different O3 metrics4 or models1. The most common approach is the use of exposure-based metrics e.g. AOT40 i.e. the accumulation of hourly O3 concentrations above 40 ppb for daylight hours during the growing season4. However, exposure-based metrics do not incorporate the effects of stomata, that are the only way of O3 entry into the plant5. Therefore, a flux-based approach is recommended e.g. by the Convention on Long Range Transboundary Air Pollution of the United Nations6 and by the National Emission Ceilings Directive of the European Union7, where the stomatal O3 uptake is estimated through models integrating the effects of climatic factors and vegetation characteristics on stomata (e.g. the DO3SE model8). Such flux metric is called Phytotoxic Ozone Dose, defined as the amount of O3 absorbed into the leaves or needles through stomata over the growing season, and above a threshold Y of uptake (PODY).

Among the many ecosystem services provided by forests, only wood production losses have been estimated so far to assess the economic impact of O3 pollution on forests9,10,11, because experimental dose–response relationships are available for estimating biomass losses12,13,14. Feng et al.11 used the AOT40-response relationship and reported that current levels of O3 across China may cause economic losses of forest production equivalent to 52.2 billion US$ in 2015. Karlsson et al.9 similarly applied the AOT40-based approach to Swedish forests and simulated that the potential annual economic loss of forest production due to O3 was 56.0 million € over the time period 1993–2003. Felzer et al.10 predicted the O3 effects on carbon sequestration in crops, pastures and forests at global scale by using the empirical function of AOT40 for gross primary production (GPP) and found that reduced CO2 uptake due to O3 exposure would increase the macroeconomic consumption cost of the greenhouse gas policy by 4.5 trillion US$ in 2100. Wood is central in a sustainable bioeconomy, e.g. forestry and extended wood-based value chains employed 4.5 million people in the European Union in 201815.

Given the limited knowledge on the economic value of O3-induced wood production losses, in particular according to a flux-based approach, the aim of this study was to develop a combined modelling approach for realistic estimates of the economic impacts of POD1-based wood losses, by using Italy as a case study. Italy is a well-known hot-spot of O3 pollution, given its central position in the Mediterranean basin in Southern Europe where climate and economic conditions promote O3 pollution16.17. In 2001, the Italian wood sectors employed 413,872 workers in 87,546 companies with a total turnover of about $35 billion, with the furniture sector accounting for $20.8 billion18. We expect that this approach and results stimulate further studies by using a harmonized methodology for a better economic understanding of the global impacts of O3 pollution on forests and the forestry sector.

Results

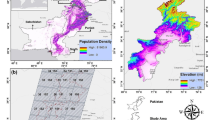
POD1 values across Italy ranged between 0.3 and 100 mmol m−2, with a spatial distribution showing lower values in the Alps mountains in the North and higher values over the peninsula and the islands where the climate is typically Mediterranean (Fig. 1A). The average value of POD1 was 20.4 mmol m−2 ranging from 8.0 mmol m−2 in Piedmont to 41.4 mmol m−2 in Sardinia (Fig. 1S).

Figure 1
figure 1

(A) Stomatal ozone uptake over a threshold of 1 nmol O3 m−2 s−1 (POD1) and (B) wood loss (%) in the POD1 scenario relative to the no ozone damage scenario (WO) estimated over a 12 × 12 km grid along Italy in the year 2005. Maps were created by QGIS (https://www.qgis.org/it/site/).

Full size image

Results suggested a significant impact of O3 (POD1) on Italian wood losses, that reached almost half of the expected wood production in the no ozone scenario (WO) at individual grid points (Fig. 1B) as well as a significant influence of the interest rate (r) on economic trend. Indeed, the total capital value of Italian forests in the WO scenario (no ozone) ranged from 8.0 to 29.5 B€ and from 2578 to 8987 € ha−1 with 2–4% of interest rate (Table 1). The POD1 scenario caused a total potential damage from 790.9 M€ to 2.85 B€ of capital value (255–869 € ha−1, on average). The annual damage ranged from 31.6 to 57.1 M€ (10–17 € ha−1 year−1, on average). The relative economic impact from WO to POD1 scenario was about 10% (total damage) and about 9% (average damage) for all interest rates. In addition, the total forest area with FEV > 0 decreased by around 1.1% from WO to POD1 (Table 2). The reduction ranged from 35,358 ha with r = 3% to 37,774 ha with r = 4% (1.1% and 1.2% of total forest area, respectively).

Table 1 Forest expectation value (FEV) under no ozone damage scenario (WO) and with a forest-type specific reduction in the annual forest increment as estimated on the basis of the phytotoxic ozone dose (POD1).
Full size table
Table 2 Total forest area (ha) with FEV > 0 and its decrease under no ozone damage scenario (WO) and phytotoxic ozone dose (POD1) scenario.
Full size table

The O3 impact on potential national wood production is reported in Table 3. According to the forest characteristics of Italy (widespread broadleaved stands, coppice management, private properties, etc.), the most represented wood assortment was firewood (from 5,449,258 to 5,603,228 m3 year−1 in WO scenario), followed by timber pole (from 818,390 to 824,274 m3 year−1), roundwood (from 587,011 to 672,446 m3 year−1) and paper mill (from 288,511 to 365,174 m3 year−1). Firewood and timber pole were strongly affected by moving from WO to POD1 scenario (on average the reduction was 7.5% and 7.4%, respectively). The decrease of roundwood and paper mill (on average 5.0% and 4.8%, respectively) was lower than that for timber pole and firewood.

Table 3 Timber production under no ozone damage scenario (WO) and phytotoxic ozone dose (POD1) scenario in Italy in 2005 and potential losses, with different interest rates r.
Full size table

The Italian administrative regions were affected by O3 in different ways (Table 4). Total damage was affected more by the forest surface than by the average POD1 value of the region, i.e. was higher in regions with higher forest areas (from 1.03 M€ in the small Aosta Valley to 191.4 M€ in the big and highly forested Tuscany, equivalent to 0.03 and 5.70 M€ year−1, respectively). The average capital value showed higher impacts in Liguria (1229 € ha−1), Campania (628 € ha−1), Calabria (568 € ha−1) and Lazio (527 € ha−1) i.e. 37, 19, 17 and 16 € ha−1 year−1, respectively. The reduction of profitable forest area, i.e. with FEV > 0, was strongly affected by the POD1 level, and was higher in Sardinia (− 10,752 ha of forest surface area, 41.4 mmol m−2 POD1), followed by Calabria (− 5811 ha, 33.2 mmol m−2), Sicily (− 3362 ha, 40.9 mmol m−2), and then by highly forested regions with relatively lower POD1 levels such as Tuscany (− 2432 ha, 20.6 mmol m−2) and Trentino-South Tyrol (− 2319 ha, 9.2 mmol m−2). In relative terms, the decrease of profitable forests still occurred in Sardinia (6.2%), Sicily (3.1%) and Calabria (2.5%) but also in regions with a limited forest coverage but high POD1 level (e.g. 2.9% of reduction in Apulia, 32.2 mmol m−2).

Table 4 Reduction of forest expectation value (FEV) and forest area from the WO to the POD1 scenario.
Full size table

Discussion

We merged an open-source add-on GIS software tool for estimating the economic value of forests19 with a classic O3 risk assessment approach6,20, and used forest inventory and WRF-CHIMERE outputs to spatially estimate the O3-induced wood losses in the year 2005. We used the accumulated stomatal O3 uptake (POD1) as a metric of O3 damage because it is considered as a better index than only O3 concentrations in the air21. However, estimating POD1 at fine scale is challenging as it requires hourly inputs22. For the first time, an economic valuation of wood losses was based on POD1 at high spatial horizontal resolution (12 km2).

Italy is known to be subject to elevated O3 pollution16 and is thus an ideal case study for applying this combined approach. In fact, the average POD1 value of Italy was 20.4 mmol m−2 with spikes up to 100 mmol m−2. Such values are higher than values estimated at individual forest stands in central and Northern Europe (Tatra mountains23, 14–16 mmol m−2; Southern Sweden24, ~ 18 mmol m−2) and similar to values simulated for East-Asian forests (continental and (sub)tropical forests20, 20–105 mmol m−2). Also East Asia is known as a hot-spot of O3 pollution25. The spatial distribution of POD1 along the Italian peninsula showed lower values in the Alpine forests in the North (on average 12 mmol m−2) and higher values in the typical Mediterranean climate of the South (on average 23 mmol m−2) and the islands (~ 41 mmol m−2). These values and the North-to-South increase are similar to what observed for the entire Europe26, as the warmer climate in the South stimulates O3 formation27. These POD1 values are well above the critical levels of 4 and 8 mmol m−2 identified by28 for the protection of deciduous broadleaves (birch and beech) and conifers (Norway spruce), respectively, stressing that most of Italian forests are exposed to severe O3 risks.

Modelling O3 impact on Italian forests showed a marked decrease of their economic value. According to applied interest rate, annual damage ranged from 31.6 to 57.0 M€ per year with a loss of capital value of about 10%. Among the few previous papers on the economic impact of O3 on forests, none used a methodology comparable with the present research [9,10,11]. However, Karlsson et al.9 indicated similar results as the potential annual economic loss for Sweden due to negative impacts of O3 on forest production was of the order of 56 M€ that is about 2.4 € ha−1 year−1, while in Italy it ranged from 3.02 to 5.46 € ha−1 year−1 (r: 2–4%). The variability of potential economic impact among Italian administrative regions reflected the strong dissimilarity of geomorphological, logistic, vegetational as well as socio-economic conditions of Italian forests29. We innovatively defined the economic damage by O3 also in terms of reduction of forest area with positive FEV. This reduction in the POD1 scenario was about 1.1–1.2% of the total forest area. This loss of stands with economic profitability may make active forest management no longer meaningful, which would result in an indirect negative effect due to the worsening of other ecosystem services30. As an example, hydrogeological problems or fire risk—which are relevant issues for the Italian territory—can increase due to a decline of silvicultural practices31. In general, trade-offs among provisioning and other forest benefits (regulating, supporting and cultural services32) can happen and they may be measured not only in biophysical but also in economic terms33. A POD1-induced loss from about 535,000 to 511,000 m3 year−1 of wood assortments was also estimated. Firewood was the most impacted product (from 421,408 to 407,915 m3 year−1 of reduction) but the structure of Italian forest chain and the high added value for the other timber outputs (e.g., roundwood) suggested a potential negative cascade effect on the whole forest chain and on ancillary activities.

Conclusions

This work is one of the first fine-scale combined models to quantify the economic impacts of O3 at national level. Results highlighted that the reduction of forest area with active management is limited to the most severely O3 polluted areas, even though significant negative effects on timber production occur all across Italy. Consequences on other forest ecosystem services and socio-economic deterioration of the forest chain, such as occupational consequences and cascade effect on satellite activities, should be evaluated. This aspect indicates that the elevated economic impact (loss of capital and annual values of forest) here presented, is still an underestimation of the total losses.

The open source software facilitates replicability as well as sensitivity analysis. Spatial analysis can take into account local peculiarities, thus helping to improve models and results, and finally resulting into guidelines to cope with the potential negative impacts of O3 pollution on forests and the forestry sector. This GIS-based application is thus a valuable tool to quantify and localize potential negative impacts. Ozone damages can interfere with the vitality of species of plant communities, as well as that of the animals, fungi, bacteria and insects that live in close association with plants or in nearby soils34. Changes induced by O3 impact on many ecological processes, affecting ecosystem services, flows, goods and values. Further activities in the definition of ecosystem-scale models suitable to extrapolate effects of O3 on productivity of trees and entire ecosystems might be addressed to economically quantify also the loss of other ecosystem services such as biodiversity, resource allocation and/or seed production.

Methodology

Study area and forest data

Data of biomass availability were obtained from the pan-European map of forest biomass increment35. The map was validated using information from the most recent and free georeferenced Italian National Forest Inventory, i.e. for the year 200536. In Italy, the total forested area was 10,467,533 ha in 2005. There was a certain variability of forest cover (in percentage) as well as vegetation, geomorphologic, logistics and socio-economic characteristics among regions (NUTS-2 level). Private forests accounted for 63.5% of the total, and coppice was the prevalent forest management (54.0%). The most common forest typology was broadleaved species (83.6% of total area), mainly oaks (23.9% of broadleaved, mostly Quercus robur and Q. cerris), as well as Fagus sylvatica (11.8%) and Castanea sativa (9%). Among the conifers (16.4% of total area), Picea abies prevailed (34.2%), in particular in the Alpine forests36.

Modelling ozone pollution

Hourly O3 concentrations and hourly meteorological data needed to calculate POD1 (i.e. solar radiation, air temperature, relative humidity, soil water content, wind speed) were simulated over the domain at 12 × 12 km of horizontal resolution by the WRF-CHIMERE modelling system, as described in26. The O3 concentrations at 20–25 m above ground level (top of the canopy) provided by CHIMERE were used to calculate PODY. For PODY, a threshold Y of 1 nmol m−2 s−1 per leaf area as recommended by6 for forest protection was applied, and computed as in6,37:

$${\text{POD1}}\left( t \right) = \mathop \smallint \limits_{SGS}^{EGS} \max \left( {\frac{Rc}{{Rb + Rc}} \times g_{sto} \times \left[ {{\text{O}}_{3} } \right] - {1, 0}} \right)dt$$
(1)

where [O3] is hourly O3 concentrations (ppb), dt is time step (1 h), SGS and EGS are the start and end date of the growing season computed as described in38, Rb is the quasi-laminar resistance (s m−1), Rc is the leaf surface resistance (s m−1), and gsto is the hourly value of stomatal conductance to O3 (mmol O3 m−2 PLA s−1, where PLA is the Projected Leaf Area) computed as following:

$$g_{sto} = g_{max} \times f_{phen} \times f_{light} \times max \left\{ {\left\{ {f_{min} } \right.,\left( {f_{temp} \times f_{VPD} \times f_{SWC} } \right.)} \right\}$$
(2)

where gmax is the maximum stomatal conductance to O3 of a plant species expressed on a total leaf surface area (mmol O3 m−2 PLA s−1). The maximum stomatal conductance (gmax) is experimentally obtained as average above the 90th or 98th percentile of gsto measurements under optimum environmental conditions for stomatal opening6,14. The functions fphen, flight, ftemp, fVPD, and fSWC are the variation in gmax with leaf age, photosynthetically flux density at the leaf surface (PPFD, μmol photons m−2 s−1), surface air temperature (T, °C), vapour pressure deficit (VPD, kPa), and volumetric soil water content (SWC, m3 m−3), respectively. The function fmin is the minimum stomatal conductance. These species-specific functions vary between 0 and 1, and are expressed as:

$$f_{light} = 1 - e^{{\left( { - light_{a} \times PPFD} \right)}}$$
(3)
$$f_{temp} = \left( {\frac{{T - T_{\min } }}{{T_{opt} - T_{\min } }}} \right)*\left[ {\left( {\frac{{T_{\max } - T}}{{T_{\max } - T_{opt} }}} \right)^{{\left( {\frac{{T_{\max } - T_{opt} }}{{T_{opt} - T_{\min } }}} \right)}} } \right]$$
(4)
$$f_{VPD} = \min \left\{ {1,\max \left[ {f_{\min } ,\left( {\frac{{(1 - f_{\min } )*(VPD_{\min } - VPD)}}{{VPD_{\min } - VPD_{\max } }}} \right) + f_{\min } } \right]} \right\}$$
(5)
$$f_{SWC} = \min \left[ {1,\max \left( {f_{\min } ,\frac{SWC - WP}{{FC - WP}}} \right)} \right]$$
(6)

where lighta is an adimensional constant; PPFD is hourly photosynthetic photon flux density estimated through the solar radiation; Topt, Tmin, and Tmax represent the optimum, minimum, and maximum temperature for gsto, respectively; VPDmin and VPDmax are minimum and maximum VPD for gsto; and WP and FC are the soil water content (SWC) at wilting point and field capacity, respectively6. WP and FC are constant and depend on the soil type obtained from a module included into the WRF-CHIMERE model. We assumed that fphen was 1 throughout the growing season (0 otherwise).

Six types of parameterization were used based on the six dominant forest types identified by land cover and climate over Italy, i.e. Alpine (for which the Boreal parameterizations in6 was used), Continental and Mediterranean with either Deciduous or Evergreen species (Table 5). After calculation of POD1, the dose–response functions specific per each forest type were applied in each 12 × 12 km grid point according to Table 6.

Table 5 Forest-type parameterization of DO3SE model according to6.
Full size table
Table 6 Forest-type dose–response functions to estimate total biomass losses (L) based on the cumulated stomatal ozone flux above a threshold of 1 mmol m−2 (POD1) according to6.
Full size table

Modelling ozone-induced wood losses

The economic value of Italian forests was quantified through a spatial-based analysis centered on the r.green.biomassfor model39. The tool is available as open-source add-on in GRASS Geographic Information System (GIS) software (https://grass.osgeo.org/grass78/manuals/addons/r.green.biomassfor.html). The model allows a quantification of wood assortments as well as their economic value by a multistep procedure. First, the so-called “technical availability” of material is quantified considering logistic (distance from forest/main roads or landing site) and geomorphological conditions (slope and terrain roughness). The combination of the above variables allows defining forest production process in terms of organization of cutting, processing and extraction. The second step introduces the economic parameters to calculate revenues from sell of assortments and full costs. Potentially available material is finally quantified on forest surfaces with economic profitability of production process. In the original version of the model, profitability was expressed as positive stumpage value (difference between revenues and costs of final harvesting / thinning). Here—in order to evaluate a long-term impact—the positive forest expectation value (FEV) (capital value of bare land plus timber at year y) was considered as index of economic profitability. FEV corresponds to the present value of cashflows arising from both the land and the tree, in perpetuity40. Input data to run r.green.biomassfor in Italy were derived from19 and are provided in Tables S1 and S2. The complete procedure was developed on raster basis with a resolution of 1 ha (squared pixel of 100 × 100 m). Wood losses due to O3 were computed taking into account the reduction of forest increment. In the present work, two scenarios were developed to quantify FEV and—as a consequence—forest surface with positive economic value and wood production: (i) a hypothetical scenario without O3 impact (WO) and (ii) a scenario based on POD1 limiting biomass production. The software r.green.biomassfor was then ran for both scenarios and results were reported at national and administrative (regions) level. FEV for each scenario s (FEVs) was calculated as in41 based on the “future revenues” approach:

$$FEV_{s} = \frac{{SV_{s} + \mathop \sum \nolimits_{m} T_{s} \cdot q^{{t_{s} - m_{s} }} + \left( {v_{s} - e_{s} } \right) \cdot \left( {\frac{{q^{{t_{s} - n_{s} }} - 1}}{r}} \right) + LEV_{s} }}{{q^{{t_{s} - n_{s} }} }}$$
(7)

where SV is stumpage value of final harvesting, T is stumpage value of intermediate thinning, t is rotation period, m is year of thinning, n is age of the forest, v and e are yearly income and cost, respectively, q = 1 + r with r interest rate, LEV is the land expectation value (bare soil) calculated as in42:

$$LEV_{s} = \frac{{SV_{s} + \mathop \sum \nolimits_{m} T_{s} \cdot q^{{t_{s} - m_{s} }} }}{{q^{{t_{s} }} - 1}} + \frac{{v_{s} - e_{s} }}{r}$$
(8)

FEVs were calculated at national and region level for both total (€) (Eq. 9) and average (€/ha) (Eq. 10) values. As POD1-based damage is accumulated over the growing season, total and average FEVs were annualized (aFEV) as expressed in Eq. (11) and Eq. (12), respectively.

$$FEV_{\omega } = \mathop \sum \limits_{i = 1}^{x} FEV_{i} \forall i \in \omega$$
(9)
$$averageFEV_{\omega } = \frac{{\mathop \sum \nolimits_{i = 1}^{x} FEV_{i} }}{{\mathop \sum \nolimits_{i = 1}^{x} i}} \,where\, i \in FEV > 0 \wedge \forall i \in \omega$$
(10)
$$aFEV_{\omega } = FEV_{\omega } \cdot r$$
(11)
$$average\_aFEV_{\omega } = averageFEV_{\omega } \times r$$
(12)

where ω is ω-th administrative level, i is i-th pixel in the map, the expression \(i \in FEV > 0 \wedge \forall i \in \omega\) represents forest surfaces with positive FEV for ω-th administrative level, and r is interest rate.

In each scenario s, the amount of timber potentially obtained was calculated on the basis of forest surface with positive FEV, forest type and partitioning (percentage) of biomass increment in each wood assortment. The analysis of economic losses was focused on forest surfaces where FEV > 0 in WO scenario because damage evaluation must compare ex-ante (WO scenario) and ex-post (POD1) situations. Therefore, in the hypothesis of timber products investigation, an economic damage exists if and only if forest area can be economically processed also in WO scenario. The main assortments considered as typical for Italy are roundwood, timber pole, paper mill and firewood19.

Long-term economic valuation (that is typical in forest sector) is very variable relative to the interest rate applied for capitalization. Therefore, a sensitivity analysis based on variation of the interest rate r was performed at national level. In other terms, economic metrics (outputs, see Table 1) were computed for three different interest rates (2%, 3% and 4%) that are appropriate in Italy on the basis of forest and forest owners’ characteristics41. Sensitivity analysis facilitates depiction of potential range of results when input variables can cause high level of uncertainty in the outputs. Regional evaluation considered—for brevity—only r = 3%43 for quantification of FEV as well as forest surface with positive FEV.

To link biomass from dose response functions to economic losses, the O3-induced biomass reductions (POD1 scenario) were attributed to the forest map by overlaying spatial locations. The forest map was created based on Corine Land Cover (CLC) polygons (Table S1). Each CLC forest polygon reports one forest category and was linked to one biogeographical region of Italy (i.e. alpine, continental or Mediterranean44). The CLC polygons were associated, through specific alphanumeric rules, to the forest types applied to compute dose–response functions (alpine deciduous, alpine evergreen, continental deciduous, continental evergreen, Mediterranean deciduous, Mediterranean evergreen). In case of lack of spatial matching among CLC polygons and POD1 forest types, a geographical extension of POD1 information was performed by means of proximity analysis (i.e. Voronoi tassellation of POD1 centroids45). The results were finally mapped by QGIS (https://www.qgis.org/it/site/).