Introduction

The successful exploitation of shale gas heavily depends on the combination of horizontal drilling, completions, and fracturing technology1,2. It has been proven that multi-stage fracturing horizontal wells constitute a very effective way to exploit low-permeability shale gas reservoirs. Due to the complex fracture network created in stimulated reservoir volume regions, it is a great challenge to accurately analyze production performance and evaluate post-fracture performance in such complex fractured reservoirs3.

Since 1972, many analytical and semi-analytical methods on production and flow behaviors in conventional gas and shale gas reservoirs have been utilized to simulate pressure transient behavior for horizontal wells with hydraulic fractures. Soliman et al.4 analyzed fluid flow mechanisms for multi-fractured horizontal wells and presented an approximate model to investigate the influence of fracture number, fracture orientation, fracture direction, fracture conductivity, and horizontal well location on flow behaviors. Larsen and Hegre5 presented two kinds of models for fractured horizontal wells with multiple fractures with finite conductivity: circular fractures with radial flow and vertical fractures with linear flow. For circular fractures, a cylindrical coordinate system is used with the perpendicular axis of the fracture coinciding with the z axis and the center of the fracture located at z = 0. The fracture size is given by the width, the well radius rw and fracture outer radius rf. For a vertical fracture, a Cartesian coordinate system is used with the x axis chosen as vertical axis, the y axis coinciding with the axis of the wellbore, and the center of the fracture located at z = 0. The fracture size is given by the width, the fracture half-length xf away from the wellbore, and the fracture half-length yf along the wellbore. Guo and Evans6 presented a randomly distributed vertical fractures model to predict production performance, and generated type curves to estimate reservoir properties and fracture characteristics. Bin et al.7 presented an improved analytical solution for fractured horizontal wells with different fracture intensities to investigate the effect of fracture properties on flow characteristics. However, due to constant rate assumption, the model cannot be applied to interpret production data. Wang et al.8 proposed a semi-analytical model in tight oil reservoirs with fractal geometries, which was used to describe complex pore sizes and random fractures in porous media. Since sorption characteristics were not incorporated into their model, the model cannot consider the effect of sorption on production. A technique was introduced by Rbeawi and Tiab9 to interpret the pressure transient behavior of fractured horizontal wells. The distribution of hydraulic fractures could be longitudinal or transverse, vertical or inclined, symmetrical or asymmetrical. Brown et al.10 and Stalgorova and Mattar11 proposed a classical tri-linear flow model to simulate production performance of fractured horizontal wells in unconventional reservoirs. However, complex geometries and sorption characteristics were not taken into account in these studies, so that they were not suitable for production performance analysis in shale gas reservoirs.

The above studies4,5,6,7,8,9,10,11 mainly focused on fluid flow in primary fractures, and ignored fluid flow inside secondary fractures and matrix. Due to the influence of induced fractures, uniform fracture models were not applicable to describe heterogeneous SRV zones. Some scholars attempted to utilize numerical models with a discrete fracture network to describe secondary fractures in SRV zones12,13,14,15. Although the production performance of a complex fracture network can be discerned through the use of numerical methods, numerical simulation is less attractive and pragmatic due to the large amount of requisite knowledge and time-consumption during the history matching process3. In contrast, the analytical model is an alternative for accurately forecasting flow behaviors and calculation efficiency.

Fractal geometry has shown potential in the analysis of flow and transport properties in porous media. Katz and Thompson16 were the pioneers to find experimental evidence that indicated that the pore spaces of a set of sandstone samples were fractals and self-similar over three to four orders of magnitude in length. Fractal theory can also describe complex fracture shape in shale gas and is easy to apply to obtain analytical solutions. Chang and Yortsos17 introduced fractal theory into petroleum engineering, and reported that the permeable fractures embedded within the matrix would be arranged in a fractal dimension. Cossio et al.18 presented a model with fractal geometry to develop a rapid and accurate semi-analytical solution for flow in a single vertical fracture that fully penetrates a homogeneous infinite-acting reservoir. Yao et al.19 proposed a fractal double-porosity model for the transient flow analysis of fluids. Kong et al.20 developed the basic formulae of seepage velocity, permeability, and porosity in both porous and fractured fractal media. Wang et al.3 presented semi-analytical modelling of flow behavior in fractured media with fractal geometry. Zhang et al.21 proposed an approach for estimating the size and equivalent permeability of fractal SRV zones for vertically fractured wells in tight reservoirs.

The proposed fluid flow models with fractal geometry3,16,17,18,19,20,21 are convenient for conducting pressure transient analysis for understanding flow in complex reservoirs22,23,24,25. Random fractures will be produced during the process of hydraulic fracturing. Fractal theory can exhaustively describe the randomness of pore sizes and gas reservoir heterogeneity24. However, most of the previous models are only involved in the aspects of pressure transient analysis in tight reservoirs, while shale multi-scale flow characteristics are not considered4,5,6,7,8,9,10,11,12. Second, gas PVT is assumed to be constant, so that the final results will lead to an assessment of errors. However, gas PVT changes with pressure in the development of shale gas reservoirs. Third, the characteristics of fractal geometry in SRV regions are not reflected in their models4,5,6,7,8,9,10,11,12.

In this paper, an improved tri-linear flow model in shale gas reservoirs with fractal geometry is presented to analyze and predict production performance of multi-fractured wells. First, multi-scale flow mechanism in shale gas reservoirs was considered in the analytical model (Fig. 1). Second, the main fractures were considered into longitudinal rectangular fractures and secondary fractures in the SRV zone were described using fractal theory. Third, gas PVT changed with reservoir pressure in this paper, and a multi-rate solution with variable pressure was also proposed to interpret real well production data measured under various production systems. Finally, the downhill Simplex method was employed to form the history matching procedure.

Figure 1
figure 1

Schematic diagram of multiscale mechanism.

Full size image

Methodology

Conceptual model

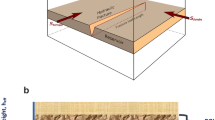
Figure 1 presents the conceptual model of stimulated reservoir volume (SRV) with fractal geometry. Many authors have presented analytical models to investigate regular fracture networks, such as the single planar hydraulic fractures network and orthogonal hydraulic fractures network4,5,6,7,8,9,10,11,12,13,14,15.

A schematic diagram of the presented model is shown in Fig. 2. Shale gas flow can be divided into three flow regions: flow in hydraulic fractures defined as region 1 (hydraulic fracture region); flow in the SRV region defined as region 2 (inner region); and flow in the OSRV region defined as region 3 (outer region). To establish mathematical models, the following basic assumptions are made:

  1. (1)

    Darcy flow occurs in hydraulic fractures;

  2. (2)

    Random fractures in SRV regions are considered using fractal geometry;

  3. (3)

    The OSRV region could be homogenous or double porosity with sorption behaviors;

  4. (4)

    Sorption characteristics are considered in the rock matrix;

  5. (5)

    The compressibility factor and viscosity change with pressure;

  6. (6)

    The Z-factor changes with pressure;

  7. (7)

    Knudsen diffusion and slippage effects are considered in the matrix model.

Figure 2
figure 2

Schematic of flow: (a) flow regions in multi-stage fractured horizontal well; (b) flow unit with SRV region and OSRV region.

Full size image

Model establishment

Different from conventional reservoirs, shale gas seepage often exhibits strong nonlinearity8. In addition, physical parameters, such as the viscosity, compressibility factor and deviation factor, are functions of pressure. However, these methods are effective for only specific problems. The viscosity, compressibility and deviation factor of shale gas change with pressure, which leads to a non-linear seepage equation. The pseudo-time and pseudo-pressure26,27,28 are defined and a detailed deduction is provided in Appendix A of the Supplementary File. These definitions can be written in the following forms:

Pseudo-pressure:

$$m(p)=\frac{{\mu }_{i}{Z}_{i}}{{p}_{i}}{\int }_{0}^{p}\frac{p}{\mu Z}\,dp$$
(1)

Pseudo-time:

$${t}_{a}={\int }_{0}^{{\rm{t}}}\frac{{\mu }_{gi}{c}_{ti}}{{\mu }_{g}(p){c}_{t}(p)}dp$$
(2)

where p is pressure, Pa; μ is viscosity, Pa▪s; cti is initial total compressibility, Pa−1; ct is total compressibility, Pa−1; t is time, s; Z is deviation factor; and Pi is initial pressure, Pa.

Matrix model

Matrix inter-porosity flow occurs in both SVR regions and OSRV regions, as shown in Fig. 2. The spherical element was assumed to flow in the matrix, and a comprehensive continuity equation with sorption can be formulated as:

$$-\frac{1}{{r}_{im}^{2}}\frac{\partial }{\partial {r}_{im}}({r}_{im}^{2}{\rho }_{im}{v}_{im})=\frac{\partial ({\rho }_{im}{\varphi }_{im})}{\partial {t}_{a}}+{\rho }_{sc}\frac{\partial {V}_{i}}{\partial {t}_{a}}$$
(3)

where Vi is sorption volume, m3/m3; ρim is gas density in the matrix, kg/m3; ρsc is standard condition gas density, kg/m3; vim is velocity in the matrix, m/s; ta is pseudo-time, s. i = o, i can represent the outer reservoir (region 3) or inner reservoir (region 2), respectively. Pseudo-time ta is defined in Eq. 2. The total compressibility in shale has been previously presented29,30 and can be expressed as:

$${c}_{t}=({c}_{g}[{S}_{gi}-{c}_{ep}]-\frac{\partial {c}_{ep}}{\partial p}+{c}_{d})$$
(4&x02010;1)
$${c}_{ep}=({c}_{f}+{c}_{w}{S}_{wi})({p}_{i}-p)$$
(4&x02010;2)
$${c}_{d}=\frac{{\rho }_{B}{B}_{g}{V}_{L}}{\varphi }(\frac{{p}_{L}}{{({p}_{L}+p)}^{2}})$$
(4&x02010;3)

where cg is gas compressibility, Pa−1; Sgi is gas saturation; cep is intermediate variables; cs is sorption compressibility, Pa−1; cf is formation compressibility, Pa−1; cw is water compressibility, Pa−1; Swi is initial water saturation; Bg is gas volume coefficient; VL is Langmuir volume, m3/kg; pL is Langmuir pressure, Pa; ρB is density of shale, kg/m3; and φ is porosity. Accounting for gas slippage and gas diffusion, gas velocity in the matrix can be expressed as:

$${v}_{im}=-\,{k}_{im}{F}_{iD}\frac{\partial {p}_{im}}{\partial {r}_{im}}=-\,{k}_{im}[(1+8\alpha {k}_{n})+{\mu }_{g}{D}_{g}{c}_{g}/{k}_{im}]\frac{\partial {p}_{im}}{\partial {r}_{im}}$$
(5)

The equation of gas state is given as:

$${\rho }_{im}=\frac{{p}_{im}M}{nZRT}$$
(6)

Substituting Eq. 1, and Eqs 4 through 6 into Eq. 3 produces the governing equation of matrix:

$$\frac{1}{{r}_{im}^{2}}\frac{\partial }{\partial {r}_{im}}({r}_{im}^{2}{k}_{im}[(1+8\alpha kn)+\frac{{\mu }_{g}{D}_{g}{c}_{g}}{kim}]\frac{\partial {m}_{im}}{\partial {r}_{im}})={\varphi }_{im}{c}_{imt}\frac{\partial {m}_{im}}{\partial {t}_{a}}$$
(7)

and

$${c}_{imt}={c}_{g}+{c}_{im}+{c}_{id}$$
(8)

where cim is matrix compressibility, Pa−1. The initial condition and boundary conditions can be given as:

$${{m}_{im}|}_{{t}_{a}=0}={m}_{i}({p}_{i})$$
(9&x02010;1)

and

$${{m}_{im}|}_{{r}_{im}=R}={m}_{if}$$
(9&x02010;2)
$${\frac{\partial {m}_{im}}{\partial {r}_{im}}|}_{{r}_{im}=0}=0$$
(9&x02010;3)

Equation 7 through 9 constitute the matrix seepage governing equation in both the SRV and OSRV regions. The dimensionless equations and solution method are provided in Appendix B.

Natural fracture model of the OSRV region (region 3)

According to the above definitions of pseudo-pressure and pseudo-time, assuming one-dimensional flow in the x direction, as shown in Fig. 3, the diffusivity equation and the associated boundary conditions for the outer reservoir are given by:

$$\frac{{\partial }^{2}{m}_{of}(p)}{\partial {x}^{2}}=\frac{{\varphi }_{of}{c}_{oft}{\mu }_{gi}}{{k}_{of}}\frac{\partial {m}_{of}(p)}{\partial {t}_{a}}+\frac{3}{R}\frac{{k}_{om}{F}_{oD}}{{k}_{of}}{\frac{\partial {m}_{om}(p)}{\partial {r}_{om}}|}_{{r}_{om}=R}$$
(10)
$${(\frac{\partial {m}_{of}(p)}{\partial x})}_{x={x}_{e}}=0$$
(11)
$${m}_{of}{(p)}_{x={x}_{f}}={m}_{If}{(p)}_{x={x}_{f}}$$
(12)

where kof is the fracture permeability in the outer region, m2; φof is fracture porosity in the outer region; kom is matrix permeability in the outer region, m2; xf is fracture half-length, m; xe is boundary length, m; coft is total compressibility in the outer region, Pa−1; and mof is fracture pseudo-pressure in the outer region, Pa. Eqs 10 through 12 constitute the natural fracture model of the OSRV region.

Figure 3
figure 3

Calculation procedure for production performance analysis.

Full size image

Natural fracture model of the SRV region (region 2)

The change in porosity and permeability in the inner region are large and heterogeneous. Therefore, the fractal model can be utilized to describe SRV behavior. Furthermore, we work exclusively in Cartesian coordinates. Thus, the fractal relationships are given as17,18:

$${k}_{If}^{Fractal}(y)={k}_{If}{(\frac{y}{{x}_{f}})}^{d-\theta -2}={k}_{If}{y}_{D}^{d-\theta -2}$$
(13&x02010;1)
$${\varphi }_{If}^{Fractal}(y)={\varphi }_{If}{(\frac{y}{{x}_{f}})}^{d-2}={\varphi }_{If}{y}_{D}^{d-2}$$
(13&x02010;2)

Assuming one-dimensional flow in the y direction, the diffusivity equation is given by:

$$\begin{array}{rcl}\frac{\partial }{\partial y}({k}_{If}^{Fractal}\frac{\partial {m}_{If}(p)}{\partial y})+{(\frac{y}{{x}_{f}})}^{d-2}\frac{{k}_{If}}{{x}_{f}}({\frac{\partial {m}_{If}(p)}{\partial x}}_{x={x}_{f}}) & = & {(\frac{y}{{x}_{f}})}^{d-2}{\varphi }_{If}{c}_{Ift}\mu \frac{\partial {m}_{If}(p)}{\partial {t}_{a}}\\ & & +\,{(\frac{y}{{x}_{f}})}^{d-2}\frac{3}{R}\frac{{k}_{Im}{F}_{ID}}{1}{\frac{\partial {m}_{\text{Im}}(p)}{\partial {r}_{Im}}|}_{{r}_{Im}=R}\end{array}$$
(14)

Substituting Eq. 13 into Eq. 14 yields:

$$\begin{array}{l}{(\frac{y}{{x}_{f}})}^{d-\theta -2}{k}_{If}[\frac{{\partial }^{2}{m}_{If}}{\partial {y}^{2}}+\frac{d-\theta -2}{y}\frac{\partial {m}_{If}}{\partial y}]+{(\frac{y}{{x}_{f}})}^{d-2}\frac{{k}_{If}}{{x}_{f}}({\frac{\partial {m}_{If}(p)}{\partial x}}_{x={x}_{f}})\\ \,={(\frac{y}{{x}_{f}})}^{d-2}{\varphi }_{If}{c}_{Ift}\mu \frac{\partial {m}_{If}(p)}{\partial t}+\,{(\frac{y}{{x}_{f}})}^{d-2}\frac{3}{R}\frac{{k}_{Im}{F}_{ID}}{1}{\frac{\partial {m}_{\text{Im}}(p)}{\partial {r}_{Im}}|}_{{r}_{Im}=R}\end{array}$$
(15)

The boundary conditions for the inner reservoir are given by:

$${(\frac{\partial {m}_{If}}{\partial y})}_{y={y}_{e}}=0$$
(16&x02010;1)

and

$${{m}_{If}|}_{y=\frac{\omega }{2}}={{m}_{F}|}_{y=\frac{\omega }{2}}$$
(16&x02010;2)

where kIf is the fracture permeability in the inner region, m2; φIf is fracture porosity in the inner region; kim is matrix permeability in the inner region, m2; xf is fracture half-length, m; cIf is fracture compressibility in the inner region, Pa−1; cIft is total compressibility of the inner region, Pa−1; mIf is fracture pseudo-pressure of the inner region, Pa; d is fractal dimension representing the dimension of fractal fracture network embedded in the Euclidean matrix; and θ is connectivity index characterizing the diffusion process.

Eqs 15 and 16 are the natural fracture model of the OSRV region, and the solution method is presented in Appendix B.

Hydraulic fracture model (region 1)

The flow in hydraulic fractures can be expressed as:

$$\frac{\partial ({k}_{F}\frac{\partial {m}_{F}(p)}{\partial x})}{\partial x}+{\frac{2{k}_{If}}{\omega }\frac{\partial {m}_{If}(p)}{\partial y}|}_{y=\frac{\omega }{2}}={\varphi }_{F}{c}_{F}{\mu }_{gi}\frac{\partial {m}_{F}(p)}{\partial {t}_{a}}$$
(17)

Inner boundary condition can be given as:

$${\frac{\partial {m}_{F}}{\partial x}|}_{x=0}=\frac{Q{\mu }_{gi}}{2wh{k}_{F}}$$
(18&x02010;1)

Outer boundary condition can be expressed as:

$${\frac{\partial {m}_{F}}{\partial x}|}_{x={x}_{f}}=0$$
(18&x02010;2)

where Q is flow rate, m3/s; cF is fracture compressibility, Pa−1; w is fracture width, m; φF is hydraulic fracture porosity; and kF is the fracture permeability, m2.

Solution of Mathematical Model

Bottom-hole pressure solution at constant rate conditions

A constant-rate solution can be obtained by using the Laplace transform method (Appendix B of the supplementary file), and we provide the solution of the non-linear difference equation using pseudo-pressure and pseudo-time definitions. The dimensionless definitions of the model and dimensionless solution at a constant rate condition are given as:

$${\bar{m}}_{FD}(p)=\frac{\pi }{{C}_{FD}s\sqrt{{\alpha }_{F}}}\frac{\cosh [\sqrt{{\alpha }_{F}}(1-{x}_{D})]}{\sinh (\sqrt{{\alpha }_{F}})}$$
(19)

where

$${\alpha }_{F}=2{\beta }_{F}/{C}_{FD}+s/{\eta }_{FD}$$
(20)
$${\beta }_{F}=-\,{(\frac{{w}_{D}}{2})}^{\gamma -1}\sqrt{{\alpha }_{{\rm{o}}}}\frac{{K}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{y}_{eD}^{\gamma }]{I}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{(\frac{{w}_{D}}{2})}^{\gamma }]-{I}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{y}_{eD}^{\gamma }]{K}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{(\frac{{w}_{D}}{2})}^{\gamma }]}{{I}_{n}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{(\frac{{w}_{D}}{2})}^{\gamma }]{K}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{y}_{eD}^{\gamma }]+{I}_{n-1}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{y}_{eD}^{\gamma }]{K}_{n}[\frac{\sqrt{{\alpha }_{o}}}{\gamma }{(\frac{{w}_{D}}{2})}^{\gamma }]}$$
(21)
$${\alpha }_{o}=\frac{{\beta }_{o}}{{C}_{RD}{y}_{eD}}+{u}_{I}$$
(22)
$${\beta }_{o}=\sqrt{{u}_{o}}\,\tanh [\sqrt{{u}_{o}}({x}_{eD}-1)]$$
(23)
$${u}_{I}=s[f(s)]=s[\frac{{\omega }_{I}}{{\eta }_{ID}}+\frac{{\lambda }_{I}{\eta }_{ID}}{5s}({\tau }_{I}\,\coth \,{\tau }_{I}-1)]$$
(24)
$${u}_{o}=s[g(s)]=s[\frac{{\omega }_{o}}{{\eta }_{oD}}+\frac{{\lambda }_{o}{\eta }_{oD}}{5s}({\tau }_{o}\,\coth \,{\tau }_{o}-1)]$$
(25)

In the above results, one-dimensional linear flow in the hydraulic fracture is considered. Flow choking within the fracture must be considered by using the following equation that was presented by Mukherjee and Economides31:

$${\bar{m}}_{FD}(p)=\frac{\pi }{{C}_{FD}s\sqrt{{\alpha }_{F}}}\frac{\cosh [\sqrt{{\alpha }_{F}}(1-{x}_{D})]}{\sinh (\sqrt{{\alpha }_{F}})}+\frac{{S}_{C}}{s}$$
(26)

SC is flow skin, and expressed as:

$${S}_{C}=\frac{{k}_{If}h}{{k}_{F}{w}_{F}}[\mathrm{ln}(\frac{h}{2{r}_{w}})-\frac{\pi }{2}]$$
(27)

Bottom-hole rate solution at constant pressure conditions

Note that the constant-pressure solution and constant-rate solution conform to the relation suggested by Van-Everdingen and Hurst32:

$${\bar{m}}_{FD}\times {\bar{q}}_{FD}=\frac{1}{{s}^{2}}$$
(28)

Therefore, the rate solution at a constant pressure condition can be obtained as:

$${\bar{q}}_{FD}=\frac{{C}_{FD}\sqrt{{\alpha }_{F}}}{s\pi }\frac{\sinh (\sqrt{{\alpha }_{F}})}{\cosh [\sqrt{{\alpha }_{F}}(1-{x}_{D})]}$$
(29)

The solutions at variable rate or variable pressure conditions

During the process of production, both the rate and pressure change with the time. Constant rate and constant pressure solutions cannot be applied to a real reservoir. Through using convolution theory29,33, the variable rate and variable pressure solutions can be given by

$${{\rm{m}}}_{wD}({t}_{Dn})=\sum _{i=1}^{n-1}\frac{q({t}_{i})}{q({t}_{n})}[{{\rm{m}}}_{FD}({t}_{Dn}-{t}_{Di-1})-{{\rm{m}}}_{FD}({t}_{Dn}-{t}_{Di})]+{{\rm{m}}}_{FD}({t}_{Dn}-{t}_{Dn-1})$$
(30)
$${q}_{wD}({t}_{Dn})=\sum _{\begin{array}{c}i=1\\ n > 1\end{array}}^{n-1}{{\rm{m}}}_{FDi}[{q}_{FD}({t}_{Dn}-{t}_{Di-1})-{q}_{FD}({t}_{Dn}-{t}_{Di})]+{q}_{FD}({t}_{Dn}-{t}_{Dn-1})$$
(31)

Calculation process

The material balance equation must be established to calculate pseudo-time and pseudo-pressure. The modified gas compressibility factor and material balance equation that were proposed by Moghadam30 for shale gas reservoirs were adopted in this paper.

The modified gas compressibility factor Z** is defined as:

$${Z}^{\ast \ast }=\frac{{\rm{p}}}{[\frac{1}{{S}_{gi}}\frac{p}{Z}({S}_{gi}-{c}_{ep}-{c}_{d})+\frac{{p}_{i}}{{Z}_{i}}(\frac{G}{{G}_{f}}-1)]\frac{{G}_{f}}{G}}$$
(32)

where the parameters cep and cd are defined in Eq. 4. The modified material balance equation can be written as:

$$\frac{p}{{Z}^{\ast \ast }}=\frac{{p}_{i}}{{Z}_{i}^{\ast \ast }}(1-\frac{{G}_{p}}{G})$$
(33)

The average pressure can be determined by taking advantage of Eqs 32 and 33, and pseudo-pressure and pseudo-time can be calculated. The entire calculation process is illustrated in Fig. 3, which shows the procedures of variable rate solution and variable pressure solution. The procedures above could be applied to interpret production data from shale gas reservoirs.

Validation of solution

The accuracy of the coupled model was validated by comparing our results with those of an analytical solution using IHS Harmony software. The settings of the reservoir and fracture properties are listed in Table 1. We selected special cases of fractal parameters d = 2 and θ = 0, which represents constant permeability and constant porosity, as the fractal geometry has been not considered in commercial software. The total analysis time is 255 d. Figures 4 and 5 present the validation results by comparing the analytical results based on the proposed fractal model with the analytical solution from commercial software10. The algorithm from IHS Harmony software was presented by Brown et al.10 in 2009. A validation of the rate solution under a constant pressure condition of 2,000 psi is shown in Fig. 4. It is apparent that the production rate and cumulative gas production obtained from the proposed model agree very well with those from the analytical solution. A validation of the pressure solution under a variable rate condition is shown in Fig. 5. Figure 5 presents five cycles of open and shut well conditions. The pressure solution associated with a variable rate and the rate solution associated with variable pressure can be calculated using Eqs 30 and 31, respectively. The same parameters are listed in Table 1, and the production rate value for open well is set to 2 MMscf. Fractal parameters remain as d = 2 and θ = 0. The solution of the pressure under variable rate conditions is consistent with the solution from the commercial software IHS Harmony.

Table 1 Data for model validation.
Full size table
Figure 4
figure 4

Validation of rate solution at constant pressure conditions for a special case (d = 2, θ = 0, f(s) = 1, g(s) = 1).

Full size image
Figure 5
figure 5

Validation of pressure solution at variable rate conditions for a special case (d = 2, θ = 0, f(s) = 1, g(s) = 1).

Full size image

Results and Discussion

Flow characteristics analysis of type curves

Flow characteristics analysis of pressure and pressure derivative curves is shown in Fig. 6 and the basic data used are shown in Table 2. It is apparent that the fluid flow in shale gas reservoirs can be classified into six stages:

  1. (1)

    The bi-linear flow regime is a straight line with a slope of 1/4 on the pressure derivative curve. The flow of gas occurs simultaneously both within hydraulic fractures and near them.

  2. (2)

    The linear flow regime is a straight line with a slope of 1/2 on the pressure derivative curve. In this period, linear flow around the fractures occupies the dominant position.

  3. (3)

    The transition flow regime (a) shows an indefinite slope line on the pressure derivative curve.

  4. (4)

    The first inter-porosity flow regime is a regime of supplementation from the shale matrix to the fracture system in the inner region. The derivative curve exhibits the first V-shaped segment.

  5. (5)

    The second inter-porosity flow regime represents the inter-porosity flow from the matrix system to the fracture system in the outer region. The pressure derivative curve shows the second V-shaped segment.

  6. (6)

    The boundary dominant flow regime is a straight line with a slope of 1 on the pressure derivative curve. In this regime, the process of inter-porosity flow is terminated, and the pressure between the matrix and fractures have increased to a state of dynamic balance.

Figure 6
figure 6

Flow characteristics of pressure and pressure derivative curves.

Full size image
Table 2 Dimensionless data for flow characteristics analysis.
Full size table

Effect of sensitive factors on flow characteristics

Figure 7 shows the influence of parameters, including the fractal dimension d; connectivity index θ; transfer coefficients of the inner region and outer region, λI and λO, respectively; storage coefficients of the inner region and outer region, ωI and ωO, respectively; and conductivity of fracture and region on pressure and pressure derivative curves. The same data are also listed in Table 2.

Figure 7
figure 7

Influence of sensitive factors on flow characteristics: (a) fractal dimension; (b) connectivity index θ; (c) inter-porosity flow coefficient of inner region λI; (d) inter-porosity flow coefficient of inner region λo; (e) storage coefficient of inner region ωI; (f) storage coefficient of inner region ωo; (g) fracture conductivity CfD; (h) fracture half-length xf.

Full size image

Influence of fractal geometry parameters on type curves

Figure 7a presents the effect of fractal dimension d on plots of type curves, wherein fractal dimension d values are set to 1.6, 2, and 2.4. A larger d represents a more complex structure of fractal natural fractures. It is concluded that the fractal dimension d has a significant impact on flow characteristics within all periods. Dimensionless pressure pD reflects pressure depletion during the production periods. From the pressure curve in Fig. 7a, it is indicated that a large fractal dimension will result in a small pressure depletion, which implies that the production rate will be enhanced under the same pressure drop. In addition, fracture morphology becomes more complex when fractal dimension d becomes large. Figure 7b presents the effect of the connectivity index of natural fractures in SRV region θ on plots of type curves. The θ values are set to 0, 0.4, and 0.8. Different from the fractal dimension, a large connectivity index will result in a large pressure depletion, which indicates that the production rate will be reduced under the same pressure drop. Moreover, a larger θ value leads to worse connectivity in the formation. In other words, pressure depletion is proportional to the connectivity index of natural fractures in the SRV region and is inversely proportional to fractal dimension.

Influence of matrix transfer and storage parameters on type curves

Figure 7c through d show the effect of the inter-porosity coefficient between the matrix and natural fractures on type curves. It reflects gas flow ability from the matrix to natural fractures in the inner region. Similarly, the inter-porosity flow coefficient of outer region λo is proportional to matrix permeability kom of the outer region, and is inversely proportional to fracture permeability kof of the outer region. Thus, it reflects the gas flow ability from the matrix to natural fractures in the outer region.

The mechanism of the theory reveals that a large inter-porosity flow coefficient reflects relatively strong matrix flow ability and weak fracture flow ability. Figure 7d presents the effect of the inter-porosity flow coefficient λo on type curves. The values are set to 0.03, 0.3, and 3. It is seen from Fig. 8d that a large λo value corresponding to strong matrix flow ability will lead to a small pressure depletion as the matrix compensates for pressure loss by supplying natural fractures. From the derivative curves of Fig. 7c and d, it is observed that flow in intermediate time is mainly affected by the inter-porosity flow coefficient.

Figure 8
figure 8

Influence of sensitive factors on production rate and cumulative production: (a) fractal dimension; (b) connectivity index θ; (c) Langmuir volume VL; (d) Langmuir pressure pL; (e) fracture half-length xf; (f) fracture conductivity CfD; (g) inter-porosity flow coefficient; (h) storage coefficient.

Full size image

Figure 7e and f show the effect of the storage coefficient of natural fractures on the type curves. The ωI values reflect natural fracture energy, which was set to 0.000001, 0.1, and 0.5 in the inner region. The ωI values reflect natural fracture energy and are set to 0.000001, 0.00001, and 0.0001in the inner region. It is known from the pressure curves of both figures that a large storage coefficient will lead to a small pressure depletion due to the storage of rich gas resources in the natural fractures. This results in an extension of the linear flow duration, which is indicated from the derivative curves of both figures. From the derivative curves of Fig. 7e and f, it could also be concluded that flow in early and medium time is mainly influenced by the storage coefficient.

Influence of fracture conductivity and region conductivity on type curves

Figure 7g shows the effect of the hydraulic fracture conductivity on the type curves. The CfD values reflect the flow ability of shale gas in hydraulic fractures and are set to 1, 5, and 20. It is observed from the pressure curves that a small fracture conductivity will lead to a large pressure depletion, which implies that the production rate will be enhanced by improving fracture conductivity. However, the production rate is improved only at an early time. It is apparent from the pressure derivative curves that there is no effect on flow in middle and late time.

Figure 7h presents the effect of the inner region conductivity CRD on type curves. The CRD values indicate flow ability of shale gas in the inner region and are set to 1, 2, and 5. CRD has an important impact on fluid flow during all production periods. According to the definition of Eq. B-29, CRD is proportional to the fracture permeability of the inner region and is inversely proportional to the fracture permeability of the outer region. The pressure curves in Fig. 7h show that a large region conductivity will lead to a large pressure depletion. It is apparent from the derivative curves that the shapes of the curves do not change as the inner region conductivity changes in the bi-linear flow period.

Effect of sensitive factors on production performance

Figure 8 shows the effects of different parameters, including fractal dimension d, connectivity index θ, Langmuir volume VL, Langmuir pressure PL, fracture half-length xf, fracture conductivity CfD, inter-porosity flow coefficient of inner region and outer region λI and λO, respectively, and storage coefficients of the inner region and outer region ωI and ωO, respectively, on production rate and cumulative production. The data used are listed in Table 3. The bottom-hole pressure was set to 2,000 psi in all cases.

Table 3 Data for sensitive parameters analysis.
Full size table

Fractal geometry

The fractal dimension values are set to 1.99, 2, and 2.01. Figure 8a presents the effect of fractal dimension d on plots of production rate and cumulative production versus time. A larger d represents a more complex structure of the fractal natural fractures. It is observed that the fractal dimension d has a significant impact on the solutions throughout the entire production period. A larger d value leads to a high production rate and a high cumulative production. In addition, as time increases, the rate first declines rapidly and then declines gradually.

Figure 8b presents the effect of the connectivity index of natural fractures in the SRV region θ on plots of production rate and cumulative production versus time. The θ values were set to 0, 0.01, and 0.2. The connectivity index reflects connectivity and tortuosity between natural fractures. It is apparent from Fig. 8b that the connectivity index of natural fractures in the SRV region has a significant impact on the solutions throughout the entire production period. As shown in Fig. 8b, a larger θ value leads to a low production rate and low cumulative production. This point implies that a larger θ reflects more complicated tortuosity, which will lead to worse connectivity in the formation.

Sorption

Figure 8c presents the effect of the Langmuir volume on production behavior. The Langmuir volume VL values are set to 100 scf/ton, 200 scf/ton, and 300 scf/ton. It is apparent from the figure that a larger VL value will result in a high production rate and cumulative production. However, the increase in cumulative production is not obvious. The cumulative productions associated with VL = 100 scf/ton, 200 scf/ton, and 300 scf/ton are Gp = 622.35 MMscf, 653.76 MMscf, and 682.26 MMscf, respectively. The fact that shale gas adsorption volume is directly proportional to the Langmuir volume will cause the shale gas adsorption volume to decrease as the Langmuir volume increases.

Figure 8d presents the effect of the Langmuir pressure pL on plots of production rate and cumulative production versus time. The pL values are set to 100 psi, 500 psi, and1200 psi. Simulation results show that production rate and cumulative production will increase as the Langmuir pressure increases. The fact that shale gas adsorption volume is inversely proportional to the Langmuir pressure will cause an increasing shale gas adsorption volume as the Langmuir pressure increases.

Fracture parameters

Figure 8e shows the effect of fracture half-length on production behavior. The fracture half-length xf was set to 141 ft, 171 ft, and 201 ft. It is apparent that a large xf will lead to a high production rate and cumulative production. A larger xf value has an important impact on enhancing production rate and cumulative production. The cumulative production of xf = 141 ft, 171 ft, and 201 ft are Gp = 570.35 MMscf, 653.76 MMscf, and 734.77 MMscf.

Fracture conductivity also has an important impact on enhancing production rate and cumulative production. Figure 8f presents the effect of fracture conductivity on production behavior. The fracture conductivity CfD values were set to 0.1, 1, and 10. It is apparent that a large CfD value will lead to a high production rate and cumulative production. The cumulative production of CfD = 0.1, 1, and 10 are Gp = 88.48 MMscf, 272.70 MMscf, and 583.31 MMscf, respectively. In the early stage, effectively increasing fracture conductivity effectively can remarkably improve the production rate and cumulative production.

Matrix transfer and storage coefficients

Figure 8g presents the effect of the inter-porosity flow coefficient of the inner region on production behavior. The fracture inter-porosity flow coefficient λI values are set to 0.1, 1, and 10. It is apparent from the figure that a large λI value will lead to a high production rate and cumulative production. Figure 8h presents the effect of the storage coefficient of the inner region on production behavior. The fracture storage coefficient ωI values are set to 0.4, 0.7, and 1. It is apparent from the figure that a large ωI value will lead to a high production rate and cumulative production.

History Matching of Production Data

Automatic history matching

Automatic parameter estimation (APE) is a mathematical process, known as multi-variable optimization, which automatically adjusts a specified set of function parameters to minimize error between the function and measured data. Minimizing the mathematical function is called the objective function. With analytical modelling, the objective function is calculated as follows.

If the Calculate Pressure mode is used:

$${E}_{{\rm{avg}}}=\frac{{\sum }_{i}(\frac{|{{\boldsymbol{(}}{p}_{calc}{\boldsymbol{)}}}_{i}-{{\boldsymbol{(}}{p}_{hist}{\boldsymbol{)}}}_{i}|}{{{\boldsymbol{(}}{p}_{hist}{\boldsymbol{)}}}_{i}})}{{n}_{hist}}$$
(34)

If the Calculate Rate mode is used:

$${E}_{{\rm{avg}}}=\frac{{\sum }_{i}(\frac{|{{\boldsymbol{(}}{{\rm{q}}}_{calc}{\boldsymbol{)}}}_{i}-{{\boldsymbol{(}}{{\rm{q}}}_{hist}{\boldsymbol{)}}}_{i}|}{{{\boldsymbol{(}}{{\rm{q}}}_{hist}{\boldsymbol{)}}}_{i}})}{{n}_{hist}}$$
(35)

where pcalc is calculated pressure for the i-th point; phist is historical pressure for the i-th point; qcalc is calculated rate for the i-th point; qhist is historical rate for the i-th point; nhist is historical point number; and Eavg reflects the difference between the calculated and historical data. Therefore, a smaller Eavg indicates a better history match.

The Simplex routine34 is a non-linear regression algorithm used for APE for reservoir and well parameters (kIf, kof, xf, CfD, SC, etc.) when modelling pressure and rate transient data. It requires only function evaluations of the objective function, and not the derivatives. Modification of the downhill Simplex method to achieve greater convergence is accomplished by imposing constraints on the parameters during the search. Estimates of the parameters are always checked against preset maximum and minimum values for each parameter. Once the routine has converged on some parameters, it is restarted with a slight perturbation away from the final values and is allowed to converge again. This ensures that the parameter estimates found are not the result of some local minimum in the residual, but rather a more global minimum.

Field examples

Case 1: Marcellus shale, U.S.A

Using our model, history matching of production data was performed based on field data. The well is a multi-stage fractured horizontal well with 12 fractures in a typical shale gas reservoir in the Marcellus shale gas field, U.S.A. The pressure data and rate data were acquired from production tests after almost one-year of production. Figure 9a shows the pressure data and rate data from Nov. 24th 2009 to Aug 6th, 2010. The basic input parameters are summarized in Table 4. We selected the fracture permeability of the inner region, the fracture permeability of the outer region, choking skin, fracture half-length, fracture conductivity, fractal dimension, inter-porosity flow coefficient of inner region, and storage coefficient of inner region as uncertain parameters of history matching, which are listed in Table 4 and marked in bold.

Figure 9
figure 9

Field example from Marcellus shale gas wells in the U.S.A.: (a) real rate and pressure data; (b) history matching of production data; (c) forecast production performance.

Full size image
Table 4 Basic data for Marcellus shale gas wells.
Full size table

Figure 9b presents the historical matching results of production data from Marcellus shale gas wells using our proposed model. Our model fits the pressure and production rate very well. The presented model can also be applied to production performance analysis in complex conditions. Table 4 gives the initial estimation of uncertain parameters in shale gas, and the final matching results are shown in Fig. 9b. The kIf value is 0.00588 mD, the kOf value is 0.000463 mD, the SC value is 0.089, the xf value is 279.086 ft, the CfD value is 15.1856, the d value is 1.96849, the λI value is 1.85974, and the ωI is 0.128578. The relative error of our model for all of the data is Eavg = 13.58%.

With the reservoir and fracture parameters determined by history matching, the production performance of the well can be predicted. In this case, the BHP was set to 631 psi from the final production data point. Figure 9c presents the predicted gas production and cumulative production. The cumulative production of the shale gas multi-fractured well with fractal geometry is estimated to be 1381.87 MMscf and the rate of well will become 0.01219 MMscf/d after 20 years. In the first five years, the rate of the well decreases rapidly, and cumulative production of the well increases dramatically. However, in the next 15 years, the rate of the well gradually decreased, and the cumulative production of the well increased slowly. From the fifth year to the twentieth year, the rate of well decreases only from 0.081876 MMscf/d to 0.01219 MMscf/d and cumulative production of well increases only from 1241.7 MMscf to 1381.87 MMscf, which does not constitute a remarkable improvement. In other words, it is not economically feasible to continue developing this shale gas well for up to 20 years.

Case 2: Fuling shale, China

The second well is also a multi-stage fractured horizontal well with 21 fractures in a typical shale gas reservoir in the Fuling high pressure shale gas field, China. The pressure and production rate data were acquired from production test performed over 474 d. Figure 10a presents the pressure and production rate profile from Jan. 7th 2016 to Apr. 24th, 2017. The basic input parameters are summarized in Table 5. The uncertain parameters of history matching are shown in Table 5 and are marked in bold.

Figure 10
figure 10

Field example from Fuling shale gas wells in China: (a) real rate and pressure data; (b) history matching of production data; (c) forecast production performance.

Full size image
Table 5 Basic data for Fuling shale gas wells.
Full size table

As shown in Fig. 10b, our model matched the BHP pressure and production rate very well from the Fuling shale gas field. Table 5 provides an initial estimation of uncertain parameters in the Fuling shale gas field, and the final matching results are shown in Fig. 10b. The kIf value is 0.00273 mD, the kOf value is 2.77e-5 mD, the SC value is 0.107, the xf value is 127.232 ft, the CfD value is 12.6512, the d value is 2.01746, the λI value is 0.28484, and the ωI is 0.0287237. The relative error of our model for all of the data is Eavg = 4.16%.

According to the results, the production performance from Fuling shale gas wells can be predicted. In this case, if the BHP is set at 6948.28 psi, Fig. 10c shows the predicted gas production and cumulative production. The cumulative production of the shale gas multi-fractured well with fractal geometry is estimated to be 1001.43 MMscf after 20 years. In the first four years, the rate of the well decreases rapidly. However, in the next 16 years, the rate of well becomes approximately stable.

Conclusions

In this study, a multi-scale flow model in shale gas reservoirs with fractal geometry was presented to investigate pressure transient response and analyze production performance, through which we examined the effects of shale rock properties and fractal characteristics. From the above analysis, the following conclusions are made:

  1. (1)

    The flow characteristics of type curves can be divided into six regimes: bi-linear flow regime, linear flow regime, transition flow regime, inter-porosity flow regime from the matrix to fractures in the inner region, inter-porosity flow regime from matrix to fractures in the outer region, and boundary dominant flow regime, respectively.

  2. (2)

    A large fractal dimension represents a complex structure of fractal natural fractures and leads to a small pressure depletion. A large connectivity index, which reflects connectivity and tortuosity among natural fractures, results in a large pressure depletion.

  3. (3)

    A large inter-porosity flow coefficient of the outer region and inner region corresponding to strong matrix flow ability will lead to a small pressure depletion because the matrix compensates for pressure loss by supplying natural fractures. A large storage coefficient results in a small pressure depletion due to rich gas resources that are stored by natural fractures.

  4. (4)

    A small fracture conductivity and a large region conductivity leads to a large pressure depletion.

  5. (5)

    A large fractal dimension, small connectivity index, large Langmuir volume, large Langmuir pressure, large fracture conductivity, large inter-porosity flow coefficient, and large storage coefficient can enhance the production rate and cumulative production of shale gas wells.

  6. (6)

    Based on a downhill Simplex algorithm, multiple uncertain parameters can be interpreted well by using the presented multi-rate solutions and multi-pressure solutions. The presented fractal model is well validated by matching real field examples.