MHD convective heat transfer in a discretely heated square cavity with conductive inner block using two-phase nanofluid model

Abstract

The problem of steady, laminar natural convection in a discretely heated and cooled square cavity filled by an alumina/water nanofluid with a centered heat-conducting solid block under the effects of inclined uniform magnetic field, Brownian diffusion and thermophoresis is studied numerically by using the finite difference method. Isothermal heaters and coolers are placed along the vertical walls and the bottom horizontal wall, while the upper horizontal wall is kept adiabatic. Water-based nanofluids with alumina nanoparticles are chosen for investigation. The governing parameters of this study are the Rayleigh number (10³ ≤ Ra ≤ 10⁶), the Hartmann number (0 ≤ Ha ≤ 50), thermal conductivity ratio (0.28 ≤ k _w  ≤ 16), centered solid block size (0.1 ≤ D ≤ 0.7) and the nanoparticles volume fraction (0 ≤ ϕ ≤ 0.04). The developed computational code is validated comprehensively using the grid independency test and numerical and experimental data of other authors. The obtained results reveal that the effects of the thermal conductivity ratio, centered solid block size and the nanoparticles volume fraction are non-linear for the heat transfer rate. Therefore, it is possible to find optimal parameters for the heat transfer enhancement in dependence on the considered system. Moreover, high values of the Rayleigh number and nanoparticles volume fraction characterize homogeneous distributions of nanoparticles inside the cavity. High concentration of nanoparticles can be found near the centered solid block where thermal plumes from the local heaters interact.

Introduction

Natural convection heat transfer in cavities is a significant phenomenon in engineering systems and important applications in operations of solar collectors, cooling of containment buildings, room ventilation, heat exchangers, storage tanks, double pane windows, etc. A comprehensive review on natural convection in cavities was made by Ostrach¹. Also, the problem of natural convection in cavities with discrete heat sources has important applications in electronic packaging, cooling of nuclear reactors, ignition of solid fuels^2,3. Kaluri and Basak⁴ and Kaluri and Basak³ considered the problem of natural convection in a discretely heated square porous cavity filled with pure fluid. They used the finite element method for solving the governing equations together with the boundary conditions and the found that the methodology of the distributed heating with multiple heat sources can be considered as an effective strategy for the optimal thermal processing of materials. The thermal conductivity of nanoparticles is higher than that of traditional fluids. Thus, nanofluids can be used in a large industrial applications such as oil industry, nuclear reactor coolants, solar cells, construction, electronics, renewable energy and many others. Also, nanoparticles are used because they stay in suspension longer than larger particles. Thus, nanofluids can be used in a large industrial applications such as oil industry, nuclear reactor coolants, solar cells, construction, electronics, renewable energy and many others. A nanofluid as a working medium has been considered by many researchers for the simple reason that it has the presence of nanoparticles resulting in higher thermal conductivity of medium and the heat transfer becoming enhanced.

Khanafer et al.⁵ reported a problem of natural convective heat transfer in cavities partially occupied by nanofluids. Two approaches based on conservation equations have been adopted in the literature to investigate the numerical simulation heat transfer of nanofluids: single-phase model (homogenous) and two phase model⁶. The single-phase approach considers the fluid phase and the nanoparticles as being in thermal equilibrium where the slip velocity between the base fluid and the nanoparticles is negligible. On the other hand, the two-phase approach assumes that the relative velocity between the fluid phase and the nanoparticles may not be zero where the continuity, momentum and energy equations of the nanoparticles and the base fluid are handled using different methods. There are number of numerical studies used the single-phase model for simulation of the nanofluids. Hu et al.⁷ studied experimentally and numerically the natural convection heat transfer in a square cavity filled with TiO₂–water nanofluids. They found that the average Nusselt number increased with the addition of nanoparticles. Sheikholeslami et al.⁸ conducted an experimental investigation on the enhancement of the heat transfer and pressure drop through a concentration of refrigerant-based nanofluid. Sheremet et al.⁹ and Alsabery et al.¹⁰ numerically investigated the natural convection heat transfer of nanofluid flow in different geometries. Recently, Alsabery et al.¹¹ numerically considered the problem of natural convection heat transfer in an inclined square cavity using the nanofluid single phase model. They found that the heat transfer rate was enhanced with the increment of the nanoparticles volume fraction. Most of the above studies are used the Maxwell-Garnett and Brinkman models to estimate the effective thermal conductivity and viscosity of the nanofluid. Sheikholeslami and Seyednezhad¹² studied the influence of electric field on nanofluid flow and natural convection in a porous media using CVFEM. However, the study of Corcione¹³ questions the validity of these models and tended to proposed a new models for estimating the effective thermal conductivity and viscosity of the nanofluid which appeared to be close to the experimental data. The results showed that the heat transfer rate enhanced with the relative concentration of nanofluid. The experimental study of Wen and Ding¹⁴ found that the slip velocity between the base fluid and particles may not be zero. Thus, the two-phase nanofluid model observed to be more accurate. Buongiorno¹⁵ proposed a non-homogeneous equilibrium model with the consideration of the effect of the Brownian diffusion and thermophoresis as two important primary slip mechanisms in nanofluid. Hamid et al.¹⁶ used the Buongiorno model to study Non-alignment stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet. Sheikholeslami et al.¹⁷ used the two-phase model of the nanofluid to investigate the thermal management for natural convection heat transfer in a 2D cavity. Garoosi et al.¹⁸ studied mixed convection heat transfer where the two-phase mixture model used to simulate the nanofluid in a two-sided lid-driven cavity with several pairs of heaters and coolers (HACs). Garoosi et al.¹⁹ used Corcione et al. model¹³ for the effective thermal conductivity and viscosity of the nanofluid to study numerically the problem of natural convection heat transfer in a heat exchanger filled with nanofluids. Very recently, Motlagh and Soltanipour²⁰ investigated numerically the problem of natural convection of nanofluids in a square cavity using the two phase model. The results of these studies indicated that the heat transfer rate enhanced with the increasing of the concentration of the nanoparticles up to 0.04.

Recently the effect of the magnetic field on convective heat transfer in cavities were considered extensively due to its wide applications such as in the polymer industry, coolers of nuclear reactors, MEMs, purification of molten metals and many other important applications which can be used to control the convection inside cavities^21,22 Pirmohammadi and Ghassemi²³ investigated numerically the effect of the magnetic field on a steady laminar natural convection flow in an inclined square cavity. Mahmoudi et al.²⁴ analysed numerically the magnetic field effect on natural convection in a two-dimensional cavity filled with nanofluid. They found that the presence of magnetic field tended to decrease the convection heat transfer. Ghasemi et al.²⁵ considered the influence of the magnetic field on natural convection in a square cavity filled with Al₂O₃-water nanofluid. They concluded that the enhancement or deterioration of the convection heat transfer by the increasing of the solid volume fraction was clearly depending on the values of Hartmann and Rayleigh numbers. Using lattice Boltzmann method, Kefayati²⁶ studied the effect of a magnetic field on natural convection in an open square cavity filled with water/alumina nanofluid where his results showed that the heat transfer decreased with the increment of Hartmann number and for various values of Rayleigh numbers and volume fractions. Sheikholeslami et al.²⁷ used the KKL model of the nanofluid to investigate the MHD effects on natural convection heat transfer in a 2D cavity filled with Al₂O₃-water nanofluid using the lattice Boltzmann method. Sheikholeslami et al.²⁸ used the same method to investigated the magnetic field effect on CuO-water nanofluid flow and heat transfer in a cavity. They considered in their study the effect of the Brownian motion on the effective thermal conductivity and they found that the enhancement in heat transfer increased as Hartmann number increase while it decreased with the increasing of Rayleigh number. Selimefendigil and Öztop²⁹ used the finite element method to study the magnetic field and internal heat generation effects on natural convection in a square cavity filled with nanofluid and having different shaped obstacles. They found that the heat transfer rate was deteriorated with the presence of the solid obstacles. Recently, Sheikholeslami and Shehzad³⁰ numerically reported the effect of external magnetic source on natural convection in a permeable media filled with Fe₃O₄-H₂O nanofluid. Using the CVFEM simulation on the problem of nanofluid migration and convective heat transfer in a 2D porous cavity with an external magnetic filed was considered by Sheikholeslami and Shehzad³¹.

Sheikholeslami and Shehzad³¹ Sivaraj and Sheremet³² considered the influence of the applied magnetic field on natural convection in an inclined square porous cavity with a heat conducting solid block. Their results indicated that the inclusion of the magnetic field decreased the heat transfer rate within the square cavity. Sheikholeslami and Rokni³³ and Sheikholeslami³⁴ investigated the Brownian motion effects on the magnetic nanofluid flow and heat transfer in a 2D porous cavity using the CVFEM modeling. They concluded that the convective flow was a reducing function of the rising of Hartmann number.

Conjugate heat transfer (CHT) for a regular fluid has very important practical engineering applications in frosting practicalities and refrigeration of the hot obtrusion in a geological framing. For example, modernistic construction of thermal insulators which are formed of two diverse thermal conductivities (solid and fibrous) materials can be modeled by the partition length and conductivity model. Kim and Viskanta³⁵ reported a conjugate convection in a differentially-heated vertical rectangular cavity filled with viscous (pure) fluids surrounded by four conducting walls. House et al.³⁶ studied the natural convective heat transfer in a square cavity with a centred heat-conducting body and they found that the heat transfer reduced with an increasing of the length of the solid body. Ha et al.³⁷ considered the effect of a centred heat-conducting body on unsteady natural convection heat transfer in a vertical cavities. Zhao et al.³⁸ studied the effect of a centred heat-conducting body on the conjugate natural convection heat transfer in a square enclosure. The results show that the thermal conductivity ratio has strong influence on the flow within the square cavity. Mahmoodi and Sebdani³⁹ used the finite volume method to investigate the conjugate natural convective heat transfer in a square cavity filled with nanofluid and containing a solid square block at the center. They concluded that the heat transfer rate decreased with an increasing of the size of the inner block for low Rayleigh numbers and increased at high Rayleigh numbers. Mahapatra et al.⁴⁰ numerically used the finite volume method to investigate the CHT and entropy generation in a square cavity in the presence of adiabatic and isothermal blocks. They found that the heat transfer enhanced with the low Rayleigh numbers and for a critical block sizes. Alsabery et al.⁴¹ used the finite deference method to study the unsteady natural convective heat transfer in nanofluid-saturated porous square cavity with a concentric solid insert and sinusoidal boundary condition. Very recently, Garoosi and Rashidi⁴² used the finite volume method to investigate the two phase model of conjugate natural convection of the nanofluid in a partitioned heat exchanger containing several conducting obstacles. They found that the heat transfer rate was significantly influenced by changing the orientation of the conductive partition from vertical to horizontal mode.

The effect of the magnetic field on natural convection in a discretely heated square cavity with a conductive inner block has not been investigated yet. Therefore, the aim of this comprehensive numerical study is to investigate the MHD natural convection of Al₂O₃-water nanofluid in a discretely heated square cavity with conductive inner block using Buongiorno’s two-phase model. The authors of the present study believe that this work is a good contribution for improving the thermal performance and the heat transfer enhancement in some engineering instruments.

Mathematical Formulation

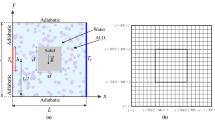
The steady two-dimensional natural convection problem in a square cavity with length L and with the cavity center inserted by a solid square with side d, as illustrated in Fig. 1. The Rayleigh number range chosen in the study keeps the nanofluid flow incompressible and laminar. Isothermal heat sources are shown by a thick red lines and the remaining parts are maintained at cold isothermal which represented by a thick blue lines. While the top horizontal wall is kept adiabatic. The boundaries of the annulus are assumed to be impermeable, the fluid within the cavity is a water-based nanofluid having Al₂O₃ nanoparticles. The Boussinesq approximation is applicable, the nanofluid physical properties are constant except for the density. By considering these assumptions, the continuity, momentum and energy equations for the laminar and steady state natural convection can be written as follows:

$$\nabla \cdot {\bf{v}}=0,$$

(1)

$${\rho }_{nf}{\bf{v}}\cdot \nabla {\bf{v}}=-\,\nabla p+\nabla \cdot {\mu }_{nf}\nabla {\bf{v}}+{(\rho \beta )}_{nf}(T-{T}_{c})\overrightarrow{g}+{\sigma }_{nf}{\bf{v}}\times \overrightarrow{{\bf{B}}},$$

(2)

$${(\rho {C}_{p})}_{nf}{\bf{v}}\cdot \nabla {T}_{nf}=-\,\nabla \cdot {k}_{nf}\nabla {T}_{nf}-{C}_{p,p}{J}_{p}\cdot \nabla {T}_{nf},$$

(3)

$${\bf{v}}\cdot \nabla \phi =-\,\frac{1}{{\rho }_{p}}\nabla \cdot {J}_{p},$$

(4)

Figure 1

(a) Physical model of convection in a square cavity, and (b) grid-points distribution in the adiabatic inner block (NY/2 − ND + 1 ≤ j ≤ NY/2 + ND + 1, NX/2 − ND + 1 ≤ i ≤ NX/2 + ND + 1).

The energy equation of the inner solid wall is

$${\nabla }^{2}{T}_{w}=\mathrm{0,}$$

(5)

where v is the velocity vector, $\overrightarrow{g}$ is the gravitational acceleration vector, $\overrightarrow{{\bf{B}}}$ represents the applied magnetic field, φ is the local volume fraction of nanoparticles and J _p is the nanoparticles mass flux. The subscripts f, nf, p and w represent the base fluid, nanofluid, solid nanoparticles and solid inner wall, respectively. Based on Buongiorno’s model nanoparticles mass flux can be written as:

$${J}_{p}={J}_{p,B}+{J}_{p,T},$$

(6)

$${J}_{p,B}=-\,{\rho }_{p}{D}_{B}\nabla \phi ,\,{D}_{B}=\frac{{k}_{b}T}{3\pi {\mu }_{f}{d}_{p}},$$

(7)

$${J}_{p,T}=-\,{\rho }_{p}{D}_{T}\nabla T,\,{D}_{T}=0.26\frac{{k}_{f}}{2{k}_{f}+{k}_{p}}\frac{{\mu }_{f}}{{\rho }_{f}T}\phi $$

(8)

where D _B and D _T are the brownian diffusion coefficient and the thermophoretic diffusivity coefficient. The thermo-physical properties of the nanofluid can be determined as follows:

The heat capacitance of the nanofluids (ρC _p ) _nf given is

$${(\rho {C}_{p})}_{nf}=(1-\phi ){(\rho {C}_{p})}_{f}+\phi {(\rho {C}_{p})}_{p}.$$

(9)

The effective thermal diffusivity of the nanofluids α _nf is given as

$${\alpha }_{nf}=\frac{{k}_{nf}}{{(\rho {C}_{p})}_{nf}}.$$

(10)

The effective density of the nanofluids ρ _nf is given as

$${\rho }_{nf}=(1-\phi ){\rho }_{f}+\phi {\rho }_{p}.$$

(11)

The thermal expansion coefficient of the nanofluids β _nf can be determined by:

$${(\rho \beta )}_{nf}=(1-\phi ){(\rho \beta )}_{f}+\phi {(\rho \beta )}_{p}.$$

(12)

The dynamic viscosity ratio of water-Al₂O₃ nanofluids for 33 nm particle-size in the ambient condition was derived in ref.¹³ as follows:

$$\frac{{\mu }_{nf}}{{\mu }_{f}}=\mathrm{1/}(1-34.87{({d}_{p}/{d}_{f})}^{-0.3}{\phi }^{1.03})\mathrm{.}$$

(13)

The thermal conductivity ratio of water-Al₂O₃ nanofluids is calculated by the Corcione model¹³ is:

$$\frac{{k}_{nf}}{{k}_{f}}=1+4.4{{\rm{Re}}}_{B}^{0.4}{{\rm{\Pr }}}^{0.66}{(\frac{T}{{T}_{fr}})}^{10}{(\frac{{k}_{p}}{{k}_{f}})}^{0.03}{\phi }^{0.66}\mathrm{.}$$

(14)

where Re _B is the brownian motion Reynolds number which is defined as:

$${{\rm{Re}}}_{B}=\frac{{\rho }_{f}{u}_{B}{d}_{p}}{{\mu }_{f}}\mathrm{.}$$

(15)

and u _B is the brownian velocity of the nanoparticle which is calculated as:

$${u}_{B}=\frac{2{k}_{b}T}{\pi {\mu }_{f}{d}_{p}^{2}}.$$

(16)

where k _b  = 1.380648 × 10⁻²³ (J/K) is the Boltzmann constant. l _f  = 0.17 nm is the mean path of fluid particles. d _f is the molecular diameter of water given as¹³

$${d}_{f}=\frac{6M}{N\pi {\rho }_{f}}.$$

(17)

where M is the molecular weight of the base fluid, N is the Avogadro number and ρ _f is the density of the base fluid at standard temperature (310 K). Accordingly, and basing on water as a base fluid, the value of d _f is obtained:

$${d}_{f}={(\frac{6\times 0.01801528}{6.022\times {10}^{23}\times \pi \times 998.26})}^{\mathrm{1/3}}=3.85\times {10}^{-10}\,{\rm{m}}\mathrm{.}$$

(18)

The electrical conductivity ratio $\frac{{\sigma }_{nf}}{{\sigma }_{f}}$ is defined by⁴³

$$\frac{{\sigma }_{nf}}{{\sigma }_{f}}=1+\frac{3(\frac{{\sigma }_{p}}{{\sigma }_{f}}-1)\phi }{(\frac{{\sigma }_{p}}{{\sigma }_{f}}+2)-(\frac{{\sigma }_{p}}{{\sigma }_{f}}-1)\phi }.$$

(19)

Now we introduce the following non-dimensional variables:

$$\begin{array}{rcl}X & = & \frac{x}{L},\,Y=\frac{y}{L},\,{\bf{V}}=\frac{{\bf{v}}L}{{\nu }_{f}},\,P=\frac{p{L}^{2}}{{\rho }_{nf}{\nu }_{f}^{2}},\,{\phi }^{\ast }=\frac{\phi }{\varphi },\,{D}_{B}^{\ast }=\frac{{D}_{B}}{{D}_{B0}},\,{D}_{T}^{\ast }=\frac{{D}_{T}}{{D}_{T0}},\\ \delta & = & \frac{{T}_{c}}{{T}_{h}-{T}_{c}},\,{\theta }_{nf}=\frac{{T}_{nf}-{T}_{c}}{{T}_{h}-{T}_{c}},\,{\theta }_{w}=\frac{{T}_{w}-{T}_{c}}{{T}_{h}-{T}_{c}},\,D=\frac{d}{L}\mathrm{.}\end{array}$$

(20)

Using the above variables yields the following dimensionless governing equations:

$$\nabla \cdot {\bf{V}}=\mathrm{0,}$$

(21)

$${\bf{V}}\cdot \nabla {\bf{V}}=-\,\nabla P+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\mu }_{nf}}{{\mu }_{f}}{\nabla }^{2}{\bf{V}}+\frac{{(\rho \beta )}_{nf}}{{\rho }_{nf}{\beta }_{f}}\frac{1}{{\rm{\Pr }}}Ra\cdot {\theta }_{nf}+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}{\bf{V}}\times {{\bf{B}}}^{\ast },$$

(22)

$$\begin{array}{rcl}{\bf{V}}\cdot \nabla {\theta }_{nf} & = & \frac{{(\rho {C}_{p})}_{f}}{{(\rho {C}_{p})}_{nf}}\frac{{k}_{nf}}{{k}_{f}}\frac{1}{{\rm{\Pr }}}{\nabla }^{2}{\theta }_{nf}+\frac{{(\rho {C}_{p})}_{f}}{{(\rho {C}_{p})}_{nf}}\frac{{D}_{B}^{\ast }}{{\rm{\Pr }}\cdot Le}\nabla {\phi }^{\ast }\cdot \nabla {\theta }_{nf}\\ & & +\,\frac{{(\rho {C}_{p})}_{f}}{{(\rho {C}_{p})}_{nf}}\frac{{D}_{T}^{\ast }}{Pr\cdot Le\cdot {N}_{BT}}\frac{\nabla {\theta }_{nf}\cdot \nabla {\theta }_{nf}}{1+\delta {\theta }_{nf}},\end{array}$$

(23)

$${\bf{V}}\cdot \nabla {\phi }^{\ast }=\frac{{D}_{B}^{\ast }}{Sc}{\nabla }^{2}{\phi }^{\ast }+\frac{{D}_{T}^{\ast }}{Sc\cdot {N}_{BT}}\cdot \frac{{\nabla }^{2}{\theta }_{nf}}{1+\delta {\theta }_{nf}},$$

(24)

$${\nabla }^{2}{\theta }_{w}=0,$$

(25)

where V is the dimensionless velocity vector (U, V), B* is the dimensionless magnetic vector (Ha² sin γ, Ha² cos γ), ${D}_{B0}=\frac{{k}_{b}{T}_{c}}{3\pi {\mu }_{f}{d}_{p}}$ is the reference Brownian diffusion coefficient, ${D}_{T0}=0.26\frac{{k}_{f}}{2{k}_{f}+{k}_{p}}\frac{{\mu }_{f}}{{\rho }_{f}\theta }\varphi$ is the reference thermophoretic diffusion coefficient, Sc = ν _f /D_B0 is Schmidt number, N _BT  = ϕD_B0T _c /D_T0(T _h  − T _c ) is the diffusivity ratio parameter (Brownian diffusivity/thermophoretic diffusivity), Le = k _f /(ρC _p ) _f ϕD_B0 is Lewis number, Ra = gρ _f β _f (T _h  − T _c )L³/(μ _f α _f ) is the Rayleigh number, $Ha={\bf{B}}L\sqrt{\frac{{\sigma }_{f}}{{\mu }_{f}}}$ is the Hartman number and Pr = ν _f /α _f is the Prandtl number. The dimensionless boundary conditions of Eqs (25) and (36) are:

$$\begin{array}{rcl}U=V & = & 0,\frac{\partial {\phi }^{\ast }}{\partial n}=-\,\frac{{D}_{T}^{\ast }}{{D}_{B}^{\ast }}\cdot \frac{1}{{N}_{BT}}\cdot \frac{1}{1+\delta {\theta }_{nf}}\frac{\partial {\theta }_{nf}}{\partial n},\,{\theta }_{nf}=1\,{\rm{on}}\,\\ & & 0.25\le X\le 0.75,Y=0,\end{array}$$

(26)

$$\begin{array}{rcl}U=V & = & 0,\frac{\partial {\phi }^{\ast }}{\partial n}=-\frac{{D}_{T}^{\ast }}{{D}_{B}^{\ast }}\cdot \frac{1}{{N}_{BT}}\cdot \frac{1}{1+\delta {\theta }_{nf}}\frac{\partial {\theta }_{nf}}{\partial n},\,{\theta }_{nf}=0\,{\rm{on}}\,\\ & & 0\le X\le 0.25\,{\rm{and}}\,0.75\le X\le 1,\,Y=0.\end{array}$$

(27)

$$\begin{array}{rcl}U=V & = & 0,\frac{\partial {\phi }^{\ast }}{\partial n}=-\,\frac{{D}_{T}^{\ast }}{{D}_{B}^{\ast }}\cdot \frac{1}{{N}_{BT}}\cdot \frac{1}{1+\delta {\theta }_{nf}}\frac{\partial {\theta }_{nf}}{\partial n},\,{\theta }_{nf}=1\,{\rm{on}}\,\\ & & 0.375\le Y\le 0.625,\,X=0,X=1,\end{array}$$

(28)

$$\begin{array}{rcl}U=V & = & 0,\frac{\partial {\phi }^{\ast }}{\partial n}=-\,\frac{{D}_{T}^{\ast }}{{D}_{B}^{\ast }}\cdot \frac{1}{{N}_{BT}}\cdot \frac{1}{1+\delta {\theta }_{nf}}\frac{\partial {\theta }_{nf}}{\partial n},{\theta }_{nf}=0\,{\rm{on}}\,\\ & & 0\le Y\le 0.375\,{\rm{and}}\,0.625\le Y\le 1,X=0,X=1.\end{array}$$

(29)

$$U=V=0,\,\frac{\partial {\phi }^{\ast }}{\partial n}=0,\,\frac{\partial {\theta }_{nf}}{\partial n}=0\,{\rm{on}}\,0\le X\le 1Y=1.$$

(30)

$${\theta }_{nf}={\theta }_{w},\,{\rm{at}}\,{\rm{the}}\,{\rm{outer}}\,{\rm{solid}}\,{\rm{square}}\,{\rm{surface}},$$

(31)

$$U=V=0,\frac{\partial {\phi }^{\ast }}{\partial n}=-\,\frac{{D}_{T}^{\ast }}{{D}_{B}^{\ast }}\cdot \frac{1}{{N}_{BT}}\cdot \frac{1}{1+\delta {\theta }_{nf}}\frac{\partial {\theta }_{nf}}{\partial n},\frac{\partial {\theta }_{nf}}{\partial n}={K}_{r}\frac{\partial {\theta }_{w}}{\partial n},X,Y\,{\rm{in}}\,[\frac{(1-D)}{2},\frac{(1+D)}{2}].$$

(32)

where K _r  = k _w /k _nf is the thermal conductivity ratio and D = d/L is the aspect ratio of inner square cylinder width to the outer square cylinder width.

The local Nusselt number evaluated at the left and bottom walls, which is defined by

$$N{u}_{l}=-\,\frac{{k}_{nf}}{{k}_{f}}{(\frac{\partial {\theta }_{nf}}{\partial X})}_{X=0},\,N{u}_{b}=-\frac{{k}_{nf}}{{k}_{f}}{(\frac{\partial {\theta }_{nf}}{\partial Y})}_{Y=0},$$

(33)

Finally, the average Nusselt numbers evaluated at the heated parts of the left, right and bottom walls of the square cavity which are given respectively by:

$${\overline{Nu}}_{l}={\int }_{0.375}^{0.625}N{u}_{l}{\rm{d}}Y,\,{\overline{Nu}}_{r}={\int }_{0.375}^{0.625}N{u}_{r}{\rm{d}}Y,\,{\overline{Nu}}_{b}={\int }_{0.25}^{0.75}N{u}_{b}{\rm{d}}X,$$

(34)

and

$${\overline{Nu}}_{nf}={\overline{Nu}}_{l}+{\overline{Nu}}_{r}+{\overline{Nu}}_{b}.$$

(35)

where $N{u}_{r}=-\,\frac{{k}_{nf}}{{k}_{f}}{(\frac{\partial {\theta }_{nf}}{\partial X})}_{X=1},$

Numerical Method and Validation

An iterative finite difference method (FDM) is employed to solve the governing Equations (25–36) subject to the boundary conditions (26–32).

Continuity equation and momentum equation:

$$\nabla \cdot {\bf{V}}=0,$$

(36)

$${\bf{V}}\cdot \nabla V=-\,\nabla P+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\mu }_{nf}}{{\mu }_{f}}{\nabla }^{2}{\bf{V}}+\frac{{(\rho \beta )}_{nf}}{{\rho }_{nf}{\beta }_{f}}\frac{1}{{\rm{\Pr }}}Ra{\theta }_{nf}+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}{\bf{V}}\times {{\bf{B}}}^{\ast },$$

(37)

Expanding the equations then yields

Continuity equation:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

(38)

Momentum equation in the X-direction:

$$\begin{array}{rcl}(\frac{{\rho }_{nf}}{{\rho }_{f}})U\frac{\partial U}{\partial X}+(\frac{{\rho }_{nf}}{{\rho }_{f}})V\frac{\partial U}{\partial Y} & = & -(\frac{{\rho }_{nf}}{{\rho }_{f}})\frac{\partial P}{\partial X}+(\frac{{\mu }_{nf}}{{\mu }_{f}})(\frac{{\partial }^{2}U}{\partial {X}^{2}}+\frac{{\partial }^{2}U}{\partial {Y}^{2}})\\ & & +\,\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(V\,\sin \,\gamma \,\cos \,\gamma -U\,{\sin }^{2}\gamma )\end{array}$$

(39)

Momentum equation in the Y-direction:

$$\begin{array}{rcl}(\frac{{\rho }_{nf}}{{\rho }_{f}})U\frac{\partial V}{\partial X}+(\frac{{\rho }_{nf}}{{\rho }_{f}})V\frac{\partial V}{\partial Y} & = & -(\frac{{\rho }_{nf}}{{\rho }_{f}})\frac{\partial P}{\partial Y}+(\frac{{\mu }_{nf}}{{\mu }_{f}})(\frac{{\partial }^{2}V}{\partial {X}^{2}}+\frac{{\partial }^{2}V}{\partial {Y}^{2}})\\ & & +\,[(\frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}})\frac{1}{Pr}Ra\theta ]+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(U\,\sin \,\gamma \,\cos \,\gamma -V\,{\cos }^{2}\gamma )\end{array}$$

(40)

Now we introduce the stream function and vorticity:

$$U=\frac{\partial {\rm{\Psi }}}{\partial Y},\,V=-\,\frac{\partial {\rm{\Psi }}}{\partial X}$$

(41)

$${\rm{\Omega }}=(\frac{\partial V}{\partial X}-\frac{\partial U}{\partial Y})$$

(42)

The stream function defined above automatically satisfies the continuity equation. The vorticity equation is obtained by eliminating the pressure between the two momentum equations, i.e. by taking the Y-derivative of the X-momentum and subtracting from it the X-derivative of the Y-momentum:

$$\begin{array}{l}(\frac{{\rho }_{nf}}{{\rho }_{f}})[\frac{\partial U}{\partial Y}\frac{\partial U}{\partial X}+U\frac{{\partial }^{2}U}{\partial Y\partial X}+\frac{\partial V}{\partial Y}\frac{\partial U}{\partial Y}+V\frac{{\partial }^{2}U}{\partial {Y}^{2}}-\frac{\partial U}{\partial x}\frac{\partial V}{\partial X}-U\frac{{\partial }^{2}V}{\partial {X}^{2}}-\frac{\partial V}{\partial X}\frac{\partial V}{\partial Y}\\ -V\frac{{\partial }^{2}V}{\partial X\partial Y}]=(\frac{{\mu }_{nf}}{{\mu }_{f}})(\frac{{\partial }^{3}U}{\partial Y\partial {X}^{2}}+\frac{{\partial }^{3}U}{\partial {Y}^{3}}-\frac{{\partial }^{3}V}{\partial {X}^{3}}-\frac{{\partial }^{3}V}{\partial X\partial {Y}^{2}})-[(\frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}})\frac{1}{{\rm{\Pr }}}Ra\frac{\partial \theta }{\partial X}]\\ +\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(\frac{\partial U}{\partial X}\,\sin \,\gamma \,\cos \,\gamma -\frac{\partial V}{\partial X}\,{\cos }^{2}\gamma -\frac{\partial V}{\partial Y}\,\sin \,\gamma \,\cos \,\gamma +\frac{\partial U}{\partial Y}\,{\sin }^{2}\gamma )\end{array}$$

(43)

which simplifies to:

$$\begin{array}{l}(\frac{{\rho }_{nf}}{{\rho }_{f}})[U(\frac{{\partial }^{2}V}{\partial {X}^{2}}-\frac{{\partial }^{2}U}{\partial Y\partial X})+V(\frac{{\partial }^{2}V}{\partial X\partial Y}-\frac{{\partial }^{2}U}{\partial {Y}^{2}})+\frac{\partial V}{\partial X}(\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y})-\frac{\partial U}{\partial Y}(\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y})]\\ =(\frac{{\mu }_{nf}}{{\mu }_{f}})[(\frac{{\partial }^{3}V}{\partial {X}^{3}}-\frac{{\partial }^{3}U}{\partial Y\partial {X}^{2}})+(\frac{{\partial }^{3}V}{\partial X\partial {Y}^{2}}-\frac{{\partial }^{3}U}{\partial {Y}^{3}})]-[(\frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}})\frac{1}{\Pr }Ra\frac{\partial \theta }{\partial x}]\\ \,\,\,+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(\frac{\partial U}{\partial Y}{\sin }^{2}\gamma +\frac{\partial U}{\partial X}\,\sin \,\gamma \,\cos \,\gamma -\frac{\partial V}{\partial Y}\,\sin \,\gamma \,\cos \,\gamma -\frac{\partial V}{\partial X}{\cos }^{2}\gamma )\end{array}$$

(44)

Using the definition of stream function we obtain:

$$\begin{array}{rcl}(\frac{{\mu }_{nf}}{{\mu }_{f}})[\frac{{\partial }^{2}{\rm{\Omega }}}{\partial {X}^{2}}+\frac{{\partial }^{2}{\rm{\Omega }}}{\partial {Y}^{2}}] & = & (\frac{{\rho }_{nf}}{{\rho }_{f}})(\frac{\partial {\rm{\Psi }}}{\partial Y}\frac{\partial \omega }{\partial X}-\frac{\partial {\rm{\Psi }}}{\partial X}\frac{\partial \omega }{\partial Y})+[(\frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}})\frac{1}{{\rm{\Pr }}}Ra\frac{\partial \theta }{\partial X}]\\ & & +\,\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {Y}^{2}}{\sin }^{2}\gamma +2\frac{{\partial }^{2}{\rm{\Psi }}}{\partial X\partial Y}\,\sin \,\gamma \,\cos \,\gamma +\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {X}^{2}}\,{\cos }^{2}\gamma )\end{array}$$

(45)

In terms of the stream function, the equation defining vorticity becomes:

$$(\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {X}^{2}}+\frac{{\partial }^{2}{\rm{\Psi }}}{\partial {Y}^{2}})=-\,{\rm{\Omega }}$$

(46)

Since the energy, volume fraction equation and block conduction do not contain the pressure variable then the velocity in these equations are easily transformed into stream function formulation.

The finite difference form of equation relating the dimensionless vorticity is:

$$(\frac{{\mu }_{nf}}{{\mu }_{f}})[\frac{{{\rm{\Omega }}}_{i+1,j}-2{{\rm{\Omega }}}_{i,j}+{{\rm{\Omega }}}_{i-1,j}}{{({\rm{\Delta }}X)}^{2}}+\frac{{{\rm{\Omega }}}_{i,j+1}-2{{\rm{\Omega }}}_{i,j}+{{\rm{\Omega }}}_{i,j-1}}{{({\rm{\Delta }}Y)}^{2}}]-{({S}_{{\rm{\Omega }}})}_{i,j}=0$$

(47)

with

$$\begin{array}{rcl}{({S}_{{\rm{\Omega }}})}_{i,j} & = & (\frac{{\rho }_{nf}}{{\rho }_{f}})[(\frac{{{\rm{\Psi }}}_{i,j+1}-{{\rm{\Psi }}}_{i,j-1}}{2{\rm{\Delta }}Y})(\frac{{{\rm{\Omega }}}_{i+\mathrm{1,}j}-{{\rm{\Omega }}}_{i-\mathrm{1,}j}}{2{\rm{\Delta }}X})-(\frac{{{\rm{\Psi }}}_{i+\mathrm{1,}j}-{{\rm{\Psi }}}_{i-\mathrm{1,}j}}{2{\rm{\Delta }}X})(\frac{{{\rm{\Omega }}}_{i,j+1}-{{\rm{\Omega }}}_{i,j-1}}{2{\rm{\Delta }}Y})]\\ & & +\,(\frac{{(\rho \beta )}_{nf}}{{(\rho \beta )}_{f}})\frac{1}{Pr}Ra(\frac{{\theta }_{i+\mathrm{1,}j}-{\theta }_{i-\mathrm{1,}j}}{2{\rm{\Delta }}X})+\frac{{\rho }_{f}}{{\rho }_{nf}}\frac{{\sigma }_{nf}}{{\sigma }_{f}}H{a}^{2}(\frac{{{\rm{\Psi }}}_{i,j+1}-2{{\rm{\Psi }}}_{i,j}+{{\rm{\Psi }}}_{i,j-1}}{{({\rm{\Delta }}Y)}^{2}}\,{\sin }^{2}\gamma \\ & & +\,\frac{{{\rm{\Psi }}}_{i+\mathrm{1,}j+1}-{{\rm{\Psi }}}_{i+\mathrm{1,}j}-{{\rm{\Psi }}}_{i-\mathrm{1,}j-1}+{{\rm{\Psi }}}_{i-\mathrm{1,}j}}{2{\rm{\Delta }}X{\rm{\Delta }}Y}\,\sin \,\gamma \,\cos \,\gamma \,+\frac{{{\rm{\Psi }}}_{i+\mathrm{1,}j}-2{{\rm{\Psi }}}_{i,j}+{{\rm{\Psi }}}_{i-\mathrm{1,}j}}{{({\rm{\Delta }}X)}^{2}}\,{\cos }^{2}\gamma )\end{array}$$

(48)

In order to solve for the value of Ω at the grid point i, j, the values of Ω at the right–hand side must be provided. B = ΔX/ΔY. This method is known as the point Gauss–Seidel method. The general formulation of the method provides:

$$\begin{array}{rcl}{{\rm{\Omega }}}_{i,j}^{k+1} & = & {{\rm{\Omega }}}_{i,j}^{k}+\frac{{\lambda }_{r}}{2(1+{B}^{2})}[{{\rm{\Omega }}}_{i+1,j}^{k}+{{\rm{\Omega }}}_{i-1,j}^{k+1}+{B}^{2}({{\rm{\Omega }}}_{i,j+1}^{k}+{{\rm{\Omega }}}_{i,j-1}^{k+1})\\ & & -2(1+{B}^{2}){{\rm{\Omega }}}_{i,j}^{k}-(\frac{{\mu }_{f}}{{\mu }_{nf}}){({\rm{\Delta }}X)}^{2}{({S}_{{\rm{\Omega }}})}_{i,j}^{k}]\end{array}$$

(49)

The computation is assumed to move through the grid points from left to right and bottom to top. Here, the superscript k denotes the iteration number. We make partition the solution domain in the X − Y plane into equal rectangles of sides ΔX and ΔY. The values of the relaxation parameter λ _r must lie in the range 0 < λ _r  < 2 for convergence. The range 0 < λ _r  < 1 corresponds to under–relaxation, 1 < λ _r  < 2 over–relaxation and λ _r  = 1 refers to the Gauss–Seidel iteration. The finite difference form of equation relating the stream function, energy and volume fraction could be treat in the same way.

The grid–points distribution at the adiabatic inner block and the square cavity is shown in Fig. 1(b), where ND is number of node points in the horizontal and vertical axis of the adiabatic inner block. The temperature conditions at the left and bottom interfaces are:

$$\begin{array}{rcl}{({\theta }_{nf})}_{\frac{NX}{2}-ND+1,j}^{k+1} & = & {({\theta }_{w})}_{\frac{NX}{2}-ND+1,j}^{k}\\ {({\theta }_{w})}_{\frac{NX}{2}-ND+1,j}^{k+1} & = & [(\frac{1}{Kr})(-{({\theta }_{nf})}_{\frac{NX}{2}-ND-1,j}^{k}+4{({\theta }_{nf})}_{\frac{NX}{2}-ND,j}^{k}-3{({\theta }_{nf})}_{\frac{NX}{2}-ND+1,j}^{k+1})\\ & & +\,4{({\theta }_{w})}_{\frac{NX}{2}-ND+2,j}^{k}-{({\theta }_{w})}_{\frac{NX}{2}-ND+3,j}^{k}]\,/3\end{array}$$

(50)

$$\begin{array}{rcl}{({\theta }_{nf})}_{i,\frac{NY}{2}-ND+1}^{k+1} & = & {({\theta }_{w})}_{i,\frac{NY}{2}-ND+1}^{k}\\ {({\theta }_{w})}_{i,\frac{NY}{2}-ND+1}^{k+1} & = & [(\frac{1}{{K}_{r}})(-{({\theta }_{nf})}_{i,\frac{NY}{2}-ND-1}^{k}+4{({\theta }_{nf})}_{i,\frac{NY}{2}-ND}^{k}-3{({\theta }_{nf})}_{i,\frac{NY}{2}-ND+1}^{k+1})\\ & & +4{({\theta }_{w})}_{i,\frac{NY}{2}-ND+2}^{k}-{({\theta }_{w})}_{i,\frac{NY}{2}-ND+3}^{k}]\,/3\end{array}$$

(51)

The convergence of the solution is assumed when the relative error for each of the variables satisfies the following convergence criterium:

$$|\frac{{{\rm{\Gamma }}}^{i+1}-{{\rm{\Gamma }}}^{i}}{{{\rm{\Gamma }}}^{i+1}}|\le \eta ,$$

where i represents the iteration number and η is the convergence criterion. In this study, the convergence criterion was set at η = 10⁻⁵. The flowchart of the solution method of MHD convective heat transfer in a square cavity with conductive inner block is presented in Fig. 2.

Figure 2

Flowchart for the solution procedure of MHD convective heat transfer in a square cavity with conductive inner block.

In the present paper, several grid testings are performed: 10 × 10, 20 × 20, 40 × 40, 60 × 60, 80 × 80, 100 × 100, 120 × 120, 140 × 140 and 160 × 160. Table 1 shows the calculated strength of the flow circulation (Ψ_min) and average Nusselt number $({\overline{Nu}}_{nf})$ at different grid sizes for Ra = 10⁵, Ha = 15, ϕ = 0.02, k _w  = 0.76 and D = 0.3. The results show insignificant differences for the 140 × 140 grids and above. Therefore, for all computations in this paper for similar problems to this subsection, the 140 × 140 uniform grid is employed.

Table 1 Grid testing for Ψ_min, Ψ_max and ${\overline{Nu}}_{nf}$ at different grid size for Ra = 10⁵, Ha = 15, ϕ = 0.02, k _w  = 0.76 and D = 0.3.

For the validation of data, the results are compared with previously published numerical results obtained by Kaluri and Basak⁴ for the case of natural convection heat transfer in discretely heated porous square cavity, as shown in Fig. 3. In addition, a comparison of the average Nusselt number is made between the resulting figure and the experimental results provided by Ho et al.⁴⁴ and the numerical results provided by Sheikhzadeh et al.⁴⁵ and by Motlagh and Soltanipour²⁰ for the case of the natural convection of Al₂O₃-water nanofluid in a square cavity using Buongiorno’s two-phase model as shown in Fig. 4. Next, a comparisons made between the present streamlines, isotherms, nanoparticles volume fraction and the average Nusselt number results and the numerical one obtained by Corcione et al.⁴⁶ are demonstrated in Fig. 5. Figure 6 presents alternative comparisons regarding the enhancement in the thermal conductivity due to the addition of the Al₂O₃ nanoparticles with two different experimental results and the numerical results of Corcione et al.⁴⁶ as well. These results provide confidence to the accuracy of the present numerical method.

Figure 3

Streamlines (a)⁴, (left), present study (right), isotherms (b)⁴, (left), present study (right) Ra = 10⁶, ϕ = 0 and D = 0.5.

Figure 4

Comparison of the mean Nusselt number obtained from present numerical simulation with the experimental results of Ho et al.⁴⁴, numerical results of Sheikhzadeh et al.⁴⁵ and numerical results of Motlagh and Soltanipour²⁰ for different values of Rayleigh numbers.

Figure 5

Corcione et al.⁴⁶ (left), present study (right) for streamlines (a) Isotherms (b) and nanoparticle distribution (c) at Ra = 3.37×10⁵, ϕ = 0.04 and D = 0.

Figure 6

Comparison of (a) thermal conductivity ratio with Chon et al.⁴⁹ and Corcione et al.⁴⁶ and (b) dynamic viscosity ratio with Ho et al.⁴⁴ and Corcione et al.⁴⁶.

Results and Discussion

In this section, we present numerical results for the streamlines, isotherms and nanoparticle distribution with various values of the nanoparticle volume fraction (0 ≤ ϕ ≤ 0.04), the Rayleigh number (10² ≤ Ra ≤ 10⁶), Hartmann number (0 ≤ Ha ≤ 50), thermal conductivity of the conductive inner block (k _w  = 0.28, 0.76, 1.95, 7 and 16) (epoxy: 0.28, brickwork: 0.76, granite: 1.95, solid rock: 7, stainless steel: 16), length of the conductive inner block (0 ≤ D ≤ 0.7), where the values of Prandtl number, Lewis number, Schmidt number, inclination angle of magnetic field, ratio of Brownian to thermophoretic diffusivity and normalized temperature parameter are fixed at Pr = 4.623, Le = 3.5 × 10⁵, Sc = 3.55 × 10⁴, $\gamma =\frac{\pi }{4}$, N _BT  = 1.1 and δ = 155. The values of the average Nusselt number are calculated for various values of Ra, ϕ and D. The thermophysical properties of the base fluid (water) and solid Al₂O₃ phases are tabulated in Table 2.

Table 2 Thermo-physical properties of water with Al₂O₃ nanoparticles at T = 310 K^20,48.

The contour level legends define the direction of the fluid heat flow (clockwise or anti-clockwise direction) and also the strength of the flow. Positive values of Ψ denotes the anti-clockwise fluid heat flow, whereas negative designates the clockwise fluid heat flow. Ψ_min represents the extreme values of the stream function. These values are important to show the minimum change of the flow.

Figure 7 presents streamlines, isotherms and nanoparticles isoconcentrations for different values of the Rayleigh number at ϕ = 0.02, Ha = 15, k _w  = 0.76 and D = 0.3. In the case of low Rayleigh number values (Fig. 6a,b) one can find a formation of six convective cells inside the cavity, namely three vortexes for left and right sides from the centered solid block. More intensive circulations are located under the solid block where heater has an essential size in comparison with two others. In this part we have an ascending convective flow in central zone of the heater and descending ones near the cooled vertical walls. An appearance of two cells on the left (clockwise circulation) and right (counter-clockwise circulation) parts of the solid block can be explained by a formation of horizontal temperature difference between the vertical heaters and cold medium descended from the upper part of cavity where we have two vertical coolers. At the same time two convective cells are formed in the upper part of the cavity due to the effects of vertical coolers. In the case of low Rayleigh numbers the heat transfer regime is a heat conduction where isotherms are quasi-parallel to the isothermal zones. Non-homogeneous distributions of nanoparticles inside the cavity for low Rayleigh numbers are due to an essential effect of thermophoresis where we have the nanoparticles motion along the heat flux from heated zones to cooled ones. Moreover, the abovementioned circulations also characterize zones of nanoparticles motion. These zones illustrate distribution of nanoparticles of different concentrations. Moderate and high values of the Rayleigh number (Fig. 7c,d) reflect more intensive nanofluid circulation inside the cavity, where all six circulations become more intensive. In these cases convective heat transfer is dominated heat transfer regime. Therefore, it is possible to observe a development of asymmetry flow and heat transfer behavior (Fig. 7c) in the case of symmetry boundary conditions with respect to the vertical line X = 0.5. For these Ra values thermal plumes become stronger and thermal boundary layers thicknesses decrease. Distributions of nanoparticles for high Ra is more homogeneous due to non-essential effect of thermophoresis. The same effect has been described earlier by Sheremet et al.⁴⁷.

Figure 7

Variation of the streamlines (left), isotherms (middle), and nanoparticle distribution (right) evolution by Rayleigh number (Ra) for ϕ = 0.02, Ha = 15, k _w  = 0.76 and D = 0.3.

Profiles of the local Nusselt number along the left and bottom walls are shown in Fig. 8. First of all, it is possible to conclude that local Nusselt number has the same values for Ra = 10³ and 10⁴ and these distributions are quasi-symmetry with respect to Y = 0.5 (Fig. 8a) and X = 0.5 (Fig. 8b) due to a domination of the heat conduction. Further growth of the Rayleigh number leads to an increase in the absolute value of the local Nusselt number and asymmetrical distribution due to more intensive convective flow and heat transfer regime. For the fixed value of Ra along the vertical wall (Fig. 8a), behavior of the local Nusselt number can be described as follows, an increase in Y from 0 to 0.375 reflects an augmentation of Nu _l due to an interaction between the hot fluid and cold bottom part of the vertical wall. Negative values of Nu _l in this part can be explained by the direction of heat flux from the fluid to the wall. For 0.375 < Y < 0.4 one can find an increase in Nu _l with successive reduction and growth of Nu _l . Such changes occur near the bottom part of the heater due to a variation of the heat flux direction and heating of the nanofluid from the vertical wall. Further decrease and increase in Nu _l occur along the heater where high values of the heat transfer rate are near the bottom and upper ends of the heater and low value is in central part where fluid is hot and, as a result temperature difference is low. A growth of Y > 0.6 repeats the bottom part distribution of Nu _l . Behavior of Nu _b (Fig. 8b) is the same like above-described for Nu _l .

Figure 8

Variation of local Nusselt number interfaces with (a) Y and (b) X for different Ra at ϕ = 0.02, Ha = 15, k _w  = 0.76 and D = 0.3.

Effects of the Rayleigh number and nanoparticles volume fraction on the average Nusselt number (see Eqs (33–35)) are shown in Fig. 9. As has been mentioned above, low Rayleigh numbers (10³ and 10⁴) illustrate a growth of the average Nusselt number with nanoparticles volume fraction, while for Ra = 10⁵ one can find a formation of maximum heat transfer rate for ϕ = 0.03. Such behavior can be explained by a formation of asymmetry convective flow and heat transfer regimes (see Fig. 7c). In the case of Ra = 10⁶ we have the heat transfer enhancement with ϕ.

Figure 9

Variation of average Nusselt number with ϕ for different Ra at Ha = 0, k _w  = 0.76 and D = 0.3.

An influence of nanoparticles volume fraction on streamlines, isotherms and nanoparticles isoconcentrations is demonstrated in Fig. 10. It should be noted that distributions of stream function and temperature does not change with ϕ. One can find only a reduction of fluid flow rate with the nanoparticles volume fraction due to an increase in the effective viscosity (see Eq. (13)). Variation of nanoparticles isoconcentrations is more essential, namely, a growth of ϕ leads to more homogeneous distributions of nanoparticles inside the cavity.

Figure 10

Variation of the streamlines (left), isotherms (middle), and nanoparticle distribution (right) evolution by nanoparticles volume fraction (ϕ) for Ra = 10⁵, Ha = 15, K _w  = 0.76 and D = 0.3.

Variations of the local Nusselt number along the left vertical wall and bottom horizontal wall are presented in Fig. 11. Nature of the local Nusselt number has been described in detail above. It is worth noting here that an increase in ϕ leads to a growth of local Nusselt number, while behavior of Nu _l and Nu _b does not change with ϕ.

Figure 11

Variation of local Nusselt number interfaces with (a) Y and (b) X for different ϕ at Ra = 10⁵, Ha = 15, k _w  = 0.76 and D = 0.3.

Figure 12 shows dependences of the average Nusselt number on the Rayleigh number and nanoparticles volume fraction (Fig. 12a) and also centered solid block size and nanoparticles volume fraction (Fig. 12b). As has been mentioned above an increase in nanoparticles volume fraction leads to the heat transfer enhancement. The rate of this heat transfer enhancement depends on the solid block sizes.

Figure 12

Variation of average Nusselt number with (a) Ra and (b) D for different ϕ at Ha = 15, k _w  = 0.76 and D = 0.3.

Figure 13 demonstrates streamlines, isotherms and isoconcentrations for different values of the Hartmann number at Ra = 10⁵, ϕ = 0.02, k _w  = 0.76 and D = 0.3. It is well-known that in the case of MHD an increase in magnetic field intensity leads to the convective flow and heat transfer suppression. Therefore, in the present analysis a growth of Ha leads to the attenuation of convective flow and heat transfer rate reduction. Moreover, for high values of Hartmann number (>10) one can find a formation of asymmetric nanofluid flow structures, temperature and nanoparticles concentration fields due to an inclined influence of magnetic field where γ = π/4. Also for high values of Hartmann number isoconcentration field becomes non-homogeneous due to a domination of heat conduction and as a results an essential effect of thermophoresis. It is interesting to note a diagonal orientation of convective cells and thermal plume for high values of Ha (≥25). Namely, convective cells for Ha = 50 are elongated from left bottom corner till right upper corner and thermal plume for Ha = 25 also has the same orientation. Such behavior is related to the effect of inclined magnetic field where an inclination angle of the magnetic field is equal to π/4. The effect of the Hartmann number on the local Nusselt number (Fig. 14) illustrates a reduction of |Nu| with Ha.

Figure 13

Variation of the streamlines (left), isotherms (middle), and nanoparticle distribution (right) evolution by Hartman number (Ha) for Ra = 10⁵, ϕ = 0.02, k _w  = 0.76 and D = 0.3.

Figure 14

Variation of local Nusselt number interfaces with (a) Y and (b) X for different Ha at Ra = 10⁵, ϕ = 0.02, k _w  = 0.76 and D = 0.3.

The average Nusselt number decreases with the Hartmann number (Fig. 15). Moreover, the heat transfer enhancement with the nanoparticles volume fraction is more essential for high values of the Hartmann number due to an intensification of the considered slip mechanisms for nanoparticles. At the same time, the maximum average Nusselt number at ϕ = 0.03 for Ha = 0 with a growth of the magnetic field intensity vanishes and the heat transfer rate becomes an increasing function of the nanoparticles volume fraction for high values of the Hartmann number. In the case of variations of the centered solid block size (Fig. 15b) one can find a significant decrease in ${\overline{Nu}}_{nf}$ with Ha for low values of block size, while an increase in D leads to a reduction of differences in the average Nusselt number between low and high values of the Hartmann number. In the case of D = 0.7 an increase in the Hartmann number does not change the heat transfer rate.

Figure 15

Variation of average Nusselt number with (a) ϕ and (b) D for different Ha at Ra = 10⁵, k _w  = 0.76 and D = 0.3.

Thermal conductivity ratio is a ratio between solid block thermal conductivity and nanofluid thermal conductivity. In the case of conjugate heat transfer problems this parameter plays an essential role, because it reflects a contribution of solid wall material in heat transfer process. Figure 16 illustrates streamlines, isotherms and isoconcentrations for different values of thermal conductivity ratio at Ra = 10⁵, ϕ = 0.02, Ha = 15 and D = 0.3. A growth of thermal conductivity ratio characterizes an increase in the thermal conductivity of solid block material, as a result this block is heated significantly from bottom and lateral heaters. In the case of k _w  = 0.28 one can find an asymmetrical nanofluid flow structures and thermal plume over the bottom heater. Orientation of these thermo-hydrodynamic structures is under the effect of the inclined magnetic field. An increase in k _w leads to more essential heating of the solid block and a formation of symmetric convective cells and thermal plume over the bottom heater. At the same time, isoconcentrations illustrate more homogeneous distributions of nanoparticles for high values of thermal conductivity of solid block.

Figure 16

Variation of the streamlines (left), isotherms (middle), and nanoparticle distribution (right) evolution by thermal conductivity of the conductive inner block (k _w ) for Ra = 10⁵, ϕ = 0.02, Ha = 15 and D = 0.3.

Profiles of the local Nusselt number along left vertical and bottom horizontal walls are shown in Fig. 17 for different values of the thermal conductivity ratio. Change of k _w leads to weak modification of Nu _l and Nu _b .

Figure 17

Variation of local Nusselt number interfaces with (a) Y and (b) X for different k _w at Ra = 10⁵, ϕ = 0.02, Ha = 15 and D = 0.3.

Figure 18 shows the variations of the average Nusselt number with k _w ,ϕ and D. An increase in kw (Fig. 18a) leads to a growth of ${\overline{Nu}}_{nf}$. In the case of different D, it is possible to highlight a non-linear effect of the thermal conductivity ratio for different values of the centered solid block sizes, namely, for D < 0.45 a growth of kw leads to the heat transfer rate reduction, while for D > 0.45 the effect is opposite.

Figure 18

Variation of average Nusselt number with (a) ϕ and (b) D for different k _w at Ra = 10⁵, Ha = 15 and D = 0.3.

The effect of solid block size on streamlines, isotherms and nanoparticles isoconcentrations as well as local and average Nusselt numbers is demonstrated in Figs 19–21. Low volume (Fig. 19a,b) of the internal solid block characterizes a formation of asymmetric thermo-hydrodynamic structures with a homogeneous nanoparticles distributions. An increase in D leads to more essential deformation of solid structures that become symmetric with a thermal plume over the bottom heater. In the case of D = 0.7 (Fig. 19d) one can find several weak circulations inside a narrow gap between solid block and cavity walls. Behavior of the local Nusselt number does not change with D (Fig. 20). In the case of the average Nusselt number we can highlight a non-linear effect of the solid block size on the heat transfer enhancement (Fig. 21).

Figure 19

Variation of the streamlines (left), isotherms (middle), and nanoparticle distribution (right) evolution by length of the conductive inner block (D) for Ra = 10⁵, ϕ = 0.02, Ha = 15 and k _w  = 0.76.

Figure 20

Variation of local Nusselt number interfaces with (a) Y and (b) X for different D at Ra = 10⁵, ϕ = 0.02, Ha = 15 and k _w  = 0.76.

Figure 21

Variation of average Nusselt number with (a) Ra and (b) ϕ for different D at Ha = 15 and k _w  = 0.76.

Conclusions

In the present study, the finite difference method (FDM) is used to study the steady laminar MHD natural convection of an alumina-water nanofluid within a discretely heated square cavity with a centered heat-conducting solid block. The governing equations in dimensionless form have been formulated using the two-phase Buongiorno nanofluid model. The detailed computational results for the flow, temperature and nanoparticles volume fraction fields within the cavity, and the local and average Nusselt numbers are shown graphically for wide ranges of the Rayleigh number, Hartmann number, thermal conductivity ratio, solid block size and nanoparticles volume fraction. The important conclusions in the study are provided below:

• 1. High values of the Rayleigh number characterize more essential circulation inside the cavity. The distribution of nanoparticles becomes more homogeneous for high Ra.

• 2. The change of the nanoparticles volume fraction illustrates more essential modification of the nanoparticles isoconcentrations where more homogeneous distribution can be obtained for high values of ϕ.

• 3. The magnetic field intensity (the Hartmann number) suppresses the convective flow and heat transfer. The heat transfer enhancement with the nanoparticles volume fraction is more essential for high values of the Hartmann number. A significant decrease in ${\overline{Nu}}_{nf}$ with Ha can be found for low values of block size, while an increase in D leads to a reduction of differences in the average Nusselt number between low and high values of the Hartmann number. In the case of D = 0.7, an increase in the Hartmann number does not change the heat transfer rate.

• 4. An increase in the thermal conductivity ratio leads to more homogeneous distributions of nanoparticles. At the same time, for D < 0.45 a growth of kw leads to a heat transfer rate reduction, while for D > 0.45 the effect is the opposite.

• 5. The effect of the centered solid block size is non-linear on the heat transfer rate.