Introduction

Preparation and coherent control of qubit states is at the heart of many quantum technologies1. Undoubtedly, quantum coherence is the most primordial non-classical effect and is at the root of many advantages displayed by quantum technologies over their classical equivalents. One of the major challenges for applications is to prepare a qubit in a state that has a controllable amount of coherence with stability in the long-time limit2. In real physical systems, quantum coherence is usually a fragile property, which is eventually destroyed by the presence of a surrounding environment3,4. It is therefore no surprise that a plethora of strategies to preserve coherence have been conceived, such as quantum error correction5, dynamical decoupling6 or feedback control7. All of these schemes are to some degree an inevitable battle against decoherence. Rather than fighting this battle, here we highlight a different counter-intuitive route to generate and preserve coherence using quantum noise.

We specifically consider a semiconductor double-quantum-dot (DQD) embedded on a substrate8,9,10,11,12,13,14 that realizes a charge qubit coupled to a phononic bath15,16. It has been previously demonstrated that properties of the DQD may be used to extract information about the phononic bath8,9. In a recent experiment10,11, the DQD and substrate were coupled to an auxiliary optical cavity, which was in turn used to experimentally characterize the spectral density of the substrate phonons. In this article, we model the dynamical evolution of these platforms and focus on their steady-state properties. Remarkably, we find that the presence of phonons autonomously drives the DQD charge qubit to a steady state that has coherence in the energy eigenbasis while retaining a significant degree of purity. This surprising result finds its explanation in the particular structure of the system–bath interaction17. Furthermore, the magnitude of steady-state coherence can be controlled by changing the experimentally tunable parameters of the qubit Hamiltonian, the detuning and the hopping. This is proven through an explicit calculation and characterization of the steady-state Bloch vector of the charge qubit as a function of the controllable Hamiltonian parameters. We also show that the coherence is robust to the presence of fermionic leads.

In addition to the obvious importance of generating coherence for quantum information processing, there is currently significant interest in harnessing coherence and exploiting it as a resource in other contexts18. In particular, coherence in the energy eigenbasis has been identified as one of the key features distinguishing quantum thermodynamics from its classical counterpart19,20,21. For example, coherence may enhance the performance of quantum refrigerators22,23,24,25 and heat engines26,27,28 or be directly converted into work29,30,31. To address this point, we conclude the article by showing that, in our set-up, the above phonon-induced steady-state coherence of the DQD can in fact be exploited to drive a mode of the surrounding cavity.

Results

Autonomous generation of steady-state coherence

The main theoretical idea behind the autonomous generation of steady-state coherence was first introduced and explored in ref. 17. In that work, sufficient conditions concerning the structure of the interaction Hamiltonian between a qubit and a bosonic bath were identified that lead to steady-state coherence. In particular, it was shown that a spin-boson model with a Hamiltonian of the form

$$\hat{{\mathcal{H}}}=\frac{{\omega }_{q}}{2}{\hat{\sigma }}_{z}+{\sum _{k}}{\Omega }_{k}{\hat{b}}_{k}^{\dagger }{\hat{b}}_{k}+\left({f}_{1}{\hat{\sigma }}_{z}+{f}_{2}{\hat{\sigma }}_{x}\right){\sum _{k}}{\lambda }_{k}\left({\hat{b}}_{k}^{\dagger }+{\hat{b}}_{k}\right)$$
(1)

autonomously leads to a non-zero steady-state value for \(\langle {\hat{\sigma }}_{x}\rangle\). Here \({\hat{\sigma }}_{x,y,z}\) denote the usual Pauli spin operators, f1, f2 ≠ 0 two generic coupling constants and \({\hat{b}}_{k}\) is the bosonic annihilation operator of the kth bath mode. The results presented in this paper stem from the crucial observation that a semiconductor DQD in contact with a phononic substrate is described exactly by a Hamiltonian of the form of Eq. (1).

The DQD charge qubit

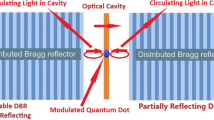
The set-up we consider is depicted schematically in Fig. 1. The DQD comprises two fermionic modes with strong repulsive interaction between them. Substrate phonons are coupled to the electric dipole moment of the DQD. The full Hamiltonian (refs 11,13,32) is then given by \(\hat{{\mathcal{H}}}={\hat{{\mathcal{H}}}}_{S}+{\hat{{\mathcal{H}}}}_{SE}+{\hat{{\mathcal{H}}}}_{E}\) with

$$\begin{array}{lll}{\hat{{\mathcal{H}}}}_{S}+{\hat{{\mathcal{H}}}}_{SE}=\left(\frac{\varepsilon }{2}+\hat{B}\right)\left({\hat{n}}_{1}-{\hat{n}}_{2}\right)+{t}_{c}\left({\hat{c}}_{1}^{\dagger }{\hat{c}}_{2}+{\hat{c}}_{2}^{\dagger }{\hat{c}}_{1}\right) + V{\hat{n}}_{1}{\hat{n}}_{2},\\ \hat{B}={\sum \limits_{k}}{\lambda }_{k}\left({\hat{b}}_{k}^{\dagger }+{\hat{b}}_{k}\right),\quad {\hat{{\mathcal{H}}}}_{E}={\sum \limits_{k}}{\Omega }_{k}{\hat{b}}_{k}^{\dagger }{\hat{b}}_{k},\end{array}$$
$${\hat{{\mathcal{H}}}}_{S}=\frac{\varepsilon }{2}\left({\hat{n}}_{1}-{\hat{n}}_{2}\right)+{t}_{c}\left({\hat{c}}_{1}^{\dagger }{\hat{c}}_{2}+{\hat{c}}_{2}^{\dagger }{\hat{c}}_{1}\right)+V{\hat{n}}_{1}{\hat{n}}_{2},\,\,{\hat{{\mathcal{H}}}}_{SE}=\hat{B}\left({\hat{n}}_{1}-{\hat{n}}_{2}\right).$$
(2)

Here \({\hat{n}}_{\ell }={\hat{c}}_{\ell }^{\dagger }{\hat{c}}_{\ell }\), \({\hat{c}}_{\ell }\) is the fermionic annihilation operator of the ℓth site and \({\hat{b}}_{k}\) is the phononic annihilation operator of the kth mode of the bath. The experimentally controllable parameters of the DQD are the detuning ε and the hopping tc. The repulsive interaction between the two sites is given by V, which is usually much larger than any other energy scale in the regime of operation. The operator \(\hat{B}\) embodies the noisy detuning due to the fluctuating phonon bath. Assuming that the latter is in a thermal state relative to an inverse temperature β, i.e. \({\rho }_{E}={Z}_{E}^{-1}\exp (-\beta {\hat{{\mathcal{H}}}}_{E})\) (\({Z}_{E}={{\rm{Tr}}}_{E}(\exp (-\beta {\hat{{\mathcal{H}}}}_{E}))\)), the noise is characterized by zero mean value, i.e. \({\langle \hat{B}(t)\rangle }_{E}=0\), and the auto-correlation function

$${\langle \hat{B}(t)\hat{B}(0)\rangle }_{E}=\int_{0}^{\infty }d\omega \left[{W}_{s}(\omega ,\beta )\cos (\omega t)-i{W}_{a}(\omega )\sin (\omega t)\right]$$
$${W}_{s}(\omega ,\beta )={{\mathfrak{J}}}_{ph}(\omega )\coth \left(\frac{\beta \omega }{2}\right),\,\,{W}_{a}(\omega )={{\mathfrak{J}}}_{ph}(\omega ),$$
(3)

where \({{\mathfrak{J}}}_{ph}(\omega )={\sum }_{k}{\lambda }_{k}^{2}\delta (\omega -{\Omega }_{k})\) is the spectral function of the phononic bath and \({\langle ...\rangle }_{E}={\rm{Tr}}({\rho }_{E}..)\). In the above equation, Ws(ω, β) and Wa(ω) represent the symmetric and the anti-symmetric parts of the noise power spectral density, respectively. The presence of Wa(ω) is the hallmark of ‘quantum noise’33. Phenomenologically setting Wa(ω) = 0 models ‘classical noise’. This, for example, is approximately the case at high temperatures, where Wa(ω) is negligible compared to Ws(ω, β).

Fig. 1: Schematic depiction of two quantum dots.
figure 1

The two quantum dots are detuned in energy by ε with inter-dot tunnelling tc and Coulomb repulsion V interacting with a substrate supporting phononic excitations.

Full size image

The system Hamiltonian \({\hat{{\mathcal{H}}}}_{S}\) can be diagonalized by transforming to the fermionic operators \({\hat{A}}_{\alpha }\), which are related to \({\hat{c}}_{\ell }\) via the following transformation,

$$\left(\begin{array}{c}{\hat{A}}_{1}\\ {\hat{A}}_{2}\end{array}\right)=\Phi \left(\begin{array}{c}{\hat{c}}_{1}\\ {\hat{c}}_{2}\end{array}\right),\,\,\Phi =\left(\begin{array}{cc}\cos (\frac{\theta }{2})\sin (\frac{\theta }{2})\\ -\sin (\frac{\theta }{2})\cos (\frac{\theta }{2})\end{array}\right),$$
$$\theta ={\tan }^{-1}\left(\frac{2{t}_{{\rm{c}}}}{\varepsilon }\right).$$
(4)

In the transformed basis, we have

$${\hat{{\mathcal{H}}}}_{S}=\frac{{\omega }_{q}}{2}({\hat{N}}_{1}-{\hat{N}}_{2})+V{\hat{N}}_{1}{\hat{N}}_{2},\,{\omega }_{q}=\sqrt{{\varepsilon }^{2}+4{t}_{c}^{2}},$$
(5)
$${\hat{{\mathcal{H}}}}_{SE}=\left[\cos \theta ({\hat{N}}_{1}-{\hat{N}}_{2})-\sin \theta ({\hat{A}}_{1}^{\dagger }{\hat{A}}_{2}+{\hat{A}}_{2}^{\dagger }{\hat{A}}_{1})\right]\hat{B},$$
$${\hat{N}}_{1}={\hat{A}}_{1}^{\dagger }{\hat{A}}_{1},\,\,{\hat{N}}_{2}={\hat{A}}_{2}^{\dagger }{\hat{A}}_{2}.$$
(6)

The DQD can be operated in the single-particle regime, i.e. where \({\hat{N}}_{1}+{\hat{N}}_{2}=1\). In this regime, the fermionic operators can be exactly mapped to Pauli spin operators,

$${\hat{\sigma }}_{z}={\hat{N}}_{1}-{\hat{N}}_{2},\,{\hat{\sigma }}_{x}={\hat{A}}_{1}^{\dagger }{\hat{A}}_{2}+{\hat{A}}_{2}^{\dagger }{\hat{A}}_{1},$$
(7)

and \({\hat{\sigma }}_{y}=i[{\hat{\sigma }}_{x},{\hat{\sigma }}_{z}]/2=-i({\hat{A}}_{1}^{\dagger }{\hat{A}}_{2}-{\hat{A}}_{2}^{\dagger }{\hat{A}}_{1})\). The resulting Hamiltonians for the DQD and the DQD–phonon couplings become, in the eigenbasis of the DQD Hamiltonian,

$${\hat{{\mathcal{H}}}}_{S}=\frac{{\omega }_{{\rm{q}}}}{2}{\hat{\sigma }}_{z},\,{\hat{{\mathcal{H}}}}_{SE}=\left({f}_{1}{\hat{\sigma }}_{z}+{f}_{2}{\hat{\sigma }}_{x}\right)\hat{B},$$
(8)

where \({f}_{1}=\cos \theta =\varepsilon /{\omega }_{q}\) and \({f}_{2}=-\sin \theta =-2{t}_{c}/{\omega }_{q}\). The above equation describes a DQD charge qubit coupled to a phononic bath. Whatever state the charge qubit is prepared in, due to the phonons, the charge qubit relaxes to a unique steady state. To determine the latter, we notice that the above Hamiltonian shares exactly the same form as Eq. (1). This means that, in a solid-state DQD charge qubit, the presence of phonons can autonomously generate coherence in the eigenbasis of the system Hamiltonian.

In general, the quantum dots experience correlated noise due to their coupling to a common phonon bath. However, this feature is not necessary for the mechanism of coherence generation considered here, in contrast to schemes for bath-induced entanglement production where environmental correlations are essential34,35,36,37. Indeed, steady-state coherences would arise even if each quantum dot were coupled to its own independent bath, as shown in Supplementary Notes. The essential ingredient for our study is the competition between the hopping between the dots and the local coupling of each quantum dot to the bath. This condition ensures that \({\hat{{\mathcal{H}}}}_{{\rm{SE}}}\) contains both \({\hat{\sigma }}_{z}\) and \({\hat{\sigma }}_{x}\) components, as required for the autonomous generation of steady-state coherence17. We now proceed to characterize this coherence and investigate its engineering and tunability via the DQD parameters ε and tc.

Steady-state properties

The state of a qubit is completely characterized by the expectation values of the three Pauli operators \({\hat{\sigma }}_{x,y,z}\). In the long-time limit, the entire set-up reaches an equilibrium steady state where the charge current, which is proportional to \(\langle {\hat{\sigma }}_{y}\rangle\), is zero. The remaining two non-zero expectation values are found to be (see ‘Methods’)

$$\langle {\hat{\sigma }}_{x}\rangle =-\frac{{\rm{sin}}\ 2\theta }{{\omega }_{q}}\left[-{\varDelta }_{s}({\omega }_{q},\beta ){\langle {\hat{\sigma }}_{z}\rangle }_{0}+{\varDelta }_{a}({\omega }_{q})-{\varDelta }_{a}(0)\right],$$
(9)
$$\langle {\hat{\sigma }}_{z}\rangle ={\langle {\hat{\sigma }}_{z}\rangle }_{0}+{\sin }^{2}\theta \left[{\varDelta }_{-}({\omega }_{q})+{\varDelta }_{+}({\omega }_{q})-\frac{\beta }{2}{{\rm{sech}}^{2}}\left(\frac{\beta {\omega }_{q}}{2}\right){\varDelta }_{s}({\omega }_{q},\beta )\right],$$
(10)

where \({\langle {\hat{\sigma }}_{z}\rangle }_{0}=-{W}_{a}({\omega }_{q})/{W}_{s}({\omega }_{{q}},\beta )=-\tanh \left(\beta {\omega }_{q}/2\right)\) and Δs(ωq, β), Δa(ωq) and Δ±(ωq, β) are the principal-value integrals defined below:

$${\varDelta }_{s}({\omega }_{q},\beta )={\mathcal{P}}\int_{0}^{\infty}{\rm{d}}\omega{W}_{s}(\omega ,\beta )\left[\frac{1}{\omega +{\omega }_{q}}-\frac{1}{\omega -{\omega }_{q}}\right],$$
(11)
$${\varDelta }_{a}({\omega }_{q})={\mathcal{P}}\int_{0}^{\infty}{\rm{d}}\omega {W}_{a}(\omega )\left[\frac{1}{\omega +{\omega }_{q}}+\frac{1}{\omega -{\omega }_{q}}\right],$$
(12)
$${\varDelta }_{\pm }({\omega }_{q},\beta )=-{\mathcal{P}}\int_{0}^{\infty}{\rm{d}}\omega \frac{{\langle {\hat{\sigma }}_{z}\rangle }_{0}{W}_{s}(\omega ,\beta )\mp {W}_{a}(\omega )}{{(\omega \pm {\omega }_{q})}^{2}}.$$
(13)

These results show that, if \(\sin 2\theta\, \ne \,0\), which corresponds to ε, tc ≠ 0, and if the noise is quantum, i.e. Wa(ω) ≠ 0, we have \(\langle {\hat{\sigma }}_{x}\rangle\, \ne \,0\). Thus, in this case, there will be coherence in the eigenbasis of the system in the equilibrium steady state. If, on the other hand, the noise were classical, i.e. Wa(ω) = 0, we would obtain \(\langle {\hat{\sigma }}_{x}\rangle =0\) and there would be no steady-state coherence. This implies that, in the high-temperature regime that corresponds to the classical limit33, no steady-state coherence will be generated. This can also be checked by taking β → 0 limit of the above results. In the opposite limit of low temperatures, βωq ≫ 1, the above formulae simplify to

$$\langle {\hat{\sigma }}_{x}\rangle =-2\sin 2\theta{\int\nolimits_{0}^{\infty }}d\omega \frac{{{\mathfrak{J}}}_{ph}(\omega )}{\omega (\omega +{\omega }_{q})}$$
(14)
$$\langle {\hat{\sigma }}_{z}\rangle =-1+2{\sin }^{2}\theta {\int \nolimits_{0}^{\infty}}d\omega \frac{{{\mathfrak{J}}}_{ph}(\omega )}{{(\omega +{\omega }_{q})}^{2}}.$$
(15)

The above equations show that, within this temperature regime, the state of the DQD becomes temperature independent. Note, however, that these expressions are only valid for temperatures well above the Kondo scale TK, where our perturbative analysis is expected to break down38,39,40. Nevertheless, TK is exponentially suppressed by weak system–bath coupling, thus providing a wide temperature regime where our results hold.

Numerical results

Above we have found that quantum noise due to phonons can be used to generate coherence in the energy eigenbasis of the DQD charge qubit for non-zero detuning. This is shown in Fig. 2, where the dynamics of \(\langle {\hat{\sigma }}_{x}(t)\rangle\) and \(\langle {\hat{\sigma }}_{y}(t)\rangle\) are plotted for two different cases showing the effects of decoherence (for ε = 0) and coherence generation (for ε = 1) (see ‘Methods’). In our calculations, we have taken the phonon spectral function as

$${{\mathfrak{J}}}_{ph}(\omega )={\gamma }_{b}\omega \left[1-{\rm{sinc}}\left(\frac{\omega }{{\omega }_{c}}\right)\right]{e}^{-{\omega }^{2}/2{\omega }_{{\rm{max}}}^{2}}.$$
(16)

The spectral functions of phonons in solid-state DQDs have been well characterized theoretically and experimentally and they vary depending on the experimental platform8,9,10,11,16. Our chosen spectral function is known to be a good description of bulk acoustic phonons in GaAs DQDs8,9,11. The frequency ωmax is the upper cut-off frequency, while ωc = cs/d, where cs is the speed of sound in the substrate and d is the distance between the two quantum dots. The dimensionless parameter γb controls the strength of coupling with phonons. The validity of our theory requires that γb ≪ 1. We have set ωc = 1 and used this as our unit of energy.

Fig. 2: Decoherence and coherence generation in DQD charge qubit due to the presence of a phononic environment.
figure 2

a Decoherence: dynamics of \(\langle {\hat{\sigma }}_{x}(t)\rangle\) and \(\langle {\hat{\sigma }}_{y}(t)\rangle\) for ε = 0, starting from an initial state with coherence \(\langle {\hat{\sigma }}_{x}(0)\rangle =0.2\), \(\langle {\hat{\sigma }}_{y}(0)\rangle =-0.2\), \(\langle {\hat{\sigma }}_{z}(0)\rangle =0\). Here the final steady state has no coherence. b Coherence generation: dynamics of \(\langle {\hat{\sigma }}_{x}(t)\rangle\) and \(\langle {\hat{\sigma }}_{y}(t)\rangle\) for ε = 1, starting from a completely mixed initial state: \(\langle {\hat{\sigma }}_{x}(0)\rangle =0\), \(\langle {\hat{\sigma }}_{y}(0)\rangle =0\), \(\langle {\hat{\sigma }}_{z}(0)\rangle =0\). Here the final steady state has coherence. Other parameters: tc = 0.5, γb = 0.03, ωmax = 10, β = 10. All energies are measured in units of ωc, which is set to 1.

Full size image

In Fig. 3, we characterize the steady state of the qubit. Since \(\langle {\hat{\sigma }}_{y}\rangle =0\), we parameterize the steady state with \(\langle {\hat{\sigma }}_{x}\rangle\) and the length of the Bloch vector

$$r=\sqrt{{\langle {\sigma }_{x}\rangle }^{2}+{\langle {\sigma }_{z}\rangle }^{2}}.$$
(17)

While \(\langle {\hat{\sigma }}_{x}\rangle\) is a measure of coherence, r is a measure of purity of the state. For a pure state, r = 1, for a completely mixed state, r = 0. Figure 3 demonstrates that tunable steady-state coherence persists with high purity across a range of temperatures and energy scales. The maximal value of \(\langle {\hat{\sigma }}_{x}\rangle\) can be achieved at low temperatures by setting the dots’ detuning to ε = ± 2tc. The sign of the coherence can be made positive or negative, depending on the sign of \(\sin 2\theta =4\varepsilon {t}_{c}/{\omega }_{q}^{2}\), as can also be seen directly from Eq. (9). Interestingly, the coherence and purity remain constant as the temperature grows up to values of order kBT ~ 0.1ωq, and then decay to zero as the temperature is further increased. It should therefore be possible to observe maximal phonon-induced steady-state coherence in a DQD system at only moderately low temperatures.

Fig. 3: The variation of \({\langle \hat{\sigma }_{x}\rangle}\) and length of Bloch vector r with several parameters of DQD charge qubit.
figure 3

a \(\langle {\hat{\sigma }}_{x}\rangle\) and 1 − r vs the detuning ε at fixed hopping tc = 0.25 at low temperature (see Eqs 14, 15), b \(\langle {\hat{\sigma }}_{x}\rangle\) and 1 − r vs the hopping tc at fixed detuning ε = 0.5 at low temperature, c \(\langle {\hat{\sigma }}_{x}\rangle\) and 1 − r vs θ at fixed ωq at low temperature. The vertical dashed lines in these plots correspond to ε = ± 2tc. d \(\langle {\hat{\sigma }}_{x}\rangle\) (top) and r (bottom) vs temperature 1/β at fixed θ = π/4 and for various chosen values of ωq. Other parameters: γb = 0.03, ωmax = 10. All energies are measured in units of ωc, which is set to 1. \(\langle {\hat{\sigma }}_{y}\rangle =0\).

Full size image

Let us make an order-of-magnitude estimate in order to demonstrate the feasibility of our proposal. We take ωq = 0.5ωc, ε = 2tc and βωq = 10, corresponding to the maximum coherence in Fig. 3. In GaAs, cs ≈ 3000m/s, so that an inter-dot separation of d = 150 nm yields ωc ≈ 20 GHz. Therefore, the maximal coherence is obtained when ε ≈ 29 μeV, tc ≈ 15 μeV and T ≈ 50 mK. These parameters are completely within reach of current experiments (for example, see refs 10,11).

Robustness to the presence of fermionic leads

Experimental set-ups such as refs 10,11 typically feature fermionic leads coupled to the DQD. In this case, even when the leads are in equilibrium, the number of particles in the DQD is not strictly conserved. However, the DQD can only be considered as a qubit in the single-particle sector. Nevertheless, we now show that steady-state coherence is robust to the presence of fermionic leads at equilibrium, i.e. at equal chemical potential μ, and at the same temperature at the substrate phonons.

The total Hamiltonian of the set-up is now given by \(\hat{{\mathcal{H}}}={\hat{{\mathcal{H}}}}_{S}+{\hat{{\mathcal{H}}}}_{SE}+{\hat{{\mathcal{H}}}}_{E}+{\hat{{\mathcal{H}}}}_{Sf}+{\hat{{\mathcal{H}}}}_{f}\), \({\hat{{\mathcal{H}}}}_{Sf}={\sum }_{\ell = 1,2}{\sum }_{r = 1}^{\infty }{\gamma }_{r\ell }\left({\hat{c}}_{\ell }^{\dagger }{\hat{B}}_{\ell r}+{\hat{B}}_{\ell r}^{\dagger }{\hat{c}}_{\ell }\right),\,{\hat{{\mathcal{H}}}}_{f}={\sum }_{\ell = 1,2}{\sum }_{r = 1}^{\infty }{{\mathcal{E}}}_{\ell r}{\hat{B}}_{\ell r}^{\dagger }{\hat{B}}_{\ell r},\) where the fermionic lead is modelled by infinite number of fermionic modes, and \({\hat{B}}_{\ell r}\) is the annihilation operator for the rth mode of the fermionic lead attached to the ℓth DQD site. For simplicity, we assume that the leads have identical, constant spectral functions \({{\mathfrak{J}}}_{\ell }^{f}(\omega )=2\pi {\sum }_{r = 1}^{\infty }{\gamma }_{\ell r}^{2}\delta (\omega -{{\mathcal{E}}}_{\ell r}),\)\({{\mathfrak{J}}}_{1}^{f}(\omega )={{\mathfrak{J}}}_{2}^{f}(\omega )=\Gamma\), for −Λ ≤ Γ ≤ Λ, and zero otherwise. Here we assume that the coupling to the leads Γ is weak, while the bandwidth Λ is assumed to be large.

At low temperatures, the number of particles in the DQD in the equilibrium steady state is governed by the chemical potential of the fermionic lead. The DQD is occupied by a single particle on average if the chemical potential is in the regime

$$-\frac{{\omega }_{q}}{2}\ll \mu \ll \frac{{\omega }_{q}}{2}+V,$$
(18)

i.e. the chemical potential is higher than ωq/2 but smaller than the charging energy of the DQD. Therefore, when Eq. (18) holds, we expect the system to display steady-state coherence if there is non-zero detuning.

To check this, we calculate \({\rm{Re}}\left(\right.\langle {\hat{A}}_{1}^{\dagger }(t){\hat{A}}_{2}(t)\rangle \left)\right.\), which corresponds to \(\langle {\hat{\sigma }}_{x}(t)\rangle\) in the single-particle sector (see ‘Methods’). The dynamics of this quantity for three different initial conditions of the DQD are shown in Fig. 4a. The three initial conditions correspond to the DQD being doubly occupied, the DQD being completely unoccupied and the completely mixed state of the charge qubit, which corresponds to \(\langle {\hat{N}}_{1}(0)\rangle =0.5\), \(\langle {\hat{N}}_{2}(0)\rangle =0.5\). None of the initial states contain any coherence in the energy eigenbasis. The chemical potential of the fermionic lead is chosen as μ = 0, which satisfies Eq. (18). For non-zero detuning, \({\rm{Re}}(\langle {\hat{A}}_{1}^{\dagger }(t){\hat{A}}_{2}(t)\rangle )\) goes to the same steady-state value given by the expression for \(\langle {\hat{\sigma }}_{x}\rangle\) in Eq. (14) for all initial conditions. Figure 4b shows the plot of the equilibrium steady-state value of \({\rm{Re}}(\langle {\hat{A}}_{1}^{\dagger }{\hat{A}}_{2}\rangle )\) as a function of μ. In the regime corresponding to Eq. (18), there is coherence in the energy eigenbasis, while beyond that regime, the coherence decays to zero. Thus we have shown that the coherence generated owing to the presence of phonons is robust to the presence of equilibrium fermionic leads, so long as the steady state of the DQD is in the single-particle sector.

Fig. 4: The robustness of phonon-induced steady-state coherence in a DQD charge qubit to the presence of fermionic leads at equilibrium.
figure 4

a Evolution of \({\rm{Re}}\left(\right.\langle {\hat{A}}_{1}^{\dagger }(t){\hat{A}}_{2}(t)\rangle \left)\right.\) in the presence of the fermionic lead is shown for three different initial conditions of the DQD with no initial coherence. The chemical potential of the fermionic lead is μ = 0. b The equilibrium steady-state value of \({\rm{Re}}\left(\right.\langle {\hat{A}}_{1}^{\dagger }{\hat{A}}_{2}\rangle \left)\right.\) as a function of μ. The vertical dashed lines show positions of μ = − ωq/2 and μ = − ωq/2 + V. The horizontal dashed lines in both a and b show the value of coherence given by the expression for \(\langle {\hat{\sigma }}_{x}\rangle\) in Eq. (14). Parameters for both plots: ε = 1, tc = 0.5, μ = 0, V = 5, β = 10, γb = 0.03, ωmax = 10, Γ = 0.06, Λ = 400. All energies are measured in units of ωc, which is set to 1.

Full size image

Application to driving a cavity

As an application, we now demonstrate that phonon-induced coherence may be used to displace an auxiliary cavity mode. Let the charge qubit be coupled to a cavity mode described by a Jaynes–Cummings-like interaction

$${\hat{{\mathcal{H}}}}_{C}={\omega }_{0}{\hat{a}}^{\dagger }\hat{a},\,\,{\hat{{\mathcal{H}}}}_{SC}=g({\hat{\sigma }}_{+}\hat{a}+{\hat{a}}^{\dagger }{\hat{\sigma }}_{-}).$$
(19)

Here ω0 is frequency of the cavity mode, \(\hat{a}\) is bosonic annihilation operator for the cavity mode, g is the cavity–DQD coupling strength and \({\hat{\sigma }}_{\pm }=({\hat{\sigma }}_{x}\pm i{\hat{\sigma }}_{y})/2\). The cavity will be further coupled with its own thermal environment, leading to a decay rate κ.

If both the cavity–DQD coupling and the cavity decay rate are small, and if the cavity is away from resonance with the DQD (i.e. ωq ≠ ω0), then we can obtain the steady-state results for the cavity up to leading order in small quantities. The results for the expectation value of the cavity field operator \(\langle \hat{a}\rangle\) and the cavity occupation \(\langle {\hat{a}}^{\dagger }\hat{a}\rangle\) to leading order are given by

$$\langle \hat{a}\rangle =-\frac{g}{2({\omega }_{0}-i\kappa )}\langle {\hat{\sigma }}_{x}\rangle ,\,\langle {\hat{a}}^{\dagger }\hat{a}\rangle \simeq \frac{1}{{e}^{\beta {\omega }_{0}}-1}+O({g}^{2}),$$
(20)

while that for \(\langle {\hat{a}}^{2}\rangle =0\). Thus it is immediately clear that the coherence of the charge qubit causes displacement of the cavity mode, given by \(\langle \hat{X}\rangle =\langle \hat{a}+{\hat{a}}^{\dagger }\rangle \simeq -2g\langle {\hat{\sigma }}_{x}\rangle /{\omega }_{0}\). However, \(\langle {\hat{a}}^{\dagger }\hat{a}\rangle\) is given by the Bose–Einstein distribution for the cavity, which ensures that no average photon current flows between the cavity and its own bosonic thermal bath. This is consistent with the fact that entire set-up is at thermal equilibrium. This means that the variance of \(\hat{X}\) is given by \({\rm{var}}(\hat{X})=\langle {\hat{X}}^{2}\rangle -{\langle \hat{X}\rangle }^{2}\simeq \coth (\beta {\omega }_{0}/2)+O({g}^{2})\). The cavity displacement \(\langle \hat{X}\rangle\), which may in principle be experimentally measured41,42, thus directly probes the steady-state coherence of the DQD. In Fig. 5, we show the real and imaginary parts of \(\langle \hat{a}\rangle\) in steady state as the DQD parameter θ is tuned. It is clear that \(\langle \hat{a}\rangle\) is non-zero when \(\langle {\hat{\sigma }}_{x}\rangle\) is non-zero.

Fig. 5: A cavity with a weak Jaynes–Cummings coupling to the DQD will be displaced due to the steady-state coherence of the DQD.
figure 5

The figure shows plots of real and imaginary parts of \(\langle \hat{a}\rangle\), as a function of DQD parameter θ with other parameters fixed. Other parameters: γb = 0.03, ωmax = 10. All energies are measured in units of ωc, which is set to 1.

Full size image

Discussion

We have theoretically demonstrated that quantum noise due to phonons in state-of-the-art DQD charge qubits autonomously generates steady-state coherence in the energy eigenbasis of the qubit at non-zero detuning. Owing to the inherently dissipative nature of this phenomenon, it represents an especially robust yet surprisingly tunable addition to the toolbox of quantum state engineering for solid-state charge qubits and promises potential to become a new resource for quantum thermodynamics. Remarkably, the magnitude and sign of the coherence can be controlled merely by manipulating the Hamiltonian parameters of the DQD, while retaining high purity. Aside from the intrinsic interest of generating quantum coherence, the resulting steady states represent useful resources in various contexts. As a simple example, we have shown that the qubit coherence in turn generates field coherence in a cavity mode that is weakly coupled to the DQD. Moreover, coherence distillation or amplification techniques could in principle be applied to generate fully coherent resource states for quantum information processing43,44,45.

We emphasize that the physics described here is a general property of spin-boson models of the type in Eq. (8). Such models can generically be used to describe dissipative two-level systems4,46,47 and can be engineered in various platforms (for examples, see refs 48,49 and citations therein). Indeed, any generic qubit Hamiltonian, \(\hat{H}=\frac{\varepsilon }{2}{\hat{\tau }}_{z}+{t}_{{{c}}}{\hat{\tau }}_{x}\) with quantum noise in the qubit parameters ε and tc can be written in the form of Eq. (8) (see Supplementary Notes for details). It follows that, at low temperatures, if f1f2 ≠ 0, which is generically true, quantum noise in qubit parameters leads to generation of steady-state coherence in the energy eigenbasis of any qubit, e.g. a superconducting qubit, a DQD spin qubit, etc. On the other hand, classical noise in qubit parameters is detrimental to such coherence. The DQD charge qubit provides an especially interesting example, since the required parameter regime corresponds to current state-of-the-art experiments10,11,12,13,14, where quantum noise in detuning is the major source of noise.

Future work will focus on a full characterization of thermodynamic properties of the set-up including an analysis of the relation between irreversible entropy production and coherence50,51, which will shed light on the thermodynamic cost of generating steady-state coherence.

Methods

Detailed methods are given in Supplementary Notes. Here we give a brief overview of the techniques.

Redfield master equation

The time evolution of the DQD qubit is modelled using a Redfield master equation, detailed in Supplementary Notes. The derivation of this equation starts from a factorized initial system-environment state ρtot(0) = ρ(0) ⊗ ρE, with ρE the thermal equilibrium state of the phononic bath and ρ(0) the initial DQD state. The Redfield equation is based on two approximations: (i) a perturbative expansion up to second order in the coupling between the DQD and the reservoir, and (ii) a Markov assumption that the reservoir memory time is short in comparison to the time scale of the DQD evolution. In the presence of fermionic leads, the same set of approximations is used but where the leads are also incorporated into the environment. The result is a master equation describing the DQD of the form

$$\frac{\partial \rho }{\partial t}=i[\rho ,{\hat{{\mathcal{H}}}}_{S}]-{{\mathcal{L}}}_{ph}\rho -{{\mathcal{L}}}_{f}\rho ,$$
(21)

where \({{\mathcal{L}}}_{ph}\) and \({{\mathcal{L}}}_{f}\), respectively, describe the effect of the phononic and fermionic reservoirs (see Supplementary Notes). The solution of Eq. (21) is used to compute the time evolution of expectation values in the main text.

Perturbation expansion of the generalized equilibrium state

As discussed in ref. 52, the predictions of the Redfield equation give results for the DQD coherence valid up to second order in \({\hat{\mathcal{H}}}_{SE}\), while the predictions for the populations are valid only to zeroth order. However, in order to discuss the purity of the qubit, we need results for both coherences and populations valid to the same order. In order to achieve this, we use the fact that an open quantum system coupled weakly to a thermal environment is generically expected to relax to the generalized equilibrium state53,54,55,56,57,58

$$\lim\limits_{t\to \infty }\rho (t)={{\rm{Tr}}}_{{\rm{E}}}\left[\frac{{{\rm{e}}}^{-\beta ({\hat{{\mathcal{H}}}}_{S}\,+\,{\hat{{\mathcal{H}}}}_{E}\,+\,{\hat{{\mathcal{H}}}}_{SE})}}{{\rm{Tr}}\left[{{\rm{e}}}^{-\beta ({\hat{{\mathcal{H}}}}_{S}\,+\,{\hat{{\mathcal{H}}}}_{E}\,+\,{\hat{{\mathcal{H}}}}_{SE})}\right]}\right],$$
(22)

which incorporates the effect of system–environment correlations. We use a perturbative expansion of Eq. (22) up to second order in \({\hat{\mathcal{H}}}_{SE}\) to obtain steady-state expectation values, as detailed in Supplementary Notes. This approach yields an identical prediction for the coherence \(\langle {\hat{\sigma }}_{x}\rangle\) as the master equation, as well as a second-order correction to the population inversion \(\langle {\hat{\sigma }}_{z}\rangle\).