Introduction

Structural phase transitions are observed in many crystal systems (including perovskites) and intrinsically driven by various lattice vibrational modes1,2. In particular, the archetype of oxides – the perovskite (ABO3) system expresses diverse structural phase transitions due to the different phonon mode softening behaviors at high-symmetry points of the first Brillouin zone, displaying different BO6 octahedral distortions3,4.

From a chemical standpoint, the Jahn-Teller effect, particularly the second-order Jahn-Teller (SOJT) effect, has been used to explain ferroelectric phase transitions driven by atomic displacements associated with zone-center (q = 0) phonon modes5. For instance, in ferroelectric perovskites, the valence band by B-site cation with empty d orbitals and the conduction band by oxygen anion with fully occupied p orbitals have different symmetries, represented by distinct irreps, \({{{\Gamma }}}_{4}^{-}\) and \({{{\Gamma }}}_{5}^{+}\), respectively6. As a consequence, the overlap between the wave functions associated with these bands is not allowed, leading to atomic displacements and the formation of chemical bonds that lower the energy through electron rearrangement. This phenomenon, known as the SOJT effect, resulting in an instability of the crystal structure and contributing to the observed phase transition.

Meanwhile, a conventional way of classifying structural distortion patterns in perovskites is to reply on the Goldschmidt tolerance factor, \(t=({r}_{A}+{r}_{B})/\sqrt{2}({r}_{B}+{r}_{{{{\rm{O}}}}})\), where rA is the radius of the A cation, rB is the radius of the B cation, and rO is the radius of the oxygen ion (anion)7. This simple geometric relationship obtained from ionic radii is closely related to their lattice vibrations since it provides some intuitive information regarding the relative distances/displacement of the ions in a perovskite unit cell. Thus, it is commonly used for predicting the phase stability (or formability) as well as describing octahedral distortion patterns in perovskite materials.

Among the various known perovskites, the Group I niobate perovskite family – especially, potassium niobate (KNbO3) and sodium niobate (NaNbO3) – is one of the promising lead-free perovskites actively studied since they show a variety of phase transition characteristics and related properties with numerous technological applications without toxicity concerns8,9. KNbO3 and NaNbO3 are typical examples that can be classified according to their phase transition patterns based on the tolerance factor.

In the case of KNbO3, whose t is 1.06 (i.e., t > 1), octahedral distortions are mainly governed by the means of Nb-site off-centering (resulting in the so-called intra-octahedral distortion). This is due to the softening of the lowest transverse optical (TO) mode at the Γ point in the first Brillouin zone, giving rise to its ferroelectric instability and the paraelectric-to-ferroelectric phase transition as temperature decreases10,11. On the other hand, for NaNbO3 whose t is 0.97 (where now t < 1), NbO6 octahedral tilting (inter-octahedral distortion) dominates over the ferroelectric instability (due to Nb-site off-centering) and undergoes the antiferrodistortive (AFD) phase transition. This is due to the dominant soft modes at the other high-symmetry points in the first Brillouin zone, resulting in more complex and diverse phase transition pathways4,12,13.

Given that t is intrinsically a simple classic geometric descriptor, it still lacks to consider many important physical contributions to phase stability (such as temperature effects) which can play a significant role in deciding the phase preference in perovskites. Accordingly, a more systematic and quantitative analysis of the complex relations between phase stability and temperature effects is needed. However, using standard density-functional theory (DFT) calculations to predict the phase stability of materials at elevated temperatures is not trivial since these calculations are typically performed using a static geometry, providing only reasonable results at 0 K temperatures.

In the first attempt to mitigate this lack, the simple harmonic approximation (HA) has been widely used to determine the phonon dispersion in many materials, but it is not applicable to strongly anharmonic solids or in the case of high-temperature phases where unstable phonon modes exist14. Going beyond the HA, the quasi-harmonic approximation (QHA), which takes into account volumetric expansions, is often used to predict phase stability at finite temperatures, but it also fails when dominant imaginary phonon frequencies appear15. In view of this, previous theoretical reports on anharmonic solids may be limited in its accuracy in the theoretical description of phase preference and lattice dynamics of high-temperature phases. Therefore, it is timely to provide a more complete and accurate picture of anharmonic lattice properties at elevated temperatures.

Recently, the self-consistent phonon (SCP) theory has received considerable attention and can treat anharmonic renormalization effects nonperturbatively, especially so for strongly anharmonic materials or high-temperature phases16,17,18. To account for the anharmonic renormalization effects in a crystal, higher-order (i.e., cubic, quartic, etc.) interatomic force constants (IFCs) should be constructed. The anharmonic terms in the IFCs can be obtained by combining the ab initio molecular dynamics (AIMD) simulation with the compressive sensing lattice dynamics (CSLD) method19,20. In this approach, the AIMD simulation gives a reliable displacement-force dataset for a given crystal structure at elevated temperatures, while the CSLD method provides an optimized sparse representation of anharmonic IFCs through cross-validation17.

Furthermore, the anharmonic self-energy correction using the phonon quasiparticle (QP) approximation has been proposed for calculating the temperature-dependent phonon dispersions more accurately in strongly anharmonic systems21. This approach can be utilized for estimating the QP peaks of the phonon spectrum for strongly anharmonic solids effectively by incorporating anharmonic renormalization effects due to the bubble self-energy from the QP approximation. In this approach, a more accurate prediction of the phase transition temperature can be realized21.

Not to mention, the dielectric constant of a crystal is also closely related to the lattice vibrations and associated structural phase transitions22. By combining the SCP approach with QP corrections, this method will be ideal in investigating temperature-dependent dielectric properties of anharmonic solids where (anti)polarity is an issue. Having said that, although there are a few studies which have attempted to calculate the temperature-dependent dielectric constant from first-principles23,24, they often poorly agree with available experiments from the lack of QP bubble self-energy corrections to the phonon dispersion.

In this study, using the SCP theory coupled to the QP approximation, we carefully investigate the anharmonic lattice dynamics of cubic KNbO3 and NaNbO3. Both the thermal expansion effects and phonon frequency shifts due to the anharmonic self-energies (as obtained using the cubic and quartic IFCs) are explicitly included to address the phonon softening behaviors. Finally, we quantitatively predict the phase transition temperature (i.e., the Curie temperature) and temperature-dependent dielectric constant for both niobates via the Lyddane-Sachs-Teller (LST) relation22,25, and are found to be in agreement with previous experimental reports.

Results and discussion

Harmonic phonon dispersions

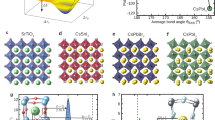
In order to investigate the lattice dynamics of the high-temperature phases of KNbO3 and NaNbO3, we first analyze the harmonic phonon dispersions of the high-symmetry cubic (\(Pm\bar{3}m\)) phase, as illustrated in Fig. 1a. According to the phonon band structures shown in Fig. 1c, d for KNbO3 and NaNbO3, respectively, they show the unstable phonon modes with imaginary frequencies at different q-points of the first Brillouin zone. These imaginary frequencies at specific modes are indicative of the magnitude of the local negative curvature (mode amplitude, Q = 0) on the potential energy surface (PES)26. The ferroelectric instability mode, the in-phase tilting mode, and the out-of-phase tilting mode play a significant role in determining phase transition patterns in the niobates4 and are portrayed in Fig. 1b. Our analysis reveals that the soft phonon modes, including the unstable modes, are highly sensitive to the unit cell volume changes. For instance, as shown in Fig. 1c, the soft phonon mode at the Γ point becomes stronger as the volume increases for KNbO3. Likewise, the soft phonon mode at the Γ point becomes stronger with increasing the unit cell volume of NaNbO3, while the corresponding soft phonon modes at the M and R points become weaker (Fig. 1d). It is noteworthy that relative strengths of phonon softening among the competing modes are altered by the modulation of the unit cell volume, and this is indicative that the volumetric change is essential in understanding the complex phase transition patterns, particularly for NaNbO3.

Fig. 1: Niobate perovskites and octahedral distortions with soft phonons.
figure 1

a Atomic structure of high-symmetry cubic (\(Pm\bar{3}m\)) niobate perovskite. b Schematic representations of dominant soft phonon modes at the Γ (0,0,0), M (0.5, 0.5, 0), and R (0.5, 0.5, 0.5) points. Harmonic phonon dispersions for c KNbO3 and d NaNbO3. The colored solid lines represent the phonon dispersions obtained from the DFT-PBEsol optimized volume (VDFT) while the gray solid lines represent the dispersions for other volumes scaling from 0.96 to 1.04 with an interval of 0.01 (from dark to lighter shades).

Full size image

Potential energy surfaces from soft phonon modes

We calculate the PESs for the ferroelectric instability mode at the Γ point, the in-phase tilting mode at the M point, and the out-of-phase tilting mode at the R point, by displacing atoms in KNbO3 and NaNbO3 along the phonon eigenvectors, as illustrated in Fig. 2. We confirm that only one double-well potential is observed at the Γ point for KNbO3, while double-well potentials are observed at all the Γ, M, and R points for NaNbO3. Regardless of the shape of the potentials, all of them exhibit large deviations from the simple harmonic approximation (shown as dashed gray lines in Fig. 2). These become more critical when the collective atomic vibrations are substantial and non-negligible, such as under high elevated temperature conditions. Instead, the potentials can be approximated by the higher fourth-order polynomials (solid gray lines in Fig. 2) which better fit the DFT data. This clearly lends support to the strong quartic anharmonicity in both oxides, especially so in NaNbO3.

Fig. 2: Potential energy surfaces (PESs) from soft phonon modes.
figure 2

PESs of a the ferroelectric instability mode at the Γ point, b the in-phase tilting mode at the M point, and c the out-of-phase tilting mode at the R point, respectively for KNbO3. The corresponding PESs for NaNbO3 is shown for d the ferroelectric instability mode at the Γ point, e the in-phase tilting mode at the M point, and f the out-of-phase tilting mode at the R point, respectively. Solid lines represent the fourth-order (quartic) polynomial fit, while the dashed lines represent the second-order (harmonic) polynomial fit. To investigate the volume dependence, the unit cell volume is scaled from 0.96 to 1.04 with an interval of 0.01 (from dark to lighter shades) based on the DFT optimized volume.

Full size image

The analysis of the anharmonic potentials in Fig. 2 provides further insights beyond the harmonic phonon dispersions and volume changes discussed earlier. In perovskites, a decrease in the unit cell volume facilitates the inter-octahedral rotations and results in stronger phonon softening effects along the unstable modes at the M or R points27. In contrast, the softening effect of the ferroelectric instability mode at the Γ point becomes relatively weaker as the unit cell volume decreases, opposing the phonon softening effects at the M or R points. Moreover, as indicated by the different energy scales of the PES, the depth of the potential wells for softening at the M and R points in NaNbO3 is much deeper than that at the Γ point. Therefore, in the case of NaNbO3, we anticipate that the octahedral tilting corresponding to softening at the M or R points will occur before the ferroelectric distortion corresponding to the mode softening at the Γ point.

Structural analysis from AIMD simulation

In order to analyze how the structure changes when subjected to the finite-temperature, we perform the ab initio molecular dynamics (AIMD) simulations with the NVT ensemble, and then we apply the normal mode decomposition28 by projecting the structural information from the AIMD trajectory onto the soft phonon modes. The displacement uℓκ of atom κ in the ℓ-th unit cell can be projected onto the specific phonon mode amplitude Qqν using the following equations:

$${Q}_{{{{\boldsymbol{q}}}}\nu }(t)=\mathop{\sum}\limits_{\kappa }{{{{\boldsymbol{u}}}}}_{\kappa }^{{{{\boldsymbol{q}}}}}(t)\cdot {{{{\boldsymbol{e}}}}}_{\kappa }^{* }({{{\boldsymbol{q}}}},\nu )\quad ,$$
(1)
$${{{{\boldsymbol{u}}}}}_{\kappa }^{{{{\boldsymbol{q}}}}}(t)=\sqrt{\frac{{M}_{\kappa }}{N}}\mathop{\sum}\limits_{\ell }{{{{\boldsymbol{u}}}}}_{\ell \kappa }(t)\exp [-i{{{\boldsymbol{q}}}}\cdot {{{\boldsymbol{r}}}}(\ell )]\quad ,$$
(2)

where \({{{{\boldsymbol{u}}}}}_{\kappa }^{{{{\boldsymbol{q}}}}}\) is the atomic displacement projected onto the wave vector q, and eκ(q, ν) is the phonon eigenvector with the mode ν. Here, N is the number of unit cells, Mκ is the atomic mass, and r(ℓ) is the equilibrium position with the lattice translation vector.

The results of the projected mode amplitudes are shown in Fig. 3. In general, NaNbO3 exhibits larger and irregular fluctuations, particularly in the M and R modes, compared to KNbO3. Notably, since our AIMD simulations are performed within the NVT ensemble using the cubic phase, we observe the switching of ferroelectric or tilting modes even at significantly lower temperatures than the experimentally reported Curie temperatures (see Supplementary Figure 5 in the Supplementary Information). This result arises from the absence of internal strain relaxation in our simulations. Furthermore, the lattice volume also plays a significant role in the softening of unstable modes. Consequently, soft phonons exhibit high sensitivity to both the AIMD temperature and the lattice volume, requiring careful consideration in determining these parameters for subsequent SCP calculations.

Fig. 3: Phonon mode projection from AIMD simulations.
figure 3

Projected mode amplitudes onto the soft modes at the Γ, M, and R points and their probability densities from the AIMD trajectories of cubic KNbO3 for 800 K with a VDFT and c 1.04VDFT and cubic NaNbO3 for 1000 K with b VDFT and d 1.04VDFT. The lighter-colored line represents the amplitudes from the full snapshot data, while the darker line represents a rolling average with a 250-snapshot interval. The probability density is calculated after 2500 steps, and the red line depicts an averaged mode amplitude from that.

Full size image

To determine the appropriate AIMD temperatures for our SCP calculations, we conduct preliminary AIMD simulations over a range of temperatures, specifically from 400 K to 1200 K with a 200 K interval. We analyze the resulting structural evolution and relative stability, supported by mode projection analysis in terms of atomic displacements and switching intervals (refer to Supplementary Table 1 and Supplementary Figures 2 – 4 in the Supplementary Information). Based on this analysis, we select an AIMD temperature of 800 K for cubic KNbO3 and 1000 K for cubic NaNbO3 as suitable for our SCP calculations. These temperatures ensure that the materials exhibit meaningful structural information while maintaining the relative stability of the cubic phase.

Temperature-dependent phonon dispersions

Next, we investigate the phonon dispersions of KNbO3 and NaNbO3 at finite temperatures using the self-consistent phonon (SCP) approach. The temperature-dependent phonon dispersions with the DFT-PBEsol optimized volume (VDFT) are presented in Fig. 4a, b for KNbO3 and NaNbO3, respectively. We find that the anharmonic contributions to the lattice vibrations, derived from the cubic and quartic IFCs, provide relatively reliable results within the framework of the SCP theory. Notably, our results reveal temperature-dependent phonon frequencies showing a significant change in the soft phonon modes especially at the low-frequency regimes. To verify the accuracy of the SCP calculations, we compare mean squared displacement (MSD) values obtained using different methods including the harmonic approximation (HA), the self-consistent phonon (SCP) calculations, and the ab initio molecular dynamics (AIMD) simulations. Our calculation results show that the MSD values calculated using the SCP method are in much better agreement with those obtained from the AIMD simulations than those calculated using the simple HA method.

Fig. 4: Temperature-dependent phonon dispersions within the SCP level.
figure 4

SCP band structures are presented for a KNbO3 and b NaNbO3 using the VDFT, respectively. Harmonic phonon dispersions are shown as dashed lines for comparison. Mean squared displacements (MSDs) as a function of temperature for c KNbO3 and d NaNbO3, accordingly. The results are obtained using the harmonic approximation (HA, shown as dashed lines), the self-consistent phonon (SCP, shown as solid lines) calculations, and the ab initio molecular dynamics (AIMD, shown as ‘x’ markers) simulations, respectively. SCP free energy versus unit cell volume curves are presented for e KNbO3 and g NaNbO3, respectively. The Birch-Murnaghan equation-of-state (BM-EOS) has been employed to fit the SCP free energy data for both structures. Lattice constants are calculated as a function of temperature for f KNbO3 and h NaNbO3, accordingly. For comparison, the experimental values of the lattice constants are adapted from References 29,30 for KNbO3 and NaNbO3, respectively.

Full size image

Figure 4 e, g depict the SCP free energies for varying volumes of KNbO3 and NaNbO3, respectively. The SCP free energy calculations are carried out in increments of 0.005 from 1 to 1.04 times the optimized DFT volume, and the results are fitted to the Birch-Murnaghan equation-of-state (BM-EOS) to obtain lattice constants as a function of temperature. The resulting lattice constants are plotted in Fig. 4f, h for KNbO3 and NaNbO3, respectively. The calculated lattice constants for KNbO3 exhibit consistency with experimental values, while a slight deviation is observed for NaNbO3, which may be attributed to the larger degree of anharmonicity in NaNbO3 as compared to KNbO3 (which will be discussed later in Fig. 5 and Table 1). This deviation suggests that the SCP free energies may be less accurate for NaNbO3 since the calculations only consider IFCs up to fourth-order terms. Despite this deviation, the lattice constants obtained from the SCP free energies are still in better agreement with the experimental values than those obtained from the DFT optimized volume (VDFT). In particular, a linear increasing relation of volume with temperature aligns well with experimental observations29,30. This highlights the significance of considering both the thermal expansion effects and anharmonicity corrections to the free energy calculations, leading to an improved description over the DFT optimized volume, VDFT.

Fig. 5: Mode-resolved degree of anharmonicity.
figure 5

Here, s of \({\sigma }_{s}^{{{{\rm{A}}}}}\) denotes a specific vibrational mode as calculated from the AIMD simulations for a cubic KNbO3 and b cubic NaNbO3 using VDFT. The anharmonic contribution to the forces are obtained from the AIMD simulations at 800 K and 1000 K for KNbO3 and NaNbO3, respectively.

Full size image
Table 1 Site-resolved degree of anharmonicity \({\sigma }_{X}^{{{{\rm{A}}}}}\), where X denotes a specific atomic site in niobate perovskites, calculated from AIMD simulations of the cubic phase of KNbO3 and NaNbO3 with VDFT.
Full size table

Anharmonicity quantification

Having demonstrated the importance of addressing anharmonicity in these niobates, we now turn our attention to numerically quantifying the degree of anharmonicity in both KNbO3 and NaNbO3. Here, we analyze the interatomic forces of the two oxides from the AIMD simulations and relate the IFCs to the lattice vibrations for the high temperature phases. Following the method proposed by Knoop et al.31, the degree of anharmonicity, \({\sigma }_{s}^{{{{\rm{A}}}}}\) can be computed quantitatively in the following fashion:

$${\sigma }^{{{{\rm{A}}}}}(T)\equiv \frac{\sigma {[{F}^{{{{\rm{A}}}}}]}_{T}}{\sigma {[F]}_{T}}=\sqrt{\frac{{\sum }_{I,\alpha }{\langle {({F}_{I,\alpha }^{{{{\rm{A}}}}})}^{2}\rangle }_{T}}{{\sum }_{I,\alpha }{\langle {({F}_{I,\alpha })}^{2}\rangle }_{T}}}\quad ,$$
(3)

where 〈⋅〉T represents the thermodynamic ensemble average, FI,α represents the force components obtained from the AIMD simulations, and \({F}_{I,\alpha }^{{{{\rm{A}}}}}\) represents their anharmonic contributions, respectively. This definition measures the standard deviation of the anharmonic force distribution and thus allows one to quantitatively analyze the difference in anharmonicity of the two niobates.

To illustrate the dominant modes responsible for the observed increase in anharmonicity, our results of the mode-resolved degree of anharmonicity, \({\sigma }_{s}^{{{{\rm{A}}}}}\) are presented in Fig. 5. As anticipated from our analysis above, the soft modes located at the Γ, M, and R points (i.e., notably for the ferroelectric mode in KNbO3 and both the ferroelectric and octahedral tilting modes in NaNbO3 shown in Fig. 5) play a prominent role in enhancing the observed anharmonicity in these oxides. In addition, a comparison of the overall magnitudes reveals that the anharmonicity in NaNbO3 is quantitatively larger than that in KNbO3. These findings are further supported by the site-resolved degree of anharmonicity data presented in Table 1. Here, the results reveal that in KNbO3, the largest anharmonic contribution arises from the forces acting on the Nb atoms, leading to a strong instability from the Nb-site off-centering ferroelectric mode.

When compared to KNbO3, both the A-site and Nb-site contributions to the degree of anharmonicity in NaNbO3 are much larger – especially so for the A-site contribution where the effect is almost doubled, giving rise to a strong instability from both ferroelectric and inter-octahedral tilting modes. This difference is mainly attributed to the size difference of the A-site cation occupying the dedocahedron network in the perovskite structure. Specifically, the Shannon ionic radii data32 indicate that the Na atom has a smaller ionic radius (1.39 Å for a 12-coordination site) as compared to the K atom (1.64 Å for the 12-coordination site). Consequently, the smaller size of the Na atom in NaNbO3 causes it to occupy a reduced space within the dedocahedron network in the perovskite structure, leading to higher anharmonicity in the structure as compared to KNbO3.

Bubble self-energy correction

So far, we have utilized the SCP theory to investigate the temperature-dependent phonon dispersions of KNbO3 and NaNbO3 in the high-symmetry cubic phase. As depicted in Fig. 4a, b, all anharmonic phonon frequencies remain positive within the temperature range, as imaginary frequencies are not allowed in the self-consistent equation of the SCP theory. However, this contradicts the experimental observation of phonon softening temperatures (see Table 2). The analysis of the anharmonic phonon frequencies from the SCP theory suggests that while it can qualitatively capture the phonon softening behavior, it cannot accurately predict the mode softening temperatures. It is thus challenging to predict precise mode softening temperatures using only the SCP theory, and further correction is necessary to obtain more accurate anharmonic phonon frequencies.

Table 2 Calculated and experimental mode softening temperatures for the phonon mode instability at the M, R, and Γ points listed for KNbO3 and NaNbO3, respectively.
Full size table

Essentially, the SCP solution given in this study itself does not include the information about the frequency-dependent bubble self-energy. Indeed, the bubble self-energy also plays a critical role in determining the phonon frequency shift as well as phonon linewidth, which are determined by the real part and imaginary part of the self-energy, respectively, represented by the phonon spectral function. To calculate the phonon spectral function Aq, the following relationship18,33 is utilized:

$${A}_{q}(\omega )\propto \frac{4{({\omega }_{q}^{{{{\rm{S}}}}})}^{2}{{\mathrm{Im}}}\,{{{\Sigma }}}_{q}^{{{{\rm{B}}}}}(\omega )}{{[{\omega }^{2}-{({\omega }_{q}^{{{{\rm{S}}}}})}^{2}+2{\omega }_{q}^{{{{\rm{S}}}}}{{\mathrm{Re}}}\,{{{\Sigma }}}_{q}^{{{{\rm{B}}}}}(\omega )]}^{2}+{[2{\omega }_{q}^{{{{\rm{S}}}}}{{\mathrm{Im}}}\,{{{\Sigma }}}_{q}^{{{{\rm{B}}}}}(\omega )]}^{2}}\quad ,$$
(4)

where \({\omega }_{q}^{{{{\rm{S}}}}}\) represents the anharmonic phonon frequencies obtained from the SCP solution, and \({{{\Sigma }}}_{q}^{{{{\rm{B}}}}}(\omega )\) denotes the frequency-dependent bubble self-energy. In Fig. 6, we present the calculated phonon spectral function for cubic KNbO3 and cubic NaNbO3 at 800 K and 1000 K, respectively, which has a direct relation to the inelastic neutron scattering (INS) measurement. Nonetheless, calculating the bubble self-energy with full frequency-dependency is computationally demanding for every set of our calculations with different temperatures and lattice volumes. To address this challenge, a recently proposed quasiparticle (QP) approximation21 has been employed, which allows one to obtain the bubble self-energy corrected phonon dispersions more efficiently. To validate this approach, we compare the phonon spectral function and the SCP dispersions with bubble self-energy correction (SCP+bubble) using the QP approximation in Fig. 6. Remarkably, the comparison between the phonon spectral function and SCP+bubble dispersions from the QP approximation demonstrates a significant agreement, confirming the validity of this method.

Fig. 6: Comparison of phonon spectral function and SCP+bubble dispersions.
figure 6

Phonon spectral function Aq(ω) of a cubic KNbO3 for T = 800 K and b cubic NaNbO3 for T = 1000 K calculated with V = VDFT. SCP dispersions with bubble self-energy correction (SCP+bubble) from the QP approximation are also presented as white solid lines.

Full size image

To achieve a more quantitative prediction of mode softening temperatures, anharmonic phonon frequencies are further corrected by solving the self-consistent equation for the bubble self-energy using the quasiparticle (QP) approximation21. We present the results with the bubble self-energy correction after scaling the DFT-optimized volume, VDFT by 1.03 and 1.02 for KNbO3 and NaNbO3 respectively, in Fig. 7a, b. In these cases, the volumes are close to VSCP(T = 800 K) for KNbO3 and VSCP(T = 1000 K) for NaNbO3, respectively. Indeed, the negative shifting of the phonon frequencies due to the bubble self-energy correction is clearly noticeable in the low frequency regime (particularly, in the vicinity of the phonon softening). In other words, when the bubble self-energies are taken into account, phonon instabilities with imaginary frequencies appear as the temperature changes. This allows one to describe the temperature-dependent phonon mode softening more realistically with improved accuracy, and this leads to a more consistent observation with experiments34,35.

Fig. 7: Temperature-dependent phonon dispersions with bubble self-energy correction (SCP+bubble) based on the QP approximation.
figure 7

SCP+bubble band structures are presented for a KNbO3 with 1.03 VDFT and b NaNbO3 with 1.02 VDFT, respectively. Harmonic phonon dispersions for the corresponding volumes are plotted with dashed lines for comparison. Squared frequencies of the soft phonon modes with VSCP are presented as a function of temperature for c KNbO3 and e NaNbO3, respectively. We note that the negative values indicating the presence of unstable modes do not have any physical meaning here. Temperature-dependent dielectric constants are obtained via the Lyddane-Sachs-Teller (LST) relation22,25 and fitted using the Curie-Weiss (CW) law38 for d KNbO3 and f NaNbO3, respectively. The calculated data with VSCP are determined by a linear interpolation of the phonon frequencies with different volumes. For comparison, experimental values of the dielectric constants are obtained from References 39,40 for KNbO3 and NaNbO3, respectively.

Full size image

Upon affirming the importance of the bubble self-energy correction, the SCP calculations with the bubble self-energy correction are then repeated while considering the effect of the volumetric changes. Figure 7c, e illustrate the dependence of the phonon mode softening on temperature as obtained by linearly interpolating the phonon frequencies from different volumes to match those using the SCP volume (VSCP) for KNbO3 and NaNbO3, respectively. More specifically, from the temperature-dependent squared phonon frequency trends, one may observe the softening of instability modes in these oxides. The mode softening temperatures obtained in the graphs are summarized in Table 2 and our theoretical predictions accurately describe the sequence of phase transitions depending on the temperature observed in the experiments34,35. From Fig. 7c, e, one can clearly show that for the case of KNbO3, a single mode softening only occurs at the Γ point, while in NaNbO3, all three modes soften at the M, R, and Γ points. Therefore, this analysis provides a way to understand the relationship between the competing soft modes and to estimate the order of phase transitions as a function of temperature (while considering volumetric changes).

Temperature-dependent dielectric relations

Besides inspecting the phonon properties of KNbO3 and NaNbO3, we further investigate and predict their temperature-dependent dielectric constants based on the anharmonic phonon dispersions described above. The SCP theory with bubble self-energy correction (SCP+bubble) provides an accurate solution which renormalizes the imaginary frequencies of the lowest TO mode at the Γ point in the HA. This approach resolves the discrepancy between the calculated dielectric constants from the typical density-functional perturbation theory (DFPT)36 and the experimental values. In particular, when we calculate the dielectric constants of the cubic phase of KNbO3 and NaNbO3 from the DFPT method, the ion-clamped dielectric constants are found to be 6.46 and 6.15, respectively, while including the ionic contributions to the dielectric constants will only yield values of 2.11 and 19.24, accordingly. These values are significantly much lower than those observed experimentally.

On the other hand, the SCP+bubble approach provides an alternative route to obtain realistic dielectric constants that are quantitatively more consistent with experimental values via the Lyddane-Sachs-Teller (LST) relation22,25 which is expressed as follows:

$$\frac{{\epsilon }_{{{{\rm{DC}}}}}}{{\epsilon }_{\infty }}=\mathop{\prod }\limits_{j=1}^{r}\frac{{{\omega }_{{{{\rm{LO}}}}}}_{j}^{2}}{{{\omega }_{{{{\rm{TO}}}}}}_{j}^{2}}\quad ,$$
(5)

where ϵDC and ϵ∞ represent the static dielectric constant and the ion-clamped dielectric constant, and \({{\omega }_{{{{\rm{LO}}}}}}_{j}\) and \({{\omega }_{{{{\rm{TO}}}}}}_{j}\) represent the phonon frequencies of the longitudinal (LO) and transverse optical (TO) modes, respectively. Here, the LO-TO splitting is achieved through the non-analytical correction using the Ewald’s method37, where the Born effective charge and the ion-clamped dielectric tensor are obtained from the DFPT calculation36 to accurately capture the long-range Coulomb interaction.

The temperature-dependent static dielectric constant for each oxide are plotted in Fig. 7d, f, while considering explicit volumetric changes. The calculated dielectric constants are fitted using the Curie-Weiss (CW) law38 where ϵ = a/(T − Tc) + c and here, a and c are fitting coefficients. This allows one to estimate the critical temperature, Tc where the dielectric anomaly occurs (see Table 3). Our results align very well with the experimental measurements39,40.

Table 3 Critical temperatures, Tc obtained from the Curie-Weiss (CW) law38 based on the SCP+bubble data with VSCP.
Full size table

With regards to KNbO3, the Tc corresponds to the point at which the paraelectric-to-ferroelectric (C → T) phase transition occurs due to the ferroelectric Nb-site off-centering only. In contrast, a more complex mode softening mechanism is found for NaNbO3 involving the mode softening at the M and R points which results in the specific tilting of the octahedra where additional Nb-site off-centering can occur in an antiparallel alignment4. This corresponds to the paraelectric-to-antiferroelectric (R → P) phase transition as captured by the Tc where the dielectric anomaly occurs. This is reflected in the mode softening at the Γ point at a much lower temperature than that at the M and R points (see Table 2). Thus, this explains the frequent observation of antiferroelectricity in NaNbO3, while only ferroelectricity is predominantly expressed in KNbO3.

Through this study, we systematically calculate and analyze the temperature-dependent phonon dispersions of KNbO3 and NaNbO3 based on the bubble self-energy corrected SCP approach. This undeniably provides a more quantitative understanding of the complex phase transitions in these perovskites. Moreover, the accurate prediction of the temperature-dependent static dielectric constants sets a solid platform to further investigate the complex relationships between the observed phase transitions and the dielectric properties in KNbO3 and NaNbO3.

Methods

Density-functional theory calculations

Density-functional theory (DFT) calculations are performed using periodic boundary conditions, employing the projector augmented wave (PAW)41,42 method as implemented in the Vienna Ab initio Simulation Package (VASP) code43,44. The PBEsol (Perdew-Burke-Ernzerhof functional revised for solids)45 exchange-correlation (xc) functional is used, treating the DFT xc energy via the generalized gradient approximation. The Kohn-Sham orbitals are expanded using a plane-wave basis set with a kinetic energy cutoff of 500 eV. Specifically, the 2p and 3s states of Na, the 3s, 3p, and 4s states of K, the 4p, 4d, and 5s states of Nb, and the 2s and 2p states of O are explicitly considered as valence states in the PAW potentials used. An 8 × 8 × 8 Γ-centered k-point grid is used to sample the irreducible Brillouin zone of the 5-atom primitive unit cell of the perovskite cubic phase. To ensure high accuracy of both energies and forces, the self-consistent loop continues until the total DFT energies and the forces are converged to 10−8 eV and 0.001 eV/Å, respectively. After optimizing the perovskite cubic unit cell, the unit cell volume is expanded from the optimized value by up to 4% with the interval of 0.5% to investigate thermal expansion effects on the phonon properties.

Calculating interatomic force constants

To construct the interatomic force constants (IFCs), we employ the supercell approach with the 2 × 2 × 2 supercell (containing 40 atoms), which is sufficient to account for the out-of-phase tilting of the NbO6 octahedra. The harmonic IFCs are first estimated by least-squares fitting using the displacement patterns extracted from the finite displacement method using an atomic displacement of 0.01 Å. In addition, the anharmonic IFCs are then predicted by the compressive sensing lattice dynamics method using a displacement-force training dataset obtained by combining the trajectories from the ab initio molecular dynamics (AIMD) simulations with additional random displacements17,19. To generate the physically reliable atomic displacements, we initially perform the AIMD simulations using a 2 × 2 × 2 Γ-centered k-point grid with a canonical (NVT) ensemble at 800 K for KNbO3 and 1000 K for NaNbO3, respectively. The simulations are performed for 10000 steps with a time step of 2 fs. We discard the initial 2500 steps from the AIMD trajectories and extract 500 sampled configurations for every 15 steps of the remaining trajectory. For the sampled configurations, we displace every individual atom by 0.05 Å in random directions to reduce cross-correlations among the sampled structures.

For the compressive sensing method, we use the adaptive LASSO46 (least absolute shrinkage and selection operator) to optimize a sparse representation of the anharmonic terms via a four-fold cross-validation process, and consider the anharmonic terms up to the fourth-order in the Taylor expansion potentials used. We set the cutoff radii of 15.0 Bohr ( ≈ 7.94 Å), which are comparable to the supercell size, for the cubic and quartic IFCs so that every n-th nearest neighbor coordination shell within the supercell boundary can be included. This ensures an equivalent number of independent parameters for different volumes considered in this study. In the regression process, we fix the harmonic IFCs calculated from the finite displacement method and optimize the anharmonic terms only. We then determine a set of linearly independent parameters by making full use of the available symmetry operations and constraints for translational invariance. The number of independent parameters (23457) is found to be 698 and 22759 for the cubic and quartic terms, respectively.

Self-consistent phonon (SCP) calculations

The self-consistent phonon (SCP) calculations at finite temperatures are performed to get temperature-dependent phonon dispersions, allowing one to deal with the anharmonic renormalization of phonon frequencies. The SCP approach is a nonperturbative way, equivalent to the many-body Green’s function theory in phonons through the use of the Dyson equation. Thus, once the IFCs are determined, we can solve the phonon many-body problem by considering both the harmonic and anharmonic contributions. The particular implementation of the SCP theory used in this study considers the loop diagram (including quartic IFCs) which is the major contributor to the anharmonic renormalization of phonon frequencies18. The self-consistent equation for the SCP theory17 can be expressed as follows:

$${({\omega }_{q}^{{{{\rm{S}}}}})}^{2}={\omega }_{q}^{2}+2{\omega }_{q}^{{{{\rm{S}}}}}{I}_{q}\quad ,$$
(6)
$${I}_{q}=\frac{1}{2}\mathop{\sum}\limits_{{q}_{1}}\frac{\hslash {{{\Phi }}}_{4}(q;-q;{q}_{1};-{q}_{1})}{4{\omega }_{q}^{{{{\rm{S}}}}}{\omega }_{{q}_{1}}^{{{{\rm{S}}}}}}\left[2n({\omega }_{{q}_{1}}^{{{{\rm{S}}}}})+1\right]\quad ,$$
(7)

where \({\omega }_{q}^{{{{\rm{S}}}}}\) represents the anharmonic phonon frequencies, Φ4(q; − q; q1; − q1) the reciprocal representation of quartic IFCs, and \(n(\omega )={({e}^{\beta \hslash \omega }-1)}^{-1}\) the Bose-Einstein distribution function. For the SCP calculations, we select a 2 × 2 × 2 grid for the q-point and an 8 × 8 × 8 grid for the q1-point in the irreducible Brillouin zone to ensure a tight convergence of the anharmonic phonon frequencies. After obtaining the anharmonic phonon frequencies from the SCP calculations, we further perform the bubble self-energy correction using the QP approximation21 by solving the following self-consistent equation:

$${{{\Omega }}}_{{{{\boldsymbol{q}}}}\nu }^{2}={({\omega }_{{{{\boldsymbol{q}}}}\nu }^{{{{\rm{S}}}}})}^{2}-2{\omega }_{{{{\boldsymbol{q}}}}\nu }^{{{{\rm{S}}}}}{{\mathrm{Re}}}\,{{{\Sigma }}}_{{{{\boldsymbol{q}}}}\nu }^{{{{\rm{B}}}}}\left[{G}^{{{{\rm{S}}}}},{{{\Phi }}}_{3}\right](\omega ={{{\Omega }}}_{{{{\boldsymbol{q}}}}\nu })\quad ,$$
(8)

where \({{\mathrm{Re}}}\,{{{\Sigma }}}_{{{{\boldsymbol{q}}}}\nu }^{{{{\rm{B}}}}}\left[{G}^{{{{\rm{S}}}}},{{{\Phi }}}_{3}\right](\omega )\) represents the real part of the bubble self-energy. Further details on the theoretical formulation of the SCP theory and the QP approximation can be found in the literature17,18,21. In this work, all phonon calculations are performed using the ALAMODE package17.