Introduction

The kagome lattice has been considered as a fertile ground to realize exotic quantum phases because of its high degree of geometric frustration and nontrivial band structures1,2,3. Particularly, when the number of electrons per site is 2/3 ± 1/6, the Fermi energy (EF) is at the van Hove singularity (vHS) such that the density of states diverges to induce various broken-symmetry phases1,2,3. The recent discovery of kagome metals of KV3Sb5, RbV3Sb5 and CsV3Sb5 (abbreviated as AV3Sb5 where A denotes alkali atoms of K, Rb and Cs)4 bring a chance to realize those phases because their EF’s are close to vHS4,5. Indeed, several studies so far have demonstrated noteworthy states such as charge density waves (CDWs)4,6,7,8,9, superconductivity10, loop currents states11,12,13 and electronic nematicity14, to name a few.

On the other hand, a recent progress in manipulating stacked two-dimensional (2D) crystals opens a new window to study phase transitions15,16,17. Owing to their anisotropic lattice structures and interactions, distinct electronic phases are realized in the same material by pressure18, a number of layers17,19 and dopings20 etc. Unlike simple lattice structures of hexagonal or rectangular shapes in typical layered materials16, newly discovered kagome metals of AV3Sb5 add another complexity of frustrating intralayer orders in studying phase transitions, thus providing a unique chance to study their interplay with extreme anisotropic interactions.

Owing to the vHS in kagome metals, CDWs occur with decreasing temperature (T) from normal metallic phase21,22. In spite of their well-established presence, a few enigmatic observations raise questions on their formation mechanism. One of anomalous behaviors is the absence of phonon softening in inelastic X-ray8, neutron21 and Raman scattering experiments23 while these results are incompatible with unstable phonon modes at M- and L-point of the Brillouin zone (BZ) in recent ab initio calculations5,24,25. Moreover, from the fact that the formation energy of CDW (ECDW)5 monotonically decreases with the size of the alkali atoms, one could naively expect that the transition temperature for CDW (TCDW) increases accordingly. However, as the size of alkali atom increases from K to Rb and to Cs, the observed TCDW first increases from 78 K to 102 K and then decreases to 94 K2, respectively, contradicting the conventional behaviors26,27.

In this work, we theoretically showed that kagome metals first develop lattice distortions within each layer at much higher temperature of T* than TCDW. Then, their phases are not fixed simultaneously with their amplitudes but fluctuate, which is shown to be inevitable owing to multiple ways of stacking CDWs between adjacent layers with the same energetic cost. As T decreases further, the phases of preformed orders eventually stop varying at TCDW. The characteristic timescale for the fluctuation is at least 105 slower than that a typical vibrational frequency of vanadium lattice. For CsV3Sb5, it is shown that a phonon softening signal exists only around L-point in a narrow temperature range around T*. Between T* and TCDW, the thermodynamic behaviors of preformed CDWs can be described by 4-states Potts model which undergoes a first-order phase transition at TCDW28. Our quantitative analysis demonstrates that the fluctuations increase as the size of alkali metal increases, thus competing with ECDW for preformed orders. So, resulting TCDW maximizes not with Cs but with Rb atom and agrees well with the experimental trend2, highlighting roles of weak interlayer interactions in determining phase transitions of layered kagome metals.

Our computations for two markedly disparate orders are made possible by developing a new large-scale molecular dynamics (MD) simulations method. A new method is specifically designed to describe lattice distortions using the relative displacements between atoms as basic variables (See Methods). Polynomial interatomic potentials are constructed using the linear regression for fitting about 2,500 basis functions to our first-principles calculation results. So, our method is accurate enough to reproduce our ab initio results very well, thus enabling us to perform large scale accurate lattice dynamics in a very long timescale.

Results

2D charge orders and their interlayer interactions

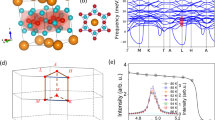
Figure 1a shows the crystal structure of AV3Sb5. Vanadium atoms form 2D kagome lattice at vertices of dashed lines in Fig. 1b, c. One thirds of Sb atoms occupy the centers of dashed hexagons and the rest two thirds are at the upper and lower plane of the kagome lattice, respectively. Alkali atoms play as spacer atoms between the layers and determine the interlayer interactions. As shown in Fig. 1c, the CDW phase has been known to form the inverse star-of-David (iSOD) structure where V atoms in 2 × 2 units are modulated into one hexagon and two triangles instead of the star-of-David structure constructed by inverting the atomic displacements of the iSOD5,25. Our ab initio calculations also prefer the former over the latter, agreeing with previous studies24,29. We note that, without interlayer interactions, the 2 × 2 CDW in each layer can take any of the four translationally equivalent structures or phases indicated by four rhombi in Fig. 1c. The interlayer interaction, however, lifts the degeneracy between those random stacking phases. In Fig. 1d, we display possible stacking orders where the different phases are denoted by different colors corresponding to those in Fig. 1c.

Fig. 1: 2 × 2 CDW of kagome metals and its low-energy stacking sequences.
figure 1

a Crystal structure of AV3Sb5 where A denotes alkali atoms of K, Rb and Cs. b Three eigenmodes of the CDW at M-points of Brillouin zone (M1, M2, and M3) for kagome shaped lattice of vanadium atoms. Blues dots are vanadium atoms and arrows denotes their displacements corresponding to each Mi(i = 1, 2, 3). c Schematic 2 × 2 CDW structures constructed from linear combinations of Mi’s where [m1, m2, m3] ≡ m1M1 + m2M2 + m3M3. Kagome lattices (dashed lines) are modulated into hexagons (blue lines) and triangles (red) forming inverse star of David structure. There are four equivalent phases of 2 × 2 CDW (rhombi with four different colors). d Low-energy stacking sequences constructed by four phases in c. The phases of CDW are distinguished by colors matching those of rhombi in c.

Full size image

We find that the same phases for neighboring layers are hardly realizable owing to the large energetic cost while the different phases are allowed and their energies for couplings are equivalent (See Supplementary Information Section 1). This implies that second-nearest-neighboring interlayer interactions should play an important role for stacking order. Without it, long-range stacking orders are absent and random stacking of CDWs would be dominant as long as the neighboring layers avoid to be the same phase (See detailed discussion in Supplementary Section 2), which contradicts experiments8,10,30. Our first-principles calculation estimates that its magnitude is order of 1 meV for 2 × 2 units in Fig. 1c. Such a small interaction may be related with possible CDW stacking faults or variations in interlayer ordering periods8,10,23,30,31. Notwithstanding its small magnitude, as we will demonstrate hereafter, it is an important interaction in freezing fluctuating charge orders of kagome metals.

From our MD simulations, we find that a interlayer correlation at temperature far above TCDW is not negligible in spite of the small negative long-rage interaction. Specifically, for CsV3Sb5 at T = 130 K, the probability that the pairs of second-nearest-neighboring layers have the same phases in the thermal ensemble turns out to be 0.66, revealing its crucial role (without it, the probability should be 0.25). From these considerations, the interlayer interactions are shown to have ambivalent characteristics depending on the interaction ranges such that nearest-neighboring layer should avoid the same phase while second-nearest-neighboring layer favors the same one.

Aforementioned formation of intralayer CDWs are captured explicitly by collecting the MD trajectories of V atom density of ρV (r;T) for a given T. In Fig. 2a, it is shown that ρV of CsV3Sb5 at T = 200 K with a simulation time of 0.4 nanoseconds perfectly match with ideal kagome lattice points. In enlarged views around the lattice point in Fig. 2b, it starts to deviate from the lattice points at T ≃ 160 K. As the temperature decreases further, it continuously deviates from the lattice points and the deviation reaches ~ 0.1 Å at T = 20 K.

Fig. 2: Preformation of CDW in CsV3Sb5.
figure 2

a Thermal distribution of vanadium atom density ρV(r; T) at T = 200 K. High (low) density regions are colored in yellow (black). b ρV(r;T) within the dotted circle in a are enlarged at the temperature range from 20 to 160 K. Green open dots denote kagome lattice points and the space of the grid (dotted lines) is 0.05 Å. c Temperature-dependent phonon spectra obtained from Sρρ(k,ω;T). In top left panel, Brillouin zone and high symmetric points of CsV3Sb5 are drawn. The spectrum at T = 20 K is multiplied by 10 for a visual clarity. The arrow in spectrum at T = 250 K indicates a soft mode. Acoustic phonon branches are invisible due to their weak intensities.

Full size image

Phonon instability

The structural instability is also reflected in the temperature-dependent phonon dispersions. At finite T, the phonon spectrum can be extracted from the density-density correlation function of Sρρ(k, ω; T) where k = (kx, ky, kz) is a crystal momentum and ω is a frequency of phonon (See Methods for details). In Fig. 2c, we plotted Sρρ(k, ω; T) of CsV3Sb5 along the high symmetric lines on (kx, ky) plane with kz = bz/2 where bz is the out-of-plane reciprocal lattice vector. At T = 250 K, a soft mode denoted by an arrow is clearly shown at L-point. As T decreases, the frequency of the soft mode approaches zero. Eventually, at T* ≃ 160 K, the structural instability develops, that may indicate a phase transitions with lattice distortions32, compatible with our simulation of ρV(r; T) in Fig. 2b. However, the structural instability here does not guarantee phase transition. Even though the local 2 × 2 CDW orders within each layer and their π-phase shift between adjacent layers can fully develops, the local CDW orders change their phases dynamically and do not spontaneously break any symmetry of the crystal. As we will see later, a global broken symmetry state occurs at much lower temperature of TCDW so that we could interpret T* as the preformation temperature of CDW.

We note that right below T*, all the softening signatures near L-point disappear as shown in Fig. 2c. At TCDW < T < T*, the preformed CDW domains have orders-of-magnitude longer lifetimes than vibrational periods as will be shown later. So, the effective phonon frequencies is essentially from the curvature of the potential around one of the four degenerate CDW phases. The phonon mode at L-point corresponding to this new metastable atomic configurations becomes harder as T decreases such that near TCDW, no softening signature can be found.

We also find that no soft modes exist along \(\overline{{{\Gamma }}{{{{{{{\rm{M}}}}}}}}}\) (Supplementary Fig. 2a), which is consistent with recent experiments reporting unexpected stability of phonon modes along \(\overline{{{\Gamma }}{{{{{{{\rm{M}}}}}}}}}\) at the transition8,21,23. Even at T > T*, the lowest M-phonon remains hard unlike L-phonon, excluding a possible preformation of CDW. At this high temperature, anharmonicity-induced phonon hardening occurs for both phonons but the effect is much stronger for M-phonon due to the enhanced interlayer force constants. If not considering the anharmonic effect, both M- and L-phonon are expected to be unstable for the structure as were demonstrated by recent first principles calculations5,24,25. We can expect that the hardening effect for phonon at U-point of BZ (2 × 2 × 4 CDW) is in-between M- and L-phonon. Indeed, the softening of dispersions at U-point around T* is less conspicuous than one at L-point (Supplementary Fig. 2b), not fully developing into instability.

Fluctuation of preformed orders

From the results so far, it seems that CsV3Sb5 undergoes a typical phase transition at T*. However, owing to large degeneracy for pairing charge orders between layers, a slow fluctuation between them proliferates across the whole layers. We note that our simulation time of 0.4 nanoseconds for the apparent ordering is long enough for simulating usual structural transitions33,34. For kagome metals, it turns out to be not. With orders-of-magnitude longer simulations time of 12 nanoseconds, we indeed found a clear signature for the fluctuation. We also confirm that the fluctuation is not an artifact from the size effect of simulation supercell (See detailed discussions in Supplementary Section 4).

The phase fluctuations are unambiguously identified by eigenmode decomposition analysis. As shown in Fig. 1b, the in-plane CDW decomposes into three symmetrically equivalent eigenmodes of Mi(i = 1, 2, 3). It can be easily checked that their linear combinations of m1(t)M1 + m2(t)M2 + m3(t)M3 can reproduce the four phases of 2 × 2 iSOD structures as shown in Fig. 1c. Here mi(t)(i = 1, 2, 3) is a time-dependent coefficient for eigenmodes of Mi where t denotes time. By inspecting temperature-dependent time evolution of mi(t) for a specific 2 × 2 supercell, we can identify slow CDW fluctuations in kagome metals (see further details in Supplementary Section 5).

Figure 3a shows a temporal evolution of m1(t) for T = 140 K. In addition to picoseconds phonon vibrations, there are clear sign changes of m1(t) in timescale of a few nanoseconds without altering its averaged absolute magnitude. This indeed indicates phase flips of CDWs. The rate of phase flips can be quantified by computing a Pearson correlation coefficient (PCC)35 for time interval of Δt, \({r}_{11}({{\Delta }}t)\equiv \frac{E[{m}_{1}(t+{{\Delta }}t){m}_{1}(t)]-E[{m}_{1}(t+{{\Delta }}t)]E[{m}_{1}(t)]}{\sigma [{m}_{1}(t+{{\Delta }}t)]\sigma [{m}_{1}(t)]},\) where E[m1] and σ[m1] are time average and standard deviation of m1, respectively. As shown in Fig. 3b, the fast phonon vibrations and the slow phase flip are manifested as picoseconds oscillation and the subsequent slow decay, respectively (For comprehensive analysis of PCCs, see Supplementary Section 5). The decay rates of r11 in Fig. 3b imply that the phase-coherence time does not exceed a few nanoseconds at 140 K and becomes longer as T decreases further. With inclusion of the phase flips, for TCDW < T < T*, the averaged local density profile of vanadium atoms of ρV should change from a Gaussian thermal ellipsoid shown in Fig. 2b into a four-peaked or non-gaussian distribution as shown in Fig. 3c. As T approaches TCDW, each peak becomes to be more distanced and eventually, the fluctuations are quenched to one of the four peaks at T = TCDW. This implies that in experiments incapable of resolving nanosecond dynamics, only the averaged properties will be observed without any symmetry-breaking feature between TCDW and T*. However, those phase fluctuations are reflected as zero frequency peak at Sρρ(k, ω; T) (see Supplementary Fig. 3), that may be accessible by inelastic neutron scattering.

Fig. 3: Fluctuation of preformed CDW.
figure 3

a Temporal fluctuation of the amplitude m1 at a specific 2 × 2 supercell for T = 140 K. The sign changes correspond to phase flips of preformed CDW. b Temporal Pearson correlation coefficient of r11(Δt) at T = 130 and 140 K. c Thermal evolution of ρV(r; T) incorporating slow phase flips. As the temperature decreases, the shape of ρV(r; T) changes from a Gaussian thermal ellipsoid (right panel, T > T*) to four-peaked distribution (two middles, TCDW < T < T*), and finally be collapsed into one of the four peaks (left) at T < TCDW.

Full size image

Critical temperatures of charge orders

Our simulations hitherto reveal that in kagome metals, TCDW is nothing but a critical temperature for a globally ordered phase by condensing the CDWs that are preformed at T*( > TCDW). Although the physical process of the phase transition is now understood, a reliable quantitative MD calculation of TCDW is undoable because the time for quenching preformed orders well exceeds our attainable simulation time. This motivates us to map our systems into an anisotropic 4-states Potts model28 to compute TCDW quantitatively using a well-established statistical method36. Due to the two well-separated time scales of dynamics (thermal vibration and phase fluctuation in Fig. 3a), if we average the atomic trajectories of preformed CDW’s over 100ps, the averaged snapshot will look like one of four 2 × 2 CDW phase in Fig. 1c, but with temperature-dependent amplitudes. The four phases become 4-states ‘spin’ variables on lattice points of layered triangular lattices as shown in Fig. 4a. So, an effective Hamiltonian for the interacting spins therein can be written as

$$H=\mathop{\sum}\limits_{\langle i,j\rangle,\alpha }{J}_{\parallel }\delta ({s}_{i,\alpha },{s}_{j,\alpha })+\mathop{\sum}\limits_{i,\alpha }{J}_{\perp }\delta ({s}_{i,\alpha },{s}_{i,\alpha+1})+\mathop{\sum}\limits_{i,\alpha }{J}_{\perp 2}\delta ({s}_{i,\alpha },{s}_{i,\alpha+2}),$$
(1)

where si,α is an effective four-states spin at i-th site of α-th layer, J∥ their effective intralayer nearest-neighboring (n.n.) interaction, J⊥ interlayer n.n. and J⊥2 every other interlayer n.n. interactions, respectively as described in Fig. 4a. Here, δ(si,α, sj,β) is zero if states of two effective spins of si,α and sj,β are different, otherwise, it is one. We note from considerations above that signs and magnitudes of the interactions should be J∥ ≪ J⊥2 < 0 < J⊥.

Fig. 4: Critical temperatures for CDW.
figure 4

a Effective lattice structure for 4-state Potts model. Effective 4-state spins locate at vertices of triangles (black circles) corresponding to 2 × 2 supercells shown in Fig. 1c. Effective intralayer (red arrow), first- (blue arrow) and second-nearest-neighboring interlayer (green arrow) interactions between spins are denoted with J∥, J⊥ and J⊥2, respectively. b, c Temperature dependent J∥(T) and J⊥(T) of AV3Sb5 (A = K, Rb, Cs), respectively. d Comparison of the experimental CDW temperatures (\({T}_{\exp }\))2 and calculated critical temperatures of T* (open squares) and TCDW (open circles) for different alkali atoms of A on abscissa.

Full size image

Unlike typical Potts models28, interaction parameters in Eq. (1) are explicit functions of temperature because amplitudes of CDW vary as the temperature changes. For T = 0, J∥(0) and J⊥(0) can be readily calculated from the energy cost forming domain wall and energy differences between different stacking, respectively (See detailed procedures in Supplementary Section 6). For T > 0, they are similarly obtained from thermally averaged potential energy of domain structure. Here, the thermal average is approximately calculated using harmonic and rigid approximations for density correlation functions (See Methods). Then, we have temperature-dependent exchange parameters of J∥(T), J⊥(T), J⊥2(T) in our 4-states Potts model. So, to compute TCDW, we need to solve the model self-consistently because temperature and the exchange parameters depend on each other. For kagome metals with alkali atoms of K and Rb, we can bypass time-consuming reference calculations by rescaling polynomial interatomic potential obtained for CsV3Sb5 without degrading accuracy (See Supplementary Section 7). We also note that the accuracy of J⊥2 from our ab initio calculation of CsV3Sb5 seems to be marginal. While the absolute magnitude of J⊥2 determines the ground state stacking structure, it turns out to play a minor role in determining TCDW. So, we set it as a parameter of J⊥2 = − 0.5J⊥ and checked that TCDW is lowered by at most 7 K when we decrease J⊥2 to be 0.

In Fig. 4b, c, the self-consistently obtained J∥(T) and J⊥(T) are shown for three kagome metals. The critical temperature for preformed orders of T* can be determined from a condition that the amplitude of intralayer CDW vanishes or that J∥(T) and J⊥(T) become zero simultaneously. As expected, the intralayer coupling of J∥(T) is largest (smallest) for CsV3Sb5 (KV3Sb5), being consistent with the lowest (largest) ECDW5. Accordingly, T* monotonically increases as the size of alkali atom increases as shown in Fig. 4d.

The J⊥ displays different temperature dependence compared with J∥(T). Since all the compounds here share the same kagome lattice layer formed by V and Sb atoms and differ by their alkali atoms, J⊥ will be dominantly set by size of the alkali atoms. Indeed, the interlayer distance for Cs compound is longest among them (Supplementary Section 1) so that it has the smallest J⊥(0) as shown in Fig. 4c. This implies that the weakest J⊥2 of Cs compound will invoke the most severe fluctuation of CDW phase among three kagome metals. We also note that as temperature approaches T*, the magnitude of J∥ is comparable to those of J⊥ as well as J⊥2. Therefore, we identify two competing features to determine thermodynamic states, i.e., the phase fluctuation of CDW counterbalances the ECDW. So, even though CsV3Sb5 has the highest T*, its TCDW can be lower than the other. Estimated T* and TCDW from Eq. (1) indeed confirm such a competitive interplay between inter- and intralayer orders, agreeing well with experimental trend as shown in Fig. 4d.

Discussion

The preformed charge order discussed so far is not measurable as discontinuities in thermodynamics variables such as a specific heat or susceptibility. Also, we expect that Raman scattering23,24,37,38 or nuclear magnetic resonance measurements39,40 may not be so easy to capture its explicit signals owing to its fluctuating phases and dynamical nature. But there might be at least three experimental signatures already indicating its existence. First, a recent X-ray diffraction experiment22 reports that the integrated peak intensity of 2 × 2 × 2 CDW order in CsV3Sb5 survives up to 160 K, well above TCDW = 94 K. In addition to that, the thermal expansion of the in-plane lattice constant shows a slope change twice at TCDW and at T = 160 K, respectively22, implying the qualitative structural changes at higher T than TCDW. Second, the coexistence of the ordered and disordered phases near TCDW is measured through nuclear magnetic resonance measurements39,40. This is consistent with a first order phase transition from our anisotropic 4-states Potts model in Eq. (1). Third one is the absence of phonon softening around TCDW8,21,23. As we already discussed, this absence is not anomaly but a consequence of preformation of CDW at much higher T*.

In addition to these indirect evidences, we may have a way to detect fluctuating charge orders directly. Because the preformed CDW not only changes the vibrational properties but also introduces slow cluster dynamics, we expect that it can be also detected as a central peak in the dynamic form factor of density fluctuation, or apparent symmetry-forbidden signals in Raman scattering reminiscing the precursor formation in ferroelectric materials41,42.

We note that our current MD methods from first-principles approaches do not show any state related with broken time-reversal-symmetry states. Within our methods, the vanadium d-orbitals have considerable out-of-plane band dispersion across the Fermi energy43 so that spin-spilt states related with them hardly develop. From these, our MD could not touch upon the various experimental signatures1,2,3,11,12,13 on time-reversal-symmetry broken phases. However, if exotic electronic and magnetic orders can couple to bond orders below TCDW, we expect that our method could reflect the corresponding structural evolutions at lower temperature.

Lastly, we point out that the tiny magnitude of J⊥2 is essential in controlling the phase fluctuation with fixed CDW amplitudes across the kagome layers. This strongly suggests that a facile engineering of thermodynamic states of kagome metals could be possible through external controls of interlayer interactions44,45 and that our current understanding of asynchronism in thermodynamics transitions of kagome metals can be applied to understand various subtle phase transitions in layered 2D crystals15,16,17,18,19,20,46.

Methods

Construction of interatomic potential

Our interatomic potential is based on the linear regression with a set of polynomial basis functions which is adequate for small displacement phonon calculations47. We note that a similar method has been used for dynamical properties of kagome metal recently48. For the interatomic potential to meet a few physical conditions such as (1) continuous translational symmetry, (2) point and space group symmetry of the crystal, (3) permutation of variables, and (4) asymptotic stability for a large displacement, basis functions are constructed as follows.

First, to meet the condition (1), we replaced the variable from the atomic displacement \({u}_{{\alpha }_{i}}\) to the relative displacement \({u}_{{\alpha }_{i}}-{u}_{{\alpha }_{i}^{{\prime} }}\) where αi is a condensed index for Cartesian components, basis atom in a unitcell and the Bravais lattice point. The index of \({\alpha }_{i}^{{\prime} }\) shares the same Cartesian component with αi but has different basis atom index and Bravais lattice point, respectively. Then, the interatomic potential of V can be written as

$$V=\mathop{\sum }\limits_{n=0}^{\infty }{V}_{n}=\mathop{\sum }\limits_{n=0}^{\infty }\frac{1}{n!}\mathop{\sum}\limits_{\{{\alpha }_{i},{\alpha }_{i}^{{\prime} }\}}{c}_{{\alpha }_{1}{\alpha }_{1}^{{\prime} }\cdots {\alpha }_{n}{\alpha }_{n}^{{\prime} }}\mathop{\prod }\limits_{i=1}^{n}({u}_{{\alpha }_{i}}-{u}_{{\alpha }_{i}^{{\prime} }}),$$
(2)

where the brace indicates that the summation runs for all indices of αi and \({\alpha }_{i}^{{\prime} }\) in the summands. The condition (2) can be straightforwardly incorporated by applying all symmetry operations R of a given crystal to Vn in Eq. (2), that can be written as

$$\tilde{V}_{n}=\frac{1}{{N}_{R}}\mathop{\sum}\limits_{R}R{V}_{n},$$

where NR is a number of symmetry operations. The condition (3) will be automatically met from linear dependence check of basis function. The condition (4) is usually ignored in phonon calculations but becomes to be critical for potentials with a huge number of variables. Since our interatomic potential has thousands of variables, without explicit consideration of the condition (4), optimization processes do not end but diverge. In general, it is hard to prove that some multivariable polynomial is bounded below but we avoid the negative divergence by forcing the highest-order basis function to be multiples of squares and by constraining their coefficients to be nonnegative during the linear regression process. Rigorously, though this approach does not guarantee the condition (4), we find that the V in Eq. (2) constructed in this way did not cause any practical problem. The resulting basis functions are sorted in ascending order by the largest distance between the two atoms in the basis function and linearly-dependent basis functions are removed by Gram-Schmidt orthogonalization.

For CsV3Sb5, we truncated the polynomial out at the 4th order and cutoff the relative distance at 10 Å for the 2nd-order basis functions and 6 Å for 3rd- and 4th-order ones. Importantly, only V displacements are used for the variables in the 3rd- and 4th-order basis function because we found that the anharmonic effect is prominent only between the V atoms due to their large displacements in CDW phases. The number of basis functions made in this way is 434, 521, and 1453 for 2nd-, 3rd- and 4th-order, respectively.

The reference configurations are collected from multiple sources to ensure reliable sampling of potential energy surfaces. We performed first-principles MD simulations of 4 × 4 × 2 supercell at 100 and 200 K for 1600 steps with a time step of 10 fs. We then collected 53 configurations from each temperature that were equally spaced in time of 300 fs. Additional 30 configurations are collected from randomly displacing ( < 0.04 Å) atomic positions from the optimized 2 × 2 × 2 CDW structure. Lastly, the linearly interpolated configurations between high-symmetric structures without CDW and the optimized 2 × 2 × 2 CDW structures are also used to collect 9 more configurations. These diverse sets of 145 configurations are found to be enough to reproduce energy landscape of low-energy stacking structures fruitfully.

The coefficients of basis functions are fitted to the calculated atomic forces. We first perform the linear regression procedure to minimize the following loss function,

$$\mathop{\sum}\limits_{i}{| {{{{{{{{\bf{A}}}}}}}}}_{i}{{{{{{{\bf{C}}}}}}}}-{{{{{{{{\bf{F}}}}}}}}}_{i}| }^{2}$$
(3)

where C is the m-dimensional coefficient vector of basis functions of \({c}_{{\alpha }_{1}{\alpha }_{1}^{{\prime} }\cdots {\alpha }_{n}{\alpha }_{n}^{{\prime} }}\) in Eq. (2), Fi is the 3N-dimensional vector of reference atomic forces in the ith configuration including N atoms, and Ai is the 3N × m matrix whose jth column is atomic forces in the configuration i calculated from the interatomic potential by fixing the coefficient of jth basis function as cj = 1 and by forcing all the other coefficients to be zeros. Here, m = m2 + m3 + m4 where mk(k = 2, 3, 4) is the number of kth-order basis functions.

For the coefficients of 4th-order basis function to be nonnegative, the coefficient vector of C obtained from Eq. (3) is again optimized using a nonlinear conjugate gradient method for the modified loss function, \({\sum }_{i}{| {{{{{{{{\bf{A}}}}}}}}}_{i}{{{{{{{\bf{D}}}}}}}}{{{{{{{\bf{C}}}}}}}}-{{{{{{{{\bf{F}}}}}}}}}_{i}| }^{2}\) where D is a m × m diagonal matrix with conditions of Dii = − 1 only when i > m2 + m3 and ci < 0 and otherwise, Dii = 1. This enforces nonnegative condition for the coefficients of 4th-order basis function.

Molecular dynamics simulation

Using the obtained interatomic potential, our molecular dynamics (MD) simulations are performed with the velocity Verlet algorithm49 for the integration of Newton’s equation of motions and simple velocity rescalings are applied for every time steps of 5 fs to incorporate the temperature effect. We have used 60 × 60 × 12 supercell for calculations in the Fig. 2 and 12 × 12 × 12 supercell for Fig. 3. All thermodynamic ensembles are collected after 100ps of thermalization steps. The density-density correlation function is given by Sρρ(k, ω; T) = ∣ρ(k, ω; T)∣2 and ρ(k, ω; T) is defined as

$$\rho ({{{{{{{\bf{k}}}}}}}},\omega ;T)=\int\nolimits_{-\infty }^{\infty }\rho ({{{{{{{\bf{k}}}}}}}},t;T){e}^{-i\omega t}dt,$$

where \(\rho ({{{{{{{\bf{k}}}}}}}},t;T)=\frac{1}{\sqrt{N}}{\sum }_{l,\kappa }{e}^{-i{{{{{{{\bf{k}}}}}}}}\cdot {{{{{{{{\bf{R}}}}}}}}}_{l,\kappa }(t;T)}\) and Rl,κ(t; T) is the position vector of basis atom κ in a unitcell Rl at the time t and temperature T.

First-principles calculations

Ab initio calculations based on density functional theory (DFT) are performed using the Vienna ab initio simulation package (VASP)50 using a plane wave basis set with a kinetic energy cutoff of 300 eV. The generalized gradient approximation with Perdew-Burke-Ernzerhof scheme51 and dispersion correction using DFT-D352 are adopted to approximate exchange-correlation functional and the projector augmented wave method53 is used for the ionic potentials. For structural optimizations and first-principles MD, 12 × 12 × 12 and 3 × 3 × 2 k-points are sampled in the Brillouin zone of CsV3Sb5, respectively and the internal atomic coordinates of CDW states were optimized until the Hellmann-Feynman forces exerting on each atom becomes less than 0.01 eV/Å.

Thermal average of potential energy

For anharmonic systems without light elements, ab initio MD simulation is a quite accurate method to investigate its thermal properties. Nevertheless, it is very time-consuming so that less demanding computational methods have been developed. The lists of those methods can be found in the recent literatures47,54. The main idea of those methods is that the original system can be approximated by the harmonic systems that minimizes the free energy of the system, and equilibrium structures and effective phonon frequencies (or effective potential) can be obtained from them. Our interest is, however, the dynamics between metastable configurations (i.e. CDW phase domains) so that the effective potential should be obtained by thermally averaging fast motions of atoms not only in the ground state configurations but also in the metastable ones.

To obtain such an average, we first assume that N-body density correlation function of \(\widetilde{\rho }\) does not vary when a ground state thermal ensemble experience a static spatial displacement, i.e., a rigid density approximation. Within this approximation, the static displacement corresponds to the metastable configuration and the thermal average can be performed using the exact \(\widetilde{\rho }\). Our second approximation is to replace the \(\widetilde{\rho }\) with \({\widetilde{\rho }}_{H}\) of an approximate harmonic system, which can be written as a closed form of normal modes54.

Procedures to obtain the effective potential from the zero-temperature interatomic potential V can be formulated as follows. For periodic systems, V can be expanded with Taylor series of atomic displacements as

$$V=\mathop{\sum }\limits_{n=0}^{\infty }{V}^{(n)}\equiv \mathop{\sum }\limits_{n=0}^{\infty }\frac{1}{n!}\mathop{\sum}\limits_{\{\alpha \}}{\phi }_{{\alpha }_{1}\cdots {\alpha }_{n}}\mathop{\prod }\limits_{i=1}^{n}{u}_{{\alpha }_{i}}$$
(4)

where αi is a condensed index for Cartesian components, basis atom in a unitcell and the Bravais lattice point. Here, \({\phi }_{{\alpha }_{1}\cdots {\alpha }_{n}}\) is a nth-order force constant and \({u}_{{\alpha }_{i}}\) is a Cartesian component of a displacement vector from a reference position chosen to be a local minimum or saddle point of V. The brace indicates that the summation runs for all indices of αi in the summands.

At finite T, the nth-order thermally averaged potential of \({V}_{T}^{(n)}\) can be written as

$${\overline{V}}_{T}^{(n)}\equiv {\langle {V}^{(n)}\rangle }_{T}=\frac{1}{n!}\mathop{\sum}\limits_{\{\alpha \}}{\phi }_{{\alpha }_{1}\cdots {\alpha }_{n}}{\langle \mathop{\prod }\limits_{i=1}^{n}{u}_{{\alpha }_{i}}\rangle }_{T}$$
(5)

where the bracket denotes the ensemble average with \(\widetilde{\rho }\). Without varying \(\widetilde{\rho }\), the average potential energy for adding a static displacement of \({{{{{{{\bf{U}}}}}}}}=({U}_{{\alpha }_{i}},\cdots \,,{U}_{{\alpha }_{n}})\) to the thermal ensemble of \({u}_{{\alpha }_{i}}\) can be written as

$${\overline{V}}_{T}^{(n)}({{{{{{{\bf{U}}}}}}}})\equiv \frac{1}{n!}\mathop{\sum}\limits_{\{\alpha \}}{\phi }_{{\alpha }_{1}\cdots {\alpha }_{n}}{\langle \mathop{\prod }\limits_{i=1}^{n}({U}_{{\alpha }_{i}}+{u}_{{\alpha }_{i}})\rangle }_{T},$$
(6)

where kth-order effective force constant is defined as \({\phi }_{{\alpha }_{1}\cdots {\alpha }_{k}}=\frac{{\partial }^{k}{\overline{V}}_{T}({{{{{{{\bf{U}}}}}}}})}{\partial {U}_{{\alpha }_{1}}\cdots \partial {U}_{{\alpha }_{k}}}.\) When we evaluate \({\langle \mathop{\prod }\nolimits_{i=1}^{n}({U}_{{\alpha }_{i}}+{u}_{{\alpha }_{i}})\rangle }_{T}\) in Eq. (6), we replace \(\widetilde{\rho }\) with \({\widetilde{\rho }}_{H}\) for which the approximate harmonic system is chosen to have the similar density correlations with the original anharmonic system. Then, using a thermally averaged potential in Eq. (6), we compute a set of harmonic frequencies from which we reconstruct a new \({\tilde{\rho }}_{H}\). So, if a self-consistency for \({\widetilde{\rho }}_{H}\) is fulfilled, we can obtain the desired thermal averaged potential of a rigidly shifted thermal ensemble. We use this method to compute the temperature-dependent interaction parameters of J∥(T) and J⊥(T) as discussed in Sec. 6 of SI.