1 Introduction

Civil engineers are always seeking solutions for urban lifeline protection and preservation of the urban architectural complex against seismic destruction [1,2,3,4]. Conventional seismic protection systems have shown their advances in seismic protection in terms of their ease of installation and low cost. The core idea for these approaches is based on the strength and stiffness of structures. In general, however, structural components with larger stiffness suffer more from seismic effects. Then, structures should be stiffer to prevent possible collapse, which increases the cost and complexity of structural design. Problems also occur in other seismic protection systems such as vulnerability against fire, problems with energy dissipation and single-mode isolation. In this regard, the availability of phononic crystals and acoustic/elastic metamaterials provide efficient solutions [5,6,7]. These artificially designed structures do not rely on the properties of buildings or infrastructures under protection. Instead, they form a stop band for waves at certain frequencies induced by interference between forward and backward waves. The seismic surface waves including Rayleigh waves and Love waves can be blocked by structures, namely, seismic metabarriers [8]. Therefore, the enclosed urban region can be protected.

Though “metamaterial” is comprised of “material” and the prefix “meta”, it is not a new material discovered or invented in the world. Instead, it is a series of novel artificially designed structures based on a variety of different mechanisms, including but not limited to Bragg resonance, local resonance, nonreciprocal, and condensed topological phases. The prefix “meta” was translated from Greek and it is similar to the meaning of “beyond”, indicating that this category of materials can exhibit extraordinary properties which were not discovered in conventional metal or inorganic nonmetal materials [9]. Typically, with a biaxial holey-structured acoustic metamaterial with multilayered and hierarchical functional units, super-resolution with deep-subwavelength local features can be demonstrated [10]. By periodically arranging unit cells in topological trivial states and topological non-trivial states in certain arrays and forming an interface between the unit cells in different states, the topologically protected wave propagation with back-scattering-, defect- and disorder-immunity can be realized [11, 12]. By applying the concepts from electromagnetic metamaterials and mimicking the related principle, a one-dimensional (1D) waveguide can be realized for water wave cloaking and mode conversion of water waves [13]. The unconventional sound absorption barriers can simultaneously exhibit sound absorption and ventilation [14]. Despite some specific examples, other interesting phenomena like acoustic topological pumping [15], Klein tunneling [16], higher-order topological states [17], indistinguishable mechanical cloaking from homogeneous surroundings [18], Willis coupling [19], and optical [20] and acoustic [21] rainbow trapping also attract engineers’ and researchers’ attention.

In earthquake engineering, seismic metamaterial which aims at efficiently tuning seismic surface Rayleigh and Love waves, and seismic bulk waves shows its advances because minimum influence of functional units and incident seismic waves on the protected buildings can be realized. The full-scale experiment carried out by Brûlé et al. [22] had a lasting impact on the development of larger-scale phononic crystals at extremely low frequency ranges. They used the Mindlin plate theory [23] to estimate the displacement field of time-harmonic surface flexural waves. They made an analogy between periodic boreholes and phononic crystals. The Bloch theorem was applied to classical civil engineering structures. Consequently, the surface Rayleigh wave at 50 Hz can be efficiently attenuated. Though 50 Hz is not within the common seismic wave frequency ranges which are always smaller than 20 Hz, this study has been considered as a starting point for using artificially designed seismic barriers to control natural vibrations. It also provided an efficient tool for transportation engineers to minimize train or vehicle-related vibration or noise [24,25,26]. However, metastructures with periodic boreholes or other periodic substructures are based on the Bragg scattering mechanism. It relies on structural periodicity and the working frequency ranges are close to the size of the repeated functional unit, indicating that the attenuation of waves in civil and transportation engineering requires a large structural size because these waves are always with large wavelengths. Therefore, new mechanisms need to be explored for effective applications in earthquake engineering.

Locally resonant phononic crystals, or acoustic metamaterials can generate bandgaps at subwavelength scale or even deep subwavelength scale which are generally comprised of heavy core coated by soft materials [27,28,29], as first reported by Liu et al. [30]. For Bragg scattering type bandgap, the interaction between the repeated unit cells is dominant. Comparatively, bandgaps in locally resonant acoustic metamaterials originate from the coupling between the long traveling wave and local resonance [31]. It should be noted that the functional unit cells in an acoustic metamaterial can be periodic [32,33,34], aperiodic [35] or graded [36]. Thus, an acoustic metamaterial can simultaneously possess Bragg scattering and local resonance bandgaps [37,38,39]. Distinguished by location, two typical seismic metamaterials can be designed, namely outer shielded metabarriers [40] and metafoundations [41,42,43]. For those shielded metamaterials on the ground, the structure always consists of an array of pillars, where the pillars can be analytically simplified as spring mass systems located within a semi-infinite space. Then the system will interact with the travelling wave, forming a surface wave bandgap. Metafoundation aims at isolating seismic waves and reducing environmental vibrations [44]. The local resonance is located below the structures, which is different from the classical multiple tuned mass dampers, efficiently leading to the reduction of structural base shear.

Seismic metamaterials are always designed based on the aforementioned mechanisms and utilizing a variety of geometrical shapes, such as snowman-like [45], H- and V-shaped [46], cross-like [47], T-shaped [48], Minkowski-like [49], Matryoshka-like [50] seismic metamaterials. These configurations generally originated from nature or artificial structures. For example, forest trees can be regarded as local resonant seismic metamaterials. Strong wave attenuation of Rayleigh waves which propagate along the surface of a semi-infinite space made of soft sedimentary soil. With the time-domain analysis, the vibration mode shapes show that the simplified tree model has a strong interaction with Rayleigh wave in certain frequency ranges. In this study, ground is assumed as a homogenous elastic media, although it is well known that the real soil condition is more complex and different from a single-layer ground. Therefore, the effects of layers of soil have been widely studied [51, 52], showing that the frequency ranges of the cut-off band gaps strongly rely on the constraint between periodic piles and the bottom layer of soil [53]. Another interesting topic concerning the application of metamaterials in transformed urbanism is metacity [54]. Similar to the forest seismic metamaterials, the buildings in urban regions can be regarded as surface resonators. Not only can an isolated building act as a seismic barrier, but also an interacting set of buildings, like a district of a city, can efficiently couple with seismic waves.

Many local resonant metamaterials combine the mechanical properties of local resonance and structural periodicity. Generally, bandgaps in lower frequency ranges originate from local resonance. A typical characteristic of these bandgaps is the narrow bandwidth. These bandgaps are of extreme research interest because the major frequency ranges for transportation are around 50 Hz, which are very close to the natural vibration frequencies of human organs and thus will lead to the occurrence of resonance. Therefore, bandwidth enlargement is significant for local resonance. It is known that the local resonance frequency is related to the properties of resonating units such as mass and equivalent spring constant. A phononic system with multiple local resonances always possesses multiple narrow local resonant bandgaps [38]. By calculating the upper and lower limits of each bandgap, it is possible to construct a system with multiple resonances exhibiting graded bandgap regions. Then, the bandgaps couple with each other and form a wide bandgap. For a wave transport medium which is an elastic half-space, the graded design will not only generate extremely large wide bandgaps but also lead to mode conversion of surface Rayleigh waves.

Realization of a metacity majorly relies on the interaction between the propagating wave and buildings, where the buildings are considered as above-ground resonant sources. Some buildings in the district will also suffer from the incident seismic waves. In this paper, inspired by naturally available pines, we design pine-like seismic metabarriers to attenuate surface Rayleigh waves at low frequency ranges. The canopy of pine can be assumed as a heavy mass while the trunk is equivalent to an elastic spring. The dispersion relation of a single unit pine is numerically obtained by applying the Bloch-Floquet periodic boundary conditions to an above-ground pine model, indicating the relation between system frequency and wavenumber. A bandgap for the surface Rayleigh wave can be observed, and the upper and lower limits of the bandgap are highlighted. The upper intersection is the coupling between bandgap and bulk shear wave while the mode shape of the lower intersection indicates the strong interaction between local resonance and travelling waves. The frequency ranges of two intersections can be efficiently tuned by altering the geometric parameters of the pine model. For waves that propagate through an array of pines with gradually varying geometric parameters, surface wave mode conversion occurs if the upper intersection frequencies of the pines decrease while the wave trapping mode will be excited when the lower intersection frequencies increase. Following this mechanism, a metamaterial barrier for mode conversion and surface wave energy reduction can be constructed. Due to the graded geometric parameters of pines, it is also found that the bandgap of the array is obviously widened. A scaled numerical model is then built to simulate a finite urban area with random buildings. A surface Rayleigh wave is excited and propagates through urban areas with or without pine array protection. Extremely low stress is observed in protected urban areas. Finally, two time-history analyses are presented based on real earthquake signals. The attenuation effect of pine-like seismic metamaterial on the Imperial Valley 1940 signal is much better than that on the Northridge 1994 signal, which implies that a wider bandgap is required for a seismic metamaterial to attenuate real earthquake signals. This paper can be further extended to more naturally available seismic metamaterials and models with more complex soil and geological conditions.

2 Naturally available metamaterial model and its dispersion relation

Starting from the analysis of naturally available forest metamaterials, the inspiration from nature for seismic metabarrier or metafoundation designs is always very attractive to researchers and engineers. Indeed, a single above-ground pillar can also be regarded as a spring-mass model [55] and the first local resonant frequency can be easily obtained. In this regard, the first resonant frequency is only tunable by varying the height of the pillar when the material properties, i.e., Young’s modulus and Poisson’s ratio, are fixed. However, previous research works always assumed simplified tree shapes while the effects of canopies were neglected. There is another type of local resonance adopted in structural design, which is a heavy mass with high mass density supported by soft bars with relatively small elastic Young’s modulus [28, 38, 56]. Here, the equivalent mass of the system is approximately assumed as the heavy mass because the mass of the soft bar is relatively small. The spring constant is dependent on the cross-sectional area and the material properties. Inspired by this design principle and considering the properties of canopies, we can also realize surface Rayleigh wave mode conversion and energy trapping, and broadband and subwavelength bandgaps.

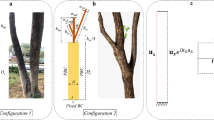
The real-life photos of several above-ground trees are given in Fig. 1a for reference and they can be found in nature. The height of trees differs from each other due to various factors such as sunlight conditions, age and planting density. Besides, the canopy shapes are also different. For simplicity and without any loss of generality, the three-dimensional pines are simplified in a two-dimensional numerical model with respect to the vertical cross-section because the major topic of this study is the attenuation of Rayleigh waves. The variation of pines provides a very useful degree of freedom for parametric tuning and design. An enlarged primary unit pine highlighted as a yellow dashed frame in Fig. 1a is shown in Fig. 1b. It includes two major parts of a tree, i.e., the trunk and canopy. Therefore, we refer to these two parts to build a numerical model, as shown in Fig. 1c.

Fig. 1
figure 1

(a) A picture of a pine forest, and (b) a single tree unit. (c) The enlarged numerical model of the tree, and (d) the whole numerical model of a tree on a semi-infinite space

Full size image

The geometric characteristics of the trunk are dependent on two parameters, i.e., the width \(w\) and the height \(H\). The construction of the canopy is more complicated. As observed in Fig. 1c, the numerical model of canopy consists of three parts, i.e., one top triangle and two trapezoids. The top triangle is a regular triangle with \(\theta = {60^\circ }\) and \({b_1} = {h_1}\). The middle trapezoid results from a regular triangle whose top vertex is located in the middle of the height of the top triangle. Neglecting the overlapped small triangle leads to an isosceles trapezoid. The bottom length of the middle trapezoid is \({b_2}\) and the height is \({h_2}\). It is not difficult to obtain the relation between \({h_1}\) and \({h_2}\), i.e., \({h_2} = {{\left( {\sqrt 3 {b_2} - {h_1}} \right)} \mathord{\left/ {\vphantom {{\left( {\sqrt 3 {b_2} - {h_1}} \right)} 2}} \right. \kern-0pt} 2}\). Similarly, the bottom trapezoid is a regular triangle, whose top vertex is located in the middle of the middle trapezoid, where the overlapped region with the middle trapezoid is neglected. The bottom length of the bottom trapezoid is \({b_3}\) and the height is \({h_3}\), and \({h_3} = {{\left( {\sqrt 3 {b_3} - {h_2}} \right)} \mathord{\left/ {\vphantom {{\left( {\sqrt 3 {b_3} - {h_2}} \right)} 2}} \right. \kern-0pt} 2}\). The length of the smallest repeated soil unit is \(a\), which determines the boundaries of the irreducible Brillouin zone of this system. Finally, in Fig. 1d, the geometric parameters of the semi-infinite space are shown, where the height is \(D\).

The seismic metamaterial consists of an array of pines in Fig. 1d, as shown in Fig. 2a. According to the design principles of above-ground seismic metamaterials [57], the local resonance frequency is dependent on the mass and equivalent spring constant. Keeping the mass density constant, the volume of the heavy mass has great effects. Similarly, cross-sectional area, height and material properties of the elastic support influence the equivalent spring constant. Therefore, we define a scale ratio \(\delta\) for each unit cell, where the geometric parameters like widths and height of the neighboring units are simultaneously enlarged or shrunk by \(\delta\). Then, the local resonance frequencies of the cells can be varied as designed.

Fig. 2
figure 2

(a) The numerical model of an array of pines with a pre-defined scale ratio. The distance between trees is the lattice constant and two line detectors are arranged on the surface of half-space to receive signals on both sides of the array. An enlarged local plot of the pine array where (b) scale ratio is smaller than 1 and (c) scale ratio is larger than 1

Full size image

As we may recall, the periodic local resonating phononic crystals show concurrent Bragg scattering bandgap and local resonance bandgaps. Therefore, prior findings utilized these two types of bandgaps for attenuating acoustic/elastic waves [37, 38]. It is noticeable that the local resonance bandgaps rely more on the resonating units, and they exist in the systems in the absence of periodicity. Based on these, Fig. 2 shows two types of seismic metabarriers, one with \(\delta < 1\) in Fig. 2b and another with \(\delta > 1\) in Fig. 2c. The general Cartesian coordinate is in vertical (Z-direction) and horizontal (X-direction) directions. Two line detectors before and after the pine arrays are set to receive the signals forward and backward of the pine arrays. For simplicity, we constructed an array with 20 pines, and we defined any of the pine units as the \({i^{th}}\) unit (from left to right and \(1 < i < 20\)). The distances between the left and right ends of Dector 1 and the center line of the first pine are \({x_3}\) and \({x_2}\), respectively. The distances between the left and right ends of Dector 2 and the center line of the last pine are \({x_2}\) and \({x_3}\), respectively. The length of the two detectors is \({x_3} - {x_2}\). A point source was established to excite Rayleigh waves in the half-infinite space and the distance between the source and the left boundary of the space is \({x_1}\). The distance between the first pine and the left boundary of the space is \({x_4}\). To absorb waves incident to the boundaries and to avoid unwanted reflected waves, low-reflecting boundaries (LRB) were set on the left, right and bottom sides of the semi-infinite space. The upper side except the regions of point source, two detectors and the pine arrays were set as free.

The dispersion relation of a unit cell characterizes the interaction between propagating waves and the structure. The passband indicates that waves with certain frequency ranges can propagate through the structure. Comparatively, the bandgap region is the frequency range where waves are attenuated by the structure, hence waves are not allowed to propagate through the structure. In the system shown in Fig. 2a, the Rayleigh wave majorly propagating on the surface. To this end, the Floquet-Bloch boundary condition can be applied to the two vertical sides and the wave vectors can be swept from \({k_x} = 0\) to \({k_x} = {\pi \mathord{\left/ {\vphantom {\pi a}} \right. \kern-0pt} a}\). Some bandgaps can also be directional while some other bandgaps can only tune one specific wave mode. Taking the elastic wave propagating in a thin plate as an example, there are antisymmetric wave modes and symmetric wave modes, like \({S_0}\), \(S{H_0}\) and \({A_0}\) modes [58]. No bandgap can be observed in the band structure, but due to the wave polarization, a full bandgap can be observed for the out-of-plane \({A_0}\) modes, while this frequency range is the pass band for the other two modes. In other words, the full band structure consists of the dispersion curves for all modes, while for some specific modes, the dispersion curves can be distinguished from other modes via proper approaches, like the well-defined out-of-plane projection [59]. Similar phenomena occur in the dispersion relation for surface Rayleigh waves, where the bandgap can only be captured with a certain range of wavenumbers [60].

In the bandgap analysis, the following parameters were assumed, width \(w = 2\) m, height of trunk \(H = 12\) m, \({b_3} = 14\) m, \({h_1} = 7.76\) m, \({h_2} = 4.85\) m, \({h_3} = 6.06\) m, lattice constant \(a = 15\) m and depth of semi-infinite space D = 150 m. The tree material properties were referred to some published data [61], where compressional velocity is \({v_{p,t}} = 2200\) m/s, shear velocity is \({v_{s,t}} = 1200\) m/s, and density is \({\rho_t} = 450\) kg/m3. The compressional velocity, shear velocity and density of soil are \({v_{p,s}} = 450\) m/s, \({v_{s,s}} = 250\) m/s and \({\rho_s} = 1800\) kg/m3, respectively. A finite element (FE) numerical model was established and analyzed by COMSOL Multiphysics.

As the analysis is restricted to 2D models, the elastic waves are limited to propagation in a 2D half-space and excitation on the surface will lead to the generation of bulk waves and surface waves. The coupling between pines and elastic waves also leads to two modes, i.e., the vertically longitudinal mode and the transverse mode. The torsional mode will not be excited. The dispersion relation of a unit pine in Fig. 1d is shown in Fig. 3a. The red dashed line indicates the shear mode and the blue lines are the mode from hybridization between pines and surface Rayleigh waves. The light ray dots are other mode shapes such as compression wave modes. No complete bandgaps can be found by sweeping the dimensionless wavenumber from 0 to 1. However, distinguished from the mode shapes, a bandgap exists for surface Rayleigh waves ranging from 5.5 to 7.4 Hz. This bandgap is determined by C and T points. The former is the intersection between the hybridization mode and the shear wave mode, and the latter is the intersection between the hybridization mode and the edge of the irreducible Brillouin zone. The displacement in the vertical direction of the pine is shown, indicating strong hybridization between above-ground resonance and surface Rayleigh wave. From the displacement field in the semi-infinite space, no interaction and coupling between the neighbouring unit cells can be captured, hence it is evident that the bandgap originates from local resonance instead of Bragg scattering. The properties based on local resonance will be rarely influenced by structural periodicity and the geometric parameters concerning local resonance frequencies can be programmable according to different demands.

Fig. 3
figure 3

a Band structure of a pine on a semi-infinite space with a vibration mode shape at the lower edge of the bandgap. b Variation of the dispersion curve by sweeping the scale ratio at a specific frequency

Full size image

Analogous to an unconventional dispersion relation in Colombi et al. [55], we demonstrate the variation of scattering and dimensionless wave number at 5 Hz. Similar to Fig. 3a, the red dashed line is the dispersion curve of shear waves and the gray shadow is the bandgap region. C and T points are also highlighted in this figure, and the geometric parameters are referred to that used in Fig. 3a. By decreasing the geometric parameters, the hybridization mode shapes will first interact with the shear mode. In this case, the surface Rayleigh wave at 5 Hz will be converted to shear waves when propagating through an array of pines where the geometric parameters become smaller. This array is always named as an inverse metabarrier [55]. The mode shape of the finite pine arrays is also shown beside the C point. Despite a small percentage of energy escaping from the mode conversion point, most Rayleigh waves stop propagating on the surface and they are diverted deep underground as bulk waves. Comparatively, for the Rayleigh wave at the same frequency, mode conversion will not occur at a pine array with gradually incresed geometric parameters. This is because an increase of geometric parameters will first cause the curve to reach T point. The surface Rayleigh wave then interacts with the local resonance mode and most of the energy will be trapped by pines, as shown in the mode shapes of the finite pine array. Besides, it should be noted that because waves at the bandgap region cannot propagate through the structure, any increase in geometric parameters will not cause the curve to reach C point and similarly, any decrease will not cause the curve to reach C point.

In civil and architectural engineering, noise induced by vehicle, machine and ground-borne vibration is mainly within the low frequency ranges. Therefore, metamaterials in low frequency ranges for vibration attenuation and noise absorption are of great research interest. We herein investigate the influence of geometric parameters and material properties of pines including canopy density \({\rho_t}\), angle of the top triangle \(\theta\) and trunk width. In the aforementioned analysis, the densities of the canopy and trunk are assumed the same. This paper aims to utilize the pine shape and to design an above-ground resonator for surface Rayleigh wave attenuation. The material properties are for easy reference and they can be adjusted according to different demands. Therefore, by sweeping the canopy density \({\rho_t}\) from 450 kg/m3 to 900 kg/m3, stepped by 50 kg/m3, as shown in Fig. 4a, we can find that both upper and lower limits of the passband are tuned to lower frequency ranges, where the slope of decrease of the lower limit is much larger, thus indicating that the bandgap becomes lower and wider. A lower bandgap with the same lattice constant will benefit the practical application of acoustic metamaterials because it means that the structure with the same occupied area can attenuate elastic waves with larger wavelengths. It is difficult to achieve in conventional civil structures like open trench barriers and filled trench barriers. We also examine the effects of varying \(\theta\) from 40° to 60°, stepped by 1°, and a similar trend of changes in bandgaps is observed in Fig. 4b. The core design principle of these two tuning methods is to change the mass of the above-ground resonators. Generally, a heavier mass generates a bandgap at lower frequency ranges. In addition, the trunk width is further tuned from 1 m to 8 m with a step of 0.5 m in Fig. 4c. The bandgap is shifted to a much higher frequency range while its width is only slightly influenced. This is due to the higher stiffness of the equivalent elastic spring. Conclusively, a lower frequency bandgap can be generated with a heavier canopy and thinner trunk.

Fig. 4
figure 4

Parametric analyses for the effects of (a) canopy density, (b) angle of the top triangle \(\theta\) and (c) trunk width \(w\) on the frequency ranges of the surface Rayleigh waves

Full size image

3 Elastic surface wave attenuation with the pine arrays

The aims of analyzing the band structures of a unit cell are to obtain the frequency ranges of the bandgap and observe the relation between different wave modes. After discussing the properties of the unit cell, we further refer to the model in Fig. 2b and c, and numerically construct an above-ground pine array on a semi-infinite space. The geometric parameters are set as \({x_1} = 60\) m, \({x_2} = 10\) m, \({x_3} = 50\) m, \({x_4} = 180\) m, respectively. The scale ratio \(\delta\) here is the size ratio between the (j + 1)-th pine and the j-th pine. The pine size decreases gradually for a scale ratio smaller than one and vice versa. Generally, wave attenuation can be identified by both band structure and transmission ratio. In Fig. 5, the transmission ratio is defined as \(\eta = 20{\log_{10}}\left( {{{\left| {{u_{out}}} \right|} \mathord{\left/ {\vphantom {{\left| {{u_{out}}} \right|} {\left| {{u_{in}}} \right|}}} \right. \kern-0pt} {\left| {{u_{in}}} \right|}}} \right)\), where \({u_{in}}\) is the displacement signal detected by the first detector and \({u_{out}}\) is the output displacement signal. In Fig. 2, the total signal is the summation of two signals for an elastic wave propagating through the pine array, i.e., the incident wave from the excitation source and the reflected wave from the pine arrays. Therefore, to examine the incident waves, one efficient approach is to remove all the pine unit cells and then record the elastic wave signal.

Fig. 5
figure 5

Broadband Rayleigh wave attenuation with a pine array. The transmission ratio varies from 3 to 10 Hz where (a) the transmission ratio is smaller than 1 and (b) the transmission ratio is larger than 1, and (c, d) the correspondingly selected mode shapes for seismic metamaterial and semi-infinite space at 7.15 Hz

Full size image

In Fig. 5, the transmission ratio is examined by sweeping Rayleigh wave frequency from 3 to 10 Hz, which is the range of interest in earthquake engineering. The blue line is the transmission ratio detected without the pine array, hence Rayleigh wave can propagate in a half-space freely. Afterwards, the pine array is employed and the red dashed line is obtained. Compared to the blue line, a significant reduction in transmission ratio can be obtained between 5 to 9 Hz. From the mathematical point of view, no real solutions are found in this region from the governing equations. Therefore, the waves are efficiently attenuated. Compared to the bandgap region in Fig. 3a, the wave attenuation region is much wider because the pines are designed as a graded array. It is known that each pine has its local resonance frequency. By carefully designing the geometric parameters of the neighbouring pines, the bandgaps of pines gradually vary and they show some overlapped regions. Then, the wave attenuation region can be regarded as the summation of all bandgaps. Figure 3b is the transmission ratio for a pine array with \(\delta > 1\), and a similar wave attenuation region is obtained. Further, in Fig. 5c and d, the mode shapes for the entire structure at 7.15 Hz are shown. The figures show the mode conversion of Rayleigh wave and excellent wave attenuation, respectively.

In Fig. 6, a quantitive study is presented for displacement fields in the vertical direction of the surface at 7 Hz and 7.75 Hz where a point displacement of 1 m is prescribed as the source. The scaling ratio is set smaller than 1 and thus mode conversion of Rayleigh wave occurs. Comparing Fig. 6a and Fig. 6b, the onset location of mode conversion for the seismic metamaterials is sensitive to the excitation frequency with the same pine array. With a higher frequency wave signal, the onset location of mode conversion shifts to the shorter pine because the local resonating frequency of a shorter pine is higher. Moreover, possible wave escape can be found for both arrays and the average displacement field for waves at 7 Hz is much smaller than that at 7.75 Hz, indicating that the efficiency of seismic metamaterial is also frequency-dependent. Figure 6c and d are the mode shapes for easy identification of the conversion location. The wavelength of a Rayleigh wave is determined by the neighbouring largest or smallest displacement field. Comparing the wavelength of a Rayleigh wave and the distance between two pines, it can be found that the former is much larger than the latter, implying significant subwavelength wave attenuation occurs in this structure. In other words, above-ground pine arrays can efficiently couple with incident surface Rayleigh waves at low frequency ranges at a relatively small geometric scale.

Fig. 6
figure 6

Quantitative analysis for surface displacement fields at (a) 7 Hz and (b) 7.75 Hz with scale ratio smaller than 1, and (c, d) the corresponding mode shapes with Rayleigh wave converted to shear bulk wave

Full size image

Wave trapping of Rayleigh waves occurs in a pine array with a scaling ratio larger than 1. Similar to the characteristics in Fig. 6, frequency-dependent wave attenuation can be captured in Fig. 7. Vertical displacement field at the trapping location dramatically decreases in a very short distance. Energy of the escaped waves at 7.75 Hz is much larger than that at 7 Hz. Compared to arrays with the scaling ratio smaller than 1, the efficiency of the array in Fig. 7 is slightly higher at both frequencies. From Fig. 7c and d, although the Rayleigh wave is strongly attenuated by the pines beyond the trapping location, the escaped waves are also able to interact with the rest of the pines. However, from the displacement fields in the pines, the interaction becomes weaker.

Fig. 7
figure 7

Quantitative analysis for surface displacement fields at (a) 7 Hz and (b) 7.75 Hz with scale ratio larger than 1, and the corresponding mode shapes at (c) 7 Hz and (d) 7.75 Hz

Full size image

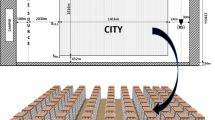
To further explore the real attenuation properties of pine-like elastic seismic metamaterials, a schematic plot for the full-size urban and suburban areas is presented in Fig. 8a. A pine array with \(\delta > 1\) is constructed between two cities, but it is closer to the city on the right. Many tall buildings with varying natural vibration frequencies ensure a summation of wide frequency bandgaps. The distance between the first building to the source, the arrangement of the buildings and the shape of the buildings are kept the same. The two cities show mirror symmetry to each other and the mirror symmetry origin is the source point. When a Rayleigh wave is excited at the source point, the city on the left will interact with incident waves directly without any protection while the city on the right will be protected by the gradient pine array. The LRB boundary condition is applied to the bottom of the half-space to avoid unwanted reflected waves. Different from the setup of the unit cell in Fig. 1 where Floquet-Bloch boundary conditions are applied, two LRB boundary conditions are applied to the left and right boundaries such that waves from the surface will not be reflected by these two boundaries. The simulated stress field is presented in Fig. 8b, where a point load at 7.28 Hz is given and determined by the bandgap frequency ranges in Fig. 3. The colour represents different levels of von Mises stress ranging from zero to the maximum value. Extremely high von Mises stress levels can be observed in the buildings for the city on the left, especially those which are closer to the point source. Comparatively, the city on the right is well protected by the pine arrays and a very low von Mises stress level in the buildings is observed. Similar phenomena are shown in Fig. 8c where the pine arrays with \(\delta < 1\) are constructed, but in Fig. 8d, surface Rayleigh wave is converted to shear bulk wave instead of directly trapped by the above-ground resonators. Conclusively, the gradient pine array with either \(\delta > 1\) or \(\delta < 1\) in suburban regions have shown significant efficiency in protecting the urban region against seismic surface wave destruction.

Fig. 8
figure 8

(a) A typical city on a semi-infinite space where urban pine arrays are arranged with a scale ratio larger than 1 to protect the city from seismic destruction. (b) Numerical mode shape at 7.28 Hz. (c) The same city with a scale ratio smaller than 1 and (d) its corresponding numerical model at 7.28 Hz

Full size image

Figure 8 presents a qualitative analysis of wave attenuation with pine-like seismic metamaterials. A further quantitative examination is demonstrated in Fig. 9, where a time transient analysis is performed. The configuration of the harmonic vertical point load can be referred to Chen et al. [60]. The blue lines are the acceleration signals received by Detector 1 and the red lines are those received by Detector 2. In Fig. 9a, the frequency of the load is 7.2 Hz, which is within the bandgap range of the structure. A significant reduction in acceleration can be observed, which means that most of the wave energy is dissipated by the pine arrays. Because waves can be reflected by different media regardless of whether the media have bandgaps or not, we further apply another source at 2 Hz. It should be noted that 2 Hz is outside the bandgap frequency ranges. It will examine the assumption that attenuation of waves is due to Snell’s law instead of bandgap, which means most of the waves can be reflected to the front of the pine arrays. From Fig. 9b, we can find that the red curves share the same shape with the blue curves. The difference is that there is a shift between two curves. This shift is the time for the wave to propagate from Detector 1 to Detector 2. Besides, the peaks and valleys of the two curves are the same, indicating weak coupling between the pine-like seismic metamaterials and propagating waves. The mode shapes at \(t = 3.07\) s are presented in Fig. 9c and d, where the waves at 2 Hz can propagate through the pine array without any influence while those at 7.2 Hz cannot reach the end of the pine array.

Fig. 9
figure 9

Time-domain analysis of a semi-infinite space protected by a pine array at (a) 7.2 Hz (within the working frequency range), and (b) 2 Hz (outside the working frequency range). The corresponding mode shape (c) at 7.2 Hz where Rayleigh wave is efficiently attenuated, and (d) at 2 Hz where Rayleigh wave passes freely

Full size image

4 Examination using real earthquake records

Two well-known earthquake records were used in this section to examine the performance of the pine-like seismic metamaterials. Firstly, the earthquake signal from Northridge 1994 was applied as an excitation source of the system. Both classical barrier and inverse barrier were employed. In Fig. 10, the curves in blue are the signals received at Detector 1 and the red curves are the attenuated signals by the pine arrays. In Fig. 10a and b, which were obtained from time-domain analysis, the peaks and valleys of the two signals seem very close to each other. Only minor reductions of accelerations can be captured in red curves at some specific time steps. Most of the signals are not affected in both cases. Therefore, the time-domain analysis indicates the failure to use pine barrier to attenuate signals from Northridge 1994. We further performed the frequency domain analysis of the system and the reason for the failure could be found, as shown in Fig. 10c and d. With both classical and inverse pine arrays, the wave amplitudes are not influenced in the low frequency ranges. Comparatively, wave components with frequencies larger than 5.5 Hz are significantly attenuated. The frequency domain analysis demonstrates that the pine arrays can only couple with certain components of the seismic waves in Northridge 1994 and it does not attenuate most of the wave components.

Fig. 10
figure 10

Time-domain analysis of pine-like seismic metamaterial using real earthquake signal, i.e., Northridge 1994, where the scale ratios are (a) larger than 1 and (b) smaller than 1. The corresponding frequency-domain analysis where the scale ratios are (c) larger than 1 and (d) smaller than 1

Full size image

From the systematic analysis of the unit cell and entire system earlier, the effectiveness of pine array is proved. As we may recall, the working frequency ranges of pine arrays are significant and they determine the attenuation properties. Therefore, for Northridge 1994 with major frequencies smaller than the array working frequency ranges, the pine array definitely fails to attenuate the waves. Further, we applied another earthquake signal, i.e., Imperial Valley 1940. Both classical and inverse pine arrays show good ability for surface Rayleigh wave attenuation. The acceleration peak can be reduced by half or more compared to its original values, as shown in Fig. 11a and b. The frequency domain analysis shows that the major wave components are in higher frequency ranges compared to Northridge 1994, as shown in Fig. 11c and d. This frequency range is consistent with the working frequency ranges of the pine arrays. Therefore, the pine arrays with gradient design are effective in attenuating surface Rayleigh waves.

Fig. 11
figure 11

Time-domain analysis of pine-like seismic metamaterial using real earthquake signal, i.e., Imperial Valley 1940, where the scale ratios are (a) larger than 1 and (b) smaller than 1. The corresponding frequency-domain analysis where the scale ratios are (c) larger than 1 and (d) smaller than 1

Full size image

5 Conclusion

In conclusion, we have designed a pine-like seismic metamaterial for efficient surface Rayleigh wave attenuation. A scale ratio is defined to tune the height and width of pines. Then, broadband bandgap is realized by coupling the bandgap regions of every pine unit in the array. Due to the interaction between local resonance and Rayleigh wave, the pine-like seismic metamaterial is able to trap and convert the low frequency Rayleigh wave at subwavelength scale. To further tune the bandgap to a much lower frequency range, a parametric sweep analysis of geometric parameters is performed. It is shown that the angle of top triangle, canopy density and trunk width can efficiently influence the bandgap region.

In addition, by analyzing the geometric parameters and dimensionless wavenumber, the relation between surface wave and bandgap can be obtained. Consequently, surface waves can be either converted to shear bulk wave or trapped on the surface by a gradient design of the pine arrays. Quantitative analysis is performed to show a significant reduction of surface displacement with pine arrays. A full-scale city model is then built. A frequency domain analysis indicates that the pine arrays in suburban areas can efficiently protect the urban region from seismic destruction. Lastly, a time-history analysis with two real earthquake signals, i.e., Northridge 1994 and Imperial Valley 1940, validates the working frequency range of the pine arrays. It highlights that the pine arrays are only efficient to attenuate earthquake waves with certain frequency ranges. This work can be further extended to many practical application scenarios such as naturally available vibration isolation devices for high-speed railways and protective barriers for significant infrastructures. Extensive studies may be conducted by considering more complex environmental and soil conditions such as water table, the porosity of the soil and tree growth induced various changes in structural parameters.