Drag on a plate perpendicular to the flow of an elasto-viscoplastic fluid

Abstract

The flow with no inertia of an elasto-viscoplastic fluid around a plate perpendicular to the flow direction was considered. Firstly, experiments were performed with a model yield stress fluid, an aqueous Carbopol gel. The viscoelastic behavior of the fluid is identified by steady and transient rheological measurements. The drag force on the plate has been measured as a function of the plate velocity in steady state and in relaxation after stopping the movement. The role of the initial stress state in the fluid was highlighted. Secondly, numerical simulations were carried out using the finite element method with Lagrangian integration points. As a first approach, the elasto-viscoplastic behaviour of the gel has been simplified by a constitutive equation based on the Maxwell and Herschel-Bulkley models. The solid–liquid transition is defined by the von Mises criterion. The comparison between experimental and numerical data are quite satisfactory.

1 Introduction

The presence of a yield stress associated with an elastic behaviour fundamentally affects the flow structure in processes. The understanding of the role of elasto-viscoplasticity is necessary to optimize the processes of these fluids and has been the subject of numerous developments in recent years [1]. We have chosen to focus on the flow of these elasto-viscoplastic (EVP) fluids around a plate perpendicular to the flow direction. This obstacle was chosen because it is a classical case in fluid mechanics and corresponds to practical applications such as the flow of complex fluids around a blade in a mixer or around fins in heat exchangers. These flow configurations can be observed for example in polymer processing or the food industry where elasto- viscoplastic fluids are commons.

The aim of the present study is to provide new experimental data on this flow configuration and, in particular, on the drag on the obstacle. The model yield stress fluid used in the experiments is finely rheologically characterized to bring out its elasto-viscoplasticity and to take into account the influence of the initial stress state in the fluid. Predictions provided by numerical simulations based on the same method as used in [2] are compared to the experimental results.

In the case of Newtonian fluids, this configuration has been the subject of numerous analytical, numerical and experimental studies. Among these, one can mention Tomotika and Aoi [3] who analytically studied the creeping flow around a flat plate parallel and perpendicular to the flow direction. They determined the analytical expressions of the drag coefficient, the streamlines and the pressure distribution on the plate. The drag coefficient of a flat plate parallel to the flow direction was calculated numerically by Tamada et al. [4] using the Navier–Stokes equations for Reynolds numbers ranging from 0.1 to 10. Dennis et al. [5] studied the flow behaviour, the streamlines, and demonstrated the formation of a vortex around the plate at higher Reynolds numbers. In et al. [6] numerically studied the two-dimensional flow around a flat plate with different angles of incidence. They determined the drag and lift coefficients for Reynolds values between 1 and 30.

Concerning shear-thinning fluids, Wu and Thompson [7] studied, numerically and experimentally, the flow around a flat plate with different angles of incidence. The authors determined the influence of inertia, flow index and angle of incidence on the drag and lift coefficients.

Let us now consider work on simple viscoplastic fluid flows, i.e. without taking into account the elastic contribution, around a plate. Brookes and Whitmore [8] experimentally studied the static drag force of a plate immersed in a Bingham fluid. They showed that this force is proportional to the immersed surface of the plate and proposed an analytical expression linking the static drag force, the frontal area and the yield stress. Other authors such as Savreux et al. [9] have numerically studied in 2D the flow of a Bingham fluid perpendicular to a flat plate. They discussed in details the morphology of the flow with negligible inertia as a function of the Oldroyd number defined as the ratio between the yield stress effects and the viscous effects, before calculating the drag coefficient and proposing analytical solutions in the high yield stress domain. Patel and Chhabra [10] used the finite element method to simulate the flow around an elliptical cylinder. The drag coefficient and the shape and size of the sheared and unsheared regions in the vicinity of the obstacle were calculated.

Ouattara et a.l [11] studied experimentally and numerically the flow of Carbopol gels around a plate with incidences between 0 and 90°. They considered Carbopol gels as simple viscoplastic fluids, without elasticity. The authors determined the drag and lift forces on the plate and quantified the effects of yield stress. The measured forces were compared with numerical results and with data from the literature. Significant differences between the experimental and numerical results were observed. The simulations were carried out using the Ansys Fluent software with an anelastic Herschel-Bulkley constitutive equation. This viscoplastic model regularised with the Papanastasiou model [12] does not allow to take the elastic contribution into account.

Jossic et al. [13] studied the morphology of Carbopol gel flows around a circular plate perpendicular to the flow direction. They determined the yielded zones and velocity profiles around the plate.

In the field of geotechnics, the stability of anchoring plates in plastic soils has been the subject of numerous studies [14,15,16]. These studies with different approaches to plasticity, seek to determine the force that can be applied to the plate before the soil fails. They made it possible to quantify the drag force in the area of dominant plastic effects.

Let us now consider work on EVP fluid flows around a plate or other geometries. Experimental and numerical works taking into account elasto-viscoplasticity is more sparse and relatively recent. Few studies concern the configuration of our present study. Our previous study [2] investigated numerically the creeping flow of an EVP fluid around a plate perpendicular to the flow direction. The same Finite Element Method with Lagrangian Integration Points (FEMLIP) and EVP constitutive equation as in the present study has been used. The influences of plasticity and elasticity on kinematic and stress fields as well as on the drag coefficient has been discussed. It should be recalled that FEMLIP has the particularity and major advantage of dissociating the material points from the calculation points, which makes it an ideal candidate for the modeling of the solid–liquid transition [17]. This makes it possible to model the elastic behaviour below the yield stress without regularisation and consequently to integrate an EVP constitutive equation more representative of the real behaviour of the Carbopol used in the experiments.

In the case of EVP fluid flow around a plate parallel to the flow direction, two studies can be cited. Ferreira et al. [18] only studied the kinematic field of the flow around a plate without calculating the drag force. They showed that elasticity modifies the shape of the yielded and unyielded zones in the vicinity of the plate. They observed a decrease in the extent of the sheared zones following an increase in speed. Furthermore, Ahonguio et al. [19] studied experimentally and numerically the creeping flow of an EVP fluid around a plate parallel to the flow direction. They quantified the influence of elasticity and yield stress on the drag force and kinematic field in the vicinity of the plate. The EVP constitutive equation and the FEMLIP method implemented are identical to those used in the present study.

Recent numerical studies have focused on the flow of an EVP fluid around different geometries such as the cylinder [20] and the sphere [21] by coupling the Saramito model [22] with the isotropic kinematic hardening (IKH) introduced by Dimitriou et al. [23]. It can be used to model the rheological behaviour of Carbopol gels. It is valid even for nonlinear deformations and predicts continuous stresses upon yielding [1]. This model has been used in numerical and experimental studies of the flow of Carbopol gels around a sphere or bubble [21, 24].

Examining the role of elasticity in the flow of a Carbopol gel around a sphere, Fraggedakis et al. [21] showed that the plastic drag decreases as the elasticity of the material increases. The flow configuration considered in the present study seems to have never been taken into account before in the literature.

The influence of the initial stress state, i.e. the residual stress state of the material resulting from its mechanical history is also analyzed. This stress state is not due to thixotropy but to the plasticity of the fluid. This aspect is all the more important as the present study is placed in the domain where the yield stress effects are important compared to viscous effects. Mougin et al. [25] showed the significant influence of the residual stress state on the dynamics of bubbles with very slow velocities in a yield stress fluid such as Carbopol gels. In this field, the shape and trajectory of bubbles are mainly controlled by the residual stress state present in the fluid. To our knowledge, the influence of this parameter in EVP fluid flows around obstacles has never been considered in the literature.

First, the experimental approach, such as the rheological characterization of the fluid, the experimental device for measuring the drag force and the experimental results are presented. Some of the experimental details are given in the studies of Ouattara et al. [11, 26, 27]. Therefore, only essential informations are presented here. The second part is dedicated to the modelling and numerical simulations. First, the configuration of the computational domain and the associated boundary and initial conditions are presented as well as the governing equations and the EVP constitutive equation. The shear-thinning contribution of the experimental fluid is taken into account in the modelling and the characteristic dimensionless numbers of the flow are introduced. The FEMLIP numerical method, already presented elsewhere [2, 17, 19] will be briefly reminded.

The analysis and discussion sections compare the numerical and experimental results during both the steady and relaxation states as well as the influence of the initial stress field on the drag force.

2 Materials and rheometry

An aqueous gel of Carbopol C940 has been chosen for the experiments. It is an easy to prepare cross-linked polyacrylic acid resin manufactured by BF Goodrich. This gel has the advantage of being transparent and is often used in fluid mechanics experiments where visualizations are needed [9, 11, 13, 25,26,27]. Often considered has model viscoplastic fluids, their rheological behavior has been the topic of numerous studies. They have shown that elasto-viscoplastic constitutive equations are more realistic to represent the flow behaviour of these fluids. A review of all these studies can be found in [28]. The influence of the physical and chemical contributions on the rheological behaviour of Carbopol based microgels have been considered. To summarize, their specific properties result from their microstructure of solvent swollen microgels [29, 30]. When the polymer concentration is high enough, they exhibit a solid–liquid transition with no or very low thixotropy [31,32,33,34]. Dimitriou et al. [23] provides a fairly comprehensive review of the literature in which the characterisation of this transition for Carbopol gels has been studied. They behave as a viscoelastic fluid below the yield stress and flow as a shear-thinning fluid above the yield stress. In addition, it is worth mentioning that their microstructure is favourable to a very weak elongational behaviour [35,36,37]. The presence of normal stresses has been observed in these gels during flow [29, 38, 39].

The rheological properties of the gel were determined with a DHR3 rheometer (TA instruments) under controlled stress in steady and dynamic regimes. In the transient regime, measurements were made with the ARES-G2 rheometer (TA instruments) working in controlled deformation. The surfaces of the cone-plate measuring cell are roughened to avoid slippage at the walls [31]. The measurements were carried out by controlling the evaporation according to techniques developed by Magnin and Piau [31, 32]. A temperature of 22 °C ± 1 °C was imposed during the experiments. The measurement uncertainties are estimated at about 7% for the rheological parameters.

Figure 1 illustrates the evolution of the shear stress $\tau$ as a function of the shear rate $\dot{\gamma }$ in steady state. It is known that the steady state shear behaviour of aqueous Carbopol gels follows the Hershel-Bulkley model described by Eq. 13. The gel used in all the experiments has the following rheological properties, a yield stress ${\tau }_{0}=115$ Pa, a consistency K = 40.4 Pa.sⁿ and a flow index n = 0.4.

Fig. 1

Steady state flow curve of the Carbopol solution. Estimate of yield stress by relaxation measurements is also presented

Figure 2 shows the evolution of the elastic G′ and viscous G″ shear moduli as a function of the shear strain. The linear domain extends to about 3% with ′ $Pa$. The latter is 19 times higher than the viscous modulus G″. Note that G′ and G″ intersect each other at a strain of about 100% corresponding to values of about 90 Pa. The stress can then be estimated at around 90 Pa, consistent with the yield stress measured in steady state.

Fig. 2

Evolution of the elastic ($G{\prime}$) and viscous ($G{\prime}{\prime}$) modulus as a function of shear strain at the frequency of 1 Hz

In addition, transient shear tests were conducted to characterize the relaxation behavior of the gel. A shear rate step is applied to the fluid and the shear stress is measured as a function of time. Figure 3 shows the time evolution of the shear stress $\tau$ during a shear rate step. Different phases can be observed: start-up, steady state and stress relaxation after stopping shear. When the shear rate returns to zero, the stress relaxes to a non-zero residual value. This characterizes the existence of a yield stress within the fluid. The behavior obtained is similar to that observed by Magnin and Piau [31] on Carbopol gels. In Fig. 1, it can be seen that the shear stress values measured at the end of relaxation regime are close to the steady state stress level measured at low shear rates, thus confirming the low thixotropy of Carbopol gels.

Fig. 3

Time evolution of the shear stress for different shear strain rates

Figure 4 shows that when shear returns to zero, the shear stress $\tau$ relaxes to a non-zero residual stress. This indicates the existence of a yield stress within the fluid. These relaxation curves can be modelled using Eq. 1. Two exponentials are needed to obtain a good fit of experimental data.

$$\tau ={\alpha }_{1}.{e}^{-\frac{t}{{t}_{1}}}+{\alpha }_{2}.{e}^{-\frac{t}{{t}_{2}}}+{\tau }_{r}$$

(1)

${\tau }_{r}$ stands for the residual stress at the end of relaxation. ${t}_{1}$ and ${t}_{2}$ are two characteristic relaxation times. ${\alpha }_{1}$ and ${\alpha }_{2}$ are two numerical coefficients quantifying the rate of decay of the stress related to the two above mentioned relaxation times. These 5 parameters are summarized in Table 1 for different shear rates. Their evolution as a function of the shear rate can be modeled using the 5 following empirical relationships, Eqs. 2, 3, 4, 5 and 6.

Fig. 4

Stress relaxation after different shear rates

Table 1 Values of the coefficients of Eq. (1) fitting stress relaxation as a function of shear rate

$${\alpha }_{1}\approx 48.3 {\dot{\gamma }}^{0.23}$$

(2)

$${\boldsymbol{\alpha }}_{2}\approx 29.5\boldsymbol{ }{\dot{{\varvec{\gamma}}}}^{0.17}$$

(3)

$${t}_{1}\approx 0. 2 {\dot{\gamma }}^{-0.71}$$

(4)

$${t}_{2}\approx 4.1 {\dot{\gamma }}^{-0.74}$$

(5)

$${{\varvec{\tau}}}_{{\varvec{r}}}\approx 87\boldsymbol{ }{\dot{{\varvec{\gamma}}}}^{0.04}$$

(6)

The regression coefficient obtained when fitting theses five equations are respectively R² = 0.98, 0.99, 0,99, 0.97 and 0.91. ${t}_{1}$ is around one order of magnitude lower than ${t}_{2}$. ${t}_{1}$ can then be related to short time scales due to the fluid elasticity (elasticity of the microgels) while ${t}_{2}$ is more likely representative of the microstructure reorganization after the fluid has been submitted to shearing. The residual stress ${\tau }_{r}$ decreases by around 20% between 0.01 and 3 s.⁻¹. The value obtained at the lowest shear rates provides a good order of magnitude of the yield stress obtained more precisely with the steady state flow curve (Fig. 1). Ahonguio et al. [38] have measured the first normal stresses ${N}_{1}$ in steady state. The experimental datA can be fitted by ${N}_{1}=93.5+120 {\dot{\gamma }}^{0.44}$

This rheometric characterization shows that two characteristic time scales are needed to model the behaviour of a Carbopol gel under relaxation. The Herschel-Bulkley model, which is purely viscoplastic and takes no account of the effects of elasticity is therefore unable to capture transient phenomena. This is why the numerical results presented below are based on the Herchel-Bulkley model coupled to the Maxwell model. It allows a finer modelling than a purely viscoplastic model.

3 Experimental set-up

The technical details of the experimental set-up for measuring the drag force have been presented in the papers by Ouattara et al. [11]. It is schematically represented in Fig. 5. The plate is moved in a free surface channel containing the yield stress fluid, by a velocity-controlled mobile trolley. The plate is instrumented with a drag force sensor.

Fig. 5

Computational domain and boundary conditions

The channel is made of transparent Plexiglas. It has a length of 3 m, a width of 22 cm and a height of 21 cm. For the plate, the length is l = 14 cm, the width a = 3 cm, and the thickness e = 0.3 cm. To prevent the yield stress fluid from sliding down, the bottom wall of the channel was covered with rough paper of roughness Ra = 120 µm. The side walls of the channel remain untreated to be as close as possible to a 2D configuration. The plate is also covered with sand paper to avoid slippage. The range of applied velocity Uo is between 0.003 and 3 mm/s.

4 Numerical modeling and non-dimensional numbers

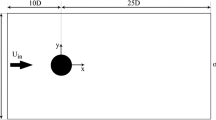
The flow considered in this study was modelled in two dimensions. Figure 5 represents the computation domain and the boundary conditions. The plate has a length $a$ without thickness. The computation domain has the dimensions $L$ in length and $H$ in height, with $L / a=6$, $H / a=5$ and $H / b=3$. The velocity profile is set to be uniform in the inlet and outlet sections and is noted ${U}_{0}$.

The boundary conditions used are as follows:

• The model is periodic, so the conditions on AC and BD are identical: ${{U}_{X}}_{1}={{U}_{X}}_{2}={U}_{0}$.

• The fluid adheres to the walls so that the velocity is zero on the surface.

• The free slip condition (${\tau }_{{{X}_{1}X}_{2}}=0$) is adopted along the section (AB). As the flow is very slow, no deformation of the free surface occurs and the free slip condition is sufficient to approximate the experimental free surface.

In general, the initial conditions have been chosen so that the stress and velocity fields are zero in the whole computational domain. This state is close to the initial state called "homogeneous state" defined in the experimental section. For some simulations, a second velocity step following the first one, as shown in Fig. 8, has been imposed. For this second velocity step the initial stress state is the one left by the plate after relaxation of the first step. This second initial state is close to the one called "inhomogeneous state" described in the experimental section.

Since the flows considered are isothermal, they are only governed by the principles of momentum and mass conservation. Since the flows are with no inertia, the momentum conservation is expressed with the Stokes equation (Eq. 7). The continuity equation (Eq. 8) expresses the mass conservation in the case of an incompressible flow.

$${\left({{\varvec{f}}}_{{\varvec{e}}{\varvec{x}}{\varvec{t}}}\right)}_{{\varvec{i}}}+{{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}},{\varvec{j}}}-{{\varvec{p}}}_{,{\varvec{i}}}=0$$

(7)

$${{\varvec{u}}}_{{\varvec{i}},{\varvec{i}}}=0$$

(8)

where ${\mathrm{f}}_{\mathrm{ext}}$, ${\uptau }_{\mathrm{ij}}$, $\mathrm{p}$ and $u$ represent the external force vector, the components of the deviatoric stress tensor, the pressure and the velocity vector respectively. ${\mathrm{X}}_{\mathrm{i}}$ and ${\mathrm{X},}_{\mathrm{i}}$ denote the component and its spatial derivative along the direction $\mathrm{i}$ of the field $\mathrm{X}$. The EVP constitutive equation used in this study has already been presented in [2, 19]. It is briefly recalled here. It should be noted that this model does not require any regularization of the yield stress and takes into account the elastic effects both below and above the yield stress. The constitutive equation is based on the Maxwell model (Eq. 9). The deviatoric stress tensor ${\varvec{\tau}}$ with components ${\tau }_{ij}$ can be expressed as a function of the apparent viscosity ${\eta }{\prime}$ the elastic modulus $\mathrm{G}$ and the strain rate tensor $\mathrm{D}$ with components ${D}_{ij}$. In this model, $D$ is the resultant of both an elastic and a viscous contribution, respectively ${D}_{e}$ and ${D}_{v}$

$${D}_{ij}={{D}_{e}}_{ij}+{{D}_{v}}_{ij}=\frac{{\widehat{\tau }}_{ij}}{2G}+\frac{{\tau }_{ij}}{2{\eta }{\prime}}$$

(9)

$\widehat{\tau }$ is the Jaumann corotational rate of the deviatoric stress tensor (Moresi et al., 2003). it makes it possible to take into account the non-linear angular deformations that deformable materials can undergo. It is used to maintain the symmetry of the deformation tensor, particularly when the solid undergoes large deformations and rotations. It therefore provides a more accurate model of the material's actual behaviour. It is defined as:

$$\widehat{\tau }=\dot{\tau }+\tau W-W\tau$$

(10)

with $W$, the material spin or vorticity tensor which corresponds to the antisymmetric part of the velocity gradient:

$$W=(\nabla u- {\nabla u}^{t})/2$$

(11)

When the stress level computed as the second invariant of the deviatoric stress tensor

$${\tau }_{II}={\left[\frac{1}{2}\tau :\tau \right]}^\frac{1}{2}$$

(12)

is above the yield stress ${\tau }_{0}$ in the sense of the von Mises criterion, the fluid exhibits a viscous behavior and shear stresses are expressed as the product of the apparent viscosity ${\eta }{\prime}$ with the viscous strain rate tensor ${D}_{v}$. Where ${\eta }{\prime}$ is expressed from the Herschel-Bulkley model (Eq. 13) using the flow index $n,$ the consistency $K,$ the yield stress ${\uptau }_{0}$

$${{\varvec{\tau}}}_{{\varvec{i}}{\varvec{j}}}=\left[\frac{{{\varvec{\tau}}}_{0}}{{{2{\varvec{D}}}_{{\varvec{v}}}}_{{\varvec{I}}{\varvec{I}}}}+{\varvec{K}}{\left({{2{\varvec{D}}}_{{\varvec{v}}}}_{{\varvec{I}}{\varvec{I}}}\right)}^{{\varvec{n}}-1}\right]{{{\varvec{D}}}_{{\varvec{v}}}}_{{\varvec{i}}{\varvec{j}}}=2{{\varvec{\eta}}}^{\boldsymbol{^{\prime}}}{{{\varvec{D}}}_{{\varvec{v}}}}_{{\varvec{i}}{\varvec{j}}}$$

(13)

The second invariant of the strain rate tensor ${{\mathrm{D}}_{\mathrm{v}}}_{\mathrm{II}}$, is defined as

$${{{\varvec{D}}}_{{\varvec{v}}}}_{{\varvec{I}}{\varvec{I}}}={\left[\frac{1}{2}\left({{\varvec{D}}}_{11}^{2}+{{\varvec{D}}}_{22}^{2}{+\boldsymbol{ }2{\varvec{D}}}_{12}^{2}\right)\right]}^\frac{1}{2}$$

(14)

Additional details regarding the discretization of Eqs. 7, 8, 9, 10, 11, 12, 13 and 14 are presented in [2] and [19].

Convergence was evaluated with three meshes: 64X32, 128X64 and 240X80 elements along the X1 and X2 axes respectively. The solution accuracy is 10⁻⁵. Their influence has been tested through the computation of the non-dimensional velocity. The differences between three meshes did not exceed 2%. The finest mesh has been selected.

The equations and boundary conditions have been made non dimensional using a for the space variables and U₀ for the velocities. This shows that the flow can be described using the dimensionless numbers listed below. They allow to evaluate the influence of the different physical parameters involved.

The Oldroyd number, also called the Bingham number in the literature, is defined as the ratio of plastic to viscous effects [40]:

$${\varvec{O}}{\varvec{d}}=\frac{{{\varvec{\tau}}}_{0}}{{{\varvec{K}}\left(\frac{{{\varvec{U}}}_{0}}{{\varvec{a}}}\right)}^{{\varvec{n}}}}$$

(15)

The Weissenberg number, defined as the ratio between the elastic and viscous effects, is expressed as follows:

$${\varvec{W}}{\varvec{i}}=\frac{{\varvec{K}}}{{\varvec{G}}}{\left(\frac{{{\varvec{U}}}_{0}}{{\varvec{a}}}\right)}^{{\varvec{n}}}$$

(16)

In this study, the Oldroyd numbers range from 5.5 to 178. The Weissenberg numbers are between 10^–8 and 10^–4.

Another dimensionless number characteristic of this flow is the flow index. It was kept constant and fixed at n = 0.4, a value identical to that of the fluid used in the experiments. The other dimensionless numbers are scaling ratios of the lengths L/a, H/a and b/a which have been kept constant throughout the present study.

The governing equations presented above with their boundary and initial conditions were solved using the FEMLIP [17]. This numerical approach makes possible to simulate all types of material behaviour in a context of large deformations. The originality of this method lies in its ability to model materials with large deformations while following the material properties in space, as well as any internal variables. It is a hybrid method that couples both an Eulerian approach for the finite element grid described by a set of fixed nodes in space and a Lagrangian approach for a set of moving particles in the grid for the material discretization of the domain of interest. A more complete description can be found in appendix as well as in [2, 19] in which the problem was solved for a Bingham fluid with n = 1. Here, the problem is solved with the same procedures but taking into account the shear-thinning behaviour of the experimental fluid, n = 0.4. The computations were carried out with a regular mesh. A time step $\Delta \mathrm{t}= {10}^{-3 }\mathrm{s}$ and a convergence criterion of ${10}^{-5}$ were fixed.

5 Results and discussion

Figure 6 represents the typical time evolution of the drag force ${F}_{d}$ exerted by the fluid on the plate, measured when a speed step is imposed. Three flow phases are observed: start-up, steady state and the relaxation of the drag force. During this last phase, the drag force gradually decreases towards a non-zero residual force. The level of this residual force is governed by the yield stress of the fluid. It is worth mentioning the similarity of the rheometer response (Fig. 3) and the drag force response (Fig. 6) to a shear rate or velocity step. Typical shear rates Uo/a applied to the plate are between 10^–4 and 10^–1 s⁻¹. The stresses or forces do not relax to zero after a mechanical load has been applied to the fluid.

Fig. 6

Time evolution of the drag force under velocity 0.003 mm.s⁻¹. Plate velocity has been stopped at 440 s

The presence of a residual stress state in the fluid raises the question of the influence of the initial state of the material on the drag force [25]. To answer this question, two initial stress states were defined. The first initial state is the one created by the passage of the plate in the channel. It is named hereafter the "inhomogeneous state". The second state, called the "homogenized state", is generated by homogenizing the fluid with a grid introduced into the channel. This process is applied along the entire length of the channel used. Homogenization of the gel in the channel is achieved by moving the grid from the bottom of the channel up to the free surface. This process was repeated for each drag force measurement.

5.1 Steady-state drag coefficient

Figure 7 shows the evolution of the numerical and experimental drag coefficients as a function of the Oldroyd number. The drag coefficient of the plate is defined by:

Fig. 7

Evolution of the non-dimensional steady state drag coefficient as a function of the Oldroyd number

$${{\varvec{C}}}_{{\varvec{d}}}^{\boldsymbol{*}}=\frac{{{\varvec{F}}}_{{\varvec{d}}}}{{{\varvec{\tau}}}_{0}.{\varvec{a}}}$$

(17)

It is observed that the drag coefficient decreases to a plateau as Od increases. At low Oldroyd numbers, viscous effects become predominant over plastic effects. At high Oldroyd numbers, plastic effects become predominant. Thus, the drag coefficient tends towards an asymptotic value governed only by the yield stress and the plate geometry. Merkak et al. [41] showed that the evolution of the drag coefficient as a function of the Oldroyd number can be described by Eq. 18.

$${{\varvec{C}}}_{{\varvec{d}}}^{\boldsymbol{*}}={{\varvec{C}}}_{{\varvec{d}},\boldsymbol{\infty }}^{\boldsymbol{*}}+\frac{{\varvec{\beta}}}{{{\varvec{O}}{\varvec{d}}}^{{\varvec{m}}}}$$

(18)

For sufficiently large Oldroyd numbers, the drag coefficient tends towards a constant value ${C}_{d,\infty }^{*}$ which depends only on the yield stress and the geometry of the obstacle. The term $\frac{\upbeta }{{\mathrm{Od}}^{\mathrm{m}}}$ represents the viscous contribution to the drag coefficient. The experimental and numerical values of ${C}_{d,\infty }^{*}$, $\beta$ and m are grouped in Table 2.

Table 2 Value of the coefficients of Eq. (18)

As mentioned in the introduction, geotechnical studies have led to several values for plate pull-out resistance in a perfectly plastic medium with different approaches. Merifield et al. [14] established a range between 11.16 and 11.86 and for Rowe and Davis [16] between 11.42 and 10.28. These values are close to the value obtained with FEMLIP (Fig. 7). Note that a value of ${C}_{d,\infty }^{*}$ = $10.41$ was obtained with the FEMLIP for a Bingham fluid (n = 1) in [2] and here 10.88 for n = 0.4 (Table 1). The flow index $n$ has a very small influence on the drag force when the plastic effects become dominant over the viscous effects.

Table 2 compares numerical and experimental values. The numerical approach tends to overestimate the drag values for large Od. If the uncertainties of the experimental measurements are taken into account, the numerical prediction is quite close to the experimental results. The deviation is the smallest at the highest viscous effects. The deviation becomes more important when yield stress effects become preponderant (Fig. 7). This discrepancy may also be due to the solid–liquid transition modelling used. The von Mises criterion used in the present study would be valid as experimentally shown by Ovarlez et al. [42] for Carbopol gels. But due to their status as model yield stress fluids, Carbopol gels have been the subject of numerous studies [23, 33, 43,44,45,46]. They have shown that, in fact, the solid–liquid transition in Carbopol gels is more sophisticated. Cheddadi et al. [47], have shown that for EVP fluid the initial state of the material is a crucial information. It is needed to obtain a steady solution in complex flow because the von Mises criterion “can be satisfied by an infinite set of combinations of the stress components that could exist inside the solid phase of the material” (sic [21]).

In addition, the yield stress would not be a constant in complex flows of Carbopol gel. Dimitriou et al. [23] experimentally examined in detail the behavior of a Carbopol gel under LAOS tests. They explain their rheometrical observations with the concept of the Isotropic Kinematic hardening where the yield stress builds up along the flow and propose a law of evolution of the yield stress (Eq. 4.1 in [21]). Fraggedakis et al. [21] have further developed this analysis. By coupling the EVP Saramito model [22] with the isotropic kinematic hardening concept they have demonstrated the influence of elasticity on the sedimentation of a sphere in a Carbopol gel. Their numerical results are in agreement with experimental observations.

It is worth mentioning, as presented in [2], that the drag force is almost entirely governed by the pressure forces at the front and back of the plate. The contribution of normal stresses to the drag force on the plate is minor.

5.2 Influence of the initial stress state of the fluid

We will now look at the drag force intensity during steady state and relaxation regimes and examine the influence of the initial stress state. For this purpose, two successive velocity steps were numerically simulated as shown in Fig. 8. Experimentally, the procedures described above is applied.

Fig. 8

Evolution of the drag coefficient during successive transient, steady and relaxation regimes as a function of non-dimensional time t* for Od = 11.5

Figure 8 shows, for Od = 11.5, the evolution of the numerically calculated drag coefficient as a function of a dimensionless time t* = t/$\lambda$, where $\lambda$ is the relaxation time of the material defined by $\lambda ={(\frac{K}{G})}^\frac{1}{n}$.

This curve was obtained by imposing a constant flow velocity until steady state is reached. The flow is then stopped and a first relaxation of the stresses towards a residual stress is observed, which results in a plateau for the drag force and thus for Cd*.

At the end of this first relaxation, the same flow rate is imposed again until a second steady state is reached. The initial stress state is no longer uniformly zero but corresponds to the one obtained at the end of the first relaxation. The flow is then stopped permanently and a second stress relaxation is observed.

In addition, the 1st steady state and the 1st relaxation state correspond to the “homogenized initial state of the gel”, and the 2nd steady state and the 2nd relaxation states, correspond to the “non-homogenized” initial stress state of the gel (Fig. 8). This protocol makes possible to highlight the influence of the initial stress state on the drag force measured in steady state. Numerically, two cases were considered. The first one corresponds to Od = 11.5 and Wi = 1.84.10^–2 and the second case, Od = 115.2 and Wi = 1.84.10^–3.

Figure 9 shows the evolution of the steady-state (Fig. 9b) and relaxation (Fig. 9a) drag coefficient as a function of Od. The experimental measurements are compared with the numerical results.

Fig. 9

Evolution of the drag coefficient as a function of the Oldroyd number in relaxation and steady state

The analysis of all these results reveals the following points. Experimentally, after shear is stopped, the stress field and thus the drag force on the plate relaxes to a non-zero stress state. The EVP modelling implemented here also predicts a residual drag force after shear. This phenomenon has also been observed in rheometry tests (Fig. 3) [29]. The results show that the difference in force level between the steady and relaxation state decreases as the shear rate decreases and thus the viscous component in the stress decreases.

Figure 9 also shows that the level of relaxation is experimentally and numerically relatively independent of Od and the imposed shear rate. This also highlights that thixotropic effects are negligible. Considering that the order of magnitude of the characteristic shear rate around the plate is Uo/a, for the tests shown, the imposed shear rate is between about 10^–4 and 10^–1 s⁻¹. As shown in the flow curve (Fig. 1) the shear stress levels corresponding to these values are close to the yield stress.

Numerically, there is a difference between regimes1 and 2 for Od = 115 which is not observed for Od = 11.5. The influence of the initial stress state is stronger when the yield stress effects are predominant. The stress levels, especially in shear, are very close to the yield stress and therefore more sensitive to the change caused by a different initial stress state. For Od = 11.5 the viscous stresses, higher than the plastic component, erase the initial state and impose the steady state stress field which relaxes to similar stress fields. A stronger effect of the initial stress state is observed experimentally than numerically. The deviations between regimes 1 and 2 are larger experimentally. One possible explanation lies in the fact that experimentally, the initial stress state effect is due to local microstructural phenomena while the numerical simulation reproduces an average behavior. These deviations are larger for the large Od as discussed above.

In summary, it appears that the initial stress state has an influence on the drag coefficient, particularly when yield stress effects are prevalent. In this area, the stress levels are close to the yield stress and therefore more sensitive to any variation imposed by the initial conditions. One possible assumption is that the drag force is mainly governed by pressure. The contribution of normal stresses from the deviatoric part of the stress tensor plays a secondary role on the drag.

Furthermore, this small influence is also due to the fact that Carbopol gels are known to be not or very weakly thixotropic [29,30,31,32]. This means that the solid–liquid transition is not sensitive to the mechanical history of the material.

5.3 Numerical results

This section analyses the stress and kinematic fields computed for the study of drag coefficients (Figs. 10 and 11).

Fig. 10

Fields of the dimensionless second invariant of the deviatoric stress tensor. Yielded regions in white, and unyielded regions in colors

Fig. 11

Fields of the dimensionless second invariant of the deviatoric stress tensor in the vicinity of the plate

First, let us consider one of the most typical consequences of yield stress, the creation of yielded and unyielded zones. For this, the field of the second invariant of the deviatoric stress tensor is made non dimensional by the yield stress:${\tau }_{II}^{*}=\frac{{\uptau }_{\mathrm{II}}}{{\uptau }_{0}}$ with ${\tau }_{II}$ defined with Eq. 12. This quantity is used to delineate the extent and shape of those yielded zones where the stresses are greater than the yield stress:${\tau }_{II}^{*}>1$. In these zones, the fluid is flowing, the strains are the sum of elastic and viscous strains. They surround the obstacle embedded in an unyielded zone and are surrounded by unyielded zones far from the plate. Figure 10 shows two types of unyielded zones. First one can observe unyielded zones stuck to the front and back of the plate, they are detailed on Fig. 11. They are not centered vertically with the plate due to the different boundary conditions on top and bottom of the simulation and also because the plate is not centered with respect to the material. One can also observe moving unyielded zones (rigid plug), located away from the plate, around a yielded zone in which high shear rate is observed with viscous deformations. In these unyielded moving zones, the deformations are elastic only. The larger the yield stress effects, the smaller the zone around the plate with viscous deformation.

For the two Od number considered, a dissymmetry of the unyielded zones upstream and downstream of the plate can be observed. It is due to the different elastic deformation history. A purely viscoplastic numerical model, that does not take into account the elastic contribution, predicts a symmetry between the upstream and downstream. This dissymmetry has been observed experimentally for Carbopol gel flow around various obstacles. For example, Jossic et al. [13] visualized the yielded zones upstream and downstream of a circular plate perpendicular to the flow of a Carbopol gel (Figs. 8a, 9a and 11a in [13]). This asymmetry will also be discussed in the study of the velocity fields.

The initial stress state appears to have an influence on the morphology of the yielded zones. As discussed above in relation to the drag coefficient, this influence is more noticeable for large Od and therefore large yield stress effects. This influence can be seen in particular on the unyielded zones stuck downstream to the plate (Fig. 11). The non-homogenized initial stress state of the gel tends to increase the yielded areas size.

This fore-aft asymmetry of the unyielded areas stuck to the plate is confirmed by the study of the non-dimensional velocity field shown in Fig. 12 for Od = 11.5. Near the upstream face there is a larger area of low velocity compared to the downstream face. These areas correspond to the unyielded regions stuck to the plate. Again, a purely viscoplastic numerical simulation would have predicted a symmetry of the velocity field. The velocities are maximal at the level of the extremities of the obstacle in the bypass zone.

Fig. 12

Non-dimensional axial velocity when Od = 11.5 (left) and Od = 115 (right)

Figure 12 represents the evolution of the non-dimensional component of the velocity along ${x}_{1}$, ${U}_{{x}_{1}}^{*}={U}_{{x}_{1}}/{U}_{0}$ as a function of the non-dimensional horizontal axis${x}_{1}^{*}={x}_{1}/a$. Examination of the velocity profile along the horizontal symmetry axis shown in Fig. 12 confirms that the velocity field is influenced by the presence of the plate over a greater distance upstream than downstream of the plate. Downstream, a region of reversed flow, often referred to as the negative wake phenomenon [48] is observed. The stronger influence of the elasticity for Od = 11.5 results in a velocity profile with an overspeed in the wake of the plate. These phenomena have been observed experimentally in the case of flows of Carbopol gels around a circular plate [11], a sphere [38] and a cylinder [49]. For example, the reader can compare Fig. 12 with Fig. 8 of [13] showing the axial velocity upstream and downstream of a circular plate for Od = 11 and 72. Figure 12 shows a similarity in behavior between numerical predictions and experimental results.

The influence of the initial stress state can be seen in the upstream and downstream axial velocity profiles represented in Fig. 12. As for unyielded regions and drag coefficient, there is little difference between regimes 1 and 2 when Od = 11.5 i.e. when viscous effects are significant (Fig. 12, left). Upstream and downstream velocity profiles are quite similar. When yield stress effects are more important, Od = 115 (Fig. 12 right), the influence of the initial state becomes significant and can be observed. The upstream profiles are slightly different, the magnitude of the velocity reached during the first steady state being smaller than that reached during the second steady state. It can also be observed that the extension in the upstream direction is a little greater. These differences are much more pronounced downstream of the plate.

6 Conclusion

The flow of an EVP fluid around a plate perpendicular to the flow direction has been studied experimentally. The focus has been made on the drag force on the plate. A Carbopol gel was chosen as an EVP model fluid. Steady-state and relaxation drag coefficients, with and without changes in the initial stress state have been measured. Additional numerical results based on the modeling of the EVP behavior of the fluid are provided. The constitutive equation is based on the Maxwell model in which the apparent viscosity is governed by the Herschel-Bulkley model. All equations are solved using the FEMLIP method. The numerical results support the experimental findings on the flow around the plate. Good agreements between experimental and numerical results are observed. Overall, the elasto-viscoplasticity contribution observed experimentally, in particular, the effect of initial stresses and residual stresses in the fluid are well represented by numerical simulations. Numerical simulations, reproducing an average behavior seems to attenuate the local microstructural behavior at the origin of the experimental observations. The observed discrepancies with numerical overestimations for large yield stress effects could be due to a simplistic modelling of the solid/liquid transition. Discrepancies could likely be reduced by the implementation of a more sophisticated numerical model such as [22].

Appendix

The finite element method with Lagrangian integration points (FEMLIP) was proposed by Moresi and Solomatov [50]. It is part of the “Particle-in-cell” methods for which numerical integration is carried out at each configuration in order to obtain the properties of the finite elements of the Gaussian integration scheme. FEMLIP is a hybrid method which couples an Eulerian and a Lagrangian approach. The Eulerian approach is used for the calculation points of the mesh. The Lagrangian approach uses a set of material points as integration points. The calculation points are a set of fixed nodes in space, connected by a finite element mesh. Material points carry material properties and mesh history variables. The material and calculation points are formally separated. To couple them, the properties of the particles are coupled to the mesh through a quadrature of non-standard elements in which the particles found in each element serve as integration points. The velocities are interpolated at the nodes of the material points which move through the fixed mesh towards a new configuration. At the end of each calculation step, the new position of the material points and history variables are obtained from finite element interpolation of nodal values. The fixed nature of the mesh makes it possible to overcome the problems of numerical diffusion which may appear in particular in the modeling of interactions between materials. For the analysis, the governing equations are discretized in space and time. The temporal discretization is carried out with an elastic time step which allows to capture all variations in elastic stresses. This step may be different from the advection time step chosen to update the particles position. The boundary conditions are directly imposed on the unknowns and belong to the nodes of the mesh.