1 Introduction

Conventional solar cells are generally based on silicon [1], thin films (CIGS [2, 3], CdTe [4], and a-Si [5, 6], and organic solar cells [7]. But recently, new types of so-called emerging solar cells, based on SnS [8, 9], Sb2Se3 [10, 11], Sb2S3 [12], Sb2(S,Se)3 [13], and so on, have emerged. The development of photovoltaic solar energy requires an increase in the conversion efficiency of the solar cells, by using materials containing nontoxic abundant elements on the earth, less expensive, and environment friendly. Thus, the abundance of antimony (Sb) and selenide (Se) in nature makes antimony selenide material (Sb2Se3) more suitable for future photovoltaic applications. However, using Sb2Se3 as an absorber material for solar cell applications has rarely been demonstrated until 2014 [14]. Thus, its use is in progress because it has the following attractive properties: bandgap between 1 and 1.2 eV [15], large absorption coefficient (> 105 cm−1), decent carrier mobility (≈10 cm2.V−1.s−1), and long carrier lifetime (≈60 ns) as well as its low toxicity and low cost [16]. From the point of view of material, Sb2Se3 has a one-dimensional (1D) crystal structure. The film growth and microstructure are very sensitive to the preparation process and experimental conditions [15]. Various approaches, including vacuum evaporation, sputtering, spin coating, electrodeposition, spray pyrolysis, chemical bath deposition vapour transport deposition [17] and rapid thermal evaporation (RTE) deposition technology [18], are used for the growth of the Sb2Se3 absorber layer.

In recent years, the power conversion efficiency (PCE) of the Sb2Se3-based solar cell went from 0.66% in 2009 [19] to 9.2% in 2019 [18]. For higher PCE, the Sb2Se3-based solar cell is typically made in the superstrate configuration. These PCEs of the solar cell are still far from the theoretical value; which may be due to the interface and current losses caused at the front contact of the solar cell. Shen et al. analysed the mechanisms of shunt current and identified the non-ohmic space-charge limited current (SCLC) as an important contribution to the nonlinear shunt current [15]. To remedy to this problem, these authors introduced a high-resistance SnO2 buffer between CdS ETM layer and the front contact (FTO) to obtain double buffer layers (also name as hybrid buffer layer). The SnO2/CdS hybrid buffer layer obtained via this strategy has the advantage to reduce the leakage current at the front of the solar cell and to improve the efficiency of Sb2Se3-based solar cells. To our knowledge, double buffer layers have already been used in CdTe solar cells to increase the efficiency of solar cells [20].

PCE of Sb2Se3-based solar cells is still far from the theoretical value as we mentioned above, according to Shockley–Queisser limit. A lot of work is still necessary in the areas of numerical simulation and experimentation to determine the key parameters that can improve the efficiency of Sb2Se3-based solar cells [21]. In this study, a numerical simulation approach is used:

  1. (i)

    To compare the experimental and simulation results as a starting point, to validate the simulation model structure. The structures of the experimental and simulated solar cells without and with a hybrid buffer layer are Glass/SnO2:F(FTO)/CdS/Sb2Se3/Au and Glass/FTO/(SnO2/CdS)/Sb2Se3/Au, respectively;

  2. (ii)

    To evaluate the effect of different electron transport material (ETM) layers which can replace CdS film, to reduce the use of cadmium sulphide which is a toxic and environmentally damaging material [20];

  3. (iii)

    To evaluate the effect of the Sb2Se3 absorber layer and the back metal contact on the solar cell performance;

  4. (iv)

    And finally, to explore the possibility of realizing a high-performance Sb2Se3-based solar cell by introducing MoSe2 as a hole transport material (HTM) layer between the Sb2Se3 absorber layer and the back metal contact. The HTM layer plays an essential role in a photovoltaic device as it improves its stability and PCE.

These points will be realised in this work using the SCAPS-1D software [22], which is generally used to design, predict, and optimize different solar cell structures.

2 Methods and materials

2.1 Methods

Besides experimental studies, simulation is a powerful tool to better understand the physics of the solar cell [23]. This approach allows the design, prediction, analysis, and optimization of solar cell performance. The SCAPS-1D software (version 3.3.10) can be used for this purpose. Its main function is to solve the fundamental equations of semiconductors (Poisson and carrier continuity equations [24,25,26]) with suitable boundary conditions at the contacts and interfaces [27]. This software does not perform calculations in the temporal domain but calculates the steady-state band diagram, recombination profile, and carrier transport in one dimension [28]. For bulk defects, which are located at the mid-gap of the semiconductor and contribute additional compensation [29], recombination currents are calculated with the Shockley–Read–Hall (SRH) model. The extension of the SRH model to the defects of the interface (or surface defects) allows carriers from both conduction and valence bands to participate in the interface recombination process [30]. The presence of interface states and band offsets in a heterostructure are related to the deposition method, atomic diffusion, and the bandgap of materials. SCAPS-1D uses the Anderson model to calculate valence and conduction band offsets [31].

2.2 Cell structure and material parameters

Figure 1 presents the solar cell structures simulated in this work. Figure 1a represents the solar cell structure used by Shen et al. in their experimental work [15]. The role of the highly resistive SnO2 buffer layer is to reduce the current loss mechanisms at the front contact of the solar cell. In superstrate device architecture, CdS layer can be growth on top of transparent conductive oxide by close-space sublimation (CSS) [32]. By replacing the rapid thermal evaporation (RTE) deposition technique [33], CSS can also be used for the deposition of the Sb2Se3 absorber on top of CdS [15], in order to limit the diffusion of Cd2+ from the buffer layer which causes severe illumination instability [32]. Figure 1b is generally used to improve the quality of the Sb2Se3 film and its low doping; and this n-i-p configuration is a possible approach to improve device performance [21, 32]. Gold (Au) and fluorine-doped tin oxide (FTO) are used as back and front contacts, respectively. A gold contact can be added via thermal evaporation [34]. Table 1 gives the SCAPS-1D parameters for the front and back contacts. Table 2 summarizes the material parameters used in SCAPS-1D for the simulations and some of them are reasonable approximations to reproduce the experimental results. Defects are deliberately added in the absorber layer (Table 2) and at the absorber/buffer interface (Table 3) to also reproduce experimental results [14]. As in many studies for perovskite-based solar cells [35,36,37,38], the absorption coefficient (α) of the Sb2Se3, ETM, and HTM layers is calculated in SCAPS-1D via Eq. 1. The optical parameters of the other layers (FTO, SnO2, and CdS) are the default files of SCAPS-1D. The default illumination spectrum is set at AM1.5. The temperature and incident light power (Ps) are set at 300 K and 100 mW/cm2, respectively.

$$\alpha = A_{\alpha } \sqrt {\left( {h\nu - E_{g} } \right)}$$
(1)
Fig. 1
figure 1

Solar cell structures: a reference cell [15] and; b proposed cell for high performance

Full size image
Table 1 Contacts parameters
Full size table
Table 2 Material properties used in the different configurations of the numerical simulation
Full size table
Table 3 Sb2Se3/Buffer interface defect properties
Full size table

where the prefactors Aα is set to be 105 cm−1.eV.−1/2

3 Results and discussion

3.1 Validation of experimental results

Before starting the analysis and optimization, we first compare the J-V characteristics of the experimental and simulated results of the Sb2Se3-based solar cell without and with the second buffer layer. SCAPS-1D software is used to analyse the output performance (open circuit voltage (VOC), short-circuit current density (JSC), fill factor (FF), and PCE) obtained experimentally by Shen et al. [15]. Figure 2a shows the comparison between the experimental and simulated J-V curves. When neglecting the resistances in the simulation cases, we obtain a PCE of 3.75% and 5.18%, respectively, for the solar cell without and with the SnO2 buffer layer. In two cases, a thickness of 550 nm, a doping concentration of 1 × 1013 cm−3, and charge mobility of 15 cm2/V.s for the Sb2Se3 absorber layer are used. Figure 2b shows the quantum efficiency (QE) simulation comparison between the Sb2Se3–based solar cell without and with the second buffer layer. The maximum efficiency in the case with SnO2 buffer layer is due to the absorption of more photons as shown in Fig. 2b, and to the decrease of the recombination rate with the presence of this layer which blocks the direct contact between FTO and Sb2Se3, and the corresponding shunt currents are reduced [15]. Table 4 resumes the output parameters obtained from the experimental and simulation results; these values are not really far from each other and agree well (deviation ε, given by Eq. 2, is less than 5%). The smallest difference can be attributed to the luck controlling the absorber thickness, bandgap, material defects, grain size, and interfaces defects [47].

$$\varepsilon = \frac{{\left| {V_{sim} - V_{\exp } } \right|}}{{V_{\exp } }}$$
(2)
Fig. 2
figure 2

a Experimental and simulated J-V characteristics, and b Quantum efficiency of the Sb2Se3-based solar cell without and with SnO2 high-resistance buffer layer

Full size image
Table 4 Output parameters of the Sb2Se3-based solar cell without and with a second SnO2 buffer layer
Full size table

We have thus validated our model as a result of a comparative analysis between the experiment and the simulation. The presence of a second buffer layer improves the performance of the cell due to the reduction of the current leakage at the front contact of the solar cell. In the following parts, we will optimize the solar cell structure of Fig. 1a.

3.2 Optimisation of the Sb2Se3-based solar cell

3.2.1 ETM layer selection

Shen et al. [15] use CdS as an ETM layer in their work. However, cadmium (Cd) is poisonous and classified as a carcinogen, both of which are harmful to the environment and humans [48]; furthermore, CdS has a narrow bandgap. In this part of the study, we will propose an alternative buffer layer to the CdS layer used in Fig. 1a. Figure 3 shows the effect of various ETM layers (CdZnS, IGZO, PCBM, WO3, WS2, ZnOS, and ZnO) on the J-V characteristic of the Sb2Se3-based solar cell, and Table 5 resumes their electrical parameters. Figure 4a shows that the PCE decreases from 7.13% (for CdZnS) to 2.91% (for ZnOS). The best PCE obtained in the case of CdZnS is due to the high mobility of the charge carriers in this layer, and to the strong electric field at the interface of the metallurgical junction (Fig. 4b) which contributes to the separation of more electron–hole pairs. Thus, for the rest of the work, we choose CdZnS as alternative ETM layer to the standard CdS layer.

Fig. 3
figure 3

Effect of various ETM layers on simulated J-V curves of the Sb2Se3-based solar cell

Full size image
Table 5 Output parameters of the Sb2Se3-based solar cell with various ETM layers
Full size table
Fig. 4
figure 4

a PCE of the Sb2Se3-based solar cell as a function of ETM layers, and b Electric field at the Sb2Se3/ETM and ETM/SnO2 interfaces of the Sb2Se3-based solar cell

Full size image

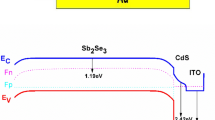
Figure 5 shows the band alignment between the Sb2Se3 absorber layer and different ETM layers. The conduction band offset (ΔEC) is an important factor for the recombination of charge carriers at ETM/Absorber interface [44]. Table 6 summarizes the different values of ΔEC obtained for the various ETM layers used in this work and SCAPS-1D uses Anderson's model (Eq. 3 [49]). ΔEC is positive for all ETMs; except for the IGZO ETM layer which leads to the formation of an energy spike at the IGZO/Sb2Se3 interface, and this acts as a barrier for the generated electrons. The lower PCE (Table 5) observed in the case of the ZnOS layer is due to the large conduction band offset (Table 6) at the ZnOS/Sb2Se3 interface; which accentuates the recombination phenomena at this interface.

Fig. 5
figure 5

Bandgap diagram at the ETM/Sb2Se3 interface of the solar cell with different ETM layers

Full size image
Table 6 Values of ΔEC for different Sb2Se3-based solar cell structures
Full size table
$${\Delta E}_{C}={\chi }_{absorber}-{\chi }_{ETM}$$
(3)

\({\chi }_{absorber}\) and \({\chi }_{ETM}\) represent the electronic affinities of the absorber and ETM layers, respectively.

3.2.2 Hybrid buffer layer thickness optimization

The thickness of the ETM layer plays a crucial role in terms of stability, efficiency, and other photovoltaic parameters of solar cells [43]. Figure 6 shows the effect of the thickness of the SnO2 and CdZnS ETM layers, which form the hybrid buffer layer, on the electrical parameters of the Sb2Se3-based solar cell. These thicknesses range from 10 to 200 nm. We can observe that JSC (Fig. 6a), VOC (Fig. 6b), and PCE (Fig. 6d) follow the same trend. The variation in the thickness of the secondary SnO2 ETM layer has very little influence on the electrical parameters of the solar cell, whatever the thickness of the primary CdZnS ETM layer. However, for CdZnS thicknesses ranging from 10 to 40 nm, JSC (Fig. 6a), VOC (Fig. 6b), and PCE (Fig. 6d) increase, which may be due to the reduction of the leakage current at the front contact, as a thin buffer layer makes this type of current prevail [50]. Above 40 nm thickness of the CdZnS layer, JSC (Fig. 6a), VOC (Fig. 6b), and PCE (Fig. 6d) decrease, which may be due to the increase of the bulk recombination phenomenon and in series resistance, and the formation of larger pinholes and uneven surface [43]. The FF (Fig. 6c) increases with the thickness of the CdZnS ETM layer, this is attributed to the lowering of series resistance with thickness [43]. The best efficiency of 7.17% (JSC = 31.72 mA/cm2, VOC = 386 mV, FF = 58.53%) of the solar cell is obtained when the thickness of the hybrid buffer layer is 50 nm (SnO2(10 nm)/CdZnS(40 nm)).

Fig. 6
figure 6

Contour plot of the solar cell electrical parameters as a function of hybrid buffer layer thickness: a JSC, b VOC, c FF, and d PCE

Full size image

3.2.3 Effect of donor concentration of CdZnS ETM layer

In this subsection, the doping concentration of the CdZnS ETM layer varies between 1017 cm−3 and 1019 cm−3 and the effect on the electrical parameters of the solar cell is shown in Fig. 7. All cell electrical parameters increase with the CdZnS doping concentration due to the increase of conductivity (more electrons are photogenerated [46]). These results are in good agreement with those obtained by Gamal et al. [51]. JSC saturation (Fig. 7a) occurs at too high doping due to the Moss-Burstein effect [52]. For the heavily doped CdZnS ETM layer with a donor concentration of 1 × 1019 cm−3, the device produces an efficiency of 7.40% (JSC = 32.40 mA/cm2, VOC = 388 mV, FF = 58.96%).

Fig. 7
figure 7

Influence of CdZnS ETM donor concentration on device output parameters: a JSC and VOC; b FF and PCE

Full size image

3.2.4 Optimisation of the Sb2Se3 absorber layer

Baig et al. [14] have shown in their works that the best PCE of the Sb2Se3-based solar cell is obtained for an acceptor density of 1013 cm−3 and a thickness of 0.300 µm for the absorber layer; thus, for the further optimization process, we use these values in this work.

3.2.4.1 Effect of the absorber’s bulk defect density

Defects are one of the main factors controlling the performance of photovoltaic devices. They control the doping level of the material, carrier lifetime, and the rate of interfacial recombination [34]. Figure 8 represents the impact of the bulk defect density of the absorber layer on the electrical parameters (JSC, VOC, FF, and PCE). The bulk defect density varies from 1011 cm−3 to 1014 cm−3. We can observe that all electrical parameters are very affected by a high defect density and decrease with the increase of this defect density, due to the increase of the recombination centers or the trapping centers of the photogenerated carriers in the active layer. This leads to reduce the lifetime of the excess electron–hole pairs [41]. Consequently, this phenomenon reduces JSC, VOC, FF, and finally PCE. Thus, the bulk defect density in the Sb2Se3 absorber material for the designed structure is set at Nt = 1011 cm−3 and the PCE of the proposed Sb2Se3-based solar cell is estimated to be 9.45% (JSC = 32.24 mA/cm2, VOC = 444 mV, FF = 66.01%).

Fig. 8
figure 8

Effect of the bulk defect density of the Sb2Se3 absorber on the output parameters of the solar cell: a JSC and VOC, b FF and PCE

Full size image
3.2.4.2 Impact of the capture cross section

In this subsection, we propose to see the effect of the capture cross sections of the defect states in the Sb2Se3 layer on the J-V characteristic (Fig. 9) and electrical parameters (Fig. 10) of the solar cell. The effects of the capture cross section, which varies from 1 × 10–14 to 8.5 × 10–9 cm2 and from 1 × 10–14 to 1.2 × 10–9 cm2 for the electrons and holes, respectively, are analysed to explore the cell performance under standard test conditions. The values of σe = 8.5 × 10–9 cm2 and σh = 1.2 × 10–9 cm2 correspond to the capture cross sections used in this work to validate the experimental model of Shen et al. [15]; and the value of 1 × 10–14 cm2 correspond to the capture cross section determined by Hobson et al. [34]. We can observe in Fig. 9 that the sections act mainly on the VOC, which decreases when the capture cross section increases, due to the increase of the recombination rate.

Fig. 9
figure 9

Effect of donor-type deep state capture cross sections in the Sb2Se3 layer on the J-V characteristic of the Sb2Se3-based solar cell

Full size image
Fig. 10
figure 10

Effect of donor-type deep state capture cross sections in the Sb2Se3 layer on the output parameters of the Sb2Se3-based solar cell: a JSC and VOC, b FF and PCE

Full size image

Figure 10 shows that the electrical parameters (JSC, VOC, FF, and PCE) follow the same trend when the capture cross section increases. They initially remain constant with the increase in the capture section and begin to decrease from a certain value. The lifetime of the charge carrier depends on the capture cross section as shown in Eqs. 4 and 5 [53]. Based on these equations, the smaller the capture cross section, the longer the lifetime and consequently, results in a longer carrier diffusion length L (Eq. 6).

$$\tau_{n} = \frac{1}{{\sigma_{h} \cdot v_{th} \cdot \left( {N_{t} - n_{r} } \right)}}$$
(4)
$$\tau_{p} = \frac{1}{{\sigma_{n} \cdot v_{th} \cdot n_{r} }}$$
(5)
$$L = \sqrt {\tau \cdot D}$$
(6)

where, \({N}_{t}\), \({n}_{r}\),\({\sigma }_{n}\), and \({v}_{th}\) are the total (occupied and unoccupied), occupied defect, hole capture cross section, and thermal velocity.

If L is more than the absorber thickness, the device performance would be superior. Equation 7 [54] gives the relation between L and the recombination current or saturation current (J0); and VOC is related to J0 as shown in Eq. 8. Thus, from Eqs. 7 and 8, we can conclude that the decrease in the capture cross section can decrease the recombination current and thus result in an improvement in VOC (Fig. 10a). FF (Fig. 10b) is also related to VOC; this is why these two electrical parameters follow the same trend. On the other hand, the decrease in the capture cross section increases the diffusion length (via Eqs. 4, 5, and 6), which leads to the increase of the JSC (Fig. 10a) through Eq. 9 [21].

$$J_{0} = A \cdot q \cdot n_{i}^{2} \left( {\frac{{D_{e} }}{{L_{e} \cdot N_{A} }} + \frac{{D_{h} }}{{L_{h} \cdot N_{D} }}} \right)$$
(7)

where NA (ND) is the acceptor (donor) doping density, L is the diffusion length, q is the elementary charge, ni is the intrinsic charge density, D represents the diffusion coefficient, and A is the area.

$$V_{OC} = \frac{{k_{B} T}}{e}\ln \left( {\frac{{J_{SC} }}{{J_{0} }} + 1} \right)\,\,{\text{where }}\frac{{k_{B} T}}{e}\,\,{\text{is thermal voltage}}$$
(8)
$$J_{ph} = J_{SC} = q \cdot G \cdot \left( {L_{n} + W + L_{p} } \right)$$
(9)

where G is the generation rate, Ln (Lp) is the electron (hole) diffusion length, and W is the width of the depletion region.

Finally, the evolution of the PCE is linked to JSC, VOC, and FF through Eq. 10; thus, the decrease of the capture cross section leads to an increase of the PCE (Fig. 10b). According to the results obtained in this study, we set the capture cross section at σe = σh = 1 × 10–14 cm2 for the optimized structure. This value of the capture cross section corresponds to that determined experimentally by Hobson et al. [34].

$$PCE = \frac{{J_{SC} \cdot V_{OC} \cdot FF}}{{P_{i} }}$$
(10)

3.2.5 Back contact work function effect

The back contact work function plays an essential role in solar cell efficiency enhancement and should be higher than 4.8 eV [55, 56], and it also plays a crucial role in determining the charge transport properties [57]. In the literature, different materials, such as Au [14], Al, Ag, and Mo [56], are used as back contact in the Sb2Se3-based solar cell. Depending on the work function of the back contact element used, this contact will become a Schottky or ohmic one [56]. In this subsection, we investigate the impact of the back contact work function on the performance of the solar cell (Fig. 11), the work function ranges from 4.40 eV to 5.80 eV. The Schottky barrier high (Фb) for the hole carriers at the back contact of the solar cell is given by Schottky–Mott rule (Eq. 11). From this equation, we can see that as the work function increases from 4.40 eV to 5.80 eV, Фb decreases from 0.81 eV to -0.59 eV, which increases the output performance of the solar cell (JSC (Fig. 11a), VOC (Fig. 11a), FF (Fig. 11b), and PCE (Fig. 11b)), this can be due to the minority carrier’s recombination reduction at the back contact and to rise in the open circuit voltage (Fig. 11a). For Фm equal or greater than 5.25 eV, the output performance of the cell is no longer affected and a PCE of 18.06% is achieved.

$$\Phi_{b} = E_{g} + \chi - \Phi_{m}$$
(11)
Fig. 11
figure 11

Simulation of output parameters of the Sb2Se3-based solar cell as a function of the back contact work function: a JSC and VOC, b FF and PCE

Full size image

where Eg and χ are the bandgap and electron affinity of the absorber layer, respectively; Фm is the work function of the metal back contact.

3.2.6 Impact of the hole transport material layer

We have seen above that a relatively low doping of the Sb2Se3 absorber does not affect the electrical parameters, which is in agreement with the results of Ayala-Mató et al. [58]. The use of an n-i-p structure compensates this low doping concentration of the Sb2Se3 absorber. In this n-i-p configuration (Fig. 1b), the p-layer is usually a hole transport material (HTM) layer, which needs high carrier mobility and should form a defect-free interface with the absorber layer to minimize carrier recombination [59]. MoSe2 material is proposed as an HTM layer, it can be formed by a molybdenum (Mo) selenization process prior to the deposition of Sb2Se3 [60]. In this subsection, by using Mo as a metal back contact (work function equal to 5.3 eV [61]), we discuss the effect of the MoSe2 HTM layer on the performance of the Sb2Se3-based solar cell. Figure 12 illustrates the variation of the output parameters of the Sb2Se3-based solar cell as a function of the thickness and bandgap, respectively, in the ranges of [0.02 µm, 0.200 µm] and [1.35 eV, 1.55 eV], of the MoSe2 HTM layer. We can observe that the MoSe2 HTM layer has very little impact on the solar cell electrical parameters. The slight increase in JSC (Fig. 12a) with MoSe2 thickness is due to the increase in the number of absorbed photons (more photogenerated carriers) and the reduction in the recombination rate in the region near the MoSe2/Mo interface. VOC (Fig. 12b) follows the same trend as JSC; in addition, the slight increase in JSC and the decrease in the recombination rate (decrease of J0) induces the increase of VOC, as these parameters are related by Eq. 8.

Fig. 12
figure 12

The electrical parameters of the solar cell as a function of the bandgap and the thickness of the MoSe2 HTM layer: a JSC, b VOC, c FF, d PCE

Full size image

We can see from Fig. 12 that increasing the MoSe2 layer bandgap slightly decreases the electrical parameters. When the value of the bandgap increases, this increases the valence band offset (Eq. 12), which limits the injection of holes and allows the recombination current flow [62] to dominate at the Sb2Se3/MoSe2 interface. However, we note that the valence band offset (0.19 eV) is less than 0.30 eV, which is very suitable to obtain lower recombination [49]. The formation of MoSe2 layer at the Sb2Se3/Mo interface improves the performance of the Sb2Se3-based solar cell. From Fig. 12, JSC varies from 33.23 to 34.37 mA/cm2 (Fig. 12a), VOC from 0.6591 to 0.6600 V (Fig. 12b), FF from 82.77 to 82.78% (Fig. 12c), and PCE from 18.13 to 18.78% (Fig. 12d). It should be noted that all electrical output parameters are high in the thick and low bandgap region of the MoSe2 HTM layer. The best performances are obtained for a thickness of 0.200 µm and a bandgap of 1.35 eV of the MoSe2 HTM layer.

$${\Delta E}_{V}={{\chi }_{HTM}-{\chi }_{{Sb}_{2}{Se}_{3}}+{E}_{g,HTM}-E}_{g,{Sb}_{2}{Se}_{3}}$$
(12)

3.2.7 Comparison of results

A thickness of 0.04 µm and a carrier concentration of 1 × 1019 cm−3 in the CdZnS ETM layer, a bulk defect density of 1 × 1011 cm−3 and a carrier capture cross section of 1 × 10–14 cm2 in the Sb2Se3 absorber layer, a thickness of 0.200 µm and a bandgap of 1.35 eV in the MoSe2 HTM layer were found to be the best parameter values of this numerical simulation and using molybdenum as back metal contact. A simulation using these values has been done to evaluate their contribution to the standard solar cell. The J-V characteristics and electrical parameters of the experimental and optimized Sb2Se3-based solar cells are shown in Fig. 13 and Table 7, respectively. We also compared our results with some simulation results from the literature on the Sb2Se3-based solar cell, as shown in Table 8.

Fig. 13
figure 13

J-V characteristics comparison of the Sb2Se3-based solar cell before and after optimization

Full size image
Table 7 Comparison of the Sb2Se3-based solar cell performance before and after optimization
Full size table
Table 8 Performance comparison of Sb2Se3-based solar cells
Full size table

3.2.8 Effect of the operating temperature

In practice, solar cells are subject to varying weather conditions. Several studies of the operating temperature impact exist in the literature [47, 63,64,65]. Thus, we will study the impact of varying the operating temperature in the range 290–470 K, on the three solar cell configurations (FTO/CdS/Sb2Se3/Au cell or cell with a single buffer layer, FTO/(SnO2/CdS)/Sb2Se3/Au cell or cell with a hybrid buffer layer, and FTO/(SnO2/CdZnS)/Sb2Se3/MoSe2/Mo cell or optimized cell) presented in this work. The results obtained from the simulations are presented in Fig. 14, we can observe that the change in temperature of the solar cell negatively affects the performance of these solar cells.

Fig. 14
figure 14

Influence of operating temperature on normalized electrical parameters as a function of the Sb2Se3-based solar cell structure: a JSC, b VOC, c FF, d PCE

Full size image

In the case of the optimized cell, the short-circuit current density (Fig. 14a) slightly increases with temperature, in the range 290 K-328 K, since the bandgap decreases and more photons have enough energy to create electron–hole pairs [65]; over 328 K, the short-circuit current density decreases. The saturation current (J0) increases with the temperature and VOC decreases [66] for all three solar cells according to Fig. 14b and Eq. 8. FF (Fig. 14c) decreases with an increase in temperature because of enhancing carrier collisions and recombination [64]. PCE (Fig. 14d) decreases with operating temperature due to the significant reduction in VOC and FF (Eq. 10).

The temperature coefficient (TC) value can be expressed by Eq. 13 [67]. TC of PCE for the cell with a single buffer layer, the cell with a hybrid buffer layer, and the optimized cell are found to be − 0.864%/K, − 0.861%/K, and − 0.324%/K, respectively. This observation shows that the Sb2Se3-based solar cell with an HTM layer is more stable than that without an HTM layer, and the one with hybrid buffer layer is slightly more stable than that with only one buffer layer.

$$TC{\text{ (part/K)}} = \left. {\frac{1}{PCE} \times \left( {\frac{\delta PCE}{{\delta T}}} \right)} \right|_{{T_{n} }}$$
(13)

where Tn is a normalization temperature set at 290 K in this work.

4 Conclusions

In summary, the Sb2Se3-based solar cell was designed, simulated, and analyzed using the SCAPS-1D simulation software (version 3.3.10). The comparison of the experimental and simulation results shows a good agreement between the J-V characteristics of the solar cell without and with the hybrid buffer layer. Thus, it is found that the PCE of the hybrid buffer layer solar cell is significantly higher than that of the single buffer layer solar cell. The introduction of the second SnO2 buffer layer between the front contact and the primary buffer layer minimizes the current leakage in the solar cell. The CdS buffer layer is widely used as an ETM layer in solar cells, but it contains environmentally harmful elements. To overcome these problems, we proposed different ETM layers (CdZnS, IGZO, PCBM, WO3, WS2, ZnOS, and ZnO) as an alternative solution. The CdZnS ETM layer demonstrated the best PCE of 7.18%, due to its high charge carrier mobility. Subsequently, in the n-p solar cell configuration, a thickness of 0.04 µm and a carrier concentration of 1 × 1019 cm−3 in the CdZnS ETM layer, a bulk defect density of 1 × 1011 cm−3 and a carrier capture cross section of 1 × 10–14 cm2 in the Sb2Se3 absorber layer were found to be the best simulation values for the optimization of the Sb2Se3-based solar cell. It was found that the output parameters increase with decreasing capture section due to the reduction in recombination rate. The low doping (1013 cm−3) of the Sb2Se3 absorber is solved using the n-i-p solar cell configuration to optimize the device performance. The use of molybdenum (Mo) as a back contact is advantageous in the case of the Sb2Se3-based solar cell because the development of the MoSe2 layer as an HTM layer, at the Sb2Se3/Mo interface boosts the device performance. The structures of the FTO/CdS/Sb2Se3/Au standard cell (cell with a single buffer layer), the FTO/(SnO2/CdS)/Sb2Se3/Au cell (cell with a hybrid buffer layer), and the FTO/(SnO2(10 nm)/CdZnS(40 nm))/Sb2Se3/MoSe2/Mo cell (optimized cell) have temperature coefficients of − 0.864%/K, − 0.861%/K, and − 0.324%/K, respectively. The operating temperature has a significant effect on the standard configuration than n-i-p configuration. The n-i-p solar cell configuration is more stable and the environmental conditions have a smaller effect on its performance.