Randomly Censored Kumaraswamy Distribution

Abstract

In this paper, inferential procedures based on classical and Bayesian framework for the Kumaraswamy distribution under random censoring model are studied. We first propose estimators for the distribution parameters, reliability function, failure rate function, and Mean time to system failure based on the maximum likelihood estimation method. Then, we calculate asymptotic confidence intervals for the parameters based on the observed Fisher’s information matrix. Also, for the parameters and reliability characteristics, Bayesian estimates are derived using the importance sampling and Gibbs sampling procedures. Highest posterior density credible intervals for the parameters are constructed using Markov Chain Monte Carlo method. Expected time on test of experiment with random censoring is also calculated. A simulation study is conducted to compare the efficiency of the derived estimates. Finally, the analysis of a real data set is presented for the illustration purpose.

1 Introduction

Censoring occurs in life-testing trials when only a subset of the test items have known exact lifetimes, and the remaining test items’ lifetimes are merely known to exceed predetermined values. There are several censoring techniques that can be utilized for life-testing. Among them, the most popular and basic methods are Type I and Type II censorings. However, periodic removals of items from the life-testing trials are not permitted by these censoring techniques.

When the object of investigation is lost or arbitrarily taken out of the experiment before it fails, this is referred to as random censoring. Alternatively, to put it another way, at the end of the experiment, some of the subjects under consideration did not experience the particular incident. For instance, some subjects in a medical study or clinical trial might not receive treatment at all and end the course of treatment before it is completed. Some participants in a sociological study become disoriented during the follow-up. In these situations, the accurate survival time also called as time to the event of interest is unknown to the experimenter. Gilbert [20] was the pioneer of the random censoring model. Afterwards, Breslow and Crowley [6] and Koziol and Green [26] have done some preliminary research on the random censoring scheme. Ghitany and Al-Awadhi [19] used randomly right censored data to generate the ML estimators of the Burr XII distribution’s parameters. Using randomly censored data, Liang [34, 35] investigated empirical Bayesian estimation for the uniform and the exponential distributions. Under random censoring, Danish and Aslam [11, 12] introduced Bayesian estimates for Weibull and generalised exponential distributions. For some recent and notable advancements, one may refer to Krishna et al. [27], Kumar and Garg [30], Garg et al. [18], Krishna and Goel [28], Kumar [29], Kumar and Kumar [31], Ajmal et al. [2] and the references therein. Besides these references, one may also refer to Chaturvedi et al. [9], Shrivastava et al. [44], Jaiswal et al. [22], where the authors have studied Bayesian analysis techniques and dynamic models. These Bayesian analysis techniques can be utilized to tackle uncertainties and variations in the data, making it suitable for situations like random censoring in reliability analysis. Also, the dynamic models can be utilized to understand how the reliability of a system changes over a certain period of time.

Kumaraswamy [33] suggested a distribution for double-bounded random processes, which have applications in hydrology. Sundar and Subbiah [48], Fletcher and Ponnambalam [16], Seifi et al. [43], Ponnambalam et al. [41], and Ganji et al. [17] conducted in-depth studies on the other applications of this distribution in related fields. Jones [23] described some of the similarities and differences between the beta and Kum distributions as well as the origins, evolution, and characteristics of the Kum distribution. He continued by enumerating the Kum distribution’s several advantages over the beta distribution. Using type II censored data, Sindhu et al. [45] derived both classical and Bayesian estimates of the shape parameter of the Kum distribution. The Kum Burr XII distribution, which is an extension of the Burr XII distribution and comprises numerous lifetime distributions as special instances, was proposed by Paranaíba et al. [40]. They have researched a range of statistical characteristics, reliability metrics, and estimation techniques for this broader class of distributions. Eldin et al. [15], Kizilaslan and Nadar [25], Dey et al. [13, 14] and Wang et al. [50] are a few additional noteworthy contributors. Recently, Mahto et al. [36] have studied statistical inference for a competing risks model when latent failure times belong to Kum distribution. Sultana et al. [47] came up with the statistical inference based on the Kum distribution under type I progressive hybrid censoring model. Chaturvedi and Kumar [8] have developed estimation procedures for the reliability functions of Kum-G Distributions based on Type I and Type II censoring schemes. Modhesh and Basheer [39] used progressively first-failure censored (PFFC) data to examine the behaviour of the entropy of random variables that follow a Kumaraswamy distribution. Abo-Kasem et al. [1] have discussed optimal sampling and statistical inferences for the Kum distribution under progressive Type-II censoring schemes. One may also refer to Kumar and Chaturvedi [32], Chaturvedi and Kumar [7], Aslam et al. [4], Younis et al. [49] and Kiani et al. [24] for a quick review of inferential procedures based on different distributions.

In this paper, inferential procedures based on classical and Bayesian framework for Kum distribution under random censoring model are considered. The rest of the paper is organized as follows: the Kum distribution is discussed in Sect. 2. Also, mathematical formulation is given for random censoring with failure and censoring time distributions. Section 3 deals with the ML estimation and ACIs of the parameters. Section 4 deals with the ETT of items. The essence of Sect. 5 is to formulate the Bayesian inferential procedure using two techniques, namely (1) importance sampling procedure under SELF using non-informative and gamma informative priors, and (2) Gibbs sampling. HPD credible intervals for the parameters are derived using MCMC method. In Sect. 6 the features of the various estimates established in this research are explored through a rigorous simulation analysis. A real data set is analyzed in support of the practical utility of the proposed methodologies in Sect. 7. Finally, some concluding thoughts and future research directions are provided in Sect. 8 Note that the statistical software R is used for computation purposes throughout the paper.

2 Random Censoring Model

Suppose the failure times $X_{1},X_{2},\ldots ,X_{n}$ are iid random variables with pdf $f_{X}(x),$ $x>0$ and cdf $F_{X}(x),$ $x>0$ respectively. Let $T_{1},T_{2},\ldots ,T_{n}$ are iid censoring times associated with these failure times with pdf $f_{T}(t),$ $t>0$ and cdf $F_{T}(t),$ $t>0$ respectively. Further, let $X_{i}'s$ and $T_{i}'s$ be mutually independent. We observe failure or censored time $Y_{i}=min(X_{i},T_{i});$ $i=1,2,\ldots ,n$ and the corresponding censor indicators $D_{i}=1 (0)$ if failure (censoring) occurs. Since, $X_{i}$ and $T_{i}$ are independent, so will be $Y_{i}$ and $D_{i},$ $i=1,2,\ldots ,n.$ As a special case, the proposed censoring model includes complete sample scenario when $T_{i}=\infty$ for all $i=1,2,\ldots ,n$ and Type I censoring scenario when $T_{i}=t_{\circ }$ for all $i=1,2,\ldots ,n$ where, $t_{\circ }$ is the pre-fixed study period. Thus, the joint pdf of Y and D is given by

$$\begin{aligned} f_{Y,D}(y,d)=\left\{ f_{X}(y)\left( 1-F_{T}(y)\right) \right\} ^{d}\left\{ f_{T}(y)\left( 1-F_{X}(y)\right) \right\} ^{1-d}. \end{aligned}$$

(1)

The marginal distributions of Y and D are obtained as

$$\begin{aligned} f_{Y}(y)=f_{X}(y)\left( 1-F_{T}(y)\right) +f_{T}(y)\left( 1-F_{X}(y)\right) ,\quad y>0 \end{aligned}$$

and

$$\begin{aligned} P[D=d]=p^{d}(1-p)^{1-d},\quad d=0,1, \end{aligned}$$

respectively, where, p stands for the probability of observing a failure and is given by

$$\begin{aligned} p=P[X\le T]=\int _{0}^{\infty }\left( 1-F_{T}(y)\right) f_{X}(y)dy. \end{aligned}$$

The Kum distribution is characterized by the pdf and cdf:

$$\begin{aligned} f(x; \alpha ,\beta )=\alpha \beta x^{\beta -1} (1-x^{\beta })^{\alpha -1};\quad 0<x<1,\ \alpha ,\beta >0, \end{aligned}$$

(2)

and

$$\begin{aligned} F(x;\alpha ,\beta )=1-(1-x^{\beta })^{\alpha }, \end{aligned}$$

(3)

respectively. Then, the corresponding reliability function, R(t),  failure rate function, h(t) and MTSF are given, respectively, by

$$\begin{aligned} R(t)= (1-t^{\beta })^{\alpha };\quad t>0, \end{aligned}$$

(4)

$$\begin{aligned} h(t)= \frac{\alpha \beta t^{\beta -1} (1-t^{\beta })^{\alpha -1}}{(1-t^{\beta })^{\alpha }} =\frac{\alpha \beta t^{\beta -1}}{1-t^{\beta }}, \end{aligned}$$

(5)

and

$$\begin{aligned} MTSF=\alpha B\left( \alpha ,1+\frac{1}{\beta }\right) , \end{aligned}$$

(6)

where, $\Gamma (a)$ stands for the gamma function and $B(a,b)=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}$ is the beta function.The present study considers that the failure time X and the censoring time T follow Kum distribution with common shape parameter $\beta .$ Let X follow $Kum(\alpha _{1},\beta )$ and T follow $Kum(\alpha _{2},\beta ),$ then, their pdfs are given by,

$$\begin{aligned} f_{X}(x,\alpha _{1},\beta )=\alpha _{1}\beta x^{\beta -1}(1-x^{\beta })^{\alpha _{1}-1};\quad 0<x<1,\ \alpha _{1},\beta >0, \end{aligned}$$

(7)

and

$$\begin{aligned} f_{T}(t,\alpha _{2},\beta )=\alpha _{2}\beta t^{\beta -1}(1-t^{\beta })^{\alpha _{2}-1};\quad 0<t<1, \ \alpha _{2},\beta >0, \end{aligned}$$

(8)

respectively. Using (1), (7) and (8), the joint density of Y and D is given by

$$\begin{aligned} f_{Y,D}(y_{i},d_{i},\alpha _{1},\alpha _{2},\beta )=\alpha _{1}^{d_{i}} \alpha _{2}^{1-d_{i}}\beta y_{i}^{\beta -1}(1-y_{i}^{\beta })^{\alpha _{1}+\alpha _{2}-1}; \quad d=0,1,\ 0<y_{i}<1. \end{aligned}$$

(9)

Thus, from (9), the marginal distribution of $Y_{i}$ is

$$\begin{aligned} f_{Y}(y)&=\sum _{d=0}^{1} f_{Y,D}(y,d) \\ &=\alpha _{1}\beta y_{i}^{\beta -1}(1-y_{i}^{\beta })^{\alpha _{1}+\alpha _{2}-1}+\alpha _{2}\beta y_{i}^{\beta -1}(1-y_{i}^{\beta })^{\alpha _{1}+\alpha _{2}-1} \\ &=(\alpha _{1}+\alpha _{2})\beta y_{i}^{\beta -1}(1-y_{i}^{\beta })^{\alpha _{1}+\alpha _{2}-1}; \quad 0<y_{i}<1. \end{aligned}$$

(10)

Hence, Y follows $Kum(\alpha _{1}+\alpha _{2},\beta ).$ The marginal distribution of $D_{i}$ is given by

$$\begin{aligned} P(D_{i}=d_{i})&=\int _{y=0}^{1}f_{Y,D}(y,d)dy \\ &=\left( \frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}}\right) ^{d_{i}} \left( \frac{\alpha _{2}}{\alpha _{1}+\alpha _{2}}\right) ^{1-d_{i}};\quad d_{i}=0,1 \\ &=p^{d_{i}}(1-p)^{1-d_{i}}, \end{aligned}$$

(11)

where, $p=P[X_{i}\le T_{i}]=\frac{\alpha _{1}}{\alpha _{1}+\alpha _{2}}.$

3 ML Estimation

In this section, we obtain MLEs of the unknown parameters of the Kum distribution using random censoring technique. Let $({\underline{y}},{\underline{d}})=(y_{1},d_{1}),(y_{2},d_{2}),\ldots , (y_{n},d_{n})$ be the randomly censored sample of size n generated from (9). Then, the likelihood function for this randomly censored sample $({\underline{y}},{\underline{d}})$ is given by

$$\begin{aligned} L({\underline{y}},{\underline{d}},\alpha _{1},\alpha _{2},\beta )&=\prod _{i=1}^{n}f_{Y,D}(y_{i},d_{i}) \\ &=\alpha _{1}^{\sum d_{i}} \alpha _{2}^{n-\sum d_{i}}\beta ^{n} \prod _{i=1}^{n}y_{i}^{\beta -1}\prod _{i=1}^{n}(1-y_{i}^{\beta }) ^{\alpha _{1}+\alpha _{2}-1} \end{aligned}$$

(12)

Taking logarithm on both the sides, we have

$$\begin{aligned} \log L&= \sum _{i=1}^{n} d_{i}\log (\alpha _{1})+(n-\sum _{i=1}^{n} d_{i}) \log (\alpha _{2})+n\log (\beta )+(\beta -1)\sum _{i=1}^{n}\log (y_{i}) \\ &\quad +(\alpha _{1}+\alpha _{2}-1)\sum _{i=1}^{n}\log (1-y_{i}^{\beta }). \end{aligned}$$

(13)

Differentiating Eq. (13) with respect to unknown model parameters $\alpha _{1},$ $\alpha _{2}$ and $\beta$ and equating them to zero, we have the normal equations as

$$\begin{aligned} \frac{\partial \log L}{\partial \alpha _{1}}&= \frac{\sum _{i=1}^{n} d_{i}}{\alpha _{1}}+\sum _{i=1}^{n}\log (1-y_{i}^{\beta })=0 \\ \implies \alpha _{1}&= \frac{-\sum _{i=1}^{n}d_{i}}{\sum _{i=1} ^{n}\log (1-y_{i}^{\beta })}, \\ \frac{\partial \log L}{\partial \alpha _{2}}&= \frac{\sum _{i=1}^{n} (n-d_{i})}{\alpha _{2}}+\sum _{i=1}^{n}\log (1-y_{i}^{\beta })=0 \end{aligned}$$

(14)

$$\begin{aligned} \implies \alpha _{2}= \frac{-\sum _{i=1}^{n}(n-d_{i})}{\sum _{i=1}^{n}\log (1-y_{i}^{\beta })}, \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial \log L}{\partial \beta }= \frac{n}{\beta } +\sum _{i=1}^{n}\log (y_{i})-(\alpha _{1}+\alpha _{2}-1) \sum _{i=1}^{n}\frac{y_{i}^{\beta }\log (y_{i})}{1-y_{i} ^{\beta }}=0. \end{aligned}$$

(16)

Substituting (14) and (15) in (16), we obtain

$$\begin{aligned} \frac{n}{\beta }+\sum _{i=1}^{n}\log (y_{i}) +\left( \frac{\sum _{i=1}^{n}d_{i}}{\sum _{i=1}^{n} \log (1-y_{i}^{\beta })} +\frac{\sum _{i=1}^{n}(n-d_{i})}{\sum _{i=1}^{n}\log (1-y_{i}^{\beta })}-1\right) \ \times \sum _{i=1}^{n}\frac{y_{i}^{\beta }\log (y_{i})}{1-y_{i}^{\beta }}=0. \end{aligned}$$

(17)

Since, it is not easy to solve Eq. (17), we need an iterative method to solve it. Let ${\widehat{\beta }}$ be the ML estimator of $\beta$ then the ML estimator of $\alpha _{1}$ and $\alpha _{2}$ are given by

$$\begin{aligned} {\widehat{\alpha }}_{1}=\frac{-\sum _{i=1}^{n}d_{i}}{\sum _{i=1}^{n}\log (1-y_{i}^{{\widehat{\beta }}})}, \end{aligned}$$

and

$$\begin{aligned} {\widehat{\alpha }}_{2}=\frac{-\sum _{i=1}^{n}(n-d_{i})}{\sum _{i=1}^{n}\log (1-y_{i}^{{\widehat{\beta }}})}. \end{aligned}$$

Then, by the invariance property of ML estimators, the ML estimator of R(t),  h(t) and MTSF are given by

$$\begin{aligned} {\widehat{R}}(t)=(1-t^{{\widehat{\beta }}}) ^{{\widehat{\alpha }}_{1}};\quad t>0, \end{aligned}$$

(18)

$$\begin{aligned} {\widehat{h}}(t)=\frac{{\widehat{\alpha }}_{1} {\widehat{\beta }} t^{{\widehat{\beta }}-1} }{(1-t^{{\widehat{\beta }}})}, \end{aligned}$$

(19)

and

$$\begin{aligned} {\widehat{MTSF}}={\widehat{\alpha }}_{1}B\left( {\widehat{\alpha }}_{1},1 +\frac{1}{{\widehat{\beta }}}\right) . \end{aligned}$$

(20)

3.1 The ACIs

In this subsection, in order to obtain ACI, we first obtain Fisher’s Information Matrix. The observed Fisher information matrix is given to evaluate the estimated variance of the ${\widehat{\alpha }}_{1}, {\widehat{\alpha }}_{2}, {\widehat{\beta }}$ respectively, and given by

$$\begin{aligned} I({\widehat{\alpha }}_{1},{\widehat{\alpha }}_{2},{\widehat{\beta }})= -\left( \begin{array}{ccc} \dfrac{\partial ^{2}\log L}{\partial \alpha _{1}^{2}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \alpha _{1}\partial \alpha _{2}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \alpha _{1}\partial \beta }\\ \dfrac{\partial ^{2}\log L}{\alpha _{2}\partial \alpha _{1}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \alpha _{2}^{2}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \alpha _{2}\partial \beta }\\ \dfrac{\partial ^{2}\log L}{\partial \beta \partial \alpha _{1}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \beta \partial \alpha _{2}} &{}\quad \dfrac{\partial ^{2}\log L}{\partial \beta ^{2}}\\ \end{array} \right) _{\alpha _{1}={\widehat{\alpha }}_{1},\alpha _{2} ={\widehat{\alpha }}_{2},\beta ={\widehat{\beta }}}. \end{aligned}$$

(21)

The second order partial derivatives are

$$\begin{aligned} \dfrac{\partial ^{2}\log L}{\partial \alpha _{1}^{2}}&= -\frac{\sum _{i=1}^{n}d_{i}}{\alpha _{1}^{2}},\\ \dfrac{\partial ^{2}\log L}{\partial \alpha _{2}^{2}}&= -\frac{(n-\sum _{i=1}^{n}d_{i})}{\alpha _{2}^{2}},\\ \frac{\partial ^{2}\log L}{\partial \beta ^{2}}&= \frac{-n}{\beta ^{2}}-(\alpha _{1}+\alpha _{2}-1)\sum _{i=1}^{n} \frac{y_{i}^{\beta }\left( \log (y_{i})\right) s^{2}}{(1-y_{i}^{\beta })^{2}},\\ \frac{\partial ^{2}\log L}{\partial \alpha _{1}\partial \alpha _{2}}&= \frac{\partial ^{2}\log L}{\partial \alpha _{2}\partial \alpha _{1}}=0,\\ \frac{\partial ^{2}\log L}{\partial \alpha _{1}\partial \beta }&= -\frac{y_{i}^{\beta }\left( \log (y_{i})\right) }{(1-y_{i}^{\beta })} =\frac{\partial ^{2}\log L}{\partial \alpha _{2}\partial \beta }\\ &= \frac{\partial ^{2}\log L}{\partial \beta \partial \alpha _{1}} =\frac{\partial ^{2}\log L}{\partial \beta \partial \alpha _{2}}. \end{aligned}$$

The estimated variance of ${\widehat{\alpha }}_{1},$ ${\widehat{\alpha }}_{2}$ and ${\widehat{\beta }}$ are the diagonal terms of $I^{-1}({\widehat{\alpha }}_{1},{\widehat{\alpha }}_{2}, {\widehat{\beta }}),$ where $I^{-1}({\widehat{\alpha }}_{1},{\widehat{\alpha }}_{2}, {\widehat{\beta }})$ is the inverse of the observed Fisher’s Information Matrix. The $(1-\alpha )100\%$ ACI for $\alpha _{1},$ $\alpha _{2}$ and $\beta$ are given by

$$\begin{aligned}{} & {} \left\{ {\widehat{\alpha }}_{1}-Z_{\alpha /2}\sqrt{var({\widehat{\alpha }}_{1})} ,\ {\widehat{\alpha }}_{1}+Z_{\alpha /2}\sqrt{var({\widehat{\alpha }}_{1})} \right\} ,\\{} & {} \left\{ {\widehat{\alpha }}_{2}-Z_{\alpha /2}\sqrt{var({\widehat{\alpha }}_{2})} ,\ {\widehat{\alpha }}_{2}+Z_{\alpha /2}\sqrt{var({\widehat{\alpha }}_{2})} \right\} , \end{aligned}$$

and

$$\begin{aligned} \left\{ {\widehat{\beta }}-Z_{\alpha /2}\sqrt{var({\widehat{\beta }})} ,\ {\widehat{\beta }} +Z_{\alpha /2}\sqrt{var({\widehat{\beta }})} \right\} , \end{aligned}$$

respectively.

4 The ETT

In this section, we discuss ETT. In lifetime experiments and reliability experiments, since time is directly related to cost, it is therefore beneficial to have an idea about the expected time of the experiment. First time in literature, the ETT for randomly censored data was introduced by Krishna et al. [27]. Let $Y_{i}=min(X_{i},T_{i});$ $i=1,2,\ldots ,n$ be the random sample of size n generated from $Kum(\alpha _{1}+\alpha _{2},\beta ).$ Let $Y_{n}=max(Y_{1},Y_{2},\ldots ,Y_{n})$ be the $n$th order statistic. Then, the cdf of $Y_{n}$ is given by

$$\begin{aligned} F_{Y_{\left( n\right) }}=P[Y_{n}\le y] =[1-(1-y^{\beta })^{\alpha _{1}+\alpha _{2}}]^{n}. \end{aligned}$$

Thus, for randomly censored Kum data, the ETT is given by

$$\begin{aligned} ETT_{RC}&=E(Y_{\left( n \right) }) \\ &=\int _{0}^{1}[1-F_{Y_{\left( n\right) }}]dy \\ &=\int _{0}^{1}[1-(1-y^{\beta })^{\alpha _{1}+\alpha _{2}}]^{n}dy. \end{aligned}$$

(22)

Then, the ML estimator of $ETT_{RC}$ is given by

$$\begin{aligned} {\widehat{ETT}}_{RC}=\int _{0}^{1}[1-(1-y^{{\widehat{\beta }}}) ^{{\widehat{\alpha }}_{1}+{\widehat{\alpha }}_{2}}]^{n}dy. \end{aligned}$$

(23)

Further, the OBTT is the maximum ordered statistic in $Y_{1},Y_{2},\ldots ,Y_{n},$ i.e.,

$$\begin{aligned} OBTT_{RC}=Y_{(n)}. \end{aligned}$$

(24)

Similarly, let $X_{(n)}$ denote the nth order statistic in the case of complete sample. Then, ETT in case of complete sample is given by

$$\begin{aligned} ETT_{CS}&= E(X_{(n)}) \\ &=\int _{0}^{1}[1-F_{X_{\left( n \right) } }]dx \\ &=\int _{0}^{1}[1-(1-x^{\beta })^{\alpha _{1}}]^{n}dx. \end{aligned}$$

(25)

Equations (23) and (25) can now be solved for different combinations of $\alpha _{1},$ $\alpha _{2},$ $\beta$ and n with the help of integral function in R software.

5 Bayesian Estimation

Here, we develop the Bayes estimates of the unknown model parameters of the randomly censored Kum distribution. In order to compute the Bayes estimates, let $\alpha _{1},$ $\alpha _{2}$ and $\beta$ independently follow the gamma priors with hyper-parameters $(a_{1},b_{1}),$ $(a_{2},b_{2}),$ and $(a_{3},b_{3}),$ respectively, with their respective pdf’s

$$\begin{aligned} g(\alpha _{1},a_{1},b_{1})&= \frac{a_{1}^{b_{1}}}{\Gamma (b_{1})} e^{-a_{1}\alpha _{1}}\alpha _{1}^{b_{1}-1};\quad a_{1},b_{1}>0,\\ g(\alpha _{2},a_{2},b_{2})&= \frac{a_{2}^{b_{2}}}{\Gamma (b_{2})} e^{-a_{2}\alpha _{2}}\alpha _{2}^{b_{2}-1};\quad a_{2},b_{2}>0,\\ g(\beta ,a_{3},b_{3})&= \frac{a_{3}^{b_{3}}}{\Gamma (b_{3})} e^{-a_{3}\beta }\beta ^{b_{3}-1};\quad a_{3},b_{3}>0. \end{aligned}$$

Following there pdf’s, we can obtain the joint prior distribution of $\alpha _{1},$ $\alpha _{2}$ and $\beta$ as

$$\begin{aligned} g(\alpha _{1},\alpha _{2},\beta )\propto e^{-(a_{1}\alpha _{1}+a_{2}\alpha _{2}+a_{3}\beta )} \alpha _{1}^{b_{1}-1}\alpha _{2}^{b_{2}-1}\beta ^{b_{3}-1}. \end{aligned}$$

(26)

Now using the likelihood function given in Eq. (12) and the joint prior given in Eq. (26), the joint posterior distribution of the parameters $\alpha _{1},$ $\alpha _{2}$ and $\beta$ is given by

$$\begin{aligned}{} & {} \pi (\alpha _{1},\alpha _{2},\beta |data) =\frac{L({\underline{y}},{\underline{d}},\alpha _{1},\alpha _{2},\beta ) g(\alpha _{1},\alpha _{2},\beta )}{\int _{0}^{\infty }\int _{0} ^{\infty }\int _{0}^{\infty }L({\underline{y}}, {\underline{d}},\alpha _{1},\alpha _{2},\beta ) g(\alpha _{1},\alpha _{2},\beta )d\alpha _{1}d\alpha _{2}d\beta } \\{} & {} \quad \implies \pi (\alpha _{1},\alpha _{2},\beta ) \propto \alpha _{1}^{\sum d_{i}} \alpha _{2}^{n-\sum d_{i}} \beta ^{n}\prod _{i=1}^{n}y_{i}^{\beta -1}\prod _{i=1}^{n}(1-y_{i}^{\beta -1}) ^{\alpha _{1}+\alpha _{2}-1}\times \alpha _{1}^{b_{1}-1} \alpha _{2}^{b_{2}-1}\beta ^{b_{3}-1} \\{} & {} \qquad \times e^{-a_{2}\alpha _{2}}e^{-a_{3}\beta } \\{} & {} \quad =\alpha _{1}^{b_{1}+\sum d_{i}-1}e^{-a_{1}\alpha _{1}}\alpha _{2} ^{n-\sum d_{i}+b_{2}-1}e^{-a_{2}\alpha _{2}}\beta ^{n+b_{3}-1} e^{-a_{3}\beta }e^{(\alpha _{1}+\alpha _{2}-1)\sum _{i=1} ^{n}log(1-y_{i}^{\beta })} \\{} & {} \qquad \times e^{(\beta -1)\sum _{i=1}^{n}log(y_{i})} \\{} & {} \quad \implies \pi (\alpha _{1},\alpha _{2},\beta )\propto \alpha _{1}^ {b_{1}+\sum d_{i}-1}e^{-\alpha _{1}\left( a_{1}-\sum _{i=1} ^{n}log(1-y_{i}^{\beta })\right) }\alpha _{2}^ {\left( n+b_{2}-\sum d_{i}-1\right) } e^{-\alpha _{2} \left( a_{2}-\sum _{i=1}^{n}log(1-y_{i}^{\beta })\right) } \\{} & {} \qquad \times \beta ^{n+b_{3}-1}e^{-\beta \left( a_{3}-\sum _{i=1} ^{n}log(y_{i}) \right) }e^{-\sum _{i=1}^{n}log(1-y_{i}^{\beta })}. \end{aligned}$$

(27)

Now, we compute the Bayes estimates under SELF. Let $\phi (\alpha _{1},\alpha _{2},\beta )$ be any function of the parameters $\alpha _{1},$ $\alpha _{2}$ and $\beta ,$ then the Bayes estimate of $\phi (\alpha _{1},\alpha _{2},\beta )$ under SELF is given by

$$\begin{aligned} \phi ^{*}&=E(\phi (\alpha _{1},\alpha _{2},\beta )|data) \\ &=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } \phi (\alpha _{1},\alpha _{2},\beta )\pi (\alpha _{1},\alpha _{2}, \beta |data)d\alpha _{1}d\alpha _{2}d\beta . \end{aligned}$$

(28)

One can clearly observe that it is not possible to obtain the closed form solution of Eq. (28). Hence, we tend to exploit two approximation methodologies, namely (i) Importance Sampling, and (ii) Gibbs Sampling, to derive the Bayes’ estimates.

5.1 Importance Sampling Technique

In this subsection, we discuss the importance sampling method to derive the Bayes estimates of the parameters and the reliability characteristics. Note that the posterior distribution given in (27) can be rewritten as

$$\begin{aligned} \pi (\alpha _{1},\alpha _{2},\beta )\propto gamma(A_{1},B_{1})\times gamma(A_{2},B_{2})\times gamma(A_{3},B_{3})\times W(\alpha _{1},\alpha _{2},\beta ), \end{aligned}$$

where, $A_{1}=a_{1}-\sum _{i=1}^{n}log(1-y_{i}^{\beta }),$ $B_{1}=b_{1}+\sum _{i=1}^{n}d_{1},$ $A_{2}=a_{2}-\sum _{i=1}^{n}log(1-y_{i}^{\beta }),$ $B_{2}=b_{2}+n-\sum _{i=1}^{n}d_{1},$ $A_{3}=a_{3}-\sum _{i=1}^{n}log(y_{i}),$ $B_{3}=n+b_{3},$ and $W(\alpha _{1},\alpha _{2},\beta )=\frac{e^{-\sum _{i=1}^{n} log(1-y_{i}^{\beta })}}{A_{1}^{B_{1}}A_{2}^{B_{2}}}.$ Now, for the computation of Bayes estimates using the importance sampling technique, following steps are used:

• Step 1. Generate $\beta ^{(1)}$ from gamma$(A_{3},B_{3}).$

• Step 2. Generate $\alpha _{1}^{(1)}$ from gamma$(A_{1},B_{1})$ using $\beta ^{(1)}$ generated in Step 1.

• Step 3. Generate $\alpha _{2}^{(1)}$ from gamma$(A_{2},B_{2})$ using $\beta ^{(1)}$ generated in Step 1.

• Step 4. Compute $W\left( \alpha ^{(1)}_{1},\alpha ^{(1)}_{2},\beta ^{(1)}\right) .$

• Step 5. Repeat steps 1 to 4, $(M-1)$ times to obtain importance samples.

Now, the approximate Bayes estimates of the parameters and reliability characteristics under SELF are given by

$$\begin{aligned} \alpha ^{*}_{1IS}&= \frac{\sum _{i=1}^{M}\alpha ^{(i)}_{1}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) },\\ \alpha ^{*}_{2IS}&= \frac{\sum _{i=1}^{M}\alpha ^{(i)}_{2}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) },\\ \beta ^{*}_{IS}&= \frac{\sum _{i=1}^{M}\beta ^{(i)}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) },\\ R^{*}_{IS}(t)&= \frac{\sum _{i=1}^{M}\left( 1-t^{\beta ^{(i)}}\right) ^{\alpha ^{(i)}_{1}} W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) },\\ h^{*}_{IS}(t)&= \frac{\sum _{i=1}^{M} \frac{\alpha ^{(i)}_{1}\beta ^{(i)} t^{\beta ^{(i)}-1}}{1-t^{\beta ^{(i)}}}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }, \end{aligned}$$

and

$$\begin{aligned} MTSF^{*}=\frac{\sum _{i=1}^{M}\alpha ^{(i)}_{1} B\left( \alpha ^{(i)}_{1},1+\frac{1}{\beta ^{(i)}}\right) W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }{\sum _{i=1}^{M}W\left( \alpha ^{(i)}_{1},\alpha ^{(i)}_{2},\beta ^{(i)}\right) }. \end{aligned}$$

5.2 MCMC Method

Here, we consider MCMC technique to compute Bayes estimates and the corresponding HPD credible intervals. The Gibbs sampling is a particular type of MCMC method (see [46]). The full posterior conditional distributions for the parameters $\alpha _{1},$ $\alpha _{2}$ and $\beta ,$ respectively, are given by

$$\begin{aligned}\pi _{1} (\alpha _{1}|\beta ,data)\propto gamma(A_{1},B_{1}), \end{aligned}$$

(29)

$$\begin{aligned} \pi _{2} (\alpha _{2}|\beta ,data)\propto gamma(A_{2},B_{2}), \end{aligned}$$

(30)

and

$$\begin{aligned} \pi _{3} (\beta |\alpha _{1},\alpha _{2},data)\propto \beta ^{n+b_{3}-1}e^{-\beta (a_{3}-\sum _{i=1}^{n}log(y_{i}))}e^{\left( \alpha _{1}+\alpha _{2}-1\right) \sum _{i=1}^{n}log(1-y_{i}^{\beta })}. \end{aligned}$$

(31)

From Eqs. (29) and (30), it can be seen that the posterior samples of $\alpha _{1}$ and $\alpha _{2}$ can be easily generated using gamma distributions, but the posterior sample of $\beta$ cannot be generated directly. For the generation of the sample of $\beta ,$ we shall use the MH algorithm, see Metropolis et al. [38] and Hastings [21]. Thus, we use the following steps to generate samples from the full conditional posterior densities given in Eqs. (29), (30) and (31), respectively:

• Step 1. Start with an initial guess of $\alpha _{1},$ $\alpha _{2}$ and $\beta ,$ say $\alpha _{1}^{(0)},$ $\alpha _{2}^{(0)}$ and $\beta ^{(0)}.$

• Step 2. Set $j=1.$

• Step 3. Generate $\beta ^{(j)}$ from $\pi _{3}(\beta |\alpha _{1}^{(j-1)},\alpha _{2}^{(j-1)},data)$ using MH algorithm with normal proposal distribution as

  • (i) Generate a candidate point $\beta _{c}^{j}$ from the proposal distribution $N(\beta ^{(j-1)},1).$

  • (ii) Generate u from Uniform(0, 1).

  • (iii) Calculate $\eta =min\left( 1,\frac{\pi _{3}(\beta _{c}^{(j)} |\alpha _{1}^{(j-1)},\alpha _{2}^{(j-1)},data)}{\pi _{3}(\beta ^{(j-1)} |\alpha _{1}^{(j-1)},\alpha _{2}^{(j-1)},data)} \right) .$

  • (iv) If $u\le \eta ,$ set $\beta ^{(j)}=\beta _{c}^{(j)}$ with acceptance probability $\eta ,$ otherwise $\beta ^{(j)}=\beta ^{(j-1)}.$

• Step 4. Generate $\alpha _{1}^{(j)}$ from $gamma(A_{1},B_{1})$ using $\beta ^{(j)}$ generated in Step 3.

• Step 5. Generate $\alpha _{2}^{(j)}$ from $gamma(A_{2},B_{2})$ using $\beta ^{(j)}$ generated in Step 3.

• Step 6. Set j = j + 1.

• Step 7. Repeat step 3 to step 6, N times, to obtain the sequence of the parameters as $\alpha _{1}^{(1)},\alpha _{2}^{(1)},\ldots ,\beta ^{(1)},$ $\alpha _{1}^{(2)},\alpha _{2}^{(2)},\ldots ,\beta ^{(2)}, \ldots ,$ $\alpha _{1}^{(N)},\alpha _{2}^{(N)}\ldots ,\beta ^{(N)}.$

We discard first $N_{\circ }=20\%$ of the N of the generated values of the parameters as the burn-in-period to obtain independent samples from the stationary distribution of the Markov chain which are typically the posterior distributions. Thus, the Bayes estimates of the parameters $\alpha _{1},$ $\alpha _{2},$ $\beta$ and reliability characteristics R(t),  h(t) and MTSF under SELF, respectively, are given by

$$\begin{aligned}{} & {} \alpha _{1GS}^{*}=\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N}\alpha _{1}^{(j)},\\{} & {} \alpha _{2GS}^{*}7\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N}\alpha _{2}^{(j)},\\{} & {} \beta _{GS}^{*}=\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N}\beta ^{(j)},\\{} & {} R_{GS}^{*}(t)=\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N} (1-t^{\beta ^{(j)}})^{\alpha _{1}^{(j)}},\\{} & {} h_{GS}^{*}(t)=\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N} \frac{\alpha _{1}^{(j)}\beta ^{(j)}t^{\beta ^{(j)}-1}}{1-t^{\beta ^{(j)}}}, \end{aligned}$$

and

$$\begin{aligned} MTSF_{GS}^{*}=\frac{1}{(N-N_{\circ })}\sum _{j=N_{\circ }+1}^{N}{\alpha }_{1}^{(j)}B\left( {\alpha }_{1}^{(j)},1+\frac{1}{{\beta }^{(j)}}\right) . \end{aligned}$$

5.3 HPD Credible Interval

In this subsection, we construct HPD credible intervals of the unknown parameters $\alpha _{1},$ $\alpha _{2}$ and $\beta ,$ respectively, by using the algorithm proposed by Chen and Shao [10]. Let $\alpha _{1(1)}<\alpha _{1(2)}<\cdots <\alpha _{1(N-N_{\circ })}$ denote the ordered form of the MCMC sample of $\alpha _{1}$ generated in the previous subsection. Thus, the $100(1-\delta )\%,$ where $0<\delta <1,$ HPD credible interval for $\alpha _{1}$ is given by

$$\begin{aligned} (\alpha _{1(j)},\alpha _{1(j+[(1-\delta )M])}), \end{aligned}$$

where j is chosen such that

$$\begin{aligned} \alpha _{1(j+[(1-\delta )M])}-\alpha _{1(j)}=\underset{1\le i\le \delta M}{min }\left( \alpha _{1(i+[(1-\delta )M])}-\alpha _{1(i)} \right) ;\quad j=1,2,\ldots ,M, \end{aligned}$$

here, [x] is the largest integer less than or equal to x. Similarly, we can construct the $100(1-\delta )\%$ HPD credible intervals for $\alpha _{2}$ and $\beta ,$ respectively.

6 Simulation Study

A Monte Carlo simulation study is conducted in this section to evaluate the effectiveness and performance of the various estimation techniques. We generate a randomly censored sample from the Kum distribution an algorithm. The steps of the algorithm are provided below:

Step 1. Generate a random sample $u_{1},u_{2},\ldots ,u_{n}$ from standard Uniform distribution, i.e., U(0, 1).

Step 2. Make a transformation to obtain failure observations $x_{i},$ $i=1,2,\ldots ,n,$

$$\begin{aligned} x_{i}=(1-(1-u_{i})^{1/\alpha _{1}})^{1/\beta }. \end{aligned}$$

Step 3. Generate another random sample $v_{1},v_{2},\ldots ,v_{n}$ from U(0, 1).

Step 4. Make another transformation to obtain censoring observations $t_{i},$ $i=1,2,\ldots ,n,$

$$\begin{aligned} t_{i}=(1-(1-v_{i})^{1/\alpha _{2}})^{1/\beta } . \end{aligned}$$

Step 5. Now obtain $y_{i}$ and $d_{i}$ by using the condition that if $x_{i}<t_{i},$ then $y_{i}=x_{i}$ and $d_{i}=1,$ else $y_{i}=t_{i}$ and $d_{i}=0.$ Hence, we obtain a randomly censored sample $(y_{i},d_{i})$ of n observations from Kum distribution.

We have generated 10,000 randomly censored samples using the aforementioned approach for various sample sizes $n=30(5)100$ and parameter values $\alpha _{1},$ $\alpha _{2},$ and $\beta$ in order to examine the behaviour of various estimates. We have used the procedure covered in Sect. 3 to calculate the average values of the ML estimators. Additionally, we have calculated the average length of the relevant CPs and the $95\%$ asymptotic confidence intervals. By taking $M=10{,}000$ as mentioned in Sect. 5, we were able to acquire the Bayes estimates using the Gibbs Sampling and importance sampling methodologies, as well as $95\%$ HPD credible intervals of the parameters. Hyperparameters are selected so that the true value of the parameter equals the mean of the prior distribution.

The average ML estimates and the average Bayes estimates of $\alpha _{1}$ with hyperparameters $a_{1}=2,$ $a_{2}=2,$ $a_{3}=3,$ $b_{1}=1,$ $b_{2}=3,$ $b_{3}=6$ and their corresponding MSE for true values of parameters $\alpha _{1} =0.5,$ $\alpha _{2}=1.5$ and $\beta =2$ are computed and the results are reported in Table 1. Comparing the estimates on the basis of MSE, from Table 1 we observe that the Bayes estimate based on Importance Sampling performs the best and ML estimate performs the least. Bayes estimate based on Gibbs sampling method lies between the two. Further, as n increases, the performance of all the estimators improve and the three estimators come close to each other. Similarly, the average ML estimate and the average Bayes estimates for $\alpha _{2}$ and their corresponding MSE are computed and the results are reported in Table 2. From Table 2 we can observe that the Bayes estimate of $\alpha _{2}$ based on the Importance Sampling performs better than the Bayes estimate based on Gibbs Sampling Method and ML estimate. However, as n increases, their MSE decreases and all the estimates become almost equally efficient. In case of $\beta ,$ for $n<60,$ Bayes estimate based on Importance sampling performs the best, ML estimate performs the least and Bayes estimate based on Gibbs sampling lies in between the two. However, for $n\ge 60,$ Bayes estimate based on Gibbs sampling performs the best, ML estimate performs the least and the Bayes estimate based on Importance sampling lies between the two. Further, for $n\ge 85,$ Bayes estimate based on Gibbs sampling performs the best, Bayes estimate based on Importance sampling performs the least and ML estimate lies between the two. Also, as sample size increases, all the estimates become almost equally efficient. The results for $\beta$ are reported in Table 3. The average length and CPs of the $95\%$ ACIs and HPD credible intervals of the three parameters are obtained for different values of n and the results are presented in Table 4. From Table 4 we observe that the length of both the intervals for $\alpha _{1},$ $\alpha _{2}$ and $\beta$ decreases as n increases, which shows the improvement in precision of the estimates as sample size increases. We also observe that the CPs of the interval estimates are much close to nominal values even for small values of n. The average length of ACI of $\alpha _{1}$ is smaller than average length of HPD credible interval, while, CP of HPD is higher than ACI. However, for $\alpha _{2}$ and $\beta ,$ the average length of HPD is smaller than the average length of ACI while, CP of ACI is higher than HPD.

For comparing the performance of ML estimate and Bayes estimate of reliability function R(t),  we obtain the average ML and Bayes estimates and their respective MSEs for $\alpha _{1} =0.5,$ $\alpha _{2}=1.5$ and $\beta =2$ and different values of n and $t=0.5$ and the results are reported in Table 5. Comparing the estimates on the basis of MSE, we observe that the Bayes estimate of R(t) based on Gibbs sampling method performs better than the ML estimate and Bayes estimate based on Importance sampling method. Also, as n increases, MSE of the three estimates decreases and the estimates become almost equally efficient. Along the similar lines, we obtain the average value of ML estimate and Bayes estimate and their MSE of the failure rate function h(t) and the results are reported in Table 6. From Table 6, on the basis of MSE, we can conclude that the Bayes estimate of h(t) based on Gibbs sampling performs better than the ML estimate and the Bayes estimate based on Importance sampling method and the estimates improve and come close to each other as n increases. Similarly, for investigating the performance of MTSF, we have obtained average ML and Bayes estimates and their respective MSEs and the results are presented in Table 7. From Table 7 we conclude that Bayes estimate of MTSF based on Gibbs sampling performs better than the Bayes estimate based on Importance sampling technique and ML estimate. Also, as n increases, MSE of the three estimates decreases and the estimates become almost equally efficient.

We have also calculated ETT based on complete sample and randomly generated sample and OBTT based on randomly generated sample as discussed in Sect. 4 for different sample sizes and the results are presented in Table 8. From Table 8, we observe that the random censoring reduces ETT and as n increases, ETT increases.

7 Real Data Analysis

We perform a real data analysis in this section. Here, we look at the data set that includes the monthly survival times (in months) of 24 patients who had Dukes’C colorectal cancer disease. This dataset was originally investigated by McIllmurray and Turkie [37]. Danish and Aslam [11] also examined this data set with a randomly censored Weibull distribution. The dataset is provided below: 3 + 6, 6, 6, 8, 12, 12, 12 +, 15 + 16 + 18 + 20 + 22 + 24, 28 + 28 + 28 + 30 + 33 + 42. The censoring times are indicated by the ‘+’ sign. To make computation easier, we first divide all observations by 50 without loss of generality. The resulting modified data are provided below: 0.06 +, 0.12, 0.12, 0.12, 0.12, 0.16, 0.16, 0.24, 0.24, 0.24 +, 0.30 +, 0.32 +, 0.36 +, 0.36 +, 0.40, 0.44 +, 0.48, 0.56 +, 0.56 +, 0.56 +, 0.60, 0.60 +, 0.66 +, 0.84.

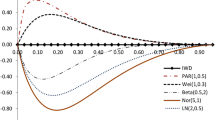
Now we compare the fitted Kum distribution with some other well-known survival models, like, exponential, Rayleigh, and Weibull distributions for Dukes’C colorectal cancer data. The ML estimates of the parameters of these distributions under random censorship model are obtained. These estimates, along with the data, are used to calculate the negative log likelihood function $-ln\,L,$ the AIC $(AIC=2\times k-2ln\,L),$ proposed by Akaike [3] and BIC $(BIC=k\times kln\,(n)-2ln\,L)$ proposed by Schwarz [42], where k is the number of parameters in the reliability model, n is the number of observations in the given data set, L is the maximized value of the likelihood function for the estimated model and KS statistic with its p-value. The lowest $-ln\,L,$ AIC,  BIC and KS statistic values and the highest p values indicate the best distribution fit. These values are listed in Table 9. It is clearly reflected from Table 9 that the Kum distribution is the best choice among other counterparts. We have also demonstrated the empirical cdf to fit the randomly censored data through the graphs. The graph of the empirical cdf along with the estimates of cdfs for randomly censored exponential, Rayleigh, Weibull and Kum distributions are represented by Fig. 1. One can observe from Fig. 1 that the estimate of cdf for Kum distribution is quite close to that proposed by empirical cdf estimator, which clearly indicates that the empirical cdf also supports the choice of Kum distribution to represent the Dukes’ C colorectal cancer data.

We now examine how to estimate the randomly censored Kum distribution’s parameters for this set of data. Here, we have $n=24$ and the effective sample size is $m=12.$ We also use the median mission time of the data, $t=0.34.$ We consequently use non-informative priors under SELF to derive the Bayes estimates of the parameters since we lack any prior knowledge. The hyperparameters for the non-informative priors are $a_{1}=b_{1}=a_{2}=b_{2}=a_{3}=b_{3}=0.$ The Gibbs sampling method and importance sampling approach are used to produce the Bayes estimates. We use $M=10{,}000$ for the importance sampling approach and $N=50{,}000$ with a burn-in-period of $N_{\circ }=10{,}000$ for the Gibbs sampling method. Furthermore, the 95% ACI and HPD credible intervals of the parameters are calculated. All results of the real data set are reported in Tables 10 and 11 respectively.

8 Concluding Remarks

In this study, we have developed estimation methods based on random censoring for the Kum distribution. Both point and interval estimations of the parameters are discussed. Extensive Monte Carlo experiments are conducted to examine the finite sample performances of the ML and the Bayes estimates based on the Importance sampling and Gibbs sampling methods. The MSE criterion is used to compare different estimates. Based on simulation experiments, we find that the ML estimator performs the least and the Bayes estimator based on importance sampling performs the best for $\alpha _{1}.$ On the other hand, the Bayes estimate based on the importance sampling approach outperforms the one based on the Gibbs sampling method and ML estimator for $\alpha _{2}.$ When $n<60,$ the Bayes estimate based on importance sampling outperforms the Bayes estimate based on Gibbs sampling and ML estimator in case of $\beta .$ Nevertheless, the Gibbs sampling based Bayes estimate outperforms the importance sampling and ML estimates for $n\ge 60.$ Furthermore, all the three estimators perform better and approach each other as n increases. Additionally, the length of CI and HPD reduces as n increases, demonstrating how the estimates’ precision improves with increasing sample size. We further find that when n increases, the estimates improve and approach each other, and that the Bayes estimates of R(t),  h(t),  and MTSF based on the Gibbs sampling perform better than the Bayes estimates based on Importance sampling and the ML estimator. Furthermore, we note that the ETT reduces with the random censoring and increases with n. Additionally, a real data set is examined to illustrate the proposed estimation techniques. The main focus of the paper is on drawing conclusions about the parameters under random censoring. An extension of the work for the cases when one encounters with random non-responses may be interesting and considered in future research, see Basit and Bhatti [5].

Table 1 Different estimates of $\alpha _{1}$

Table 2 Different estimates of $\alpha _{2}$

Table 3 Different estimates of $\beta$

Table 4 The $95\%$ asymptotic confidence and HPD credible intervals

Table 5 Different estimates of R(t) for $t=0.5$

Table 6 Different estimates of h(t) for $t=0.5$

Table 7 Different estimates of MTSF

Table 8 The estimation of ETT or OBTT

Table 9 Goodness-of-fit tests for the Dukes’ C colorectal cancer data

Table 10 The ML and Bayes estimates of the parameters and reliability characteristics for the Dukes’ C colorectal cancer data set

Table 11 The $95\%$ asymptotic confidence and HPD credible intervals of the parameters for the Dukes’ C colorectal cancer data set

Fig. 1

The empirical and fitted cdfs of different competing models for Dukes’C colorectal cancer data