General Soliton and (Semi-)Rational Solutions of a (2+1)-Dimensional Sinh-Gordon Equation

Abstract

In this paper, we investigate solutions of a (2+1)-dimensional sinh-Gordon equation. General solitons and (semi-)rational solutions are derived by the combination of Hirota’s bilinear method and Kadomtsev-Petviashvili hierarchy reduction approach. General solutions are expressed as $N\times N$ Gram-type determinants. When the determinant size N is even, we generate solitons, line breathers, and (semi-)rational solutions located on constant backgrounds. In particular, through the asymptotic analysis we prove that the collision of solitons are completely elastic. When N is odd, we derive exact solutions on periodic backgrounds. The dynamical behaviors of those derived solutions are analyzed with plots. For rational solutions, we display the interaction of lumps. For semi-rational solutions, we find the interaction solutions between lumps and solitons.

1 Introduction

The study of solitons, breathers, rational solutions and their interactions is a main topic in the field of soliton theory and attracts great attention in recent years. Various explicit physical meaning solutions of integrable equations are found, such as algebra solitons, lumps, line breathers, rogue waves and peakon solutions, and so on. Studies of solitons are not only restricted in (1+1)-dimensional integrable equations. In fact, (2+1)-dimensional integrable systems have richer dynamic properties and they are more relevant to real world physics. Many (2+1)-dimensional integrable systems have been extensively studied, such as Davey-Stewartson (DS) equation [1,2,3], Mel’nikov equation [4], dispersive long wave equation [5], Fokas equation [6], et al. A variety of powerful methods have been developed to solve integrable equations, such as inverse scattering method [7], Darboux transformation method (DT) [8], Hirota’s bilinear method [9], the dressing method [10], Riemann-Hilbert method [11], Kadomtsev-Petviashvili (KP) hierarchy reduction method [12] and so on. Among these methods, the KP reduction technique in conjunction with Hirota’s bilinear method is very powerful to construct (semi-)rational solutions. This approach has been applied to many integrable systems [1,2,3,4, 13,14,15,16] to derive rational and semi-rational solutions. These pioneer works inspire us to study dynamics of (2+1)-dimensional nonlinear integrable equations.

In 1987, the sinh-Gordon equation, $q_{xt}+\sinh q=0$, was extended to (2+1)-dimension by the inverse spectral transform [17]. The extended (2+1)-dimensional sinh-Gordon equation reads

$$\begin{aligned} \bigg (e^{-q}\Big (e^q(q_{xt}+\sinh q)\Big )_x\bigg )_x=\sigma ^2\bigg (e^{-q}\int ^{x}_{-\infty }(e^q)_ydx\bigg )_{yt} -\frac{1}{2}\sigma ^2\bigg (\Big (e^{-q}\int ^{x}_{-\infty }(e^q)_ydx\Big )^2\bigg )_{xt},\quad \sigma ^2=\pm 1. \end{aligned}$$

(1)

In [18], Lou proposed the following (2+1)-dimensional extended sinh-Gordon equation

$$\begin{aligned} \left\{ \begin{aligned}&\bigg (\alpha \phi _{yt}+e^{-2\phi }(e^{2\phi }\phi _{xt})_{x}\bigg )_{y}=-(s_{x}e^{2\phi })_{xx},\\&\bigg (e^{2\phi }\Big (\phi _{xt}-\frac{1}{2}Ce^{2\phi }+\frac{1}{2}Ce^{-2\phi }\Big )\bigg )_{x}+\alpha e^{2\phi }\phi _{yt}+\alpha e^{2\phi }(e^{2\phi }s)_{x}=0. \end{aligned} \right. \end{aligned}$$

(2)

This equation is related to the first negative KP equation by a two-dimensional Miura transformation. Here, C is arbitrary constant, $\alpha ^2=-1$ and $\alpha ^2=1$ correspond to the KP I and KP II equation, respectively. In [19], by setting $2\phi =\omega , C=\frac{1}{2}, \alpha =1,s=\theta$, the (2+1)-dimensional sinh-Gordon equation (2) is rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\bigg (e^{\omega }\Big (\omega _{xt}-\sinh \omega \Big )\bigg )_{x} +e^{\omega }\omega _{yt}=-2e^{2\omega }(\theta _{x}+\omega _{x}\theta ),\\&(\theta _{x}e^{\omega })_{xx}+\frac{1}{2}\Big (\omega _{y} +\omega _{xx}+\frac{1}{2}\omega ^{2}_{x}\Big )_{yt}=0. \end{aligned} \right. \end{aligned}$$

(3)

Upon the dependent variable transformation

$$\begin{aligned} \omega (x,y,t)=2\ln \frac{F(x,y,t)}{G(x,y,t)},\quad \theta (x,y,t) =2\int ^{-\infty }_{x}\Big (\ln G(\xi ,y,t)\Big )_{yt}\bigg (\frac{G(\xi ,y,t)}{F(\xi ,y,t)}\bigg )^{2}d\xi , \end{aligned}$$

(4)

the sinh-Gordon equation (3) is transformed into the following bilinear form [19]

$$\begin{aligned} \left\{ \begin{aligned}&(D_{y}+D^{2}_{x})F\cdot G=0,\\&(D^{2}_{x}D_{t}+D_{y}D_{t}+2D_{x})F\cdot G=0. \end{aligned} \right. \end{aligned}$$

(5)

Besides, a bilinear Bäcklund transformation, Wronskian solutions and Pfaffian generalization of this equation were derived in [19]. Integrable discretization of the (2+1)-dimensional extended sinh-Gordon equation (3) was investigated in [20]. By using Hirota’s bilinear method and KP hierarchy reduction technique, the rational solutions of algebraic solitons in the Gram determinant form are constructed in [21]. However, to the best of our knowledge, general solitons, line breathers, lumps on the constant and periodic backgrounds of the (2+1)-dimensional sinh-Gordon equation (3) have not been reported yet.

In this paper, we consider general solitons, line breather solutions and (semi-)rational solutions of the (2+1)-dimensional sinh-Gordon equation (3). We derive lump solutions and further explore semi-rational solutions consisting of lumps and solitons. Moreover, the dynamical behaviors of solitons, line breathers and lumps both on constant and periodic backgrounds are studied.

This paper is organized as follows. In Section 2, we present the general solitons and (semi-)rational solutions of the sinh-Gordon equation. These solutions are expressed as $N\times N$ Gram-type determinant. In Section 3, we demonstrate the dynamic behaviors of solitons on the constant and periodic backgrounds, respectively. In Section 4, we present the line breather solutions on the constant and periodic grounds. In Section 5, the dynamics of rational solutions on the constant and periodic background are illustrated. In Section 6, semi-rational solutions of interactions of lumps and solitons are investigated. Finally we give the conclusion and discussion.

2 General Solitons and (Semi-)Rational Solutions in Determinant Form

In this part, we give the general solitons and (semi-)rational solutions of the sinh-Gordon Eq. (3). Bilinear sinh-Gordon equation (5) can be obtained from the following KP hierarchy equations

$$\begin{aligned}&(D_{x_1}^2-D_{x_2})\tau _{n+1}\cdot \tau _n=0, \end{aligned}$$

(6)

$$\begin{aligned}&( D_{x_{-1}}(D_{x_1}^2-D_{x_2})-4D_{x_1})\tau _{n+1}\cdot \tau _n=0, \end{aligned}$$

(7)

under the variables transformation $x_1=-x,x_2=-y,x_{-1}=\frac{t}{2},$ and $\tau _n=F, \,\tau _{n+1}=G$ (see ref. [21]). The rational algebraic solitons in the Gram-type determinant form of the sinh-Gordon equation (5) are presented in [21]. In the following we give more general soliton and (semi-)rational solutions.

Theorem 1

The bilinear sinh-Gordon equation (5) admits solutions

$$\begin{aligned} F=\tau _{n+1},\quad G=\tau _{n}, \end{aligned}$$

(8)

where $\tau _{n}=\det _{1\le i,j\le N}(m^{(n)}_{i,j})$. The elements are defined as following

$$\begin{aligned}&m^{(n)}_{i,j}=c_{i}\delta _{i,j}e^{-\xi _{i}-\eta _{j}}\nonumber \\&+\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\sum ^{n_{i}}_{k=0}a_{i,k}\Big (p_{i}\partial p_{i}+\xi '_i+n\Big )^{n_{i}-k}\times \sum ^{n_{j}}_{l=0}b_{j,l}\Big (q_{j}\partial q_{j}+\eta '_j-n\Big )^{n_{j}-l}\frac{1}{p_{i}+q_{j}}, \end{aligned}$$

(9)

where

$$\begin{aligned}&\xi '_{i}=-p_{i}x-2p^{2}_{i}y-\frac{1}{2p_{i}}t, \end{aligned}$$

(10)

$$\begin{aligned}&\eta '_{j}=-q_{j}x+2q^{2}_{j}y-\frac{1}{2q_{j}}t, \end{aligned}$$

(11)

$$\begin{aligned}&\xi _{i}=-p_{i}x-p^{2}_{i}y+\frac{1}{2p_{i}}t+\xi _{i,0}, \end{aligned}$$

(12)

$$\begin{aligned}&\eta _{j}=-q_{j}x+q^{2}_{j}y+\frac{1}{2q_{j}}t+\eta _{j,0}. \end{aligned}$$

(13)

Here, N is a positive integer, $n_i,n_j$ are nonnegative integers, $\delta _{i,j}$ is the Kronecker delta, and $c_i,p_i,q_j,\xi _{i,0},\eta _{j,0}$ are arbitrary parameters.

The Gram determinant solutions can be obtained from solutions the KP hierarchy equations by introducing differential operators applied to those parameters of elements in the determinant [21]. The proof of the above theorem is similar to that in [21] and we omit the details here.

Remark 1

Four types of solutions (8) in Theorem 1 will be discussed under the following different parameter constraints:

$\textrm{I}$. soliton solutions as $c_i\ne 0, n_i=0,i=1,...,N$;

$\textrm{II}$. line breathers as $c_i\ne 0, n_i=0,i=1,...,N$;

$\textrm{III}$. rational solutions (lumps) as $c_i=0, \sum ^{N}_{k=1}n_k\ge 1, i=1,...,N$;

$\textrm{IV}$. semi-rational solutions (mixed solutions of lumps and solitons) as $\sum ^{N}_{i=1}|c_i|>0,\sum ^{N}_{k=1}n_k\ge 1$.

Remark 2

To construct solitons, line breathers, rational and semi-rational solutions on the constant background, we set the size of the determinants to be even in Theorem 1. Meanwhile, to derive solutions on the periodic background, we take the odd size of the determinants.

In the following, we take appropriate parameter constraints to construct solitons, line breathers and lumps of the sinh-Gordon equation (3).

3 Dynamics of the Soliton Solutions

In this part, we study the dynamic behaviors of the soliton solutions of the sinh-Gordon equation (3) on constant and periodic backgrounds, respectively. To this end, we take parameters $n_{i}=0, (i=1,2,...,N)$ in Theorem 1.

3.1 One-Soliton Solutions

To obtain one-soliton solutions on the constant background, we take $N=1$ in Theorem 1. Then the first order determinant reads as

$$\begin{aligned} m^{(n)}_{1,1}=c_{1}+\Big (-\frac{p_1}{q_1}\Big )^{n}\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}},\quad n=0,1, \end{aligned}$$

(14)

where

$$\begin{aligned} \xi _1+\eta _1=-(p_1+q_1)x+(q^{2}_{1}-p^2_1)y+\Big (\frac{1}{2p_{1}}+\frac{1}{2q_{1}}\Big )t+\xi _{1,0}+\eta _{1,0}, \end{aligned}$$

(15)

and $p_1,q_1,\xi _{1,0},\eta _{1,0}$ are arbitrary complex numbers. Let us consider the potential $\omega _x$, where

$$\begin{aligned} \omega _x=2\Big (\ln \frac{F}{G}\Big )_x=\frac{2(p_1+q_1)^{2}}{q_1(p_1+q_1)e^{-\xi _1-\eta _1} +\frac{-p_1}{p_1+q_1}e^{\xi _1+\eta _1}+q_1-p_1}. \end{aligned}$$

(16)

Here we require $p_1q_1<0$ and $p_1+q_1>0$ to avoid singularity. We remark here that the last equation can be rewritten as

$$\begin{aligned} \omega _x=\frac{2(p_1+q_1)^{2}}{2\sqrt{-p_1q_1}\cosh (-\xi _1-\eta _1+\theta )+q_1-p_1}, \end{aligned}$$

as $p_1<0,q_1>0$ or

$$\begin{aligned} \omega _x=\frac{2(p_1+q_1)^{2}}{-2\sqrt{-p_1q_1}\cosh (-\xi _1-\eta _1+\theta )+q_1-p_1}, \end{aligned}$$

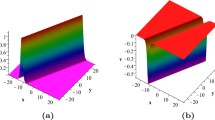
as $p_1>0,q_1<0$, where $\exp (\theta )=(p_1+q_1)\sqrt{-\frac{q_1}{p_1}}$. Plots of one-soliton solutions (16) under different parameters are shown in Fig. 1 with different parameters.

We set $p_1=\alpha +\beta \textrm{i},c_1=\lambda \textrm{i}$ and $q_1=-p_1^*$ with real $\alpha ,\beta ,\lambda$. The tau functions F and G have the expression

$$\begin{aligned}&F=c_{1}+\Big (-\frac{p_1}{q_1}\Big )\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}}=\lambda \textrm{i}-\frac{\alpha +\beta \textrm{i}}{2\beta \textrm{i}(-\alpha +\beta \textrm{i})}\exp \Big [-2\beta \textrm{i}\Big (x+2\alpha y+\frac{t}{2(\alpha ^2+\beta ^2)}\Big )+\xi _{1,0}+\eta _{1,0}\Big ], \end{aligned}$$

(17)

$$\begin{aligned}&G=c_{1}+\frac{1}{p_{1}+q_{1}}e^{\xi _{1}+\eta _{1}}=\lambda \textrm{i}+\frac{1}{2\beta \textrm{i}}\exp \Big [-2\beta \textrm{i}\Big (x+2\alpha y+\frac{t}{2(\alpha ^2+\beta ^2)}\Big )+\xi _{1,0}+\eta _{1,0}\Big ]. \end{aligned}$$

(18)

Substituting F and G into the potential $\omega _x$ leads to

$$\begin{aligned} \omega _x=\frac{16\beta ^3\lambda \exp (-2\textrm{i}\zeta +\xi _{1,0} +\eta _{1,0})}{(-\alpha -\textrm{i}\beta )\exp (-4\textrm{i}\zeta +2\xi _{1,0}+2\eta _{1,0}) +4\alpha \beta \lambda \exp (-2\textrm{i}\zeta +\xi _{1,0}+\eta _{1,0})+4\beta ^2\lambda ^2(-\alpha +\textrm{i}\beta )}, \end{aligned}$$

(19)

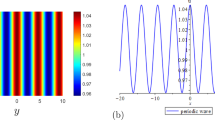
where $\zeta =\beta x+2\alpha \beta y+\frac{\beta }{2(\alpha ^2+\beta ^2)}t$. In this case, solution (19) is periodic with periods $\pi /\beta$ in x, $\pi /2\alpha \beta$ in y and $2\pi (\alpha ^2+\beta ^2)/\beta$ in t. Figures of this periodic one-soliton solution are depicted in Fig. 2.

Fig. 1

One-soliton solution $\omega _x$ (16) with parameter values a $p_1=-2,q_1=3,c_1=1,y=1,\xi _{1,0}=\eta _{1,0}=0$; b $p_1=4,q_1=-3,c_1=1,y=2,\xi _{1,0}=\eta _{1,0}=0$

Fig. 2

Profiles of periodic one-soliton (19) with parameters $\alpha =\beta =1,c_1=1,y=1,\xi _{1,0}=\eta _{1,0}=0$; b Density plot of $\omega _x$

3.2 Two-Soliton Solutions on the Constant Background

For $N=2$, we take $c_1=c_2=1$ in Theorem 1. The tau function solutions F and G are expressed by $2\times 2$ determinants

$$\begin{aligned} F&=\begin{vmatrix} 1-\frac{p_1}{q_1}\frac{1}{p_1+q_1}e^{\xi _{1}+\eta _{1}}&-\frac{p_1}{q_2}\frac{1}{p_1+q_2}e^{\xi _{1}+\eta _{2}} \\ -\frac{p_2}{q_1}\frac{1}{p_2+q_1}e^{\xi _{2}+\eta _{1}}&1-\frac{p_2}{q_2}\frac{1}{p_2+q_2}e^{\xi _{2}+\eta _{2}} \end{vmatrix} \nonumber \\&=1-\frac{p_1}{q_1}\frac{1}{p_1+q_1}e^{\zeta _1}-\frac{p_2}{q_2}\frac{1}{p_2+q_2}e^{\zeta _2} +\frac{p_1p_2}{q_1q_2}\frac{(p_1-p_2)(q_1-q_2)}{(p_1+q_1)(p_1+q_2)(p_2+q_1)(p_2+q_2)}e^{\zeta _1+\zeta _2}, \end{aligned}$$

(20)

$$\begin{aligned} G&=\begin{vmatrix} 1+\frac{1}{p_1+q_1}e^{\xi _{1}+\eta _{1}}&\frac{1}{p_1+q_2}e^{\xi _{1}+\eta _{2}} \\ \frac{1}{p_2+q_1}e^{\xi _{2}+\eta _{1}}&1+\frac{1}{p_2+q_2}e^{\xi _{2}+\eta _{2}} \end{vmatrix} \nonumber \\&=1+\frac{1}{p_1+q_1}e^{\zeta _1}+\frac{1}{p_2+q_2}e^{\zeta _2}+\frac{(p_1-p_2)(q_1-q_2)}{(p_1+q_1)(p_1+q_2)(p_2+q_1)(p_2+q_2)}e^{\zeta _1+\zeta _2}, \end{aligned}$$

(21)

with

$$\begin{aligned} \zeta _i=\xi _i+\eta _i=-(p_i+q_i)x+(q^{2}_{i}-p^2_i)y +\Big (\frac{1}{2p_{i}}+\frac{1}{2q_{i}}\Big )t+\xi _{i,0}+\eta _{i,0},\quad i=1,2. \end{aligned}$$

(22)

In what follows, we analyze the asymptotic behaviors of two-soliton solutions. For convenience, we set $y=0$ and then the potential $\omega _x$ is expressed as

$$\begin{aligned} \omega _x=2\frac{A_1e^{\zeta _1}+A_2e^{\zeta _2}+A_{12}e^{\zeta _1+\zeta _2} +A_{112}e^{2\zeta _1+\zeta _2}+A_{122}e^{\zeta _1+2\zeta _2}}{1+B_1e^{\zeta _1}+B_2e^{\zeta _2}+B_{11}e^{2\zeta _1}+B_{22}e^{2\zeta _2} +B_{12}e^{\zeta _1+\zeta _2}+B_{112}e^{2\zeta _1+\zeta _2}+B_{122}e^{\zeta _1+2\zeta _2}+B_{1122}e^{2\zeta _1+2\zeta _2}}, \end{aligned}$$

(23)

where

$$\begin{aligned}&A_1=\frac{p_{1}+q_{1}}{q_{1}},\quad A_2=\frac{p_{2}+q_{2}}{q_{2}},\quad B_{1}=\frac{-p_1+q_1}{q_1(p_1+q_1)},\quad B_{2}=\frac{-p_2+q_2}{q_2(p_2+q_2)},\\&A_{112}=\frac{-p_1(p_1-p_2)(q_1-q_2)(p_2+q_2)}{q_1q_2(p_1+q_1)^2(p_1+q_2)(p_2+q_1)},\quad A_{122}=\frac{-p_2(p_1-p_2)(q_1-q_2)(p_1+q_1)}{q_1q_2(p_1+q_2)(p_2+q_1)(p_2+q_2)^2},\\&B_{11}=\frac{-p_1}{q_1(p_1+q_1)^2},\quad B_{22}=\frac{-p_2}{q_2(p_2+q_2)^2},\quad B_{112}=\frac{-p_1(-p_2+q_2)(p_1-p_2)(q_1-q_2)}{q_1q_2(p_1+q_1)^2(p_1+q_2)(p_2+q_1)(p_2+q_2)},\\&B_{122}=\frac{-p_2(-p_1+q_1)(p_1-p_2)(q_1-q_2)}{q_1q_2(p_1+q_1)(p_1+q_2)(p_2+q_1)(p_2+q_2)^2},\quad B_{1122}=\frac{p_1p_2(p_1-p_2)^2(q_1-q_2)^2}{q_1q_2(p_1+q_1)^2(p_1+q_2)^2(p_2+q_1)^2(p_2+q_2)^2}. \end{aligned}$$

Without loss of generality, we assume $p_i+q_i>0, (i=1,2)$ and $p_2q_2<p_1q_1<0$. We denote the left-moving soliton along $\zeta _1=0$ as Soliton 1 and the right-moving soliton along $\zeta _2=0$ as Soliton 2. The asymptotic behaviours for the two-soliton solutions are analysed in the following.

Before collision ($t\rightarrow -\infty$):

Soliton 1 ($\zeta _1\approx 0,\zeta _2\rightarrow +\infty$)

$$\begin{aligned} \omega _x&\rightarrow \frac{2(p_1+q_1)^2}{(q_1-p_1)+2\sqrt{-p_1q_1}\cosh (\zeta _1-\theta _1)}, \end{aligned}$$

(24)

where $\theta _1$ is defined by $\exp (\theta _1)=\frac{(p_1+q_1)(p_1+q_2)(p_2+q_1)}{(p_1-p_2)(q_1-q_2)}\sqrt{-\frac{q_1}{p_1}}.$

Soliton 2 ($\zeta _2\approx 0,\zeta _1\rightarrow -\infty$)

$$\begin{aligned} \omega _x&\rightarrow \frac{2(p_2+q_2)^2}{(q_2-p_2)+2\sqrt{-p_2q_2}\cosh (\zeta _2-\theta _2)}, \end{aligned}$$

(25)

where $\theta _2$ is defined by $\exp (\theta _2)=(p_2+q_2)\sqrt{-\frac{q_2}{p_2}}$.

After collision ($t\rightarrow +\infty$):

Soliton 1 ($\zeta _1\approx 0,\zeta _2\rightarrow -\infty$)

$$\begin{aligned} \omega _x&\rightarrow \frac{2(p_1+q_1)^2}{(q_1-p_1)+2\sqrt{p_1q_1}\cosh (\zeta _1-\theta _3)}, \end{aligned}$$

(26)

where $\theta _3$ is defined by $\exp (\theta _3)=(p_1+q_1)\sqrt{-\frac{q_1}{p_1}}$.

Soliton 2 ($\zeta _2\approx 0,\zeta _1\rightarrow +\infty$)

$$\begin{aligned} \omega _x&\rightarrow \frac{2(p_2+q_2)^2}{(q_2-p_2)+2\sqrt{p_2q_2}\cosh (\zeta _2-\theta _4)}, \end{aligned}$$

(27)

where $\theta _4$ is defined by $\exp (\theta _4)=\frac{(p_2+q_2)(p_1+q_2)(p_2+q_1)}{(p_1-p_2)(q_1-q_2)}\sqrt{-\frac{q_2}{p_2}}.$

From the asymptotic analysis, we find that the collision of two solitons is completely elastic, i.e., their shapes and velocities keep unchanged after the interaction. In particular, Soliton 1 has a phase shift $\theta$ and Soliton 2 has an opposite phase shift $-\theta$ with $\exp (\theta )=\frac{(p_1+q_2)(p_2+q_1)}{(p_1-p_2)(q_1-q_2)}$ after the collision. We depict the plots of the interaction of two solitons and the corresponding density plots on the constant background in Figs. 3, 4 and 5, respectively. We observe three types of two-soliton solutions. Figure 3 displays the interaction of two bright solitons. Figure 4 shows the interaction of two solitons both under the horizon. Figure 5 exhibits the interaction of two solitons with one under the horizon and the other above the horizon.

Fig. 3

Two-soliton solution $\omega _x$ on the constant background at $y=0$ and the corresponding density plot with parameters $p_1=-1, q_1=\frac{5}{3}, p_2=-\frac{1}{5}, q_2=\frac{3}{5},\xi _{i,0}=\eta _{i,0}=0,c_1=c_2=1$

Fig. 4

Two-soliton solution $\omega _x$ on the constant background at $y=0$ and the corresponding density plot with parameters $p_1=2, q_1=-\frac{5}{4}, p_2=1, q_2=-\frac{3}{5},\xi _{i,0}=\eta _{i,0}=0,c_1=c_2=1$

Fig. 5

Two-soliton solution $\omega _x$ on the constant background at $y=0$ and the corresponding density plot with parameters $p_1=-1, q_1=2, p_2=5, q_2=-3,\xi _{i,0}=\eta _{i,0}=0,c_1=c_2=1$

3.3 Two-Soliton Solutions on the Periodic Background

In order to derive two-soliton solutions on the periodic background, we take $N=3$ and $q_3=-p_3^*$ in Theorem 1. Then the tau functions F and G have the following determinant expressions

$$\begin{aligned} F=\begin{vmatrix} m^{(1)}_{1,1}&m^{(1)}_{1,2}&m^{(1)}_{1,3} \\ m^{(1)}_{2,1}&m^{(1)}_{2,2}&m^{(1)}_{2,3} \\ m^{(1)}_{3,1}&m^{(1)}_{3,2}&m^{(1)}_{3,3} \end{vmatrix},\quad G=\begin{vmatrix} m^{(0)}_{1,1}&m^{(0)}_{1,2}&m^{(0)}_{1,3} \\ m^{(0)}_{2,1}&m^{(0)}_{2,2}&m^{(0)}_{2,3} \\ m^{(0)}_{3,1}&m^{(0)}_{3,2}&m^{(0)}_{3,3} \end{vmatrix}, \end{aligned}$$

(28)

with entries

$$\begin{aligned} m^{(n)}_{i,j}=c_i\delta _{i,j}+\Big (-\frac{p_i}{q_j}\Big )^{n}\frac{1}{p_{i}+q_{j}}e^{\xi _{i}+\eta _{j}},\quad 1\le i,j\le 3,\quad n=0,1. \end{aligned}$$

(29)

We put $p_3=\alpha +\beta \textrm{i},\, q_3=-\alpha +\beta \textrm{i},\,c_1=c_2=1,c_3=\lambda \textrm{i}$, and

$$\begin{aligned}&\xi _i+\eta _i=-(p_i+q_i)x+(q^{2}_{i}-p^2_i)y+\Big (\frac{1}{2p_{i}}+\frac{1}{2q_{i}}\Big )t+\xi _{i,0}+\eta _{i,0},\quad i=1,2, \end{aligned}$$

(30)

$$\begin{aligned}&\xi _3+\eta _3=-2\beta \textrm{i}\Big [x-2\alpha y-\frac{1}{2(\alpha ^2+\beta ^2)}t\Big ]+\xi _{3,0}+\eta _{3,0}. \end{aligned}$$

(31)

We choose $p_1,q_1,p_2, q_2$ the same values as those in Fig. 3 and $p_3=-q_3^{*}=2+5\textrm{i},c_3=2\textrm{i}$. Then we can generate two solitons on the periodic background (see Fig. 6).

Fig. 6

Two-soliton solution $\omega _x$ on the periodic background at $y=0$ and the corresponding density plot with parameters $p_1=-1, q_1=\frac{5}{3}, p_2=-\frac{1}{5}, q_2=\frac{3}{5},p_3=2+5\textrm{i},q_3=-2+5\textrm{i},\xi _{i,0}=\eta _{i,0}=0,c_1=c_2=1,c_3=2\textrm{i}$

4 Dynamics of the Line Breather Solutions

In this part, we study the dynamics of line breather solutions of sinh-Gordon equation (3) on both constant and periodic backgrounds. To construct line breather solutions, we take parameters $n_{i}=0,i=1,2,...,N$. For simplicity, we consider the line breather solutions on constant and periodic backgrounds by setting $N=2$ and 3, respectively.

4.1 Line Breather Solutions on the Constant Background

To construct line breather solutions of sinh-Gordon equation (3) on the constant background, we choose $p_i,q_i, (i=1,2,...,N)$ to be purely imaginary and $p_i\ne -q_i$. For $N=2$, we set $p_1=q_2=p\textrm{i},q_1=p_2=q\textrm{i},c_1=\alpha +\beta \textrm{i},c_2=-c_1^*$, where $p,q,\alpha ,\beta$ are real numbers, $p\ne -q$ and $\beta$ are nonzero. The potential $\omega _x$ has the expression

$$\begin{aligned} \omega _x=2\Big (\ln \frac{F}{G}\Big )_x, \end{aligned}$$

(32)

where

$$\begin{aligned} F&= \begin{vmatrix} (\alpha +\beta \textrm{i})e^{-\xi _{1}-\eta _{1}}-\frac{p\textrm{i}}{q\textrm{i}}\frac{1}{p\textrm{i}+q\textrm{i}}&-\frac{p\textrm{i}}{p\textrm{i}}\frac{1}{p\textrm{i}+p\textrm{i}}\\ -\frac{q\textrm{i}}{q\textrm{i}}\frac{1}{q\textrm{i}+q\textrm{i}}&(-\alpha +\beta \textrm{i})e^{-\xi _{2}-\eta _{2}}-\frac{q\textrm{i}}{p\textrm{i}}\frac{1}{q\textrm{i}+p\textrm{i}} \end{vmatrix}\nonumber \\&=-(\alpha ^2+\beta ^2)e^{-\xi _1-\eta _1-\xi _2-\eta _2}\Big [1-\frac{p}{q}b_1e^{\xi _1+\eta _1} -\frac{q}{p}b_2e^{\xi _2+\eta _2}+b_{12}e^{\xi _1+\eta _1+\xi _2+\eta _2}\Big ], \end{aligned}$$

(33)

$$\begin{aligned} G&=\begin{vmatrix} (\alpha +\beta \textrm{i})e^{-\xi _{1}-\eta _{1}}+\frac{1}{p\textrm{i}+q\textrm{i}}&\frac{1}{p\textrm{i}+p\textrm{i}} \\ \frac{1}{q\textrm{i}+q\textrm{i}}&(-\alpha +\beta \textrm{i})e^{-\xi _{2}-\eta _{2}}+\frac{1}{q\textrm{i}+p\textrm{i}} \end{vmatrix}\nonumber \\&=-(\alpha ^2+\beta ^2)e^{-\xi _1-\eta _1-\xi _2-\eta _2}\Big [1+b_1e^{\xi _1+\eta _1} +b_2e^{\xi _2+\eta _2}+b_{12}e^{\xi _1+\eta _1+\xi _2+\eta _2}\Big ], \end{aligned}$$

(34)

and

$$\begin{aligned}&\xi _1+\eta _1=(p+q)\Big [-\textrm{i}x+(p-q)y-\frac{\textrm{i}}{2pq}t\Big ]+\xi _{1,0}+\eta _{1,0}, \end{aligned}$$

(35)

$$\begin{aligned}&\xi _2+\eta _2=(p+q)\Big [-\textrm{i}x+(q-p)y-\frac{\textrm{i}}{2pq}t\Big ]+\xi _{2,0}+\eta _{2,0}, \end{aligned}$$

(36)

$$\begin{aligned}&b_{1}=\frac{1}{(p+q)(-\beta +\alpha \textrm{i})},\quad b_{2}=\frac{1}{(p+q)(-\beta -\alpha \textrm{i})},\quad b_{12}=-\frac{(p-q)^2}{4pq(p+q)(\alpha ^2+\beta ^2)}. \end{aligned}$$

(37)

To illustrate the dynamics of $\omega _x$ (32), we select the parameters $\alpha =0,\beta =-1,p=\frac{1}{10},q=\frac{2}{5},y=0$. In this case, the line breather solution admits

$$\begin{aligned} \omega _x=\frac{50\textrm{i}\Big (4e^{\frac{3\textrm{i}}{4}(2x+25t)} +9e^{\frac{\textrm{i}}{4}(2x+25t)}\Big )}{\Big (4e^{\frac{\textrm{i}}{2}(2x+25t)} -34e^{\frac{\textrm{i}}{4}(2x+25t)}-9\Big )\Big (4e^{\frac{\textrm{i}}{2}(2x+25t)}+16e^{\frac{\textrm{i}}{4}(2x+25t)}-9\Big )}. \end{aligned}$$

(38)

with the periods $\frac{2\pi }{p+q}$ in x and $\frac{4pq\pi }{p+q}$ in t. The plot of the line breather is depicted in Fig. 7 with parameter values $\alpha =0,\beta =-1,p=\frac{1}{10},q=\frac{2}{5},y=0$. One can find that the figure appears periodicity. The maximum and minimum value of $|\omega _x|$ under these parameters are approximately 1.5152 and 0.3332, respectively.

Fig. 7

Line breather solution $\omega _x$ (38) on the constant background and the corresponding density plot with parameters $\alpha =0,\beta =-1,p=\frac{1}{10},q=\frac{2}{5},y=0$

4.2 Line Breather Solutions on the Periodic Background

For $N=3$, we choose $p_i,q_j, i,j=1,2,3$ to be purely imaginary and $p_1=q_2=p\textrm{i},q_1=p_2=q\textrm{i},p_3=q_3=m\textrm{i},c_1=\alpha +\beta \textrm{i},c_3=c_2=-c_1^*$ to construct line breather solutions on the periodic background. In this case, we have potential $\omega _x=2\Big (\ln \frac{F}{G}\Big )_x,$ where

$$\begin{aligned} F&=\begin{vmatrix} (\alpha +\beta \textrm{i})e^{-\xi _{1}-\eta _{1}}-\frac{p}{q}\frac{1}{p\textrm{i}+q\textrm{i}}&-\frac{1}{2p\textrm{i}}&-\frac{p}{m}\frac{1}{p\textrm{i}+m\textrm{i}} \\ -\frac{1}{2q\textrm{i}}&(-\alpha +\beta \textrm{i})e^{-\xi _{2}-\eta _{2}}-\frac{q}{p}\frac{1}{q\textrm{i}+p\textrm{i}}&-\frac{q}{m}\frac{1}{q\textrm{i}+m\textrm{i}} \\ -\frac{m}{q}\frac{1}{m\textrm{i}+q\textrm{i}}&-\frac{m}{p}\frac{1}{m\textrm{i}+p\textrm{i}}&(-\alpha +\beta \textrm{i})e^{-\xi _{3}-\eta _{3}}-\frac{1}{2m\textrm{i}} \end{vmatrix}, \end{aligned}$$

(39)

$$\begin{aligned} G&=\begin{vmatrix} (\alpha +\beta \textrm{i})e^{-\xi _{1}-\eta _{1}}+\frac{1}{p+q}&\frac{1}{2p\textrm{i}}&\frac{1}{p\textrm{i}+m\textrm{i}} \\ \frac{1}{q+q}&(-\alpha +\beta \textrm{i})e^{-\xi _{2}-\eta _{2}}+\frac{1}{q\textrm{i}+p\textrm{i}}&\frac{1}{q\textrm{i}+m\textrm{i}}\\ \frac{1}{m\textrm{i}+q\textrm{i}}&\frac{1}{m\textrm{i}+p\textrm{i}}&(-\alpha +\beta \textrm{i})e^{-\xi _{3}-\eta _{3}}+\frac{1}{2m\textrm{i}} \end{vmatrix}. \end{aligned}$$

(40)

Here $\xi _1,\xi _2,\xi _3,\eta _1,\eta _2,\eta _3$ are given by (10)–(13). By taking the same parameter values as those in Fig. 7 and $p_3=q_3=\textrm{i},c_3=-\textrm{i}$, $\omega _x$ owns the expression

$$\begin{aligned} {\begin{matrix} \omega _x=&(58436224e^{2\textrm{i}(2x+13t)}+182613200e^{\frac{1}{4}\textrm{i}(22x+83t)} -156241008e^{\frac{1}{4}\textrm{i}(14x+79t)}-16008300e^{\frac{3}{4}\textrm{i}(2x+25t)}\\ &-786671424e^{\frac{3}{2}\textrm{i}(2x+9t)}+410879700e^{\frac{3}{4}\textrm{i}(6x+11t)} +123268068e^{\frac{1}{4}\textrm{i}(10x+29t)}-4428675e^{\frac{1}{4}\textrm{i}(2x+25t))}\\ &+36374184e^{\textrm{i}(t+2x)})/[(47432e^{\frac{3}{2}\textrm{i}(2x+9t)} -23716e^{\frac{1}{2}\textrm{i}(2x+25t)}-403172e^{\frac{1}{4}\textrm{i}(10x+29t)}+70686e^{\frac{1}{4}\textrm{i}(2x+25t)}\\ &-106722e^{\textrm{i}(t+2x)}+6561)(47432e^{\frac{3}{2}\textrm{i}(2x+9t)} +23716e^{\frac{1}{2}\textrm{i}(2x+25t)}+189728e^{\frac{1}{4}\textrm{i}(10x+29t)}\\ &+33264e^{\frac{1}{4}\textrm{i}(2 x+25t)}-106722e^{\textrm{i}(t+2x)}-6561)]. \end{matrix}} \end{aligned}$$

(41)

We depict the line breather solution (41) on the periodic background (see Fig. 8). The line breathers on the periodic background exhibit higher amplitudes than those on the constant background. As shown in Fig. 8, the maximum and the minimum values of $|\omega _x|$ are approximately 4.8392 and 0.1342, respectively.

Fig. 8

Line breather solution $\omega _x$ (41) on the periodic background and the corresponding density plot with parameters $\alpha =0,\beta =-1,p=\frac{1}{10},q=\frac{2}{5},p_3=q_3=\textrm{i},c_3=-\textrm{i},y=0$

5 Dynamics of the Rational Solutions

In this part, we derive rational solutions to the sinh-Gordon equation (3) and investigate dynamic behaviors. In order to obtain rational solutions, we take $c_i=0,(n _i=1,i=1,2...,)$ in Theorem 1. Rational solutions of algebraic soliton types to the sinh-Gordon equation (3) were studied in [5], but lump type rational solutions have not been reported. In the following we consider lump type rational solutions to the potential $\frac{F}{G}$ both on constant and periodic backgrounds.

5.1 Rational Solutions on the Constant Background

We take the determinant size $N=2$ and then

$$\begin{aligned} F= \begin{vmatrix} m^{(1)}_{1,1}&m^{(1)}_{1,2} \\ m^{(1)}_{2,1}&m^{(1)}_{2,2} \end{vmatrix},\quad G=\begin{vmatrix} m^{(0)}_{1,1}&m^{(0)}_{1,2} \\ m^{(0)}_{2,1}&m^{(0)}_{2,2} \end{vmatrix}, \end{aligned}$$

(42)

with matrix entries

$$\begin{aligned}&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\bigg [\Big (\xi _i'+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\times \Big (\eta _j'+b_{j,1}-\frac{q_{j}}{p_{i}+q_{j}}-n\Big ) \nonumber \\&+\frac{p_{i}q_{j}}{(p_{i}+q_{j})^2}\bigg ]\frac{1}{p_{i}+q_{j}},\quad i,j=1,2. \end{aligned}$$

(43)

Here $\xi '_i,\eta '_j$ are defined in (10)-(13), and $a_{i,1}, b_{j,1}, p_i, q_j$ are arbitrary complex numbers. Actually, when we take $q^*_1=p_1,q^*_2=p_2,p_2+q_2=-(p_1+q_1),a_{1,1}=a_{2,1}=b_{1,1}=b_{2,1}=0,y=0$, the regularity of $\frac{F}{G}$ can be verified by a similar process in [4].

By taking $p_1=q^*_1=\frac{7}{10}-\frac{7}{10}\textrm{i},p_2=q^*_2=-\frac{7}{10}+\frac{7}{10}\textrm{i},y=0$, we get

$$\begin{aligned} \frac{F}{G}=\frac{-390625t^4+(-3001250x^2+3062500\textrm{i})t^2+12005000xt-5764801x^4 -11764900\textrm{i}x^2+6002500}{390625t^4+3001250t^2x^2+5764801x^4+6002500}. \end{aligned}$$

(44)

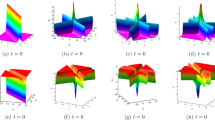
The positivity of the denominator ensures the regular property of the rational solution (44). Figure 9 displays lumps on the constant background. The figure depicts four peaks and four troughs. When $|p_1|=|p_2|$, the density plot Fig. 9f demonstrates that the center part is almost a circle. When $|p_1|\ne |p_2|$, the density plots Fig. 9d and e show that the center part is close to an ellipse.

Fig. 9

Rational solutions of F/G given by (42) and the corresponding density plots on the constant background with parameters $y=0,a_{1,1}=a_{2,1}=b_{1,1}=b_{2,1}=0,\xi _{i,0}=0,\eta _{j,0}=0$, a $p_{1}=q^*_{1}=1-\frac{\textrm{i}}{2},p_2=q^*_2=-1+\frac{\textrm{i}}{2}$; b $p_{1}=q^*_{1}=\frac{1}{2}+\textrm{i},p_2=q^*_2=-\frac{1}{2}-\textrm{i}$; c $p_{1}=q^*_{1}=\frac{7}{10}-\frac{7}{10}\textrm{i},p_2=q^*_2=-\frac{7}{10}+\frac{7}{10}\textrm{i}$; d, e and f are density plots corresponding to a–c respectively

5.2 Rational Solutions on the Periodic Background

In order to construct rational solutions to the sinh-Gordon equation (3) on the periodic background, we take $N=3$, $q_3=-p^*_3$ and $p_3,c_3$ to be purely imaginary in Theorem 1. Then the tau functions are expressed by

$$\begin{aligned} F=\begin{vmatrix} m^{(1)}_{1,1}&m^{(1)}_{1,2}&m^{(1)}_{1,3} \\ m^{(1)}_{2,1}&m^{(1)}_{2,2}&m^{(1)}_{2,3} \\ m^{(1)}_{3,1}&m^{(1)}_{3,2}&m^{(1)}_{3,3} \\ \end{vmatrix},\quad G=\begin{vmatrix} m^{(0)}_{1,1}&m^{(0)}_{1,2}&m^{(0)}_{1,3} \\ m^{(0)}_{2,1}&m^{(0)}_{2,2}&m^{(0)}_{2,3} \\ m^{(0)}_{3,1}&m^{(0)}_{3,2}&m^{(0)}_{3,3} \\ \end{vmatrix}, \end{aligned}$$

(45)

with matrix entries

$$\begin{aligned}&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\bigg [\Big (\xi '_i+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\Big (\eta '_j+b_{j,1}-\frac{q_{j}}{p_{i}+q_{j}}-n\Big )\nonumber \\&+\frac{p_{i}q_{j}}{(p_{i}+q_{j})^2}\bigg ]\frac{1}{p_{i}+q_{j}},\hspace{1em}i,j=1,2, \end{aligned}$$

(46)

and

$$\begin{aligned} \left\{ \begin{aligned}&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\Big (\xi '_i+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\frac{1}{p_{i}+q_{j}},\quad i=1,2;j=3,\\&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\Big (\eta '_j+b_{j,1} -\frac{q_{j}}{p_{i}+q_{j}}-n\Big )\frac{1}{p_{i}+q_{j}},\quad j=1,2;i=3,\\&m^{(n)}_{i,j}=c_{i}e^{-\xi _i-\eta _j}+\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\frac{1}{p_{i}+q_{j}},\quad i=j=3. \end{aligned} \right. \end{aligned}$$

(47)

Here $\xi _i,\eta _j,\xi '_i,\eta '_j$ are defined in (10)-(13), and $a_{i,1}, b_{j,1}, p_i, q_j$ are arbitrary complex numbers.

By taking the same parameter values of $p_i,q_i, \,i=1,2$ as those in Fig. 9 and $q_3=-p^*_3$, $p_3,c_3$ to be purely imaginary, we generate the rational solutions on the periodic background (see Fig. 10).

Fig. 10

Rational solutions F/G given by (45) and the corresponding density plots on the periodic background with parameters, a $p_{3}=-q^*_{3}=-3\textrm{i},c_3=5\textrm{i}$; b $p_{3}=-q^*_{3}=-3\textrm{i},c_3=5\textrm{i}$; c $p_{3}=-q^*_{3}=-\frac{3}{2}\textrm{i},c_3=5\textrm{i}$, and other parameter values are same as in Fig. 9. Besides, d–f are density plots corresponding to a–c respectively

6 Dynamics of the Semi-Rational Solutions

In this part, we study the dynamics of semi-rational solutions on the constant and periodic backgrounds to the sinh-Gordon equation. For this purpose, we set $c_i\ne 0,n_i=1,i=1,2...,$ in Theorem 1 and then the matrix entries $m^{(n)}_{i,j}$ are combinations of polynomials and exponential functions. In the following, we consider the potential $\frac{F}{G}$ and construct semi-rational solutions that consist of lumps and solitons.

6.1 Semi-Rational Solutions on the Constant Background

We take $N=2$ in Theorem 1 to construct semi-rational solutions of the sinh-Gordon equation (3) on the constant background. In this case, the tau functions F and G are determinants

$$\begin{aligned} F=\begin{vmatrix} m^{(1)}_{1,1}&m^{(1)}_{1,2} \\ m^{(1)}_{2,1}&m^{(1)}_{2,2} \end{vmatrix},\quad G=\begin{vmatrix} m^{(0)}_{1,1}&m^{(0)}_{1,2} \\ m^{(0)}_{2,1}&m^{(0)}_{2,2} \end{vmatrix}, \end{aligned}$$

(48)

with entries

$$\begin{aligned} m^{(n)}_{i,j}=&c_i\delta _{i,j}e^{-\xi _i-\eta _j}+\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\bigg [\Big (\xi _i'+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\nonumber \\&\times \Big (\eta _j'+b_{j,1}-\frac{q_{j}}{p_{i}+q_{j}}-n\Big ) +\frac{p_{i}q_{j}}{(p_{i}+q_{j})^2}\bigg ]\frac{1}{p_{i}+q_{j}},\quad i,j=1,2. \end{aligned}$$

(49)

and $a_{i,1}, b_{j,1}, p_i, q_j$ are arbitrary complex numbers. Similar as subsection 5.1, the potential F/G is regular when $q^*_1=p_1,q^*_2=p_2,(p_2+q_2)=-(p_1+q_1),a_{1,1}=a_{2,1}=b_{1,1}=b_{2,1}=0,c_2=-c^*_1$. By setting $p_{1}=q^*_{1}=\frac{7}{10}-\frac{7}{10}\textrm{i},p_2=q^*_2=-\frac{7}{10}+\frac{7}{10}\textrm{i}$ and $c_2=-c^*_1=2+2\textrm{i}$, the semi-rational solution F/G depicts the interaction between solitons and lumps. As shown in Fig. 11, one soliton stands under the horizon, while the other one locates above the horizon with its amplitude decreasing as $y\rightarrow 0$ and merges into the background around $y=0$. As $y>0$, the soliton travels below the horizon and its amplitude becomes larger.

Fig. 11

Semi-rational solutions F/G given by (48) and the corresponding density plots on the constant background with parameters $a_{1,1}=a_{2,1}=b_{1,1}=b_{2,1}=0,\xi _{i,0}=0,\eta _{j,0}=0,c_1=-c^*_2=2+2\textrm{i},p_{1}=q^*_{1}=\frac{7}{10}-\frac{7}{10}\textrm{i},p_2=q^*_2=-\frac{7}{10}+\frac{7}{10}\textrm{i}$

6.2 Semi-Rational Solutions on the Periodic Background

Semi-rational solutions of the sinh-Gordon equation (3) on the periodic background are derived by setting $N=3$, $q_3=-p^*_3$ and $p_3,c_3$ to be purely imaginary in Theorem 1. In this case, we have

$$\begin{aligned} F= \begin{vmatrix} m^{(1)}_{1,1}&m^{(1)}_{1,2}&m^{(1)}_{1,3} \\ m^{(1)}_{2,1}&m^{(1)}_{2,2}&m^{(1)}_{2,3} \\ m^{(1)}_{3,1}&m^{(1)}_{3,2}&m^{(1)}_{3,3} \\ \end{vmatrix},\quad G=\begin{vmatrix} m^{(0)}_{1,1}&m^{(0)}_{1,2}&m^{(0)}_{1,3} \\ m^{(0)}_{2,1}&m^{(0)}_{2,2}&m^{(0)}_{2,3} \\ m^{(0)}_{3,1}&m^{(0)}_{3,2}&m^{(0)}_{3,3} \\ \end{vmatrix}, \end{aligned}$$

(50)

with entries

$$\begin{aligned} m^{(n)}_{i,j}=&c_i\delta _{i,j}e^{-\xi _i-\eta _j}+\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\bigg [\Big (\xi _i'+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\nonumber \\&\times \Big (\eta _j'+b_{j,1}-\frac{q_{j}}{p_{i}+q_{j}}-n\Big )+\frac{p_{i}q_{j}}{(p_{i}+q_{j})^2}\bigg ] \frac{1}{p_{i}+q_{j}},\quad i,j=1,2, \end{aligned}$$

(51)

and

$$\begin{aligned} \left\{ \begin{aligned}&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\Big (\xi '_i+a_{i,1} -\frac{p_{i}}{p_{i}+q_{j}}+n\Big )\frac{1}{p_{i}+q_{j}},\quad i=1,2;j=3,\\&m^{(n)}_{i,j}=\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\Big (\eta '_j+b_{j,1} -\frac{q_{j}}{p_{i}+q_{j}}-n\Big )\frac{1}{p_{i}+q_{j}},\quad j=1,2;i=3,\\&m^{(n)}_{i,j}=c_{i}e^{-\xi _i-\eta _j}+\Big (-\frac{p_{i}}{q_{j}}\Big )^{n}\frac{1}{p_{i}+q_{j}},\quad i=j=3. \end{aligned} \right. \end{aligned}$$

(52)

Here $\xi _i,\eta _j,\xi '_i,\eta '_j$ are defined in (10)–(13), and $a_{i,1}, b_{j,1}, p_i, q_j$ are arbitrary complex numbers.

Setting $q_3=-p^*_3=-\textrm{i}, c_3=2\textrm{i}$ and $p_i, q_i, \,(i=1,2)$ the same values as those in Fig. 11, we derive semi-rational solutions consisting of solitons and lumps on the periodic background. The plots are shown in Fig. 12.

Fig. 12

Semi-rational solutions F/G given by (50) and the corresponding density plots on the periodic background with parameters $p_{3}=-q^*_{3}=-\textrm{i},c_3=-2\textrm{i}$, and other parameter values are same as those in Fig. 11

7 Conclusion

The KP hierarchy reduction method is a powerful method to investigate exact solutions of integrable equations and present Gram determinant structures of $N-$soliton solutions. Based on this approach, we give rational and semi-rational solutions in the $N\times N$ determinant form of the sinh-Gordon equation. Under different size of the determinant and parameters constraints, we obtain soliton solutions, line breathers, lump solutions and their interactions. For even N, we present local solutions on constant backgrounds. For odd N, we construct solutions on the periodic background. We study dynamic behaviors for solitons, line breathers, lumps and their interactions on both the constant and periodic backgrounds. Here the periodic backgrounds are caused by the trigonometric functions. Recently, solitons and rational solutions on elliptic functions attract much attention. How to construct solutions of the sinh-Gordon equation on those elliptic functions is left to be studied.