1 Introduction

Lorentzian geometry gets in contact with modern differential geometry and mathematical physics of general relativity by giving the invariants of Lorentzian geometry. Actually relativity theory is stated in terms of Lorentzian geometry and is really interesting subject for scientists interested in expanding universe and big bang etc. [1]. The theory of curves and surfaces is still the most important topic in differential geometry and has been investigated by many geometers until now. Furthermore, it is possible to find different applications of curves in almost every science field. Helix is the one of the well known curves in the literature which has very remarkable and different applications. For example, explanation of DNA, carbon nano-tube, nano-springs.

Investigation the differential geometric properties of a given curve, we generally use Serret Frenet frame fields of the curve. Actually, Serret Frenet formulas help us understand the kinematic properties of a particle moving along a continuous, differentiable curve in Euclidean space. Especially, the formulas describe the derivatives of the tangent, normal and binormal unit vectors in terms of each other. Curvature and torsion are functions defined along curve and are the coefficients of well-known Serret Frenet formulas. Meanly, the curvature function \(\kappa\) and torsion function \(\tau\) are used to describe the behavior of the curve. Physically, we can think of a space curve as being obtained from a straight line by bending (curvature) and twisting (torsion) [2].

Dynamics is a science that studies body motion. Kinematics, as a sub branch of dynamics, deals with the geometry and time dependent aspects of motion without considering the forces causing the motion. Among the most important terms whose mathematical and geometric applications are examined in these areas are force, moment or torque, velocity, acceleration and momentum. These terms can be defined in different ways. Force can basically be defined as the effect of one object on another. It is the force applied to an object that causes the object to move or deform. Moment or torque is expressed as a measure of the rotational, bending, or torsional motion of a force applied to an object. Velocity is defined as the time rate of change of position. The time rate of increase of velocity is termed acceleration. The net force is obtained by the combined effect of all the forces acting on an object. The fact that the net force acting on an object is zero does not mean that there are no forces acting on the object. An object is said to be in equilibrium if it is either at rest or is moving in a straight line with a constant speed. Therefore, the first law states that if the net force acting on a body is zero, the body is in equilibrium [3].

Position vector field is used in physics, kinematics, geometry, dynamics. In geometry, a position vector, also known as location vector. One of the most important subjects of differential geometry is to determine the position vector of a moving point. This is important for the point of view, because the trajectory of that point is a curve or a surface. There are many studies on the characterization of curves using the curvature and torsion functions in different spaces. In the studies of [4, 5], constant ratio curves in Euclidean spaces and some of their characterizations are expressed. Furthermore, the definition of constant ratio curve is given in the lower manifolds of Euclidean space in [6] and the Riemannian surfaces are discussed in [7]. In addition, [8] studied the relationship between rectifying curves and twisted curves in Euclidean space. As a continuation of this work, some geometrical properties of rectifying curves are given [9]. In addition [10], rectifying, normal and oscillatory curves are studied in three-dimensional compact Lie groups.

Among the current studies, the most striking ones are the studies on the characterization of the twisted curves. If the curvature and torsion functions of the curve \(\wp\)are different from zero, the curve \(\wp\) is called a twisted curve. In the study [6], it is stated that each twisted curve can be given in the following form

$$\begin{aligned} \wp \left( s\right) =r_{0}\left( s\right) t\left( s\right) +r_{1}\left( s\right) n\left( s\right) +r_{2}\left( s\right) b\left( s\right) \end{aligned}$$

where \(r_{0},r_{1},r_{2}:I\rightarrow {\mathbb {R}}\) are differentiable functions. Using the above representation of the twisted curves, the characterizations of curves with constant curvature functions are investigated in [11]. The planes spanned by vector fields \(\{t,n\},\) \(\{t,b\}\) and \(\{n,b\}\) are known as osculating, rectifying and normal plane of the curve, respectively. The position vector of the curve \(\wp\) which lies its rectifying, osculating and normal plane is called rectifying, osculatory and normal curve, respectively [8].

The curve \(\wp\) is called a W curve, if its curvature and torsion functions are constant. The simplest examples of curves with constant curvature functions are circles, hyperbolas as planar curves with constant curvature functions and helices as non-planar curves with constant curvature functions. Curves with constant curvature functions in the Minkowski 3-space are classified by Walrave in [12]. Moreover, curves with constant curvature functions in the Minkowski 3-space are investigated in [13,14,15,16].

Firstly, characterization of W curves in Euclidean space is examined in [17, 18]. The position vector of given W curve is obtained as follows

$$\begin{aligned} \wp (s)=\frac{1}{{\kappa }^{2}+{\tau }^{2}}({\tau }^{2}st(s)-\kappa n(s)+\kappa \tau sb(s)) \end{aligned}$$

with differentiable functions \(r_{0}\left( s\right) ,r_{1}\left( s\right) ,r_{2}\left( s\right)\). These differentiable functions are given by

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\tau -c_{1}\kappa \mathrm {\cos }{\left( as\right) \ }+c_{2}\kappa \mathrm {\sin }{\left( as\right) \ }+{{\frac{{\tau }^{2}}{a^{2}}}}s,\\ r_{1}\left( s\right)&=c_{1}a\sin {\left( as\right) \ }+c_{2} a\mathrm {\cos }{\left( as\right) \ }-\frac{\kappa }{a^{2}},\\ r_{2}\left( s\right)&=c_{0}\kappa +c_{1}\tau \mathrm {\cos }{\left( as\right) \ }-c_{2}\tau \sin {\left( as\right) \ }+{{\frac{\kappa \tau }{a^{2} }}}s \end{aligned}$$

where \(a=\sqrt{{\kappa }^{2}+{\tau }^{2}}\) and \(c_{i}\) are real constants for \(0\le i\le 2\). Then, the characterization of spacelike W curves was discussed in [13]. In study [19], position vector of spacelike curve is obtained as linear combinations of their Serret Frenet vectors with differentiable functions depending on values of curvature and torsion. Moreover, Erdogdu and Yavuz examined null Cartan W curves and then the position vector of a null Cartan curve stated by a linear combination of its pseudo orthogonal frame with differentiable functions in [20]. The position vector of W curve mates are stated by a linear combination of its Frenet frame with differentiable functions are investigated in the studies [19, 21].

The position vector extends from the origin to the particle, while the velocity vector indicates the direction of motion of the particle. Other variables suitable for describing a moving particle can be stated by means of these fundamental variables. The motion of a particle moving about a center of force can be given by the angular momentum, which is defined to be the vector product of the position and momentum vectors [22]. Vectorial momentums of any space curve as t-dual, n-dual and b-dual curves are defined as follows

$$\begin{aligned} {\tilde{\wp }}_{w}(s)=\wp \left( s\right) \times w\left( s\right) \end{aligned}$$

in [23]. Let a force F act on a single particle at a point P whose position vector with respect to the origin O is given by r. Then, the moment of the force acting on the particle with respect to the origin O is defined as the vector product

$$\begin{aligned} \Upsilon =r \times F. \end{aligned}$$

This vector quantity is called the moment of force (or torque). The angular momentum L of the particle with respect to the origin O is defined by

$$\begin{aligned} L=r\times p \end{aligned}$$

such that a particle of mass m and linear momentum p at a position r relative to the origin O. The magnitude of the angular momentum vector is

$$\begin{aligned} l=\left\| r\right\| \left\| p\right\| \sin \theta \end{aligned}$$

where \(\theta\) is the angle between linear momentum p and position vector r. The torque vector is stated as the variation of the angular moment of the object with respect to time during the motion of the object. The rate of change of the angular momentum vector can be obtained by the sum of the torques of all the forces acting on all the particles. The position vector of the particle on which the force acts must be used for each torque. The torque of a force around a point is basically a measure of how effective the force would be at causing a rotation around that point, because of above equation depends on the magnitude of the force, the distance from the center of rotation to the point where the force is applied, and the angle [3]. By the definition of vector product, the torque is perpendicular to the plane formed by the position vector and force. Therefore, the position vector and torque are closely related. In addition, torque helps us dynamically to define the properties of vector. There are studies in many fields related to position vector and torque vector. Tunçer defined the X-torque curves, X-equilibrium curves, X-moment curves, X-gyroscopic curves as new curves derived from a regular space curve by using the Frenet vectors of a space curve and its position vector [24]. Moreover, Tunçer introduced the vectorial moments as w-dual curve in the study [23]. In addition to all these studies, the position vector field also has important applications in dynamics and mechanics [25].

Since kinematics deals with geometry and time-dependent aspects of motion without considering the forces that cause motion, the aim of this study is to geometrically consider the basic concepts of kinematics, force, torque, equilibrium, moment. For this purpose, the findings and results obtained in the study are stated as below.

In this paper, after giving the necessary informations to understand timelike curves in Minkowski space, the position vector of a timelike curve \(\wp\) is stated by a linear combination of its Serret Frenet frame with differentiable functions. Then, the vectorial momentum of timelike curve \(\wp\) is investigated by force with tangential direction. Also, the definition of tangential dual curve of the curve \(\wp\) is stated by using these differentiable functions. Moreover, the relation between Serret Frenet frame, curvature and torsion of tangential dual curve \({\tilde{\wp }}_{t}\) and the timelike curve \(\wp\) are stated, respectively. Thus, tangential torque curve of timelike curve \(\wp\) is defined and examined. New dynamically and physical results are introduced depending on the torque of the timelike curve \(\wp\) and the direction of tangent vector component of curve. Since W curves are the most general of planar and non-planar constant curvature timelike curves, they are specifically included in this study. Then, the position vector of a timelike W curve is again stated by a linear combination of its Serret Frenet frame with differentiable functions. Therefore, solution of differential equation of the position vector of the timelike W curve with two different case: \(\kappa ^{2}-\tau ^{2}=0\) and \(\kappa ^{2}-\tau ^{2}\ne 0\). A brief summary of the consequences is given and the necessary and sufficient conditions of a timelike W curve to be a rectifying, osculatory and normal curve are stated, respectively. By using the differentiable functions obtained as a result of these solutions, tangential dual and torque curve of the timelike W curve are obtained. Based on this, depending on the tangential dual and torque curve of the timelike W curve, results are given for two different cases separately. Afterwards, an example is given to explain the results.

2 Basic of Timelike Curves in Minkowski

In this section, some informations which are necessary to understand the overall study are stated.

Minkowski 3-space is the real space with Lorentzian product

$$\begin{aligned} \left\langle \overrightarrow{u},\overrightarrow{v}\right\rangle _{L} =-u_{1}v_{1}+u_{2}v_{2}+u_{3}v_{3} \end{aligned}$$

where \(\overrightarrow{u}=\left( u_{1},u_{2},u_{3}\right)\), \(\overrightarrow{v}=\left( v_{1},v_{2},v_{3}\right) \in {\mathbb {R}} ^{3}\). Since Lorentzian product is not positively defined, we may classify the vectors in \({\mathbb {E}}_{1}^{3}\) as follows:

If \({\left\langle \overrightarrow{u},\overrightarrow{u}\right\rangle }_{L}>0\), \({\left\langle \overrightarrow{u},\overrightarrow{u}\right\rangle }_{L}<0\) or \({\left\langle \overrightarrow{u},\overrightarrow{u}\right\rangle }_{L}=0,\) then \(\overrightarrow{u}\) is called a spacelike, timelike or null vector, respectively. For each \(\overrightarrow{u}\in {\mathbb {E}}_{1}^{3}\), the norm of \(\overrightarrow{u}\) vector is defined

$$\begin{aligned} \left\| \overrightarrow{u}\right\| \varvec{=}\sqrt{\left| {\left\langle \overrightarrow{u},\overrightarrow{u}\right\rangle } _{L}\right| }. \end{aligned}$$

If \({\left\langle \overrightarrow{u},\overrightarrow{v}\right\rangle }_{L}=0\) then \(\overrightarrow{u}\) and \(\overrightarrow{v}\) vectors are said to be orthogonal.

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a regular curve. If the vector \(\wp ^{\prime }\left( s\right)\) is a timelike vector for \(\forall s\in I\), then \(\wp\) is called timelike curve. And if \(\left\langle \wp ^{\varvec{^{\prime }}}\left( s\right) ,\wp ^{\varvec{^{\prime }} }\left( s\right) \right\rangle _{L}=-1\), then \(\wp\) is called unit speed timelike curve. If \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) is a unit speed timelike curve, then

$$\begin{aligned} t\left( s\right) =\wp ^{\prime }\left( s\right) \end{aligned}$$

vector is the unit tangent vector of \(\wp\). So that

$$\begin{aligned} n\left( s\right) =\frac{\wp ^{\prime \prime }\left( s\right) }{\left\| \wp ^{\prime \prime }\left( s\right) \right\| } \end{aligned}$$

is the principal normal vector of \(\wp\). Finally,

$$\begin{aligned} b\left( s\right) =t\left( s\right) \times _{L}n\left( s\right) \end{aligned}$$

is the binormal vector of \(\wp\). The curvature and torsion functions of \(\wp\) are defined as

$$\begin{aligned} \kappa \left( s\right) =\sqrt{{\left\langle \wp ^{\prime \prime }\left( s\right) ,\wp ^{\prime \prime }\left( s\right) \right\rangle }_{L}}, \\ \tau \left( s\right) ={\left\langle n^{\prime }\left( s\right) ,b\left( s\right) \right\rangle }_{L}, \end{aligned}$$

respectively. The Serret Frenet formulas for the unit speed timelike curve \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) are as follows:

$$\begin{aligned} \left[ \begin{array}{c} t^{^{\prime }}\left( s\right) \\ n^{^{\prime }}\left( s\right) \\ b^{^{\prime }}\left( s\right) \end{array} \right] =\left[ \begin{array}{ccc} 0 &{} \kappa \left( s\right) &{} 0\\ \kappa \left( s\right) &{} 0 &{} \tau \left( s\right) \\ 0 &{} -\tau \left( s\right) &{} 0 \end{array} \right] \ \left[ \begin{array}{c} t\left( s\right) \\ n\left( s\right) \\ b\left( s\right) \end{array} \right] \end{aligned}$$

where t, n, b are Serret Frenet vector fields of \(\wp\) [2].

3 Vectorial Moments of Timelike Curves with Tangential Direction

In this section, the circular or hyperbolic angle between linear momentum p and position vector R which changes depending on casual character of these vectors are defined. Moreover tangential dual curve of the unit speed timelike curve is defined. The relation between Serret Frenet frame, curvature and torsion of tangential dual curve \({\tilde{\wp }}_{t}\) and the timelike curve \(\wp\) are obtained. Then, tangential torque curve of timelike curve \(\wp\) is defined and investigated. Finally, dynamically and physical results are introduced depending on the torque of timelike curve \(\wp\) and the direction of tangent vector component of curve.

Definition 1

Let a force F act on a single particle in Minkowski space at a point P whose position vector with respect to the origin O is given by R. Then, the moment of the force acting on the particle with respect to the origin O is defined as the vector product

$$\begin{aligned} \Upsilon =R {\times }_{L}F. \end{aligned}$$

This vector quantity is called the moment of force (or torque).

Definition 2

Let a particle of mass m and linear momentum p at a position R relative to the origin O be given in Minkowski space. The angular momentum L of the particle with respect to the origin O is defined by

$$\begin{aligned} L=R\times _{L}p. \end{aligned}$$

The magnitude of the angular momentum vector is

$$\begin{aligned} l=\left\| r\right\| \left\| p\right\| \sin \theta \end{aligned}$$

or

$$\begin{aligned} l=\left\| r\right\| \left\| p\right\| \sinh \theta \end{aligned}$$

where \(\theta\) is circular or hyperbolic angle between linear momentum p and position vector R which changes depending on casual character of these vectors.

The physical quantities, moment of a force and angular momentum, have an important relation between them. It is the rotational analogue of the relation between force and linear momentum. For deriving the relation in the context of a single particle, we differentiate

$$\begin{aligned} L=R\times _{L}p \end{aligned}$$

with respect to time,

$$\begin{aligned} \frac{dL}{dt}=\frac{dR}{dt}\times _{L}p+R\times _{L}\frac{d}{dt}p. \end{aligned}$$

Now, the velocity of the particle is

$$\begin{aligned} v=\frac{dR}{dt} \end{aligned}$$

and

$$\begin{aligned} p=mv. \end{aligned}$$

This implies that

$$\begin{aligned} \frac{dR}{dt}\times _{L}p=v {\times }_{L}mv=0. \end{aligned}$$

Then, we see

$$\begin{aligned} R\times _{L}\frac{dp}{dt}=R\times _{L}F=\Upsilon \end{aligned}$$

since \(\frac{dp}{dt}=F.\) Therefore, we obtain

$$\begin{aligned} \frac{dL}{dt}=\Upsilon \end{aligned}$$

which means that the moment of force is the rate of change of angular momentum.

Definition 3

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike curve with nonzero curvature functions \(\kappa\), \(\tau\) and Serret Frenet frame field \(\{t,n,b\}.\) The curve

$$\begin{aligned} {\tilde{\wp }}_{t}({\tilde{s}})=\wp (s) {\times }_{L}t(s) \end{aligned}$$

is called tangential dual curve of the curve \(\wp .\) \({\tilde{s}}\) is the arclength parameter of tangential dual curve. By using the position vector representation of the curve \(\wp\), we may write

$$\begin{aligned} {\tilde{\wp }}_{t}({\tilde{s}})=-r_{2}(s)n(s)+r_{1}(s)b(s). \end{aligned}$$

The following theorem gives the relations between Serret Frenet frame fields of \(\wp\) and \({\tilde{\wp }}_{t}.\)

Theorem 4

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a given unit speed timelike curve with position vector

$$\begin{aligned} \wp \left( s\right) =r_{0}\left( s\right) t\left( s\right) +r_{1}\left( s\right) n\left( s\right) +r_{2}\left( s\right) b\left( s\right) \end{aligned}$$

Serret Frenet frame, curvature and torsion of tangential dual curve \({\tilde{\wp }}_{t}:I\rightarrow {\mathbb {E}}_{1}^{3}\) are expressed as follows:

$$\begin{aligned} {\widetilde{t}}&=-\frac{(r_{2}t+r_{0}b)}{\sqrt{\left| r_{0}{}^{2} -r_{2}{}^{2}\right| }},\\ {\widetilde{n}}&=\pm \frac{r_{0}(r_{2}-\tau r_{0}r_{1}-\kappa r_{1} r_{2})t-(r_{0}{}^{2}-r_{2}{}^{2})(\tau r_{0}+\kappa r_{2})n+r_{2}(r_{2}-\tau r_{0}r_{1}-\kappa r_{1}r_{2})b}{\sqrt{\left| r_{0}{}^{2}-r_{2}{} ^{2}\right| }\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2} )^{2}+(r_{1}r_{2}\kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2})^{2}\right| }},\\ {\widetilde{b}}&=\frac{(\kappa r_{0}r_{2}+\tau r_{0}^{2})t+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})n+(\tau r_{0}r_{2}+\kappa r_{2}^{2})b}{\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2} )^{2}\right| }} \end{aligned}$$

and

$$\begin{aligned} {\widetilde{\kappa }}=\frac{\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0} ^{2})^{2}+(r_{1}r_{2}\kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2})^{2}\right| }}{\kappa \left| r_{0}{}^{2}-r_{2}{} ^{2}\right| ^{\frac{3}{2}}}, \\ {\widetilde{\tau }}=\frac{r_{2}(\kappa ^{\prime }r_{2}-\tau ^{\prime }r_{0} )-2\tau \left( -r_{2}+\kappa ^{2}r_{2}^{3}+\tau ^{2}r_{0}^{2}r_{2}+\tau r_{0}r_{1}+\kappa r_{1}r_{2}+2\kappa \tau r_{0}r_{2}^{2}\right) }{\kappa \left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2} )^{2}\right| }. \end{aligned}$$

Here \(\kappa\) and \(\tau\) are nonzero curvature functions and \(\{t,n,b\}\) is Serret Frenet frame of the curve \(\wp .\)

Proof

Assume that \({\tilde{\wp }}_{t}:I\rightarrow {\mathbb {E}}_{1}^{3}\) is tangential dual curve of \(\wp ,\) so we can define \({\tilde{\wp }}_{t}\) as follows

$$\begin{aligned} {\tilde{\wp }}_{t}(s)=-r_{2}(s)n(s)+r_{1}(s)b(s). \end{aligned}$$

Taking derivative of the above equation according to s, we find

$$\begin{aligned} {\tilde{\wp }}_{t}^{\prime }=-r_{2}^{\prime }n-r_{2}(\kappa t-\tau b)+r_{1} ^{\prime }b+r_{1}(\tau n). \end{aligned}$$

Then we obtain

$$\begin{aligned} {\tilde{\wp }}_{t}^{\prime }=-\kappa (r_{2}t-r_{0}b). \end{aligned}$$

The norm of the above equation is given by

$$\begin{aligned} \left\| {\tilde{\wp }}_{t}^{\prime }\right\| =\kappa \sqrt{\left| r_{0}^{2}-r_{2}^{2}\right| }. \end{aligned}$$

Therefore, we obtain the tangent vector field of tangential dual curve as follows:

$$\begin{aligned} {\widetilde{t}}=-\frac{(r_{2}t+r_{0}b)}{\sqrt{\left| r_{0}{}^{2}-r_{2}{} ^{2}\right| }}. \end{aligned}$$

Then we also find

$$\begin{aligned} {\tilde{\wp }}_{t}^{\prime \prime }=(-\kappa ^{\prime }r_{2}-\kappa \tau r_{1})t+(-\kappa ^{2}r_{2}-\kappa \tau r_{0})n+(-\kappa ^{\prime }r_{0} -\kappa +\kappa ^{2}r_{1})b \end{aligned}$$

and

$$\begin{aligned} {\tilde{\wp }}_{t}^{\prime } {\times }_{L}{\tilde{\wp }}_{t}^{\prime \prime }=\kappa ^{2}((\kappa r_{0}r_{2}+\tau r_{0}^{2})t+(r_{1}r_{2}\kappa +r_{0} r_{1}\tau -r_{2})n+(\tau r_{0}r_{2}+\kappa r_{2}^{2})b). \end{aligned}$$

Again, the norm of the above equation is given by

$$\begin{aligned} \left\| {\tilde{\wp }}_{t}^{\prime } {\times }_{L}{\tilde{\wp }}_{t} ^{\prime \prime }\right\| =\kappa ^{2}\sqrt{\left| -(\kappa r_{0} r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2}\kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2})^{2}\right| }. \end{aligned}$$

Then we obtain binormal vector field of tangential dual curve as follows:

$$\begin{aligned} {\widetilde{b}}=\frac{(\kappa r_{0}r_{2}+\tau r_{0}^{2})t+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})n+(\tau r_{0}r_{2}+\kappa r_{2}^{2})b}{\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2} )^{2}\right| }}. \end{aligned}$$

We know that

$$\begin{aligned} {\widetilde{t}}{\times }_{L}{\widetilde{b}}=\mp {\tilde{n}}. \end{aligned}$$

Thus, we find

$$\begin{aligned} {\tilde{n}}=\pm \frac{r_{0}(r_{2}-\tau r_{0}r_{1}-\kappa r_{1}r_{2})t-(r_{0} {}^{2}-r_{2}{}^{2})(\tau r_{0}+\kappa r_{2})n+r_{2}(r_{2}-\tau r_{0} r_{1}-\kappa r_{1}r_{2})b}{\sqrt{\left| r_{0}{}^{2}-r_{2}{}^{2}\right| }\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2} \kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2} )^{2}\right| }}. \end{aligned}$$

By some calculations, we obtain the curvature as follows

$$\begin{aligned} {\widetilde{\kappa }}&=\frac{\left\| {\tilde{\wp }}_{t}^{\prime } {\times }_{L}{\tilde{\wp }}_{t}^{\prime \prime }\right\| }{\left\| {\tilde{\wp }}_{t}^{\prime }\right\| ^{3}}\\&=\frac{\kappa ^{2}\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2} )^{2}+(r_{1}r_{2}\kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2})^{2}\right| }}{(\kappa \sqrt{\left| r_{0}{}^{2}-r_{2}{} ^{2}\right| })^{3/2}}\\&=\frac{\sqrt{\left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1} r_{2}\kappa +r_{0}r_{1}\tau -r_{2})^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2} )^{2}\right| }}{\kappa \left| r_{0}{}^{2}-r_{2}{}^{2}\right| ^{\frac{3}{2}}}. \end{aligned}$$

Finally, the torsion function of the tangential dual curve is given by

$$\begin{aligned} {\widetilde{\tau }}&=\frac{\left\langle {\tilde{\wp }}_{t}^{\prime } {\times }_{L}{\tilde{\wp }}_{t}^{\prime \prime },{\tilde{\wp }}_{t} ^{\prime \prime \prime }\right\rangle _{L}}{\left\| {\tilde{\wp }}_{t}^{\prime } {\times }_{L}{\tilde{\wp }}_{t}^{\prime \prime }\right\| ^{2}}\\&=\frac{r_{2}(\kappa ^{\prime }r_{2}-\tau ^{\prime }r_{0})-2\tau \left( -r_{2}+\kappa ^{2}r_{2}^{3}+\tau ^{2}r_{0}^{2}r_{2}+\tau r_{0}r_{1}+\kappa r_{1}r_{2}+2\kappa \tau r_{0}r_{2}^{2}\right) }{\kappa \left| -(\kappa r_{0}r_{2}+\tau r_{0}^{2})^{2}+(r_{1}r_{2}\kappa +r_{0}r_{1}\tau -r_{2} )^{2}+(\tau r_{0}r_{2}+\kappa r_{2}^{2})^{2}\right| }. \end{aligned}$$

\(\square\)

Definition 5

Let \({\tilde{\wp }}_{t}:I\rightarrow {\mathbb {E}}_{1}^{3}\) be the tangential dual curve of timelike curve \(\wp\). The curve \(\Gamma _{t}\left( {\tilde{s}}\right) =\frac{d{\tilde{\wp }}_{t}\left( s\right) }{ds}\) is defined as tangential torque curve of \(\wp\) where \({\tilde{s}}\) is the arclength parameter. The tangential torque curve \(\Gamma _{t}\) is obtained as follows

$$\begin{aligned} \frac{d{\tilde{\wp }}_{t}\left( s\right) }{ds}=-\kappa (s)\left( r_{2} (s)t(s)+r_{0}(s)b(s)\right) . \end{aligned}$$

Corollary 6

If the following equality is satisfied

$$\begin{aligned} \frac{d{\tilde{\wp }}_{t}\left( s\right) }{ds}=0, \end{aligned}$$

then timelike curve of \(\wp\) is a tangential moment conservative curve.

Corollary 7

The vector \(\Gamma _{t}\) always lies in rectifying plane of the timelike curve \(\wp .\) Moreover, tangential torque curve is perpendicular to the principal normal vector of the timelike curve \(\wp .\)

Remark 8

Let the parameter \({\tilde{s}}\) be the arclength parameter of tangential torque curve \(\Gamma _{t}.\) Then there is a relation between the arclength parameters of both the tangential torque curve \(\Gamma _{t}\) and timelike curve of \(\wp\) which is given as follows

$$\begin{aligned} \frac{ds}{d{\tilde{s}}}=\mp \frac{1}{\sqrt{-\left( -\kappa ^{\prime }r_{2} +\kappa \tau r_{1}\right) ^{2}+\left( -\kappa ^{2}r_{2}+\kappa \tau r_{0}\right) ^{2}+\left( -\kappa ^{\prime }r_{0}-\kappa +\kappa ^{2} r_{1}\right) ^{2}}}. \end{aligned}$$

Definition 9

If the tangential torque curve \(\Gamma _{t}\) and t are of the same direction at each points of the curve \(\wp ,\) then the curve is defined as an unstable tangential equilibrium curve. At the same time, if the tangential torque curve \(\Gamma _{t}\) and t are of the opposite direction at each points of the curve \(\wp ,\) then the curve defined as a stable tangential equilibrium curve.

Definition 10

If the tangential torque curve \(\Gamma _{t}\) doesn’t have any component on t(s), then the curve is defined as a neutral tangential equilibrium curve.

Definition 11

If the tangential torque curve \(\Gamma _{t}\) and t are perpendicular at each points of the curve \(\wp ,\) then the curve is defined as a tangential gyroscopic curve.

Corollary 12

When the position vector of the timelike curve \(\wp\) is the osculatory curve, it is also the tangential gyroscopic curve.

4 Differential Equations and It’s Solutions of the Position Vector of the Timelike W Curve

In this section, the characterization of a timelike curve \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) given by arc length parameter is investigated in terms of its curvature and torsion functions. Suppose that the position vector of the curve \(\wp\) is stated as follows:

$$\begin{aligned} \wp \left( s\right) =r_{0}\left( s\right) t\left( s\right) +r_{1}\left( s\right) n\left( s\right) +r_{2}\left( s\right) b\left( s\right) . \end{aligned}$$
(1)

If we take the derivative of both sides of Eq. (1) with respect to the arc length parameter with the use of Serret Frenet formulas stated in Sect. 2, then we obtain

$$\begin{aligned} \wp ^{\prime }\left( s\right)&=\left( r_{0}^{\prime }\left( s\right) +\kappa (s)r_{1}\left( s\right) \right) t\left( s\right) \\&\quad +\left( \kappa (s)r_{0}\left( s\right) +r_{1}^{\prime }\left( s\right) -\kappa (s)r_{2}\left( s\right) \right) n\left( s\right) \\&\quad +\left( \tau (s)r_{1}\left( s\right) +r_{2}^{\prime }\left( s\right) \right) b\left( s\right) . \end{aligned}$$

Since \(\wp ^{\prime }(s)=t(s),\) then we obtain the following nonhomogeneous linear differential system of equations:

$$\begin{aligned} r_{0}^{\prime }\left( s\right) +\kappa (s)r_{1}\left( s\right) =1, \end{aligned}$$
$$\begin{aligned} r_{1}^{\prime }\left( s\right) +\kappa (s)r_{0}\left( s\right) -\kappa (s)r_{2}\left( s\right) =0, \end{aligned}$$
(2)
$$\begin{aligned} r_{2}^{\prime }\left( s\right) +\tau (s)r_{1}\left( s\right) =0. \end{aligned}$$

Characterization of a given unit speed timelike W curve differ according to the values of curvature and torsion. These different situations are discussed separately in following theorems. Readers are encouraged to refer to [26] for details of methods for solving systems of first order nonhomogeneous linear differential systems of equations.

Theorem 13

Assume that \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) is a given unit speed timelike twisted curve. If \(\wp\) is a W curve with \(\kappa ^{2}-\tau ^{2}>0\), then the position vector \(\wp \left( s\right)\) is stated with the following differentiable functions:

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\tau +c_{1}\kappa \cosh (\beta s)+c_{2} \kappa \sinh (\beta s)-\frac{\tau ^{2}}{\beta ^{2}}s,\\ r_{1}\left( s\right)&=-c_{2}\beta \cosh (\beta s)-c_{1}\beta \sinh (\beta s)+\frac{\kappa }{\beta ^{2}},\\ r_{2}\left( s\right)&=c_{0}\kappa +c_{1}\tau \cosh (\beta s)+c_{2}\tau \sinh (\beta s)-\frac{\kappa \tau }{\beta ^{2}}s, \end{aligned}$$

where \(\beta ^{2}=\kappa ^{2}-\tau ^{2},\) \(\beta \in {\mathbb {R}} ^{+}\) and \(c_{i}\) are arbitrary constants for \(0\le i\le 2\).

Proof

Suppose that \(\wp\) is a W timelike curve with \(\kappa ^{2}-\tau ^{2}>0\). This means that the coefficients of differential equations given in Eq. (2) are also constants. Thus,

$$\begin{aligned} \left[ \begin{array}{c} r_{0}^{\prime }\left( s\right) \\ r_{1}^{\prime }\left( s\right) \\ r_{2}^{\prime }\left( s\right) \end{array} \right] =\left[ \left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} \tau \\ 0 &{} -\tau &{} 0 \end{array} \right] \right] \left[ \begin{array}{c} r_{0}\left( s\right) \\ r_{1}\left( s\right) \\ r_{2}\left( s\right) \end{array} \right] +\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

The eigenvalues and eigenvectors of the matrix of nonhomogeneous linear system of the above equation are found as follows:

$$\begin{aligned} {\lambda }_{1}=0\Rightarrow V_{1}=\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] , \\ {\lambda }_{2}=\beta \Rightarrow V_{2}=\left[ \begin{array}{c} \kappa \\ -\beta \\ \tau \end{array} \right] , \\ {\lambda }_{3}=-\beta \Rightarrow V_{3}=\left[ \begin{array}{c} \kappa \\ \beta \\ \tau \end{array} \right] \end{aligned}$$

where \(\kappa ^{2}-\tau ^{2}=\beta ^{2}.\) Then we find the homogeneous solution of the system as follows:

$$\begin{aligned} X_{h}\left( s\right)&=c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +d_{1}e^{\beta s}\left[ \begin{array}{c} \kappa \\ -\beta \\ \tau \end{array} \right] +d_{2}e^{-\beta s}\left[ \begin{array}{c} \kappa \\ \beta \\ \tau \end{array} \right] \\&=c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +d_{1}(\cosh (\beta s)+\sinh (\beta s))\left[ \begin{array}{c} \kappa \\ -\beta \\ \tau \end{array} \right] \\&\quad +d_{2}(\cosh (\beta s)-\sinh (\beta s)\left[ \begin{array}{c} \kappa \\ \beta \\ \tau \end{array} \right] \end{aligned}$$

where \(c_{0}\), \(d_{1}\), \(d_{2}\) are arbitrary constants. Rewriting the constants as follows

$$\begin{aligned} d_{1}+d_{2}=c_{1}, \\ d_{1}-d_{2}=c_{2}, \end{aligned}$$

we obtain

$$\begin{aligned} X_{h}\left( s\right) =c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +c_{1}\left[ \begin{array}{c} \kappa \cosh (\beta s)\\ -\beta \sinh (\beta s)\\ \tau \cosh (\beta s) \end{array} \right] +c_{2}\left[ \begin{array}{c} \kappa \sinh (\beta s)\\ -\beta \cosh (\beta s)\\ \tau \sinh (\beta s) \end{array} \right] . \end{aligned}$$

The fundamental matrix of the nonhomogeneous linear differential system of the equation is obtained as

$$\begin{aligned} \varphi \left( s\right) =\left[ \begin{array}{ccc} \tau &{} \kappa \cosh (\beta s) &{} \kappa \sinh (\beta s)\\ 0 &{} -\beta \sinh (\beta s) &{} -\beta \cosh (\beta s)\\ \kappa &{} \tau \cosh (\beta s) &{} \tau \sinh (\beta s) \end{array} \right] . \end{aligned}$$

By the equality \(X_{p}\left( s\right) =\varphi \left( s\right) u\left( s\right) ,\) we may find the vector valued function \(u\left( s\right)\) by following equation

$$\begin{aligned} \varphi \left( s\right) u^{\prime }\left( s\right) =\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

Actually, solving \(3\times 3\) linear equation by Crammer’s method, we find the particular solution of Eq. (2) as follows:

$$\begin{aligned} X_{p}\left( s\right) =\left[ \begin{array}{c} -\frac{\tau ^{2}}{\beta ^{2}}s\\ \frac{\kappa }{\beta ^{2}}\\ -\frac{\kappa \tau }{\beta ^{2}}s \end{array} \right] . \end{aligned}$$

Since \(X_{g}(s)=X_{h}(s)+X_{p}(s),\) then it is seen that

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\tau +c_{1}\kappa \cosh (\beta s)+c_{2} \kappa \sinh (\beta s)-\frac{\tau ^{2}}{\beta ^{2}}s,\\ r_{1}\left( s\right)&=-c_{2}\beta \cosh (\beta s)-c_{1}\beta \sinh (\beta s)+\frac{\kappa }{\beta ^{2}},\\ r_{2}\left( s\right)&=c_{0}\kappa +c_{1}\tau \cosh (\beta s)+c_{2}\tau \sinh (\beta s)-\frac{\kappa \tau }{\beta ^{2}}s. \end{aligned}$$

So, we get the proof. \(\square\)

Theorem 14

Suppose that \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) is a given unit speed timelike twisted curve. If \(\wp\) is a W curve with \(\kappa ^{2}-\tau ^{2}<0\), then the position vector \(\wp \left( s\right)\) is stated with the following differentiable functions:

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\tau +\kappa c_{1}\cos (\alpha s)+\kappa c_{2}\sin (\alpha s)+\frac{\tau ^{2}}{\alpha ^{2}}s,\\ r_{1}\left( s\right)&=c_{1}\alpha \sin (\alpha s)-c_{2}\alpha \cos (\alpha s)-\frac{\kappa }{\alpha ^{2}},\\ r_{2}\left( s\right)&=c_{0}\kappa +c_{1}\tau \cos (\alpha s)+c_{2}\tau \sin (\alpha s)+\frac{\kappa \tau }{\alpha ^{2}}s \end{aligned}$$

where \(-\alpha ^{2}=\kappa ^{2}-\tau ^{2},\) \(\alpha \in {\mathbb {R}} ^{+}\) and \(c_{i}\) are arbitrary constants for \(0\le i\le 2\).

Proof

Suppose that \(\wp\) is a W timelike curve with \(\kappa ^{2}-\tau ^{2}>0\). This means that the coefficients of differential equations given in Eq. (2) are also constant. We may write as follows:

$$\begin{aligned} \left[ \begin{array}{c} r_{0}^{\prime }\left( s\right) \\ r_{1}^{\prime }\left( s\right) \\ r_{2}^{\prime }\left( s\right) \end{array} \right] =\left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} \tau \\ 0 &{} -\tau &{} 0 \end{array} \right] \left[ \begin{array}{c} r_{0}\left( s\right) \\ r_{1}\left( s\right) \\ r_{2}\left( s\right) \end{array} \right] +\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

The eigenvalues and eigenvectors of the matrix of nonhomogeneous linear system of the above equation are found as follows:

$$\begin{aligned} {\lambda }_{1}=0\Rightarrow V_{1}=\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] , \end{aligned}$$
$$\begin{aligned} {\lambda }_{2}=\alpha i\Rightarrow V_{2}=\left[ \begin{array}{c} \kappa \\ -\alpha i\\ \tau \end{array} \right] , \end{aligned}$$
(3)
$$\begin{aligned} {\lambda }_{3}=-\alpha i\Rightarrow V_{3}=\left[ \begin{array}{c} \kappa \\ \alpha i\\ \tau \end{array} \right] \end{aligned}$$

where \(-\alpha ^{2}=\kappa ^{2}-\tau ^{2}.\) Thus, we have found the homogeneous solution as follows

$$\begin{aligned} X_{h}\left( s\right)&=c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +d_{1}e^{\alpha si}\left[ \begin{array}{c} \kappa \\ -\alpha i\\ \tau \end{array} \right] +d_{2}e^{-\alpha si}\left[ \begin{array}{c} \kappa \\ \alpha i\\ \tau \end{array} \right] \\&=c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +d_{1}(\cos (\alpha s)+i\sin (\alpha s))\left[ \begin{array}{c} \kappa \\ -\alpha i\\ \tau \end{array} \right] +d_{2}(\cos (\alpha s)\\&\quad -i\sin (\alpha s))\left[ \begin{array}{c} \kappa \\ \alpha i\\ \tau \end{array} \right] \end{aligned}$$

where \(c_{0}\), \(d_{1}\), \(d_{2}\) are arbitrary constants. By assuming the followings

$$\begin{aligned} d_{1}+d_{2}=c_{1}, \\ i(d_{1}-d_{2})=c_{2}, \end{aligned}$$

we obtain the homogeneous solution as

$$\begin{aligned} X_{h}\left( s\right) =c_{0}\left[ \begin{array}{c} \tau \\ 0\\ \kappa \end{array} \right] +c_{1}\left[ \begin{array}{c} \kappa \cos \left( \alpha s\right) \\ \alpha \sin \left( \alpha s\right) \\ \tau \cos \left( \alpha s\right) \end{array} \right] +c_{2}\left[ \begin{array}{c} \kappa \sin \left( \alpha s\right) \\ -\alpha \cos \left( \alpha s\right) \\ \tau \sin \left( \alpha s\right) \end{array} \right] . \end{aligned}$$

The fundamental matrix of the nonhomogeneous linear differential system of the equation can be written as

$$\begin{aligned} \varphi \left( s\right) =\left[ \begin{array}{ccc} \tau &{} \kappa \cos \left( \alpha s\right) &{} \kappa \sin \left( \alpha s\right) \\ 0 &{} \alpha \sin \left( \alpha s\right) &{} -a\cos \left( \alpha s\right) \\ \kappa &{} \tau \cos \left( \alpha s\right) &{} \tau \sin \left( \alpha s\right) \end{array} \right] . \end{aligned}$$

By the use of the equality \(X_{p}\left( s\right) =\varphi \left( s\right) u\left( s\right) ,\) we find the vector values function \(u\left( s\right)\) by following equation

$$\begin{aligned} \varphi \left( s\right) u^{\prime }\left( s\right) =\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

We find the particular solution of Eq. (2) as follows:

$$\begin{aligned} X_{p}\left( s\right) =\left[ \begin{array}{c} \frac{\tau ^{2}}{\alpha ^{2}}s\\ -\frac{\kappa }{\alpha ^{2}}\\ \frac{\kappa \tau }{\alpha ^{2}}s \end{array} \right] . \end{aligned}$$

Since \(X_{g}(s)=X_{h}(s)+X_{p}(s),\) then it is seen that

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\tau +\kappa c_{1}\cos (\alpha s)+\kappa c_{2}\sin (\alpha s)+\frac{\tau ^{2}}{\alpha ^{2}}s,\\ r_{1}\left( s\right)&=c_{1}\alpha \sin (\alpha s)-c_{2}\alpha \cos (\alpha s)-\frac{\kappa }{\alpha ^{2}},\\ r_{2}\left( s\right)&=c_{0}\kappa +c_{1}\tau \cos (\alpha s)+c_{2}\tau \sin (\alpha s)+\frac{\kappa \tau }{\alpha ^{2}}s. \end{aligned}$$

\(\square\)

Corollary 15

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a given unit speed timelike W curve with \(\tau ^{2}-\kappa ^{2}\ne 0.\) The followings are obtained:

  1. (i)

    \(\wp\) is a rectifying curve if and only if \(\kappa =0,\)

  2. (ii)

    \(\wp\) is a osculatory curve if and only if \(\kappa \tau =0,\)

  3. (iii)

    \(\wp\) is a normal curve if and only if \(\tau =0,\) where \(\kappa\) is the curvature and \(\tau\) is the torsion of the curve \(\wp .\)

Theorem 16

Let \(\wp :I \rightarrow \mathbb{E}_{1}^{3}\) be a unit speed timelike twisted curve. If \(\wp\) is a W curve with \(\tau =\kappa\), then the position vector \(\wp (s)\) is stated with the following differentiable functions:

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\left( \frac{\kappa ^{2}}{2}s^{2}+1\right) -c_{1}s\kappa -c_{2}\frac{\kappa ^{2}}{2}s^{2}+s+\frac{\kappa ^{2}}{6} s^{3},\\ r_{1}\left( s\right)&=-c_{0}\kappa s+c_{1}+c_{2}\kappa s-\frac{\kappa }{2}s^{2},\\ r_{2}\left( s\right)&=c_{0}\frac{\kappa ^{2}}{2}s^{2}-c_{1}\kappa s-c_{2}\left( \frac{\kappa ^{2}}{2}s^{2}-1\right) +\frac{\kappa ^{2}}{6}s^{3} \end{aligned}$$

where \(c_{i}\) are arbitrary constants for \(0\le i\le 2\).

Proof

Suppose that \(\wp\) is a W timelike curve with \(\kappa =\tau\). This means that the coefficients of differential equations given are also constant. We may write the equations as follows:

$$\begin{aligned} \left[ \begin{array}{c} r_{0}^{\prime }\left( s\right) \\ r_{1}^{\prime }\left( s\right) \\ r_{2}^{\prime }\left( s\right) \end{array} \right] =\left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} \kappa \\ 0 &{} -\kappa &{} 0 \end{array} \right] \left[ \begin{array}{c} r_{0}\left( s\right) \\ r_{1}\left( s\right) \\ r_{2}\left( s\right) \end{array} \right] +\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

Considering the coefficient matrix

$$\begin{aligned} A=\left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} \kappa \\ 0 &{} -\kappa &{} 0 \end{array} \right] , \end{aligned}$$

we can find

$$\begin{aligned} \varphi (s)=e^{As}=\left[ \begin{array}{ccc} \frac{1}{2}s^{2}\kappa ^{2}+1 &{} -s\kappa &{} -\frac{1}{2}s^{2}\kappa ^{2}\\ -s\kappa &{} 1 &{} s\kappa \\ \frac{1}{2}s^{2}\kappa ^{2} &{} -s\kappa &{} 1-\frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] . \end{aligned}$$

Therefore, the homogeneous solution of the system has been found as follows:

$$\begin{aligned} X_{h}\left( s\right) =c_{0}\left[ \begin{array}{c} \frac{1}{2}s^{2}\kappa ^{2}+1\\ -s\kappa \\ \frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] +c_{1}\left[ \begin{array}{c} -s\kappa \\ 1\\ -s\kappa \end{array} \right] +c_{2}\left[ \begin{array}{c} -\frac{1}{2}s^{2}\kappa ^{2}\\ s\kappa \\ 1-\frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] \end{aligned}$$

where \(c_{0}\), \(c_{1}\), \(c_{2}\) are arbitrary constants. With the use of the equality \(X_{p}\left( s\right) =\varphi \left( s\right) u\left( s\right) ,\) we may find the vector values function \(u\left( s\right)\) by following equation

$$\begin{aligned} \varphi \left( s\right) u^{\prime }\left( s\right) =\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

We find the particular solution of Eq. (2) as follows:

$$\begin{aligned} X_{p}\left( s\right) =\left[ \begin{array}{c} \frac{1}{6}s^{3}\kappa ^{2}+s\\ -\frac{1}{2}s^{2}\kappa \\ \frac{1}{6}s^{3}\kappa ^{2} \end{array} \right] . \end{aligned}$$

Since \(X_{g}(s)=X_{h}(s)+X_{p}(s),\) then it is seen that

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\left( \frac{\kappa ^{2}}{2}s^{2}+1\right) -c_{1}s\kappa -c_{2}\frac{\kappa ^{2}}{2}s^{2}+s+\frac{\kappa ^{2}}{6}s^{3},\\ r_{1}\left( s\right)&=-c_{0}\kappa s+c_{1}+c_{2}\kappa s-\frac{\kappa }{2}s^{2},\\ r_{2}\left( s\right)&=c_{0}\frac{\kappa ^{2}}{2}s^{2}-c_{1}\kappa s-c_{2}\left( \frac{\kappa ^{2}}{2}s^{2}-1\right) +\frac{\kappa ^{2}}{6}s^{3}. \end{aligned}$$

So, we get the proof. \(\square\)

Theorem 17

Let \(\wp :I \subset \mathbb {R} \rightarrow \mathbb{E}_{1}^{3}\) be a unit speed timelike twisted curve. If \(\wp\) is a W curve with \(\tau =-\kappa\), then the position vector \(\wp (s)\) is stated with the following differentiable functions:

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\left( \frac{\kappa ^{2}}{2}s^{2}+1\right) -c_{1}\kappa s+c_{2}\frac{\kappa ^{2}}{2}s^{2}+s+\frac{\kappa ^{2}}{6} s^{3}\\ r_{1}\left( s\right)&=-c_{0}\kappa s+c_{1}-c_{2}\kappa s-\frac{\kappa }{2}s^{2},\\ r_{2}\left( s\right)&=-c_{0}\frac{\kappa ^{2}}{2}s^{2}+c_{1}\kappa s-c_{2}\left( \frac{\kappa ^{2}}{2}s^{2}-1\right) -\frac{\kappa ^{2}}{6}s^{3} \end{aligned}$$

where \(c_{i}\) are arbitrary constants for \(0\le i\le 2\).

Proof

Suppose that \(\wp\) is a W timelike curve with \(\kappa =\tau\). Then,

$$\begin{aligned} \left[ \begin{array}{c} r_{0}^{\prime }\left( s\right) \\ r_{1}^{\prime }\left( s\right) \\ r_{2}^{\prime }\left( s\right) \end{array} \right] =\left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} -\kappa \\ 0 &{} \kappa &{} 0 \end{array} \right] \left[ \begin{array}{c} r_{0}\left( s\right) \\ r_{1}\left( s\right) \\ r_{2}\left( s\right) \end{array} \right] +\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

Considering the coefficient matrix

$$\begin{aligned} A=\left[ \begin{array}{ccc} 0 &{} -\kappa &{} 0\\ -\kappa &{} 0 &{} -\kappa \\ 0 &{} \kappa &{} 0 \end{array} \right] , \end{aligned}$$

we can find

$$\begin{aligned} \varphi (s)=e^{As}=\left[ \begin{array}{ccc} \frac{1}{2}s^{2}\kappa ^{2}+1 &{} -s\kappa &{} \frac{1}{2}s^{2}\kappa ^{2}\\ -s\kappa &{} 1 &{} -s\kappa \\ -\frac{1}{2}s^{2}\kappa ^{2} &{} s\kappa &{} 1-\frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] . \end{aligned}$$

Therefore, the homogeneous solution of the system has been found as follows:

$$\begin{aligned} X_{h}\left( s\right) =c_{0}\left[ \begin{array}{c} \frac{1}{2}s^{2}\kappa ^{2}+1\\ -s\kappa \\ -\frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] +c_{1}\left[ \begin{array}{c} -s\kappa \\ 1\\ s\kappa \end{array} \right] +c_{2}\left[ \begin{array}{c} \frac{1}{2}s^{2}\kappa ^{2}\\ -s\kappa \\ 1-\frac{1}{2}s^{2}\kappa ^{2} \end{array} \right] \end{aligned}$$

where \(c_{0}\), \(c_{1}\), \(c_{2}\) are arbitrary constants. With the use of the equality \(X_{p}\left( s\right) =\varphi \left( s\right) u\left( s\right) ,\) we may find the vector values function \(u\left( s\right)\) by following equation

$$\begin{aligned} \varphi \left( s\right) u^{\prime }\left( s\right) =\left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

We find the particular solution of Eq. (2) as

$$\begin{aligned} X_{p}\left( s\right) =\left[ \begin{array}{c} \frac{\kappa ^{2}}{6}s^{3}+s\\ -\frac{\kappa }{2}s^{2}\\ -\frac{\kappa ^{2}}{6}s^{3} \end{array} \right] . \end{aligned}$$

Since \(X_{g}(s)=X_{h}(s)+X_{p}(s),\) then it is seen that

$$\begin{aligned} r_{0}\left( s\right)&=c_{0}\left( \frac{\kappa ^{2}}{2}s^{2}+1\right) -c_{1}\kappa s+c_{2}\frac{\kappa ^{2}}{2}s^{2}+s+\frac{\kappa ^{2}}{6} s^{3},\\ r_{1}\left( s\right)&=-c_{0}\kappa s+c_{1}-c_{2}\kappa s-\frac{\kappa }{2}s^{2},\\ r_{2}\left( s\right)&=-c_{0}\frac{\kappa ^{2}}{2}s^{2}+c_{1}\kappa s-c_{2}\left( \frac{\kappa ^{2}}{2}s^{2}-1\right) -\frac{\kappa ^{2}}{6}s^{3}. \end{aligned}$$

So, we get the proof. \(\square\)

Corollary 18

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve with \(\tau ^{2}-\kappa ^{2}=0.\) The followings are obtained:

  1. (i)

    \(\wp\) is a rectifying curve if and only if \(\kappa =0,\)

  2. (ii)

    \(\wp\) is an osculatory curve if and only if \(\kappa =0,\)

  3. (iii)

    \(\wp\) can not be a normal curve, where \(\kappa\) is the curvature and \(\tau\) is the torsion of the curve \(\wp .\)

5 Differential Equation Solution of the Position Vector of the Vectorial Moments of Tangential Timelike W Curves

In this section, we investigate tangential direction curve of timelike W curves in two different case. In first case, we consider that \(\tau ^{2}-\kappa ^{2}\ne 0\) (or \(\frac{\tau }{\kappa }\ne \pm 1).\) As second case, we consider the \(\tau ^{2}-\kappa ^{2}=0\) (or \(\frac{\tau }{\kappa }=\pm 1)\) which corresponds to \(\tau =\varepsilon \kappa\) where \(\varepsilon =\pm 1.\)

5.1 Case 1

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau ^{2}-\kappa ^{2}\ne 0\). By solution of system of differential equation, we obtain

$$\begin{aligned} r_{0}(s)&=\frac{\tau ^{2}s}{\tau ^{2}-\kappa ^{2}},\nonumber \\ r_{1}(s)&=-\frac{\kappa }{\tau ^{2}-\kappa ^{2}}, \nonumber \\ r_{2}(s)&=\frac{\kappa \tau s}{\tau ^{2}-\kappa ^{2}}. \end{aligned}$$
(4)

Therefore, we may write

$$\begin{aligned} \wp (s)=\left( \frac{\tau ^{2}s}{\tau ^{2}-\kappa ^{2}}\right) t(s)+\left( -\frac{\kappa }{\tau ^{2}-\kappa ^{2}}\right) n(s)+\left( \frac{\kappa \tau s}{\tau ^{2}-\kappa ^{2}}\right) b(s). \end{aligned}$$

On the other hand, we obtain tangential direction dual curve of \(\wp\) as follows:

$$\begin{aligned} {\tilde{\wp }}_{t}(s)=-\left( \frac{\kappa \tau s}{\tau ^{2}-\kappa ^{2}}\right) n(s)+\left( -\frac{\kappa }{\tau ^{2}-\kappa ^{2}}\right) b(s). \end{aligned}$$

Theorem 19

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau ^{2}-\kappa ^{2}\ne 0\). Serret Frenet frame and curvature, torsion of tangential dual curve \({\tilde{\wp }}_{t}:I\rightarrow {\mathbb {E}}_{1}^{3}\) are given as follows:

$$\begin{aligned} {\widetilde{t}}(s)&=-\frac{(\kappa t(s)+\tau b(s))}{\sqrt{\left| \kappa ^{2}-\tau ^{2}\right| }},\\ {\widetilde{n}}(s)&=\pm \frac{-2\kappa \tau ^{2}t(s)-s(\kappa ^{4}-\tau ^{4})n(s)-2\kappa \tau ^{2}b(s)}{(\kappa ^{2}-\tau ^{2})\sqrt{\left| s^{2}(\kappa ^{4}-\tau ^{4})(\kappa ^{2}+\tau ^{2})+4\kappa ^{2}\tau ^{2}\right| }},\\ {\widetilde{b}}(s)&=\frac{s\tau (\kappa ^{2}+\tau ^{2})t(s)+2\kappa \tau n(s)+s\kappa (\kappa ^{2}+\tau ^{2})b(s)}{\sqrt{\left| s^{2}(\kappa ^{4} -\tau ^{4})(\kappa ^{2}+\tau ^{2})+4\kappa ^{2}\tau ^{2}\right| }} \end{aligned}$$

and

$$\begin{aligned} {\widetilde{\kappa }}=\frac{\sqrt{\left| s^{2}(\kappa ^{4}-\tau ^{4} )(\kappa ^{2}+\tau ^{2})+4\kappa ^{2}\tau ^{2}\right| }}{\sqrt{\left| \kappa ^{2}-\tau ^{2}\right| }\kappa \tau s^{2}}, \\ {\widetilde{\tau }}=2\left( \frac{1}{s}+\frac{-4\kappa ^{2}\tau ^{2}+2(\kappa ^{2} -\tau ^{2})^{2}}{s(s^{2}(\kappa ^{4}-\tau ^{4})(\kappa ^{2}+\tau ^{2})+4\kappa ^{2}\tau ^{2})}\right) . \end{aligned}$$

Proof

The proof can be done by using Eq. (4) and Theorem 13. \(\square\)

Remark 20

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau ^{2}-\kappa ^{2}\ne 0\). The tangential torque curve \(\Gamma _{t}\) is obtained as follows

$$\begin{aligned} \Gamma _{t}\left( {\tilde{s}}\right) =\frac{-\kappa ^{2}\tau s}{\tau ^{2} -\kappa ^{2}}t(s)+\frac{-\kappa \tau ^{2}s}{\tau ^{2}-\kappa ^{2}}b(s). \end{aligned}$$

Corollary 21

Since tangential torque curve is always a rectifying curve, there can never be a stable tangential equilibrium curve, unstable tangential equilibrium curve, neutral tangential equilibrium curve and tangential gyroscopic curves.

5.2 Case 2

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau =\varepsilon \kappa\) and \(\varepsilon =\pm 1\). By solution of system of Eq. (3), we obtain

$$\begin{aligned} r_{0}(s)&=\frac{\kappa ^{2}}{6}s^{3}+s,\nonumber \\ r_{1}(s)&=-\frac{\kappa }{2}s^{2}, \nonumber \\ r_{2}(s)&=\varepsilon \frac{\kappa ^{2}}{6}s. \end{aligned}$$
(5)

Therefore, we may write position vector as follows:

$$\begin{aligned} \wp (s)=\left( \frac{\kappa ^{2}}{6}s^{3}+s\right) t(s)+\left( -\frac{\kappa }{2}s^{2} \right) n(s)+\left( \varepsilon \frac{\kappa ^{2}}{6}s\right) b(s). \end{aligned}$$

On the other hand we obtain tangential direction curve of \(\wp\) as follows:

$$\begin{aligned} {\tilde{\wp }}_{t}(s)=-\left( \varepsilon \frac{\kappa ^{2}}{6}s\right) n(s)+\left( -\frac{\kappa }{2}s^{2}\right) b(s). \end{aligned}$$

Theorem 22

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau =\varepsilon \kappa\) and \(\varepsilon =\pm 1\). Serret Frenet frame and curvature, torsion of tangential dual curve \({\tilde{\wp }}_{t}:I\rightarrow {\mathbb {E}}_{1}^{3}\) are given as follows:

$$\begin{aligned} {\widetilde{t}}(s)&=-\frac{\kappa \sqrt{3}}{6}\frac{(\varepsilon \kappa ^{2}s^{2}t(s)+(\kappa ^{2}s^{2}+6)b(s))}{\sqrt{\kappa ^{2}s^{2}+3}},\\ {\widetilde{n}}(s)&=\pm \frac{2\varepsilon \kappa s(s^{2}\kappa ^{2} +6)(s^{2}\kappa ^{2}+3)t(s)-4\varepsilon (s^{2}\kappa ^{2}+3)^{2}n(s)+s^{3} \kappa ^{3}(s^{2}\kappa ^{2}+4)b(s)}{2(s^{2}\kappa ^{2}+3)\sqrt{s^{2}\kappa ^{2}(s^{4}\kappa ^{4}+60)+12(s^{4}\kappa ^{4}+9)}},\\ {\widetilde{b}}(s)&=\frac{\varepsilon (s^{2}\kappa ^{2}+6)(s^{2}\kappa ^{2}+3)t(s)-3\varepsilon s^{3}\kappa ^{3}(s^{2}\kappa ^{2}+4)n(s)+s^{2} \kappa ^{2}(s^{2}\kappa ^{2}+3)b(s)}{\sqrt{3}\sqrt{s^{2}\kappa ^{2}(s^{4} \kappa ^{4}+60)+12(s^{4}\kappa ^{4}+9)}} \end{aligned}$$

and

$$\begin{aligned} {\widetilde{\kappa }}(s)=\frac{\sqrt{s^{2}\kappa ^{2}(s^{4}\kappa ^{4} +60)+12(s^{4}\kappa ^{4}+9)}}{2s\kappa (s^{2}\kappa ^{2}+3)^{3/2}}, \\ {\widetilde{\tau }}(s)=\frac{12(12s^{4}\kappa ^{4}+2s^{6}\kappa ^{6}-63)}{s^{3}(s^{2}\kappa ^{2}+3)(s^{2}\kappa ^{2}(s^{4}\kappa ^{4}+60)+12(s^{4} \kappa ^{4}+9))}. \end{aligned}$$

Proof

The proof can be done by using Equation 5 and Theorem 16 and Theorem 17. \(\square\)

Remark 23

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve where \(\tau =\varepsilon \kappa\) and \(\varepsilon =\pm 1\). The tangential torque curve \(\Gamma _{t}\left( {\tilde{s}}\right)\) is obtained as follows

$$\begin{aligned} \Gamma _{t}\left( {\tilde{s}}\right) =\frac{-\varepsilon \kappa ^{3}s^{3}}{6}t(s)-\frac{\kappa ^{3}s^{3}+6\kappa s}{6}b(s). \end{aligned}$$

Corollary 24

Similar to Case 1, since tangential torque curve is always a rectifying curve, there can never be a stable tangential equilibrium curve, unstable tangential equilibrium curve, neutral tangential equilibrium curve and tangential gyroscopic curves.

6 Example

Let \(\wp :I\rightarrow {\mathbb {E}}_{1}^{3}\) be a unit speed timelike W curve with following parametric expression

$$\begin{aligned} \wp (s)=(\sqrt{2}\sinh s,\sqrt{2}\cosh s,s). \end{aligned}$$

Then the Frenet frame is obtained

$$\begin{aligned} t(s)&=(\sqrt{2}\cosh s,\sqrt{2}\sinh s,1),\\ n(s)&=(\sinh s,\cosh s,0),\\ b(s)&=(\cosh s,\sinh s,\sqrt{2}) \end{aligned}$$

where the curvature and torsion of the curve are

$$\begin{aligned} \kappa (s)=\sqrt{2}\,\text { and }\,\tau (s)=-1, \end{aligned}$$

respectively. Thus we get

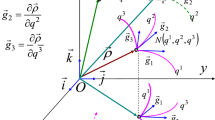
$$\begin{aligned} r_{0}\left( s\right) =-{s,}\text { }r_{1}\left( s\right) =\sqrt{2},\text { }r_{2}\left( s\right) =\sqrt{2}s \end{aligned}$$

with the use of Theorem 13 where \(c_{0}=c_{1}=c_{2}=0\). An illustration of the position vector of timelike W curve is given in  Fig. 1.

Fig. 1
figure 1

Position vector of timelike W curve

Full size image

Tangential dual curve of \(\wp\) obtained as follows:

$$\begin{aligned} {\tilde{\wp }}_{t}(s)&=-(\sqrt{2}s)(\sinh s,\cosh s,0)+(\sqrt{2})(\cosh s,\sinh s,\sqrt{2}),\\&=\left( \sqrt{2}\cosh s-\sqrt{2}s\sinh s,\sqrt{2}\sinh s-\sqrt{2}s\cosh s,2\right) . \end{aligned}$$

Moreover, tangential dual curve of \(\wp\) is illustrated in  Fig. 2. 

Fig. 2
figure 2

Tangential dual curve

Full size image

Then, tangential direction torque timelike W curve \(\Gamma _{t}\left( {\tilde{s}}\right)\) is obtained as follows

$$\begin{aligned} \Gamma _{t}\left( {\tilde{s}}\right)&=-2s(\sqrt{2}\cosh s,\sqrt{2}\sinh s,1)+\sqrt{2}s(\cosh s,\sinh s,\sqrt{2}),\\&=\left( -\sqrt{2}s\cosh s,-\sqrt{2}s\sinh s,0\right) . \end{aligned}$$

7 Conclusions

According to all findings of this paper, we can summarize the following results.

In this paper, we focus on investigating the position vector of a timelike curve \(\wp\) by a linear combination of its Serret Frenet frame with differentiable functions. As a different perspective, we investigated the contribution of the position vector in the dynamically in Minkowski space. With this point of view, we first investigated the vectorial momentum of timelike curve \(\wp\) by force with tangential direction. Also, the definition of tangential dual curve of the curve \(\wp\) is stated by using these differentiable functions. Thus, tangential torque curve of timelike curve \(\wp\) is defined and examined. Some results are stated depending on the torque of the timelike curve \(\wp\) and the direction of the tangent vector component of the curve. Therefore, the position vector of a timelike W curve \(\wp (s)\) can be stated as follows:

$$\begin{aligned} \wp \left( s\right) =\frac{\tau ^{2}}{\tau ^{2}-\kappa ^{2}}st\left( s\right) -\frac{\kappa }{\tau ^{2}-\kappa ^{2}}n\left( s\right) +\frac{\kappa \tau }{\tau ^{2}-\kappa ^{2}}b\left( s\right) \end{aligned}$$

where \(\tau ^{2}-\kappa ^{2}\ne 0.\) Moreover, \(\wp\) is a rectifying curve if and only if \(\wp\) is a straight line. Then, \(\wp\) is a osculatory curve if and only if \(\wp\) is a straight line or a part of circle. The necessary and sufficient condition of \(\wp\) to be a normal curve is being a part of circle. On the other hand, the position vector \(\wp (s)\) can be stated as follows:

$$\begin{aligned} \wp \left( s\right) =\left( s+\frac{\kappa ^{2}}{6}s^{3}\right) t\left( s\right) -\frac{\kappa }{2}s^{2}n\left( s\right) +\frac{\kappa ^{2}}{6}sb\left( s\right) \end{aligned}$$

where \(\tau =\kappa .\) Furthermore, if \(\wp\) is a W curve with \(\tau =-\kappa\), then the position vector \(\wp (s)\) can be stated as follows:

$$\begin{aligned} \wp \left( s\right) =\left( s+\frac{\kappa ^{2}}{6}s^{3}\right) t\left( s\right) -\frac{\kappa }{2}s^{2}n\left( s\right) -\frac{\kappa ^{2}}{6}sb\left( s\right) . \end{aligned}$$

Combining above two cases, if \(\tau ^{2}-\kappa ^{2}=0,\) then we have also obtained the following states. \(\wp\) is a rectifying or osculatory curve if and only if \(\wp\) is a straight line. Finally, it is not possible of \(\wp\) to be a normal curve. By using the differentiable functions obtained as a result of these solutions, tangential dual and torque curve of the timelike W curve is obtained. Based on this, depending on the tangential dual and torque curve of the timelike W curve, results are given for two different cases separately. Afterwards, an example to explain the results is given.

The difference of this study from others is that new dynamically and physical results are stated depending on the torque of the timelike curve \(\wp\) and the direction of the tangent vector component of the curve. Thus, this study will accompany the scientists who will conduct new studies on similar subjects as a important resource since it is one of the first studies on this subject. In this context, the present paper gives an extraordinary view of the timelike curve. The results obtained in this study can also be examined for different frames and spaces. Similarities and differences can be interpreted by comparing them. In addition, new results can be generated by changing the character of the curve. All these are open problems for future studies.