1 Introduction

In this section, we will discussed some basics of the topic.

1.1 Medical Diagnosis and Fundamental Theories

Medical diagnosis is a difficult procedure that entails figuring out what is causing a patient's symptoms in the first place and selecting the best course of action. Even while improvements in medical research have greatly increased the accuracy of diagnoses, there are still a number of difficulties and possible issues that might occur. Key concerns in medical diagnosis include the following:

Diagnostic interpretation of symptoms, physical findings, and test results is frequently subjective and varies amongst medical specialists. Based on their expertise and experience, various physicians may come to different judgments. Limited information: patients occasionally may not offer a full or accurate medical history, which might make a diagnosis more difficult. In addition, access to patient data may be restricted for healthcare professionals, especially if the patient has seen a number of healthcare professionals or if access to medical records is difficult. Uncommon illnesses: it can be challenging to diagnose uncommon diseases since many of their symptoms are similar to those of more widespread ailments. These illnesses may not be regularly seen by doctors, which might cause delayed or missing diagnosis. Diagnostic mistakes: diagnostic mistakes can happen for a number of reasons, such as insufficient or inaccurate interpretation of test data, poor communication between healthcare professionals, cognitive biases, or a lack of experience with unusual illness presentations. Time restrictions: in some medical settings, doctors only have a limited amount of time to spend with each patient, which may compromise the accuracy of the diagnostic procedure. Due to time constraints, people may take short cuts or rely too much on heuristics, which might lead to delayed or incorrect diagnoses. Diagnostic test accessibility and dependability: depending on the healthcare institution and geographic region, diagnostic test accessibility and dependability might change. False-positive or false-negative findings can happen, which might result in inaccurate diagnosis or pointless additional research. Complex cases: some medical illnesses have difficult-to-diagnose symptoms or involve numerous organ systems. In certain situations, a multidisciplinary approach and cooperation amongst several professionals may be necessary [1].

It is necessary to make ongoing improvements in medical education, expand patient access to comprehensive information, implement quality assurance measures, encourage interdisciplinary collaboration, and take advantage of technological advancements like artificial intelligence to support precise and prompt diagnosis to address these issues [2].

A mathematical approach called fuzzy set theory addresses ambiguity and imprecision in decision-making. Fuzzy set theory can assist in addressing some of the difficulties and complications associated with medical diagnosis. Here are some ways that fuzzy set theory might simplify medical diagnosis: handling uncertainty: the representation and manipulation of ambiguity and uncertainty in data and information are both possible using fuzzy set theory. It can be challenging to label symptoms or test findings as positive or negative for a particular ailment when they fall into a grey area during a medical diagnosis. Fuzzy set theory offers a method for quantifying and thinking through this ambiguity, enabling more adaptable and subtle diagnosis. Granularity and partial membership: the fuzzy set theory supports the idea of partial membership, which denotes that an element may partially belong to a set. This can be helpful in making a diagnosis in medicine when symptoms or test findings do not cleanly fall into a certain category. Gradations of membership may be represented using fuzzy sets, making the diagnostic procedure appear more realistic. Expert information may be included into the diagnosis process using fuzzy set theory, together with linguistic factors. Subjective evaluations and professional judgement are frequently used in medical diagnosis. Fuzzy sets offer a structure for encoding and integrating this knowledge, facilitating more precise and comprehensible diagnostic judgements. Fuzzy set theory is capable of handling partial or erroneous data. Patient data may be incomplete or test findings may be ambiguous or imprecise while making a medical diagnosis. When accurate or complete information is not available, the diagnostic process can still proceed because of fuzzy sets' ability to represent and manipulate imperfect data. Systems for making decisions: the development of decision support systems for making medical diagnoses can use fuzzy set theory. These systems may evaluate patient data, symptoms, and test results using fuzzy logic and fuzzy inference techniques, giving physicians insightful analysis and suggestions. These systems can aid in helping to make more precise and trustworthy diagnostic judgements by combining uncertainty and expert knowledge. The application of fuzzy set theory in medical diagnostics has advantages, but it must be carefully considered and validated. To create and evaluate efficient diagnostic models and algorithms, collaboration between specialists in fuzzy set theory and medical domain expertise is essential. Pattern recognitions applications regarding fuzzy set theory are discussed in [3]. For other decision making, applications of fuzzy set theory in different applied sciences, one can see [4,5,6,7,8].

1.2 Description of Problem

Healthcare workers frequently meet a number of prevalent diseases and health disorders in Saudi Arabia, as they do in every other nation. Following are a few of the prevalent diseases in Saudi Arabia, such as diabetes, cardiovascular diseases: heart disease, respiratory diseases, obesity, gastrointestinal disorders and the most important different types of cancers. Among all the cancers, ovarian cancer is one of the most critical and dangerous cancer. The female reproductive organs known as the ovaries, which also produce the hormones oestrogen and progesterone, are the site of ovarian cancer. The stages of ovarian cancer show how far the disease has gone from the ovaries to other bodily organs. The FIGO (International Federation of Gynaecology and Obstetrics) staging system is the one that is most frequently used to describe ovarian cancer. It divides ovarian cancer into the I, II, III, and IV stages [9,10,11,12,13,14]. Here is an overview of the different stages of ovarian cancer:


Stage I: Only the ovaries are affected by the malignancy in stage I. Stage IB denotes the presence of cancer in both ovaries, whereas stage IA denotes the disease is restricted to one ovary. The lymph nodes or other surrounding organs have not been infected by the cancer cells.


Stage II: The cancer in stage II has progressed past the ovaries but is still located inside the pelvic area. Stage IIB denotes that the disease has progressed to other pelvic tissues, whereas stage IIA denotes involvement of the uterus or fallopian tubes.


Stage III: In stage III, the disease has progressed past the pelvis and may now also affect the abdominal lining or lymph nodes. Stage IIIA denotes the involvement of the lymph nodes located beneath the peritoneum or the dissemination to the small pelvis. The spread to the peritoneum (the lining of the abdomen) outside of the little pelvis is referred to as stage IIIB. In stage IIIC, cancer cells are seen in the lymph nodes in the abdomen or close to the aorta.


Stage IV: Stage IV refers to the progression of cancer to distant organs outside of the abdomen, such as the liver, lungs, or other organs. Stage IVA shows the presence of cancer cells in the fluid around the lungs, and stage IVB indicates the spread to other distant organs.

Subcategories may exist within each stage to offer further information about the severity of the malignancy. These subgroups may take into account elements including tumor size, organ involvement nearby, and the quantity of malignant lymph node cells. It is vital to remember that the prognosis and treatment choices for ovarian cancer are greatly influenced by the disease's stage. Stages I and II of ovarian cancer often have a better prognosis and a higher likelihood of responding to treatment, but stages III and IV are more difficult to treat and have a worse prognosis.

In terms of problems in medical diagnosis in Saudi Arabia, some common challenges include:


Limited access to healthcare: despite considerable infrastructure improvements in the healthcare sector, Saudi Arabia may still have access issues, especially in outlying or rural areas. Accurate and prompt diagnosis may be hampered by limited access to healthcare facilities and specialists.


Language and cultural barriers: Saudi Arabia is a multicultural nation with a sizable expat population. Language and cultural obstacles can occasionally make it difficult for patients and healthcare professionals to communicate effectively, which could have an impact on how accurately a diagnosis is made.


Diagnostic errors and misinterpretation: diagnostic blunders can happen in Saudi Arabia's healthcare system as well as any other. Misdiagnosis or a delay in diagnosis may be caused by variables such insufficient patient data, a lack of consultation time, and cognitive biases.


Limited awareness and screening: some diseases, like some cancers, may have lower rates of early identification because of a lack of screening or awareness campaigns. As a result, the disease may be diagnosed at a later stage and be at a more advanced form.


Electronic health record integration: although Saudi Arabia has made steps to introduce EHRs across the country, there may still be issues with interoperability and data sharing across healthcare providers. The diagnostic procedure may be impacted by patient information that is illegible or incomplete.

Saudi Arabia keeps making investments in technology adoption, medical education, and healthcare infrastructure to address these issues. To increase diagnosis accuracy, efforts are being made to improve patient access to healthcare services, improve patient information systems, and support ongoing medical education [15,16,17,18,19,20,21,22,23].

A typical fuzzy set that provides for a more expressive depiction of uncertainty is called an intuitionistic fuzzy set (IFS). IFSs, which were first Eulalia Szmidt and Janusz Kacprzyk [24], introduced include extra information about the hesitation and uncertainty that are present during decision-making processes. Each element of the universe of discourse is given a membership degree in an IFS, which indicates how much it is a part of the set, and a non-membership degree, which indicates how little it is a part of the set. The level of uncertainty or hesitation in assigning the membership and non-membership degrees is also represented by the hesitation degree in an IFS.

It is possible to trace the origins of intuitionistic fuzzy sets to the growth of fuzzy set theory. Reference [25] developed fuzzy set theory, which offered a mathematical framework for dealing with ambiguity and uncertainty in problem-solving. Researchers eventually came to the conclusion that conventional fuzzy sets were insufficient to accurately represent the full nature of doubt, because they did not clearly take into consideration the reluctance or uncertainty related to membership and non-membership.

By adding hesitation degrees, their work attempted to improve the modelling capabilities of fuzzy sets. This gave decision-makers the chance to admit that they lacked the knowledge or confidence necessary to give elements exact degrees of membership and non-membership.

Intuitionistic fuzzy sets provide a more thorough depiction of uncertainty than other fuzzy settings. While intuitionistic fuzzy sets include hesitation and non-membership degrees to reflect extra dimensions of uncertainty, traditional fuzzy sets solely take membership degrees into account. For decision-making tasks involving vagueness, ambiguity, and incomplete knowledge, intuitionistic fuzzy sets are more adaptable and expressive due to the additional dimension of uncertainty [26,27,28,29,30].

Using a variety of factors, the TOPSIS approach (Technique for Order Preference by Similarity to Ideal Solution) helps choose the greatest choice from a group of alternatives. It offers a ranking or preference order after taking into account both the advantages and disadvantages of each solution.

The TOPSIS method's value comes from its capacity to handle decision-making issues involving various criteria and options. It is especially useful when making decisions under conditions of ambiguity or imprecision. The TOPSIS technique enables decision-makers to take into consideration trade-offs and conflicts among various criteria by taking into account both positive and negative criteria [31,32,33,34,35,36,37,38]. Some other decision making methods can be surveyed from [39,40,41,42].

The TOPSIS method has several advantages that contribute to its significance:


Comprehensive evaluation: the TOPSIS technique takes several factors into account at once and provides a full assessment of the options. It lets decision-makers to compare how each alternative performs across several dimensions, promoting better informed decision-making. Flexibility: both quantitative and qualitative criteria may be handled by the TOPSIS technique due to its adaptability. It may be used to solve a variety of decision issues since it can handle several sorts of data, including fuzzy sets, linguistic phrases, and numerical values. Intuitive interpretation: the results are interpreted using the TOPSIS approach in a simple and understandable manner. The alternatives are ranked according to how close they are to the perfect solution and how distant they are from the undesirable ideal option. Decision-makers may quickly find the best solutions thanks to this rating. Consideration of uncertainty: by adding fuzzy sets or other strategies for modelling uncertainty, the TOPSIS method may deal with uncertainty in decision-making. It gives decision-makers a more accurate appraisal of the options by allowing them to adjust for inaccurate or missing information.

The TOPSIS approach may now be used to solve complicated choice issues by combining it with intuitionistic fuzzy soft sets (IFSS). To deal with ambiguity, uncertainty, and incompleteness in decision-making, IFSS offers a mathematical framework. Decision-makers may successfully manage ambiguous and imprecise information by combining IFSS with the TOPSIS technique, producing more solid and dependable decision outputs. In conclusion, the TOPSIS technique is crucial since it provides a systematic process for making decisions based on a variety of factors. It gives understandable rankings, accommodates different forms of data, and enables decision-makers to take into account both the advantages and disadvantages of choices. Its capacity to manage uncertainty is increased when combined with intuitionistic fuzzy soft sets, thereby expanding its range of applications in actual decision-making situations [43,44,45].

1.3 Significant Contributions

Because fuzzy logic can handle imprecision and uncertainty, it allows computers to simulate human decision-making. Its importance stems from its capacity to handle imprecise and lacking data, which makes it indispensable in domains, such as pattern recognition, artificial intelligence, and control systems. Fuzzy logic improves systems' efficiency and adaptability by offering a framework for handling uncertainty, which produces more clever and flexible solutions. It spurs innovation in a variety of industries with applications ranging from sophisticated robotics to home appliances. An effective mathematical framework for modeling uncertainty, ambiguity, and vagueness in decision-making processes is intuitionistic fuzzy soft sets, which combine intuitionistic fuzzy sets and soft sets. Elements in intuitionistic fuzzy soft sets have degrees of hesitation, non-membership, and membership, which allows for a more thorough representation of complicated data. This hybrid approach is extremely useful in domains, such as expert systems, decision analysis, and pattern recognition, where precise and nuanced handling of imprecise or incomplete data is crucial. It allows intuitive reasoning with uncertain information.

The TOPSIS method is very important, especially in the context of intuitionistic fuzzy soft sets. This approach provides an organized way to make decisions in situations where imprecision and uncertainty are prevalent, which is a feature that many real-world issues share. When intuitionistic fuzzy soft sets are involved, TOPSIS helps choose the best option among a range of options for elements with varying degrees of membership, non-membership, and hesitation. Decision-makers can rank alternatives according to how close they are to the ideal solution while taking both optimistic and pessimistic viewpoints using TOPSIS, which helps them manage the complexity inherent in intuitionistic fuzzy soft sets. As a result, this approach is useful for navigating decision-making processes and guarantees that decisions are made with knowledge, even in circumstances where there is uncertainty and ambiguity.

Because it can manage intricate decision-making processes with several criteria and uncertainties, the TOPSIS method is very useful in the diagnosis of ovarian cancer. Numerous factors, including the patient's age, family history, the severity of their symptoms, the size of the tumor, and different biomarkers, must be taken into account when diagnosing ovarian cancer. Healthcare workers can combine these various criteria using TOPSIS, giving each a weight according to its relative importance. TOPSIS is able to efficiently rank the most indicative factors and determine the most likely diagnosis by comparing the individual patient profiles to an ideal diagnostic outcome. This article is divided into further five sections arranged as follows;

Section 2 consists of the literature review of the proposed model.

Section 3 consists of the fundamental theories to propose new model.

Section 4 consists of the proposed aggregation operators for the intuitionistic fuzzy soft sets.

Section 5 consists of the case study and Sect. 6 consists of the conclusion of the study.

2 Literature Review

Szmidt and Kacprzyk [46] introduce several intuitionistic fuzzy set aggregation operators and discusses their applications in multicriteria decision-making problems. Reference [47] This paper focuses on the development of intuitionistic fuzzy aggregation operators for information fusion in medical diagnosis applications, considering uncertainty and hesitancy in decision-making. In [48], authors presents various intuitionistic fuzzy aggregation operators suitable for group decision-making processes and explores their effectiveness in handling uncertainty and hesitancy. In [49], authors investigates the application of intuitionistic fuzzy aggregation operators in decision-making based on the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method, [50] selections using temporal IF information are made using an accumulation of infinite chains of intuitionistic fuzzy sets, Ref. [51] new aggregation operations, complex intuitionistic fuzzy sets, and decision-making implementations of these methods are found in this article, Ref. [52] introduces few aggregation operators, such as IFOWG, IFHG, and IFWG, are new geometric aggregation operators that extend the WG and OWG operators to accommodate environments where the given arguments are IFS. In this article, the created operators are demonstrated using a few numerical examples. The application of the IFHG operator to multiple attribute decision-making based on intuitionistic fuzzy sets is provided as our final point.

In Ref. [53], authors presented the I-GIFOWA operator is introduced in this study. With all the traits of both the generalized IFOWA and the induced IFOWA operators, it is a new aggregation operator that generalized the IFOWA operator. To address the situation when the provided arguments are interval-valued intuitionistic fuzzy sets. They also create methods to use interval-valued intuitionistic fuzzy or intuitionistic fuzzy information to tackle group multiple attribute decision making issues. To demonstrate the usefulness of the created methodologies, we finally describe their implementation, [54] demonstrate the accessibility and benefits of the suggested technique in comparison to certain current methods, a real-world scenario is provided. To use the ambiguous and imprecise information, the suggested aggregation operators are more generalized than the ones now in use. Several current operators are viewed as special examples of the one that is being suggested. Finally, the suggested approach will give the decision-maker a range of options, so they may access the best options, Ref. [55] researched how to aggregate IVIF data. Based on the IIFWGA and the IIFHGA operators, a method for MAGDM with IVIF information is devised, Ref. [56] investigated are the dynamic multiple attribute decision making (DMADM) issues using IF data. Two new aggregation operators’ dynamic intuitionistic fuzzy weighted geometric (DIFWG) operator and uncertain dynamic intuitionistic fuzzy weighted geometric (UDIFWG) operator are proposed. The concepts of IF variable and uncertain IF variable are defined, Ref. [57] the scoring function and accuracy function are set up such that any two linguistic IF values (LIFVs) can be compared to one another. To demonstrate the effectiveness of the suggested strategy in MAGDM, a numerical example is given, Ref. [58] offers aggregation methods that capture how preferences and criteria interact when complex intuitionistic fuzzy (CIF) conditions are present. We investigate the decision-making (DM) process in the CIF set environment and offer an approach to resolve the numerous criteria DM challenges to make the potential application easier [59]. Thermal energy storage application discussed via fuzzy TOPSIS approached in this article. In (Extension of the TOPSIS for group decision-making under fuzzy environment) authors extended the TOPSIS method for different fuzzy environments. In (Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method) authors discussed type-2 TOPSIS method and their applications in decision-making process. In (The interval-valued fuzzy TOPSIS method and experimental analysis), authors extended the TOPSIS approach to interval-valued fuzzy environment. For other detail articles on [60,61,62,63].

3 Basic Results

Because soft set theory can deal with the ambiguity and uncertainty present in real-world data and decision-making processes, it is highly significant in many fields. In contrast to the strict boundaries between elements assumed in traditional set theory, degrees of membership are allowed in soft sets, offering a more flexible and realistic depiction of uncertainty. Soft sets are useful in many different fields, including data analysis, image processing, pattern recognition, and decision making because of their adaptability. They provide a framework for modeling imprecise information, enabling more accurate and nuanced reasoning in scenarios where precise data may be hard to come by or unavailable.

Definition 1.

[64] A mapping \(F:\varepsilon \to {\mathbb{H}}^{\mho }\) is known as a SS, where \({\mathbb{H}}^{\mho }\) be a family of all subsets of a universe of discourse \(\mho\) and \(\epsilon\) is a set of attributes.

A hybrid extension of fuzzy sets and soft sets, fuzzy soft sets combine the ideas of vagueness and uncertainty into one cohesive framework. Fuzzy soft sets allow elements to have varying degrees of membership to various sets, as well as a degree of hesitation, which represents the inherent uncertainty in the element's classification. This combination makes it possible for fuzzy soft sets to represent complex decision-making situations where ambiguity and uncertainty coexist. Fuzzy soft sets are versatile, because they can handle imprecise and incomplete information, which makes it possible to represent real-world data in a more flexible and nuanced manner. This makes them especially helpful in domains where it can be challenging to define exact boundaries between elements, such as pattern recognition, decision analysis, and data mining.

Definition 2.

[65] \({\mathbb{H}}^{\mho }\) be a family of all fuzzy subsets over U and \(\varepsilon\) be a set of attributes. Let \(\mho \varepsilon\), then a pair \((F, \mho )\) is called FSS over U. Where F is a mapping such as \(F:\mho \to {\mathbb{H}}^{\mho } .\)

To handle uncertainty, vagueness, and ambiguity in decision-making contexts, intuitionistic fuzzy soft sets represent a sophisticated extension of intuitionistic fuzzy sets and soft sets, combining the features of both. Element degrees of membership, non-membership, and hesitation in intuitionistic fuzzy soft sets reflect the subtlety of their classification. Comparing this tripartite representation to conventional fuzzy or soft sets enables a more thorough modeling of uncertainty. Applications for intuitionistic fuzzy soft sets can be found in a variety of domains, including expert systems, pattern recognition, and decision analysis, where it's necessary to manage complex and uncertain data efficiently. Intuitionistic fuzzy soft sets provide a flexible framework for reasoning with imprecise and incomplete data, enabling more robust and informed decision-making processes that lead to advancements across a range of domains.

Definition 3.

A mapping F:U \(\to I{\mathbb{H}}^{\mho }\) is known as an IFSS and defined as F \({u}_{u}\left(e\right)= \left\{({u}_{u}, {T}_{\mho }({u}_{u})\right.| {u}_{u}\in \mho \}\) where \({T}_{\mho }\left({u}_{u}\right)\ \, and \, \ {T}_{\mho }\left({u}_{u}\right)\) are the MD and NMD respectively for all \({u}_{u}\in \mho\ and\ 0\le {T}_{\mho }({u}_{u) ,} {T}_{u}\left({u}_{u}\right), {T}_{\mho }\left({u}_{u}\right)+{T}_{\mho }({u}_{u})\le 1.\) Where \(I{\mathbb{H}}^{\mho }\) be a set of all intuitionistic fuzzy subsets of \(\mho .\)

Definition 4.

Let \((F,\mho )\) and \((G, B)\) be two IFSSs over \(\mho\). Then, some basic operations under IFSS defined as follows:

  1. 1)

    I \(\mho \, us \, subset \, of \, \beta \, and \, {T}_{F\left(e\right)}\le {T}_{G\left(e\right)} \, and \, {T}_{F\left(e\right)}\ge {T}_{G\left(e\right) } \, for \, all \, e\in \, \mho , \, then \, \left(F, \mho \right)\subseteq \left(G ,B\right).\)

  2. 2)

    If (F, U) \(\subseteq ( G,B )\) and \(( G, B)\) is subset of \((F,\mho )\) then\(F(\mho ) = (G,B)\).

  3. 3)

    Let \(F(\mho ) = \left\{\left({u}_{u}, {T}_{\mho }\left({u}_{u}\right), {T}_{\mho }\left({u}_{u}\right)\right|{u}_{u}\in \mho \right\}.\)

Definition 6.

For an IFSV \({\beta }_{uj}=\left({\sigma }_{uj}, {\phi }_{uj}\right)\) score function is defined as

$$S\left({\beta }_{uj}\right)={\sigma }_{uj}-{\phi }_{uj}$$
(1)

4 Proposed Aggregation Operators

This section contains the development of the proposed AOs based on the AATRM and AATCRM. IFSAAWA and IFSAAWG operators for the aggregation of the family of various IFSVs are presented in this section.

Definition 7

For the family of IFSVs \({\beta }_{uj}=\left({\sigma }_{uj},{\phi }_{uj}\right); \, u=1, 2, . . . , n, \, j=1, 2,...,m\). Then IFSAAWA operator is created as follows:

$$\text{IFSAAWA} \, \left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)={\oplus }_{j=1}^{m}{\zeta }_{j}({\oplus }_{u=1}^{n}{\varrho }_{u}{\beta }_{uj})$$

where the weight vectors are denoted by \({\zeta }_{j} , {\varrho }_{u}>0, \sum_{j=1}^{m}{\zeta }_{j}=1\) and \(\sum_{u=1}^{n}{\varrho }_{u}=1.\)

Theorem 1

IFSAAWA operator yields the aggregated value of the collection of IFSVs, which is still an IFSV and is given by

$$\text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\mathit{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\mathit{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right)$$
(2)

Proof

Let \({\beta }_{uj}=\left({\sigma }_{uj}, {\phi }_{uj}\right)\) be a collection of IFSVs. Then, utilizing IFSV operating laws, we have

$${\varrho }_{u}\beta =\left(1-{e}^{-{\left({\varrho }_{u}{\left(-\mathit{ln}\left(1-\sigma \right)\right)}^{\mu }\right)}^{\frac{1}{\mu }}}, {e}^{-{\left({\varrho }_{u}{\left(-\mathit{ln}\left(\phi \right)\right)}^{\mu }\right)}^{\frac{1}{\mu }}}\right)$$

In addition

$${\oplus }_{u=1}^{n}{\varrho }_{u}{\beta }_{uj}=\left(1-{e}^{{-\left({\sum }_{u=1}^{n}{{\varrho }_{u}\left(-\mathit{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)}^{\frac{1}{\mu }}}, {e}^{{-\left({\sum }_{u=1}^{n}{{\varrho }_{u}\left(-\mathit{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)}^{\frac{1}{\mu }}}\right)$$

In addition, we have

$${\oplus }_{j=1}^{m}{\zeta }_{j}({\oplus }_{u=1}^{n}{\varrho }_{u}{\beta }_{uj})=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right)$$

Therefore

$$\text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right)$$

Some basic properties of the proposed IFSAAWA operator are stated as follows.

Theorem 2.

If \({\beta }_{uj},{\delta }_{uj}; \, u=\text{1,\,2},\dots ,n, j=\text{1,\,2},\dots ,m,\) are IFSVs. Then, some properties are stated as follows.

  1. i)

    Idempotency: If all the IFSVs are identical, \(u.e., \beta uj=\beta\) for all \(u, j,\) then

    $$\text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)=\beta$$
  2. ii)

    Monotonicity: Let \({\beta }_{uj}=\left({\sigma }_{uj}, {\phi }_{uj}\right)\) and \({\delta }_{uj}=\left({\tau }_{uj}, {\upsilon }_{uj}\right)\) be two collections of the IFSVs such that \({\sigma }_{uj}\le {\tau }_{uj}\) and \({\phi }_{uj}\ge {\upsilon }_{uj}\) then \(\text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)\le \text{IFSAAWA}\left({\delta }_{11}, {\delta }_{12},...,{\delta }_{nm}\right)\).

  3. iii)

    Boundedness: Let \({\beta }^{-}=\left(\underset{j}{\text{min}}\underset{u}{\text{min}}\left\{{\sigma }_{uj}\right\},\underset{j}{\text{max}}\underset{u}{\text{max}}\left\{ {\phi }_{uj}\right\}\right)\) and \({\beta }^{+}=\left(\underset{j}{\text{max}}\underset{u}{\text{max}}\left\{{\sigma }_{uj}\right\},\underset{j}{\text{min}}\underset{u}{\text{min}}\left\{ {\phi }_{uj}\right\}\right)\). Then \({\beta }^{-}\le \text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)\le {\beta }^{+}\).

Proof

Idempotency: If all \({\beta }_{uj}\) are same i.e., \({\beta }_{uj}=\beta =\left(\sigma ,\phi \right), \forall u,j\) then using Eq. 2, we have

$$\text{IFSAAWA}\left({\beta }_{11}, {\beta }_{12},...,{\beta }_{nm}\right)=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right) =\left(1-{e}^{-\left(-\text{ln}\left(1-\sigma \right)\right)}, {e}^{-\left(-\text{ln}\left(\phi \right)\right)}\right)=\left(\sigma ,\phi \right).$$

Proof

Monotonicity: Since we have \({\sigma }_{uj}\le {\tau }_{uj}\), therefore, for all \(u,j\), we have

$$\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\ge \sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\tau }_{uj}\right)\right)}^{\mu }$$

In the same way, we get

$${e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\ge {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\tau }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}$$

Similarly, we have

$$1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\le 1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\tau }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}$$

Similarly, we can prove for the NMD. Hence, the proof is completed.

Proof

Boundedness: Since for all \(u, j\) we have \({\beta }^{-}\le {\beta }_{uj}\le {\beta }^{+}\); therefore, using monotonicity property, we get \({\beta }^{-}\le \text{IFSAAWA}\left({\beta }_{11},{\beta }_{12},\dots ,{\beta }_{nm}\right)\le {\beta }^{+}\).

5 Diagnosis of Cancer by TOPSIS Technique

In this section, we demonstrate how TOPSIS may be used in an IFS environment. We will first write the stepwise TOPSIS technique using the developed AOs and then discuss its application in the diagnosis of the stages of cancer.

5.1 Algorithm of TOPSIS for Diagnosis of Stages of Ovarian Cancer

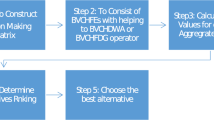
In the following, the methodology to apply the TOPSIS technique to diagnose the stages of ovarian cancer is formulized. In this subsection, the TOPSIS technique is extended to the information in the form of the IFSS. Stepwise TOPSIS is provided as follows;

Step 1: The problem should be pinpoint. Consider \(E=\left\{{E}_{i}\right\}\) is the team of the experts, \(P=\left\{{p}_{i}\right\}\) are the attributes or symptoms diagnose, and \(S=\left\{{s}_{i}\right\}\) are the stages of the ovarian cancer.

Step 2: Construct the weighted decision matrix of the attributes with the help of the weight values of the special terms obtained from the experts. Note that expert assigns the values to each attribute according to their weightage based on the special terms stated in Table 1. Consider \(H={\left({\beta }_{ij}\right)}_{l\times m}\) is the weighted decision matrix obtained from the decision expert using the fuzzy values of the special terms.

Table 1 Fuzzy weights of the special terms of the ovarian cancer
Full size table

Step 3: The matrix obtained from the previous step is may have different types of the attributes. To convert the attributes in the similar nature, normalize the weighted decision matrix obtained from previous step. We use we normalize the matrix \(N={\left({n}_{ij}\right)}_{l\times m}\) where \({n}_{ij}=\frac{{w}_{ij}}{{\sum }_{i=1}^{l}{w}_{ij}^{2}}\) and then acquire the weight vector \(W=\left({\zeta }_{j}\right)\) where \({\zeta }_{j}=\frac{{\sum }_{i=1}^{l}{n}_{ij}}{l{\sum }_{k=1}^{m}{n}_{ik}}\).

Step 4: Extract the decision matrices in the form of the IFSS in which each parameter is assigned a value in the form of IFSS. Consider \({E}_{i}=\left({\sigma }_{ij},{\phi }_{ij}\right)\) is the family of the decision matrices obtained from the expert in which they assign the values to the stages of the ovarian cancer according to the advised tests and physical condition of the patient based on some criteria. Then we obtain the aggregated matrix \(A\) from the family of the decision matrices using the proposed weighted AOs:

$$A=\left({\sigma }_{ij}^{\prime},{\phi }_{ij}^{\prime}\right)=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right)$$
(3)

Step 5: We find the ideal solutions, i.e., positive idea solution (PIS) and negative ideal solution (NIS) as follows:

$$\text{PIS}=\left({\sigma }_{k}^{+},{\phi }_{k}^{+}\right)=\left(\underset{j}{\text{max}}{\sigma }_{i}^{\prime},\underset{j}{\text{min}}{\phi }_{i}^{\prime}\right)$$
(4)
$$\text{NIS}=\left({\sigma }_{k}^{-},{\phi }_{k}^{-}\right)=\left(\underset{j}{\text{min}}{\sigma }_{i}^{\prime},\underset{j}{\text{max}}{\phi }_{i}^{\prime}\right)$$
(5)

Step 6: Find the negative and positive distance from the ideal solution for each alternative as follows:

$${D}^{+}=\sqrt{\sum\limits_{k=1}^{m}\left(\left({\sigma }_{kj}-{\sigma }_{kj}^{+}\right)+\left({\phi }_{kj}-{\phi }_{kj}^{+}\right)\right)}$$
(6)

In addition

$${D}^{-}=\sqrt{\sum\limits_{k=1}^{m}\left(\left({\sigma }_{kj}-{\sigma }_{kj}^{-}\right)+\left({\phi }_{kj}-{\phi }_{kj}^{-}\right)\right)}$$
(7)

Step 7: Find the coefficient of closeness as follows:

$${C}_{j}=\frac{{D}_{j }^{-}}{{D}_{j }^{-}+{D}_{j }^{+}}$$
(8)

Step 8: Finally, we rank the alternatives in ascending or descending orders as our choice.

The stepwise procedure is given in Fig. 1 as follows.

Fig. 1
figure 1

Stepwise flowchart

Full size image

5.2 Case Study

A doctor determines a patient's cancer stage to plan therapy and predict prognosis using the findings of diagnostic exams, imaging scans, and samples obtained following surgery. The medical professional treating you will probably use the staging systems developed by the American Joint Committee on Cancer (AJCC) or the International Federation of Gynaecology and Obstetrics (FIGO), which offer comparable data, for ovarian cancer. These techniques assist medical professionals in determining a tumor's stage depending on its location and if it has migrated to surrounding lymph nodes or to other parts of the body.

Based on this information, doctors will divide the cancer into substages of A, A1, A2, B, or C and give an overall Stage of 1–4. A lower number frequently denotes more localised cancer, whereas a higher number denotes more widespread cancer. This staging system covers fallopian tube cancer as well as main peritoneal cancer.

Another point about staging: in general, the pathological stage or surgical stage of ovarian cancer is referred to as the stage. Tissue samples that have been surgically removed and biopsied play a key role in determining this. A doctor may determine the cancer's clinical stage if surgery is not an option using imaging and a physical examination. Following a surgical biopsy, the data will help determine the pathological stage of the patient's cancer.

5.2.1 Understanding Survival Rates for Ovarian Cancer Stages

Many ovarian cancer patients are curious about the prognosis for their stage of the disease. A better prognosis is typically linked to early stage disease rather than advanced stage disease. A person's prognosis may also be revealed by additional information discovered after surgery or treatment. People who can have all visible tumors removed after surgery, for instance, typically live longer than those whose disease cannot be properly excised. Details on the precise kind of ovarian cancer (serous, clear cell, etc.) and its grade, tumour mutations, a person's genetic background, and the effectiveness of treatment can provide further prognostic information. Patients should talk to their doctors about the state of their illness, the features of their tumour, and how these aspects impact their prognosis.

5.2.1.1 Stage 1 Ovarian Cancer

When a person has stage 1 ovarian cancer, it indicates the cancer has not progressed to other organs and has only been identified in one or both ovaries or fallopian tubes. Only 17% of ovarian cancer patients receive a Stage 1 diagnosis. Cancer is confined to the ovary (or ovaries), or the fallopian tubes. Some details are provided as follows.

Stage 1a: One ovary only has cancer that is contained therein, or one fallopian tube alone has cancer that is contained therein.

Stage 1b: The outer surfaces of either the ovaries or the fallopian tubes do not have cancer.

Stage 1c: Cancer affects one or both ovaries or fallopian tubes, and either the tumour lining is torn out during surgery (1C1), cancer is found on the outside of the ovary or fallopian tube (1C2), or cancer is found in fluid (a condition known as ascites) or washings from the abdomen or pelvis (1C3).

5.2.1.2 Stage 2 Ovarian Cancer

Primary peritoneal cancer that is limited to the pelvis is referred to as stage 2 ovarian cancer, as is cancer that has been found in one or both ovaries or fallopian tubes and has spread to other areas of the pelvis. At 19% of instances, ovarian cancer at stage 2 is found. Stage 2 ovarian cancer is either a primary peritoneal cancer that is restricted to the pelvis or has been discovered in one or both ovaries or fallopian tubes and has progressed to other areas of the pelvis. Ovarian cancer at stage 2 is discovered in 19% of cases.

Stage 2a: The uterus has been reached or entered by cancer.

Stage 2b: Other areas of the pelvis contain cancer, but only within the pelvis.

5.2.1.3 Stage 3 Ovarian Cancer

When ovarian cancer is in stage 3, one or both ovaries have been determined to be positive, and the cancer has progressed to other regions of the abdomen and/or adjacent lymph nodes. When the disease has reached the liver's outer layer, it is also referred to as Stage 3 ovarian cancer. Ovaries, fallopian tubes, or primary peritoneal cancer that affects pelvic or para-aortic lymph nodes without spreading to other locations in the abdomen or pelvis are all examples of cancers that can affect these organs.

Stage 3a: The malignancy may be in one or both ovaries, the fallopian tubes, or the major peritoneum if there is proof of tiny implants outside the pelvic region. The metastasis of the malignancy may have potentially damaged pelvic or aortic lymph nodes.

Stage 3b: If you have primary peritoneal cancer, one or both of your ovaries, one or both of your fallopian tubes, or another type of cancer where the cancer has visibly spread to organs outside of your pelvis, it must be less than 2 cm in size. In addition, lymph nodes in the pelvis or around the aorta may have been affected by the cancer.

Stage 3c: Ovarian, fallopian tube, or primary peritoneal carcinoma with deposits greater than 2 cm that have obviously metastasized to organs outside the pelvic region. In addition, the cancer may have progressed to the liver or spleen's surface or to lymph nodes in the pelvic or para-aortic region.

5.2.1.4 Stage 4 Ovarian Cancer

When ovarian cancer is found to be at Stage 4, it has gone to distant areas such the lungs, the inner section of the liver, or other organs. Ovarian cancer in Stage 4 also refers to cancer cells found in the fluid surrounding the lungs.

Stage 4a: Malignant pleural effusion is a condition in which there are cancer cells in the fluid surrounding the lungs but they have not yet moved to organs like the spleen, liver, or lymph nodes outside of the abdomen.

Stage 4b: Cancer can be found in lymph nodes outside of the pelvis or abdomen, the spleen, the liver, or other locations that are not part of the peritoneal cavity.

5.3 About Cancer Grading

A pathologist classifies cancer as Grade 1, 2, or 3 by examining cancer cells under a microscope. Grade 3 cancer cells are very abnormal, and high-grade cancer cells are more prone to spread. Although chemotherapy may still be used to treat these cancers, grade 1 tumors are typically less aggressive. However, it is very difficult to diagnose the stage of the ovarian cancer. There are chances of uncertainty to diagnose the stages. Hence, to overcome the chances of uncertainty we use the well-known method "TOPSIS" for selecting the unbeatable choice from the point of view to make thorough, unanimous, and intelligent selections.

Example 1

Consider \(E=\left({D}_{1},{D}_{2},{D}_{3},{D}_{4}\right)\) be the expert team, the set of patients is \(V=\left\{{p}_{1},{p}_{2},{p}_{3},{p}_{4}\right\}\) and \(\mathcal{D}=\left\{{\eta }_{1},{\eta }_{2},{\eta }_{3},{\eta }_{4}\right\}\) is the set of parameters. Consider \({w}_{ij}\) be the weight allocated by \({D}_{i}\) to \({\eta }_{j}\) with the help of the variables provided in Table 1. Consider the matrix \(P={\left({w}_{ij}\right)}_{l\times m}\) denotes the weights assigned to the parameters.

The matrix of the parameter is as follows:

$$P={\left({w}_{ij}\right)}_{l\times m }=\left(\begin{array}{c}{s}_{1},{s}_{2},{s}_{3},{s}_{4}\\ {s}_{2},{s}_{3},{s}_{1},{s}_{4}\\ {s}_{1},{s}_{2},{s}_{3},{s}_{1}\\ {s}_{1},{s}_{3},{s}_{2},{s}_{4}\end{array}\right)=\left(\begin{array}{c}\text{0.2,0.3,0.4,0.5}\\ \text{0.3,0.4,0.2,0.5}\\ \text{0.2,0.3,0.4,0.2}\\ \text{0.2,0.4,0.3,0.5}\end{array}\right)$$

In case of the presence of the cost type attribute, normalize the weighted decision matrix. We cannot separate cost and benefit type attribute. Hence, we use the do not normalize here, because there is not any cost type attribute. Hence, we normalize the matrix \(N={\left({n}_{ij}\right)}_{l\times m}\) where \({n}_{ij}=\frac{{w}_{ij}}{{\sum }_{i=1}^{l}{w}_{ij}^{2}}\) and then acquire the weight vector \(W=\left({\omega }_{j}\right)\) where \({\omega }_{i}=\frac{{\sum }_{i=1}^{l}{n}_{ij}}{l{\sum }_{k=1}^{m}{n}_{ik}}\). The \(W={\omega }_{j}=\left(0.1607, 0.25, 0.2955, 0.2036\right)\) is acquired. Consider the experts provide the following four tables. Each expert provides the values to each patient in the form of the IFSN such that \(\text{PFSN}=\left(\sigma ,\phi \right)\). The four matrices are given as follows (Tables 2, 3).

Table 2 For expert \({D}^{\left(1\right)}\)
Full size table
Table 3 For expert \({D}^{\left(2\right)}\)
Full size table

The mean proportional matrix is obtained using the following expression (Tables 4, 5):

Table 4 For expert \({D}^{\left(3\right)}\)
Full size table
Table 5 For expert \({D}^{\left(4\right)}\)
Full size table
$$A={\left[{p}_{jk}\right]}_{l\times m}=\left(1-{e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left(1-{\sigma }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}, {e}^{-{\left(\sum_{j=1}^{m}{\zeta }_{j}\left(\sum_{u=1}^{n}{\varrho }_{u}{\left(-\text{ln}\left({\phi }_{uj}\right)\right)}^{\mu }\right)\right)}^{\frac{1}{\mu }}}\right)$$

Now, we obtain the PIS and NIS in the form of the IFSS from Table 6 as follows:

Table 6 Aggregated decision matrix using the proposed weighted AOs
Full size table
$$\text{PIS}=\left(\left(0.0506, 0.0421\right),\left(0.0594, 0.0378\right),\left(0.0522, 0.0441\right),\left(0.0542, 0.0374\right)\right)$$

And

$$\text{NIS}=\left(\left(0.0490, 0.0541\right),\left(0.0445, 0.0495\right),\left(0.04178, 0.04639\right),\left(0.0468, 0.0505\right)\right)$$

With the help of the PIS and NIS evaluated above we find the distance of each stage from the PIS and NIS. Then we evaluate the coefficient of the closeness as in Table 7 as follows.

Table 7 PIS, NIS, and coefficient of closeness
Full size table

Table 7 states the PIS, NIS, and coefficient of closeness based on which we rank the stages of the ovarian cancer. We may finally conclude that the patient is suffering from the stage 3 of the ovarian cancer. Note that this ranking is based on the information fusion with the help of the developed weighted AOs.

As we can observer that the developed model consists of the parameter \(\mu\). Due to the involvement of the parameter the developed AOs become very flexible in the fusion of the information. However, it is possible that the result may change by variating the values of the parameter. Table 8 represents the results obtained after the variation of the value of the parameter.

Table 8 Results obtained by changing the values of \(\mu\)
Full size table

Table 8 shows the results obtained by changing the values of the parameters. Interestingly, the stage 3 is diagnosed at different values of the parameter. The graphical representation of Table 8 is given as follows.

Figure 2 shows the results obtained by changing the values of the parameters. Interestingly, the stage 3 is diagnosed at different values of the parameter. It is also important to note that the change in the values of the involve parameter does not affect the ranking of the alternatives. However, if we change the values of the weights of the attributes or the weights of the experts the ranking of the alternatives will must be changed accordingly.

Fig. 2
figure 2

Graphical effect of the change in the values of \(\mu\)

Full size image

The obtained results are also compared with some existing operators as follows.

Table 9 shows the comparison between different operators. We have applied the different existing operators developed by other scholars and obtained the similar results. It shows the significance of the proposed model.

Table 9 Comparison between different operators
Full size table

6 Conclusion

In this study, the new AOs have been developed based on the IFSS. Some of their properties are stated. Then the developed AOs are used to diagnose the stage of the ovarian cancer with the help of the TOPSIS technique. Some important points of the study are given as follows.

The developed AOs are based on the IFSS which is the latest framework to deal with the uncertainty in the information. The proposed AOs consist of the parameter due to which they become very flexible. The change in the results is observed in Table 8. The results are also shown graphically in Fig. 1. The developed model is applied in the diagnosis of the stage of the ovarian cancer with the help of very famous technique known as TOPSIS. The diagnosis of any disease is full of the uncertainty due to the involvement of the human opinion. To reduce this uncertainty the TOPSIS is structured based on the IFSS. The developed approach is significant, because it reduces the uncertainty when the information is analyzed. In future, this study can be used for the framework such that [68,69,70]. The proposed model also be generalized to the frameworks in the future [71,72,73]. Further one can study [74, 75] for recent work of the topic and for their extensions.