Effect of gas spacing and resonance frequency on theoretical performance of thermoacoustic refrigerators

Abstract

In this paper, the design and analysis of 500 W thermoacoustic refrigerators for the temperature difference of 28 K using helium and air are discussed. Helium is the best working gas, but air is chosen to study the possibility of replacing helium for the future cost-effective refrigerator since it is much cheaper than helium. Heat and work flow equations of thermoacoustic refrigerators are discussed. The refrigerator models are optimized by normalizing the design parameters using Rott’s linear thermoacoustic theory. The effect of gas spacing expressed in terms of the thermal penetration depth in stack-heat exchanger unit at 85% porosity is discussed. The effect of the resonance frequency of air on the stack-heat exchanger sheets spacing and thickness and on the theoretical performance is discussed. The effect of the resonance frequency of air on the theoretical performance at 200 Hz, 300 Hz, and 400 Hz is discussed. The cooler shows better COP of 1.72 at 300 Hz for air and 1.53 at 400 Hz for helium. The theoretical results are compared with the DeltaEC software results. The DeltaEC predicts cooling power and COP of 347 W at 1.02 for helium and 224 W at 0.79 for air, respectively.

1 Introduction

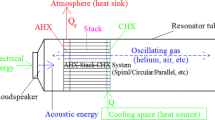
Thermoacoustic refrigeration uses thermoacoustic effect, which is the conversion of heat energy to sound energy and vice versa. The standing wave stack-based thermoacoustic refrigerators use the commercially available loudspeaker to produce sound energy to create refrigeration effect, known as LDTAR systems. The acoustic work pumps heat from cold space via cold heat exchanger to ambient heat exchanger. The challenge with the LDTAR system is the poor electro-acoustic efficiency of loudspeaker, which is about 3%. To improve the electro-acoustic efficiency, the loudspeaker is modified with the back volume gas spring (BVGS) system. The modified commercial loudspeaker is known as an acoustic driver, which will have an efficiency of about 50% as found in the literature [1,2,3]. Thermoacoustic refrigeration is an eco-friendly emerging technology for cooling applications. Because of its inherent advantages and simplicity in its construction, it is considered as the best alternative to the current vapor compression refrigeration systems. In the last three decades, research on thermoacoustic refrigeration has gained the attention of the researchers to optimize the design and development of thermoacoustic refrigerators ranging from Hofler’s 3 W to less than 500 W, as found elsewhere [3,4,5,6]. The schematic of the thermoacoustic refrigerator with the BVGS system is shown in Fig. 1. The acoustic driver generates a standing sound wave in the pressurized gas (helium or air or any other inert gas usually at 10 bar) contained in a closed resonator tube. The oscillating gas causes temperature differences across the stack. The cold and ambient heat exchangers (CHX and AHX) are placed at either side of the stack. The gas surrounding the CHX (maximum rarefaction region) absorbs heat and is pumped to the AHX (maximum compression region) through the micro pores of the stack.

Fig. 1

The schematic of the thermoacoustic refrigerator

The whole resonator tube and the BVGS system are assumed to be covered with the multi-layer superinsulation to avoid heat dissipation losses. Thermoacoustic heat pumping mechanism with Pv and Ts diagrams similar to the Brayton cycle, except for heat addition at the end of compression, and heat rejection at the end of the expansion process are shown in Fig. 2. The AHX maintained at room temperature by circulating cooling water through copper tubing system, which rejects heat to the atmosphere. The gas has adiabatic compresses (1–2) and the hot gas rejects heat to the surrounding AHX sheets at constant pressure (2–3). The gas expands adiabatically during the reverse stroke of the loudspeaker (3–4), and the cold gas surrounding the CHX sheets absorbs heat which is connected to the cooling chamber at constant pressure (4–1).

Fig. 2

The Pv and Ts diagrams of the thermoacoustic refrigerator

1.1 Heat and work flow equations in a thermoacoustic refrigerator

As shown in Fig. 1, the acoustic power input (W_a) to the resonator is dissipated into the following components: the resonator left to AHX (W_rax), the AHX (W_ax), the stack (W_s), the CHX (W_cx), and the resonator right to CHX (W_rcx). The acoustic power dissipated in the stack pumps heat, whereas the acoustic power dissipated in the heat exchangers and in the resonator portion manifests as thermoacoustic losses and acts as additional heat loads on the AHX and CHX. For the adiabatic oscillating gas parcel, let W_rax = Q_rax, W_ax = Q_ax, W_s = Q_s, W_cx = Q_cx, and W_rcx = Q_rcx be the heat loads on the AHX and CHX [7]. The heat extracted by the stack Q_es is the sum of heat absorbed from cooling space Q via CHX and the additional heat loads of Q_cx and Q_rcx, which is given by:

$${Q}_{es}=Q+{Q}_{cx}+{Q}_{rcx}$$

(1)

The heat pumped by the stack Q_ps is the sum of the heat extracted by the stack Q_es, and heat load of the stack Q_s is given by:

$${Q}_{ps}={Q}_{es}+{Q}_{s}=\left(Q+{Q}_{cx}+{Q}_{rcx}\right)+{Q}_{s}$$

(2)

The heat rejected by the AHX, Q_r is the sum of the Q_ps and Q_ax and Q_rax is given by:

$${Q}_{r}={Q}_{ps}+{\mathrm{Q}}_{\mathrm{ax}}+{Q}_{r\mathrm{a}x}$$

(3)

Using Eq. (2) in (3),

$${Q}_{r}=\left(Q+{Q}_{cx}+{Q}_{rcx}+{Q}_{s}\right)+{Q}_{\mathrm{a}x}+{Q}_{r\mathrm{a}x}$$

(4)

The COP of the refrigerator is given by:

$$\mathrm{COP}=\frac{Q}{E}=\left(\frac{Q}{{Q}_{es}}.\frac{{Q}_{es}}{{W}_{s}}.\frac{{W}_{s}}{{W}_{\mathrm{a}}}.\frac{{W}_{\mathrm{a}}}{{W}_{e}}\right)=\left(\epsilon .{\mathrm{COP}}_{s}.{\eta }_{\mathrm{a}s}.{\eta }_{e\mathrm{a}}\right)$$

(5)

where ϵ = Q/Q_es is the effectiveness of the CHX, COP_s = Q_es/W_s is the COP of the stack, η_as = W_s/W_a is the acoustic power efficiency of the stack, and η_ea = W_a/W_e is the electro-acoustic efficiency of the driver. The total heat rejected by the AHX with BVGS system Q_R is the sum of Q_r and Q_l (heat lost by loudspeaker), is given by:

$${Q}_{R}={Q}_{r}+{Q}_{\mathrm{l}}$$

(6)

In this paper, an attempt is made to design and optimize 500 W thermoacoustic refrigerators using helium and air as working substances at 10 bar pressure for a temperature difference of 28 K. The dimensional normalization of parameters is applied using the linear thermoacoustic theory for a temperature difference of 28 K at 3% drive ratio (ratio of acoustic pressure amplitude to average gas pressure). The objectives of the current research work are to study the effect of helium and air gas spacing expressed in terms of the thermal penetration depth in stack-heat exchanger unit at 85% porosity and to study the effect of increasing the resonance frequency of air from 200 to 400 Hz in the step of 100 Hz on the stack-heat exchanger sheets spacing and thickness and on the theoretical performance of coolers compared to the published literature [3]. The other objectives are to compare the performance of the cooler with helium and air as working gases and to verify the capability of air replacing helium as working gas expressed in terms of COP, cooling power, and power density. The velocity of air is much smaller than helium, leading to a decrease in cooling power, and in addition, it also decreases the length and volume of the refrigerator. The decrease in the volume of the refrigerator increases power density, which is an advantage as found in the published literature [3]. The cost of the compressed dry air cylinder to meet the required operating pressure of 12 bar is much cheaper than helium. Hence, checking the possibility of using dry air as a replacement for helium to reduce the cost of the future practical refrigerator is justified.

2 Design and optimization of stack-heat exchanger system

As shown in Fig. 1, the geometry of the stack, AHX, and CHX is the same, but the length and material used for construction vary. The diameter, porosity, half-stack sheet spacing and thickness, half-AHX and CHX sheet spacing, and thickness are the same. The design and optimization guidelines are the same for both the stack and heat exchangers (AHX and CHX).

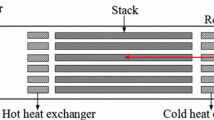
The AHX and CHX are placed on either side of the stack leaving a small gap of about less than 5 mm between the stack and the heat exchangers to avoid heat conduction which decreases the performance of the refrigerator. The stack is enclosed in the stack holder. The stack holder must have rigidity and low thermal conductivity. The stack holder must withstand 10 bar dynamic pressure, and it should be rigidly connected to the AHX and CHX using flanges on either side of the stack using rubber O-rings to avoid gas leakage and thermal contact. The POM-Ertacetal (H) 2 mm thickness material meets the above requirements since it offers higher mechanical strength, hardness, stiffness, creep resistance, wear resistance and lower thermal expansion rate, and thermal conductivity of 0.31 Wm⁻¹ K⁻¹ and density of 1410 kgm⁻³. The material for the stack must be chosen such that it should have low thermal conductivity and rigidity to sustain the oscillation of the 10-bar pressurized gas. The low thermal conductivity material avoids the conduction of heat in the reverse direction from AHX to CHX if there is a direct contact between the stack and heat exchangers. Hence, the commercial, locally available, and cheaper Mylar stack material is the best choice with the thermal conductivity, k_s = 0.16 Wm⁻¹ K⁻¹, density, ρ_s = 1349.6 kgm⁻³ and specific heat, C_ps = 1065.6 Jkg⁻¹ K⁻¹. The copper material is chosen for the thin sheets of AHX and CHX and the holder of the heat exchanger, which is rigid and has better thermal conductivity. The properties of the copper material are as follows: thermal conductivity k = 398.68 Wm⁻¹ K⁻¹; density, ρ = 9000 kgm⁻³; and specific heat, C_p = 420 Jkg⁻¹ K⁻¹. The stack can have the geometries of circular pores stack, circular stack, pin array stack, parallel plates stack, and spiral pores stack as shown in Fig. 3. In the literature, it is found that the pin array and parallel plates stack structures are efficient over other geometries [5, 8, 9]. The pin array stack structure is the most efficient stack compared to the parallel plates stack since it experiences the least frictional losses between the oscillating gas and the stack sheets, which avoids gas turbulence. The construction of the micropore stack structures of the circular pores stack, circular stack, pin array stack, and parallel plates stack is very difficult, less precise, and laborious to fabricate manually or with the known fabrication methods used elsewhere [5, 6]. The construction of these micropores stack structures can be easily made with the required accuracy and precision using the latest 3D printing technology. The 3D printing of the spiral stack is not expensive and can be quickly fabricated, cheap, and consistent with the design. Consequently, the 3D-printed stack is more reliable and provides repeatable outcomes.

Fig. 3

The various geometries of the thermoacoustic refrigerator stack

The Mylar thin sheet is attached to the 6-mm PVC rod and spirally wound over it using the nylon spacer lines which separate the stack sheets with a spacing distance equal to 2y (Fig. 3).

In the current research work, we choose to design a 500-W refrigerator for the temperature difference of 28 K with helium and air. The thermophysical properties of the oscillating gas depend on the operating parameters chosen in the design of the cooler (Table 1). The choice of operating parameters listed in Table 1 depends on the theoretical and practical limitations discussed elsewhere [5, 6, 10, 11]. The porosity ε of the stack and heat exchanger system is the portion of the cross-sectional area along the length of the stack-heat exchanger system open for the gas to oscillate given by:

$$\varepsilon =\frac{y}{y+l}=0.85$$

(7)

where y and l are the half-stack/HX sheet spacing and thickness of the spiral stack, respectively. The portion blocked for the gas oscillation in the stack-heat exchanger system is the blockage ratio, B is given by:

Table 1 Design parameters and thermophysical properties of gas

$$B=\frac{l}{y+l}=1-\varepsilon =0.15$$

(8)

From the literature [12, 13], it was stated to use the half-stack/HX spacing y of δ_k to 2δ_k in order not to alter the acoustic field. Using Eq. (7), with 85% porosity, the variation of stack sheet spacing and thickness versus thermal penetration depth with helium and air is given in Table 2. The derived parameters and the values used in the design process are given in Table 3.

Table 2 Stack-heat exchanger sheet spacing and thickness as a function of thermal penetration depth

Table 3 Derived parameters used in the design process

The design parameters are made dimensionless called normalized parameters help the designer in simplifying the design process by minimizing the number of design parameters involved in optimizing the cooler. The normalized design parameters of thermoacoustic refrigerator are given in Table 4. Using the data given in Table 1, the dimensionless parameters are determined as follows: D is 0.03 for both helium and air, γ is 1.67 for helium and 1.4 for air, σ is 0.68 for helium and 0.71 for air, and θ_n is 0.0972 for both helium and air.

Table 4 Normalized design parameters of a thermoacoustic refrigerator

The critical temperature gradient between AHX and CHX is the temperature difference at which the stack does not pump heat, given by:

$${\theta }_{c} = \frac{\left(y-1\right) \varepsilon. {T}_{\mathrm{mg}}.{l}_{3\mathrm{n}}}{\mathrm{tan}\left(X_\mathrm{n}\right)}$$

(9)

The normalized critical temperature gradient, Γ, is the ratio of the temperature gradient across the stack θ to the critical temperature gradient,θ_c, given by:

$$\Gamma = \frac{\theta }{{\theta }_{\mathrm{c}}}=\frac{{\theta }_{\mathrm{n}}.\mathrm{ tan}{\mathrm{X}}_{\mathrm{n}}}{\left(\gamma -1\right) \varepsilon. {l}_{3\mathrm{n}}}$$

(10)

In the literature, it is found that the Γ should be less than one for the stack to pump heat and behave as a refrigerator for both helium and air.

In this paper, we have derived the normalized cooling power and acoustic power equations (Q_ns and W_ns) by considering the stack heat capacity ratio, and the effect of thermal conductivity of both gas and stack. This decreases the performance of the stack by reverse conduction of heat from AHX to CHX as compared to the published results [1, 4]. Using the dimensionless and normalized parameters given in Table 4, the normalized cooling power and acoustic power equations from the Rott’s thermoacoustic theory [14, 15] are given by:

$${Q}_{\mathrm{ns}}=\frac{{-\delta }_{\mathrm{kn}}.{D}^{2}.\mathrm{sin}\left(2{X}_{\mathrm{n}}\right)}{8\gamma (1+{\varepsilon }_{\mathrm{s}})\left(1+\sigma \right)\Lambda }\times \left[\Gamma \frac{1+\sqrt{\sigma }+\sigma }{1+\sqrt{\sigma }}-\left(1+\sqrt{\sigma }-{\sqrt{\sigma }\delta }_{kn}\right)\right]-{\Lambda }^{1}$$

(11)

$${W}_{\mathrm{ns}}=\frac{{-\delta }_{kn}.{l}_{3\mathrm{n}}.{D}^{2}}{4\gamma }\left[\frac{\left(\gamma -1\right)\varepsilon .{cos}^{2}({X}_{\mathrm{n}})}{(1+{\varepsilon }_{\mathrm{s}})}\left(\frac{\Gamma }{\left(1+\sqrt{\sigma }\right)\Lambda }-1\right)- \frac{\sqrt{\sigma }.{sin}^{2}{(X}_{\mathrm{n}})}{\varepsilon. \Lambda } \right]$$

(12)

The terms ε_s, Λ, and Λ¹ in Eqs. (11) and (12) are the normalized stack heat capacity correction factor and the gas and stack heat conduction correction factors, respectively, given by:

$${\varepsilon }_{\mathrm{s}}=\sqrt{\frac{{\rho }_{g}.{c}_{pg}{.k}_{g}}{{\rho }_{s}{c}_{ps}{k}_{s}}}$$

(13)

$$\Lambda =1-{\delta }_{vn}+0.5{\delta }_{vn}^{2}$$

(14)

$${\Lambda }^{1}=\frac{{T}_{\mathrm{mg}}.c}{P.u.{l}_{3\mathrm{n}}}(\varepsilon {k}_{\mathrm{g}}+(1-{\varepsilon )k}_{\mathrm{s}})$$

(15)

Using the normalized equations from Eqs. (11, 12, 13, 14 and 15), the COP of the spiral stack is given by the ratio of the normalized cooling power output to the normalized acoustic power input given by:

$${\mathrm{COP}}_{\mathrm{s}}=\frac{{Q}_{\mathrm{ns}}}{{W}_{\mathrm{ns}}}$$

(16)

Using the data given in Tables 1, 2, 3, and 4 in Eqs. (11) and (12) for the NSLCC values of l_3n and X_n from 0.1 to 0.5 in the steps of 0.1, the Q_ns and W_ns for the stack are determined for the three spiral stack sheets spacing, 2y equal to 2δ_k, 3δ_k, and 4δ_k (Table 2) for helium and air working gases. Using Eq. (16), the COP_s of the spiral stack is determined, and using the normalized cooling power equation given in Table 4Q_n = Q/(PuA₁), the cross-sectional area, A₁, and diameter of the stack, d₁, are determined with helium and air gases for the required cooling power, Q of 500 W refrigerator. The best NSLCC for helium and air as a function of half-spiral stack sheets spacing (y = δ_k, 1.5δ_k, and 2δ_k) is chosen at the highest performance of the stack with the lowest value of stack diameter d₁. The highest performance of the stack with the lowest stack diameter improves the performance and power density of the cooler as found elsewhere [16,17,18,19]. At this criterion, the spiral stack is optimized by choosing the best NSLCC for helium and air for the half-stack sheets spacing of y = δ_k, 1.5δ_k, and 2δ_k and the results are given in Table 5. Referring to Table 5, the performance and diameter of the stack increase with an increase in half-stack sheets spacing y. For helium, the half-stack sheet spacing of y = 2δ_k is the best since it has the COP_s of 3.49 with the stack diameter d₁ = 26 cm (Table 5) which improves both performance and power density of the cooler. But for air, the half-stack sheet spacing of y = 2δ_k results with the COP_s of 5.71 at the stack diameter d₁ = 45.4 cm. This is because of the smaller wavelength of air (1.7 m) compared to helium (2.5 m) (Table 3), which improves the power density of the cooler.

Table 5 The specifications and performance parameters of the spiral stack-heat exchanger system as a function of working gas and frequency optimized at y = 2δ_k

Hence, for air working gas, the half-stack sheet spacing of y = 2δ_k is also best considering both performance and power density. The acoustic power input to the stack W_s for heat pumping is calculated using the normalized equation W_n = W_s/(PuA₁) given in Table 5.

With reference to Fig. 1, the diameter of the AHX and CHX is the same as that of the stack diameter d₁. The spiral geometry of the CHX and AHX is shown in Fig. 4 which is the same as that of the spiral stack (Fig. 3), but the length and material used for construction differ as discussed above. The thin copper sheet was first glued to the 6-mm diameter copper rod and spirally wound over the rod using copper spacer lines. Upon acoustic power input by the driver into the resonator, the length of the acoustic displacement amplitude of the oscillating gas at the cold end of the stack during forward and backward movement of gas 2x₁ is given by:

Fig. 4

The spiral geometry of the CHX and AHX

$${2x}_{1}=\frac{{2P}_{\mathrm{a}}\mathrm.{sin}(c.x)}{\varepsilon .\rho. u.\omega }$$

(17)

In Eq. (17), x is the position of the CHX at the cold end of the stack away from the driver. The length of the CHX (l₄) equal to the length of the oscillating gas (2x₁) is determined using the values given in Tables 1 and 3 in Eq. (17). As discussed in Section 1 of Eq. (6), the AHX rejects all the heat input to the resonator system and the heat lost by the driver with BVGS system (Fig. 1). It is found that the AHX rejects twice the heat supplied by the CHX [5, 6, 20]. Hence, the length of the AHX l₂ is equal to 2l₄. Based on the above discussion the theoretical lengths of CHX and AHX are found to be 6 mm and 12 mm, respectively, for helium and 3 mm and 6 mm, respectively, for air. By considering the practical difficulties encountered in accommodating the temperature sensors over these small lengths of CHX and AHX during construction [6, 21, 22], the actual lengths of CHX and AHX for both helium and air are taken to be 10 mm and 20 mm, respectively. Using the normalized equations given in Table 4 the stack center position X, the spacing between driver and AHX l₁ and stack length l₃ are determined (Table 5) using wave number c given in Table 3. The normalized acoustic power dissipation in the CHX and AHX (W_ncx and W_nax) is obtained using Eq. (12) by setting the temperature gradient term Γ = 0 and using the normalized lengths (l_2n and l_4n) and center positions (X_2n and X_4n) of the cold and ambient heat exchangers. The acoustic power dissipated in the CHX and AHX is calculated using the equations W_cx = W_ncx (PuA₁) and W_ax = W_nax (PuA₁), respectively, with helium and air (Table 5).

3 Resonator design and optimization

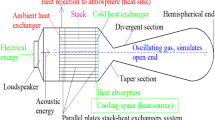
Resonator is a solid tube which connects the loudspeaker and stack-heat exchanger unit and stack-heat exchanger unit with a taper section and buffer volume. The stainless-steel thin sheet of 0.5 mm is the best choice for 10 bar pressure for avoiding threading and gas leakage problems encountered with Delrin material during experimentation is found elsewhere [6]. The properties of the stainless thin sheets are as follows: thermal conductivity k = 14.15 Wm⁻¹ K⁻¹, density ρ = 7922.5 kgm⁻³ and specific heat C_p = 448.28 Jkg⁻¹ K⁻¹. The resonator length must be small as possible to minimize the heat dissipation losses which improves performance and power density [23, 24]. Hence, the total length of resonator L_t should be less than or equal to the quarter-wavelength resonator given by:

$${L}_{\mathrm{t}}=\frac{\lambda }{n}$$

(18)

where λ is the wavelength of working gas and n = 1, 2, 3, 4 which decides the length of resonator. The acoustic power dissipation per unit surface area of the resonator left to AHX (l₁) and right to CHX (L₂ to r_h) as shown in Fig. 5 is w_r is given by:

Fig. 5

The geometry of the stack-heat exchanger’s system, driver, and TDH resonator system

$${w}_{r}=0.25{\rho }_{h}.{u}_{1}^{2}.{\delta }_{\mathrm{v}}.\omega +0.25\frac{{p}_{1}^{2}\left(\gamma -1\right){\delta }_{\mathrm{k}}. \omega }{{\rho }_{h}.{u}^{2}}$$

(19)

The amplitude of pressure and velocity inside the resonator tube at a distance x measured from the loudspeaker position at the mean center position of l₁, L₂, L₃, and r_h is given by:

$${p}_{1}={P}_{\mathrm{a}}\mathrm{cos}(c.x)$$

(20)

and

$${u}_{1}=\frac{{P}_{\mathrm{a}}\mathrm{sin}(c.x)}{\varepsilon \rho u}$$

(21)

The total acoustic power dissipation W_r in these four resonator components as heat loads on AHX (W_rax) and CHX (W_rcx) is determined by multiplying Eq. (19) with their individual internal surface area given by:

$${W}_{\mathrm{r}}={W}_{\mathrm{rax}}+{W}_{\mathrm{rcx}}$$

(22)

The power density of the resonator is the ratio of the required cooling capacity of the cooler Q to the total volume of the resonator V_t given by:

$${P}_{\mathrm{v}}=\frac{Q}{{V}_{\mathrm{t}}}$$

(23)

The whole length of the resonator outer surface and stack holder must be well insulated with the multi-layered super insulation to avoid heat leak losses with the surrounding environment at steady state condition. Hence, the total acoustic power dissipation in AHX, stack, CHX, and resonator, W_t is given by:

$${W}_{\mathrm{t}}={{W}_{\mathrm{ax}}+W}_{\mathrm{s}}+{W}_{\mathrm{cx}}+{W}_{\mathrm{r}}$$

(24)

At steady state conditions, the total heat rejection rate Q_r on AHX is given by:

$${Q}_{r}={W}_{\mathrm{t}}+ Q$$

(25)

The theoretical performance parameters of the cooler are given by:

$$\mathrm{COP}=\frac{Q}{{W}_{\mathrm{t}}}$$

(26)

$$\mathrm{COPC}=\frac{{T}_{\mathrm{cx}}}{\theta }$$

(27)

$$\mathrm{COPR}=\frac{\mathrm{COP}}{\mathrm{COPC}}$$

(28)

In this section, the attempts are made to optimize the length, internal surface area, and volume of the TDH resonator right to CHX (Fig. 5) with helium and air working gases discussed. The TDH resonator is chosen since it has a compact size, better performance, and power density compared to the TSDH designs discussed elsewhere [25,26,27]. Referring to Fig. 5, the length of the taper section L₂ is chosen to be 20 mm, and the radius of the hemisphere r_h is chosen to be equal to the radius of large diameter tube d₁. These lengths are chosen based on the compact size and shape providing space for accommodating instrumentation between taper and divergent sections of the resonator. The diameter ratio d_r = d₂/d₁ at the throat section is chosen based on the minimum resonator losses and better performance by avoiding gas turbulence in the taper and divergent sections of the resonator [4, 5, 23, 24]. The length of the large resonator tube L₁ for helium and air is the sum of the lengths of l₁ to l₄ (Table 5) given in Table 6. The parameters which decide the performance (COP and COPR), power density P_v, and total length of the resonator L_t are the diameter ratio d_r and the length of the divergent section L₃. In this section, the d_r and L₃ are optimized such that the diverging angle θ₂ in the buffer volume should be small as possible to avoid gas turbulence in the resonator [3, 5, 8]. The small diverging angle results in minimum acoustic power dissipation in the resonator right to taper (W_rcx) leading to improved performance and power density of the cooler. Based on the above criteria, the diameter ratio d_r at the throat section is 16% for both helium (400 Hz) and air (200 Hz). The diameter ratio d_r increases with an increase in the frequency of air (20% at 300 Hz and 25% at 400 Hz) (Table 6). The increase in the frequency of air decreases the wavelength λ (Table 3) which in turn decreases the length of the divergent section L₃ (Table 6). The decrease in length of the divergent section decreases the total length of the resonator L_t which increase the diverging angle θ₂. The decrease in total length of the resonator L_t for air improves power density P_v and decreases resonator dissipation W_r. This in turn increases the total acoustic dissipation W_t in the resonator because of the increase in acoustic power dissipation in the stack W_s (Table 5) due to the acoustic resistance of the low velocity of the oscillating air (Table 1). The increase in acoustic resistance in the stack increases the heat rejection rate Q_r at the AHX, leading to a decrease in COP and COPR of air (Table 6). The geometrical and theoretical results (VLT, VRT, V_r, V_t, COP, and COPR) as a function of working gas and resonance frequency are given in Table 6.

Table 6 Geometrical results and theoretical performance credentials of the optimized TDH resonators as a function of working gas and resonance frequency

4 DeltaEC results

DeltaEC (Design environment for low-amplitude thermo-acoustic Energy Conversion) [28] is a computer program which integrates one-dimensional wave equation, heat flow equation, and acoustic power flow equation of the oscillating fluid in the resonator for the complex geometry of the cooler. Using DeltaEC, the designer can test the performance of the theoretically optimized cooler for validation. The advantage of DeltaEC is that the designer can predict the performance of any required geometrical model of the thermoacoustic system (engine or cooler) by iteratively adjusting the guesses and geometrical dimensions of the components for convergence. DeltaEC uses thermoacoustic segments for the loudspeaker, ducts, HHX, CHX, stack, cones, compliances, and reverse polish notation (RPN) segments for calculating the unknown parameters. The targets are set for the required thermoacoustic components of the model. The use of thermoacoustic segments and RPN segments with guesses and targets for the thermoacoustic engine and cooler is found elsewhere [3, 18, 28]. DeltaEC is specially designed for predicting the performance of low-amplitude thermoacoustic engine or cooler where the drive ratio of the oscillating fluid D is less than or equal to 3% [25]. The accuracy of the DeltaEC results decreases with an increase in drive ratio because of an increase in the turbulence of the oscillating fluid in the resonator tube [18]. In the current research work, the oscillating fluid is helium and air operating with 10 bar pressure and a drive ratio of 3%. By default, DeltaEC assumes isothermal conditions for all the thermoacoustic segments except the stack-heat exchanger unit with no heat leak losses between the resonator outer surface and the surrounding environment.

With reference to Fig. 5, the commercial loudspeaker attached to the resonator duct left to AHX has a length of l₁. The commercially moving coil loudspeakers available in the market have poor electro-acoustic efficiency of about 3% [1, 2]. The loudspeakers dedicated for thermoacoustic coolers can have an efficiency of 50–90% possible [21, 29]. This can be made possible by modifying the commercial loudspeaker with the back volume filled with the same oscillating gas in the resonator tube at 10 bar pressure (Fig. 5). The back volume acts as a gas spring to match the driver frequency with the resonator frequency to improve the efficiency of driver [5, 30]. In the current research work, the common electromechanical parameters of the four commercial loudspeakers chosen based on the stack diameter d₁ (Table 5) are given in Table 7. The electrical resistance R_e, inductance L_e, force factor Bl, moving mass m, and mechanical resistance R_m are assumed to be the same for these four types of drivers. The gas spring stiffness s which depends on driver frequency f_d is determined (Table 8) by:

Table 7 The common electromechanical parameters of the drivers chosen in DeltaEC for helium and air

Table 8 DeltaEC simulation results of the optimized TDH resonator designs as a function of working gas and resonance frequency

$$s=4{\pi }^{2}{\left({f}_{d}\right)}^{2}m$$

(29)

Referring to Fig. 5, the back volume for the oscillating gas (helium and air) at the four cross-sectional areas of back volumes A_b of loudspeakers equal to their cross-sectional area of the vibrating diaphragm A_d is given by:

$${V}_{b}=\frac{\gamma P{A}_{b}^{2}}{s}$$

(30)

The volume of the BVGS system V_b and its length l_b with helium and air as a function of resonance frequency are calculated using Eq. (30) and given in Table 8. In DeltaEC the AHX and CHX temperatures are targeted to 301 K and 273 K, respectively. This results with the mean temperature of the AHX and CHX T_mx at 287 K. In Table 1, the mean temperature of the oscillating gas T_mg is 288 K (1 Kelvin higher than T_mx) as per the published literature [3, 5]. The DeltaEC predicts the average gas temperature of the oscillating gas T, the mean temperature of gas across heat exchanger T_mg, and the mean temperature of heat exchanger T_mx (Table 8). It is found that the T_mg is about 0.4 to 2.6 Kelvin higher than the T_mx with helium and air. The electroacoustic efficiency of the driver is higher for helium compared to air because of its higher velocity of gas oscillation (Table 1) and increases with the increase in resonance frequency f of air. The DeltaEC predicts the electrical power input to the speaker E, the cooling power of refrigerator at CHX Q, and the total heat rejected Q_R by the AHX with BVGS system (Table 8). The Q_R is defined as:

$${Q}_{R}=E+Q$$

(31)

The electrical power input to speaker E in DeltaEC calculation is given by:

$$E = {Q}_{1}+ {W}_{\mathrm{a }}$$

(32)

where Q_l is the heat lost by loudspeaker during energy conversion, and W_a is the acoustic power output of speaker is given by:

$${W}_{\mathrm{a} }= {Q}_{rax}+ {Q}_{ax }+ {Q}_{s}+ {Q}_{cx} + {Q}_{rcx}$$

(33)

Using RPN segments in DeltaEC, the COP and COPR of the cooler are determined using the Eqs. (26, 27 and 28).

The effect of cooling power on the operating and performance parameters of the cooler using helium and air with the BVGS system is given in Table 9. It is found that the cooling power Q is directly proportional to the frequency f, mean temperature of gas T, mean temperature of gas across heat exchanger T_mg, mean temperature of heat exchanger T_mx, electroacoustic efficiency of driver η_ea, and the total heat rejected by the AHX Q_R. But the temperature difference across the stack θ decreases with an increase in cooling power Q. At the constant AHX temperature of 301 K, the refrigeration effect in the cooling chamber (Fig. 1) decreases as the CHX temperature increase with the increase in cooling power (Table 9). The COP is inversely proportional to the temperature difference across the stack θ, but the COPR is decrease at 500 W for helium and 300 W for air. This is because of the increase in the CHX temperature due to the increase in acoustic turbulence of the oscillating helium and air in the resonator right to CHX (Fig. 5).

Table 9 Variation of performance parameters as a function of cooling power for the optimized TDH resonator operating with helium and air

The variation of the dynamic pressure amplitude P_a and solid material temperature T_s of the cooler along the length of the resonator with air oscillating at 300 Hz frequency is given in Figs. 6 and 7. DeltaEC confirms a 3% drive ratio near the driver and decreases gradually in the stack-heat exchanger unit and then decreases drastically in the resonator right to taper (Fig. 6). The internal solid surface temperature T_s remains constant in the resonator section left to AHX and a small drop in temperature is observed in the AHX and decreases drastically in the stack unit. Furthermore, the temperature of the resonator surface right to CHX remains constant (Fig. 7).

Fig. 6

Dynamic pressure amplitude of air along the length of the resonator

Fig. 7

Variation of the solid temperature along the length of the duct, stack-heat exchanger unit, and resonator system

5 Discussion

In this section, the design and optimization results of studying the effect of resonance frequency and gas spacing in stack-heat exchanger unit on thermoacoustic refrigerators using helium and air working gases are discussed. The cooler design is optimized for a temperature difference of 28 K and cooling power of 500 W operating at 10 bar pressure with a driving ratio of 3%. Referring to Tables 3 and 5, the wavelength λ is much larger than the stack length l₃, so that the acoustic field is not significantly disturbed by the presence of the stack in the resonator. The thermal and viscous penetration depths are smaller than the spacing in the stack 2y (Tables 1 and 2), which simplifies Rott’s functions [14, 15]. The temperature difference θ = 28 K is smaller than the mean temperature of gas T_mg = 288 K (Table 1), and hence, the thermophysical properties of oscillating gas remain constant within the stack length. Referring to Table 5, the normalized critical temperature gradient is Γ < 1 for all the cases, which confirms that the thermoacoustic system behaves as a refrigerator [5, 15].

Referring to Eqs. (11, 12, 13, 14, 15 and 16), the normalized cooling power equation (Q_n) and normalized acoustic power equation (W_n) are derived by considering the stack heat capacity ratio (ε_s) and the thermal conductivity of stack sheets (k_s) at 85% porosity (Eq. (15)) compared to the published literature [1, 5, 31, 32]. This improves the accuracy of the theoretical results (Eq. (16)) by deducting the reverse conduction of heat from AHX to CHX. It acts as an additional heat load on CHX, leading to an increase in acoustic power dissipation W_cx in the CHX (Table 5).

With reference to Tables 6, 7, and 8, the theoretical results (COP and COPR) are higher than the DeltaEC results since the theoretical design assumes that the driver provides the necessary acoustic power input W_a to the resonator without BVGS system (Figs. 1 and 5). It neglects the electromechanical properties of the driver and its losses. It also neglects the effect of damping because of the variations in the resonator size and shape (tapering, convergent-divergent section, and hemisphere) cause turbulence, acoustic resistance, and flow losses of the oscillating gas. This affects the resonance frequency f, the sound velocity u, and hence the total resonator length L_t as found in the published literature [33].

6 Conclusions

In this paper, the design of 500 W thermoacoustic coolers for a temperature difference of 28 K using helium and air operating with 10 bar pressure subjected to 3% drive ratio at the constant AHX temperature of 301 K is discussed. The effect of gas spacing (2y) as a function of thermal penetration depth (δ_k) and resonance frequency (f) is discussed in Section 2. The stack-heat exchanger sheets spacing 2y = 4δ_k is the best for both helium and air considering better stack sheets spacing and thickness (Table 2), which makes the construction easier, and improves the performance of the stack (Table 5). The increase in resonance frequency of air decreases the viscous and thermal penetration depths (Table 1) which in turn decreases the stack sheet spacing and thickness (Table 2). The stack diameter and performance of the stack decrease with an increase in frequency because of an increase in acoustic power input to the stack due to the acoustic turbulence of the oscillating gas (Table 5). For the resonator with air has a 38% reduction in length and a 2.2% reduction in total volume, leading to a 12.4% increase in COP and 3.7% increase in power density compared to helium (Table 6).

The DeltaEC predicts a 35.4% decrease in cooling power, a 21.9% decrease in COP, and a 48.6% decrease in electroacoustic efficiency of the driver for air, leading to a 60.6% increase in electrical power input to the driver and a 28.4% increase in total heat rejected by the AHX with BVGS system compared to helium (Table 8). This is because of the increase in acoustic resistance due to the low velocity of the oscillating air compared to helium (Table 1). Referring to Table 9, at 500-W cooling power, the DeltaEC predicts the temperature difference of 21 K for helium and 1 K for air. This leads to an increase in the CHX temperatures of 6.7 °C at the COP of 1.36 for helium, and 26.7 °C at the COP of 1.43 for air, which in turn increases the temperature of the cooling chamber (Fig. 1). This is because of the increase in acoustic nonlinearities of the oscillating gas due to acoustic impedance and gas turbulence at higher cooling power of the refrigerator as discussed in Section 5. The cooler shows an increase in power density of 61.2% with helium and 91.8% with air compared to the published literature found elsewhere [3]. Similarly, the DeltaEC predicts a 58.4% increase in cooling power and an 8.6% increase in COP for helium, and a 61.2% increase in cooling power and a 36.6% increase in COP for air compared to the published results [3]. The design and optimization methodology discussed in this paper will guide the designer in optimizing the design and development of the efficient and low-cost eco-friendly thermoacoustic refrigerators in the near future.

7 Nomenclature

AHX Ambient heat exchanger

A_b Cross-sectional area of back volume of loudspeaker, cm²

A_d Cross-sectional area of vibrating diaphragm of loudspeaker, cm²

A_t Total resonator surface area, cm²

A₁ Cross-sectional area of stack, m²

Bl Force factor, NA⁻¹ or T-m

BVGS Back volume gas spring

CHX Cold heat exchanger

COP Coefficient of performance of cooler

COPC Carnot’s coefficient of performance

COPR Coefficient of performance relative to Carnot’s

COP_S Coefficient of performance of stack

c Wave number of gas, cym⁻¹

C_p Specific heat of gas at constant pressure, Jkg⁻¹ K⁻¹

C_v Specific heat of gas at constant volume, Jkg⁻¹ K⁻¹

D Drive ratio

d₁ Stack diameter, mm

d₂ Throat diameter, mm

d_r Diameter ratio, d₂/d₁

E Electrical power input to loudspeaker, W

f Resonator frequency, Hz

f_d Driver frequency, Hz

Gas A Gas area in resonator system, m²

HX Heat exchanger

k_g Thermal conductivity of gas, Wm⁻¹ K⁻¹

k_s Thermal conductivity of stack, Wm⁻¹ K⁻¹

L₁ Length of large diameter tube, m

L₂ Length of taper, m

L₃ Length of divergent section, m

LDTAR Loudspeaker driven thermoacoustic refrigerator

L_e Electrical inductance of loudspeaker, H

L_t Total resonator length, mm

l Half-sheet thickness of spiral stack-heat exchangers, µm

2l Sheet thickness of spiral stack-heat exchangers, µm

l₁ Distance between loudspeaker and ambient heat exchanger, mm

l₂ Length of ambient heat exchanger, mm

l₃ Length of stack, mm

l₄ Length of cold heat exchanger, mm

l_b Length of back volume system, mm

m Moving mass of driver, g

NSLCC Normalized stack length and center combination

P Average gas pressure, bar

P_a Acoustic or dynamic pressure amplitude, bar

P_v Power density of cooler, Wm⁻³

Q Cooling power of refrigerator, W

Q_l Heat lost by loudspeaker, W

Q_r Heat rejected by ambient heat exchanger without BVGS system, W

Q_RTotal heat rejected by ambient heat exchanger with BVGS system, W

R_m Mechanical resistance of loudspeaker, Nsm⁻¹

R_e Electrical resistance of loudspeaker, Ω

r_h Hemispherical radius, mm

s Loudspeaker spring stiffness, Nm⁻¹

T Average gas temperature, K

TDH Taper and divergent section terminated with hemispherical end

TSDH Taper with small tube and divergent section terminated with hemispherical end

T_cx Temperature of cold heat exchanger, K

T_ax Temperature of ambient heat exchanger, K

T_mg Mean temperature of gas between heat exchangers, K

T_mx Mean temperature of ambient and cold heat exchangers, K

u Velocity of oscillating gas, ms⁻¹

VLT Volume left to taper, L

VT Volume of taper, L

VRT Volume right to taper, L

V_r Resonator volume ratio, VRT/VLT

V_t Total resonator volume, L

W_a Acoustic power input to resonator, W

W_r Acoustic power dissipation in resonator, W

W_s Acoustic power dissipation in stack, W

W_ax Acoustic power dissipation in ambient heat exchanger, W

W_rax Acoustic power dissipation in resonator left to ambient heat exchanger, W

W_cx Acoustic power dissipation in cold heat exchanger, W

W_rcx Acoustic power dissipation in resonator right to cold heat exchanger, W

W_t Total acoustic power dissipated in stack, heat exchangers, and resonator, W

w Acoustic power loss per unit surface area of resonator, Wm⁻²

X Stack center position, mm

y Half-gas spacing in stack-heat exchanger sheet, µm

2y Gas spacing in stack-heat exchanger sheet, µm

8 Greek Symbol

δ_k Thermal penetration depth, mm

δ_v Viscous penetration depth, mm

ε Porosity of stack-heat exchanger system

β Thermal expansion coefficient, K⁻¹

γ Ratio of specific heats

Γ Normalized critical temperature gradient

ρ Mass density of gas, kgm⁻³

η_eaElectro-acoustic efficiency of the loudspeaker, %

σ Gas Prandtl number

λ Wavelength of the oscillating gas, m

$\omega$ Angular frequency of acoustic wave, rads⁻¹

$\mu$ Dynamic viscosity of working gas, kgm⁻¹s⁻¹

θ Temperature difference between hot and cold heat exchangers, K

θ_c Critical temperature difference between hot and cold heat exchangers, K

θ_n Normalized temperature gradient between hot and cold heat exchangers

θ₂ Diverging angle in the buffer volume, degree

9 Subscripts

c Critical

n Normalized

s Stack

t Total