Riemannian geometric approach to optimal binocular rotation, pyramid based interpolation and bio-mimetic pan-tilt movement

Abstract

Over the past several years, we have been studying the problem of optimally rotating a rigid sphere about its center, where the rotation is actuated by a triplet of external torques acting on the body. The control objective is to repeatedly direct a suitable radial vector, called the gaze vector, towards a stationary point target in IR³. The orientation of the sphere is constrained to lie in a suitable submanifold of SO(3). Historically, the constrained rotational movements were studied by physiologists in the nineteenth century, interested in eye and head movements. In this paper we revisit the gaze control problem, where two visual sensors, are tasked to simultaneously stare at a point target in the visual space. The target position changes discretely and the problem we consider is how to reorient the gaze directions of the sensors, along the optimal pathway of the human eyes, to the new location of the target. This is done by first solving an optimal control problem on the human binocular system. Next, we use these optimal control and show that a pan-tilt system can be controlled to follow the gaze trajectory of the human eye requiring a nonlinear static feedback of the pan and tilt angles and their derivatives. Our problem formulation uses a new Riemannian geometric description of the orientation space. The paper also introduces a new, pyramid based interpolation method, to implement the optimal controller.

1 Introduction

In this paper we consider the Binocular Sensory Control problem, where each sensor is tasked to mimic the movement dynamics of the human eye. Typically we assume that the centers of the sensors are fixed in space and the sensor gaze directions rotate to inspect point targets that are located in 3D. The gaze directions are always constrained to pass through a point and the goal of the sensing mechanism is to initially start with a target fixed in its view and to switch to an alternate target in the visual field in a unit interval of time, assumed to be [0,1]. The paper analyses rotation for a binary pair of sensors and the goal is to compute optimal control over the chosen fixed time interval, extending two of our prior papers [1, 2]. In our earlier research, binocular eye rotation has also been studied as a cascade of version and vergence eye movement applied to the two eyes separately (see [3] and [4]). This paper also extends [5], a recently published paper by the authors on Riemannian geometric formulation for the optimal control of binocular eye motion. The optimal control, we show, can be implemented by a pyramid based linear interpolation introduced in this paper.

Anatomy of the eye is such that it is only able to rotate with three degrees of freedom [6, 7], but is unable to translate [8]. The eye movement system is a relatively simple mechanical control system compared to other complex human movement systems [9]. Modeling the dynamics of monocular eye rotation has been an important goal in Neuroscience (see [10] for a short review article on how brain controls the eye movement) and Biomechanics [11]. Since the early half of the 19^th century [12, 13], scientists have tried to create dynamic models in order to understand various eye movement trajectories (see [14] for some historical details). Starting from some of the initial papers of [15], the principles from geometry, for example as in [16–18], are central to many of the key questions in nonlinear systems theory (see [19]), applied to rotational dynamics. Specific to the eye movement control system, we would also like to refer to [20–22] and many references therein. For a single eye, optimization problems associated with gaze control [23], have been extended to optimal control problems studied by [24–26].

In the last few decades, there has been considerable research on exactly how the eye rotations are controlled. It was well known since the 19^th century by physiologists such as Helmholtz, Listing and Donders that when head is kept fixed, the axes of rotation is confined to a plane called the Listing’s plane (see [27–29]). Questions arise as to how the Listing’s constraint is satisfied by the ‘motion controller’. Current literature seems to support the view that the constraint is met by active neural control in the brain (see [23, 29–34]) as opposed to an alternative view that the constraints are forced by mechanical properties of the eye plant using muscle pulleys [35, 36]. In this paper and many of our earlier papers [5, 25] geometric methods were used to study optimal control problems within the constrained space (called the configuration space) using a Riemannian formulation. We demonstrate that the synthesized control, to be viewed as actively generated by the neural circuit in the brain, continues to enforce for example the Listing’s constraint (and an additional co-planarity constraint to be introduced later in this paper), even when implemented on the ambient space SO(3) ¹.

Geometric methods have a long history in the study of eye movement rotation (see [27, 28, 37, 38]). Riemannian geometry (see [39, 40]) has been introduced for monocular optimal control problems on the configuration spaces LIST in [6] and DOND in [24]. We have recently (see [5]) extended the Riemannian geometric formulation to binocular control problems, wherein a configuration space LBIN for the binocular eye pair is described as a subset of SO(3)×SO(3). In this paper, we first recall from [5] the construction of the optimal eye rotation controller for the binocular eye pair. We then propose that these controllers can be implemented using a straightforward pyramid [41] based interpolation scheme, where the plan is to synthesize the control function as a convex combination of four corner points of a pyramid. Controlling the binocular system to each of the four corner points can be learnt and kept in the memory to be used subsequently as a lookup table. Finally we replace the eye-pair with a pair of mechanical visual sensors, capable of rotating, only along pan and tilt. We describe a simple control strategy, to track the optimal (human) gaze pathway, using the mechanical pan/tilt system (see [26] and Fig. 3 for a figure of generalized gimbal. For a pan/tilt system the axial rotation angle ϕ₃ is constrained to zero)². Hence a mechanical pan/tilt system is able to follow human eye movement only up to its gaze direction but cannot follow the changing roll of the eye.

Next we briefly talk about the importance of a mechanical system following the human eye. In one line of research [42], a mechanical system, such as a humanoid robot, tries to generate human like behaviors in robots by recording and mimicking human motions in the execution of a particular task. For example, a human instructor can explain the process of assembling a device with several parts distributed over a table [43], and his associated gaze behaviors are learnt and encoded in dynamic gaze controllers implemented in a robot [44]. Human gaze behavior can also be replicated in a robot by directly programming the control laws into the robot. For example in [45] a neurophysiological model of human saccadic motion was implemented in a robot head where each eye had pan/tilt mobility. Although the emphasis of this paper is not on humanoid robots, we show how a pan/tilt system can imitate the human ocular movements upto gaze directions only, without an explicit reprogramming of its controllers, requiring only a nonlinear static feedback.

Finally, we outline the sections of this paper. In Section 2, we introduce notations that describe the axis-angle parametrization [6, 24, 25] of unit quaternion. Section 3 describes a recently introduced Riemannian metric on the configuration space LBIN for the binocular pair of human eyes [5]. Using the Riemannian metric from Section 3, we write down the controlled Euler-Lagrange equation in Section 4. The control variables are the external torque vector functions applied to each of the two eyes and the problem we propose is to optimally control (using a suitably chosen cost function), the rotation of the eye-pair, in time interval [0,1], so that the fixated target point in the visual space switches between two points. To solve for the optimal control, an associated Two Point Boundary Value Problem needs to be solved and in our prior papers [5, 26], such a boundary value problem has been solved using a program called COMSOL [46]. In [5], many examples are showcased where the eye centers are kept horizontal, i.e. the head is kept straight relative to the torso. In Section 5, an example is introduced where the head is tilted sideways i.e., the separation vector joining the two eyes contained in the Listing’s Plane³. In Section 6, we propose a pyramid based interpolation to approximate the control torque function required to transfer the binocular gaze point from an a priori chosen initial point to a final point. This final point is assumed to be contained within a cubic interval in the visual space. The main point of the interpolation algorithm is that the optimal control does not have to be computed for every new final point. It is enough to have precomputed the optimal control for each of the eight corner points of the cube, eventually suitably recombining four of the corner points on a pyramid by convex combination. This procedure needs to be scaled up by discretizing the visual space into tiles of cubes and the associated optimal control functions, with final gaze points at the corner points of every cube, stored in the form of a look-up table. In Section 7, we introduce Tait-Bryan parametrization with the explicit goal of talking about pan/tilt/roll type of rotation [26] on SO(3). We compute the controlled Euler-Lagrange’s equation with external torque as the associated control vector. We also repeat the same calculation when the roll component is forced to zero and we have a mechanical pan/tilt system with only two degrees of freedom for rotation.

In Section 8, we mainly show how an optimal control computed for the binocular system can be used as an input to a pair of pan-tilt system, where the goal is to match the gaze trajectories of the two systems point by point. Typically this step of biomimetic matching requires a dynamic feedback. Under the specific hypothesis that the axes of the binocular system of eyes satisfy Listing’s condition, the feedback structure can be reduced to a nonlinear static feedback. We also show via simulation that re-parameterizing SO(3) from axis-angle to Tait-Bryan parametrization does not change the optimal gaze trajectories of the binocular system on the human eyes. In Section 9 we briefly discuss three main topics introduced in this paper. In the first topic we point out why it is impractical to solve a two point boundary value problem in real time, every time a control function is required to be computed. It is desirable, specifically for the purpose of inspecting targets in the visual space, to have the control functions pre-computed over a fixed initial and a discrete set of final target points. The required control is synthesized using interpolation based approximation. The second topic we point out is that for a certain class of binocular optimal control, the control function has a linear structure. This simplifies parameterizing and tabulating the control. The third topic we introduce is biomimetic control of a pair of mechanical visual sensors, and how pan/tilt rotation can be used to track the gaze direction of human eyes, using a feedback control. The feedback structure is particularly simple (nonlinear static) when eye axes are constrained to a Listing’s plane. Finally, Section 10 concludes the paper emphasizing the importance of pyramid based interpolation and bio-mimetic pan/tilt rotation.

2 Notations and terminology

We start this section by introducing the axis-angle parametrization (see Fig. 1) of quaternions, where the notations are borrowed from [6] and [24, 25]. This parameterization is particularly used in our study of human eye rotation control. In later part of this paper, we have also introduced Tait-Bryan parametrization [26] in order to talk about Bio-Mimetic pan/tilt movement.

Fig. 1

Axis-angle parametrization under Listing’s constraint q₃=0. The Listing’s plane is described by z=0. Angle θ is the angle subtended between the positive axis of rotation on the Listing’s plane and the positive x-axis. Angle ϕ is the anticlockwise rotation about the positive axis of rotation

Let us begin with the space of quaternions denoted by Q, see [47] and write each q∈Q as $q_{0}\vec {\mathbf {1}} + q_{1}\vec {\mathbf {i}}+q_{2}\vec {\mathbf {j}}+q_{3}\vec {\mathbf {k}}$. Space of unit quaternions will be identified with the unit sphere S³, and can be written as

$$ \begin{aligned} q= {\cos\left(\frac{\phi}{2}\right)\vec{\mathbf{1}} + \sin\left(\frac{\phi}{2}\right)n_{1}\vec{\mathbf{i}} + \sin\left(\frac{\phi}{2}\right)n_{2}\vec{\mathbf{j}} + \sin\left(\frac{\phi}{2}\right)n_{3}\vec{\mathbf{k}}}, \end{aligned} $$

(1)

where ϕ∈[0,2π] is an angle variable and n=(n₁,n₂,n₃) is a unit axis vector in $\mathbb {R}^{3}$. We denote by rot, the standard map from S³ into SO(3) which maps the quaternion q to an orthogonal matrix that rotates a vector in $\mathbb {R}^{3}$ around the axis of rotation n by a counterclockwise angle ϕ (see Fig. 1). It is easy to verify (see (3) in [25]) that

$$ \begin{aligned} &\qquad\qquad\qquad\qquad\qquad \mathbf{rot}(q)=\\ &{\left[\begin{array}{ccc} q_{0}^{2}+q_{1}^{2}-q_{2}^{2} - q_{3}^{2} & 2(q_{1}q_{2}-q_{0}q_{3}) & 2(q_{1}q_{3}+q_{0}q_{2})\\ 2(q_{1}q_{2}+q_{0}q_{3}) & q_{0}^{2}+q_{2}^{2}-q_{1}^{2} - q_{3}^{2} & 2(q_{2}q_{3}-q_{0}q_{1})\\ 2(q_{1}q_{3}-q_{0}q_{2}) & 2(q_{2}q_{3}+q_{0}q_{1}) & q_{0}^{2}+q_{3}^{2}-q_{1}^{2} - q_{2}^{2} \end{array}\right].} \end{aligned} $$

(2)

The orthogonal matrix (2) can be associated with the orientation of a rotating rigid body as follows:

Each column of (2) is a mutually orthogonal unit vector. We can associate the three column vectors to three body coordinates that describe the orientation.

The rotating rigid body, viz. the human eye, has a specific ‘gaze direction’, a vector whose direction is what we propose to control. We use the convention that the gaze direction is given by the third column of the rotation matrix (2). We therefore have the following projection map, projecting the orientation matrix (2) to a gaze direction vector

$$\mathbf{proj}: \mathbf{SO(3)} \rightarrow \mathbf{S^{2}},$$

where

$$\mathbf{rot(q)}\longmapsto \left[ \begin{array}{c} 2(q_{1}q_{3}+q_{0}q_{2})\\ 2(q_{2}q_{3}-q_{0}q_{1})\\ q_{0}^{2}+q_{3}^{2}-q_{1}^{2}-q_{2}^{2} \end{array} \right]. $$

(3)

Typically our interest is to control the gaze vector (3) so that it is pointing towards a suitable point target (see Fig. 2 where a pair of eyes are pointing towards a target). As has been commented in Section 1, additional constraints on the quaternion q need to be imposed (such as the Listing’s constraint given by q₃=0 or perhaps a more general Donders’ constraint [26]), so that the constrained orientation matrix with a specific gaze direction is unique (see [48]). For pan/tilt rotation (see [26]), considered later in the paper, the Listing’s constraint is replaced by Fick Gimbal constraint q₀q₃=−q₁q₂.

Fig. 2

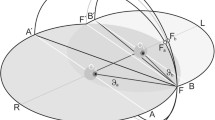
Figure detailing locations of the two eyes of the binocular system, gazing at a point target in space. The centers of the left and the right eyes are located respectively at (0,0,0) and (0,1,0). Note that the center of the inertial coordinate is assumed to coincide with the left eye center, upward-pointing axis is the positive x-axis while the forward-pointing axis is the positive z-axis. The y-axis joins the centers of the two eyes and the direction from left to right is chosen positive. Curly arrows (in blue) indicate the positive (clockwise, viewed from the axis center) rotation about each axis. The blue dot is the target, and the two red arrows are the eye-gaze directions

The pan/tilt system is a part of a generalized gimbal system (see Fig. 3) already introduced in [26], where the parametrization of the associated quaternion uses the Tait-Bryan angles ϕ₁,ϕ₂ and ϕ₃⁴. In this paper, two pan/tilt systems (see Fig. 11) are controlled simultaneously, so that it bio-mimetically follows the gaze directions (but not the roll) of the binocular human eyes, optimally saccading between two target points in the visual space.

Fig. 3

The generalized gimbal and the Tait-Bryan angles ϕ₁,ϕ₂ and ϕ₃. Fick Gimbal models a mechanical pan-tilt system and is a special case of the generalized gimbal when the axial rotation angle ϕ₃ (rotation about axis 3) is constrained to 0. It can only mimic eye movements up to gaze direction using a pan-tilt feedback

3 Riemannian metric on the space L B I N

This section is essentially replicated from [5]. We begin by considering parametrization of a point in S³, as introduced in (1) and further describe the unit vector n, the axis of rotation, as

$$ n=(\cos\theta \cos\alpha \quad\sin\theta \cos\alpha \quad\sin\alpha), $$

(4)

where θ∈[0,π] and $\alpha \in \left [-\frac {\pi }{2},\frac {\pi }{2}\right ].$ The parameterization (1), (4) together describes, what is known in [25], as the axis-angle parameterization of S³ and SO(3) using the mapping ‘ rot’ (essentially the three axis-angle parameters are θ,ϕ and α). In order for the orientation of a single eye to satisfy Listing’s constraint, q₃=0, we impose α=0, forcing the axis of rotation to always lie on the Listing’s plane z=0. This reduces the quaternion in (1) to the form (see [6])

$$ q=\cos\frac{\phi}{2} \vec{\mathbf{1}}+\sin\frac{\phi}{2} \left[\cos\theta \,\vec{\mathbf{i}}+\sin\theta \, \vec{\mathbf{j}} \right] + 0 \,\vec{\mathbf{k}}. $$

(5)

We now introduce two such quaternions, one for the left eye q^L and other for the right eye q^R, described as

$$ q^{L}=\cos\frac{\phi^{L}}{2} \vec{\mathbf{1}}+\sin\frac{\phi^{L}}{2} \left[\cos\theta^{L} \vec{\mathbf{i}} +\sin\theta^{L} \vec{\mathbf{j}} \right] + 0 \,\vec{\mathbf{k}} $$

(6)

and

$$ q^{R}=\cos\frac{\phi^{R}}{2} \vec{\mathbf{1}}+\sin\frac{\phi^{R}}{2} \left[\cos\theta^{R} \vec{\mathbf{i}}+\sin\theta^{R} \vec{\mathbf{j}} \right] + 0 \,\vec{\mathbf{k}}. $$

(7)

The pair (q^L,q^R) is thus an element of S³×S³. Note that the gaze directions corresponding to the left and the right eye are given by

$$ g_{L}=\left(\sin \theta^{L} \sin \phi^{L}\quad - \cos \theta^{L} \sin \phi^{L} \quad\cos\phi^{L}\right), $$

(8)

$$ g_{R}=\left(\sin \theta^{R} \sin \phi^{R}\quad - \cos \theta^{R} \sin \phi^{R} \quad\cos\phi^{R}\right). $$

(9)

Let us now assume that the left and the right eye has centers separated by the vector e=(x,y,z)=(0,1,0) as shown in Fig. 2. The figure shows that the centers of the left and the right eyes are located respectively at (0,0,0) and (0,1,0). The configuration space of the binocular system is now described by imposing that the vectors g_L,g_R and e are coplanar. Such a co-planarity condition will impose that the gaze directions of the left and the right eyes always meet at a point. Thus we have

$$ \cos \phi^{R} \sin \theta^{L} \sin \phi^{L}= \cos \phi^{L} \sin \theta^{R} \sin \phi^{R}. $$

(10)

We denote by LBIN (L stands for Listing, BIN stands for Binocular), the subset of SO(3)×SO(3) where the orientation matrices separately obey Listing’s Law and together the corresponding gaze directions satisfy the co-planarity condition (10). Equivalently, LBIN is a subset of LIST×LIST (see [6]) where the gaze directions of each component satisfy (10). Let ρ be the mapping

$${} \rho:[0,\pi] \times [0,2\pi] \times [0,\pi] \rightarrow \mathbf{S^{3}} \times \mathbf{S^{3}} $$

(11)

described as

$${} \rho(\theta^{L},\phi^{L},\theta^{R}) = \\\left[ \left[\begin{array}{c} \cos{\frac{\phi^{L}}{2}}\\\cos{\theta^{L}}\sin{\frac{\phi^{L}}{2}}\\\sin{\theta^{L}}\sin{\frac{\phi^{L}}{2}}\\0 \end{array}\right], \left[\begin{array}{c} \cos{\frac{\phi^{R}}{2}}\\\cos{\theta^{R}}\sin{\frac{\phi^{R}}{2}}\\\sin{\theta^{R}}\sin{\frac{\phi^{R}}{2}}\\0 \end{array}\right] \right], $$

(12)

where from (10) we have

$${} \phi^{R}=\tan^{-1} \left\{ \frac{\sin \theta^{L} \sin \phi^{L}}{\sin \theta^{R} \cos \phi^{L}} \right\}. $$

(13)

Note that the co-planarity condition (10) or (13) can change when the separation vector e changes. This will be the case when the two sensors are fixed but their centers are located at a different set of points.

A Riemannian metric on LBIN is easily induced from SO(3)×SO(3). We define elements g_ij of the symmetric Riemannian matrix ⁵G_LB as ⁶

$$ \begin{array}{c} g_{11}=\left\langle\frac{\partial}{\partial\theta^{L}},\frac{\partial}{\partial\theta^{L}}\right\rangle,\;\; g_{12}=\left\langle\frac{\partial}{\partial\theta^{L}},\frac{\partial}{\partial\phi^{L}}\right\rangle,\\ g_{13}=\left\langle\frac{\partial}{\partial\theta^{L}},\frac{\partial}{\partial\theta^{R}}\right\rangle,\;\; g_{22}=\left\langle\frac{\partial}{\partial\phi^{L}},\frac{\partial}{\partial\phi^{L}}\right\rangle,\\ g_{23}=\left\langle\frac{\partial}{\partial\phi^{L}},\frac{\partial}{\partial\theta^{R}}\right\rangle,\;\; g_{33}=\left\langle\frac{\partial}{\partial\theta^{R}},\frac{\partial}{\partial\theta^{R}}\right\rangle \end{array} $$

(14)

and compute⁷ the Riemannian metric g given by

$${} g = \left(\dot{\theta^{L}}\,\, \dot{\phi^{L}}\,\, \dot{\theta^{R}}\right) G_{LB} \left(\begin{array}{c} \dot{\theta^{L}}\\ \dot{\phi^{L}}\\ \dot{\theta^{R}} \end{array}\right), $$

(15)

where G is the corresponding Riemannian matrix of inner products (see [6] for a single eye and [5] for a binocular system of two eyes).

4 Euler-Lagrangian formulation of binocular eye movement

Since a Riemannian metric defines kinetic energy on the manifold, we use g in (15) to define the Lagrangian $\mathcal {L}=\frac {1}{2}\; g$ of the binocular system⁸. The controlled Euler-Lagrange equations are given by

$$\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{\mu}} - \frac{\partial\mathcal{L}}{\partial \mu} = \tau_{\mu}, $$

(16)

where μ∈{θ^L,ϕ^L,θ^R}. It follows from [25] that (16) can be written as,

$$G_{LB}\ddot{\Theta} + \dot{G}_{LB}\dot{\Theta} - \nabla_{\Theta}^{T}\mathcal{L} = \tau, $$

(17)

where G_LB is the Riemannian matrix, ∇_Θ is the gradient $\left (\frac {\partial }{\partial {\theta ^{L}}},\frac {\partial }{\partial {\phi ^{L}}}, \frac {\partial }{\partial {\theta ^{R}}}\right), \Theta = \left (\theta ^{L},\phi ^{L},\theta ^{R}\right)^{T}$, and τ is the 3-vector of generalized torques τ_μ. Further as [25] describes, we define the external torque vector T (a 6-vector), in the inertial coordinate to be,

$$ \tau = M_{LB}^{T}T, $$

(18)

and⁹

$$ M_{LB}^{T}M_{LB} = 4\;G_{LB}. $$

(19)

Remark 1

The columns of the matrix M are called the Euler basis vectors, see [49], where T has been described as the resultant moment relative to the center of mass on the body.

Now we setup our dynamical system for the binocular eye rotation by defining

$$ Z(t)=\left[z_{1},z_{2},z_{3},z_{4},z_{5},z_{6}\right]^{T} = \left[\theta^{L},\dot{\theta^{L}},\phi^{L},\dot{\phi^{L}},\theta^{R},\dot{\theta^{R}}\right]^{T}. $$

(20)

We require that the states go from some a priori agreed Z(0) to Z(1) while minimizing the control energy in a fixed interval of time

$$ \int_{0}^{1} \frac{1}{2}\| T\|^{2}\,dt, $$

(21)

where T is the vector of external torques given by Eq. (22).¹⁰

$$ T=\left[T_{x}^{L}, T_{y}^{L}, T_{z}^{L}, T_{x}^{R}, T_{y}^{R}, T_{z}^{R}\right]^{T}. $$

(22)

We denote the costate variables by,

$$ \Lambda =\left[\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6}\right]^{T} $$

(23)

and define the Hamiltonian as,

$$ \mathcal{H}(Z,\Lambda)= \Lambda^{T}\cdot\dot{Z} -\displaystyle{\frac{1}{2} T^{T} T}. $$

(24)

Using the Hamilton’s equations [17], the system

$$ \begin{aligned} \frac{d}{dt} \left[\begin{array}{c} Z\\ \Lambda \end{array}\right] = F\left[z_{1},\dots,z_{6},\lambda_{1},\dots,\lambda_{6}, T_{x}^{L}, T_{y}^{L}, T_{z}^{L}, T_{x}^{R}, T_{y}^{R}, T_{z}^{R}\right] \end{aligned} $$

(25)

is now obtained. Using Eqs. (17), (18), and (20), one can recast (24) as

$$ \begin{aligned} \mathcal{H} = &\Lambda_{1}^{T} [\dot{z}_{1} - z_{2}\,\, \dot{z}_{3} - z_{4}\,\, \dot{z}_{5} - z_{6}] \\ &+ \Lambda_{2}^{T} \left[ G_{LB}^{-1}(M_{LB}^{T} T - \dot{G}_{LB}\dot{Z}_{1} + \nabla_{Z_{1}}^{T}\mathcal{L}) - \dot{Z}_{2} \right] - \frac{1}{2} T^{T} T, \end{aligned} $$

(26)

where Λ₁=[λ₁,λ₃,λ₅]^T,Λ₂=[λ₂,λ₄,λ₆]^T,Z₁=[z₁,z₃,z₅]^T, and Z₂=[z₂,z₄,z₆]^T. Finally using the Pontryagin’s Maximum Principle, the expressions for optimal external torques (see [6]) are obtained:

$$ \frac{\partial H}{\partial T} = \Lambda_{2}^{T} G_{LB}^{-1}M^{T}_{LB} - T^{T} = 0, $$

(27)

which we write symbolically as

$$ \left[T_{x}^{L}, T_{y}^{L}, T_{z}^{L}, T_{x}^{R}, T_{y}^{R}, T_{z}^{R}\right] = \left[\lambda_{2} \; \lambda_{4} \; \lambda_{6}\right]\;G_{LB}^{-1} M_{LB}^{T}. $$

(28)

The control torques can now be eliminated from the state space system (25) and we obtain the following dynamical system

$$ \frac{d}{dt} \left[\begin{array}{c} Z\\ \Lambda \end{array}\right] = \tilde{F}[Z, \Lambda]. $$

(29)

Since we know only the initial and the final value of Z, we have a two-point boundary value problem (BVP). The resulting problem is solved using COMSOLMultiphysics program (see [46])¹¹. The computed Z and Λ variables are plugged in (28) to obtain the optimal vector T, which is denoted by T_BVP.

The optimal vector has been computed for a large number of examples in [5] where the gaze of the binocular eye pair moves between target points going from ‘left to right’, ‘bottom to top’ and ‘near to far’ in the visual field. The corresponding visual trajectories and the optimal torque trajectories have been plotted. The eye centers are assumed fixed and located on the (horizontal) y−axis. This would be the case when the vector separating the two eyes is parallel to the ground. In the next section we discuss one simulation when the head is fixed but tilted.

5 Optimal eye movement when head is fixed and tilted

The main message of this section is the following. Although in Section 4 we had said that the optimal external torque controls are computed by solving a BVP using COMSOL, it is often possible to approximate the external torque function using a linear function. This had been the case in various examples discussed in [5]¹², where separation vector between the two eyes are horizontal. In this section we consider a case when the head is tilted (see Fig. 4) and the eye separation vector is not horizontal. We demonstrate via simulation that ‘a linear approximation is still good’.

Fig. 4

The centers of the two eyes are not horizontal, because the head is tilted. This changes the co-planarity condition (10) and subsequently the Riemannian matrix G_LB in (14)

Example 1: Eye separation vector is not horizontal, i.e., the head is tilted

Let us assume a binocular system as in Fig. 4 where the left eye is centered at (0,0,0) and the right eye is centered at (1,1,0). The separation vector e is given by (1,1,0) and the co-planarity of g_L,g_R, and e is appropriately defined. The angle variable ϕ^R needs to be redefined in comparison to (13) and this changes the Riemannian matrix G_LB in (15). We now consider the two point boundary value problem sketched in Section 4 assuming the initial and final values of the angles (θ^L,ϕ^L,θ^R) are respectively $\left (\frac {\pi }{4},\frac {\pi }{8}, \frac {\pi }{6} \right)$ and $\left (\frac {\pi }{3},\frac {\pi }{5}, \frac {\pi }{4} \right)$. The time derivatives of the angle variables are assumed to be 0 at the initial and final times. As indicated in Section 4, we use COMSOL to calculate the optimal trajectories for $\left (\theta ^{L}(t), \phi ^{L}(t), \theta ^{R}(t)\right), \left (\dot {\theta }^{L}(t), \dot {\phi }^{L}(t), \dot {\theta }^{R}(t)\right)$ (see Fig. 5) and using the co-planarity condition (not explicitly described in this section), the variable $\phi ^{R}(t), \dot {\phi }^{R}(t)$. The optimal trajectories of states and costates are plugged in (28) to solve for the optimal external torque vector $T_{BVP}(t)=\left (T_{x}^{L}(t), T_{y}^{L}(t), T_{z}^{L}(t), T_{x}^{R}(t), T_{y}^{R}(t), T_{z}^{R}(t)\right)$ (see Fig. 6).

Fig. 5

The right eye is located on the Listing’s plane of the left eye centered at (0,0,0). The right eye is centered at (1,1,0). The separation vector between the two eyes are on the coronal or the frontal plane but not parallel to the y-axis (horizontal axis). The angles θ^L,ϕ^L,θ^R shifts from $\left (\frac {\pi }{4},\frac {\pi }{8}, \frac {\pi }{6}\right)$ to $(\frac {\pi }{3},\frac {\pi }{5}, \frac {\pi }{4})$. The figure shows the generalized angles and the generalized velocities when the input external torques are computed by solving the Boundary Value Problem and compared with the corresponding trajectories when the input external torques are approximated by a linear function

Fig. 6

The external torques are plotted for the example discussed in Fig. 5. The optimal external torques computed from the Boundary Value Problem and the linear approximation of the external torque functions are practically indistinguishable

As was noted in [5], the graph of T_BVP(t) appears linear from the figure and we approximate this function by T_LIN(t)=T_BVP(0)[1−2t] where t∈[0,1]. The approximate linear function is plotted in Fig. 6 (using the symbol +) and T_LIN(t) and T_BVP(t) appear indistinguishable.

Let us now consider an initial value problem by combining Eqs. (16) and (18) to obtain

$$ \frac{d}{dt}\frac{\partial\mathcal{L}}{\partial\dot{\mu}} - \frac{\partial\mathcal{L}}{\partial \mu} = M_{LB}^{T}T_{LIN}(t). $$

(30)

Initial conditions for (30) are chosen by setting $\theta ^{L}(0)=\frac {\pi }{4}, \phi ^{L}(0)=\frac {\pi }{8}, \theta ^{R}(0)=\frac {\pi }{6}, \dot {\theta }^{L}(0)=0, \dot {\phi }^{L}(0)=0, \dot {\theta }^{R}(0)= 0$. The initial value problem is now solved and the the results are plotted in Fig. 5 using the symbol +. Once again, these trajectories mimic very close to the optimal trajectories.

6 Approximating the optimal external torque function using pyramid based interpolation

In the last Section 5 we observed via simulation that for the binocular human eye movement, the optimal external torque functions have a linear graph. We have demonstrated this ‘linearity’ when the eye separation vector lies on the frontal plane, which in our construction also happens to be the Listing’s plane of the two eyes. In this section we go back to Fig. 2 and consider the binocular system where the eye centers are at (0,0,0) and (0,1,0). Assume that initially the eyes are focused at the point C (see Fig. 7). The task is to move the gaze optimally to another final point D. However the exact location of point D is uncertain and we shall assume that it could be any where on or inside a cube CU with corners at D₁,D₂,⋯,D₈. The main point of this section is to illustrate the following: If we denote by T_CD the optimal control of transferring the gaze from C to D, then T_CD can be approximated by a linear pyramid based interpolation using four of the optimal control functions from $T_{CD_{i}}, i=1,..,8$. First of all we write CU as a union of six pyramids PY_i,i=1,⋯,6 where any two pyramids may intersect only at their surfaces. We now ascertain the membership of D in one of the six pyramids and call this pyramid PY. The corner points of the pyramid PY are four of the eight points D₁,D₂,⋯,D₈. Assume without any loss of generality that these corner points are D₁,D₂,D₃,D₄. We claim that T_CD is approximated by a convex combination of $T_{CD_{i}}, i=1,2,3,4$. Via simulation we show the effectiveness of the proposed approximation. We now digress a little and describe how a cube can be written as a union of six pyramids.

Fig. 7

The final point D is uncertain but assumed to be contained within the cube CU. There are 8 paths transferring the initial gaze point C to a terminal gaze point D_i,i=1,2,⋯,8. The figure shows paths to D₁,D₄ and D for illustration

6.1 Pyramid construction

We start our discussion with a cube CU of edge distance 1 unit (see Fig. 8). Assume that one corner of the cube is at (a,b,c) chosen in such a way that D lies in the interior of the unit cube. The other corners are at the following 7 points: (a+1,b,c),(a,b+1,c),(a,b,c+1),(a+1,b+1,c),(a+1,b,c+1),(a,b+1,c+1),(a+1,b+1,c+1).

Fig. 8

A cube CU of edge distance 1 unit. Corner points are (a,b,c), (a+1,b,c),(a,b+1,c),(a,b,c+1),(a+1,b+1,c),(a+1,b,c+1),(a,b+1,c+1),(a+1,b+1,c+1)

We claim that CU can be decomposed into 6 pyramids $PY_{1}, \dots, PY_{6}$ such that $\cup _{i = 1}^{6} PY_{i} = CU$ and $\check {PY}_{i} \cap \check {PY}_{j}$ is empty for $i,j = 1, \dots 6, \, i \neq j$. Here $\check {PY}_{i}$ is the interior of $PY_{i},\, i= 1, \dots 6$. Each pyramid that we construct in IR³ has 4 vertices. Let us now write down the following unordered triplets of elements, using tokens $\bar {a}, \bar {b}, \bar {c}, \overline {a+1}, \overline {b+1}$ and $\overline {c+1}$¹³. Let us now generate the following array of 6 rows of 4 triplets as follows:

Array I:

• 1. $(\bar {a},\bar {b},\bar {c}), (\overline {a+1},\bar {b},\bar {c}),(\overline {a+1},\overline {b+1},\bar {c}), (\overline {a+1},\overline {b+1},\overline {c+1})$

• 2. $(\bar {b},\bar {a},\bar {c}), (\overline {b+1},\bar {a},\bar {c}),(\overline {b+1},\overline {a+1},\bar {c}), (\overline {b+1},\overline {a+1},\overline {c+1})$

• 3. $(\bar {c},\bar {a},\bar {b}), (\overline {c+1},\bar {a},\bar {b}),(\overline {c+1},\overline {a+1},\bar {b}), (\overline {c+1},\overline {a+1},\overline {b+1})$

• 4. $(\bar {a},\bar {c},\bar {b}), (\overline {a+1},\bar {c},\bar {b}),(\overline {a+1},\overline {c+1},\bar {b}), (\overline {a+1},\overline {c+1},\overline {b+1})$

• 5. $(\bar {b},\bar {c},\bar {a}), (\overline {b+1},\bar {c},\bar {a}),(\overline {b+1},\overline {c+1},\bar {a}), (\overline {b+1},\overline {c+1},\overline {a+1})$

• 6. $(\bar {c},\bar {b},\bar {a}), (\overline {c+1},\bar {b},\bar {a}),(\overline {c+1},\overline {b+1},\bar {a}), (\overline {c+1},\overline {b+1},\overline {a+1})$.

Note that the above array of triplets follow a pattern. In the first column of the array, the tokens $\bar {a}, \bar {b}, \bar {c}$ are ordered in each of its possible 6 combinations. The second column of the array is same as the first column of the array except that the first element of a triplet in the second column is obtained by incrementing the first element of the corresponding triplet in the first column.

Likewise, the third column of the array is same as the second column of the array except that the second element of a triplet in the third column is obtained by incrementing the second element of the corresponding triplet in the second column.

Finally, the fourth column of the array is same as the third column of the array except that the third element of a triplet in the fourth column is obtained by incrementing the third element of the corresponding triplet in the third column.

For every triplet in Array I, the unordered triplets of tokens are now reordered by removing the overbar and writing a or a+1 to the left of b or b+1 which is written to the left of c or c+1. We perform this operation for each triplet of tokens in the above Array I term by term. We now get the following Array II of 6 rows of 4 ordered triplets of elements.

Array II:

• 1. (a,b,c),(a+1,b,c),(a+1,b+1,c),(a+1,b+1,c+1)

• 2. (a,b,c),(a,b+1,c),(a+1,b+1,c),(a+1,b+1,c+1)

• 3. (a,b,c),(a,b,c+1),(a+1,b,c+1),(a+1,b+1,c+1)

• 4. (a,b,c),(a+1,b,c),(a+1,b,c+1),(a+1,b+1,c+1)

• 5. (a,b,c),(a,b+1,c),(a,b+1,c+1),(a+1,b+1,c+1)

• 6. (a,b,c),(a,b,c+1),(a,b+1,c+1),(a+1,b+1,c+1).

For every triplet in Array II, we treat each element of a triplet as coordinates of a point in IR³. We define PY_i,i=1,⋯,6 as the i^th pyramid generated by the four points of the i^th row, to be treated as corner points. The 6 pyramids are generated one for each row of Array II. We now state and prove the following theorem.

Theorem 1

Let D be a point in $\mathbb {R}^{3}$ with coordinates D=(x,y,z). Let CU be the unit cube as described in this subsection. If x−a≠y−b≠z−c and D is in CU, then D belongs uniquely to one of the six pyramids PY₁,PY₂,PY₃,PY₄,PY₅,PY₆.

Proof

First of all we show that for (x,y,z) to lie in the pyramid PY_i, i=1,⋯,6 the coordinates (x−a,y−b,z−c) needs to satisfy certain inequality. This is now described for each of the six pyramids.

For the pyramid PY₁, we write down the convex combination of four corner points from the first row of Array II, and obtain

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a+1,b,c) + \mu_{3}(a+1,b+1,c)\\ &+ \mu_{4}(a+1,b+1,c+1)\\ =& (a+\mu_{2}+ \mu_{3}+\mu_{4}, b+ \mu_{3}+\mu_{4}, c + \mu_{4}). \end{array} $$

Note that μ_i-s are all non-negative and μ₁+μ₂+μ₃+μ₄=1. Thus, all points in PY₁ has the property that

$$ x-a\geq y-b \geq z-c. $$

(31)

Repeating the above calculations and without writing the details, we obtain the following. For PY₂ the convex combination is

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a,b+1,c) + \mu_{3} (a+1,b+1,c)\\ &+ \mu_{4}(a+1,b+1,c+1)\\ =& (a+ \mu_{3}+\mu_{4}, b+ \mu_{2}+ \mu_{3}+\mu_{4}, c + \mu_{4}). \end{array} $$

All points in PY₂ has the property that

$$ y-b\geq x-a \geq z-c. $$

(32)

For PY₃ the convex combination is

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a,b,c+1) + \mu_{3} (a+1,b,c+1)\\ &+ \mu_{4}(a+1,b+1,c+1)\\ =& (a+ \mu_{3}+\mu_{4}, b+\mu_{4}, c + \mu_{2}+ \mu_{3}+\mu_{4}). \end{array} $$

All points in PY₃ has the property that

$$ z-c\geq x-a \geq y-b. $$

(33)

For PY₄ the convex combination is

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a+1,b,c) + \mu_{3} (a+1,b,c+1)\\&+ \mu_{4}(a+1,b+1,c+1) \end{array} $$

$$= (a+ \mu_{2}+\mu_{3}+\mu_{4}, b+\mu_{4}, c + \mu_{3}+ \mu_{4}). $$

All points in PY₄ has the property that

$$ x-a\geq z-c \geq y-b. $$

(34)

For PY₅ the convex combination is

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a,b+1,c) + \mu_{3} (a,b+1,c+1)\\ &+ \mu_{4}(a+1,b+1,c+1)\\ =& (a+ \mu_{4}, b+\mu_{2}+\mu_{3}+\mu_{4}, c + \mu_{3}+ \mu_{4}). \end{array} $$

All points in PY₅ has the property that

$$ y-b\geq z-c \geq x-a. $$

(35)

For PY₆ the convex combination is

$$\begin{array}{*{20}l} &\mu_{1}(a,b,c) + \mu_{2}(a,b,c+1) + \mu_{3} (a,b+1,c+1)\\ &+ \mu_{4}(a+1,b+1,c+1)\\ =& (a+ \mu_{4}, b+\mu_{3}+\mu_{4}, c + \mu_{2} + \mu_{3}+ \mu_{4}). \end{array} $$

All points in PY₆ has the property that

$$ z-c \geq y-b \geq x-a. $$

(36)

Since the coordinates x−a,y−b and z−c are distinct, by assumption, it would follow that one and only one of the six inequalities described in (31), (32), (33), (34), (35), (36) would be satisfied. □

Remark 2

When the coordinates of D−(a,b,c) are not distinct, then D is at the surface of more than one of the six pyramids. The details are quite evident and is omitted.

6.2 Approximating external torque via interpolation

Recall that T_CD(t) is the external torque of transferring the gaze point of the binocular system from C to D in IR³. Typically T_CD(t) is calculated by solving a boundary value problem (using COMSOL) as outlined in Sections 4 and 5. In this section we argue that T_CD(t) need not be calculated once for every D in IR³. Using pyramid based linear interpolation, we can approximate T_CD(t) from $T_{CD_{i}}(t), i=1,\cdots,8$ by writing

$$ T_{CD}(t) \; \approx \; \sum_{i=1}^{4} \; \mu_{i} \; T_{CD_{i}}(t), $$

(37)

where μ_i,i=1,2,3,4 are unique coefficients obtained as follows. If D belongs to one of the six pyramids with corner points at D₁,D₂,D₃ and D₄, (assumed without any loss of generality), then μ_i-s are obtained uniquely by solving

$$D \; = \; \mu_{1} D_{1} + \mu_{2} D_{2} + \mu_{3} D_{3} + \mu_{4} D_{4}. $$

Our final step in the interpolation based approximation is valid when the graph of the functions $T_{CD_{i}}, i=1,\cdots,8$ are linear (see Section 5). Using the ‘linearity’ of the external torque function we modify (37) as follows.

$$ T_{CD}(t) \; \approx \; \left[ \sum_{i=1}^{4} \; \mu_{i} \; T_{CD_{i}}(0) \right] \left(1-2t \right). $$

(38)

Example 2: (Final gaze point is in the interior of the corresponding pyramid)

In this example we consider the binocular system where the left eye is at (0,0,0) and the right eye is at (0,1,0). The two eyes are initially gazing at a target located at (1,2,1). The goal is to optimally move the gaze to a new target located at (5.7,−0.5,2.3). By solving the boundary value problem, we compute and plot the optimal trajectories of the generalized angles (Fig. 9(a), solid lines) and generalized velocities (Fig. 9(b), solid lines). The optimal gaze trajectory is shown in (Fig. 9(c), blue, dotted line). Finally the optimal external torques are graphed in (Fig. 9(d), solid lines). Note that these graphs are straight lines.

Fig. 9

Example 2: Both sensors are on the y-axis located at (0,0,0) and (0,1,0). The gaze point shifts from (1,2,1) to (5.7,−0.5,2.3). The final point is an interior point in the pyramid with corner points at (5,−1,2), (7,−1,2), (7,1,2), (7,1,4)

We now use pyramid based interpolation to approximate the optimal external torque function. First of all we construct a cube that contains the point (5.7,−0.5,2.3). The vertices of the cube are chosen at the following eight points:

$$\begin{array}{*{20}l} &(5,-1,2,), \, (5,-1,4),\, (5,1,4),\,(5,1,2),\, (7,-1,2),\\& (7,-1,4),\,(7,1,4),\,(7,1,2). \end{array} $$

(39)

It turns out that the point (5.7,−0.5,2.3) is contained in the pyramid with corner points at

$$(5,-1,2),\,(7,-1,2),\,(7,1,2),\,(7,1,4). $$

We now use the approximation formula (38) to obtain a linear interpolation of the external torque function $T_{INT}^{L}$ and $T_{INT}^{R}$. In (Fig. 9(d), dotted lines) the graphs of $T_{INT}^{L}$ and $T_{INT}^{R}$ are plotted. Finally we use (30) and the linear interpolation $T_{INT}^{L}$ and $T_{INT}^{R}$ to solve for the generalized angles and velocities (see (Fig. 9(a), dotted lines) and (Fig. 9(b), dotted lines)). We plot the gaze trajectory in (Fig. 9(c), red, dotted lines) for the interpolated external torque function. $\square$

Example 3: (Final gaze point is on the surface of the corresponding pyramid)

In this example, we have the binocular system with sensors located as in Example 2. The goal is to optimally move the gaze from an initial gaze at (1,2,1) to a final gaze point at (6,0,4). We proceed by solving the boundary value problem, compute and plot the optimal trajectories of the generalized angles (Fig. 10(a), solid lines) and generalized velocities (Fig. 10(b), solid lines). The optimal gaze trajectory is shown in (Fig. 10(c), blue, dotted line). Finally the optimal external torques are graphed in (Fig. 10(d), solid lines). Once again, as in Example 2, these graphs are straight lines.

Fig. 10

Example 3: Both sensors are on the y-axis located at (0,0,0) and (0,1,0). The gaze point shifts from (1,2,1) to (6,0,4). The final point is on one surface of the pyramid with corner points at (5,−1,2), (5,−1,4), (7,−1,4), (7,1,4)

Pyramid based interpolation is now used as in Example 2. It turns out that the final point (6,0,4) is on the surface on the cube (39) and specifically on the surface of the pyramid with corner points at

$$(5,-1,2),\,(5,-1,4),\,(7,-1,4),\,(7,1,4).$$

We now use the approximation formula (38) to obtain a linear interpolation of the external torque function $T_{INT}^{L}$ and $T_{INT}^{R}$. In (Fig. 10(d), dotted lines) the graphs of $T_{INT}^{L}$ and $T_{INT}^{R}$ are plotted. Finally we use (30) and the linear interpolation $T_{INT}^{L}$ and $T_{INT}^{R}$ to solve for the generalized angles and velocities (see (Fig. 10(a), dotted lines) and (Fig. 10(b), dotted lines)). We plot the gaze trajectory in (Fig. 10(c), red, dotted lines) for the interpolated external torque function. $\square$

Remark 3

The main difference between examples 2 and 3 is the location of the final target point. In the former, the target point is in the interior of the associated pyramid and in the latter, it is on the surface. The main point to observe, and it is the essence of the two simulations, is evident from Figs. 9(c) and 10(c). ‘The trajectory of the gaze point does not deviate appreciably even when the input control in the form of external torque is computed using a linear interpolation from four corner points of an associated pyramid’. Thus control can be synthesized using a lookup table and one does not have to execute a more demanding COMSOL, in real time.

Remark 4

Our final remark of this section is about the approximation formula (38). Recall from (28) that

$$\begin{array}{*{20}l} &\left[T_{x}^{L}(0), T_{y}^{L}(0), T_{z}^{L}(0), T_{x}^{R}(0), T_{y}^{R}(0), T_{z}^{R}(0)\right] \\&= [\lambda_{2}(0) \; \lambda_{4}(0) \; \lambda_{6}(0)]\;G_{LB}^{-1}(0) M_{LB}^{T}(0). \end{array} $$

(40)

Let us define the symbols

$$T_{CD}(0)\;=\; \left[T_{x}^{L}(0), T_{y}^{L}(0), T_{z}^{L}(0), T_{x}^{R}(0), T_{y}^{R}(0), T_{z}^{R}(0)\right] $$

$$\lambda \;=\; [\lambda_{2}(0) \; \lambda_{4}(0) \; \lambda_{6}(0)] $$

and

$$W \;=\; G_{LB}^{-1}(0) M_{LB}^{T}(0). $$

We can rewrite (40) symbolically as

$$ T_{CD}(0) \;=\; \lambda \; W, $$

(41)

where the matrix W is a 3×6 matrix whose entries depend only on the initial gaze point C and not on the final gaze point D (see [5]). The vector λ, on the other hand, is a 1×3 vector whose entries depend both on C and D.

We can rewrite (38), using (41), as follows.

$$ T_{CD}(t) \; \approx \; \left[ \sum_{i=1}^{4} \; \mu_{i} \; \lambda_{i} \right]\;W\; \left(1-2t \right). $$

(42)

Note in (42) that when C is fixed, then W is fixed but λ_i depends on D_i, the corner points of the pyramid. The points λ_i,i=1,⋯,8 in IR³ form the corner points of a cuboid, which can be calculated apriori. We make the following statemnt about the interpolation algorithm.

For every cube CU (with corner points D_i) there is a cuboid CB (with corner points λ_i) that can be precalculated and stored. This cuboid is dependent on the initial point C.

7 Rotation dynamics with Tait-Bryan parameterization

In this section we introduce Tait-Bryan (TB) parameterization [50,51] and make connection with Fick Gimbals and Pan-Tilt rotation. Our introduction will be brief and we will refer the readers to a previous paper [26], see also Figs. 3 and 11.

Fig. 11

A mechanical binosensing system gazing at a target. This figure is exactly same as Fig. 2 where the eye balls are replaced by a mechanical pan-tilt system

In the TB parameterization there are three angle variables ϕ₁,ϕ₂ and ϕ₃ where ϕ₁ is the angle of rotation about axis 1 (see Fig. 3), ϕ₂ is the angle of rotation about axis 2 rotated by ϕ₁-rotation about axis 1. Rotations about axis 1 and axis 2 are respectively called Pan and Tilt. Finally ϕ₃ is the angle of Axial rotation about axis 3 rotated by the previous two rotations. The three angle variables ϕ₁,ϕ₂ and ϕ₃ completely parameterizes the orientation space SO(3). As in Eqs. (1) and (4), for the axis-angle parameterization, we now have the following unit quaternion for the TB parameterization (See (9) in [26]).

$$ \begin{aligned} q(\phi_{1},\phi_{2},\phi_{3}) = \left(\begin{array}{c} \sin\frac{\phi_{1}}{2}\sin\frac{\phi_{2}}{2}\sin\frac{\phi_{3}}{2} + \cos\frac{\phi_{1}}{2}\cos\frac{\phi_{2}}{2}\cos\frac{\phi_{3}}{2} \\ \cos\frac{\phi_{1}}{2}\sin\frac{\phi_{2}}{2}\cos\frac{\phi_{3}}{2} + \sin\frac{\phi_{1}}{2}\cos\frac{\phi_{2}}{2}\sin\frac{\phi_{3}}{2} \\ \sin\frac{\phi_{1}}{2}\cos\frac{\phi_{2}}{2}\cos\frac{\phi_{3}}{2} - \cos\frac{\phi_{1}}{2}\sin\frac{\phi_{2}}{2}\sin\frac{\phi_{3}}{2} \\ \cos\frac{\phi_{1}}{2}\cos\frac{\phi_{2}}{2}\sin\frac{\phi_{3}}{2} - \sin\frac{\phi_{1}}{2}\sin\frac{\phi_{2}}{2}\cos\frac{\phi_{3}}{2} \end{array}\right), \end{aligned} $$

(43)

where the angles $\phi _{1} \in [-\pi, \pi ], \phi _{2} \in \left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$, and ϕ₃∈[−π,π]. Using the unit quaternion (43), a left invariant Riemannian metric on SO(3) can now be written (see Eqs. (26), (27) in [26]) as

$$ g \;=\; \left[ d\phi_{1} \;\; d\phi_{2} \;\; d\phi_{3} \right] \; G_{TB} \; \left[ d\phi_{1} \;\; d\phi_{2} \;\; d\phi_{3} \right]^{T}, $$

(44)

where

$$ G_{TB} \;=\; \left(\begin{array}{ccccc} \frac{1}{4} && 0 && - \frac{1}{4} \sin \phi_{2}\\ 0 && \frac{1}{4} && 0 \\ - \frac{1}{4} \sin \phi_{2} && 0 && \frac{1}{4} \end{array} \right). $$

(45)

Using the Riemannian metric (44) for SO(3), the associated Euler-Lagrange Eq. (16) is given by¹⁴

$$\begin{array}{*{20}l} \left(\begin{array}{c} \ddot{\phi}_{1} \\ \ddot{\phi}_{3} \end{array} \right) =& \left(\begin{array}{cc} \tan \phi_{2} & \sec \phi_{2} \\ \sec \phi_{2} & \tan \phi_{2} \end{array} \right) \left(\begin{array}{c} \dot{\phi}_{1} \\ \dot{\phi}_{3} \end{array} \right) \dot{\phi}_{2} \\&+ 4 \sec^{2} \phi_{2} \left(\begin{array}{cc} 1 & \sin \phi_{2} \\ \sin \phi_{2} & 1 \end{array} \right) \left(\begin{array}{c} \tau_{\phi_{1}} \\ \tau_{\phi_{3}} \end{array} \right), \end{array} $$

(46)

$$ \ddot{\phi}_{2} = - \cos \phi_{2} \; \dot{\phi}_{1} \; \dot{\phi}_{3} \;+\; 4 \tau_{\phi_{2}}. $$

(47)

The vector $\tau = [\tau _{\phi _{1}}, \tau _{\phi _{2}}, \tau _{\phi _{3}}]^{T}$ is the generalized torque vector. If we now define T=[T₁,T₂,T₃]^T to be the external torque vector, in the inertial coordinate, the two vectors τ and T can now be related by a formula similar to (18) written as follows

$$ \tau \;=\; M_{TB}^{T} \; T, $$

(48)

where M_TB is the M-matrix for the TB parameterization described as follows (already reported in page 323, [25])

$$ M_{TB}\;=\; \left(\begin{array}{ccccc} 0 && \cos \phi_{1} && \cos \phi_{2} \sin \phi_{1} \\ 1 && 0 && -\sin \phi_{2} \\ 0 && - \sin \phi_{1} && \cos \phi_{1} \cos \phi_{2} \end{array} \right). $$

(49)

The Eqs. (46)-(48), describe rotation dynamics on SO(3) with the external torque vector T as the control. As in Eqs. (20)-(29), we can setup a dynamical system for the monocular unconstrained eye rotation on SO(3). We can also require the states to go from a priori agreed initial state to a final state in a unit interval of time minimizing the control energy (21). Repeating the steps in Section 4, an optimal external torque T can now be computed using COMSOL to solve the associated two point boundary value problem BVP (see also [24–26]).

In order to describe human eye-rotation, the orientation space is not the unrestricted SO(3) but a submanifold LIST (see [25] and Fig. 15) of SO(3). We now parameterize LIST using TB parametrization.

Example 4: LIST using Tait-Bryan parametrization Using the quaternion parametrization (43), it follows that the Listing’s constraint q₃=0 is described by

$$ \tan \frac{\phi_{3}}{2} \;=\; \tan \frac{\phi_{1}}{2} \; \tan \frac{\phi_{2}}{2}. $$

(50)

Let us now define

$$\begin{array}{@{}rcl@{}} \Delta_{1} \;&=&\; \sin \frac{\phi_{1}}{2} \; \sin \frac{\phi_{2}}{2}, \\ \Delta_{2} \;&=&\; \cos \frac{\phi_{1}}{2} \; \cos \frac{\phi_{2}}{2}. \end{array} $$

(51)

Substituting the Listing’s constraint (50) into the quaternion (43), we obtain the following parametrization of LIST in the TB parametrization

$$ \left[ \begin{array}{c} \Delta_{1}^{2} + \Delta_{2}^{2} \\ \sin \frac{\phi_{2}}{2} \; \cos \frac{\phi_{2}}{2} \\ \sin \frac{\phi_{1}}{2} \; \cos \frac{\phi_{1}}{2} \; \cos \phi_{2} \\ 0 \end{array} \right] \bigg/ \sqrt{\Delta_{1}^{2} + \Delta_{2}^{2}}. $$

(52)

$\square$

Note that in the parametrization (52) of LIST, only the pan (ϕ₁) and tilt (ϕ₂) are used. Construction of a left invariant Riemannian metric on LIST in the TB parametrization would now be standard [6] and the details are not elaborated here.

Example 5: Euler-Lagrange equation for the Pan-Tilt system We now impose the Fick Gimbal constraint ϕ₃=0 into the TB quaternion (43). Recall that for a Fick Gimbal, the axial rotation angle ϕ₃ is permanently frozen to zero. The Fick Gimbal quaternion is described as follows.

$$ \rho_{fick}(\phi_{1},\phi_{2})\;=\; \left(\begin{array}{c} \cos \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \\ \cos \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \\ \sin \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \\ -\sin \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \end{array} \right). $$

(53)

We now write

$$ \frac{\partial \rho_{fick}}{\partial \phi_{1}}\;=\; \frac{1}{2}\left(\begin{array}{c} -\sin \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \\ -\sin \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \\ \cos \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \\ -\cos \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \end{array} \right) $$

(54)

and

$$ \frac{\partial \rho_{fick}}{\partial \phi_{2}}\;=\; \frac{1}{2}\left(\begin{array}{c} -\cos \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \\ \cos \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \\ -\sin \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \\ -\sin \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2} \end{array} \right). $$

(55)

Computing the inner products we write

$$ \left<\frac{\partial \rho_{fick}}{\partial \phi_{i}}, \frac{\partial \rho_{fick}}{\partial \phi_{i}}\right> \;=\; \frac{1}{4}, \;\; i=1,2 $$

(56)

and

$$ \left<\frac{\partial \rho_{fick}}{\partial \phi_{1}}, \frac{\partial \rho_{fick}}{\partial \phi_{2}}\right> \;=\; 0. $$

(57)

From (56) and (57) we write the Riemannian matrix ¹⁵

$$G_{FG} \;=\; \left(\begin{array}{cc} \frac{1}{4} & 0 \\ 0 & \frac{1}{4} \end{array} \right). $$

We choose the potential energy V to be zero and the kinetic energy

$$\mathbf{KE} \;=\; \frac{1}{8} \left(\dot{\phi}_{1}^{2} + \dot{\phi}_{2}^{2}\right), $$

and we write the Lagrangian as

$$\mathbf{\mathcal{L}} \;=\; \frac{1}{8} \left(\dot{\phi}_{1}^{2} + \dot{\phi}_{2}^{2}\right). $$

The Euler-Lagrange’s Eq. (16) for the Pan-Tilt system is now written as

$$ \frac{1}{4} \ddot{\phi}_{1} \;=\; \tau_{\phi_{1}}, \;\; \frac{1}{4} \ddot{\phi}_{2} \;=\; \tau_{\phi_{2}}. $$

(58)

Finally we would like to relate the external torque vector T=(T₁,T₂,T₃)^T to the generalized torque $\tau =(\tau _{\phi _{1}}, \tau _{\phi _{2}})^{T}$. This is done by first calculating the M-matrix M_FG.

Let q=[q₀,q₁,q₂,q₃]^T be the Fick Gimbal quaternion (53) and let us define $\tilde {\omega } = [0, \omega _{1}, \omega _{2}, \omega _{3}]^{T}$, where ω_i-s are the components of the angular velocity vector. It follows from [52] and has also been used in [25] that

$$ \dot{q} \;=\; \frac{1}{2} \tilde{\omega} \bullet q, $$

(59)

where ∙ denotes quaternion multiplication. Substituting the parameters of the Fick Gimbal quaternion (53) into (59) and carrying out the algebraic computation we write

$$ \left(\begin{array}{ccc} -q_{2} && -q_{1}\\ q_{3} && q_{0}\\ q_{0} && q_{3} \\ -q_{1} && -q_{2} \end{array} \right) \left(\begin{array}{c} \dot{\phi}_{1} \\ \dot{\phi}_{2} \end{array} \right) \;=\; \left(\begin{array}{ccccc} -q_{1} && -q_{2} && -q_{3}\\ q_{0} && q_{3} && -q_{2}\\ -q_{3} && q_{0} && q_{1} \\ q_{2} && -q_{1} && q_{0} \end{array} \right) \left(\begin{array}{c} \omega_{1} \\ \omega_{2} \\ \omega_{3} \end{array} \right). $$

(60)

Solving (60) we write

$$\left(\begin{array}{c} \omega_{1} \\ \omega_{2} \\ \omega_{3} \end{array} \right) \;=\; M_{FG} \left(\begin{array}{c} \dot{\phi}_{1} \\ \dot{\phi}_{2} \end{array} \right), $$

where

$$M_{FG} \;=\; \left(\begin{array}{cc} 0 & 1\\1 & 0\\0 & 0 \end{array} \right). $$

It would now follow from a relation similar to (18) that $\tau _{\phi _{1}} = T_{2}$ and $\tau _{\phi _{2}} = T_{1}$. The Euler-Lagrange’s equation for the Pan-Tilt system (58) now reduces to

$$ \frac{1}{4} \ddot{\phi}_{1} \;=\; T_{2}, \;\; \frac{1}{4} \ddot{\phi}_{2} \;=\; T_{1}. $$

(61)

For the purpose of the next section, we shall define

$$T_{FG} = [T_{2}, T_{1}]^{T}, $$

from (61) and write the following Pan-Tilt dynamics

$$ \left(\begin{array}{c} \ddot{\phi}_{1} \\ \ddot{\phi}_{2} \end{array} \right) = 4 \; T_{FG}. $$

(62)

$\square$

8 Biomimetic Pan-Tilt movement following the optimal gaze trajectories of the human binocular system

Our goal in this section is to control the Pan-Tilt dynamics (62) so that the gaze of the pan tilt system matches the gaze of the human ocular system. Since the ocular dynamics on SO(3) satisfies (46)-(48), roughly speaking, we need to match the angle variables ϕ₁ and ϕ₂ in (62) with the same variables in (46) and (47). Note that the angle ϕ₃ is frozen permanently to zero for the pan-tilt system, and therefore cannot match the axial movements of the human eye i.e., ϕ₃ in (46).

Let us rewrite part of the dynamical system (46)-(48) as follows

$$ \left(\begin{array}{c} \ddot{\phi}_{1} \\ \ddot{\phi}_{2} \end{array} \right) \;=\; 4F_{TB} \;+\; 4 H_{TB} M_{TB}^{T} T, $$

(63)

where M_TB is defined in (49) and we define

$$F_{TB} \;=\; \frac{1}{4} \left[ \begin{array}{c} \tan{\phi_{2}} \; \dot{\phi}_{1} \dot{\phi}_{2} \;+\; \sec{\phi_{2}} \; \dot{\phi}_{3} \dot{\phi}_{2} \\ - \cos{\phi}_{2} \; \dot{\phi}_{1} \dot{\phi}_{3} \end{array} \right] $$

and

$$H_{TB} \;=\; \left[ \begin{array}{ccc} \sec^{2} \phi_{2} & 0 & \sec^{2} \phi_{2} \sin \phi_{2} \\ 0 & 1 & 0 \end{array} \right]. $$

In order to match the Fick Gimbal dynamics (62) with the SO(3) dynamics (63) the right hand sides have to match and we get the following

$$ T_{FG} \;=\; F_{TB} \;+\; H_{TB} M_{TB}^{T} T, $$

(64)

where T is any external torque input to the ocular dynamics on SO(3). The Eq. (64) can be viewed as a torque-transformer, which transforms the external torque T for the SO(3)-system to T_FG, the torque input to the Pan-Tilt-system. The equality (64) would ensure that the angle variables ϕ₁ and ϕ₂ of the two systems match, provided they have the same initial conditions.

In order to implement the torque-transformer, we will need $\dot {\phi }_{3}$ which unfortunately is not available to the Pan-Tilt system. Hence, we will need a $\dot {\phi }_{3}$-generator to be implemented with the following equation:

$$\begin{array}{*{20}l} \ddot{\phi}_{3} =& \sec{\phi_{2}} \; \dot{\phi}_{1} \dot{\phi}_{2} \;+\; \tan{\phi_{2}} \; \dot{\phi}_{3} \dot{\phi}_{2} \\&+ \left[4 \sec^{2} \phi_{2} \; \sin \phi_{2}, 0, 4 \sec^{2} \phi_{2}\right] M_{TB}^{T} T. \end{array} $$

Implementation of the torque-transformer and the $\dot {\phi }_{3}$ generator has been sketched in Fig. 12.

Fig. 12

The torque-transformer is a static device. The $\dot {\phi }_{3}$-generator is a dynamical system requiring T and ρ as input. $\rho =\left [\phi _{1}, \dot {\phi }_{1}, \phi _{2}, \dot {\phi }_{2} \right ]^{T}$, consists of Pan, Tilt angles and their derivatives. T is the external torque input to the unconstrained monocular plant. T_FG is the external torque input to the mechanical pan-tilt device that follows the human eye gaze movement

If T = T^∗ is chosen in such a way that the angle variables ϕ₁,ϕ₂ and ϕ₃ satisfy the Listing’s constraint (50) one can compute $\dot {\phi }_{3}$ explicitly as

$$ \dot{\phi}_{3} \;=\; \frac{\tan \frac{\phi_{1}}{2} \sec^{2} \frac{\phi_{2}}{2}}{1+ \tan^{2} \frac{\phi_{1}}{2} \tan^{2} \frac{\phi_{2}}{2}} \dot{\phi}_{2} + \frac{\tan \frac{\phi_{2}}{2} \sec^{2} \frac{\phi_{1}}{2}}{1+ \tan^{2} \frac{\phi_{1}}{2} \tan^{2} \frac{\phi_{2}}{2}} \dot{\phi}_{1}. $$

(65)

As shown in Fig. 13 that in this case the $\dot {\phi }_{3}$ generator is implemented by a pan-tilt feedback requiring variables ϕ₁,ϕ₂ and their derivatives.

Fig. 13

The torque-transformer is a static device. The $\dot {\phi }_{3}$-generator is a static system requiring ρ as input. T^∗ is chosen such that the states ϕ₁,ϕ₂,ϕ₃ evolve on LIST. ρ and T_FG are as described in Fig. 12

Remark 5

In this remark we would like to put into perspective how we have synthesized and implemented the external torque optimal control. First of all note that in Section 4 we have proposed to synthesize the optimal control for the binocular system where the axes of human eye rotation satisfy Listing’s law and the eye gazes always remain coplanar together with its separation vector. The associated space LBIN is parametrized using axis-angle parameters as a subset of SO(3)×SO(3) (see Fig. 14). The optimal control vector T is a 6-vector, the first 3 components of T is the optimal control to the left eye (call it T_left) and the next 3 components are likewise for the right eye (call it T_right). In Examples 1, 2, 3, the optimal control vector is computed where we show that the control functions can be approximated by a pyramid based interpolation scheme. It turns out that if we apply the optimal control T_left to an unrestricted rotation dynamics (viz. (46)-(48)) on SO(3) with initial condition on LIST, the integral curves of the dynamical system would evolve on LIST (see Fig. 15). The same can be said for the optimal control T_right. In fact the gaze trajectory of the two eyes are precisely the gaze trajectory computed on LBIN using COMSOL. In the next example we have verified this fact even when the parametrization on SO(3) uses Tait-Bryan parametrization. Finally we demonstrate in Fig. 13 that using optimal control T^∗, which is either T_left or T_right one can make a mechanical pan-tilt device follow the gaze directions of the human eye.

Fig. 14

LBIN is shown as a subset of the ambient space SO(3)×SO(3). LBIN is to be viewed as a parametrization of the binocular system

Fig. 15

LIST is shown as a subset of the ambient space SO(3). LIST is to be viewed as a parametrization of the monocular system

Example 6: On the ambient space SO(3), a single eye can be optimally controlled while satisfying Listing.

The point we illustrate in this example is that the optimal controller synthesis is independent of the choice of the parametrization (axis-angle or Tait-Bryan) of the manifold and whether or not the state variables are allowed to evolve on the constrained manifold (LBIN or LIST) or respectively the ambient manifold (SO(3)×SO(3) or SO(3)) (see Figs. 14, 15).

We consider an example¹⁶ from [5] wherein we have a binocular system with eye centers located as in Fig. 2. The goal is to shift the gaze point from (7,2,4) to (3,2,8) using a dynamical system in the form of (17), (18) while minimizing a cost function (21). The optimal control was obtained in [5] and its graph was plotted (see Fig. 13 in [5]). The problem was solved on LBIN using axis-angle parametrization. The optimal control vector T, from (22) is now separated between the left and the right eye and applied separately to (46)-(48), a dynamical system on SO(3) described using Tait-Bryan parametrization. Solving the initial value problem (46)-(48), with the input torque obtained from T as indicated, we show that the gaze direction vector of each eye follow a trajectory identical to what was obtained as solution to the optimal control problem in [5]. In Fig. 16(a) we show that the gaze points of the two binocular systems are identical. We also show that the solution to the initial value problem actually evolved in LIST (see Fig. 16(b)) although it was solved on SO(3). It shows that the optimal controller is able to maintain the LBIN constraints (specifically the Listing’s constraint on any of the two eyes) although these constraints are not mechanically imposed on the eye pair.

Fig. 16

Solving an initial value problem with using the external torques obtained Both sensors are on the y-axis located at (0,0,0) and (0,1,0). The gaze point shifts from (7,2,4) to (3,2,8)

9 Discussion

Synthesis of the optimal control function, encountered in eye and head rotation problems, as introduced in many of our earlier papers [5,6,24–26,53] requires solving a Two Point Boundary Value Problem. These boundary value problems are typically computationally intensive (see text books [54] and [55]), and require the framework of a recursive solver, for example one based on the algorithm of [56]. In our research, we had started with MATLAB Toolbox [6] to solve boundary value problems, Pseudospectral Methods [4,57–59] and subsequently used the COMSOL Program already indicated in section 4. In any application, wherein a binocular gaze directing robot would be used for target localization, inspection and reaching¹⁷, it is not very convenient to have to solve a boundary value problem for every chosen pair of initial and final points. This is because the iterative solution to the two point boundary value problem, required to solve for the optimal control, suffers from singularity issues and do not always converge. Often parameters in the COMSOL Program, and in the KNITRO solver, that we have used for pseudospectral methods, require tweaking. The configuration space LBIN may need to be re-parameterized to avoid singularities. The point we would like to put forward in this paper is that it is convenient to precompute the control function for a fixed initial point and over a set of discretely chosen final points, viz. the corner points of a cube. In real time, the gaze directing controller uses the precomputed control functions as a lookup table and computes the required control for its own action using a pyramid based interpolation. Solutions to the Boundary Value Problems, once solved, does not have to be recomputed.

When the centers of the eyes in the binocular system remain stationary and on the Listing’s plane, we have illustrated in this paper and also in [5] that the optimal control function has a Linear structure, described in (42). The angular velocities of the two eyes increase to a peak value before reducing back to zero, as is typically observed in eye saccades [33]. The optimal control to the binocular system is entirely parameterized by its initial value at t=0. It has not been shown rigorously, all the possible conditions under which the linear structure of the optimal control is maintained¹⁸.

Either for the purpose of optimal control or otherwise, it is important to mimic human movements and is a subject of research in social robotics in particular [61]. Specific to human gaze and eye movement, it is possible to control a pair of mechanical pan/tilt system even though the underlying configuration spaces of the human eye and the mechanical pan/tilt system are different¹⁹. In spite of the difference, the part of the two configuration spaces, that control the gaze/pointing direction can be identified and controlled (as depicted in Fig. 12). The main point is that the controller T_FG for the mechanical system does not have to be recomputed but instead it can be generated from the control input to the human eye, by a suitable dynamic feedback (64), called the $\dot {\phi }_{\mathbf {3}}$-generator. When the axes of the eye movement are restricted to the Listing’s plane, the feedback structure can be simplified to a static feedback (65) and the implementation details are shown in Fig. 13.

10 Conclusion

This paper has revisited the optimal binocular gaze control problem recently introduced in the Riemannian setting by the authors. It is shown that the optimal control function can be approximated by a pyramid based interpolation scheme, hence does not need to be solved in real time. Some level of discretization for the final target point will be allowed. The paper also introduces a new Biomimetic pan-tilt rotation control, where a pair of mechanical eyes are tasked to follow the human binocular gaze trajectory. The paper shows that if the optimal control to the human binocular system is known, the same can be used with a mechanical pair of eyes, with an appropriate nonlinear static feedback.