1 Introduction

Sulfamethoxazole (SMX) is a common human and veterinary antibiotic. Due to its great importance, at least as a member of the sulfonamide family, production and usage, as well as concentrations and environmental sources and sinks of SMX, have been presented and summarized in various reviews [1,2,3,4,5,6]. Highly variable concentrations of SMX (\(\mathrm{LOQ}< c / \mathrm{ng}\; L^{-1} < 16,700\)) are found in rivers worldwide [7], with a reported mean concentration of \(\overline{c} = 76\; \mathrm{ng}\; \mathrm{L}^{-1}\) (\(c_\mathrm{median} = 14\; \mathrm{ng}\; \mathrm{L}^{-1}\)) [8] and a range of \(\overline{c} < 10 - 60\; \mathrm{ng}\; \mathrm{L}^{-1}\) [9] in European Rivers. Due to its frequent usage in medication, concentrations of SMX are discussed as a marker for the origin of wastewater (i.e., WWTP-effluent) [10].

As early as 1994, direct photolysis was first described as a potential degradation pathway of SMX in aqueous solutions by Zhou and Moore in a landmark paper [11]. However, the obvious potential of SMX as a chemical actinometer for natural sunlight [12] was not further explored. In a wealth of work in the following years, in addition to direct photolysis (e.g., [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]), the degradation of SMX via bimolecular processes initiated by light together with, e.g., hydrogen peroxide [31, 37, 38], ozone [19, 39,40,41,42], chlorine [34], chlorine dioxide [43], a combination of ozone and hydrogen peroxide [20, 44] or by UV/persulfate [33] was published. A general overview of the removal of SMX from aqueous solutions is given in [45], an overview of the many transformation products reported in the literature in [46].


In the early papers by Zhou and Moore [11, 12], significant key points of direct photolysis of SMX have already been addressed. For the first time the importance of the second dissociation constant of SMX (\(\mathrm{p}K_\mathrm{a2} = 5.6\)) in explaining the pH-dependent UV spectra, rate constants, and quantum yields was discussed. Furthermore, the separation of main products by preparative HPLC, characterization by, e.g., NMR-spectroscopy and the degradation by sun-light of SMX depending on the season was presented. The cleavage of the bond connecting the sulfonamide and isoxazole part and addition of water was recognized as the source of the main products sulfanilic acid (SUA) and 3-amino-5-methylisoxazole (AMI). In addition, the well-known photochemical isomerization of the isoxazole part [47] of SMX via an azirine intermediate [48, 49] was used to explain the formation of the corresponding oxazole-derivative, hereafter referred to as ISO:

scheme 1

As with the 3-aminoisoxazoles [50], the energetically preferred tautomer in SMX is present as an amine. In contrast, ISO is preferentially present as an imine [11]. Although the formation of ISO has been found to be one of the major photoproducts of SMX and has been reported in numerous subsequent publications [21, 33, 37, 51,52,53,54], the correct imine structure is often ignored.

In addition to the rearrangement of SMX, the hydrolysis of the azirine intermediate as a competitive reaction provided an explanation of an assumed ring-opening product with molar mass \(M = 271\; \mathrm{g}\; \mathrm{mol}^{-1}\) (TP271) [11]. However, besides the adoption of the original structure [21, 54, 55], and although TP271 was characterized by, e.g., NMR-spectroscopy, in later investigations, different structures for TP271 were suggested [23, 33, 52, 54, 56, 57].

Missing experiments of the photolysis of ISO and contradictory statements on structures and products were the starting point of the investigations presented here. The study includes

  • the analysis of SMX and ISO and UV-spectra and properties of ISO,

  • a kinetic analysis of the pH-dependent photolysis of SMX and ISO including the main products,

  • an overview of available pH-dependent quantum yields of SMX including recommended values and a comparison with corresponding quantum yields of ISO,

  • an assessment of the many reported structures of TP271 by DFT methods,

  • concentrations found for SMX and ISO in surface waters from a River in North-Germany.

2 Experimental

2.1 Analytical procedures

Sulfamethoxazole (SMX) and all other compounds were analysed by LC–MSMS (HPLC 1200, Agilent, with dual pump, autosampler, column oven and mass spectrometer 6430, Agilent). Conditions HPLC: column Agilent Poroshell 120 SB-C18 4.6 \(\times\) 30 mm; particle size 2.7 \(\upmu \hbox {m}\); eluent: A = methanol, B = 0.1% formic acid, \(0'{-}3'\): 5% A, \(3'{-}6'\): gradient to 80% A, \(6'{-}6.1'\): gradient to 5% A, \(6.1'{-}9'\): 5% A; \({T} = 25 \; ^{\circ }\hbox {C}\); injection \(\hbox {volume} = 5 \, \upmu \hbox {L}\); needle wash; flow rate = 1 mL/min. Conditions mass spectroscopy: ESI-head, positive mode, source parameters: \({T} = 350 \; ^{\circ }\hbox {C}\), gas flow = 10 L/min, p(nebulizer) = 35 psi, capillary voltage = 4000 V. LC–MSMS parameter and exemplified chromatograms are summarized in the Supplementary Information (SI, Table S1 and Figure S1). Quantification was performed with external calibration solutions relative to internal standards (IS) sulfamethoxazole-D4 (SMX-D4), sulfanilic acid-D4 (SUA-D4) and aniline-d5 (ANI-D5) in the range of \(c = 0 - 1000\; \upmu \mathrm{g/L}\) for all compounds using linear calibration functions. Therefore, usually in \(100\; \upmu \hbox {L}\)-inserts \(V=45\; \upmu \mathrm{L}\) of a sample is combined with \(V=5\; \upmu \mathrm{L}\) of the IS-mixture (\(c_0 = 1000\; \upmu \mathrm{g/L}).\)

Sum formulas of isomers and transformation products were checked by high-resolution mass spectrometry (HRMS, Thermo Scientific, Dionex UltiMate UHPLC system with LTQ Orbitrap-XL).

UV-spectra (double-beam spectrometer Lambda 45 with pre monochromator, Perkin Elmer) were measured with a resolution of 2 nm in 1 nm steps at d = 1 cm in quartz cuvettes at ambient temperature with the solvent as reference. The wavelength accuracy has been checked by a holmium filter to be better than \(\Delta \lambda =\pm 1\) nm.

UV-spectra (d = 1 cm) were obtained with concentrations in the range of \(5 - 20 \; \mathrm{mg}\; \mathrm{L}^{-1}\) versus the corresponding solvent. For the measurement of the \(\mathrm{p}K_\mathrm{a}\)-value of ISO (\(c_0\) = 10 mg/L), mixtures of phosphoric acid (0.1 M), potassium dihydrogenphosphate (0.1 M) and sodium hydroxide (0.1 M) were used to prepare pH-values \(3.5 \le \mathrm{pH} \le 11\), determined by a pH-electrode SenTix 940-3 and SenTix Mic-D (WTW, Weinheim, Germany) after calibration with standard buffer solutions at pH = 4 and 7. The \(\mathrm{p}K_\mathrm{a}\)-value was evaluated using the Henderson–Hasselbalch equation as mean value of absorbances at 7 pH-values from 18 wavelengths between 207 and 281 nm.

For the measurements of \(\mathrm{log}(K_\mathrm{D})\) (distribution coefficient octanol/buffer) suitable prepared and with octanol saturated buffer solutions and n-octanol, saturated with the corresponding buffer solution, were used. Mixtures of n-octanol and buffer (V = 0.5–2 mL) of ISO with concentrations of \(c_0 = \; 10{-}400 \; \upmu \mathrm{g}\; \mathrm{L}^{-1}\) were shaken (Heidolph Reax 2) at \(T = \; 20 \pm 2 \; ^{\circ }\hbox {C}\) for 2 h in Eppendorf safe-lock tubes (2 mL). After centrifugation (centrifuge miniSpin, Eppendorf) for 5 min at 10,000 rpm the n-octanol phase was directly analysed by LC–MSMS.

2.2 Photolysis in the laboratory, actinometry and quantum yields

The setup for photolysis experiments is described elsewhere [58]. In brief, photolysis experiments were performed with a photolysis apparatus on an optical bench (Amko, Tornesch,Germany) with a Xe lamp XBO 1000 (Osram, Germany). The electrical power of the light source was always set to 500 W (± 2%). Light was focused by mirrors through an optical glass-filter with known absorbance into a stoppered quartz cuvette (d = 1 cm) with the corresponding solution (\(V_\mathrm{start} = 3135\; \upmu \mathrm{L}\)) equipped with a stirring bar in a cuvette holder with magnetic stirrer. The distance between light source and cuvette was 70 cm. The Xe lamp and mirrors were cooled by tap water, cooling of the cuvette (\(T = 293 \pm 1\; \mathrm{K}\)) was accomplished by a thermostat (Type Petite Fleur, Huber, Germany). Experiments always started with an equilibrium period to stabilize the light source and temperature in the stirred solution (5–10 min). Within the equilibrium period, the light beam was shut off with a shutter behind the optical filter. After taking three dark samples within 2 min (\(V = 45 \;\upmu \mathrm{L}\)) for irradiation time t = 0 s, the shutter was opened and the solution was irradiated. Usually 10 samples were removed (\(V = 45 \;\upmu \mathrm{L}\)) after a given irradiation time (accuracy of about 1 s) within a maximum irradiation time of t = 500 min. Always air saturated solutions were used from solutions stirred at least 60 min before start in the dark at room temperature. Oxygen concentrations were determined by an oxygen digital IDS-sensor FDO (WTW, Weinheim, Germany).

A second, identical optical bench was used for irradiation by a (not cooled) monochromatic mercury-light source (UVP PenRay Lamp, \(\lambda = 254\; \mathrm{nm}\), Analytik Jena US) in a distance of 56 mm to the entrance window of the thermostated cuvette. To remove the 185 nm line of the PenRay lamp a home-made optical filter prepared from microscope slides (quartz-glass, d = 3 mm) was used.

Relative light intensities were obtained with a SpectraWiz Spectrometer (Black-Comet C-25 Spectrometer, StellarNet Inc., USA). Actinometric measurements for both polychromatic and monochromatic light sources using iron(III)oxalate are described in detail elsewhere [59].

Details in the calculation of quantum yields for the experimental setups discussed above are available in [58, 59]. For the low concentrations used in this study quantum yields \(\Phi\) (dimensionless [60]) were calculated from Eq. (1) in steps of \(\Delta \lambda = 1\; \mathrm{nm}\). Parameters in Eq. (1) are the rate constant \(k_\mathrm{exp}\) (in \(\mathrm{s}^{-1}\)) from the photolysis of the compound, the spectral photon irradiance on amount basis \(I_\lambda\) (in \(\mathrm{mol}\; \mathrm{s}^{-1}\; \mathrm{cm}^{-2}\; \mathrm{nm}^{-1}\)) from actinometry, the molar decadic absorption coefficient \(\epsilon _\lambda\) (in \(\mathrm{L} \; \mathrm{mol}^{-1}\;\mathrm{cm}^{-1}\)) from UV-spectroscopy and the conversion factor 2303. From this definition the quantum yield is, therefore, the fraction of the experimental rate constant, \(k_\mathrm{exp}\), and the theoretical maximal rate const, \(k_{\Phi = 1}\), with a quantum yield for a primary process of \(\Phi = 1\)

$$\begin{aligned} \Phi = \frac{k_\mathrm{exp}}{2303 \displaystyle \sum \nolimits _{\lambda \mathrm{(start)}}^{\lambda \mathrm{(end)}} I_\lambda \epsilon _\lambda \; \Delta \lambda } = \frac{k_\mathrm{exp}}{k_{\Phi = 1}} \end{aligned}$$
(1)

In Eq. (1) \(\lambda \mathrm{(start)}\) is defined by the onset of the light spectrum and \(\lambda \mathrm{(end)}\) by the end of the UV-spectrum.

Based on the available data for different light sources (vide infra), it can be expected for SMX and at least assumed for ISO that the quantum yield is wavelength independent.

2.3 Analysis in river samples

Concentrations of SMX and ISO from 5 sampling campaigns between February 2020 and September 2021 (winter and summer) were used. Therefore, 80 samples obtained in a small river in the northern part of Germany (River Wietze, length about 45 km) with two main inflows and with in sum 3 WWTP as exclusive sources of SMX were quantified after SPE-enrichment and analysis by LC–MSMS as described in [61]. A map of the sampling points and detailed concentrations are summarized in the SI (Table S4 and S5 and Figure S9).

2.4 Compounds and solutions

Formic acid (98–100%), phosphoric acid (85%), sodium hydroxide (\(>99\%\)) and potassium dihydrogenphosphate (100%) were purchased from Merck and VWR (Germany) and solvents (acetonitrile, methanol) were purchased from VWR in the highest available quality (\(>99.7\%\)) and were used as received. Potassium trioxalatoferrate(III) trihydrate (Alfa Aesar, 99%) was recrystallized from water. Ultra pure water with a specific resistance of 18.2 \(\hbox {M}\Omega\) cm was produced from a water-purification system (OmniaTap UV, Stakpure, Germany).

Sulfamethoxazole (abbreviated SMX, supplier Ehrenstorfer, purity 99.0%), 4-amino-N-(5-methyl-2-oxazolyl)benzenesulfonamide (ISO, TLC Pharmaceutical Std., 99.6%), sulfanilic acid (SUA, TCI, \(>99\) %), 3-amino-5-methylisoxazole (AMI, TCI, > 97%), 2-amino-5-methyloxazole (AMO, Vlada Chem, > 95%) and aniline (ANI, Aldrich, 99.5%) were used as received. Sulfamethoxazole-D4 (SMX-D4, HPC Standards, 99.5%), sulfanilic acid-D4 (SUA-D4, TRC, 98.0%) and aniline-D5 (ANI-D5, CIL, \(\ge\) 98%) were used as internal standards in the LC–MSMS analysis.

Stock solutions of SMX, ISO, SUA, AMI, AMO and ANI in acetonitrile with concentrations of \(c\mathrm{(stock)} = 1000\; \mathrm{mg} \;\mathrm{L}^{-1}\) each and SMX-D4, SUA-D4 and ANI-D5 in acetonitrile with concentrations of \(c\mathrm{(stock)} = 100\; \mathrm{mg} \;\mathrm{L}^{-1}\) (for ANI-D5 \(1000\; \mathrm{mg} \;\mathrm{L}^{-1}\)) each were stored in the dark at \(T = -25 \; ^{\circ }\hbox {C}\) and were used in the preparation of dilutions and for calibration solutions. Diluted working solutions (\(c_0 = 1000 \; \upmu \mathrm{g} \; \mathrm{L}^{-1}\)) for photolysis experiments were always freshly prepared from stock solutions and the corresponding solvent (e.g., dist. water, buffer).

2.5 Description of the kinetic model

This study focused especially on the direct photolysis of SMX and ISO in buffered solutions with start concentrations below \(c \le \; 2 \, \upmu \mathrm{M}\) (\(\le \; 500 \, \upmu \mathrm{g}\, \mathrm{L}^{-1}\)) and without additives to prevent for instance the formation of OH-radicals. For the photon flux of the polychromatic Xe-light source and within the time range of \(t \le 500\) minutes loss reactions of AMI, AMO und SUA were negligible and set to zero. However, as discussed below, in photolysis reactions starting with ISO, a loss of AMO in basic solutions at pH = 8.5 was found. In a global model, equations summarized in the SI (Chapter S4.2 and S4.3) were used in parallel in a non-linear fit [62] for both cases starting with SMX or ISO. These cases include all compounds and for the fit relative concentrations of c(SMX), c(ISO), c(AMI), c(AMO), c(SUA) and c(ISO2) (see below for the discussion of the isomer ISO2) were used by division of the absolute concentrations by the start concentration \(c_0\mathrm{(SMX)}\) or \(c_0(\text{ ISO})\), respectively. All equations are based on \(1{\mathrm{st}}\)-order kinetics and are derived from the description of fundamental consecutive and parallel reactions [63]. The reaction scheme and the assignment of the rate constants for the case \(c_0({\rm SMX}) > 0\) and \(c_0(\text{ ISO}) = 0\) is shown in Fig. 5. The rate constant \(k = k_1 + k_2 + k_\mathrm{SUA} + k_S\) describes the loss of SMX, the rate constant \(k' = k_3 + k_\mathrm{ISO2} + k_I\) the loss of ISO. The rate constant \(k_1\) describes the formation of ISO, \(k_2\) the formation of AMI (and the corresponding equimolar formation of SUA), \(k_3\) the formation of AMO (and the equimolar formation of SUA), \(k_\mathrm{S}\) unknown loss reactions for SMX and \(k_\mathrm{I}\) corresponding unknown loss reactions for ISO. These rate constants are involved for both basic and acidic conditions starting with SMX. Starting from ISO, all rate constants directly related to SMX are zero and the scheme, therefore, simplifies drastically (see SI Chapter S4.2 and S4.3).

In the case of \(c_0\mathrm{(SMX)} > 0\) in addition three special rate constants were included into the kinetic scheme. For basic conditions it was found that \(c\mathrm{(SUA)} > c\mathrm{(AMI)} + c\mathrm{(AMO)}\) and it was necessary to include an additional formation reaction for SUA, represented by \(k_\mathrm{SUA}\). From the accuracy of the experimental data it was not possible to distinguish formation reactions of SUA directly from SMX or ISO or via (unknown) intermediate products. For simplicity reasons an additional formation of SUA from SMX was used comparable to the formation of AMI but with unknown products from the original isoxazole ring in SMX. For both acidic and basic conditions very low, and therefore, highly uncertain concentrations of a further isomer of SMX (ISO2) were found in the photolysis of SMX and ISO. However, for basic conditions even LC–MSMS areas (and estimated concentrations) were too low to be quantifiable. This unknown isomer is also formed from ISO without delay, typical for a direct formation and not as a product of a subsequent reaction (see the Sect. 3). Therefore, a direct formation from ISO is assumed with the rate constant \(k_\mathrm{ISO2}\) and the loss reaction \(k'_\mathrm{ISO2}\).

In the case of \(c_0(\text{ ISO}) > 0\) besides \(k_\mathrm{SUA}\) in addition a rate constant for the loss of AMO (\(k_\mathrm{AMO}\)) at high pH was necessary.

2.6 Quantum chemical calculations

Using density-functional theory (DFT), it is possible to predict Gibbs free energies of molecules starting from their geometry as input purely theoretically.

At finite temperatures, the description of a molecule by a single geometric (and corresponding electronic) structure can be unrealistic. With increasing molecular flexibility, a large number of conformers may exists within a very narrow energy window. All significantly populated conformers at a given temperature form a conformer ensemble (CRE) that determines the properties of the system. The population of conformer i is given by the Boltzmann distribution:

$$\begin{aligned} p_i = \frac{e^{\frac{-G_i}{kT}}}{\sum _i^\mathrm{conf.}{e^{\frac{-G_i}{kT}}}}, \end{aligned}$$
(2)

where \(p_i\) is the probability of a given conformer to be populated, \(G_i\) is the Gibbs free energy of conformer i, k is the Boltzmann constant and T the temperature of the system. Due to the flexibility of the investigated molecules, it was necessary to extensively screen their conformational space as described in [64]. CREs were created with the general force field GFN-FF [65] and irrelevant conformers were sorted out using the semiempirical GFN2-xTB [66] method using the CREST [67] program. The resulting CRE was then re-ranked on a higher DFT level of theory using the r2SCAN-3c [68] composite method. All these steps were paired with an implicit solvation model [69,70,71] for water, to take solvation effects into account.


The Gibbs free energies of the amine and imine tautomers of SMX and ISO, as well as of the TP271 derivatives were finally calculated as a Boltzmann weighted average over the energies of the relevant conformers as

$$\begin{aligned} \overline{G} = \sum _{i}^\mathrm{conf.}{p_i G_i}. \end{aligned}$$
(3)

Dipole moments for AMO, AMI, ISO and SMX were calculated accordingly by averaging over all relevant conformers.

The pKa value of AMO was calculated also at the r2SCAN-3c level from the CREs of the corresponding acid and base as described in [72]. The accuracy of this approach is estimated to be about \(\pm 0.5\) \(\mathrm{p}K_\mathrm{a}\) units for a wide range of molecules.

3 Results and discussion

3.1 Overview of compounds considered

LC–MSMS parameters and exemplary chromatograms are summarized in the SI (Table S1 and Figure S1, Figure S2) with detection limits in the range of DL = 2–7 nM. Only substances available as reference compounds and known to be products in the direct photolysis of SMX (and assumed of ISO) were used in the quantitative kinetic analysis. Therefore, ISO, 3-amino-5-methylisoxazole (AMI) and sulfanilic acid (SUA) were considered in the photolysis of SMX and the corresponding oxazole-derivative 2-amino-5-methyloxazole (AMO) and again SUA in the photolysis of ISO.

In addition to a large number of products formed by direct and indirect photolysis of SMX and detected by HRMS in assumed low concentrations, e.g., [21, 43, 56, 73], only a few products are available as reference compounds. These compounds include human metabolites, such as nitroso, nitro and hydroxylated derivatives of SMX [21, 74], also discussed in biotic degradation reactions [75], formed in, e.g., ozonolysis or indirect photolysis reactions [37, 42, 76,77,78] and explicitly avoided in this work and not considered in detail. In agreement with other studies [14, 33, 55, 57, 79], aniline was not found in any of the samples from experiments performed here. However, these results are in contradiction to experiments, where aniline is formed in the photolysis of SMX [11, 21, 42, 43]. It is interesting to note that the seldom reported and in this study not considered product (5-methyl-1,2-oxazol-3-yl)sulfamic acid in the photolysis of SMX [21, 42, 43] was always found together with aniline. Furthermore, unlike other sulfonamides, elimination of \({\mathrm{SO}}_2\) does not play a role for SMX [80].

Besides SMX and ISO another isomer of SMX (ISO2) was found in the photolysis of SMX and ISO. The sum formula of this third isomer was obtained via HRMS. The mass-to-charge ratio for protonated SMX and isomers is m/z (theo, \(\mathrm{C}_{10}\mathrm{H}_{12}\mathrm{N}_3\mathrm{O}_3\mathrm{S}^+\)) = 254.05939, the experimental value for all isomers was identical to m/z (\(\text{[SMX+H] }^+ = \text{[ISO+H] }^+ = \text{[ISO2+H] }^+\)) = 254.0602 (\(\Delta m/z = 3\; \mathrm{ppm}\)). The isomer ISO2 is formed from ISO and was, therefore, found in both photolysis reactions starting with SMX or ISO. The retention time of ISO2 (\(t_\mathrm{r} = 6.16\; \mathrm{min}\), see also SI, Figure S2) was the highest retention time of all compounds analysed (SI, Figure S1) and ISO2 is assumed to be the amine tautomer of ISO (vide infra). Very low concentrations of ISO2, estimated from the response of ISO, were found in the range of 0.1–0.5 mol% of ISO.

The last compound considered in more detail is the transformation product TP271, found at a retention time of 3.1 min. The sum formula of TP271 was obtained by comparison of the theoretical mass-to-charge ratio for protonated TP271 (m/z (theo, \(\mathrm{C}_{10}\mathrm{H}_{14}\mathrm{N}_3\mathrm{O}_4\mathrm{S}^+\)) = 272.06995) with the experimental value of the only peak in the chromatogram of m/z (\(\text{[TP271+H] }^+\)) = 272.0689 (\(\Delta m/z = -4\; \mathrm{ppm}\)). TP271 was characterized in [11] and the formation was explained as a byproduct in a hydrolysis reaction of the azirine-derivative leading to ISO (see Fig. 7). A theoretical study was performed (Sect. 3.5) to assess the thermodynamic stability using standard Gibbs free energies calculated for numerous products reported in the literature (see Sect. 1).

3.2 Properties of SMX and ISO and UV-spectra

Some basic properties of SMX and ISO are summarized in Table 1. Sulfonamides possess two dissociation equilibria [14, 81,82,83]. The equilibrium between cationic and neutral SMX is characterized by \(\mathrm{p}K_\mathrm{a1} = 1.6\) [14], the equilibrium between neutral and anionic SMX by \(\mathrm{p}K_\mathrm{a2} = 5.6\) [81]. The \(\mathrm{p}K_\mathrm{a2}\) of ISO was determined in this study to be \(\mathrm{p}K_\mathrm{a2} = 7.0 \pm 0.1\) (see UV-spectra in the SI, Figure S6). The protonation at the amine group of 4-amino-benzenesulfonamide is \(\mathrm{p}K_\mathrm{a} = 1.78\) [84] and comparable to the first \(\mathrm{p}K_\mathrm{a1}\) of known sulfonylamides [14, 81]. Hence, for ISO a \(\mathrm{p}K_\mathrm{a1}\) comparable to known sulfonylamides can be assumed and indeed no further change in the UV-spectra of ISO was found between \(3.5< \mathrm{pH} < 6\). As additional information the \(\mathrm{p}K_\mathrm{a} = \; 3.28\) (at \(T = 20\; ^{\circ }\hbox {C}\)) of SUA [85], the \(\mathrm{p}K_\mathrm{a} = \; 0.47\) of AMI [50] and the theoretically determined \(\mathrm{p}K_\mathrm{a} = \; 6.60\) of AMO should be mentioned.

Table 1 Properties of SMX and ISO
Full size table

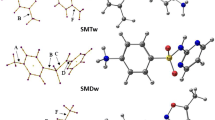
As for AMO and AMI, theoretical calculations indicated a prefered population of the amine tautomer for SMX (\(\Delta G^{-{\ominus }-}_{{\mathrm{imine}}\rightarrow \text{ amine }} = - 6.4\; \mathrm{kcal}\; \mathrm{mol}^{-1}\)). On the other hand, for ISO a preferred population of the imine tautomer (\(\Delta G^{-{\ominus }-}_{\text{ amine }\rightarrow \text{ imine }} = - 4.8\; \mathrm{kcal}\; \mathrm{mol}^{-1}\)) was found (see Fig. 1).

Fig. 1
figure 1

DFT calculated standard Gibbs free reaction enthalpies \(\Delta _\mathrm{R} G^{-{\ominus }-}\) of the amine and imine tautomers of SMX and ISO relative to the most stable ISO isomer

Full size image

These results are in agreement with qualitative experimental findings for AMI [50] and SMX and ISO [11]. Calculated dipole moments for the imine tautomers of AMO, AMI, ISO and SMX were found to be higher (but for SMX nearly comparable) than the corresponding amine-tautomers (see SI, Table S2). The imine tautomers discussed in this study can thus be assumed to be at least slightly more polar than the amine tautomers.

Corresponding differences could also be found for the octanol/water distribution constants \(K_\mathrm{OW}\) and \(K_\mathrm{D}\) by DFT calculations (see Table 1). For the imine tautomers of SMX and ISO \(\mathrm{log}(K_\mathrm{OW})\) are much lower and negative compared to the amine tautomers. Accordingly experimental values of \(\mathrm{log}(K_\mathrm{D})\) between pH = 5–9 for ISO are always negative with \(\mathrm{log}(K_\mathrm{OW}) = -1.15\) calculated by DFT. The reverse is true for SMX with positive \(\mathrm{log}(K_\mathrm{D})\) for pH \(< \mathrm{p}K_\mathrm{a2}\) [89] and \(\mathrm{log}(K_\mathrm{OW}) = 0.89\) [90].

Fig. 2
figure 2

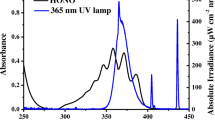
Molar decadic absorption coefficients (left scale) of ISO in buffered solutions at pH = 3.5 (pH \(\ll \mathrm{p}K_\mathrm{a2}\)) and at pH = 8.5 (pH \(\gg \mathrm{p}K_\mathrm{a2}\)). For comparison a typical spectrum of the polychromatic Xe-light source used in this study and a sun-spectrum (calculated with the STAR model [93]) for the 21.6.2021 at 52.3 \(^{\circ }\hbox {N}\), 10.4 \(^{\circ }\hbox {E}\), 11 UTC (right scale) is shown

Full size image

UV-spectra of SUA [54], AMI [50, 54] and SMX [20, 21, 26, 52, 54] with molar decadic absorption coefficients at different pH-values are available in the literature in agreement with values presented in this study (SI, Figure S5 and Figure S7). In addition the up to now not published UV-spectra for AMO are also included in the SI (Figure S7).

The UV-spectra of ISO below and above \(\mathrm{p}K_\mathrm{a2}\) are shown in Fig. 2, qualitatively discussed for pH \(< \mathrm{p}K_\mathrm{a2}\) in the literature [11]. The UV spectrum of ISO (and completely analogous for SMX) in acetonitrile is virtually identical to the UV spectrum of the neutral compound in the aqueous phase. The shoulder (at 243 nm) in the UV-spectrum of ISO at pH=3.3 is an indicator of the imine structure [11].

3.3 Photolysis of SMX and ISO

No other isomer (i.e., no ISO) was found in stock solutions of SMX, and a very low impurity of \(< 0.1\) mol% of SMX was found in stock solutions of ISO (SI, Figure S2). The kinetic curves obtained from two measurements each with the polychromatic Xe-light source for pH = 3.7 and pH=8.8 are shown in Figs. 3 and 4 (a typical spectrum of the polychromatic Xe-light source is shown in Fig. 2).

Fig. 3
figure 3

Normalized concentrations and kinetics of compounds quantified in the photolysis of SMX with a Xe-light source at pH = 3.7, \(T = 20\;^{\circ }\hbox {C}\) and \(c_0({\rm SMX}) \pm \sigma = (1.92 \pm 0.05)\; \upmu \mathrm{M}\). Lines are from a global model with all compounds involved, summarized in Fig. 5, Table 2 and the SI (Table S3). Note the different scalings of the ordinates

Full size image
Fig. 4
figure 4

Normalized concentrations and kinetics of compounds quantified in the photolysis of SMX with a Xe-light source at pH \(= 8.8\), \(T = 20\;^{\circ }\hbox {C}\) and \(c_0({\rm SMX}) \pm \sigma = (2.10 \pm 0.04)\; \upmu \hbox {M}\). Lines are from a global model with all compounds involved, summarized in Fig. 5, Table 2 and the SI (Table S3). Note the different scalings of the ordinates

Full size image

The kinetic scheme used is shown in Fig. 5, the rate constants obtained for all reactions involved from the overall fit of the reactions in Fig. 5 are summarized in the SI (Table S3 and Chapter S4.2 and S4.3) and for the calculation of the quantum yields of SMX and ISO in Table 2. The different yields (in percent) given in Fig. 5 of the compounds formed in acidic and basic solution were calculated by the fraction of the corresponding formation-rate constant and the loss-rate constant of SMX or ISO.

In acidic aqueous solution, AMI and SUA are formed from SMX in equimolar concentration. However, in basic solution a lower concentration of AMI than for SUA is obtained with a consequently additional formation for SUA (8 mol%) with unknown reaction of the original isoxazole ring. For simplicity, it was assumed that this additional pathway forms SUA directly and not via unknown intermediates. The SUA fraction of 20 mol% formed in basic solution and about 30 mol% in acidic solution is in agreement with values in [14] (35 mol% at pH=2) and [21] (20 mol%, but pH not specified). In [73] the direct photolysis of a high mass concentration of \(c({\rm SMX}) = 100 \; \mathrm{mg}\; \mathrm{L}^{-1}\) in unbuffered water leads to comparable mass concentrations of AMI and SUA of about \(10 \; \mathrm{mg}\; \mathrm{L}^{-1}\), i.e., in a molar ratio of \({\mathrm{AMI:SUA}} \approx 2:1\). Only a very low yield of 2% for AMI (but a higher yield of 11% of (5-methyl-1,2-oxazol-3-yl)sulfamic acid and 5% of aniline) was reported in [21]. In our measurements AMI was found to be stable in all solutions at different pH-values and for different light sources.

Due to the \(\mathrm{p}K_\mathrm{a} = 3.28\), the formation of SUA has a significant impact in unbuffered water on the development of the direct photolysis of SMX and ISO, especially if high start concentrations are used. An example is shown in the SI (Figure S8) for the development of the pH-value in the photolysis of ISO with the Hg-light source. Even for moderately concentrated start concentrations of \(c({\rm ISO}) = 13 \; \upmu \mathrm{M}\) (= 3.3 mg/L) a change of almost \(\Delta \mathrm{pH} = 0.8\) covering the important pH = 7 (i.e., \(\mathrm{p}K_\mathrm{a2}\) of ISO) was found.

Fig. 5
figure 5

Results of the photolysis of SMX with a Xe-light source at pH \(= 8.8\) (see Fig. 4, equation arrows in blue) and at pH \(= 3.6\) (see Fig. 3, equation arrows in red) at \(T = 20\;^{\circ }\hbox {C}\). Percentages are fractions of the different reaction channels in basic (in blue) and in acidic (in red) solution

Full size image

The formation of ISO in the photolysis of SMX, first reported in [11, 12], was also stated in [21, 33, 52, 54, 55], in [51] the time development of ISO was monitored by LC–MSMS.

In no case a photochemical back reaction of ISO to SMX was observed in this study. The yield of ISO of 28 mol% found in acidic solution is comparable to the estimated yield of 30 mol% given in [11]. In [15] the analysis of the reaction solution by LC–MSMS indicated that ISO was not formed through a OH-mediated reaction. Besides photolysis, other formation reactions of ISO in the dark are known. ISO is reported to be formed by microbially initiated one-electron reductive cleavage of the isoxazole N–O bond in SMX via the azirine intermediate [94] or in an electro-Fenton process [95]. AMO was assumed in addition or besides AMI [14], and assumed as a possible product (only at pH = 9) from ISO [37]. As for all other reaction pathways, the formation of AMO is pH dependent. Concentrations of AMO found in this study were low and rate constants of the formation and loss of AMO (see SI, Table S3) are uncertain. AMO was stable in acidic solutions using the polychromatic and the monochromatic light source, but was photolysed in basic solution. Concentrations of AMO in photolysis experiments of SMX with start concentrations of \(2\; \upmu \mathrm{M}\) were too low to be used in the evaluation of rate constants (see Fig. 4). From an independent performed photolysis of AMO with the Xe-light source at \(\hbox {pH}=8.5\) and the photolysis starting from ISO at pH=8.8 (see SI, Table S3) a highly uncertain rate constant of \(k_\mathrm{AMO} \pm \sigma = (0.007 \pm 0.004) \; \mathrm{min}^{-1}\) (considering different photon irradiances by about a factor of 2) with \(\Phi _\mathrm{AMO} \pm \sigma = (0.1 \pm 0.06)\) was obtained.

Besides SMX and ISO a third isomer ISO2 was detected and concentrations were estimated from the response of SMX and ISO. Concentrations at pH = 3.7 are already low (about 0.5 mol% with respect to and starting from SMX and 2 mol% with respect to and starting from ISO) and were too low at pH=8.8 to be quantified. The kinetics of the formation of ISO2 starting from SMX and ISO is shown in the SI, Figure S3. As expected ISO2 is directly formed starting from ISO and in a consecutive reaction via ISO starting from SMX. This kinetic behaviour supports, therefore, the assumption that ISO2 is formed from ISO. Furthermore, and as already stated above, ISO2 degrades in a dark reaction at \(\mathrm{T} = 20\; ^{\circ }\hbox {C}\) in acidic solution as the only compound investigated with a lifetime of \(\tau = 109\; \mathrm{h}\) (see SI, Figure S4). These experimental facts and, in addition, the highest retention time of all isomers suggest that ISO2 may be the relatively non-polar amine tautomer of ISO (see Fig. 1).

3.4 Quantum yields

To evaluate the quantum yields of ISO, quantum yields of SMX were also measured for comparison. All experiments were performed at \(T = 20\; ^{\circ }\hbox {C}\) and were, furthermore, carried out with the polychromatic Xe light source and the monochromatic Hg lamp. An extraordinary number of quantum yields for SMX have been reported in the literature, some of which are contradictory. The unusually large database prompted us to calculate recommended quantum yields below (\(\Phi _\mathrm{N}\)) and above (\(\Phi _\mathrm{A}\) ) the \(\mathrm{p}K_\mathrm{a2}\) from the available data. However, contrary to the large number of quantum yields of SMX in aqueous solutions, surprisingly, no quantum yields of SMX in organic solvents are known. In addition to prospective measurements in various organic solvents (data not discussed here), the quantum yields of SMX and ISO in acetonitrile were determined.

Table 2 Quantum yields \(\Phi\) and corresponding rate constants k (in \(\mathrm{min}^{-1}\)) of sulfamethoxazole (SMX) and the isomer of SMX (ISO) from 11 kinetic runs in buffered aqueous solutions at 20 \(^{\circ }\hbox {C}\)
Full size table

Quantum yields of SMX and ISO in aqueous solutions with necessary parameters such as rate constants and photon irradiances are summarized in Table 2. With the given errors, quantum yields independent of the light source were obtained for all pH values and mean values were used.

The mean quantum yield of SMX determined in this study for both light sources (polychromatic Xe-lamp and monochromatic Hg-light source) at \(\hbox {pH}=3.7\) is \(\Phi _\mathrm{N} = 0.15 \pm 0.01\), at \(\hbox {pH}=8.6\) \(\Phi _\mathrm{A} = 0.03 \pm 0.001\). As discussed above, a \(\hbox {pH}=3.7\) is assumed to be above \(\mathrm{p}K_\mathrm{a1}\) of ISO. The corresponding quantum yield of ISO determined in this study for both light sources at \(\hbox {pH}=3.7\) is \(\Phi _\mathrm{N} = 0.06 \pm 0.02\), at \(\hbox {pH}=8.6\) \(\Phi _\mathrm{A} = 0.05 \pm 0.01\).

Quantum yields in acetonitrile from two independent measurements starting from SMX and ISO are \(\Phi = 0.12\) (SMX) and \(\Phi = 0.09\) (ISO) and are thus comparable to the corresponding quantum yields \(\Phi _\mathrm{N}\). However, in contrast to the measurements in the acidic environment, a very low yield of 1% of ISO but a high yield of 55% of AMI is found in acetonitrile.

With the dissociation fraction \(\alpha\) and the quantum yields of the neutral species, \(\Phi _\mathrm{N}\), and the anionic species, \(\Phi _\mathrm{A}\), the apparent quantum yield is \(\Phi = \Phi _\mathrm{N} \cdot (1 - \alpha )\) + \(\Phi _\mathrm{A} \cdot \alpha\). Substitution of the dissociation fraction \(\alpha\) from the Henderson–Hasselbalch equation leads to

$$\begin{aligned} \Phi = \Phi _\mathrm{N} + \frac{\Phi _\mathrm{A} - \Phi _\mathrm{N}}{10^{\mathrm{p}K_\mathrm{a2} - pH} + 1} \end{aligned}$$
(4)
Fig. 6
figure 6

Plot of \({N}=30\) recommended pH-dependent quantum yields \(\Phi\) of SMX versus pH (\(3 \le \mathrm{pH} \le 9\)). All quantum yields found in the literature are shown in the insert excluding values around \(\mathrm{p}K_\mathrm{a1}\), at undefined pH-values (i.e., pure water) and below \(\Phi < 0.001\). Circles = quantum yields using monochromatic light sources, squares = quantum yields using polychromatic light sources, filled symbols = this work. The solid line is the result from a fit of Eq. (4), the dotted lines are values for \(\Phi \pm 2\sigma\). Any error bars given are not shown for clarity

Full size image

In sum \({N}=69\) pH-dependent quantum yields of SMX were found in the literature (details in an Excel-sheet in the SI). Quantum yields of SMX at or below \(\mathrm{p}K_\mathrm{a1}\) with \(\Phi \approx 0\) [14, 23, 36] and quantum yields in water [15,16,17, 25, 29] with undefined pH were excluded. From the remaining (\({N}=58\)) quantum yields published in [11,12,13,14,15, 17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] recommended values (\(N=30\)) were used from [11, 12, 14, 18, 20, 21, 24, 26, 27, 31,32,33,34,35,36] in a non-linear fit from Eq. (4) to obtain \(\Phi _\mathrm{A}\) and \(\Phi _\mathrm{N}\) (see Fig. 6).

Quantum yields of SMX using values from monochromatic light sources only (\({N}=19\)) are \(\Phi _\mathrm{N} \pm 2\sigma = 0.19 \pm 0.03\) and \(\Phi _\mathrm{A} \pm 2\sigma = 0.040 \pm 0.014\), from polychromatic light sources only (\({N}=11\)) are \(\Phi _\mathrm{N} \pm 2\sigma = 0.13 \pm 0.05\) and \(\Phi _\mathrm{A} \pm 2\sigma = 0.057 \pm 0.028\) and for all values (\({N}=30\)) \(\Phi _\mathrm{N} \pm 2\sigma = 0.17 \pm 0.03\) and \(\Phi _\mathrm{A} \pm 2\sigma = 0.046 \pm 0.014\) (fit shown in Fig. 6). The quantum yields for the different light sources, identical within measurement errors, imply that both \(\Phi _\mathrm{N}\) and \(\Phi _\mathrm{A}\) for SMX and ISO do not depend on wavelength. Accordingly, SMX as well as ISO are examples of compounds that satisfy the Kasha–Vavilov rule [96, 97].

3.5 Formation of TP271

As already discussed in the Introduction, closely related to the formation of ISO from SMX is a side reaction of the intermediate azirine derivative shown in Fig. 7.

Fig. 7
figure 7

Possible products from the azirine-derivative formed as intermediate after photolysis of SMX. Cleavage of the bonds A and B in the azirine derivative and subsequent hydrolysis or rearrangement leads to 6 different compounds (including the back-reaction to SMX itself). The product TP271d was never mentioned in the literature, for differences in \(\Delta G\) see Table 3

Full size image

The formation of the transformation product TP271, described and characterized in [11], was explained from the hydrolysis of the azirine derivative. Homolytic cleavage at bond A (see Fig. 7) leads to ISO, cleavage at bond B provides the back reaction to SMX. A heterolytic cleavage and reaction with water at bonds A and B yields four potential products. TP271 [11] and the never described isomer TP271d are reached via pathway A, while TP271b, described in [94], as well as TP271e, reported in [23], are obtained via pathway B.

For deriving the structure of TP271, NMR spectra, MS spectra and chemical methods were used [11], for all other alternative structures shown in Table 3 no evidence other than MS fragments or even only MRM transitions were used. To assess the importance of isomers TP271a–TP271h reported in the literature in comparison with TP271 \(\Delta _\mathrm{R} G^{-{\ominus }-}\) was calculated relative to TP271. \(\Delta _\mathrm{R} G^{-{\ominus }-}\) thus corresponds to the reaction of the isomers TP271a–TP271h to TP271, respectively. The calculated data summarized in Table 3 show, that the thermodynamically most stable isomer is TP271. Accordingly, the quantum mechanical calculations provide very strong arguments that the given structures for TP271a–TP271h as transformation products in the direct photolysis of SMX are not correct. Thus, if a transformation product with the molecular formula \(\mathrm{C}_{10}\mathrm{H}_{13}\mathrm{N}_{3}\mathrm{O}_{4}\mathrm{S}\) is found in the direct photolysis of SMX, it is very likely to be TP271.

Table 3 Transformation products with a molar mass of \(M= 271 \; \mathrm{g}\; \mathrm{mol}^{-1}\) reported in the literature and their \(\Delta _\mathrm{R} G^{-{\ominus }-}\)-values (in \(\mathrm{kcal}\; \mathrm{mol}^{-1}\)) calculated in this study by DFT relative to TP271
Full size table

3.6 Environmental concentrations in river water

SMX and ISO were also analysed as part of campaigns in 2020/2021 in the Wietze, a small river in Northern Germany (latitide \(52.6 \; ^{\circ }\hbox {N}\)). Details on sampling and preparation of the aqueous samples for analysis by LC–MSMS are compiled in [61]. The sampling area, location of the sample sites, and details of the concentrations obtained are summarized in the SI (Chapter S5).

Survey measurements between February 2020 and September 2021 provided mean daily concentrations for SMX in the river water ranging from \(c = 43 - 337 \; \mathrm{ng}\; \mathrm{L}^{-1}\), strongly dependent on the volume flow of the Wietze River and thus also on the season. As expected variations in concentrations of SMX in the effluent of the largest WWTP were much lower with values of \(c = 319 - 748 \; \mathrm{ng}\; \mathrm{L}^{-1}\). In none of the analysed 80 samples ISO could be found above the limit of quantification (\(LOQ = 2 \; \mathrm{ng}\; \mathrm{L}^{-1}\)).

On June 28, 2021 ten monitoring sites in a special “summer campaign” were sampled in a section of the Wietze River without tributaries over a distance of 9 km. In these measurements with a \(\hbox {pH} = 7.7\) mean concentrations were \(c({\rm SMX}) \pm \sigma = (121 \pm 17)\; \mathrm{ng}\; \mathrm{L}^{-1}\) and \(c({\rm ISO}) \pm \sigma = (8 \pm 2)\; \mathrm{ng}\; \mathrm{L}^{-1}\). The concentrations of ISO are consistent compared to the concentrations of SMX due to the 17% yield in the basic environment (see Fig. 5) and the higher degradation rate constant of ISO relative to SMX (see Table 2).

Even for the special “summer campaign” for none of the compounds a decrease (SMX) or increase (ISO) of the concentration in the watercourse of the Wietze could be proven. A rough estimation of the minimum half-life of SMX (and ISO) is possible from the uncertainty of concentrations found. A minimum half-life for SMX in surface water is obtained for \(t =\; 5\; \mathrm{h}\) (calculated from the distance of 9 km and a flow rate of \(v =\; 0.5 \; \mathrm{m}\; \mathrm{s} ^{-1}\)) and an assumed maximum decrease in concentration of 20%. However, this half-life, valid for the time of measurement, must be corrected and increases by about a factor of 2–3, since all measurements were made over noon with maximum solar radiation and the day–night cycle must be considered. Taking all these factors into account the minimum half-life of SMX in the Wietze River for a summer day is \(t_{1/2} \gg 45\; \mathrm{h}\).

For comparison qualitative information about the abiotic degradation of SMX with a light source simulating sunlight [22, 56, 98] and calculated and measured half-lives for sunlight are available. Reported half-lives of SMX in the literature are highly variable. Even for similar time periods and latitudes, values are given that differ by more than a factor of 10. Thus, pH plays a significant role in addition to the quantum yield itself (for calculated values). SMX, and thus presumably ISO, is predominantly degraded even in natural waters via direct photolysis [14, 98]. In addition, the concentrations of nitrate and DOC (e.g., also via an internal filter effect [13]) as well as morphological parameters such as water depths influence the half-lives in model scenarios or in laboratory measurements.

Thus, for the latitude \(47 \; ^{\circ }\hbox {N}\) in acidic solution half-lives with \(t_{1/2} = \; 10.4\; \mathrm{and} \; 44\; \mathrm{h}\) (summer/winter) [21] or for the latitude \(50 \; ^{\circ }\hbox {N}\) in acidic solution \(t_{1/2} = \; 58\; \mathrm{h}\) for winter [14] were given. Much higher half-lives at pH=7 of \(t_{1/2} = \; 300\; \mathrm{h} \; \mathrm{and} \; 750\; \mathrm{h}\) (summer/winter) for latitude \(22.3 \; ^{\circ }\hbox {N}\) are calculated in [27] via the SMART model and in [30] at \(\hbox {pH}=7\) for the summer period of \(t_{1/2} =\; 96 - 2160\; \mathrm{h}\) using the Apex model for variable water parameters.

Furthermore, half-lives measured in sunlight (May–June) for Minneapolis (USA, latitude \(45 \; ^{\circ }\hbox {N}\)) in buffer solutions were given as \(t_{1/2} = \; 5\; \mathrm{h}\) (\(\hbox {pH}=5.3\)) and \(t_{1/2} = \; 35\; \mathrm{h}\) (\(\hbox {pH}=6.9\)) [14] and for Sydney (Australia, latitude \(33.55 \; ^{\circ }\hbox {S}\)) in acidic solution as \(t_{1/2} = \; 1\; \mathrm{and}\; 9.6\; \mathrm{h}\) (summer/winter) [12].

4 Conclusions

The predominant presence of the tautomeric amine structure in SMX and the imine structure in ISO defines the properties of both compounds and should always be correctly reproduced. The direct photolysis of SMX and of ISO below and above the respective \(\mathrm{p}K_\mathrm{a}\) value proceeds at different rates with different yields of the analysed compounds. The yield for ISO from photolysis of SMX above \(\mathrm{p}K_\mathrm{a2}\) is only about half as large (17 mol%) compared to the yield in the acidic range (28 mol%). Using the products SUA, AMI and ISO, the mass balance found for the photolysis of SMX in the acidic range (pH \(< \mathrm{p}K_\mathrm{a2}\) is roughly 60%, and only 40% in the basic range. In the corresponding photolysis of ISO using the products SUA and AMO, the mass balance is extremely poor in all pH ranges with \(< 15\)%.

Concentrations of SMX and ISO were further measured in natural samples from a surface water body in the Wietze river, a typical river in the North German Plain. A degradation of SMX or an increase of ISO could not be found in the Wietze river even in a summer campaign in 2021 for a, however, small flow distance of 9 km. In agreement with the measured quantum yield of ISO from SMX for pH \(> \mathrm{p}K_\mathrm{a2}\) of \(\Phi = 0.05\), the mean concentrations of ISO are low at \(c({\rm ISO}) = 8\; \mathrm{ng}\; \mathrm{L}^{-1}\) compared with the mean concentrations for SMX of \(c({\rm SMX}) = 120\; \mathrm{ng}\; \mathrm{L}^{-1}\). From the analytical uncertainties half-lives of SMX and ISO in the range of days for the summer months for latitudes in the northern part of Germany were estimated. Assuming a degradation of both compounds by direct photolysis and the reduction of available sun-light intensities in winter half-lives of both compounds in a surface water in winter are assumed to be in the range of weeks.

The found quantum yields of SMX and of ISO are independent of the wavelength within the experimental errors. However, various measurements reported in the literature on the quantum yields of SMX are doubtful or not comparable with other values due to insufficient specification of, e.g., the pH value. Thus, out of 69 quantum yields found, only roughly half were used to calculate the quantum yield of the anionic and the neutral form of SMX.

Besides the formation of ISO from SMX, a competing reaction is the formation of the transformation product TP271. Many alternative structures, often insufficiently characterised, have been reported in the literature (products TP271a-TP271h). A quantum mechanical calculation of the free enthalpies of these products yields the result that all alternative structures are significantly higher in energy and must, therefore, be regarded as insignificant.