Besov regularity of inhomogeneous parabolic PDEs

Abstract

We study the regularity of solutions of parabolic partial differential equations with inhomogeneous boundary conditions on polyhedral domains $D\subset \mathbb {R}^3$ in the specific scale $\ B^{\alpha }_{\tau ,\tau }, \ \frac{1}{\tau }=\frac{\alpha }{3}+\frac{1}{p}\$ of Besov spaces. The regularity of the solution in this scale determines the order of approximation that can be achieved by adaptive numerical schemes. We show that for all cases under consideration the Besov regularity is high enough to justify the use of adaptive algorithms. Our results are in good agreement with the forerunner (Dahlke and Schneider in Anal Appl 17:235–291, 2019), where parabolic equations with homogeneous boundary conditions were investigated.

1 Introduction

This paper is concerned with the regularity theory of partial differential equations (=PDEs) of parabolic type. The analysis of parabolic PDEs has a long history and a lot of results concerning existence and uniqueness of solutions are known. However, in most cases, an analytic expression of the solution is not available, so that numerical algorithms for the constructive approximation of the unknown solution up to a given tolerance are needed. Our main goal here is to justify the use of adaptive schemes when solving parabolic PDEs numerically, in particular on non-smooth domains $\Omega \subset \mathbb {R}^d$. As a prototype of our investigations one may think of the heat equation with inhomogeneous initial boundary conditions, i.e.,

$$\begin{aligned} \frac{\partial u}{\partial t}-\Delta u= f \quad \text {in} \quad (0,T]\times \Omega ,\quad u=g \quad \text {on} \quad [0,T]\times \partial \Omega , \quad u|_{t=0}=u_0 \quad \text {in} \quad \Omega ,\nonumber \\ \end{aligned}$$

(1.0.1)

where u is the unknown solution describing the distribution of heat over time, the right hand side f represents an outer heat source, g is some adequate function defined on the boundary, and $u_0$ is a function which represents the initial temperature at time $t = 0$. We treat more general parabolic PDEs of higher order in the course of our investigations as well.

We are interested in regularity properties of the unknown solution u in specific nonstandard smoothness spaces, i.e., the so-called adaptivity scale of Besov spaces

$$\begin{aligned} B^{\alpha }_{\tau ,\tau }(\Omega ), \quad \frac{1}{\tau }=\frac{\alpha }{d}+\frac{1}{2}, \quad \alpha >0, \end{aligned}$$

(1.0.2)

where $\alpha >0$ stands for the smoothness of the solution and $\tau$ displays its integrability. The smoothness in these scales of spaces is related with the achievable convergence order of adaptive algorithms. To briefly explain the concept, in an adaptive strategy the choice of the underlying degrees of freedom is not a priori fixed but depends on the shape of the unknown solution. In particular, additional degrees of freedom are only spent in regions where the numerical approximation is still ‘far away’ from the exact solution.

On the other hand, it is the regularity of the solution in the scale of (fractional) Sobolev spaces $H^s(\Omega )$, where now s indicates the smoothness of u, which encodes information on the convergence order for nonadaptive (uniform) methods. Thus, we can justify the use of adaptivity if the smoothness of the exact solution of a given PDE within the scale of Besov spaces is high enough compared to its classical Sobolev smoothness, i.e., when $\alpha >s$.

For elliptic PDEs there are a lot of positive results in this context. For example, for the Poisson equation with homogeneous Dirichlet conditions it is well-known that if the domain under consideration, the right-hand side, and the coefficients are sufficiently smooth, then the problem is completely regular and there is no reason why the Besov smoothness should be higher than the Sobolev smoothness. However, on nonsmooth (e.g. polyhedral) domains, the situation changes completely. On these domains, singularities at the boundary may occur that diminish the Sobolev regularity of the solution significantly, cf. [6, 17, 18, 20] (but can be compensated by suitable weight functions). However, recent studies show that these boundary singularities do not influence the Besov regularity too much, cf. [7, 8], so that for certain nonsmooth domains the use of adaptive algorithms is completely justified. In [29] the authors contributed to these studies and also obtained positive results for the Poisson equation with inhomogeneous (Dirichlet, Neumann as well as mixed) boundary conditions.

Concerning parabolic PDEs not much is known in this respect so far. A first step in this direction was done by Aimar et al. [1] and later on continued in [2, 3]. These studies are limited to the heat equation with zero Dirichlet boundary conditions, i.e., (1.0.1) with $g=u_0=0$. Moreover, in [10, 11] the authors obtained Besov regularity estimates for more general linear and nonlinear parabolic PDEs but again for zero Dirichlet boundary conditions only. In good agreement with the elliptic setting in all parabolic problems studied it turns out that (again) adaptivity pays off.

Unfortunately, all results established so far for parabolic PDEs do not deal with inhomogeneous boundary conditions, which is very restrictive in view of possible applications. It is our intention to close this gap now with our investigations.

As a main tool for establishing our results we work with weighted Sobolev spaces defined on domains of polyhedral type D, whose importance in this context comes from the fact that the weights can compensate the above mentioned singularities of the solutions at the boundary. Our specific weighted Sobolev spaces (which will be briefly refered to as V-spaces in the sequel) are taken from Maz’ya, Rossmann [26] and can be seen as a refinement of the well-known Kondratiev spaces. However, in contrast to the Kondratiev spaces, our V-spaces here invoke mixed weights, which reflect in a more subtle way the distance(s) to the vertices and edges of the underlying polyhedral domain.

Kondratiev spaces have been heavily used for regularity studies in the past, since they are very much related with Besov spaces in the adaptivity scale (1.0.2), in the sense that powerful embedding results exist, see, e.g. [19].

For our purposes, in Theorem 2.10 we transfer these embeddings to the setting of our V-spaces and obtain

$$\begin{aligned} V_{\varvec{\beta },\delta }^{l,p}(D)\cap B_{p,p}^s(D)\hookrightarrow B_{\tau ,\tau }^{\alpha }(D), \quad \alpha <\min \Big \{{l},{3(l-|\delta ^+|)}, {3s} \Big \},\quad \frac{1}{\tau }=\frac{\alpha }{3}+\frac{1}{p} , \end{aligned}$$

(1.0.3)

subject to some further restrictions on the parameters. In particular, the parameter l above denotes the smoothness and p the integrability of the function considered, whereas $\varvec{\beta },\delta$ are exponents related with the weights measuring the distance to the vertices and edges of the domain D of polyhedral type. As can be seen from (1.0.3), having established regularity in the scale of V-spaces as well as fractional Sobolev spaces (using the coincidence $B^{s}_{2,2}(D)=H^s(D)$) in turn yields Besov regularity of the solution under consideration.

Having this in mind we process as follows: first we improve and generalize the findings from [10, 28] for parabolic PDEs with homogeneous boundary conditions from Kondratiev to V-spaces.

Afterwards, in order to obtain regularity results for parabolic PDEs with inhomogeneous initial boundary conditions, we adapt the proofs from [28] by reducing the inhomogenous parabolic problem to a similar (easier) one, where only homogeneous boundary terms appear (e.g. for the heat equation in (1.0.1) this leads to a similar problem with new boundary term ${\tilde{g}}=0$, a new right hand side ${\tilde{f}}$ and initial condition ${\tilde{u}}_0$, which then depend on g). There are similar strategies to reduce inhomogeneous elliptic problems to homogeneous ones, but for parabolic equations this is technically more involved and requires a more subtle analysis (in particular in view of the regularity of g). With this reduction strategy we are then able to establish Sobolev and weighted Sobolev regularity results for parabolic PDEs with inhomogeneous boundary conditions. These together with our embedding result (1.0.3) finally allow us to establish Besov and Hölder–Besov regularity for our parabolic problems.

The paper is organized as follows. In Sect. 2 we introduce the relevant function spaces needed for our investigations, in particular, the weighted Sobolev spaces (V-spaces), Besov spaces, and certain Banach-space valued function spaces as well as Hölder-spaces.

In Sect. 3 we provide regularity results in Sobolev spaces with and without time derivatives for the inhomogeneous parabolic problem. Afterwards we establish regularity results the scale of V-spaces for the homogeneous as well as the inhomogeneous problem. Then using our embedding result we deduce regularity in the scales of (Hölder-)Besov spaces. Finally, we give a short discussion and comparison of our findings with the forerunners from [28].

2 Preliminaries

Notation

We start by collecting some general notation used throughout the paper. As usual, $\mathbb {N}$ stands for the set of all natural numbers, $\mathbb {N}_0={\mathbb {N}}\cup \{0\}$, $\mathbb {Z}$ denotes the integers, and $\mathbb {R}^d$, $d\in \mathbb {N}$, is the d-dimensional real Euclidean space with |x|, for $x\in \mathbb {R}^d$, denoting the Euclidean norm of x. Moreover, by $[\cdot ]$ we denote the floor function $[x]:=\max \{m\in \mathbb {Z}: \, m\le x\}$ for $x\in \mathbb {R}$. Let $\mathbb {N}_0^d$ be the set of all multi-indices, $\alpha = (\alpha _1, \ldots ,\alpha _d)$ with $\alpha _j\in \mathbb {N}_0$ and $|\alpha |:= \sum _{j=1}^d \alpha _j$. Then for partial derivatives we write $\partial ^\alpha f=\frac{\partial ^{|\alpha |}f}{\partial x^\alpha }$. Furthermore, $B_r(x)$ is the open ball of radius $r >0$ centered at x.

We denote by c a generic positive constant which is independent of the main parameters, but its value may change from line to line. The expression $A\lesssim B$ means that $A \le c\,B$. If $A \lesssim B$ and $B\lesssim A$, then we write $A \sim B$.

Throughout the paper ’domain’ always stands for an open and connected set. The test functions on a domain $\Omega$ are denoted by $C^{\infty }_0(\Omega )$. Let $L_p(\Omega )$, $1\le p\le \infty$, be the Lebesgue spaces on $\Omega$ as usual. We denote by ${C}(\Omega )$ the space of all bounded continuous functions $f:\Omega \rightarrow \mathbb {R}$ and ${C}^k(\Omega )$, $k\in \mathbb {N}_0$, is the space of all functions $f\in {C}(\Omega )$ such that $\partial ^{\alpha }f\in {C}(\Omega )$ for all $\alpha \in \mathbb {N}_0$ with $|\alpha |\le k$, endowed with the norm $\sum _{|\alpha |\le k}\sup _{x\in \Omega }|\partial ^{\alpha }f(x)|$.

Moreover, the set of distributions on $\Omega$ will be denoted by ${\mathcal {D}}'(\Omega )$, whereas ${\mathcal {S}}'(\mathbb {R}^d)$ denotes the set of tempered distributions on $\mathbb {R}^d$.

Lipschitz diffeomorphism and Lipschitz domain

We say that the one-to-one mapping $\Phi :\mathbb {R}^d\rightarrow \mathbb {R}^d$ is a Lipschitz diffeomorphism, if the components $\Phi _k(x)$ of $\Phi (x)=(\Phi _1(x),\ldots ,\Phi _d(x))$ are Lipschitz functions on $\mathbb {R}^d$ and

$$\begin{aligned} | \Phi (x)-\Phi (y)|\sim |x-y|\quad \text {for} \quad x,\, y \in \mathbb {R}^d \quad \text {with} \quad |x-y|\le 1 , \end{aligned}$$

where the equivalence constants are independent of x and y. Then the inverse of $\Phi$ is also a Lipschitz diffeomorphism on $\mathbb {R}^d$. We define a Lipschitz domain according to [28, Def. 2.1.1] as follows: Let $\Omega$ be a bounded domain in $\mathbb {R}^d$ with boundary $\Gamma =\partial \Omega$. Then $\Omega$ is said to be a (bounded) Lipschitz domain, if there exist N open balls $K_1,\ldots ,K_N$ such that $\ \bigcup _{j=1}^N K_j \supset \Gamma$ and $K_j\cap \Gamma \ne \emptyset$ if $j=1,\ldots ,N$, with the following property: for every ball $K_j$ there are Lipschitz diffeomorphisms $\psi ^{(j)}$ such that $\psi ^{(j)}:\, K_j \longrightarrow V_j$ for $j=1,\ldots ,N$, where $V_j:=\psi ^{(j)}(K_j)$ and

$$\begin{aligned} \psi ^{(j)}(K_j\cap \Omega )\subset \mathbb {R}^d_+,\quad \psi ^{(j)}(K_j\cap \Gamma )\subset \mathbb {R}^{d-1}. \end{aligned}$$

Sobolev and fractional Sobolev spaces

Let $m \in \mathbb {N}_0$ and $1\le p \le \infty$. Then $W^{m}_p(\Omega )$ denotes the standard $L_p$-Sobolev spaces of order m on the domain $\Omega$, equipped with the norm

$$\begin{aligned} \Vert \, u \, |W^m_{p}(\Omega )\Vert := \Big (\sum _{|\alpha |\le m} \int _\Omega |\partial ^\alpha u(x)|^p\,dx\Big )^{1/p}. \end{aligned}$$

By $\mathring{W}^m_{p}(\Omega )$ we denote the closure of ${\mathcal {D}}(\Omega )$ in $W^m_p(\Omega )$, where ${\mathcal {D}}(\Omega )$ stands for the collection of all infinitely differentiable functions with support compactly contained in $\Omega$.

If $p=2$ we shall also write $H^m(\Omega )$ instead of $W^m_2(\Omega )$. Moreover, for $s\in \mathbb {R}$ we define the fractional Sobolev spaces ${H}^s(\mathbb {R}^d)$ as the collection of all $u\in {\mathcal {S}}'(\mathbb {R}^d)$ such that

$$\begin{aligned} \Vert u|{H}^s(\mathbb {R}^d)\Vert := \Vert {\mathcal {F}}^{-1}((1+|\xi |^2)^{s/2} {\mathcal {F}}u )|L_2(\mathbb {R}^d) \Vert <\infty , \end{aligned}$$

where ${\mathcal {F}}$ denotes the Fourier transform with inverse ${\mathcal {F}}^{-1}$. These spaces partially coincide with the classical Sobolev spaces for $s=m$ with $m\in \mathbb {N}_0$. Corresponding spaces on domains can be defined via restrictions of functions from ${H}^s(\mathbb {R}^d)$ equipped with the norm

$$\begin{aligned} \Vert u|{H}^s(\Omega )\Vert := \inf \left\{ \Vert g|{H}^s(\mathbb {R}^d) \Vert :\, g\in {H}^s(\mathbb {R}^d),\, g|_{\Omega }=u \right\} . \end{aligned}$$

If, additionally, $\Omega \subset \mathbb {R}^d$ is a bounded Lipschitz domain, then for $s=m+\sigma$ with $m\in \mathbb {N}_0$ and $\sigma \in (0,1)$, an alternative norm comes from the Sobolev–Slobodeckij spaces and is given by

$$\begin{aligned} \Vert u|H^s(\Omega )\Vert = \Vert u|H^m(\Omega )\Vert + \displaystyle \sum _{|\alpha |=m} \left( \int _{\Omega } \int _{\Omega } \frac{|\partial ^{\alpha }u(x)-\partial ^{\alpha }u(y) |^2}{|x-y |^{d+2\sigma }} \,dx\,dy \right) ^{1/2} <\infty . \end{aligned}$$

This follows from the extension operator in [17, Thm. 1.2.10] and the fact that the corresponding spaces defined on $\mathbb {R}^d$ coincide, cf. [33, Sect. 2.3.5].

The following definition of domains of polyhedral type can be found in [26, Def. 4.1.1].

Definition 2.1

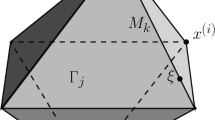
A bounded domain $D\subset \mathbb {R}^3$ is said to be a domain of polyhedral type if

• (i) the boundary $\partial D$ consists of smooth (of class $C^{\infty }$) open two-dimensional manifolds $\Gamma _j$ (the faces of D), $j = 1,\ldots ,n$, smooth curves $M_k$ (the edges), $k = 1,\ldots ,d$, and vertices $x^{(1)},\ldots ,x^{(d')}$,

• (ii) for every $\xi \in M_k$ there exist a neighborhood ${\mathcal {U}}_{\xi }$ and a diffeomorphism (a $C^{\infty }$ mapping) $\kappa _{\xi }$ which maps $D\cap {\mathcal {U}}_{\xi }$ onto ${\mathcal {D}}_{\xi }\cap B_1$, where ${\mathcal {D}}_{\xi }$ is a dihedron and $B_1$ is the unit ball,

• (iii) for every vertex $x^{(j)}$ there exist a neighborhood ${\mathcal {U}}_j$ and a diffeomorphism $\kappa _j$ mapping $D\cap {\mathcal {U}}_j$ onto $K_j\cap B_1$, where $K_j$ is a cone with edges and vertex at the origin.

The set $M_1\cup \cdots \cup M_d\cup \{ x^{(1)},\ldots ,x^{(d')} \}$ of the singular boundary points is denoted by S.

Remark 2.2

• We do not exclude the cases $d=0$ and $d'=0$. In the latter case, the set S consists only of smooth non-intersecting edges. In Fig. 1 we can see a typical domain of polyhedral type, the so called Fichera corner. Figures 2 and 3 illustrate the cases when $d=0$ and $d'=0$, respectively.

• Not every domain of polyhedral type is a Lipschitz domain. An easy counterexample is given by two cuboids lying on top of each other, cf. [15, Example 6.5].

Fig. 1

A domain of polyhedral type

Fig. 2

The case $d=0$

Fig. 3

The case $d'=0$

2.1 Weighted Sobolev spaces for domains of polyhedral type

In order to study the regularity of parabolic PDEs in weighted Sobolev spaces on domains of polyhedral type we introduce in this subsection the space $V_{\varvec{\beta },\delta }^{l,p}(D)$ using [26, Subsec. 4.1.2] with D being a bounded domain of polyhedral type.

Definition 2.3

Let $D\subset \mathbb {R}^3$ be a bounded domain of polyhedral type with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$. We denote the distance of x from the edge $M_k$ by $r_k(x)$ and the distance from the vertex $x^{(j)}$ by $\rho _j(x)$. Furthermore, we denote by $X_j$ the set of all indices k such that the vertex $x^{(j)}$ is an end point of the edge $M_k$. Let ${\mathcal {U}}_1,\ldots ,{\mathcal {U}}_{d'}$ be domains in $\mathbb {R}^3$ such that

$$\begin{aligned} {\overline{D}}\subset {\mathcal {U}}_1\cup \cdots \cup {\mathcal {U}}_{d'},\quad x^{(i)} \notin \overline{{\mathcal {U}}}_j\,\,\text {if}\,\, i\ne j,\quad \text {and}\quad \overline{{\mathcal {U}}}_j \cap {\overline{M}}_k=\emptyset \, \,\text {if}\,\, k\notin X_j. \end{aligned}$$

Then for $l\in \mathbb {N}_0$, $1<p<\infty$, $\varvec{\beta }=(\beta _1,\ldots ,\beta _{d'})\in \mathbb {R}^{d'}$ and $\delta =(\delta _1,\ldots ,\delta _{d})\in \mathbb {R}^d$, we define $V_{\varvec{\beta },\delta }^{l,p}(D)$ as the closure of the set $C_0^{\infty }({\overline{D}}{\setminus }S)$ with respect to the norm

$$\begin{aligned} \Vert u|V_{\varvec{\beta },\delta }^{l,p}(D)\Vert =\left( \displaystyle \sum _{j=1}^{d'} \int _{D\cap {\mathcal {U}}_j} \sum _{|\alpha |\le l}\rho _j^{p(\beta _j-l+|\alpha |)} \prod _{k\in X_j} \left( \frac{r_k}{\rho _j} \right) ^{p(\delta _k-l+|\alpha |)} |\partial _x^{\alpha }u|^p\, dx \right) ^{1/p}. \end{aligned}$$

(2.1.1)

Remark 2.4

We collect some remarks and properties of the weighted Sobolev spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$.

• The space $V_{\varvec{\beta },\delta }^{l,p}(D)$ is Banach space. The proof can be derived from a generalized result e.g. from [23, p. 18, Thm. 3.6].

• $V_{\varvec{\beta },\delta }^{l,p}(D) \subset L_p(D)$ for $l\ge \beta _j,\, j=1,\ldots ,d'$ and $l\ge \delta _k,\, k=1,\ldots ,d$.

• Similarly as in [30, Rem. 2.2, Subsec. 2.1] it can be shown that a function $\varphi \in C^l(D)$ is a pointwise multiplier in $V_{\varvec{\beta },\delta }^{l,p}(D)$, i.e., for $u\in V_{\varvec{\beta },\delta }^{l,p}(D)$ we have

  $$\begin{aligned} \Vert \varphi u|V_{\varvec{\beta },\delta }^{l,p}(D)\Vert \le c \Vert u|V_{\varvec{\beta },\delta }^{l,p}(D)\Vert . \end{aligned}$$

• The weighted Sobolev spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$ are refinements of the Kondratiev spaces ${\mathcal {K}}_{a,p}^m(D)$, cf. [9, Rem. 4 (ii)].

• The space $V_{\varvec{\beta },\delta }^{l,p}(D)$ does not depend on the choice of the domains ${\mathcal {U}}_j$, cf. [26, Subsec. 4.1.2, p. 142].

• If $s,\,t\in \mathbb {R}$, then by $V_{\varvec{\beta }+s,\delta +t}^{l,p}(D)$ we mean the space $V_{\varvec{\beta }',\delta '}^{l,p}(D)$ with the weight parameters $\varvec{\beta }'=(\beta _1+s,\ldots ,\beta _{d'}+s )$ and $\delta '=(\delta _1+t,\ldots ,\delta _d+t)$.

• For $p=2$ we use the abbreviation $V_{\varvec{\beta },\delta }^{l}(D):=V_{\varvec{\beta },\delta }^{l,2}(D)$.

• The closure of the set $C_0^{\infty }(D)$ in $V_{\varvec{\beta },\delta }^{l,p}(D)$ is denoted by $\mathring{V}_{\varvec{\beta },\delta }^{l,p}(D)$.

• The space $V_{\varvec{\beta },\delta }^{-l,p}(D)$ denotes the dual space of $\mathring{V}_{-\varvec{\beta },-\delta }^{l,p'}(D)$, $p'=p/(p-1)$, with respect to the dual pairing $\langle \cdot , \cdot \rangle _{D}:=\langle \cdot , \cdot \rangle _{ V_{\varvec{\beta },\delta }^{-l,p}(D)\times \mathring{V}_{-\varvec{\beta },-\delta }^{l,p'}(D)}$. This space is provided with the norm

  $$\begin{aligned} \Vert u|V_{\varvec{\beta },\delta }^{-l,p}(D) \Vert =\sup \{ | \langle u,v\rangle _D |\, : \, v \in \mathring{V}_{-\varvec{\beta },-\delta }^{l,p'}(D) , \, \Vert v| V_{-\varvec{\beta },-\delta }^{l,p'}(D) \Vert =1 \}. \end{aligned}$$

• Moreover, for $l\ge 1$ we denote by $V_{\varvec{\beta },\delta }^{l-1/p,p}(\Gamma _j)$ the trace space for $V_{\varvec{\beta },\delta }^{l,p}(D)$ on the face $\Gamma _j$ of D. The corresponding norm is defined as

  $$\begin{aligned} \Vert u|V_{\varvec{\beta },\delta }^{l-1/p,p}(\Gamma _j) \Vert =\inf \{\Vert v| V_{\varvec{\beta },\delta }^{l,p}(D)\Vert : \, v\in V_{\varvec{\beta },\delta }^{l,p}(D),\ v=u \text { on } \Gamma _j \}. \end{aligned}$$

We provide embeddings between the spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$, which will be needed later on when establishing our regularity results. First, we recall [26, Lem. 4.1.3].

Lemma 2.5

Let $l,\,l'$ be nonnegative integers and $1<p\le q<\infty$ such that $l-3/p\ge l'-3/q$. Then we have the embedding

$$\begin{aligned} V_{\varvec{\beta },\delta }^{l,p}(D)\hookrightarrow V_{\varvec{\beta }',\delta '}^{l',q}(D), \end{aligned}$$

if $\beta _j-l+3/p\le \beta _j'-l'+3/q$ for $j=1,\ldots ,d'$, and $\delta _k-l+3/p \le \delta '_k-l'+3/q$ for $k=1,\ldots ,d$.

Remark 2.6

• An analogous result holds for the trace spaces $V_{\varvec{\beta },\delta }^{l-1/p,p}(\Gamma _j)$ in view of [26, Lem. 4.1.5].

• Lemma 2.5 holds for arbitrary integers $l,l'$ when $p=q=2$. This follows from the following consideration:

  Let $l'\le l\le 0$, $\beta _j-l\le \beta _j'-l'$ for $j=1,\ldots ,d'$, and $\delta _k-l \le \delta '_k-l'$ for $k=1,\ldots ,d$. Then, applying Lemma 2.5 we obtain

  $$\begin{aligned} \mathring{V}_{-\varvec{\beta }',-\delta '}^{-l'}(D) \hookrightarrow \mathring{V}_{-\varvec{\beta },-\delta }^{-l}(D). \end{aligned}$$

  Since the spaces $V_{\varvec{\beta },\delta }^{l}(D),\,V_{\varvec{\beta }',\delta '}^{l'}(D)$ are the dual spaces of $\mathring{V}_{-\varvec{\beta },-\delta }^{-l}(D)$ and $\mathring{V}_{-\varvec{\beta }',-\delta '}^{-l'}(D)$, respectively, it follows that

  $$\begin{aligned} V_{\varvec{\beta },\delta }^{l}(D)\hookrightarrow V_{\varvec{\beta }',\delta '}^{l'}(D). \end{aligned}$$

  (2.1.2)

  It remains to consider the case when $l'\le 0 \le l$. Then applying Lemma 2.5 and (2.1.2) we have the embeddings

  $$\begin{aligned} V_{\varvec{\beta },\delta }^{l}(D)\hookrightarrow V_{\varvec{\beta }'-l',\delta '-l'}^{0}(D)\hookrightarrow V_{\varvec{\beta }',\delta '}^{l'}(D). \end{aligned}$$

  (2.1.3)

  Therefore, (2.1.2) and (2.1.3) prove the claim.

Lemma 2.5 and Remark 2.6 yield the following special cases which we shall use later on.

Corollary 2.7

For $l\ge 0$ we have the embeddings

$$\begin{aligned} V_{0,0}^{l}(D)&\hookrightarrow V_{\varvec{\beta },\delta }^{0}(D) \quad \text {if}\quad -l \le \beta _j\quad \text {and}\quad -l\le \delta _k, \nonumber \\ V_{\varvec{\beta },\delta }^{0}(D)&\hookrightarrow V_{0,0}^{-l}(D) \quad \text {if}\ \ \quad \beta _j \le l \quad \ \text {and}\quad \ \ \delta _k\le l, \end{aligned}$$

(2.1.4)

for all $j=1,\ldots ,d'$ and $k=1,\ldots ,d$.

2.2 Besov spaces via wavelets

Under certain restrictions on the parameters, the Besov spaces $B_{p,q}^s$, defined by the classical approach via higher order differences or alternatively by the Fourier-analytical approach coincide and even allow an equivalent characterization in terms of wavelet decompositions, see e.g. [33, 34] and also [5, 25]. Therefore, in this section we introduce Besov spaces via wavelet decompositions as in [19, Sec. 2, p. 563], since this characterization is extremely convenient for our purposes when providing embedding results between weighted Sobolev and Besov spaces later on. Consider the wavelet construction of Daubechies, see e.g. [13, 14], with the mother function $\eta$ and the scaling function $\phi$, which satisfy the following conditions:

$$\begin{aligned} \mathrm{(i)}&\quad \text { compact support:} \quad \text { supp}\,\eta ,\phi \subset [-N,N]^d,\\ \mathrm{(ii)}&\quad \text { moment conditions:}\quad \displaystyle \int _{\mathbb {R}^d} x^{\alpha }\eta (x)dx=0 \, \ \text { for }\ \, \alpha \in \mathbb {N}_0^d,\ |\alpha |\le r,\\ \mathrm{(iii)}&\quad \text { sufficiently high smoothness:}\quad \eta ,\phi \in C^r(\mathbb {R}^d). \end{aligned}$$

We set $\psi ^0=\phi$, $\psi ^1=\eta$, define E as the set of the nontrivial vertices of $[0,1]^d$, and put

$$\begin{aligned} \psi ^e(x_1,\ldots ,x_d):=\displaystyle \prod _{j=1}^d \psi ^{e_j}(x_j)\, \text { for }\, e\in E. \end{aligned}$$

Moreover, let $\Psi ':=\{\psi ^e: \, e\in E \}$ and consider the set of dyadic cubes,

$$\begin{aligned} {\mathcal {D}}=\{I_{j,k}:=2^{-j}k+2^{-j}[0,1]^d: \, k\in \mathbb {Z}^d, \, j\in \mathbb {Z}\}. \end{aligned}$$

Now we put $\Lambda '={\mathcal {D}}^+\times \Psi '$, where ${\mathcal {D}}^+$ is the set of the dyadic cubes with measure at most 1. Furthermore, we use the notation ${\mathcal {D}}_j:=\{I\in {\mathcal {D}}: \, |I|=2^{-jd}\}$. The functions from $\Psi '$ are rescaled in the following way:

$$\begin{aligned} \psi _{I_{j,k}}:=\psi _{j,k}:=2^{jd/2}\psi (2^j\cdot -k) \quad \text {with}\quad I_{j,k}\in {\mathcal {D}},\, k\in \mathbb {Z}^d, \, j\in \mathbb {Z},\, \psi \in \Psi '. \end{aligned}$$

Then the set $\{ \psi _I:\, I\in {\mathcal {D}},\, \psi \in \Psi ' \}$ forms an orthonormal basis in $L_2(\mathbb {R}^d)$. Let Q(I) denote some dyadic cube of minimal size such that $\text {supp}\,\psi _I\subset Q(I)$ for every $\psi \in \Psi '$. Then we can write every function $f\in L_2(\mathbb {R}^d)$ as

$$\begin{aligned} f=P_0f+\displaystyle \sum _{(I,\psi )\in \Lambda '} \langle f,\psi _I\rangle \psi _I, \end{aligned}$$

where $P_0$ is the orthogonal projector onto the closure of the span of the function $\Phi (x)=\phi (x_1)\cdots \phi (x_d)$ and its integer shifts $\Phi (\cdot -k),\, k\in \mathbb {Z}^d$, in $L_2(\mathbb {R}^d)$. It will be convenient to include ${\phi }$ into the set $\Psi '$. We use the notation ${\phi }_I:=0$ for $|I|<1$, ${\phi }_I={\phi }(\cdot -k)$ for $I=k+[0,1]^d$, and can simply write

$$\begin{aligned} f=\displaystyle \sum _{(I,\psi )\in \Lambda } \langle f,\psi _I\rangle \psi _I, \quad \text {where} \quad \Lambda ={\mathcal {D}}^+\times \Psi ,\, \Psi =\Psi '\cup \{ \Phi \}. \end{aligned}$$

With these considerations we can now define Besov spaces $B^s_{p,q}(\mathbb {R}^d)$ by decay properties of the wavelet coefficients, if the parameters fulfill certain conditions, as follows.

Definition 2.8

Let $0<p,q<\infty$ and $s>\max \left( 0,d(\frac{1}{p}-1)\right)$. Choose $r\in \mathbb {N}$ such that $r > s$ and construct a wavelet Riesz basis as described above. Then the function $f\in L_p(\mathbb {R}^d)$ belongs to the Besov space $B_{p,q}^s(\mathbb {R}^d)$ if it admits a decomposition of the form

$$\begin{aligned} f=P_0f+\displaystyle \sum _{(I,\psi )\in \Lambda '} \langle f,\psi _I\rangle \psi _I \end{aligned}$$

(convergence in ${\mathcal {S}}'(\mathbb {R}^n)$) with

$$\begin{aligned} \Vert f|B_{p,q}^s(\mathbb {R}^d)\Vert&:=\Vert P_0f|L_p(\mathbb {R}^d)\Vert +\displaystyle \left( \sum _{j=0}^{\infty }2^{j\left( s+d\left( \frac{1}{2}-\frac{1}{p}\right) \right) q}\Bigg ( \sum _{(I,\psi )\in {\mathcal {D}}_j\times \Psi '}|\langle f,\psi _I\rangle |^p \Bigg )^{q/p} \right) ^{1/q}\\&<\infty . \end{aligned}$$

Corresponding spaces on domains $\Omega \subset \mathbb {R}^d$ can be defined by restriction via

$$\begin{aligned} B_{p,q}^s(\Omega ):=\{ f\in {\mathcal {D}}'(\Omega ):\, \exists \, g \in B_{p,q}^s(\mathbb {R}^d), \, g|_{\Omega }=f\}, \end{aligned}$$

normed by

$$\begin{aligned} \Vert f|B_{p,q}^s(\Omega )\Vert :=\displaystyle \inf _{g|_{\Omega }=f}\Vert g|B_{p,q}^s(\mathbb {R}^d)\Vert . \end{aligned}$$

Remark 2.9

• We mention that according to [27] for a bounded Lipschitz domain $\Omega$ there exists a universal extension operator $E:B_{p,q}^s(\Omega )\longrightarrow B_{p,q}^s(\mathbb {R}^d)$ satisfying

  $$\begin{aligned} \Vert Eu|B_{p,q}^s(\mathbb {R}^d)\Vert \lesssim \Vert u|B_{p,q}^s(\Omega )\Vert . \end{aligned}$$

• Moreover, when $p=q=2$ the Besov spaces coincide with the fractional Sobolev spaces, i.e., in this case we have the coincidence $B^s_{2,2}(\Omega )=H^s(\Omega )$, $s>0$.

• For $r=0,\, p=q$ we use the convention $B_{p,p}^0(\Omega ):=L_p(\Omega )$ in view of the embedding $B_{p,p}^s(\Omega )\hookrightarrow L_p(\Omega )$ for $s>0$ and $0<p<\infty$.

Using the wavelet characterization of the Besov spaces, in [29, Thm. 3.1, Sec. 3] we established an embedding result on polyhedral cones, which displays the close relation between the V- and Besov spaces, respectively. Applying localization arguments we now generalize this embedding for domains of polyhedral type, which will be one of our main tools when investigating the Besov regularity of solutions for the parabolic problems.

Theorem 2.10

(Embeddings on domains of polyhedral type) Let D be a bounded domain of polyhedral type in $\mathbb {R}^3$ with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$. Moreover, let $s>0$, $l\in \mathbb {N}_0$, $1< p<\infty$, $\varvec{\beta }=(\beta _1,\ldots ,\beta _{d'})\in \mathbb {R}^{d'}$ with $l> \max _{j=1,\ldots ,d'}\beta _j$ and $\delta =(\delta _1,\ldots ,\delta _d)\in \mathbb {R}^d$ with $|\delta ^+|=\sum _{j=1}^d \max (\delta _j,0)$. Then we have a continuous embedding

$$\begin{aligned} V_{\varvec{\beta },\delta }^{l,p}(D)\cap B_{p,p}^s(D)\hookrightarrow B_{\tau ,\tau }^r(D),\quad \frac{1}{\tau }=\frac{r}{3}+\frac{1}{p}, \end{aligned}$$

(2.2.1)

where

$$\begin{aligned} r<\min \Big \{{l},{3(l-|\delta ^+|)}, {3s} \Big \}. \end{aligned}$$

Proof

Step 1: The weighted Sobolev space $V_{\beta ,\delta }^{l,p}(K)$ can be seen as a subcase of Definition 2.1 for the bounded polyhedral cone K with edges $M_1,\ldots ,M_d$, since K is also a domain of polyhedral type, where now $d'=1$, $\varvec{\beta }=\beta \in \mathbb {R}$, $X_1=\{1,\ldots ,d\}$ in the norm (2.1.1), and the integral domain $D\cap {\mathcal {U}}_1$ is now K itself with ${\mathcal {U}}_1$ being the unit ball around the vertex of the cone.

Moreover, according to their definition, domains of polyhedral type D can be covered by domains ${\mathcal {U}}_1,\ldots ,{\mathcal {U}}_{d'}$ such that

$$\begin{aligned} D\subset {\mathcal {U}}_1\cup \cdots \cup {\mathcal {U}}_{d'},\quad x^{(i)}\notin {\mathcal {U}}_j\quad \text {if}\quad i\ne j, \quad {\mathcal {U}}_j\cap {\overline{M}}_k=\emptyset \quad \text {if}\quad k\notin X_j, \end{aligned}$$

i.e., if $M_k$ is not adjacent to $x^{(j)}$. Since the diffeomorphisms $\kappa _j$ in Definition 2.1 are $C^{\infty }$ (and therefore also Lipschitz-diffeomorphisms), we have $|\kappa _j(x)-\kappa _j(y)|\sim |x-y|$ and $|\kappa _j^{-1}(x)-\kappa _j^{-1}(y)|\sim |x-y|$ for $|x-y|\le 1$. This yields

$$\begin{aligned} \left\| u|V_{\varvec{\beta },\delta }^{l,p}(D)\right\| ^p&= \displaystyle \sum _{j=1}^{d'} \int _{D\cap {\mathcal {U}}_j} \sum _{|\alpha |\le l}\rho _j(x)^{p(\beta _j-l+|\alpha |)} \prod _{k\in X_j} \left( \frac{r_k(x)}{\rho _j(x)} \right) ^{p(\delta _k-l+|\alpha |)} |\partial _x^{\alpha }u(x)|^p\, dx\nonumber \\&\sim \displaystyle \sum _{j=1}^{d'} \int _{\kappa _j(D\cap {\mathcal {U}}_j)} \sum _{|\alpha |\le l}\rho _j(\kappa _j^{-1}(y))^{p(\beta _j-l+|\alpha |)} \prod _{k\in X_j} \left( \frac{r_k(\kappa _j^{-1}(y))}{\rho _j(\kappa _j^{-1}(y))} \right) ^{p(\delta _k-l+|\alpha |)}\nonumber \\&\quad \cdot |\partial _y^{\alpha }u(\kappa _j^{-1}(y))|^p |\det D(\kappa _j^{-1})(y)|\, dy \nonumber \\&\sim \displaystyle \sum _{j=1}^{d'} \left\| u\circ \kappa _j^{-1}|V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))\right\| ^p \end{aligned}$$

(2.2.2)

using the transformation theorem, where $\kappa _j(D\cap {\mathcal {U}}_j)$ is a bounded polyhedral cone according to Definition 2.3 and $\delta ^{(j)}$ contains the components of $\delta$ related to the edges of the cone $\kappa _j(D\cap {\mathcal {U}}_j)$, i.e., the components with indices from $X_j$.

Since the definition of the spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$ is independent of the covering ${\mathcal {U}}_j$, cf. Remark 2.4, we can take a slightly larger covering ${\mathcal {U}}_j':=\{ x\in \mathbb {R}^3: \,\text {dist} (x,{\mathcal {U}}_j)<\varepsilon \} \supset {\mathcal {U}}_j$ such that

$$\begin{aligned} D\subset {\mathcal {U}}'_1\cup \cdots \cup {\mathcal {U}}'_{d'},\quad x^{(i)}\notin {\mathcal {U}}'_j\quad \text {if}\quad i\ne j, \quad {\mathcal {U}}'_j\cap {\overline{M}}_k=\emptyset \quad \text {if}\quad k\notin X_j, \end{aligned}$$

where $\varepsilon >0$ is sufficiently small. Furthermore, we can take a subordinated family $\{ \psi _j' \}_{j=1}^{d'}$ of smooth functions satisfying

$$\begin{aligned} 0\le \psi _j'\le 1,\quad \text {supp}\, \psi _j'\subset {\mathcal {U}}'_j,\quad \psi _j' \equiv 1\quad \text {on}\quad {\mathcal {U}}_j, \end{aligned}$$

for $j=1,\ldots ,d'$, and define a resolution of unity subject to ${\mathcal {U}}'_j$ as follows:

$$\begin{aligned} \eta _j(x):=\frac{\psi _j'(x)}{\sum _{j=1}^{d'}\psi _j'(x)} \quad \text {with}\quad \textrm{supp}\, \eta _j\subset {\mathcal {U}}'_j,\quad j=1,\ldots ,d' \quad \text {and}\quad \sum _{j=1}^{d'}\eta _j(x)=1 \end{aligned}$$

(2.2.3)

for $x\in D$. The functions $\eta _j$ are well defined since $\sum _{j=1}^{d'}\psi _j'(x)$ is non-zero for all $x\in {\mathcal {U}}_j$, $j=1,\ldots ,d'$. Furthermore, since every point in D is covered at least once and at most $d'$-times by ${\mathcal {U}}_j$, we have for $x\in D$ that

$$\begin{aligned} \frac{1}{d'}\le \eta _j(x)\le 1. \end{aligned}$$

(2.2.4)

We now show that the following norms are equivalent:

$$\begin{aligned} \left\| u|V_{\varvec{\beta },\delta }^{l,p}(D)\right\| \sim \left( \displaystyle \sum _{j=1}^{d'} \Vert (\eta _j u)\circ \kappa _j^{-1}| V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))\Vert ^p \right) ^{1/p}. \end{aligned}$$

(2.2.5)

Using (2.2.2), (2.2.3), (2.2.4), and the fact that the functions $\eta _j\in C^{\infty }$ are pointwise multipliers in the spaces $V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))$, we calculate

$$\begin{aligned} \left\| u|V_{\varvec{\beta },\delta }^{l,p}(D)\right\| ^p&\sim \sum _{k=1}^{d'} \sum _{j=1}^{d'} \left\| (\eta _k u)\circ \kappa _j^{-1}|V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))\right\| ^p\\&\sim \displaystyle \sum _{j=1}^{d'} \Vert (\eta _j u)\circ \kappa _j^{-1}| V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j)) \Vert ^p\\&\sim \displaystyle \sum _{j=1}^{d'} \Vert \eta _j u | V_{\beta _j,\delta ^{(j)}}^{l,p}(D\cap {\mathcal {U}}_j) \Vert ^p \sim \left\| u|V_{\varvec{\beta },\delta }^{l,p}(D)\right\| ^p, \end{aligned}$$

which shows (2.2.5).

Step 2: As for the Besov spaces involved in the embedding (2.2.1), we can apply the localization principle from [34, Thm. 2.4.7(ii)] to $B_{p,p}^s(D)$. In particular a close inspection of the proof of that theorem together with [34, Sect. 2.4.7, Rem. 2] yields that our functions $\eta _j$ can be used for the localization, since we have a good control of their supports and derivatives. This altogether shows

$$\begin{aligned} \Vert u|B_{p,p}^s(D) \Vert ^p \sim \displaystyle \sum _{j=1}^{d'} \Vert \eta _j u|B_{p,p}^s(D\cap {\mathcal {U}}_j)\Vert ^p \sim \displaystyle \sum _{j=1}^{d'} \Vert (\eta _j u)\circ \kappa _j^{-1}|B_{p,p}^s(\kappa _j(D\cap {\mathcal {U}}_j))\Vert ^p, \end{aligned}$$

(2.2.6)

where the latter step was proven (even for anisotropic Besov spaces) in [21, Thm. 23]. A corresponding estimate holds for the term with $B_{\tau ,\tau }^r(D)$.

Step 3: In [29, Thm. 3.1] we have shown that on polyhedral cones it holds

$$\begin{aligned} V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))\cap B_{p,p}^s(\kappa _j(D\cap {\mathcal {U}}_j)) \hookrightarrow B_{\tau ,\tau }^r(\kappa _j(D\cap {\mathcal {U}}_j)), \end{aligned}$$

hence,

$$\begin{aligned}&\Vert (\eta _j u)\circ \kappa _j^{-1}|B_{\tau ,\tau }^r(\kappa _j(D\cap {\mathcal {U}}_j))\Vert \\&\quad \lesssim \Vert (\eta _j u)\circ \kappa _j^{-1}|V_{\beta _j,\delta ^{(j)}}^{l,p}(\kappa _j(D\cap {\mathcal {U}}_j))\Vert +\Vert (\eta _j u)\circ \kappa _j^{-1}|B_{p,p}^s(\kappa _j(D\cap {\mathcal {U}}_j))\Vert . \end{aligned}$$

Taking the pth power on both sides and summing over $j=1,\ldots ,d'$ together with (2.2.5) and (2.2.6) we obtain the desired result

$$\begin{aligned} \Vert u|B_{\tau ,\tau }^r(D) \Vert&\lesssim \Vert u|V_{\varvec{\beta },\delta }^{l,p}(D) \Vert +\Vert u|B_{p,p}^s(D) \Vert \sim \max \left( \Vert u|V_{\varvec{\beta },\delta }^{l,p}(D) \Vert ,\Vert u|B_{p,p}^s(D) \Vert \right) . \end{aligned}$$

$\square$

Remark 2.11

We briefly discuss the role of $\varvec{\beta }$ and $\delta$, where for simplicity we assume that $\varvec{\beta }$ has the same components, i.e., $\varvec{\beta }=(\beta ,\ldots ,\beta )$ for some $\beta \in \mathbb {R}$. In particular, these two parameters “compensate” possible singularities at the vertices or at the edges of the domain of polyhedral type D with the help of the weight functions $\rho _j$ and $r_k$, respectively. Moreover, in order to deal with $L_p$ functions we require that $\beta _j\le l$ for all $j=1,\ldots ,d'$ and $\delta _i\le l$ for all $i=1,\ldots ,d$, cf. Remark 2.4 (the second condition is incorporated in the even more restrictive inequality $0\le r<3(l-|\delta ^+|)$). Moreover, by using [26, Lem. 4.1.3], we see that

$$\begin{aligned} V^{l,p}_{\varvec{\beta },\delta }(D)\hookrightarrow V^{l,p}_{\varvec{\beta },\delta ^{'}}(D)\quad \text {if}\quad \delta _k\le \delta _k^{'} \end{aligned}$$

(2.2.7)

for all $k=1,\ldots , d$, which implies $|\delta |\le |\delta '|$. Furthermore, the smaller $|\delta ^+|$, the greater the smoothness parameter $r<3(l-|\delta ^+|)$ can be chosen. The embedding (2.2.7) of the V-scale is reflected in the condition for r, since decreasing values of $|\delta ^+|$ correspond to shrinking V-spaces, which then in turn can be embedded into smaller Besov spaces, i.e. with larger smoothness parameters r (and hence a growing upper bound for r can be observed).

The dependence on $\varvec{\beta }$ is slightly different. Also in this context from [26, Lem. 4.1.3] we deduce for $\varvec{\beta }'=(\beta ',\ldots ,\beta ')\in \mathbb {R}^{d'}$ that

$$\begin{aligned} V^{l,p}_{\varvec{\beta },\delta }(D)\hookrightarrow V^{l,p}_{\varvec{\beta }^{'},\delta }(D)\quad \text {if}\quad \beta \le \beta ^{'}. \end{aligned}$$

Therefore, in this case we see that for every (fixed) l we can choose any $\beta <l$ with the effect that the resulting space $V^{l,p}_{\varvec{\beta },\delta }(D)$ still embeds into the same Besov space with smoothness $r<\min \{l,3(l-|\delta ^+|)\}$ independent of $\varvec{\beta }$ (again ignoring the dependence on s for the moment). Moreover, the weight parameter $\varvec{\beta }$ (connected to the distances to the vertices of D) not playing any role in the condition on r (besides the requirement $\max _{j=1,\ldots ,d'}\beta _j=\beta <l$ needed for the embedding into $L_p$) is analogous to previous results for smooth cones, cf. [12, Sec. 2], where the singular set is just a point (of dimension 0).

2.3 Banach-space valued function spaces

In order to investigate parabolic problems in the sequel we introduce some Banach-valued function spaces following [28, Subsec. 2.2.2].

Definition 2.12

Let X be a Banach space and $I\subset \mathbb {R}$ some interval. We denote by $L_p(I,X)$, $1\le p\le \infty$, the space of (equivalence classes of) measurable functions $u\,:\,I\rightarrow X$ such that the mapping $t\mapsto \Vert u(t)\Vert _X$ belongs to $L_p(I)$, which is endowed with the norm

$$\begin{aligned} \Vert u|L_p(I,X)\Vert = {\left\{ \begin{array}{ll} \displaystyle \left( \int _I \Vert u(t)|X \Vert ^p \,dt \right) ^{1/p}\quad &{}\text {if}\quad p<\infty ,\\ \displaystyle \mathop {\mathrm {ess\,sup}}\limits _{t\in I} \Vert u(t)|X\Vert \quad &{}\text {if}\quad p=\infty . \end{array}\right. } \end{aligned}$$

Furthermore, for $m\in \mathbb {N}_0$ we denote by $W_p^m(I,X)$ the space of all functions $u\in L_p(I,X)$, whose weak derivatives of order $0\le k\le m$ belong to $L_p(I,X)$, normed by

$$\begin{aligned} \Vert u|W_p^m(I,X)\Vert = {\left\{ \begin{array}{ll} \left( \displaystyle \sum _{k=0}^m \Vert \partial _{t^k}u|L_p(I,X)\Vert ^p \right) ^{1/p} \quad &{}\text {if}\quad p<\infty ,\\ \displaystyle \max _{0\le k \le m} \Vert \partial _{t^k}u|L_{\infty }(I,X)\Vert \quad &{}\text {if}\quad p=\infty . \end{array}\right. } \end{aligned}$$

Moreover, if $p=2$ we write $H^m(I,X):= W_2^m(I,X)$.

Remark 2.13

The spaces $L_p(I,X)$ and $W_p^m(I,X)$ are Banach spaces, cf. [10, Subsec. 2.2, p. 10].

In particular, for $D_{T}=(0,T] \times D$ with D being some domain of polyhedral type we abbreviate

$$\begin{aligned} L_p(D_T)&:=L_p([0,T], L_p(D)),\\ H^1([0,T], H^m, (H^m)')&:= L_2([0,T],H^m(D))\cap H^1([0,T],(H^{m}(D))') \quad \text {and}\\ H^1([0,T], {H}^m, L_2)&:= L_2([0,T],H^m(D))\cap H^1([0,T],L_2(D)), \end{aligned}$$

where $(H^{m}(D))'$ denotes the dual space of $H^m(D)$. Moreover, we put

$$\begin{aligned} H^1([0,T], \mathring{H}^m, H^{-m}):=L_2([0,T],\mathring{H}^m(D)) \cap H^1([0,T],H^{-m}(D)), \end{aligned}$$

normed by

$$\begin{aligned} \Vert u| H^1([0,T], \mathring{H}^m, H^{-m}) \Vert = \Vert u|L_2([0,T],\mathring{H}^m(D)) \Vert + \Vert u| H^1([0,T],H^{-m}(D))\Vert , \end{aligned}$$

(2.3.1)

where $\mathring{H}^m(D)$ denotes the closure of ${\mathcal {D}}(D)$ in $H^m(D)$ and $H^{-m}(D)$ stands for the dual space $(\mathring{H}^m(D))'$. Moreover, the pairing $(\cdot , \cdot )_{L_2(D)}$ (or $(\cdot ,\cdot )$ if there is no danger of confusion) denotes the inner product in $L_2(D)$ whereas $\langle \cdot , \cdot \rangle$ is the dual pairing of $\mathring{H}^m(D)$ and $H^{-m}(D)$ or $H^m(D)$ and $(H^{m}(D))'$, respectively. Furthermore, we define the space

$$\begin{aligned} H^1([0,T], {H}^m, H^{-m})&:= L_2([0,T],H^m(D))\cap H^1([0,T],H^{-m}(D)) \end{aligned}$$

normed as in (2.3.1) with obvious modifications.

Since $\mathring{H}^m(D)\hookrightarrow H^m(D)$ and $(H^m(D))'\hookrightarrow H^{-m}(D)$ we have the embeddings

$$\begin{aligned} H^1([0,T], H^m, (H^m)')&\hookrightarrow H^1([0,T], {H}^m, H^{-m})\qquad \text {and}\\ H^1([0,T], \mathring{H}^m, H^{-m})&\hookrightarrow H^1([0,T], {H}^m, H^{-m}), \end{aligned}$$

where the respective norms for the spaces considered in the second embedding are essentially the same.

For later use we need also the following embedding theorem which is a direct consequence of the proof of [28, Thm. 2.4.12].

Theorem 2.14

Let $X,\,X_1,\,X_2$ be Banach spaces such that $X_1\cap X_2 \hookrightarrow X$. Moreover, let $k\in \mathbb {N}_0$, $0<p\le \infty$, and $0<T<\infty$. Then the following embedding holds

$$\begin{aligned} W^k_p([0,T],X_1)\cap W^k_p([0,T],X_2) \hookrightarrow W^k_p([0,T],X). \end{aligned}$$

Furthermore, for $u\in W^k_p([0,T],X_1) \cap W^k_p([0,T],X_2)$ we have the estimate

$$\begin{aligned} \Vert u| W^k_p([0,T],X)\Vert&\lesssim \Vert u| W^k_p([0,T],X_1)\cap W^k_p([0,T],X_2)\Vert \\&\sim \Vert u| W^k_p([0,T],X_1)\Vert + \Vert u| W^k_p([0,T],X_2)\Vert . \end{aligned}$$

In the sequel we shall need the following Banach-space valued Hölder spaces, which can be also found in [28, Subsec. 2.2.2].

Definition 2.15

(Hölder spaces) Consider a Banach space X and an interval $I = [0,T]\subset \mathbb {R}$ with $T<\infty$. We write C(I, X) for the space consisting of all bounded and (uniformly) continuous functions $u: I\rightarrow X$ normed by

$$\begin{aligned} \Vert u|C(I,X)\Vert :=\displaystyle \max _{t\in I} \Vert u(t)|X\Vert . \end{aligned}$$

Moreover, we say that $u\in C^k(I,X)$, $k\in \mathbb {N}_0$, if u has a Taylor expansion

$$\begin{aligned} u(t+h)=u(t)+u'(t)h+\frac{1}{2}u''(t)h^2+\cdots +\frac{1}{k!}u^{(k)}(t)h^k+r_k(t,h) \end{aligned}$$

for all $t+h$, $t\in I$ such that $u^{(j)}(t)$ depends continuously on t for all $j = 0,\ldots ,k$ and $\lim _{|h|\rightarrow 0}\frac{\Vert r_k(t,h)|X\Vert }{|h|^k}=0.$ The space $C^k(I,X)$ is then equipped with the following norm

$$\begin{aligned} \Vert u|C^k(I,X)\Vert :=\displaystyle \sum _{j=0}^k \Vert u^{(j)}|C(I,X)\Vert . \end{aligned}$$

Given $\alpha \in (0,1)$, we denote by $C^{\alpha }(I,X)$ the Hölder space containing all $u \in C(I,X)$ such that

$$\begin{aligned} \Vert u|{\mathcal {C}}^{\alpha }(I,X)\Vert&:= \Vert u|C(I,X)\Vert +|u|_{C^{\alpha }(I,X)} :=\Vert u|C(I,X)\Vert + \displaystyle \sup _{\begin{array}{c} t,s\in I,\\ t\ne s \end{array}} \frac{\Vert u(t)\!-\!u(s)|X\Vert }{|t-s|^{\alpha }}\!<\!\infty . \end{aligned}$$

Consequently, ${\mathcal {C}}^{k,\alpha }(I,X)$ contains all functions $u \in C(I,X)$ such that

$$\begin{aligned} \Vert u|{\mathcal {C}}^{k,\alpha }(I,X)\Vert :=\Vert u|C^k(I,X)\Vert +|u^{(k)}|_{C^{\alpha }(I,X)}<\infty . \end{aligned}$$

Remark 2.16

• (i) We have the following embedding

  $$\begin{aligned} H^1([0,T], H^m, (H^m)')\hookrightarrow C([0,T],L_2(D)). \end{aligned}$$

  (2.3.2)

  This can be shown as follows: For real Hilbert spaces V, H such that $V\hookrightarrow H=H' \hookrightarrow V'$ with dense embeddings it holds that

  $$\begin{aligned} u\in L_2([0,T],V), \quad u'\in L_2([0,T],V')\quad \text {implies} \quad u\in C([0,T],H), \end{aligned}$$

  (2.3.3)

  cf. [35, Thm. 25.5]. For $u\in H^1([0,T], H^m, (H^m)')$ we have $u\in L_2([0,T],H^m(D))$ and $u'\in L_2([0,T],(H^m(D))')$. Then choosing $V=H^m(D)$ and $H=L_2(D)$ in (2.3.3) with $H^m(D)\hookrightarrow L_2(D)\hookrightarrow (H^{m}(D))'$ dense, we obtain (2.3.2).

  Moreover, in a similar way we can show that

  $$\begin{aligned} H^1([0,T], \mathring{H}^m, H^{-m}) \hookrightarrow C([0,T],L_2(D)), \end{aligned}$$

  (2.3.4)

  choosing $V=\mathring{H}^m(D)$ and $H=L_2(D)$ in (2.3.3), since $\mathring{H}^m(D)\hookrightarrow L_2(D)\hookrightarrow (H^{-m}(D))$ with dense embeddings.

• (ii) Furthermore, for some (quasi-)Banach space Y with $X\hookrightarrow Y$ it holds that

  $$\begin{aligned} C^k(I,X) \hookrightarrow C^k(I, Y ) \quad \text {and}\quad {\mathcal {C}}^{k,\alpha }(I,X)\hookrightarrow {\mathcal {C}}^{k,\alpha }(I,Y), \end{aligned}$$

  (2.3.5)

  see e.g. in [28, Remark 2.2.4]. Moreover, for $1<p<\infty$ and $m\in \mathbb {N}$, we have a generalized version of Sobolev’s embedding theorem,

  $$\begin{aligned} W^m_p(I,X)\hookrightarrow {\mathcal {C}}^{m-1,1-\frac{1}{p}}(I,X), \end{aligned}$$

  (2.3.6)

  cf. [28, Thm. 2.2.5].

For later use we provide the following auxiliary embedding result which is a generalization of [16, Thm. 4, § 5.9.2].

Lemma 2.17

Let D be an open bounded Lipschitz domain, $m\in \mathbb {N}_0$, and $k\in \mathbb {N}$. Suppose that $u\in L_2([0,T],H^{m+2k}(D))$ with $\partial _t u\in L_2([0,T],H^m(D))$. Then

$$\begin{aligned} u\in C([0,T],H^{m+k}(D)), \end{aligned}$$

and the following estimate holds

$$\begin{aligned} \Vert u| C([0,T],H^{m+k}(D))\Vert \le C\left( \Vert u|L_2([0,T],H^{m+2k}(D)) \Vert + \Vert \partial _t u|L_2([0,T],H^m(D)) \Vert \right) , \end{aligned}$$

(2.3.7)

where the constant C is independent of u.

Proof

The proof is based on the proof in [16, Thm. 4, § 5.9.2] with suitable modifications according to our needs. We consider first $m=0$, in which case

$$\begin{aligned} u\in L_2([0,T],H^{2k}(D)),\quad \partial _t u\in L_2([0,T],L_2(D)) . \end{aligned}$$

We select a bounded open set $V \supset \supset D$ and construct the corresponding extension ${\bar{u}}:=Eu$ using the extension operator from [31, Chap. VI, §3.1, Thm. 5] (in particular, we have $\textrm{supp}(Eu)\subset V$, see [31, Formula (31) on p. 191]). Moreover, since

$$\begin{aligned} \Vert {\bar{u}}|H^{2k}(V) \Vert \lesssim \Vert {u}|H^{2k}(D) \Vert \end{aligned}$$

we see that ${\bar{u}}\in L_2([0,T],H^{2k}(V))$ and

$$\begin{aligned} \Vert {\bar{u}} | L_2([0,T],H^{2k}(V))\Vert \le C \Vert {u} | L_2([0,T],H^{2k}(D))\Vert , \end{aligned}$$

(2.3.8)

for an appropriate constant C independent of u. Moreover, since E is a universal extension operator, it is also an extension operator from $L_2(D)$ into $L_2(V)$, and hence, by a similar argument as in [16, Thm. 4, § 5.9.2] we obtain that $\partial _t{\bar{u}}\in L_2([0,T],L_2(V))$ with the estimate

$$\begin{aligned} \Vert \partial _t{\bar{u}} | L_2([0,T],L_2(V))\Vert \le C \Vert \partial _t{u} | L_2([0,T],L_2(D))\Vert . \end{aligned}$$

(2.3.9)

We proceed by assuming for the moment that ${\bar{u}}$ is a smooth function. We then compute

$$\begin{aligned} \left| \frac{d}{dt}\left( \displaystyle \sum _{|\alpha |\le k} \int _V |\partial _x^{\alpha }{\bar{u}}|^2\, dx\right) \right|&=2 \left| \sum _{|\alpha |\le k}\int _V \partial _x^{\alpha }{\bar{u}}\, \partial _x^{\alpha }(\partial _t{\bar{u}})\, dx \right| =2 \left| \sum _{|\alpha |\le k}\int _V \partial _x^{2\alpha }{\bar{u}}\, \partial _t{\bar{u}}\, dx \right| \nonumber \\&\le 2 \sum _{|\alpha '|\le 2k}\int _V \left| \partial _x^{\alpha '}{\bar{u}}\, \partial _t{\bar{u}} \right| \, dx\nonumber \\&\le 2 \sum _{|\alpha '|\le 2k} \Vert \partial _x^{\alpha '}{\bar{u}}|L_2(V)\Vert \cdot \Vert \partial _t {\bar{u}}|L_2(V) \Vert \nonumber \\&\le 2 \Vert {\bar{u}}|H^{2k}(V)\Vert \cdot \Vert \partial _t {\bar{u}}|L_2(V) \Vert \nonumber \\&\le \Vert {\bar{u}}|H^{2k}(V)\Vert ^2+\Vert \partial _t {\bar{u}}|L_2(V) \Vert ^2, \end{aligned}$$

(2.3.10)

where we used Hölder’s inequality, the inequality $2ab\le a^2+b^2$, and the fact that there is no boundary term when we integrate by parts, since the extension ${\bar{u}}$ has compact support within V. Integrating both sides of (2.3.10) w.r.t. the time-variable t from $s_1$ to $s_2$ for $0\le s_1 \le s_2\le T$ we obtain

$$\begin{aligned} \displaystyle \int _{s_1}^{s_2} \left| \frac{d}{dt}\left( \displaystyle \sum _{|\alpha |\le k} \int _V |\partial _x^{\alpha }{\bar{u}}|^2\, dx\right) \right| \, dt&\le \int _{s_1}^{s_2} \Vert {\bar{u}}|H^{2k}(V)\Vert ^2\, dt+ \int _{s_1}^{s_2} \Vert \partial _t {\bar{u}}|L_2(V) \Vert ^2 \, dt\nonumber \\&\le \int _{0}^{T} \Vert {\bar{u}}|H^{2k}(V)\Vert ^2\, dt+ \int _{0}^{T} \Vert \partial _t {\bar{u}}|L_2(V) \Vert ^2 \, dt\nonumber \\&=\Vert {\bar{u}}|L_2([0,T],H^{2k}(V))\Vert ^2 + \Vert \partial _t{\bar{u}}|L_2([0,T],L_2(V))\Vert ^2. \end{aligned}$$

(2.3.11)

Since (2.3.11) holds for arbitrary $0\le s_1 \le s_2\le T$ we choose them such that one of $s_1,\, s_2$ provides the minimum of $\Vert {\bar{u}}(\cdot )|H^{k}(V)\Vert$ and the other one provides the maximum. We denote them by $t_{\max }$ and $t_{\min }$, respectively. Then for the left-hand side of (2.3.11) we calculate w.l.o.g. for $s_1=t_{\min }$, $s_2=t_{\max }$ that

$$\begin{aligned} \int _{t_{\min }}^{t_{\max }} \left| \frac{d}{dt}\left( \displaystyle \sum _{|\alpha |\le k} \int _V |\partial _x^{\alpha }{\bar{u}}|^2\, dx\right) \right| \, dt&\ge \left| \int _{t_{\min }}^{t_{\max }} \frac{d}{dt}\left( \displaystyle \sum _{|\alpha |\le k} \int _V |\partial _x^{\alpha }{\bar{u}}|^2\, dx\right) \, dt \right| \nonumber \\&= \left| \Vert {\bar{u}}(t_{\max })|H^k(V)\Vert ^2- \Vert {\bar{u}}(t_{\min })|H^k(V)\Vert ^2 \right| \nonumber \\&= \Vert {\bar{u}}(t_{\max })|H^k(V)\Vert ^2- \Vert {\bar{u}}(t_{\min })|H^k(V)\Vert ^2. \end{aligned}$$

(2.3.12)

Moreover, we have

$$\begin{aligned} T\Vert {\bar{u}}(t_{\min })|H^k(V)\Vert \le \Vert {\bar{u}}|L_2([0,T],H^k(V))\Vert \le \Vert {\bar{u}}|L_2([0,T],H^{2k}(V))\Vert . \end{aligned}$$

(2.3.13)

Considering (2.3.11), (2.3.12), and (2.3.13) we deduce

$$\begin{aligned} \Vert {\bar{u}}(t_{\max })|H^k(V)\Vert&\le \Vert {\bar{u}}(t_{\min })|H^k(V)\Vert +\Vert {\bar{u}}|L_2([0,T],H^{2k}(V))\Vert + \Vert \partial _t{\bar{u}}|L_2([0,T],L_2(V))\Vert \nonumber \\&\le C \left( \Vert {\bar{u}}|L_2([0,T],H^{2k}(V))\Vert + \Vert \partial _t{\bar{u}}|L_2([0,T],L_2(V))\Vert \right) , \end{aligned}$$

(2.3.14)

where C depends only on T. The estimate (2.3.14) together with (2.3.8) and (2.3.9) yields the desired result,

$$\begin{aligned} \displaystyle \max _{0\le t\le T}\Vert u(t)|H^k(D)\Vert \le C \left( \Vert {u} | L_2([0,T],H^{2k}(D))\Vert +\Vert \partial _t{u} | L_2([0,T],L_2(D))\Vert \right) . \end{aligned}$$

(2.3.15)

The case when u is not smooth follows by approximating u using a mollifier, i.e., $u^{\varepsilon }=\eta _{\varepsilon }*u$, as in in [16, Thm. 4, § 5.9.2]. As above it follows in this case that $u\in C([0,T], H^k(D))$.

It remains to show the case when $m\ge 1$, which can be reduced to the case when $m=0$ as follows. Let $\alpha$ be a multiindex of order $|\alpha |\le m$ and set $v_{\alpha }:=\partial _x^{\alpha }u$. Then

$$\begin{aligned} v_{\alpha }\in L_2([0,T],H^{2k}(D)),\quad \partial _t v_{\alpha }\in L_2([0,T],L_2(D)). \end{aligned}$$

Hence, we can apply (2.3.15), with u replaced by $v_{\alpha }$, and sum over all indices $|\alpha |\le m$ which leads to the desired estimate (2.3.7). This completes the proof. $\square$

2.4 The fundamental parabolic problems

We present the fundamental parabolic problems with homogeneous and inhomogeneous boundary conditions, that we want to consider in the sequel. Let $D\subset \mathbb {R}^3$ be some domain of polyhedral type with faces $\Gamma _j$, $j=1,\ldots ,n$. For $0<T<\infty$ put $D_{T}=(0,T] \times D$ and $\Gamma _{j,T}=[0,T]\times \Gamma _j$.

Parabolic problem with homogeneous boundary conditions. Let $m\in \mathbb {N}$. We consider the following initial-boundary value problem,

Here f is a function given on $D_T$, $\nu$ denotes the exterior normal to $\Gamma _j$, and the partial differential operator L is given by

$$\begin{aligned} L(t,x,\partial _x)=\displaystyle \sum _{|\alpha |,|\beta |=0}^m {(-1)^{|\alpha |}} \partial _x^{\alpha }(a_{\alpha \beta }(t,x)\partial _x^{\beta }), \end{aligned}$$

(2.4.1)

where $a_{\alpha \beta }$ are bounded real-valued functions from $C^{\infty }(D_T)$ with $a_{\alpha \beta }=a_{\beta \alpha }$. Furthermore, the operator L is assumed to be uniformly elliptic with respect to $t\in [0,T]$, i.e.,

$$\begin{aligned} \displaystyle \sum _{|\alpha |,|\beta |=m} a_{\alpha \beta } \xi ^{\alpha } \xi ^{\beta }\ge c|\xi |^{2m}\quad \text {for all}\quad (t,x)\in D_T,\quad \xi \in \mathbb {R}^3. \end{aligned}$$

Let us denote by

$$\begin{aligned} B(t,u,v)=\int _D \displaystyle \sum _{|\alpha |,|\beta |=0}^m a_{\alpha \beta }(t,x) (\partial _x^{\beta }u) (\partial _x^{\alpha } v)\, dx \end{aligned}$$

the time-dependent bilinear form. In the sequel, w.l.o.g. we suppose that $B(t,\cdot ,\cdot )$ satisfies

$$\begin{aligned} B(t,u,u)\ge \mu \Vert u |H^m(D) \Vert ^2 \end{aligned}$$

(2.4.2)

for all $u\in \mathring{H}^m(D)$ and a.e. $t\in [0,T]$. Moreover, we set

$$\begin{aligned} B_{\partial _{t^k}}(t,u,v)= \int _D \displaystyle \sum _{|\alpha |,|\beta |=0}^m \frac{\partial a_{\alpha \beta }(t,x)}{\partial t^k}\partial _x^{\beta }u(t,x) \partial _x^{\alpha } v(t,x)\,dx. \end{aligned}$$

(2.4.3)

Finally, we explain what is meant by the weak solution of problem ($P_{\text {hom}}$).

Definition 2.18

Given $f\in L_2([0,T],H^{-m}(D))$ a function u satisfying

$$\begin{aligned} u\in L_2([0,T],\mathring{H}^{m}(D)),\quad \partial _t u \in L_2([0,T],H^{-m}(D)) \end{aligned}$$

is called a weak solution of problem ($P_{\text {hom}}$) if, and only if, $u(0,\cdot )=0$ in D and the equality

$$\begin{aligned} \langle \partial _t u(t,\cdot ),v \rangle +B(t,u,v)= \langle f(t,\cdot ),v\rangle \end{aligned}$$

holds for all $v\in \mathring{H}^m(D)$ and a.e. $t\in [0,T]$.

It is also our intention to study inhomogeneous versions of ($P_{\text {hom}}$). Therefore, we modify ($P_{\text {hom}}$) as follows.

Parabolic problem with inhomogeneous boundary conditions. Let $m\in \mathbb {N}$. We consider the following initial-boundary value problem,

where g and $u_0$ are functions given on $D_T$ and D, respectively, and f, L are as explained before for problem ($P_{\text {hom}}$). We wish to point out here that the condition on the coefficients $a_{\alpha \beta }$ of L to be smooth is quite strong and can probably be weakened. This requires a careful check of the subsequent regularity results. However, the since presentation is already quite technical and not easy to read, we decided to merely focus on the (necessary) regularity assumptions regarding the right hand side f as well as the initial and boundary conditions $u_0$ and g, respectively.

Remark 2.19

In analogy to Definition 2.18 we can define what is meant by a weak solution of the inhomogeneous problem ($P_{\text {inhom}}$) as follows. Let ${\tilde{f}}=f-\frac{\partial }{\partial t} g- L(t,x,\partial _x)g$. We say that u is a weak solution of ($P_{\text {inhom}}$) if for ${\tilde{f}}\in L_2([0,T],H^{-m}(D))$ and $g\in H^1([0,T], H^m, (H^m)')$ the function $u-g$ satisfies

$$\begin{aligned} u-g\in L_2([0,T],\mathring{H}^{m}(D)),\quad \partial _t (u-g) \in L_2([0,T],H^{-m}(D)) \end{aligned}$$

(2.4.4)

with

$$\begin{aligned} (u-g)(0,\cdot )=u_0(\cdot )-g(0,\cdot )\quad \text {in}\quad D, \end{aligned}$$

(2.4.5)

and the equality

$$\begin{aligned} \langle \partial _t (u-g)(t,\cdot ),v \rangle +B(t,u-g,v)= \langle {\tilde{f}}(t,\cdot ),v\rangle \end{aligned}$$

holds for all $v\in \mathring{H}^m(D)$ and a.e. $t\in [0,T]$. By our conditions (2.4.4) on $u-g$, in view of (2.3.4) we see that $u-g\in C([0,T], L_2(D))$, and thus the equality (2.4.5) makes sense.

2.5 Operator pencils

Following [26, Subsec. 4.1.6] and [28, Sec. 3.5] we now consider the operator pencils generated by the boundary value problem for elliptic equations (also with inhomogeneous boundary conditions for later use)

$$\begin{aligned} Lu=f \ \text { in }\ D,\qquad \frac{\partial ^{k-1}u}{\partial \nu ^{k-1}}=g_{j,k}\ \text { on }\ \Gamma _j, \end{aligned}$$

(2.5.1)

for $j=1,\ldots ,n$ and $k=1,\ldots ,m$, where $D\subset \mathbb {R}^3$ is a domain of polyhedral type with faces $\Gamma _j$. We assume that

$$\begin{aligned} L(x,\partial _x)=\displaystyle \sum _{|\alpha |\le 2m} A_{\alpha }(x)\partial _x^{\alpha } \end{aligned}$$

is a uniformly elliptic differential operator of order 2m with smooth coefficients $A_{\alpha }$.

Operator pencils

The boundary value problem (2.5.1) generates two types of operator pencils, $A_{\xi }(\lambda )$ and ${\mathfrak {A}}_j(\lambda )$, for the edge points and vertices of D, respectively.

1. Operator pencils $A_{\xi }(\lambda )$ for edges: Let $\xi$ be a point on an edge $M_k$, and let $\Gamma _{k_+},\, \Gamma _{k_-}$ be the faces of D adjacent to $\xi$. Then by ${\mathcal {D}}_{\xi }$ we denote the dihedron which is bounded by the half-planes $\mathring{\Gamma }_{k_{\pm }}$ tangent to $\Gamma _{k_{\pm }}$ at $\xi$ and the edge $\mathring{M}_{\xi }= \overline{\mathring{\Gamma }}_{k_+}\cap \overline{\mathring{\Gamma }}_{k_-}$. Furthermore, let $r,\varphi$ be polar coordinates in the plane perpendicular to $\mathring{M}_{\xi }$ such that

$$\begin{aligned} \mathring{\Gamma }_{k_{\pm }}=\left\{ x\in \mathbb {R}^3: \ r>0, \ \varphi =\pm \frac{\theta _{\xi }}{2}\right\} . \end{aligned}$$

Then we define the operator $A_{\xi }(\lambda )$ as follows:

$$\begin{aligned} A_{\xi }(\lambda ) U(\varphi )=r^{2m-\lambda } \mathring{L}(\xi ,\partial _x)u, \end{aligned}$$

(2.5.2)

where $u(x) = r^{\lambda }U(\varphi )$ and

$$\begin{aligned} \mathring{L}(\xi ,\partial _x)=\displaystyle \sum _{|\alpha |= 2m} A_{\alpha }(\xi )\partial _x^{\alpha } \end{aligned}$$

denotes the principal part of the differential operator $L(x,\partial _x)$ with coefficients frozen at $\xi$. The operator $A_{\xi }(\lambda )$ realizes a continuous mapping

$$\begin{aligned} H^{2m}(I_{\xi })\rightarrow L_2(I_{\xi }) \end{aligned}$$

for every $\lambda \in \mathbb {C}$, where $I_{\xi }$ denotes the interval $(-\theta _{\xi }/2,+\theta _{\xi }/2)$. We denote by $\delta _+(\xi )$ and $\delta _-(\xi )$ the greatest positive real numbers such that the strip

$$\begin{aligned} m-1-\delta _-^{(\xi )}< \text {Re}\,\lambda < m-1+\delta _+^{(\xi )} \end{aligned}$$

(2.5.3)

is free of eigenvalues of the pencil $A_{\xi }(\lambda )$. Furthermore, we define

$$\begin{aligned} \delta _{\pm }^{(k)}=\displaystyle \inf _{\xi \in M_k}\delta _{\pm }^{(\xi )} \end{aligned}$$

(2.5.4)

for $k=1,\ldots ,d$.

2. Operator pencils ${\mathfrak {A}}_i(\lambda )$ for vertices: Let $x^{(i)}$ be a vertex of D, and let $J_i$ be the set of all indices j such that $x^{(i)}\in {\overline{\Gamma }}_j$. By our assumptions in Definition 2.1, there exist a neighborhood ${\mathcal {U}}$ of $x^{(i)}$ and a diffeomorphism $\kappa$ mapping $D\cap {\mathcal {U}}$ onto $K_i\cap B_1$ and $\Gamma _k\cap {\mathcal {U}}$ onto $\mathring{\Gamma }_k\cap B_1$ for $k\in J_i$, where

$$\begin{aligned} K_i=\{ x:\, x/|x|\in \Omega _i \} \end{aligned}$$

is a cone with vertex at the origin, and $\mathring{\Gamma }_k=\{ x:\, x/|x|\in \gamma _k \}$ are the faces of this cone. Without loss of generality, we may assume that the Jacobian matrix $\kappa '(x)$ is equal to the identity matrix I at the point $x^{(i)}$. We introduce spherical coordinates $\rho =|x|,\, \omega = x/|x|$ in $K_i$, and define

$$\begin{aligned} {\mathfrak {A}}_i(\lambda ) U(\omega )=\rho ^{2m-\lambda } \mathring{L}(x^{(i)},\partial _x)u , \end{aligned}$$

(2.5.5)

where $u(x)=\rho ^{\lambda }U(\omega )$, $U\in \mathring{H}^{m}(\Omega _i)$. The operator ${\mathfrak {A}}_i(\lambda )$ realizes a continuous mapping

$$\begin{aligned} \mathring{H}^{m}(\Omega _i)\rightarrow H^{-m} (\Omega _i) \end{aligned}$$

for arbitrary $\lambda \in \mathbb {C}$.

Remark 2.20

(Operator pencils for parabolic problems) Since we shall study parabolic PDEs, where the differential operator $L(t, x,\partial _x)$ additionally depends on the time t, we have to work with operator pencils $A_{\xi }(\lambda , t)$ and ${\mathfrak {A}}_i(\lambda , t)$ in this context. The philosophy is to fix $t \in [0, T]$ and define the pencils as above: We replace (2.5.2) by

$$\begin{aligned} A_{\xi }(\lambda ,t) U(\varphi )=r^{2m-\lambda } \mathring{L}(t,\xi ,\partial _x)u, \end{aligned}$$

and work with $\delta _{\pm }^{(\xi )}(t)$ and $\delta _{\pm }^{(k)}(t)=\displaystyle \inf _{\xi \in M_k}\delta _{\pm }^{(\xi )}(t)$ in (2.5.3) and (2.5.4), respectively. Moreover, we put

$$\begin{aligned} \delta _{\pm }^{(k)}= \displaystyle \inf _{t\in [0,T]} \delta _{\pm }^{(k)}(t),\quad k=1,\ldots ,l. \end{aligned}$$

Similar for ${\mathfrak {A}}_i(\lambda , t)$, where now (2.5.5) is replaced by

$$\begin{aligned} {\mathfrak {A}}_i(\lambda ,t) U(\omega )=\rho ^{2m-\lambda } \mathring{L}(t,x^{(i)},\partial _x)u. \end{aligned}$$

3 Regularity results for parabolic PDEs

In this section we study the regularity of parabolic partial differential equations in weighted Sobolev spaces and (Hölder-)Besov spaces on domains of polyhedral type. We extend the works of Maz’ya and Rossmann [26] (where only elliptic problems were considered), Luong and Loi [24] (whose results were established on polyhedral cones only), and Schneider [28] (where regularity in Kondratiev spaces was studied, which are contained in our scale of weighted Sobolev spaces).

To provide Besov regularity for the parabolic problem with inhomogeneous boundary conditions we first shall prove two Sobolev regularity theorems (without and with time derivatives) for the inhomogeneous problem based on the homogeneous case from [28]. Then we give regularity assertions in V-spaces for homogeneous and inhomogeneous problems for domains of polyhedral type D. Finally, we deduce Besov and Hölder–Besov regularity by applying the embedding $V_{\varvec{\beta },\delta }^{l,2}(D)\cap H^s(D)\hookrightarrow B^r_{\tau ,\tau }(D)$ subject to some restrictions on the parameters.

3.1 Known auxiliary results

For our regularity assertions we rely on known results for elliptic equations when fixing the time parameter t. Therefore, we consider first the elliptic problem (2.5.1) (also with inhomogeneous boundary conditions for later use) and provide a lemma on the regularity of its solutions in domains of polyhedral type, which is a direct consequence of [26, Cor. 4.1.10, Thm. 4.1.11].

Lemma 3.1

Let $D\subset \mathbb {R}^3$ be a domain of polyhedral type and ${\tilde{\gamma }}, \gamma '\ge m$. Moreover, let $u\in V_{{\tilde{\varvec{\beta }}},{\tilde{\delta }}}^{{\tilde{\gamma }}}(D)$ be a solution of (2.5.1), where

$$\begin{aligned}&f\in V_{{\tilde{\varvec{\beta }}},{\tilde{\delta }}}^{{\tilde{\gamma }}-2m}(D)\cap V_{\varvec{\beta }',\delta '}^{\gamma '-2m}(D),\\&g_{j,k}\in V_{{\tilde{\varvec{\beta }}},{\tilde{\delta }}}^{{\tilde{\gamma }}-k+1/2}(\Gamma _j)\cap V_{\varvec{\beta }',\delta '}^{\gamma '-k+1/2}(\Gamma _j), \end{aligned}$$

for all $j=1,\ldots ,n$ and $k=1,\ldots ,m$. Suppose that the closed strip between the lines $\text {Re}\, \lambda ={\tilde{\gamma }}-{\tilde{\beta }}_j-3/2$ and $\text {Re}\, \lambda =\gamma '-\beta _j'-3/2$ is free of eigenvalues of the pencil ${\mathfrak {A}}_j(\lambda )$ for $j=1,\ldots ,d'$ and that

$$\begin{aligned} -\delta _+^{(k)}<{\tilde{\delta }}_k-{\tilde{\gamma }}+m<\delta _-^{(k)},\quad \quad -\delta _+^{(k)}<\delta _k'-\gamma '+m<\delta _-^{(k)} \end{aligned}$$

for $k=1,\ldots ,d$. Then $u\in V_{\varvec{\beta }',\delta '}^{\gamma '}(D)$ and the following inequality holds

$$\begin{aligned} \Vert u| V_{\varvec{\beta }',\delta '}^{\gamma '}(D) \Vert \le C \left( \Vert f| V_{\varvec{\beta }',\delta '}^{\gamma '-2m}(D)||+ \displaystyle \sum _{j,k} \Vert g_{j,k}|V_{\varvec{\beta }',\delta '}^{\gamma '-k+1/2}(\Gamma _j)\Vert \right) , \end{aligned}$$

where C is a constant independent of u, f and $g_{j,k}$.

Later on we rely also on the following lemma from [28, Lem. 5.2.1].

Lemma 3.2

(Continuity of bilinear form) Assume that $F(t,\cdot ,\cdot ):\mathring{H}^m(D) \times \mathring{H}^m(D)\rightarrow \mathbb {R}$ is a bilinear map satisfying

$$\begin{aligned} |F(t,u,v)|\le C \Vert u|\mathring{H}^m(D)\Vert \Vert v|\mathring{H}^m(D)\Vert \end{aligned}$$

for all $t\in [0,T]$ and all $u,v\in \mathring{H}^m(D)$, where C is a constant independent of $u,\,v$, and t. Assume further that $F(\cdot , u, v)$ is measurable on [0, T] for each pair $u, v \in \mathring{H}^m(D)$. Assume that $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ satisfies $u(0)\equiv 0$ and

$$\begin{aligned} \langle \partial _t u(t),v\rangle +B(t,u(t),v)=\displaystyle \int _0^t F(\tau ,u(\tau ),v) \, d\tau \end{aligned}$$

for a.e. $t \in [0, T]$ and all $v \in \mathring{H}^m(D)$. Then $u\equiv 0$ on $[0,T]\times D$.

We recall [28, Thm. 5.2.2], which guarantees the existence (and uniqueness) of the weak solution of the homogeneous problem ($P_{\text {hom}}$) and provides Sobolev regularity without time derivatives for it.

Theorem 3.3

(Sobolev regularity without time derivatives for homogeneous problem) Let $f\in L_2([0,T],H^{-m}(D))$. Then problem ($P_{\text {hom}}$) has a unique weak solution u in the space $H^1([0,T], \mathring{H}^m, H^{-m})$ and the following estimate holds

$$\begin{aligned} \Vert u|H^1([0,T], \mathring{H}^m, H^{-m}) \Vert \le C \Vert f| L_2([0,T],H^{-m}(D))\Vert , \end{aligned}$$

where C is a constant independent of u and f.

The above theorem can be strengthened as follows to include Sobolev regularity results for the time derivatives as well, cf. [28, Thm. 5.2.3].

Theorem 3.4

(Sobolev regularity with time derivatives for homogeneous problem) Let $l\in \mathbb {N}_0$ and assume that the right hand side f of problem ($P_{\text {hom}}$) satisfies

$$\begin{aligned} f\in H^l([0,T],H^{-m}(D))\quad \text {and} \quad \partial _{t^k}f(0,x)=0 \quad \text {for}\quad k=0,\ldots ,l-1. \end{aligned}$$

Then the weak solution u in the space $H^1([0,T], \mathring{H}^m, H^{-m})$ of problem ($P_{\text {hom}}$) has derivatives with respect to t up to order l satisfying

$$\begin{aligned} \partial _{t^k}u \in H^1([0,T], \mathring{H}^m, H^{-m})\quad \text {for}\quad k=0,\ldots ,l, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \sum _{k=0}^l \Vert \partial _{t^k}u|H^1([0,T], \mathring{H}^m, H^{-m})\Vert \le C \displaystyle \sum _{k=0}^l \Vert \partial _{t^k}f| L_2([0,T],H^{-m}(D))\Vert , \end{aligned}$$

where C is a constant independent of u and f.

3.2 Regularity results in Sobolev spaces for the inhomogeneous problem

In this section we generalize Theorems 3.3 and 3.4 to the inhomogeneous setting. Our main strategy for proving our regularity results in Sobolev spaces with inhomogeneous boundary conditions will be to reduce the inhomogeneous problem to a similar one with homogeneous boundary conditions. We briefly illustrate the concept for elliptic PDEs.

Consider the problem

$$\begin{aligned} Lu&=f \quad \text {in} \quad D,\nonumber \\ u&=g\quad \text {on} \quad \partial D, \end{aligned}$$

(3.2.1)

where $g\in H^m(D)$ is the inhomogeneous boundary condition and L an elliptic differential operator of the form (2.4.1) (independent of the time parameter t). Using the variational formulation, a weak solution of (3.2.1) is a function $u\in H^m(D)$ such that $u-g\in \mathring{H}^m(D)$, i.e., $u=g$ on $\partial D$ in the trace sense, satisfying

$$\begin{aligned} \displaystyle \int _D Lu \varphi \, dx= \sum _{|\alpha |,|\beta |\le m} \int _D a_{\alpha \beta } \partial ^{\alpha }u \partial ^{\beta }\varphi \, dx := B(u,\varphi )= \int _D f\varphi \, dx = \langle f,\varphi \rangle \end{aligned}$$

(3.2.2)

for all $\varphi \in \mathring{H}^m(D)$. This can be rewritten in terms of $w:=u-g$. Then the corresponding (homogeneous) problem is to find $w\in \mathring{H}^m(D)$ such that

$$\begin{aligned} B(w,\varphi )=\langle f,\varphi \rangle -B(g,\varphi ) =: \langle F, \varphi \rangle \quad \text {for all}\quad \varphi \in \mathring{H}^m(D). \end{aligned}$$

(3.2.3)

Therefore, instead of solving (3.2.2) we solve (3.2.3) in order to obtain a weak solution for (3.2.1). For parabolic PDEs this works in a similar (slightly more technical) manner.

Using the above described strategy we start with generalizing Theorem 3.3 to the inhomogeneous setting. The proof follows closely [28, Thm. 5.2.2] and [16, Sect. 7.1.2] subject to suitable modifications.

Theorem 3.5

(Sobolev regularity without time derivatives for inhomogeneous problem) Let D be a bounded Lipschitz domain of polyhedral type. Moreover, assume $f\in L_2([0,T],H^{-m}(D))$ and let the initial-boundary conditions satisfy $g\in H^1([0,T], H^m, (H^m)')$ and $u_0\in L_2(D)$.

Then problem ($P_{\text {inhom}}$) has a unique weak solution u in $H^1([0,T], {H}^m, H^{-m})$ and the following estimate holds

$$\begin{aligned}&\Vert u|H^1([0,T], {H}^m, H^{-m})\Vert \nonumber \\&\quad \le C \left\{ \Vert f|L_2([0,T],H^{-m}(D))\Vert + \Vert g|H^1([0,T], H^m, (H^m)')\Vert +\Vert u_0|L_2(D)\Vert \right\} , \end{aligned}$$

(3.2.4)

where C is a constant independent of $f,\,g,\,u_0$, and u.

Remark 3.6

The restriction of the boundary data g at time $t=0$ makes sense: By our assumptions $g(0,\cdot )\in L_2(D)$ is well-defined, since by (2.3.2) we have

$$\begin{aligned} g\in H^1([0,T], H^m, (H^m)')&= L_2([0,T],H^m(D))\cap H^1([0,T],(H^{m}(D))')\\&\hookrightarrow C([0,T],L_2(D)). \end{aligned}$$

Proof

First we show the uniqueness of the solution. Let $u_1,\, u_2\in H^1([0,T], {H}^m, H^{-m})$ be two weak solutions of ($P_{\text {inhom}}$). Then $w_1=u_1-g,\,w_2=u_2-g\in H^1([0,T], \mathring{H}^m, H^{-m})$ are two weak solutions of the following homogeneous problem

$$\begin{aligned} \left\{ \begin{array}{rll} \partial _t w_i+ Lw_i &{}= f-\partial _t g- Lg=:F \quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w_i}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,...,m,\, j=1,...,n,\\ w_i|_{t=0} &{}= u_0- g(0,\cdot ) \quad &{}\text {on} \quad D, \end{array} \right\} \end{aligned}$$

(3.2.5)

with the new right hand side $F\in L_2([0,T],H^{-m}(D))$. In this case we have for $i=1,2$ that

$$\begin{aligned} \langle \partial _t w_i,\varphi \rangle + B(t,w_i,\varphi ) =\langle F, \varphi \rangle \quad \text {for all}\quad \varphi \in \mathring{H}^m(D), \end{aligned}$$

(3.2.6)

where $B(t,w,\varphi )=\displaystyle \int _{D} L w(t,x)\varphi (x) \, dx$ and $\langle F, \varphi \rangle =\langle f,\varphi \rangle -\langle \partial _t g,\varphi \rangle -B(t,g,\varphi )$. Subtraction yields

$$\begin{aligned} \langle \partial _t w_1-\partial _t w_2,\varphi \rangle +B(t,w_1-w_2,\varphi )&=0 \quad \text {for all}\quad \varphi \in \mathring{H}^m(D), \\ (w_1-w_2)(0,x)&=0 \quad \text {in}\quad D. \end{aligned}$$

Applying Lemma 3.2 to $w_1-w_2$ with the bilinear form $F\equiv 0$ on $\mathring{H}^m(D)\times \mathring{H}^m(D)$, gives $w_1-w_2\equiv 0$ on $D_T$. Therefore,

$$\begin{aligned} u_1\equiv u_2\quad \text {on}\quad [0,T]\times D, \end{aligned}$$

which proves the uniqueness of the solution of problem ($P_{\text {inhom}}$).

Now we turn towards proving the existence of a solution. By the assumption $a_{\alpha \beta }=a_{\beta \alpha }$ for $|\alpha |,|\beta |\le m$, L is formally a self-adjoint operator. Moreover, the Rellich–Kondrachov Theorem tells us that the embedding $\mathring{H}^m(D)\hookrightarrow L_2(D)$ is compact (in particular, this holds for bounded Lipschitz domains and therefore also for bounded Lipschitz domains of polyhedral type).

From this we deduce that the operator $L(0,x,\partial _x)$ possesses a set $\{\psi _k\}_{k=1}^{\infty }$ consisting of all its eigenfunctions, which is not only an orthogonal basis of $\mathring{H}^m(D)$ but also an orthonormal basis of $L_2(D)$. We refer to [15, Thm. 8.39] in this context (with $X=\mathring{H}^m, \, Y=L_2$; the fact that the embedding $\mathring{H}^m(D)\hookrightarrow L_2(D)$ is compact is crucial here). We now want to approximate w, the solution of problem (3.2.6). For each positive integer N consider the function

$$\begin{aligned} w^N(t,x)=\sum _{k=1}^N C^N_k(t)\psi _k(x), \end{aligned}$$

(3.2.7)

where $\left\{ C_k^N(t)\right\} _{k=1}^N$ is the solution of the ordinary differential equation system

$$\begin{aligned} (\partial _t w^N, \psi _k)+B(t,w^N,\psi _k)&= \langle f,\psi _k\rangle -\langle \partial _t g,\psi _k\rangle -B(t,g,\psi _k), \end{aligned}$$

(3.2.8)

$$\begin{aligned} C_k^N(0)&= (u_0-g(0,\cdot ),\psi _k), \end{aligned}$$

(3.2.9)

for $k=1,\ldots , N$. After multiplying both sides of (3.2.8) by $C_k^N(t)$, taking the sum with respect to k from 1 to N, and integrating with respect to t from 0 to T ($T>0$), we arrive at

$$\begin{aligned}&\int _0^T (\partial _t w^N, w^N)\, dt +\int _0^T B(t,w^N,w^N)\, dt\ \\&\quad = \int _0^T\langle f,w^N\rangle \, dt -\int _0^T\langle \partial _t g,w^N\rangle \, dt -\int _0^T B(t,g,w^N) \, dt. \end{aligned}$$

From this we deduce

$$\begin{aligned}&\int _0^T\frac{\partial }{\partial t}\Vert w^N(t)|L_2(D)\Vert ^2\,dt+2\int _0^T B(t,w^N,w^N)\, dt\nonumber \\&\qquad =2\int _0^T\langle f,w^N\rangle \, dt-2 \int _0^T\langle \partial _t g,w^N\rangle \, dt - 2 \int _0^T B(t,g,w^N) \, dt, \end{aligned}$$

(3.2.10)

where we applied [32, Chap. III, Lem. 1.2] for the first term, since $w^N\in L_2([0,T],\mathring{H}^m(D))$ and $\partial _t w^N \in L_2([0,T],H^{-m}(D))$.

The equality (3.2.10) yields

$$\begin{aligned}&\Vert w^N(T)|L_2(D)\Vert ^2- \Vert w^N(0)|L_2(D)\Vert ^2 +2\int _0^T B(t,w^N,w^N)\, d t \nonumber \\&\quad =\underbrace{2\int _0^T\langle f,w^N\rangle \, d t}_{=:I} - \underbrace{ 2 \int _0^T\langle \partial _t g,w^N\rangle \, dt}_{=:II} -\underbrace{2 \int _0^T B(t,g,w^N) \, dt}_{=:III}. \end{aligned}$$

(3.2.11)

Applying Young’s inequality, i.e., $ab\le \frac{1}{2}\left( \varepsilon a^2+\frac{b^2}{\varepsilon } \right)$, we can estimate term I by

$$\begin{aligned} \left| 2\int _0^T\langle f,w^N\rangle \, d t\right|&\le 2\int _0^T \Vert f|H^{-m}(D)\Vert \Vert w^N|\mathring{H}^m(D)\Vert \, d t \nonumber \\&\le \varepsilon \Vert w^N|L_2([0,T],H^m(D))\Vert ^2+\frac{1}{\varepsilon }\Vert f|L_2([0,T],H^{-m}(D))\Vert ^2. \end{aligned}$$

(3.2.12)

For term II we similarly obtain that

$$\begin{aligned} \left| 2\int _0^T\langle \partial _t g,w^N\rangle \, d t\right|&\le 2\int _0^T \Vert \partial _t g|(H^{m}(D))'\Vert \Vert w^N|H^m(D)\Vert \, d t \nonumber \\&\le \varepsilon \Vert w^N|L_2([0,T],H^m(D))\Vert ^2+\frac{1}{\varepsilon }\Vert \partial _t g|L_2([0,T],(H^{m}(D))')\Vert ^2. \end{aligned}$$

(3.2.13)

Applying Hölder’s and again Young’s inequality, we estimate for term III

$$\begin{aligned} \left| 2\int _0^T B(t,g,w^N)\, dt \right|&\le c \int _0^T \Vert g|H^m(D)\Vert \Vert w^N|H^m (D)\Vert \, dt \nonumber \\&\le c' \left\{ \varepsilon \Vert w^N|L_2([0,T],H^{m}(D))\Vert ^2+ \frac{1}{\varepsilon } \Vert g|L_2([0,T],H^{m}(D))\Vert ^2 \right\} , \end{aligned}$$

(3.2.14)

since $B(t,g,w^N)$ consists of the derivatives of $g,\, w^N\in H^m(D)$ of order less or equal m and the coefficients $a_{\alpha ,\beta }$ of L (and their derivatives) are smooth and therefore bounded in D.

Using the coercivity of the bilinear form B, cf. (2.4.2), on the left-hand side in (3.2.11) we estimate

$$\begin{aligned} 2\int _0^T B(t,w^N,w^N)\, dt&\ge 2 \mu \int _0^T \Vert w^N| H^m(D)\Vert ^2 \, dt \nonumber \\&=2 \mu \Vert w^N|L_2([0,T],H^{m}(D)) \Vert ^2. \end{aligned}$$

(3.2.15)

Therefore, choosing $0< 3\varepsilon <2\mu$ we get from (3.2.11)–(3.2.15) that

$$\begin{aligned}&\Vert w^N|L_2([0,T],H^m(D))\Vert ^2 \nonumber \\&\quad \le \frac{c}{\varepsilon } \Bigg \{ \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 +\Vert \partial _t g|L_2([0,T],(H^{m}(D))')\Vert ^2 \nonumber \\&\qquad +\Vert g|L_2([0,T],H^{m}(D))\Vert ^2 \Bigg \} \nonumber \\&\qquad + \underbrace{c' \displaystyle \sup _{0\le t\le T} \Vert w^N(t)|L_2(D)\Vert ^2}_{=:IV}. \end{aligned}$$

(3.2.16)

We now estimate term IV as follows: Put

$$\begin{aligned} \eta (t)&:=\Vert w^N(t)|L_2(D)\Vert ^2,\\ \xi (t)&:= \Vert f(t)|H^{-m}(D)\Vert ^2+\Vert \partial _t g(t)|(H^{m}(D))'\Vert ^2+\Vert g(t)|H^{m}(D)\Vert ^2. \end{aligned}$$

Then (3.2.10) and similar estimates as in (3.2.12)–(3.2.16) (this time without integration over t) show that

$$\begin{aligned} \eta '(t)&=\frac{d}{d t}\Vert w^N(t)|L_2(D)\Vert ^2 \le 2\Big ( \big |\langle f,w^N\rangle - \langle \partial _t g,w^N\rangle - B(t,g,w^N) \big | \Big )\\&\le c\Big ( \Vert f(t)|H^{-m}(D)\Vert ^2+ \Vert \partial _t g(t)|(H^{m}(D))'\Vert ^2+ \Vert g(t)|H^{m}(D)\Vert ^2 +\Vert w^N(t)|H^m(D)\Vert ^2 \Big ) \\&= c_1 \eta (t)+c_2 \xi (t), \end{aligned}$$

for a.e. $0\le t\le T$, where we used that $B(t,w^N,w^N)$ in (3.2.10) is non-negative due to (2.4.2). For the functions $\eta$ and $\xi$ we now can apply the differential form of Gronwall’s inequality, cf. [16, App. B.2], which yields the estimate

$$\begin{aligned} \eta (t)\le e^{c_1 t} \left( \eta (0)+c_2 \int _0^t \xi (s)\, ds \right) , \quad \text {for} \quad 0\le t\le T. \end{aligned}$$

(3.2.17)

We now estimate the term $\eta (0)$ using the definition of $w^N$ and the fact that $\{\psi _k\}_{k=1}^{\infty }$ is an orthonormal basis in $L_2(D)$ and obtain

$$\begin{aligned} \eta (0)&=\Vert w^N(0)|L_2(D)\Vert ^2= \bigg \Vert \displaystyle \sum _{k=1}^{N} C_k^N (0) \psi _k |L_2(D)\bigg \Vert ^2 \\ {}&\le \sum _{k=1}^{\infty } (u_0-g(0,\cdot ),\psi _k)^2\le \Vert u_0|L_2(D)\Vert ^2 +\Vert g(0,\cdot )|L_2(D)\Vert ^2. \end{aligned}$$

Then we obtain from (3.2.17) the estimate

$$\begin{aligned} \sup _{0\le t\le T} \Vert w^N(t)|L_2(D)\Vert ^2&\le c \Big \{ \Vert u_0|L_2(D)\Vert ^2+\Vert g(0,\cdot )|L_2(D)\Vert ^2 + \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2\\&\quad +\Vert \partial _t g|L_2([0,T],(H^{m}(D))')\Vert ^2+ \Vert g|L_2([0,T],H^{m}(D))\Vert ^2 \Big \}. \end{aligned}$$

This inserted in (3.2.16) yields

$$\begin{aligned} \Vert w^N|L_2([0,T],H^m(D))\Vert ^2&\le c' \Big \{ \Vert u_0|L_2(D)\Vert ^2+ \Vert g(0,\cdot )|L_2(D)\Vert ^2\nonumber \\&\quad +\Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 \nonumber \\&\quad +\Vert \partial _t g|L_2([0,T],(H^{m}(D))')\Vert ^2 + \Vert g|L_2([0,T],H^{m}(D))\Vert ^2 \Big \}. \end{aligned}$$

(3.2.18)

Now fix any $v\in \mathring{H}^m(D)$ with $\Vert v|H^m(D)\Vert \le 1$, and write $v=v_1+v_2$, where $v_1\in \textrm{span}(\psi _1,\ldots , \psi _N)$ and $(v_2,\psi _l)_{L_2(D)}=0$, for $l=1,\ldots , N$. Since the functions $\left\{ \psi _l\right\} _{l=1}^N$ are orthogonal in $\mathring{H}^m(D)$, $\Vert v_1|{H}^m(D)\Vert \le \Vert v|{H}^m(D)\Vert \le 1$. We obtain from (3.2.8) that

$$\begin{aligned} (\partial _t w^N, v_1)+B(t,w^N,v_1)=\langle f,v_1\rangle -\langle \partial _t g,v_1\rangle - B(t,g,v_1). \end{aligned}$$

Therefore,

$$\begin{aligned} \langle \partial _t w^N,v\rangle =(\partial _t w^N,v)=(\partial _t w^N,v_1)=\langle f,v_1\rangle - \langle \partial _t g,v_1\rangle -B(t,g,v_1) -B(t,w^N,v_1). \end{aligned}$$

Since $\Vert v_1|{H}^m(D)\Vert \le 1$, we see that

$$\begin{aligned} |\langle \partial _t w^N,v\rangle |\lesssim \Vert f|H^{-m}(D)\Vert + \Vert \partial _t g|(H^{m}(D))'\Vert +\Vert g|H^{m}(D)\Vert + \Vert w^N|L_2(D)\Vert , \end{aligned}$$

thus,

$$\begin{aligned} \Vert \partial _t w^N | H^{-m}(D) \Vert \lesssim \Vert f|H^{-m}(D)\Vert + \Vert \partial _t g|(H^{m}(D))'\Vert +\Vert g|H^{m}(D)\Vert + \Vert w^N|L_2(D)\Vert . \end{aligned}$$

Integration over t together with (3.2.18) yields

$$\begin{aligned}&\Vert \partial _t w^N |L_2([0,T],H^{-m}(D))\Vert ^2\nonumber \\&\quad \lesssim \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 +\Vert \partial _t g|L_2([0,T],(H^{m}(D))')\Vert ^2\nonumber \\&\qquad +\Vert g|L_2([0,T],H^{m}(D))\Vert ^2 +\Vert u_0|L_2(D)\Vert ^2 + \Vert g(0,\cdot )|L_2(D)\Vert ^2\nonumber \\&\quad \lesssim \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2+ \Vert g|H^1([0,T], H^m, (H^m)')\Vert ^2 +\Vert u_0|L_2(D)\Vert ^2, \end{aligned}$$

(3.2.19)

where in the last step we used the embedding $H^1([0,T], H^m, (H^m)')\hookrightarrow C([0,T],L_2(D))$ for the term $\Vert g(0,\cdot )|L_2(D)\Vert ^2$. Now using (3.2.18), (3.2.19) and the triangle inequality we get for $u^N=w^N+g$ that

$$\begin{aligned}&\Vert u^N|H^1([0,T], {H}^m, H^{-m})\Vert ^2\\&\quad \le \Vert w^N|H^1([0,T], {H}^m, H^{-m})\Vert ^2+ \Vert g|H^1([0,T], {H}^m, H^{-m})\Vert ^2\\&\quad \lesssim \Vert w^N|L_2([0,T],H^m(D))\Vert ^2+\Vert \partial _t w^N|L_2([0,T],H^{-m}(D))\Vert ^2\\&\qquad + \Vert g|H^1([0,T], H^m, (H^m)')\Vert ^2\\&\quad \lesssim \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 + \Vert g|H^1([0,T], H^m, (H^m)')\Vert ^2 +\Vert u_0|L_2(D)\Vert ^2, \end{aligned}$$

where in the second step we use the fact that $H^1([0,T], H^m, (H^m)')\hookrightarrow H^1([0,T], {H}^m, H^{-m})$ since $(H^m(D))'\hookrightarrow H^{-m}(D)$. Moreover, the appearing constant is independent of $f,\,g,\, u_0$ and N.

We see that $\{u^N\}_{N=1}^{\infty }$ is a uniformly bounded sequence in the reflexive space $H^1([0,T], {H}^m, H^{-m})$, thus, by the same arguments as in [16, Ch. 7, Thm. 3] we conclude that there exists a subsequence $\{u^{N_l}\}_{l=1}^{\infty }$ of $\{u^N\}_{N=1}^{\infty }$ which weakly converges to a weak solution $u\in H^1([0,T], {H}^m, H^{-m})$ of problem ($P_{\text {inhom}}$). In particular, this solution satisfies

$$\begin{aligned}&\Vert u|H^1([0,T], {H}^m, H^{-m})\Vert ^2 \\&\quad \lesssim \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 + \Vert g|H^1([0,T], H^m, (H^m)')\Vert ^2 +\Vert u_0|L_2(D)\Vert ^2, \end{aligned}$$

and satisfies the initial-boundary conditions

$$\begin{aligned} u(0,x)=u_0(x) \quad \text {in} \quad D \quad \text {and}\quad \frac{\partial ^{k-1}u}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}}= \frac{\partial ^{k-1}g}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}}, \ k=1,\ldots , m, \ j=1,\ldots , n, \end{aligned}$$

using $w=u-g$, (3.2.5) and the construction from (3.2.7), (3.2.9). This completes the proof. $\square$

To prove the generalization of Theorem 3.4 to the inhomogeneous setting we will need the following auxiliary lemma whose proof is based on [4, Lem. 4.3] with suitable modifications for our needs and which is related to the following problem:

Problem ($P_3$) has the advantage that it is easier to handle since now homogeneous boundary conditions appear.

Lemma 3.7

(Sobolev regularity with first time derivatives) Let D be a bounded Lipschitz domain of polyhedral type. Moreover, assume

$$\begin{aligned} f\in X \quad \text {where} \quad X=H^1([0,T],H^{-m}(D)) \quad \text {or}\quad X=L_2(D_T) \end{aligned}$$

and

$$\begin{aligned} \varphi _0 \in \mathring{H}^m(D). \end{aligned}$$

Then problem ($P_3$) has a unique weak solution w in $H^1([0,T], {H}^m, L_2):=L_2([0,T],H^{m}(D))\cap H^1([0,T], L_2(D))$ and the following estimate holds

$$\begin{aligned} \Vert w|H^1([0,T], {H}^m, L_2)\Vert\le & {} C\left\{ \Vert f|X\Vert +\Vert \varphi _0|\mathring{H}^m(D)\Vert \right\} , \end{aligned}$$

where C is a constant independent of $f,\,\varphi _0$ and w.

Remark 3.8

Later on we shall apply Lemma 3.7 to $\varphi _0:= u_0-g(0,\cdot )\in \mathring{H}^m(D)$ in order to relate problem ($P_3$) with our inhomogeneous problem ($P_{\text {inhom}}$). Thus, for the function $u_0$ we require $u_0\in {H}^m(D)$ and for g we require that it is smooth enough such that

$$\begin{aligned} g(0,\cdot )\in H^m(D). \end{aligned}$$

This is satisfied if

$$\begin{aligned} g&\in H^1([0,T], {H}^{2m}, L_2):=L_2([0,T],H^{2m}(D))\cap H^1([0,T], L_2(D))\nonumber \\&\hookrightarrow C([0,T],H^m(D)), \end{aligned}$$

(3.2.20)

cf. Lemma 2.17 concerning the embedding. Furthermore, in this case we have the estimate

$$\begin{aligned} \Vert w|H^1([0,T], {H}^m, L_2)\Vert&\le C\left\{ \Vert f|X\Vert +\Vert \varphi _0|\mathring{H}^m(D)\Vert \right\} \nonumber \\&\le C\left\{ \Vert f|X\Vert + \Vert g|H^1([0,T], {H}^{2m}, L_2)\Vert +\Vert u_0|H^m(D)\Vert \right\} , \end{aligned}$$

Proof

Step 1: Let us consider first the case $f \in L_2(D_T)$. We use the same construction as in (3.2.7) but now for each positive integer N consider the function

$$\begin{aligned} w^N(t,x)=\sum _{k=1}^N C^N_k(t)\psi _k(x), \end{aligned}$$

(3.2.21)

where $\left\{ C_k^N(t)\right\} _{k=1}^N$ is the solution of the ordinary differential equation system

$$\begin{aligned} (\partial _t w^N, \psi _k)+B(t,w^N,\psi _k)&= \langle f,\psi _k\rangle , \end{aligned}$$

(3.2.22)

$$\begin{aligned} C_k^N(0)&= \Vert \psi _k|\mathring{H}^m(D) \Vert ^{-2} (\varphi _0,\psi _k)_{\mathring{H}^m(D)}, \end{aligned}$$

(3.2.23)

for $k=1,\ldots , N$. Here the pairing $(\cdot , \cdot )_{\mathring{H}^m(D)}$ denotes the inner product in $\mathring{H}^m(D)$. Multiplying both sides of (3.2.22) by $2\frac{dC_k^N}{dt}$, then taking the sum with respect to k from 1 to N, and afterwards integrating with respect to t from 0 to T, we arrive at

$$\begin{aligned}&2 \Vert \partial _t w^N|L_2(D_T) \Vert ^2+ \displaystyle \sum _{|\alpha |,|\beta |\le m} \int _{D_T} a_{\alpha \beta }(t,x) \frac{\partial }{\partial t} (\partial _x^{\beta }w^N \partial _x^{\alpha }w^N) \,dx\, dt\\&\quad = 2 \int _0^T ( f,\partial _t w^N )_{L_2(D)} \, dt. \end{aligned}$$

Here we used that $\langle f,\partial _t w^N \rangle =( f,\partial _t w^N )_{L_2(D)}$ for $f(t,\cdot ) \in L_2(D)\subset H^{-m}(D)$ and $\partial _t w^N(t,\cdot ) \in \mathring{H}^m (D)$. Using integration by parts with respect to t we obtain

$$\begin{aligned}&2\Vert \partial _t w^N|L_2(D_T) \Vert ^2+B(T,w^N,w^N)\nonumber \\&\quad =B(0,w^N,w^N)+\displaystyle \int _0^T B_{\partial _t}(t,w^N,w^N)\, dt+ 2\int _0^T (f,\partial _t w^N )_{L_2(D)} \, dt. \end{aligned}$$

(3.2.24)

Since $a_{\alpha \beta }, \frac{\partial a_{\alpha \beta }}{\partial _t}$ are bounded on $D_T$, from (3.2.21), (3.2.23), Cauchy’s and Young’s inequalities we obtain

$$\begin{aligned} |B(0,w^N,w^N)|&\le c \Vert w^N(0,\cdot ) |\mathring{H}^m(D) \Vert ^2 \le c \Vert \varphi _0 |\mathring{H}^m(D) \Vert ^2, \end{aligned}$$

(3.2.25)

$$\begin{aligned} \left| \int _0^T B_{\partial _t}(t,w^N,w^N)\, dt\right|&\le c \Vert w^N|L_2([0,T],\mathring{H}^m(D))\Vert ^2, \end{aligned}$$

(3.2.26)

$$\begin{aligned} \left| 2 \displaystyle \int _0^T ( f,\partial _t w^N )_{L_2(D)} \, dt\right|&\le \varepsilon \Vert \partial _t w^N |L_2(D_T) \Vert ^2 +c(\varepsilon ) \Vert f |L_2(D_T) \Vert ^2. \end{aligned}$$

(3.2.27)

Furthermore, we use the estimate (3.2.18) replacing $u_0-g(0,\cdot )$ by $\varphi _0$ and g by the zero function and obtain

$$\begin{aligned} \Vert w^N|L_2([0,T],H^m(D))\Vert ^2 \le c ( \Vert \varphi _0|L_2(D)\Vert ^2+ \Vert f|L_2([0,T],H^{-m}(D))\Vert ^2 ). \end{aligned}$$

(3.2.28)

In view of (3.2.24), (3.2.27), (3.2.28), and (2.4.2) we deduce

$$\begin{aligned} \Vert \partial _t w^N|L_2(D_T) \Vert ^2 \le C \left( \Vert \varphi _0 |\mathring{H}^m(D) \Vert ^2+ \Vert f |L_2(D_T) \Vert ^2 \right) . \end{aligned}$$

(3.2.29)

Combining (3.2.28) and (3.2.29) we obtain

$$\begin{aligned} \Vert w^N|H^1([0,T], {H}^m, L_2)\Vert ^{{2}}\le C' \left( \Vert \varphi _0 |\mathring{H}^m(D) \Vert ^2+ \Vert f |L_2(D_T) \Vert ^2 \right) , \end{aligned}$$

where $C'$ is a constant independent of $N,\, f$, and $\varphi _0$. Hence, we see that $\{w^N\}_{N=1}^{\infty }$ is a uniformly bounded sequence in the reflexive space $H^1([0,T], {H}^m, L_2)$. Thus, by the same arguments as in [16, Ch. 7, Thm. 3] we conclude that there exists a subsequence $\{w^{N_l}\}_{l=1}^{\infty }$ of $\{w^N\}_{N=1}^{\infty }$ which weakly converges to a weak solution $w\in H^1([0,T], {H}^m, L_2)$ of problem ($P_3$). In particular, this solution satisfies

$$\begin{aligned} \Vert w|H^1([0,T], {H}^m, L_2)\Vert \le C' \left( \Vert \varphi _0 |\mathring{H}^m(D) \Vert + \Vert f |L_2(D_T) \Vert \right) , \end{aligned}$$

which proves the lemma for $X=L_2(D_T)$.

Step 2: Now let $f\in H^1([0,T],H^{-m}(D))$. Applying [16, Sec. 5.9, Thm. 2, (iii)] to the complete normed vector space $X=H^{-m}(D)$ we obtain

$$\begin{aligned} \Vert f (t,\cdot )| H^{-m}(D)\Vert ^2 \le C \Vert f | H^1([0,T],H^{-m}(D))\Vert ^2,\quad t\in [0,T], \end{aligned}$$

(3.2.30)

where the constant C depends only on T.

Similarly to (3.2.24) we obtain

$$\begin{aligned}&2\Vert \partial _t w^N|L_2(D_T) \Vert ^2+B(T,w^N,w^N)\nonumber \\&\quad =B(0,w^N,w^N)+\displaystyle \int _0^T B_{\partial _t}(t,w^N,w^N)\, dt+ 2 \int _0^T \langle f,\partial _t w^N \rangle \, dt. \end{aligned}$$

(3.2.31)

Noting that $\int _0^T\langle f,\partial _t w^N \rangle \, dt=- \int _0^T\langle \partial _t f, w^N \rangle \, dt+ \langle f, w^N \rangle |_0^T$, using (3.2.30) and Young’s inequality twice we calculate

$$\begin{aligned} \left| \displaystyle \int _0^T\langle f,\partial _t w^N \rangle \, dt \right|&\le C(\varepsilon )\Vert \partial _t f|L_2([0,T],H^{-m}(D)) \Vert ^2 +\frac{\varepsilon }{2} \Vert w^N|L_2([0,T],\mathring{H}^{m}(D)) \Vert ^2\nonumber \\&\quad +\Vert f(T,\cdot )| H^{-m}(D)\Vert \cdot \Vert w^N(T,\cdot )| H^{m}(D)\Vert \nonumber \\&\quad + \Vert f(0,\cdot )| H^{-m}(D)\Vert \cdot \Vert w^N(0,\cdot )| H^{m}(D)\Vert \nonumber \\&\le C(\varepsilon ,\varepsilon ') \Vert f|H^1([0,T],H^{-m}(D)) \Vert ^2 +\frac{\varepsilon }{2}\Vert w^N|L_2([0,T],\mathring{H}^{m}(D)) \Vert ^2\nonumber \\&\quad + \frac{\varepsilon '}{2} \left( \Vert w^N(T,\cdot )| H^{m}(D)\Vert ^2+\Vert w^N(0,\cdot )| H^{m}(D)\Vert ^2 \right) . \end{aligned}$$

(3.2.32)

Combining (3.2.25), (3.2.26), (3.2.28), (3.2.32) together with the coercivity of the bilinear form B, cf. (2.4.2), for $0<\varepsilon ', {\varepsilon } <\mu$ we obtain from (3.2.31) that

$$\begin{aligned} \Vert \partial _t w^N|L_2(D_T) \Vert ^2 \le C \left( \Vert f|H^1([0,T],H^{-m}(D)) \Vert ^2 + \Vert \varphi _0|\mathring{H}^m(D)\Vert ^2\right) . \end{aligned}$$

(3.2.33)

Finally, combining (3.2.28) and (3.2.33) yields

$$\begin{aligned} \Vert w^N|H^1([0,T], {H}^m, L_2)\Vert \le C'\left( \Vert f|H^1([0,T],H^{-m}(D))\Vert +\Vert \varphi _0|\mathring{H}^m(D)\Vert \right) . \end{aligned}$$

By the same argument as in Step 1 above, we conclude the existence of a convergent subsequence of $\{w^N\}_{N=1}^{\infty }$ to a function $w\in H^1([0,T], {H}^m, L_2)$ and obtain the assertion of the lemma for the case $f\in H^1([0,T],H^{-m}(D))$. $\square$

Remark 3.9

For later use we remark that if $\varphi \in \mathring{H}^{m}(D)$ and $f=f_1+f_2$ with $f_1\in H^1([0,T],H^{-m}(D))$, $f_2\in L_2(D_T)$, then one can decompose problem ($P_3$) into two parts

$$\begin{aligned} \left\{ \begin{array}{rll} \partial _t w_1+ (-1)^m Lw_1 &{}= f_1 \quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w_1}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,...,m,\, j=1,...,n,\\ w_1|_{t=0} &{}= c\varphi _0 \quad &{}\text {on} \quad D, \end{array} \right\} \end{aligned}$$

(3.2.34)

and

$$\begin{aligned} \left\{ \begin{array}{rll} \partial _t w_2+ (-1)^m Lw_2 &{}= f_2\quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w_2}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,...,m,\, j=1,...,n,\\ w_2|_{t=0} &{}= (1-c)\varphi _0\quad &{}\text {on} \quad D, \end{array} \right\} \end{aligned}$$

(3.2.35)

where $c\in \mathbb {R},\, 0\le c\le 1$.

Then if $w_1,\,w_2$ are the solutions of (3.2.34) and (3.2.35), respectively, we deduce from Lemma 3.7 that $w=w_1+w_2$ is the solution of ($P_3$) and the following inequality holds

$$\begin{aligned} \Vert w|H^1([0,T], {H}^m, L_2)\Vert \le C\left\{ \Vert f_1|H^1([0,T],H^{-m}(D))\Vert +\Vert f_2| L_2(D_T)\Vert +\Vert \varphi _0|\mathring{H}^m(D)\Vert \right\} . \end{aligned}$$

We now generalize Theorem 3.4 to inhomogeneous boundary conditions. We rely on the proof of the homogeneous case from [28, Thm. 5.2.3] and [4, Thm. 3.1] with suitable modifications. First we have to introduce the so called compatibility conditions appearing in [4, Sec. 3] modified according to our needs:

Definition 3.10

(Compatibility conditions) Using the notations from problem ($P_{\text {inhom}}$) we define

$$\begin{aligned} F:= f-\partial _t g- Lg, \qquad \varphi :=u_0- g(0,\cdot ), \end{aligned}$$

and

$$\begin{aligned} \varphi _0&:=\varphi ,\quad \varphi _1:=F(0,\cdot )- L(0,x,\partial _x)\varphi _0, \quad \ldots ,\\ \varphi _l&:=\partial _{t^{l-1}}F(0,\cdot )- \displaystyle \sum _{k=0}^{l-1}{l-1 \atopwithdelims ()k}L_{t^{l-1-k}}(0,x,\partial _x)\varphi _k, \end{aligned}$$

where

$$\begin{aligned} L_{t^k}(t,x,\partial _x)=\displaystyle \sum _{|\alpha |,|\beta |\le m} {(-1)^{|\alpha |}}\partial ^{\alpha }_x\left( \partial _{t^k} a_{\alpha \beta }(t,x) \partial ^{\beta }_x \right) . \end{aligned}$$

We say that the l-th-order compatibility conditions are fulfilled if $\partial _{t^k}F\in L_2([0,T],{H}^{(l-k)2m}(D))$ for $k=0,\ldots , l$, and additionally, it holds that $\varphi \in \mathring{H}^{(2\,l+1)m}(D)$,

$$\begin{aligned} \varphi _0,\ldots ,\varphi _{l-1}\in \mathring{H}^{2m}(D),\quad \text {and}\quad \varphi _l\in \mathring{H}^m(D). \end{aligned}$$

Remark 3.11

Note that such compatibility conditions are not needed in Theorem 3.5 since this would simply correspond to require that $u_0 -g(0,\cdot )=0$ on $\partial D$ (no further conditions in terms of derivatives w.r.t. time are needed). However, since $g(0,\cdot )$ and $u_0$ by the assumptions belong to $L_2(D)$ (and are therefore not defined pointwise) such a condition is not necessary (does not make sense) in this context.

With these compatibility conditions we are now able to generalize Theorem 3.4 for the inhomogeneous problem ($P_{\text {inhom}}$) as follows.

Theorem 3.12

(Sobolev regularity with time derivatives for inhomogeneous problem) Let D be a bounded Lipschitz domain of polyhedral type. Moreover, let $l\in \mathbb {N}_0$ and assume that the right hand side f of problem ($P_{\text {inhom}}$) satisfies

$$\begin{aligned} \partial _{t^k} f\in L_2([0,T],H^{(l-k)2m}(D)), \qquad k=0,\ldots , l. \end{aligned}$$

For g we assume

$$\begin{aligned} \partial _{t^k}g \in L_2([0,T],H^{(l+1-k)2m+m}(D)), \qquad k=0,\ldots , l+1. \end{aligned}$$

(3.2.36)

Moreover, let $u_0\in {H}^{(2l+1)m}(D)$ and the l-th order compatibility conditions be satisfied. Then the weak solution $u\in H^1([0,T], {H}^m, L_2)$ of Problem ($P_{\text {inhom}}$) has derivatives with respect to t up to order l satisfying

$$\begin{aligned} \partial _{t^k}u\in H^1([0,T], {H}^m, L_2)\quad \text {for}\quad k=0,\ldots , l. \end{aligned}$$

Moreover, we have the estimate

$$\begin{aligned}&\displaystyle \sum _{k=0}^l \Vert \partial _{t^k}u|H^1([0,T], {H}^m, L_2)\Vert \nonumber \\&\quad \le C\Bigg (\sum _{k=0}^l\Vert \partial _{t^k} f|L_2([0,T],H^{(l-k)2m}(D))\Vert \nonumber \\&\qquad + \sum _{k=0}^{l+1}\Vert \partial _{t^k} g|L_2([0,T],H^{(l+1-k)2m+m}(D))\Vert +\Vert u_0|{H}^{(2l+1)m}(D)\Vert \Bigg ), \end{aligned}$$

(3.2.37)

where C is a constant independent of $f,\,g,\,u_0$, and u.

Proof

We define the function $w:=u-g$ and consider the following equivalent problem to problem ($P_{\text {inhom}}$):

$$\begin{aligned} \left\{ \begin{array}{lll} \partial _t w+ Lw &{}= f-\partial _t g- Lg=:F \quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,...,m,\, j=1,...,n,\\ w|_{t=0} &{}= u_0- g(0,\cdot ) \quad &{}\text {on} \quad D. \end{array} \right\} \end{aligned}$$

(3.2.38)

In particular, problem (3.2.38) has the advantage that it is easier to handle compared to problem ($P_{\text {inhom}}$), since now homogeneous boundary conditions appear. In what follows, we will show the theorem by induction on l and additionally prove that the following equalities hold:

$$\begin{aligned} \partial _{t^k}w(0,\cdot )=\varphi _k, \quad k=0,\ldots , l, \end{aligned}$$

and

$$\begin{aligned} \langle \partial _{t^{l+1}} w,\eta \rangle +\displaystyle \sum _{k=0}^l{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k} w,\eta )&= (\partial _{t^l}F,\eta ) \nonumber \\&=\langle \partial _{t^l} f,\eta \rangle - \langle \partial _{t^{l+1}} g,\eta \rangle \nonumber \\&\quad -\sum _{k=0}^l{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}g ,\eta ) \end{aligned}$$

(3.2.39)

for all $\eta \in \mathring{H}^m(D)$. The case $l=0$ follows directly from Lemma 3.7 (and Theorem 3.5) which for $F\in L_2(D_T)$ and $\varphi _0=u_0-g(0,\cdot )\in \mathring{H}^m(D)$ gives the estimate

$$\begin{aligned} \Vert w|H^1([0,T], {H}^m, L_2)\Vert \lesssim \Vert F|L_2(D_T)\Vert +\Vert \varphi _0|\mathring{H}^m(D)\Vert . \end{aligned}$$

(3.2.40)

In particular, $F\in L_2(D_T)$ follows from $f\in L_2(D_T)$ and the fact that the assumptions on g imply $\partial _t g\in L_2([0,T],L_2(D))$ and $Lg\in L_2([0,T],L_2(D))$.

Therefore, we obtain

$$\begin{aligned} \Vert F|L_2(D_T)\Vert&\lesssim \Vert f|L_2(D_T)\Vert +\Vert \partial _t g|L_2(D_T)\Vert + \Vert Lg|L_2(D_T)\Vert \\&\lesssim \Vert f|L_2(D_T)\Vert +\sum _{k=0}^1\Vert \partial _{t^k}g|L_2([0,T], H^{(1-k)2m{+m}}(D))\Vert , \end{aligned}$$

which inserted in (3.2.40) and using the embedding (3.2.20) gives

$$\begin{aligned}&\Vert w|H^1([0,T], {H}^m, L_2)\Vert \\&\quad \lesssim \Vert f|L_2(D_T)\Vert +\sum _{k=0}^1\Vert \partial _{t^k}g|L_2([0,T], H^{(1-k)2m{+m}}(D))\Vert +\Vert u_0|H^m(D)\Vert . \end{aligned}$$

This proves the claim for $l=0$. Assuming that the assumptions hold for $l-1$, i.e.,

$$\begin{aligned} \partial _{t^k}u\in H^1([0,T], {{H}^{m}}, L_2)\quad \text {for}\quad k=0,\ldots , l-1, \end{aligned}$$

together with

$$\begin{aligned}&\displaystyle \sum _{k=0}^{l-1} \Vert \partial _{t^k}u|H^1([0,T], {{H}^{m}}, L_2)\Vert \nonumber \\&\quad \lesssim \Bigg (\sum _{k=0}^{l-1}\Vert \partial _{t^k} f|L_2([0,T], H^{(l-1-k)2m}(D))\Vert \nonumber \\&\qquad + \sum _{k=0}^{l}\Vert \partial _{t^k}g|L_2([0,T], H^{((l-1)+1-k)2m+m}(D))\Vert \nonumber \\&\qquad +\Vert u_0|H^{(2(l-1)+1)m}(D)\Vert \Bigg ), \end{aligned}$$

and $\ \partial _{t^k}w(0,\cdot )=\varphi _k,\quad k=0,...,l-1,$

$$\begin{aligned} \langle \partial _{t^{l}} w,\eta \rangle +\displaystyle \sum _{k=0}^{l-1}{l-1 \atopwithdelims ()k} B_{\partial _{t^{l-1-k}}}(t,\partial _{t^k} w,\eta )= (\partial _{t^{l-1}}F,\eta ), \end{aligned}$$

we will prove them for l ($l\ge 1$). We consider first the following problem: find a function $v\in {H^1([0,T], \mathring{H}^m, H^{-m})}$ satisfying $v(0,\cdot )=\varphi _l$ and

$$\begin{aligned}&\langle \partial _t v,\eta \rangle +B(t,v,\eta )\nonumber \\&\quad =(\partial _{t^l}F,\eta )- \displaystyle \sum _{k=0}^{l-1}{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}w,\eta ) \nonumber \\&\quad =\langle \partial _{t^l} f,\eta \rangle -\displaystyle \sum _{k=0}^{l-1}{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}(u-g),\eta )-\langle \partial _{t^{l+1}} g,\eta \rangle -\sum _{k=0}^l{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}g ,\eta )\nonumber \\&\quad = \langle \partial _{t^l} f,\eta \rangle -\displaystyle \sum _{k=0}^{l-1}{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}u,\eta )-\langle \partial _{t^{l+1}} g,\eta \rangle -B(t,\partial _{t^l}g,\eta )\nonumber \\&\quad =: \langle {\widetilde{F}}(t),\eta \rangle . \end{aligned}$$

(3.2.41)

for all $\eta \in \mathring{H}^m(D)$ and a.e. $t\in [0,T]$. (Note that the idea here is that by construction we want $v=\partial _{t^l}w=\partial _{t^l}(u-g)$.) We show that the functional ${\widetilde{F}}(t)$, $t\in [0,T]$ on the right hand side of belongs to ${\widetilde{F}}\in L_2([0,T], H^{-m}(D))$: From the inductive hypothesis, the fact that

$$\begin{aligned} \Vert {\widetilde{F}}(t)|H^{-m}(D)\Vert =\displaystyle \sup _{\eta \in \mathring{H}^m(D), \Vert \eta |\mathring{H}^m(D)\Vert \le 1}|\langle {\widetilde{F}}(t),\eta \rangle |, \end{aligned}$$

together with $(H^m(D))'\hookrightarrow H^{-m}(D)$ and (2.4.3), we see that

$$\begin{aligned}&\Vert {\widetilde{F}}|L_2([0,T],H^{-m}(D))\Vert \\&\quad \le \Vert \partial _{t^l}f|L_2([0,T], H^{-m}(D))\Vert + \Vert \partial _{t^{l+1}}g|L_2([0,T], (H^{m}(D))')\Vert \\&\qquad + \Vert \partial _{t^{l}}g|L_2([0,T],H^m(D)) \Vert \\&\qquad +C\displaystyle \sum _{k=0}^{l-1}\Vert \partial _{t^k}u|L_2([0,T],H^m(D))\Vert \\&\quad \lesssim \Vert \partial _{t^l}f|L_2(D_T)\Vert + \Vert \partial _{t^l}g| H^1([0,T], {H}^{2m}, L_2)\Vert \\&\qquad + \sum _{k=0}^{l-1} \Vert \partial _{t^k} f|L_2([0,T],H^{(l-1-k)2m}(D))\Vert + \sum _{k=0}^{l}\Vert \partial _{t^k} g|L_2([0,T],H^{(l-k)2m+m}(D))\Vert \\&\qquad +\Vert u_0|H^{(2(l-1)+1)m}(D)\Vert \\&\quad \le C' \Bigg ( \sum _{k=0}^l \Vert \partial _{t^k} f|L_2([0,T],H^{(l-k)2m}(D))\Vert + \sum _{k=0}^{l+1}\Vert \partial _{t^k}g|L_2([0,T],H^{(l+1-k)2m+m}(D))\Vert \\&\qquad +\Vert u_0|H^{(2l+1)m}(D)\Vert \Bigg ), \end{aligned}$$

where $C'$ is a constant independent of $f,\, g,\, u_0$, and u.

Hence, according to Theorem 3.5 the problem (3.2.41) has a solution $v\in {H^1([0,T],} {{\mathring{H}^m}, H^{-m})}$ with

$$\begin{aligned} \Vert v|H^1([0,T], {\mathring{H}^m}, H^{-m})\Vert&\le C(\Vert {\widetilde{F}}|L_2([0,T], H^{-m}(D))\Vert + \Vert \varphi _l|H^m(D)\Vert ), \end{aligned}$$

where C is a constant independent of $f,\, g,\, u_0$ and u.

We put now

$$\begin{aligned} \gamma (t,x)=\int _0^tv(\tau ,x)\, d \tau + \varphi _{l-1}(x), \qquad t\in [0,T], \ x\in D. \end{aligned}$$

Then we have $\gamma (0,\cdot )=\varphi _{l-1}$, $\partial _t \gamma =v$, $\partial _t \gamma (0,\cdot )=v(0,\cdot )=\varphi _l$. Note that

$$\begin{aligned} B(t,\partial _t \gamma , \eta )=\frac{\partial }{\partial t}B(t,\gamma ,\eta )- B_{\partial _{t}}(t,\gamma ,\eta ), \end{aligned}$$

(3.2.42)

and

$$\begin{aligned} \frac{\partial }{\partial t} \left( \displaystyle \sum _{k=0}^{l-2}{l-1\atopwithdelims ()k}B_{\partial _{t^{l-1-k}}}(t,\partial _{t^k}w,\eta )\right) = \sum _{k=0}^{l-1}{l\atopwithdelims ()k}B_{\partial _{t^{l-k}}}(t, \partial _{t^k}w,\eta )-B_{\partial _{t}} (t,\partial _{t^{l-1}} w,\eta ). \end{aligned}$$

(3.2.43)

Using (3.2.42) and (3.2.43) we rewrite (3.2.41) as follows

$$\begin{aligned}&\langle \partial _{t^2}\gamma ,\eta \rangle +\frac{\partial }{\partial t}B(t,\gamma ,\eta ) \nonumber \\&\qquad =(\partial _{t^l}F,\eta )+B_{\partial _t}(t,\gamma -\partial _{t^{l-1}}w,\eta )- \frac{\partial }{\partial t}\displaystyle \sum _{k=0}^{l-2}{l-1\atopwithdelims ()k} B_{\partial _{t^{l-1-k}}}(t,\partial _{t^k}w,\eta ). \end{aligned}$$

(3.2.44)

Since $L_{t^{k}}=\displaystyle \sum _{|\alpha |,|\beta |=0}^m {(-1)^{|\alpha |}}\partial _x^{\alpha }(\partial _{t^{k}} a_{\alpha \beta } \partial _x^{\beta } )$ we deduce from (2.4.3) that

$$\begin{aligned} B_{\partial _{t^k}}(t,\omega ,\eta )=\displaystyle \int _D L_{t^{k}}(t,x,\partial _x)\omega \eta \, dx \end{aligned}$$

(3.2.45)

for all $\omega \in \mathring{H}^{2m}(D)$, $\eta \in \mathring{H}^m(D)$, and all $t\in [0,T]$. From the compatibility conditions and (3.2.45) we see that

$$\begin{aligned} (\varphi _l,\eta )= (\partial _{t^{l-1}}F(0),\eta )- \displaystyle \sum _{k=0}^{l-1}{l-1\atopwithdelims ()k} B_{\partial _{t^{l-1-k}}}(0,\varphi _k,\eta ). \end{aligned}$$

(3.2.46)

Using (3.2.46), the fact that $\gamma (0,\cdot )=\varphi _{l-1}$, $\partial _t\gamma (0,\cdot )=\varphi _{l}$, $\partial _{t^k}w(0,\cdot )=\varphi _k$ for $k=0,...,l-1,$ and integrating (3.2.44) with respect to t from 0 to t we obtain

$$\begin{aligned}&\langle \partial _{t}\gamma ,\eta \rangle +B(t,\gamma ,\eta ) \nonumber \\&\qquad = (\partial _{t^{l-1}}F,\eta )+\displaystyle \int _0^t B_{\partial _t}(\tau ,\gamma -\partial _{t^{l-1}}w,\eta )\, d\tau - \sum _{k=0}^{l-2}{l-1\atopwithdelims ()k} B_{\partial _{t^{l-1-k}}}(t,\partial _{t^k}w,\eta ), \end{aligned}$$

(3.2.47)

where most of the ‘boundary terms’ corresponding to $t=0$ after integration cancel out. Put $z=\gamma -\partial _{t^{l-1}}w$. Then $z(0,\cdot )=0$ since $\partial _{t^{l-1}}w(0,\cdot )=\gamma (0,\cdot )=\varphi _{l-1}$. It follows from the inductive assumption (3.2.39) with l replaced by $l-1$ and (3.2.47) that

$$\begin{aligned} \langle \partial _t z(t,\cdot ),\eta \rangle +B(t,z(t,\cdot ),\eta )=\displaystyle \int _0^t B_{\partial _{t}}(\tau ,z(\tau ,\cdot ),\eta )\, d\tau , \end{aligned}$$

(3.2.48)

for all $\eta \in \mathring{H}^m(D)$.

Moreover, $z\in H^1([0,T], \mathring{H}^m, H^{-m})$, since $v=\partial _t \gamma \in H^1([0,T], \mathring{H}^m, H^{-m})$ and $\partial _{t^{l-1}}w=\partial _{t^{l-1}}(u-g)\in H^1([0,T], \mathring{H}^m, L_2):=L_2([0,T],\mathring{H}^m(D))\cap H^1([0,T],L_2(D))\hookrightarrow H^1([0,T], \mathring{H}^m, H^{-m})$ according to the induction assumption on u and the conditions on g.

Now applying Lemma 3.2, we can see from (3.2.48) that $z\equiv 0$ on $[0,T]\times D$. This implies $\partial _{t^l}(u-g)=\partial _{t^l}w=\partial _t \gamma =v\in {H^1([0,T], \mathring{H}^m, H^{-m})}$, and hence, $\partial _{t^l}u\in {H^1([0,T], H^m, {H^{-m}})}$, since according to our assumptions $\partial _{t^l}g\in {H^1([0,T], H^m, (H^m)')}$. It remains to show that in fact we actually have $\partial _{t^l}u\in H^1([0,T], {H}^m, L_2)$. For this we rewrite (3.2.41) as

$$\begin{aligned} \langle \partial _t v,\eta \rangle +B(t,v,\eta ) = \langle {\widehat{F}}_1,\eta \rangle +\langle {\widehat{F}}_2,\eta \rangle , \end{aligned}$$

where ${\widehat{F}}_1(t)$, ${\widehat{F}}_2(t)$, $t\in [0,T]$ are the functionals defined by

$$\begin{aligned} \langle {\widehat{F}}_1,\eta \rangle&:= \langle \partial _{t^l}f,\eta \rangle -\langle \partial _{t^{l+1}} g,\eta \rangle , \qquad \eta \in \mathring{H}^m(D), \nonumber \\ \langle {\widehat{F}}_2,\eta \rangle&:= -B(t,\partial _{t^l}g,\eta )-\displaystyle \sum _{k=0}^{l-1}{l\atopwithdelims ()k} B_{\partial _{t^{l-k}}}(t,\partial _{t^k}u,\eta ), \qquad \eta \in \mathring{H}^m(D). \end{aligned}$$

(3.2.49)

Since $\partial _{t^{l+1}}g\in L_2(D_T)$ and $\partial _{t^l}f\in L_2(D_T)$ we see immediately that ${\widehat{F}}_1$ in fact belongs to $L_2(D_T)$. Moreover, we see from (3.2.49) that ${\widehat{F}}_2$ belongs to $H^1([0,T],H^{-m}(D))$: We deduce ${\widehat{F}}_2, \ \partial _t {\widehat{F}}_2\in L_2([0,T], H^{-m}(D))$, from (3.2.49) and

$$\begin{aligned} \langle \partial _t {\widehat{F}}_2,\eta \rangle&:= -B_{\partial _t}(t,\partial _{t^l}g,\eta )-B(t,\partial _{t^{l+1}}g,\eta ) \nonumber \\&\quad -\displaystyle \sum _{k=0}^{l-1}{{l+1}\atopwithdelims ()k} B_{\partial _{t^{l+1-k}}}(t,\partial _{t^k}u,\eta )-lB_{\partial _t}(t, \partial _{t^l}u,\eta ). \end{aligned}$$

(3.2.50)

using the regularity assumptions $\partial _{t^{l}}g\in L_2([0,T],H^{2m+m}(D))$, $\partial _{t^{l+1}}g\in L_2([0,T],H^{m}(D))$, and $\partial _{t^k}u\in L_2([0,T], H^{m}(D))$ for all $k=0,\ldots , l$.

Thus, from Remark 3.9 after Lemma 3.7 we conclude $v=\partial _{t^l}(u-g)\in H^1([0,T], {H}^m, L_2)$, which implies $\partial _{t^l}u\in H^1([0,T], {H}^m, L_2)$. The desired estimate (3.2.37) holds since $\Vert {\widehat{F}}_1|L_2(D_T)\Vert$, $\Vert {\widehat{F}}_2|H^1([0,T],H^{-m}(D))\Vert$ and $\Vert \varphi _l|H^m(D)\Vert$ can be estimated by the right hand side of (3.2.37). This finally completes the proof. $\square$

Remark 3.13

Note that the regularity conditions (3.2.36) on g in Theorem 3.12 are necessary since we require $\partial _{t^{l+1}}g\in L_2([0,T],H^{m}(D))$ in (3.2.50).

3.3 Regularity results in weighted Sobolev spaces

In this subsection we provide regularity assertions for the weak solution of problems ($P_{\text {hom}}$) and ($P_{\text {inhom}}$) in the spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$. Forerunners for the homogeneous case can be found in [24, Thm. 3.3], where the underlying domain is a polyhedral cone, and in [28, Thms. 5.2.9, 5.2.12], where corresponding regularity results are proven on domains of polyhedral type in the scale of Kondratiev spaces (which is contained in the scale of V-spaces). We now want to generalize these results to the more general spaces $V_{\varvec{\beta },\delta }^{l,p}(D)$ where the underlying domain is of polyhedral type for both, the homogeneous and the inhomogeneous setting.

3.3.1 Weighted Sobolev regularity for the homogeneous problem

We first investigate the regularity in weighted Sobolev spaces for the parabolic problem ($P_{\text {hom}}$) on domains of polyhedral type.

Theorem 3.14

($A_{\text {hom}}$: Regularity in V-spaces of homogeneous problem) Let $D\subset \mathbb {R}^3$ be a bounded Lipschitz domain of polyhedral type with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$. Let $\gamma \in \mathbb {N}$ with $\gamma \ge 2m$ and put $\gamma _m:=\left[ \frac{\gamma -1}{2m}\right]$. Furthermore, let $\delta \in \mathbb {R}^d$, $\varvec{\beta }\in \mathbb {R}^{d'}$ with ${\delta _k\in [-m,m]}$ for $k=1,\ldots ,d$ and $\beta _j\in [-m,m]$ for $j=1,\ldots ,d'$. Assume that the right hand side f of problem ($P_{\text {hom}}$) satisfies

• (i) $\partial _{t^k} f\in L_2(D_T)\cap L_2([0,T], V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D) )$, $k=0,\ldots , \gamma _m$,    and    $\partial _{t^{\gamma _m+1}} f\in L_2(D_T)$,

• (ii) $\partial _{t^k} f(0,x)=0$,    $k=0,\ldots , {\gamma _m}.$

Moreover, suppose that the closed strip between the lines $\text {Re}\, \lambda =m-3/2$ and $\text {Re}\, \lambda = 2m(\gamma _m-i)-\beta _j+2m-3/2$ is free of eigenvalues of the pencil ${\mathfrak {A}}_j(\lambda )$ for $j=1,\ldots ,d',\, i=0,\ldots ,\gamma _m$ and that

$$\begin{aligned} -\delta _-^{(k)}< 2m(\gamma _m-i)-\delta _k+m <\delta _+^{(k)} \end{aligned}$$

for $k=1,\ldots ,d$ and $i=0,\ldots ,\gamma _m$. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ (with time-derivatives $\partial _{t^k}u\in H^1([0,T], \mathring{H}^m, H^{-m}) \text { for } k=1,\ldots ,\gamma _{m}+1$) of problem ($P_{\text {hom}}$) we have

$$\begin{aligned} \partial _{t^{l+1}} u\in L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-l)}(D)) \end{aligned}$$

for $l=-1,0,\ldots , \gamma _m$. In particular, for the derivatives $\partial _{t^{l+1}} u$ up to order $\gamma _m+1$ we have the a priori estimate

$$\begin{aligned}&\sum _{l=-1}^{\gamma _m} \Vert \partial _{t^{l+1}} u|{L_2([0,T], V_{\varvec{\beta },\delta }^{2m(\gamma _m-l)}(D))}\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)} (D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert , \end{aligned}$$

(3.3.1)

where the constant is independent of u and f.

Remark 3.15

The existence of the solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ with derivatives $\partial _{t^k}u\in H^1([0,T], \mathring{H}^m, H^{-m}) \,\text {for}\, k=1,\ldots ,\gamma _{m}+1$ in Theorem 3.14 follows from Theorems 3.3 and 3.4 with $l=\gamma _m+1$.

Proof

We prove the theorem by induction. In particular, we first show the claim for the induction basis $\gamma =2m$. Then we proceed with the induction step from $\gamma -1$ to $\gamma$ with $l=\gamma _m$, and finally, we make a backwards induction from $l=\gamma _m,\gamma _m-1,\ldots ,i$ to $l=i-1$ with arbitrary $\gamma$.

Let $\gamma =2m$, then we have $\gamma _m=0$. Since by our assumptions $f, \partial _t f\in L_2(D_T)\hookrightarrow L_2([0,T],H^{-m}(D))$ it follows from Theorem 3.4 that $\partial _t u(t)\in \mathring{H}^m(D)$. Furthermore, according to [26, p. 143, and Lem. 3.1.6] and Lemma 2.5 one obtains that $\mathring{H}^m(D)\subset V_{0,0}^m(D)\subset V_{\varvec{\beta },\delta }^0(D)$ if $-m\le \beta _j$ for all $j=1,\ldots ,d'$ and $-m\le \delta _k$ for all $k=1,\ldots ,d$. In this case Theorem 3.4 gives the estimate

$$\begin{aligned} \Vert \partial _t u|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert&\lesssim \Vert \partial _t u|L_2([0,T],\mathring{H}^m(D))\Vert \nonumber \\&\lesssim \sum _{k=0}^1\Vert \partial _{t^k}f|L_2([0,T],H^{-m}(D))\Vert \lesssim \sum _{k=0}^1\Vert \partial _{t^k}f|L_2(D_T)\Vert . \end{aligned}$$

(3.3.2)

Moreover, we have

$$\begin{aligned} Lu=f-\partial _{t}u, \end{aligned}$$

where for fixed t the right hand side belongs to $V_{\varvec{\beta },\delta }^0(D)$ and according to (2.1.4) also to $V_{0,0}^{-m}(D)$ if $\beta _j\le m,\, j=1,\ldots ,d'$ and $\delta _k\le m,\, k=1,\ldots ,d$. Thus, an application of Lemma 3.1 (with ${\tilde{\gamma }}=m$, ${\tilde{\delta }}_k=0$, $k=1,\ldots ,d$, $\tilde{\beta _j}=0$, $j=1,\ldots ,d'$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$) gives $u(t)\in V_{\varvec{\beta },\delta }^{2m}(D)$ with the a priori estimate

$$\begin{aligned} \Vert u(t)|V_{\varvec{\beta },\delta }^{2m}(D)\Vert \lesssim \Vert f(t)|V_{\varvec{\beta },\delta }^0(D)\Vert +\Vert \partial _t u(t)|V_{\varvec{\beta },\delta }^0(D)\Vert . \end{aligned}$$

Now integration w.r.t. the parameter t together with (3.3.2) proves the claim for $\gamma =2m$, i.e.,

$$\begin{aligned} \Vert u|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert \lesssim \Vert f|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert +\sum _{k=0}^1\Vert \partial _{t^k}f|L_2(D_T)\Vert . \end{aligned}$$

Assume inductively that our assumption holds for $\gamma -1$. This means, in particular, that we have the following a priori estimate

$$\begin{aligned}&\sum _{l=-1}^{(\gamma -1)_m} \Vert \partial _{t^{l+1}} u|{L_2([0,T],V^{2m((\gamma -1)_m-l)}_{\varvec{\beta }, \delta }(D))}\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{(\gamma -1)_m}\Vert \partial _{t^k} f|{L_2([0,T], V^{2m((\gamma -1)_m-k)}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{(\gamma -1)_m+1} \Vert \partial _{t^k} f|{L_2(D_T)}\Vert . \end{aligned}$$

(3.3.3)

We are going to show that the claim then holds for $\gamma$ as well. If $l=\gamma _m$ by our assumptions on f we have $\partial _{t^{k}} f\in L_2(D_T)\hookrightarrow L_2([0,T],H^{-m}(D))$ for $k=0,\ldots , \gamma _m+1$, and by Theorem 3.4 together with (2.1.4) and $\mathring{H}^m(D)=\mathring{V}_{0,0}^m(D)$, cf. [26, p. 143], we have

$$\begin{aligned} \partial _{t^{\gamma _m+1}}u(t)\in \mathring{H}^m(D)\subset V^0_{\varvec{\beta },\delta }(D)\quad \text {for} \quad {-m\le \beta _j,\, -m\le \delta _k}, \end{aligned}$$

where $j=1,\ldots ,d'$ and $k=1,\ldots ,d$. In particular, Theorem 3.4 provides us with the a priori estimate

$$\begin{aligned} \Vert \partial _{t^{\gamma _m+1}}u|L_2([0,T], V^0_{\varvec{\beta },\delta }(D))\Vert&\lesssim \Vert \partial _{t^{\gamma _m+1}}u|L_2([0,T], \mathring{H}^m(D))\Vert \nonumber \\&\lesssim \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f| L_2([0,T],H^{-m}(D))\Vert \lesssim \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f| L_2(D_T)\Vert , \end{aligned}$$

which shows the claim for $l=\gamma _m$ and arbitrary $\gamma$. Hence, the claim holds for $l=\gamma _m$. We now proceed by backwards induction. Suppose now the result holds for $\gamma$ and $l=\gamma _m, \gamma _m-1, \ldots , i$ where $0\le i\le \gamma _m$. We show that it then also holds for $i-1$. Differentiating ($P_{\text {hom}}$) i-times gives

$$\begin{aligned} L (\partial _{t^i}u)=\partial _{t^i}f-\partial _{t^{i+1}}u-\sum _{k=0}^{i-1}{i\atopwithdelims ()k}\partial _{t^{i-k}}L (\partial _{t^k}u), \end{aligned}$$

(3.3.4)

where $\partial _{t^{i-k}}L= \sum _{|\alpha |,|\beta |=0}^m (-1)^{|\alpha |}\partial _x^{\alpha }(\partial _{t^{i-k}} a_{\alpha \beta } \partial _x^{\beta } )$. From our initial assumptions on f we see that $\partial _{t^i}f(t)\in V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)$ and from the inductive assumptions it follows that $\partial _{t^{i+1}}u(t)\in V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)$ and

$$\begin{aligned} \partial _{t^{(k-1)+1}}u&\in L_2([0,T],V^{2m((\gamma -1)_m-(k-1))}_{\varvec{\beta },\delta }(D)) \hookrightarrow L_2([0,T],V^{2m(\gamma _m-i+1)}_{\varvec{\beta },\delta }(D)), \end{aligned}$$

(3.3.5)

where we used Lemma 2.5 and the fact that $(\gamma -1)_m-(k-1)\ge \gamma _m-i+1$ for $k=0,\ldots , i-1$. The differential operator $\partial _{t^{i-k}} L$ diminishes the space regularity by 2m since its coefficients $a_{\alpha \beta }$ are smooth functions. Thus, from (3.3.5) we see that

$$\begin{aligned} \partial _{t^{i-k}}L (\partial _{t^k}u)\in L_2([0,T],V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)), \end{aligned}$$

hence, the right hand side of (3.3.4) belongs to $L_2([0,T],V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D))$ and by (2.1.4) also to $L_2([0,T],V^{-m}_{0,0}(D))$ since $\beta _j\le m$, $\delta _k\le m$ for $j=1,\ldots ,d'$ and $k=1,\ldots ,d$. An application of Lemma 3.1 (now with $\gamma '=2m(\gamma _m-(i-1))$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$ and again taking ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0$ for $j=1,\ldots ,d'$ and ${\tilde{\delta }}_k=0$ for $k=1,\ldots ,d$) yields

$$\begin{aligned} \partial _{t^{(i-1)+1}}u(t)\in V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D). \end{aligned}$$

Moreover, we have the a priori estimate

$$\begin{aligned}&\Vert \partial _{t^{(i-1)+1}}u(t)| V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}f(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}u(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{k=0}^{i-1}\Vert \partial _{t^{i-k}}L(\partial _{t^k}u)(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}f(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}u(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{k=0}^{i-1}\Vert (\partial _{t^k}u)(t)|V^{2m(\gamma _m-i+1)}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}f(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}u(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{k=0}^{i-1}\Vert (\partial _{t^k}u)(t)|V^{2m((\gamma -1)_m-(k-1))}_{\varvec{\beta },\delta }(D)\Vert , \end{aligned}$$

where we used (3.3.5) in the last step. Integration w.r.t. the parameter t together with the inductive assumptions on $\partial _{t^{i+1}}u$ and $\partial _{t^k} u$ (cf. (3.3.3)) gives the a priori estimate

$$\begin{aligned}&\Vert \partial _{t^{(i-1)+1}}u| L_2([0,T],V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \Vert \partial _{t^{i}} f|{L_2([0,T], V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D))}\Vert +\Vert \partial _{t^{i+1}} u|{L_2([0,T], V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D))}\Vert \\&\qquad + \sum _{k=0}^{i-1}\Vert \partial _{t^k}u|L_2([0,T],V^{2m((\gamma -1)_m-(k-1))}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T], V^{2m(\gamma _m-k)}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert \\&\qquad + \sum _{k=0}^{(\gamma -1)_m}\Vert \partial _{t^k} f|{L_2([0,T], V^{2m((\gamma -1)_m-k)}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{(\gamma -1)_m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert \\&\quad \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T], V^{2m(\gamma _m-k)}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert , \end{aligned}$$

where in the last step we used the fact that $(\gamma -1)_m\le \gamma _m$. This shows that the claim is true for $i-1$ and completes the proof. $\square$

Remark 3.16

(Restrictions on the parameter $\delta$) We discuss the restrictions on the parameter $\delta =(\delta _1,\ldots , \delta _d)$ appearing in Theorem 3.14. For simplicity, let the domain of polyhedral type D be a polyhedron with straight edges and faces where $\theta _k$ denotes the angle at the edge $M_k$. Then we require for $\delta _k,\, k=1,\ldots ,d$ that

$$\begin{aligned}&(1)\quad -\delta _-^{(k)}<2m(\gamma _m-i)-\delta _k+m<\delta _+^{(k)},\quad i=0,\ldots ,\gamma _m,\\&(2) \quad -m\le \delta _k\le m. \end{aligned}$$

We consider the case of the heat equation when $m=1$ and $\delta _{\pm }^{(k)}=\frac{\pi }{\theta _k}$, cf. [22, Subsect. 2.1.1] or [24, Sect. 4]. For general angles $\theta _k$ we obtain the restrictions

$$\begin{aligned}&(1)\quad -\frac{\pi }{\theta _k}<2(\gamma _1-i)-\delta _k+1< \frac{\pi }{\theta _k},\quad i=0,\ldots ,\gamma _1,\\&(2)\quad -1\le \delta _k\le 1, \end{aligned}$$

which are satisfied if

$$\begin{aligned} \max \bigg ( 2(\gamma _1-i)-\frac{\pi }{\theta _k}+1,-1 \bigg )<\delta _k\le 1, \quad i=0,\ldots ,\gamma _1. \end{aligned}$$

(3.3.6)

To guarantee that such $\delta _k$’s exist we require

$$\begin{aligned} 2\gamma _1-\frac{\pi }{\theta _k}+1<1 \quad \text {i.e., } \quad \gamma _1< \frac{\pi }{2\theta _k}, \end{aligned}$$

(3.3.7)

which shows that the greater the angle $\theta _k$, the smaller $\gamma _1$ (and thus $\gamma$) has to be in order to satisfy the assumptions. In particular, for the extremal case $\theta _k=2\pi$ we require $\gamma _1=0$ (i.e., $\gamma =2$ and $\frac{1}{2}<\delta _k\le 1$) whereas for $\theta _k=\frac{\pi }{4}$ we obtain $\gamma _1<2$ (i.e., $\gamma <4$ with $-1<\delta _k\le 1$ for $\gamma =3$). Moreover, if $\gamma _1=0$ in (3.3.6) then $\max \big ( 2(\gamma _1-i)-\frac{\pi }{\theta _k}+1,-1 \big )=\max \big (1-\frac{\pi }{\theta _k},-1\big )$. In this case it is always possible to find suitable $\delta _k$’s, since $1- \frac{\pi }{\theta _k}<1$ is always satisfied. If $\gamma _1=1$ (and $i=0$) then $\max \big ( 2(\gamma _1-i)-\frac{\pi }{\theta _k}+1,-1 \big )=\max \big (3-\frac{\pi }{\theta _k},-1\big )$. In this case we require that

$$\begin{aligned} 3-\frac{\pi }{\theta _k}<1 \quad \Longleftrightarrow \quad \theta _k< \frac{\pi }{2}. \end{aligned}$$

Thus, in this case we can find suitable $\delta _k$’s only for not too great angles, in particular, only for angles smaller than $\frac{\pi }{2}.$

Furthermore, if we have a non-convex angle $\theta _k>\pi$ then only $\gamma _1=0$ is allowed, and hence, $\gamma =2$ is required with $\max \big (1-\frac{\pi }{\theta _k},-1\big )=1-\frac{\pi }{\theta _k}<\delta _k\le 1$. In this case it is possible to find suitable $\delta _k$’s but they cannot be negative since $1-\frac{\pi }{\theta _k}>0$.

From the above discussion we see that the shape of the domain limits strongly the regularity of the solutions even for smooth data.

In general, we see that the largest angle of the edges determines the maximal (possible) range for the smoothness $\gamma$, which can be considered. For every vertex $x_j$, $j=1,\ldots , d'$, we can use that the truncation near the vertex is a polyhedral cone, and hence, for the edges at this vertex we can use the formula $\theta _{j_1}+\cdots +\theta _{j_l}=(l-2)\pi$. For fixed l the maximum of the angles is the smallest in the case of a polyhedron having the same angles, i.e., $\theta =\theta _{j_i}=\frac{l-2}{l}\pi$, $i=1,\ldots , l$. We see that the greater l is, the greater is also $\theta$. Therefore, the ’best’ case (when one wishes to consider large values of $\gamma$) is the tetrahedron with angles $\theta =\frac{\pi }{3}$.

We now present our second result concerning weighted Sobolev regularity for the parabolic problem ($P_{\text {hom}}$) on domains of polyhedral type, where the right–hand side f now is arbitrarily smooth with respect to time.

Theorem 3.17

($B_{\text {hom}}$: Regularity in V-spaces of homogeneous problem) Let $D\subset \mathbb {R}^3$ be a bounded Lipschitz domain of polyhedral type with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$ and let $\eta \in \mathbb {N}$ with $\eta \ge 2m$. Moreover, let $\delta \in \mathbb {R}^d$ with $\delta _k\in [-m,m],\, k=1,\ldots ,d$, and $\varvec{\beta }\in \mathbb {R}^{d'}$ with $\beta _j\in [-m,m],\, j=1,\ldots ,d'$. Assume that the right hand side f of problem ($P_{\text {hom}}$) satisfies

• (i) $f\in \bigcap _{l=0}^{\infty }H^l([0,T], L_2(D)\cap V^{\eta -2m}_{\varvec{\beta },\delta }(D))$,

• (ii) $\partial _{t^l} f(0,x)=0$,    $l\in \mathbb {N}_0.$

Furthermore, suppose that the closed strip between the lines $\text {Re}\, \lambda =m-3/2$ and $\text {Re}\, \lambda =\eta -\beta _j-3/2$ is free of eigenvalues of the pencil ${\mathfrak {A}}_j(\lambda )$ for $j=1,\ldots ,d'$ and that

$$\begin{aligned} \eta -m-\delta _k< \delta _+^{(k)} \end{aligned}$$

for $k=1,\ldots ,d$. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ (with time-derivatives $\partial _{t^k}u\in H^1([0,T], \mathring{H}^m, H^{-m})$ for all $k\in \mathbb {N}$) of ($P_{\text {hom}}$) we have

$$\begin{aligned} \partial _{t^{l}} u\in L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\quad \text {for all}\quad l\in \mathbb {N}_0. \end{aligned}$$

In particular, for the derivatives $\partial _{t^k} u$, $k=0,\ldots , l$, we have the a priori estimate

$$\begin{aligned}&\sum _{k=0}^{l} \Vert \partial _{t^{k}} u|{L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))}\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{l+(\eta -2m)}\Vert \partial _{t^k} f|{L_2([0,T], V^{\eta -2m}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{l+1+(\eta -2m)}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert , \end{aligned}$$

(3.3.8)

where the constant is independent of u and f.

Proof

We prove the theorem by induction. In particular, we first show the theorem for $\eta =2m$ and $l=0$. Then from the induction assumption $\eta =2m,\, k=0,\ldots ,l-1$ we make an induction step to $\eta =2m,\, k=l$. Afterwards, with the induction assumption $\eta -1,\, l\in \mathbb {N}_0$ we prove the theorem for arbitrary $\eta \ge 2m$ and $l\in \mathbb {N}_0$.

Let $\eta =2m$. Since by our assumptions $f, \partial _t f\in L_2(D_T)\hookrightarrow L_2([0,T],H^{-m}(D))$ it follows from Theorem 3.4, [26, p. 143, and Lem. 3.1.6], and (2.1.4) that $\partial _t u(t) \in \mathring{H}^m(D)\subset V^0_{\varvec{\beta },\delta }(D)$ if $-m\le \beta _j,\, j=1,\ldots ,d'$ and $-m\le \delta _k,\, k=1,\ldots ,d$. In this case Theorem 3.4 gives the estimate

$$\begin{aligned} \Vert \partial _t u|L_2([0,T],V^0_{\varvec{\beta },\delta }(D))\Vert&\lesssim \Vert \partial _t u|L_2([0,T],\mathring{H}^m(D))\Vert \nonumber \\&\lesssim \sum _{k=0}^1\Vert \partial _{t^k}f|L_2([0,T],H^{-m}(D))\Vert \lesssim \sum _{k=0}^1\Vert \partial _{t^k}f|L_2(D_T)\Vert . \end{aligned}$$

(3.3.9)

Moreover, since

$$\begin{aligned} Lu=f-\partial _{t}u=:F, \end{aligned}$$

(3.3.10)

where for fixed t the right hand side F(t) belongs to $V^0_{\varvec{\beta },\delta }(D)$ (and due to the fact that $\beta _j,\,\delta _k \le m$, we have $\partial _t u(t) \in \mathring{H}^m(D)\hookrightarrow V^0_{\varvec{\beta },\delta }(D)\hookrightarrow V^{-m}_{0,0}(D)$, thus, also $F(t)\in V^{-m}_{0,0}(D)$) an application of Lemma 3.1 (with ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0,\, j=1,\ldots ,d'$, ${\tilde{\delta }}_k=0,\, k=1,\ldots ,d$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$) gives $u(t)\in V^{2m}_{\varvec{\beta },\delta }(D)$ with the a priori estimate

$$\begin{aligned} \Vert u(t)|V^{2m}_{\varvec{\beta },\delta }(D)\Vert&\lesssim \Vert f(t)|V^0_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _t u(t)|V^0_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Now integration w.r.t. the parameter t and (3.3.9) prove the claim for $\eta =2m$ and $l=0$, i.e.,

$$\begin{aligned} \Vert u|L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert \lesssim \Vert f|L_2([0,T],V^0_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^1\Vert \partial _{t^k}f|L_2(D_T)\Vert . \end{aligned}$$

We now assume that the claim is true for $\eta =2m$ and $k=0,\ldots , l-1$. Then differentiating ($P_{\text {hom}}$) l-times gives

$$\begin{aligned} L (\partial _{t^l}u)=\partial _{t^l}f-\partial _{t^{l+1}}u-\sum _{k=0}^{l-1}{l\atopwithdelims ()k}\partial _{t^{l-k}}L (\partial _{t^k}u)=:F_2. \end{aligned}$$

(3.3.11)

By our initial assumptions $\partial _{t^l}f(t)\in V^0_{\varvec{\beta },\delta }(D)$ and $\partial _{t^{l+1}}u(t)\in \mathring{H}^m(D)\hookrightarrow V^0_{\varvec{\beta },\delta }(D)$. Moreover, the inductive assumptions provide us with $\partial _{t^k}u(t)\in V^{2m}_{\varvec{\beta },\delta }(D)$, thus, $\partial _{t^{l-k}}L(\partial _{t^k}u)(t)\in V^{0}_{\varvec{\beta },\delta }(D)$ and we see that $F_2(t)\in V^{0}_{\varvec{\beta },\delta }(D)$. Applying Lemma 3.1 (again with ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0,\, j=1,\ldots ,d'$, ${\tilde{\delta }}_k=0,\, k=1,\ldots ,d$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$) gives $\partial _{t^l}u(t)\in V^{2m}_{\varvec{\beta },\delta }(D)$ and we have the following a priori estimate

$$\begin{aligned}&\Vert \partial _{t^l}u(t)| V^{2m}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}f(t)| V^{0}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}u(t)|V^{0}_{\varvec{\beta },\delta }(D)\Vert + \sum _{k=0}^{l-1} \Vert \partial _{t^{l-k}}L (\partial _{t^k}u)(t)|V^{0}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}f(t)| V^{0}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}u(t)|\mathring{H}^m(D)\Vert + \sum _{k=0}^{l-1} \Vert (\partial _{t^k}u)(t)|V^{2m}_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. t, our inductive assumptions, and Theorem 3.4 give

$$\begin{aligned} \Vert \partial _{t^l}u| L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert \lesssim \sum _{k=0}^{l}\Vert \partial _{t^k}f| L_2([0,T],V^{0}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{l+1}\Vert \partial _{t^k}f| L_2(D_T)\Vert . \end{aligned}$$

Assume now inductively that our assumption holds for $\eta -1$ and all derivatives $l\in \mathbb {N}_0$. We are going to show first that the claim then holds for $\eta$ and $l=0$ as well. Looking at (3.3.10) we see that $f(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$ and by our inductive assumption and Lemma 2.5 we obtain $\partial _t u(t)\in V^{\eta -1}_{\varvec{\beta },\delta }(D) \hookrightarrow V_{\varvec{\beta },\delta }^{\eta -2m}(D)$ for $m\ge 1$. Therefore, $F(t)\in V_{\varvec{\beta },\delta }^{\eta -2m}(D)$ and an application of Lemma 3.1 (with ${\tilde{\gamma }}=m,\, {\tilde{\beta }}_j=0,\, j=1,\ldots ,d',\, {\tilde{\delta }}_k=0,\, k=1,\ldots ,d,\, \gamma '=\eta ,\, \varvec{\beta }'=\varvec{\beta },\, \delta '=\delta$) gives $u(t) \in V_{\varvec{\beta },\delta }^{\eta }(D)$ with a priori estimate

$$\begin{aligned} \Vert u(t)| V^{\eta }_{\varvec{\beta },\delta }(D)\Vert&\lesssim \Vert f(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t}u(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert \\&\lesssim \Vert f(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \Vert \partial _{t}u(t)|V^{\eta -1}_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. the parameter t and our inductive assumptions show that the claim is true for $\eta$ and $l=0$, i.e.,

$$\begin{aligned}&\Vert u| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{k=0}^{1+(\eta -1-2m)}\Vert \partial _{t^k}f| L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{2+(\eta -1-2m)}\Vert \partial _{t^k}f| L_2(D_T)\Vert \\&\quad = \sum _{k=0}^{\eta -2m}\Vert \partial _{t^k}f| L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{1+(\eta -2m)}\Vert \partial _{t^k}f| L_2(D_T)\Vert . \end{aligned}$$

Suppose now that it is true for $\eta$ and derivatives $k=0,\ldots , l-1$. Differentiating ($P_{\text {hom}}$) l-times again gives (3.3.11). From our initial assumptions on f we see that $\partial _{t^l}f(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$ and from the inductive assumptions it follows that $\partial _{t^{l+1}}u(t)\in V^{\eta -1}_{\varvec{\beta },\delta }(D)\hookrightarrow V^{\eta -2m}_{\varvec{\beta },\delta }(D)$. Moreover, by the inductive assumptions $\partial _{t^k}u(t)\in V^{\eta }_{\varvec{\beta },\delta }(D)$ for $k=0,\ldots , l-1$, and therefore,

$$\begin{aligned} \partial _{t^{l-k}}L (\partial _{t^k}u)(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D). \end{aligned}$$

This shows that the right hand side in (3.3.11) satisfies $F_2(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$. Applying Lemma 3.1 again (with ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0$, ${\tilde{\delta }}_k=0$, $\gamma '=\eta$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$) gives $u(t)\in V^{\eta }_{\varvec{\beta },\delta }(D)$ with a priori estimate

$$\begin{aligned}&\Vert \partial _{t^l}u(t)| V^{\eta }_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}f(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}u(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \sum _{k=0}^{l-1} \Vert \partial _{t^{l-k}}L (\partial _{t^k}u)(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}f(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \Vert \partial _{t^{l+1}}u(t)|V^{\eta -1}_{\varvec{\beta },\delta }(D)\Vert + \sum _{k=0}^{l-1} \Vert (\partial _{t^k}u)(t)|V^{\eta }_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. the parameter t together with our inductive assumptions gives

$$\begin{aligned}&\Vert \partial _{t^l}u| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \Vert \partial _{t^l}f|L_2([0,T], V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert \\&\qquad +\sum _{k=0}^{l+1+(\eta -1-2m)}\Vert \partial _{t^k}f| L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{l+2+(\eta -1-2m)}\Vert \partial _{t^k}f| L_2(D_T)\Vert \\&\qquad + \sum _{k=0}^{l-1+(\eta -2m)}\Vert \partial _{t^k}f| L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{l-1+1+(\eta -2m)}\Vert \partial _{t^k}f| L_2(D_T)\Vert \\&\quad \lesssim \sum _{k=0}^{l+(\eta -2m)}\Vert \partial _{t^k}f| L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{l+1+(\eta -2m)}\Vert \partial _{t^k}f| L_2(D_T)\Vert , \end{aligned}$$

which finishes the proof. $\square$

Remark 3.18

In Theorem 3.17 compared to Theorem 3.14 we require for $\delta _k,\, k=1,\ldots ,d$ only the parameter restrictions

$$\begin{aligned} (1)\ \eta -m-\delta _k<\delta _+^{(k)} \quad \text {and}\quad (2)\ -m\le \delta _k\le m, \end{aligned}$$

where $\eta \ge 2m$. Focusing again on the heat equation with $m=1$ and $\delta _+^{(k)}=\frac{\pi }{\theta _k}$ this is satisfied if we assume

$$\begin{aligned} \max \bigg ( \eta -1-\frac{\pi }{\theta _k},-1 \bigg ) <\delta _k\le 1. \end{aligned}$$

Hence, we require

$$\begin{aligned} \eta -1-\frac{\pi }{\theta _k}<1 \quad \Longleftrightarrow \quad \eta < 2+\frac{\pi }{\theta _k}. \end{aligned}$$

Let now an angle $\theta _k$ of D be non-convex, i.e., $\theta _k>\pi$, then only $\eta =2$ is possible at best. Moreover, the restriction $1-\frac{\pi }{\theta _k}< \delta _k\le 1$ leads to the same situation that we already discussed in Remark 3.16.

On the other hand, for smaller angles we obtain a better result compared to Theorem 3.14: If $\theta _k=\frac{\pi }{4}$ (or slightly below) then $\eta <6$ is allowed (compared to $\gamma _1<2$ in Theorem 3.14 and hence, maximal regularity of u being $2(\gamma _1+1)=4$) and suitable $\delta _k$’s can be chosen.

Again we refer to the discussion in Remark 3.16 in this context. As was also mentioned there we deduce from the above considerations that the ’best’ possible range for $\eta$ is obtained for a tetrahedron with angles $\theta =\frac{\pi }{3}$: In this case $\eta <2+3=5$, and thus, $2\le \eta \le 4$ with $-1<\delta _k\le 1$ for $\eta =2,3$ and $0<\delta _k\le 1$ for $\eta =4$.

3.3.2 Weighted Sobolev regularity for the inhomogeneous problem

We now generalize Theorem 3.14 to inhomogeneous boundary conditions. The proof is based on the homogeneous case subject to suitable modifications.

Theorem 3.19

($A_{\text {inhom}}$: Regularity in V-spaces of inhomogeneous problem) Let $D\subset \mathbb {R}^3$ be a bounded Lipschitz domain of polyhedral type with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$. Let $\gamma \in \mathbb {N}$ with $\gamma \ge 2m$ and put $\gamma _m:=\left[ \frac{\gamma -1}{2m}\right]$. Furthermore, let $\delta \in \mathbb {R}^d$, $\varvec{\beta }\in \mathbb {R}^{d'}$ with ${\delta _k\in [-m,m]}$ for $k=1,\ldots ,d$ and $\beta _j\in [-m,m]$ for $j=1,\ldots ,d'$. Assume that $f,\,g,\, u_0$ of problem ($P_{\text {inhom}}$) satisfy

• (i) $\partial _{t^k} f\in L_2([0,T],H^{(\gamma _m+1-k)2m}(D)\cap V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D) )$, $k=0,\ldots , \gamma _m$,    and

  $\partial _{t^{\gamma _m+1}} f\in L_2(D_T)$,

• (ii) $\partial _{t^k}g\in L_2([0,T],H^{(\gamma _m+2-k)2m+m}(D)\cap V_{\varvec{\beta },\delta }^{2m(\gamma _m+1-k)}(D) )$, $k=0,\ldots ,\gamma _m+1$,    and    $\partial _{t^{\gamma _m+2}}g\in L_2([0,T],H^m(D))$,

• (iii) $u_0\in H^{(2(\gamma _m+1)+1)m}(D),$

and the $(\gamma _m+1)$-st order compatibility conditions from Definition 3.10 hold. Moreover, suppose that the closed strip between the lines $\text {Re}\, \lambda =m-3/2$ and $\text {Re}\, \lambda = 2\,m(\gamma _m-i)-\beta _j+2m-3/2$ is free of eigenvalues of the pencil ${\mathfrak {A}}_j(\lambda )$ for $j=1,\ldots ,d',\, i=0,\ldots ,\gamma _m$ and that

$$\begin{aligned} -\delta _-^{(k)}< 2m(\gamma _m-i)-\delta _k+m <\delta _+^{(k)} \end{aligned}$$

for $k=1,\ldots ,d$ and $i=0,\ldots ,\gamma _m$. Then for the weak solution $u\in H^1([0,T], {H}^m, {L_2})$ (with derivatives $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\gamma _m+1$) of problem ($P_{\text {inhom}}$) we have

$$\begin{aligned} \partial _{t^{l+1}} u\in L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-l)}(D)) \end{aligned}$$

for $l=-1,0,\ldots , \gamma _m$. In particular, for the derivatives $\partial _{t^{l+1}} u$ up to order $\gamma _m+1$ we have the a priori estimate

$$\begin{aligned}&\sum _{l=-1}^{\gamma _m} \Vert \partial _{t^{l+1}} u|{L_2([0,T], V_{\varvec{\beta },\delta }^{2m(\gamma _m-l)}(D))}\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)} (D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2([0,T],H^{(\gamma _m+1-k)2m}(D))}\Vert \nonumber \\&\qquad + \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1-k)} (D))}\Vert \nonumber \\&\qquad +\sum _{k=0}^{\gamma _m+2}\Vert \partial _{t^k} g|{L_2([0,T],H^{(\gamma _m+2-k)2m+m}(D))}\Vert \nonumber \\&\qquad + \Vert u_0|H^{(2(\gamma _m+1)+1)m}(D) \Vert , \end{aligned}$$

(3.3.12)

where the constant is independent of $f,\,g,\,u_0$, and u.

Remark 3.20

The existence of the solution $u\in H^1([0,T], {H}^m, {L_2})$ with $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\gamma _m+1$ in Theorem 3.19 follows from Theorems 3.5 and 3.12 with $l=\gamma _m+1$.

Proof

We prove the theorem by induction. In particular, we first show the claim for the induction basis $\gamma =2m$. Then we proceed with the induction step from $\gamma -1$ to $\gamma$ with $l=\gamma _m$, and finally, we make a backwards induction from $l=\gamma _m,\gamma _m-1,\ldots ,i$ to $l=i-1$ with arbitrary $\gamma$.

We define the function $w:=u-g$ and consider again the following equivalent problem to problem ($P_{\text {inhom}}$):

$$\begin{aligned} \left\{ \begin{array}{rll} \partial _t w+ Lw &{}= f-\partial _t g- Lg=:F \quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,...,m,\, j=1,...,n,\\ w|_{t=0} &{}= u_0- g(0,\cdot ) \quad &{}\text {on} \quad D. \end{array} \right\} \end{aligned}$$

(3.3.13)

Let $\gamma =2m$, then we have $\gamma _m=0$. Since by our assumptions $f,\, \partial _t g\in L_2([0,T],H^{2m}(D))$ and $g\in L_2([0,T],H^{4m}(D))$, we have $F\in L_2([0,T],H^{2m}(D))$. Moreover, from $\partial _t f,\,\partial _{t^2}g\in L_2([0,T],L_2(D))$ and from the assumptions on g above we obtain that $\partial _t F\in L_2(D_T)$. Finally, applying Lemma 2.17 to g, since $g\in L_2([0,T],H^{4m}(D))$, $\partial _t g\in L_2([0,T],H^{2m}(D))$ we deduce

$$\begin{aligned} g\in C([0,T],H^{3m}(D)), \end{aligned}$$

(3.3.14)

with the estimate

$$\begin{aligned} \Vert g|C([0,T],H^{3m}(D))\Vert \lesssim \Vert g| L_2([0,T],H^{4m}(D))\Vert + \Vert \partial _t g|L_2([0,T],H^{2m}(D)) \Vert . \end{aligned}$$

(3.3.15)

Hence, we obtain $u_0-g(0,\cdot )\in H^{3m}(D)$. Thus, it follows from Theorem 3.12 that $w(t),\, \partial _t w(t)\in {\mathring{H}^m(D)}$. Furthermore, according to [26, p. 143, and Lem. 3.1.6] and Lemma 2.5 one obtains that $\mathring{H}^m(D)\subset V_{0,0}^m(D)\subset V_{\varvec{\beta },\delta }^0(D)$ if $-m\le \beta _j$ for all $j=1,\ldots ,d'$ and $-m\le \delta _k$ for all $k=1,\ldots ,d$. In this case Theorem 3.12 gives the estimate

$$\begin{aligned}&\Vert \partial _t w |L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \lesssim \Vert \partial _t w|L_2([0,T],\mathring{H}^m(D))\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert +\Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert . \end{aligned}$$

(3.3.16)

Moreover, we have

$$\begin{aligned} Lw=F-\partial _{t}w, \end{aligned}$$

where for fixed t the right hand side belongs to $V_{\varvec{\beta },\delta }^0(D)$ (cf. (3.3.16) and the initial assumptions on $f,\,g,\,u_0$) and according to (2.1.4) also to $V_{0,0}^{-m}(D)$ if $\beta _j\le m,\, j=1,\ldots ,d'$ and $\delta _k\le m,\, k=1,\ldots ,d$. Thus, an application of Lemma 3.1 (with ${\tilde{\gamma }}=m$, ${\tilde{\delta }}_k=0$, $k=1,\ldots ,d$, $\tilde{\beta _j}=0$, $j=1,\ldots ,d'$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$) gives $w(t)\in V_{\varvec{\beta },\delta }^{2m}(D)$ with the a priori estimate

$$\begin{aligned} \Vert w(t)|V_{\varvec{\beta },\delta }^{2m}(D)\Vert \lesssim \Vert F(t)|V_{\varvec{\beta },\delta }^0(D)\Vert +\Vert \partial _t w(t)|V_{\varvec{\beta },\delta }^0(D)\Vert . \end{aligned}$$

Now integration w.r.t. the parameter t together with (3.3.16) yields

$$\begin{aligned}&\Vert w|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert \lesssim \Vert F|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \nonumber \\&\quad +\sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert + \Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert . \end{aligned}$$

(3.3.17)

From (3.3.16) together with (3.3.17) we obtain

$$\begin{aligned}&\displaystyle \sum _{l=-1}^{0} \Vert \partial _{t^{l+1}} w|{L_2([0,T], V_{\varvec{\beta },\delta }^{-2ml}(D))}\Vert \lesssim \sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert \nonumber \\&\quad +\Vert F|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert +\Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert . \end{aligned}$$

(3.3.18)

Using that $u=w+g$ from (3.3.18), the initial assumptions and the fact that the differential operator L diminishes the space regularity by 2m we calculate

$$\begin{aligned}&\displaystyle \sum _{l=-1}^{0} \Vert \partial _{t^{l+1}} u|{L_2([0,T], V_{\varvec{\beta },\delta }^{-2ml}(D))}\Vert \\&\quad \lesssim \sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert +\Vert F|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \\&\qquad \quad + \sum _{k=0}^1\Vert \partial _{t^{k}}g|L_2([0,T],V_{\varvec{\beta },\delta }^{2m(1-k)}(D))\Vert +\Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert \\&\quad \lesssim \Vert f|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert +\sum _{k=0}^1\Vert \partial _{t^{k}}g|L_2([0,T],V_{\varvec{\beta },\delta }^{2m(1-k)}(D))\Vert \\&\qquad \quad + \sum _{k=0}^1\Vert \partial _{t^k}f|L_2([0,T],H^{(1-k)2m}(D))\Vert +\sum _{k=0}^2\Vert \partial _{t^k}g|L_2([0,T],H^{(2-k)2m}(D))\Vert \\&\qquad \quad + \Vert u_0|H^{3m}(D)\Vert , \end{aligned}$$

where we used (3.3.15) in the last step. This shows the claim for the induction basis $\gamma =2m$.

Assume inductively that our assumption holds for $\gamma -1$. This means, in particular, that we have the following a priori estimate

$$\begin{aligned}{} & {} \sum _{l=-1}^{(\gamma -1)_m} \Vert \partial _{t^{l+1}} u|{L_2([0,T], V_{\varvec{\beta },\delta }^{2m((\gamma -1)_m-l)}(D))}\Vert \nonumber \\{} & {} \quad \lesssim \sum _{k=0}^{(\gamma -1)_m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m((\gamma -1)_m-k)} (D))}\Vert \nonumber \\{} & {} \qquad +\sum _{k=0}^{(\gamma -1)_m+1}\Vert \partial _{t^k} f|{L_2([0,T],H^{((\gamma -1)_m+1-k)2m}(D))}\Vert \nonumber \\{} & {} \qquad + \sum _{k=0}^{(\gamma -1)_m+1}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m((\gamma -1)_m+1-k)} (D))}\Vert \nonumber \\{} & {} \qquad +\sum _{k=0}^{(\gamma -1)_m+2}\Vert \partial _{t^k} g|{L_2([0,T],H^{((\gamma -1)_m+2-k)2m+m}(D))}\Vert + \Vert u_0|H^{(2((\gamma -1)_m+1)+1)m}(D) \Vert .\nonumber \\ \end{aligned}$$

(3.3.19)

We are going to show that the claim then holds for $\gamma$ as well. Let $l=\gamma _m$. Then by our assumptions on $f,\,g$ using that $\partial _{t^k} (Lg)= \sum _{r=0}^k {k \atopwithdelims ()r} (\partial _{t^{k-r}}L)(\partial _{t^r}g)$ (where $\partial _{t^{k-r}}L= \sum _{|\alpha |,|\beta |=0}^m (-1)^{|\alpha |}\partial _x^{\alpha }(\partial _{t^{k-r}} a_{\alpha \beta } \partial _x^{\beta })$) and the fact that the differential operators $\partial _{t^i}L$ diminish the space regularity by 2m for $i=0,\ldots ,k$ (since the coefficients $a_{\alpha \beta }$ are smooth functions), we have $\partial _{t^{k}} F\in L_2([0,T],H^{(\gamma _m+1-k)2m}(D))$ for $k=0,\ldots , \gamma _m+1$.

Moreover, since $g\in L_2([0,T],H^{(\gamma _m+2)2m}(D))$ and $\partial _{t}g \in L_2([0,T],H^{(\gamma _m+1)2m}(D))$ we deduce from Lemma 2.17 that $g\in C([0,T],H^{(2(\gamma _m+1)+1) m}(D))$ with the a priori estimate

$$\begin{aligned}&\Vert g| C([0,T],H^{(2(\gamma _m+1)+1) m}(D))\Vert \nonumber \\&\quad \lesssim \Vert g|L_2([0,T],H^{(\gamma _m+2)2m}(D)) \Vert + \Vert \partial _{t}g|L_2([0,T],H^{(\gamma _m+1)2m}(D)) \Vert . \end{aligned}$$

(3.3.20)

This implies that $u_0-g(0,\cdot )\in H^{(2(\gamma _m+1)+1) m}(D)$. Then by Theorem 3.12 together with (2.1.4) and $\mathring{H}^m(D)=\mathring{V}_{0,0}^m(D)$, cf. [26, p. 143], we have

$$\begin{aligned} \partial _{t^{\gamma _m+1}}w(t)\in {\mathring{H}^m(D)}\subset V^0_{\varvec{\beta },\delta }(D)\quad \text {for} \quad {-m\le \beta _j,\, -m\le \delta _k}, \end{aligned}$$

where $j=1,\ldots ,d'$ and $k=1,\ldots ,d$. In particular, Theorem 3.12 provides us with the a priori estimate

$$\begin{aligned}&\Vert \partial _{t^{\gamma _m+1}}w |L_2([0,T], V^0_{\varvec{\beta },\delta }(D))\Vert \lesssim \Vert \partial _{t^{\gamma _m+1}}w|L_2([0,T], \mathring{H}^m(D))\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} F| L_2([0,T],H^{(\gamma _m+1-k)2m}(D))\Vert + \Vert u_0-g(0,\cdot )| H^{(2(\gamma _m+1)+1) m}(D)\Vert , \end{aligned}$$

from which we obtain

$$\begin{aligned}&\Vert \partial _{t^{\gamma _m+1}}u |L_2([0,T], V^0_{\varvec{\beta },\delta }(D))\Vert \nonumber \\&\quad \lesssim \Vert \partial _{t^{\gamma _m+1}}g |L_2([0,T], V^0_{\varvec{\beta },\delta }(D))\Vert +\underbrace{\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} F| L_2([0,T],H^{(\gamma _m+1-k)2m}(D))\Vert }_{=:I} \nonumber \\&\qquad + \underbrace{ \Vert u_0-g(0,\cdot )| H^{(2(\gamma _m+1)+1) m}(D)\Vert }_{=:II}. \end{aligned}$$

(3.3.21)

We first estimate term I and calculate

$$\begin{aligned} I&\lesssim \displaystyle \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f| L_2([0,T],H^{(\gamma _m+1-k)2m}(D))\Vert + \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^{k+1}} g| L_2([0,T],H^{(\gamma _m+1-k)2m}(D))\Vert . \end{aligned}$$

(3.3.22)

For term II we use (3.3.20) and obtain

$$\begin{aligned} II&\lesssim \Vert u_0| H^{(2(\gamma _m+1)+1) m}(D)\Vert + \Vert g|L_2([0,T],H^{(\gamma _m+2)2m}(D)) \Vert \nonumber \\&\quad + \Vert \partial _{t}g|L_2([0,T],H^{(\gamma _m+1)2m}(D)) \Vert , \end{aligned}$$

which together with (3.3.21) and (3.3.22) shows the claim for $l=\gamma _m$ and arbitrary $\gamma$. Hence, the claim holds for $l=\gamma _m$. We now proceed by backwards induction. Suppose now the result holds for $\gamma$ and $l=\gamma _m, \gamma _m-1, \ldots , i$, where $0\le i\le \gamma _m$. We show that it then also holds for $i-1$. Differentiating (3.3.13) i-times gives

$$\begin{aligned} L (\partial _{t^i}w)=\partial _{t^i}F-\partial _{t^{i+1}}w-\sum _{r=0}^{i-1}{i\atopwithdelims ()r}\partial _{t^{i-r}}L (\partial _{t^r}w). \end{aligned}$$

(3.3.23)

From our initial assumptions on f and g we see that $\partial _{t^i}F(t)\in V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)$ and from the initial assumptions on g together with the inductive assumptions it follows for $w=u-g$ that $\partial _{t^{i+1}}w(t)\in V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)$ and

$$\begin{aligned} \partial _{t^{(r-1)+1}}w \in&L_2([0,T],V^{2m((\gamma -1)_m-(r-1))}_{\varvec{\beta },\delta }(D)) \hookrightarrow L_2([0,T],V^{2m(\gamma _m-i+1)}_{\varvec{\beta },\delta }(D)), \end{aligned}$$

(3.3.24)

where we used Lemma 2.5 and the fact that $(\gamma -1)_m-(r-1)\ge \gamma _m-i+1$ for $r=0,\ldots , i-1$. Since the differential operator $\partial _{t^{i-k}} L$ diminishes the space regularity by 2m, from (3.3.24) we see that

$$\begin{aligned} \partial _{t^{i-r}}L (\partial _{t^r}w)\in L_2([0,T],V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)). \end{aligned}$$

Hence, the right hand side of (3.3.23) belongs to $L_2([0,T],V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D))$ and by (2.1.4) also to $L_2([0,T],V^{-m}_{0,0}(D))$ since $\beta _j\le m$, $\delta _k\le m$ for $j=1,\ldots ,d'$ and $k=1,\ldots ,d$. An application of Lemma 3.1 (now with $\gamma '=2m(\gamma _m-(i-1))$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$ and again taking ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0$ for $j=1,\ldots ,d'$ and ${\tilde{\delta }}_k=0$ for $k=1,\ldots ,d$, since $\partial _{t^{(i-1)+1}}w(t)\in \mathring{H}^m(D)\subset V^m_{0,0}(D)$) yields

$$\begin{aligned} \partial _{t^{(i-1)+1}}w(t)\in V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D). \end{aligned}$$

Moreover, we have the a priori estimate

$$\begin{aligned}&\Vert \partial _{t^{(i-1)+1}}w(t)| V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}F(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}w(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{r=0}^{i-1}\Vert \partial _{t^{i-r}}L(\partial _{t^r}w)(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}F(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}w(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{r=0}^{i-1}\Vert \partial _{t^r}w(t)|V^{2m(\gamma _m-i+1)}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^i}F(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{i+1}}w(t)|V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \\&\qquad + \sum _{r=0}^{i-1}\Vert \partial _{t^r}w(t)|V^{2m((\gamma -1)_m-(r-1))}_{\varvec{\beta },\delta }(D)\Vert , \end{aligned}$$

where we used (3.3.24) in the last step. From that we obtain

$$\begin{aligned}&\Vert \partial _{t^{(i-1)+1}}u(t)| V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D)\Vert \nonumber \\&\quad \lesssim \Vert \partial _{t^{(i-1)+1}}g(t)| V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D)\Vert + \Vert \partial _{t^i}f(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \nonumber \\&\qquad +\Vert \partial _{t^{i+1}}g(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^i}(Lg)(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \nonumber \\&\qquad + \Vert \partial _{t^{i+1}}u(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert + \sum _{r=0}^{i-1}\Vert \partial _{t^r}u(t)|V^{2m((\gamma -1)_m-(r-1))}_{\varvec{\beta },\delta }(D)\Vert \nonumber \\&\qquad + \sum _{r=0}^{i-1}\Vert \partial _{t^r}g(t)|V^{2m((\gamma -1)_m-(r-1))}_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

(3.3.25)

Using the fact that

$$\begin{aligned} \Vert \partial _{t^i}(Lg)(t)| V^{2m(\gamma _m-i)}_{\varvec{\beta },\delta }(D)\Vert \lesssim \displaystyle \sum _{r=0}^i \Vert \partial _{t^r}g(t)| V^{2m(\gamma _m-{r}+1)}_{\varvec{\beta },\delta }(D)\Vert , \end{aligned}$$

and integrating (3.3.25) w.r.t. the parameter t together with the inductive assumptions on $\partial _{t^{i+1}}u$ and $\partial _{t^r} u$ (cf. (3.3.19)) we obtain the a priori estimate

$$\begin{aligned}&\Vert \partial _{t^{(i-1)+1}}u| L_2([0,T],V^{2m(\gamma _m-(i-1))}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)} (D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2([0,T],H^{(\gamma _m+1-k)2m}(D))}\Vert \\&\qquad + \sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1-k)} (D))}\Vert \\&\qquad +\sum _{k=0}^{\gamma _m+2}\Vert \partial _{t^k} g|{L_2([0,T],H^{(\gamma _m+2-k)2m+m}(D))}\Vert \\&\qquad + \Vert u_0|H^{(2(\gamma _m+1)+1)m}(D) \Vert , \end{aligned}$$

where we used $(\gamma -1)_m\le \gamma _m$. This shows that the claim is true for $i-1$, which completes the proof. $\square$

We now generalize Theorem 3.17 to inhomogeneous boundary conditions. The proof is again based on the homogeneous case subject to suitable modifications.

Theorem 3.21

($B_{\text {inhom}}$: Regularity in V-spaces of inhomogeneous problem) Let $D\subset \mathbb {R}^3$ be a bounded Lipschitz domain of polyhedral type with edges $M_1,\ldots ,M_d$ and vertices $x^{(1)},\ldots ,x^{(d')}$ and let $\eta \in \mathbb {N}$ with $\eta \ge 2m$. Moreover, let $\delta \in \mathbb {R}^d$ with $\delta _k\in [-m,m],\, k=1,\ldots ,d$, and $\varvec{\beta }\in \mathbb {R}^{d'}$ with $\beta _j\in [-m,m],\, j=1,\ldots ,d'$. Furthermore, let $l\in \mathbb {N}_0$ be an arbitrary large fixed number. Assume that the right hand side of problem ($P_{\text {inhom}}$) satisfies

• (i) $\partial _{t^k}f\in L_2([0,T],H^{(\eta -2m+l+1-k)2m}(D)\cap V^{\eta -2m}_{\varvec{\beta },\delta }(D))$ for all $k=0,\ldots ,\eta -2m+l$, and $\partial _{t^{\eta -2m+l+1}}f\in L_2(D_T)$,

• (ii) $\partial _{t^k}g\in L_2([0,T],{ H^{(\eta -2m+l+2-k)2m+m}(D)}\cap V^{\eta }_{\varvec{\beta },\delta }(D))$ for all $k=0,\ldots ,\eta -2m+l+1$, and $\partial _{t^{\eta -2m+l+2}}g\in L_2([0,T],H^m(D))$,

• (iii) $u_0\in H^{(2(\eta -2m+l+1)+1)m}(D),$

and the $({\eta -2m+l+1})$-st order compatibility conditions from Definition 3.10 hold. Moreover, suppose that the closed strip between the lines $\text {Re}\, \lambda =m-3/2$ and $\text {Re}\, \lambda =\eta -\beta _j-3/2$ is free of eigenvalues of the pencil ${\mathfrak {A}}_j(\lambda )$ for $j=1,\ldots ,d'$ and that

$$\begin{aligned} \eta -m-\delta _k< \delta _+^{(k)} \end{aligned}$$

for $k=1,\ldots ,d$. Then for the weak solution $u\in H^1([0,T], {H}^m, {L_2})$ (with $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\eta -2m+l+1$) of ($P_{\text {inhom}}$) we have

$$\begin{aligned} \partial _{t^{k}} u\in L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D)),\quad k=0,\ldots ,l. \end{aligned}$$

In particular, for the derivatives of u up to order l we have the a priori estimate

$$\begin{aligned}&\sum _{k=0}^{l} \Vert \partial _{t^{k}} u|{L_2([0,T], V_{\varvec{\beta },\delta }^{\eta }(D))}\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^{l+\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{\eta -2m} (D))}\Vert + \sum _{k=0}^{l+1+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{{\eta }} (D))}\Vert \nonumber \\&\qquad +\sum _{k=0}^{l+1+\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],{H^{(\eta -2m+l+1-k)2m}(D))}}\Vert \nonumber \\&\qquad +\sum _{k=0}^{l+2+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],{H^{(\eta -2m+l+2-k)2m+m}(D))}}\Vert \nonumber \\&\qquad + \Vert u_0|{H^{(2(\eta -2m+l+1)+1)m}(D)} \Vert , \end{aligned}$$

(3.3.26)

where the constant is independent of $f,\,g,\,u_0$, and u.

Remark 3.22

The existence of the solution $u\in H^1([0,T], {H}^m, {L_2})$ with $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\eta -2m+l+1$ in Theorem 3.21 follows from Theorems 3.5 and 3.12 replacing l by $\eta -2m+l+1$.

Proof

We prove the theorem by induction. In particular, we first show the theorem for $\eta =2m$ and $l=0$. Then from the induction assumption $\eta =2m,\, k=0,\ldots ,l-1$ we make an induction step to $\eta =2m,\, k=l$. Afterwards, with the induction assumption $\eta -1,\, l\in \mathbb {N}_0$ we prove the theorem for arbitrary $\eta \ge 2m$ and $l\in \mathbb {N}_0$.

We define the function $w:=u-g$ and consider again the following equivalent problem to problem ($P_{\text {inhom}}$):

$$\begin{aligned} \left\{ \begin{array}{lll} \partial _t w+ Lw &{}= f-\partial _t g- Lg=:F \quad &{}\text {on}\quad D_T,\\ \frac{\partial ^{k-1}w}{\partial \nu ^{k-1} } \big |_{\Gamma _{j,T}} &{}=0 \quad &{}\text {for} \quad k=1,\ldots ,m,\, j=1,\ldots ,n,\\ w|_{t=0} &{}= u_0- g(0,\cdot ) \quad &{}\text {on} \quad D. \end{array} \right\} \end{aligned}$$

(3.3.27)

Let $\eta =2m$ and $l=0$. Since by our assumptions $F\in L_2([0,T],H^{2m}(D)),\, \partial _t F\in L_2(D_T),\, u_0-g(0,\cdot )\in H^{3m}(D)$, cf. (3.3.14), it follows from Theorem 3.12, [26, p. 143, and Lem. 3.1.6], and (2.1.4) that $w(t),\,\partial _t w(t) \in \mathring{H}^m(D)\subset V^0_{\varvec{\beta },\delta }(D)$ if $-m\le \beta _j,\, j=1,\ldots ,d'$ and $-m\le \delta _k,\, k=1,\ldots ,d$. In this case Theorem 3.12 gives the estimate

$$\begin{aligned}&\Vert \partial _t w |L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \lesssim \Vert \partial _t w|L_2([0,T],\mathring{H}^m(D))\Vert \nonumber \\&\quad \lesssim \sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert +\Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert . \end{aligned}$$

(3.3.28)

Moreover, we have

$$\begin{aligned} Lw=F-\partial _{t}w, \end{aligned}$$

(3.3.29)

where for fixed t the right hand side belongs to $V_{\varvec{\beta },\delta }^0(D)$ (cf. (3.3.28) and the initial assumptions on $f,\,g$) and according to (2.1.4) also to $V_{0,0}^{-m}(D)$ if $\beta _j\le m,\, j=1,\ldots ,d'$ and $\delta _k\le m,\, k=1,\ldots ,d$. Thus, an application of Lemma 3.1 (with ${\tilde{\gamma }}=m$, ${\tilde{\delta }}_k=0$, $k=1,\ldots ,d$, $\tilde{\beta _j}=0$, $j=1,\ldots ,d'$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$, since $w(t) \in \mathring{H}^m(D)\subset V^0_{\varvec{\beta },\delta }(D)$) gives $w(t)\in V_{\varvec{\beta },\delta }^{2m}(D)$ with the a priori estimate

$$\begin{aligned} \Vert w(t)|V_{\varvec{\beta },\delta }^{2m}(D)\Vert \lesssim \Vert F(t)|V_{\varvec{\beta },\delta }^0(D)\Vert +\Vert \partial _t w(t)|V_{\varvec{\beta },\delta }^0(D)\Vert . \end{aligned}$$

Now integration w.r.t. the parameter t together with (3.3.28) yields

$$\begin{aligned} \Vert w|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert&\lesssim \Vert F|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \nonumber \\&\qquad +\sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert \nonumber \\&\qquad + \Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert . \end{aligned}$$

(3.3.30)

Using that $u=w+g$ from (3.3.30), the initial assumptions and the fact that the differential operator L diminishes the space regularity by 2m we calculate

$$\begin{aligned}&\Vert u|{L_2([0,T], V_{\varvec{\beta },\delta }^{2m}(D))}\Vert \\&\quad \lesssim \sum _{k=0}^1\Vert \partial _{t^k}F|L_2([0,T],H^{(1-k)2m}(D))\Vert +\Vert F|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert \\&\qquad + \Vert g|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert +\Vert u_0-g(0,\cdot )|H^{3m}(D)\Vert \\&\quad \lesssim \Vert f|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert + \Vert \partial _t g|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert + \Vert g|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert \nonumber \\&\qquad + \sum _{k=0}^1\Vert \partial _{t^k}f|L_2([0,T],H^{(1-k)2m}(D))\Vert + \sum _{k=0}^1\Vert \partial _{t^{k+1}}g|L_2([0,T],H^{(1-k)2m}(D))\Vert \nonumber \\ {}&\qquad +\sum _{k=0}^1\Vert \partial _{t^k}(Lg)|L_2([0,T],H^{(1-k)2m}(D))\Vert + \Vert u_0|H^{3m}(D)\Vert +\Vert g(0,\cdot )|H^{3m}(D)\Vert \nonumber \\&\quad \lesssim \Vert f|L_2([0,T],V_{\varvec{\beta },\delta }^0(D))\Vert +\sum _{k=0}^1\Vert \partial _{t^k}f|L_2([0,T],H^{(1-k)2m}(D))\Vert \nonumber \\&\qquad +\sum _{k=0}^1\Vert \partial _{t^{k}}g|L_2([0,T],V_{\varvec{\beta },\delta }^{2m}(D))\Vert \\&\qquad +\sum _{k=0}^2\Vert \partial _{t^k}g|L_2([0,T],H^{(2-k)2m+m}(D))\Vert + \Vert u_0|H^{3m}(D)\Vert , \end{aligned}$$

where we used again (3.3.15) in the last step. This shows the claim for the induction basis $\eta =2m$ and $l=0$.

We now assume that the claim is true for $\eta =2m$ and $k=0,\ldots , l-1$. Then differentiating (3.3.27) l-times gives

$$\begin{aligned} L (\partial _{t^l}w)= \partial _{t^l}F-\partial _{t^{l+1}}w-\sum _{r=0}^{l-1}{l\atopwithdelims ()r}\partial _{t^{l-r}}L (\partial _{t^r}w) =:F_2. \end{aligned}$$

(3.3.31)

By our initial assumptions $\partial _{t^l}F(t)\in V^0_{\varvec{\beta },\delta }(D)$ and $\partial _{t^{l+1}}w(t)\in \mathring{H}^m(D)\hookrightarrow V^0_{\varvec{\beta },\delta }(D)$. Moreover, the inductive assumptions provide us with $\partial _{t^r}w(t)\in V^{2m}_{\varvec{\beta },\delta }(D),\, r=0,\ldots ,l-1$, thus, $\partial _{t^{l-r}}L(\partial _{t^r}u)(t)\in V^{0}_{\varvec{\beta },\delta }(D)$ and we see that $F_2(t)\in V^{0}_{\varvec{\beta },\delta }(D)$. Applying Lemma 3.1 (again with ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0,\, j=1,\ldots ,d'$, ${\tilde{\delta }}_k=0,\, k=1,\ldots ,d$, $\gamma '=2m$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$, since $\partial _{t^l}w(t)\in \mathring{H}^m(D)\subset V_{0,0}^m(D)$) gives $\partial _{t^l}w(t)\in V^{2m}_{\varvec{\beta },\delta }(D)$ and we have the following a priori estimate

$$\begin{aligned}&\Vert \partial _{t^l}w(t)| V^{2m}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}F(t)| V^{0}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}w(t)|V^{0}_{\varvec{\beta },\delta }(D)\Vert + \sum _{r=0}^{l-1} \Vert \partial _{t^{l-r}}L (\partial _{t^r}w)(t)|V^{0}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}F(t)| V^{0}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}w(t)|\mathring{H}^m(D)\Vert + \sum _{r=0}^{l-1} \Vert \partial _{t^r}w(t)|V^{2m}_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. t, our inductive assumptions, the embedding $\mathring{H}^m(D)\subset V^0_{\varvec{\beta },\delta }(D)$ and Theorem 3.12 give (using again that $u=w+g$)

$$\begin{aligned}&\Vert \partial _{t^l}u| L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \Vert \partial _{t^l}g| L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert +\Vert \partial _{t^l}F| L_2([0,T],V^{0}_{\varvec{\beta },\delta }(D))\Vert + {\Vert \partial _{t^{l+1}}u|L_2([0,T],{{H}^m}(D))\Vert } \\&\qquad + \Vert \partial _{t^{l+1}}g|L_2([0,T],{{H}^m}(D))\Vert +\sum _{r=0}^{l-1} \Vert \partial _{t^r}u|L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert \\&\qquad +\sum _{r=0}^{l-1} \Vert \partial _{t^r}g|L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{r=0}^{l+1} \Vert \partial _{t^r}g|L_2([0,T],V^{2m}_{\varvec{\beta },\delta }(D))\Vert +\sum _{k=0}^{l}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{0} (D))}\Vert \\&\qquad +\sum _{k=0}^{l+2}\Vert \partial _{t^k} g|{L_2([0,T],H^{(l+2-k)2m+m}(D))}\Vert +\sum _{k=0}^{l+1} \Vert \partial _{t^k}f| L_2([0,T],H^{(l+1-k)2m}(D))\Vert \\&\qquad +\Vert u_0|H^{(2(l+1)+1)m}(D) \Vert . \end{aligned}$$

This shows the claim for $\eta =2m$ and arbitrary l.

Assume now inductively that our assumption holds for $\eta -1$ and all derivatives $l\in \mathbb {N}_0$. We are going to show first that the claim then holds for $\eta$ and $l=0$ as well. Looking at (3.3.29) we see that $F(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$ and by our inductive assumption and Lemma 2.5 we obtain $\partial _t w(t)\in V^{\eta -1}_{\varvec{\beta },\delta }(D) \hookrightarrow V_{\varvec{\beta },\delta }^{\eta -2m}(D)$ for $m\ge 1$. Therefore, $F(t)-\partial _t w(t)\in V_{\varvec{\beta },\delta }^{\eta -2m}(D)$. Hence, an application of Lemma 3.1 (with ${\tilde{\gamma }}=m,\, {\tilde{\beta }}_j=0,\, j=1,\ldots ,d',\, {\tilde{\delta }}_k=0,\, k=1,\ldots ,d,\, \gamma '=\eta ,\, \varvec{\beta }'=\varvec{\beta },\, \delta '=\delta$, since $w(t)\in \mathring{H}^m(D)\subset V_{0,0}^m(D)$) gives $w(t) \in V_{\varvec{\beta },\delta }^{\eta }(D)$ with a priori estimate

$$\begin{aligned} \Vert w(t)| V^{\eta }_{\varvec{\beta },\delta }(D)\Vert&\lesssim \Vert F(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t}w(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert \\&\lesssim \Vert F(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t}u(t)|V^{\eta -1}_{\varvec{\beta },\delta }(D)\Vert + \Vert \partial _{t}g(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. the parameter t and our inductive assumptions show that the claim is true for $\eta$ and $l=0$, i.e.,

$$\begin{aligned}&\Vert u| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \Vert g| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert + \Vert F|L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert \\&\qquad + \Vert \partial _{t}u|L_2([0,T],V^{\eta -1}_{\varvec{\beta },\delta }(D))\Vert +\Vert \partial _{t}g|L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{k=0}^{1+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{{\eta }} (D))}\Vert +\sum _{k=0}^{\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{\eta -2m} (D))}\Vert \\&\qquad +\sum _{k=0}^{1+\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],H^{(\eta -2m+1-k)2m}(D))}\Vert \\&\qquad +\sum _{k=0}^{2+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],H^{(\eta -2m+2-k)2m+m}(D))}\Vert + \Vert u_0|H^{(2(\eta -2m+1)+1)m}(D) \Vert , \end{aligned}$$

where we used $V^{\eta -2m}_{\beta ,\delta }(D)\hookrightarrow V^{\eta -1-2m}_{\beta ,\delta }(D)$.

Suppose now that it is true for $\eta$ and derivatives $r=0,\ldots , l-1$. Differentiating ($P_{\text {inhom}}$) l-times again gives (3.3.31). From our initial assumptions on $f,\,g$ we see that $\partial _{t^l}F(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$ and from the inductive assumptions it follows that $\partial _{t^{l+1}}w(t)\in V^{\eta -1}_{\varvec{\beta },\delta }(D)\hookrightarrow V^{\eta -2m}_{\varvec{\beta },\delta }(D)$. Moreover, by the inductive assumptions $\partial _{t^r}w(t)\in V^{\eta }_{\varvec{\beta },\delta }(D)$ for $r=0,\ldots , l-1$, and therefore,

$$\begin{aligned} \partial _{t^{l-r}}L (\partial _{t^r}w)(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D). \end{aligned}$$

This shows that the right hand side in (3.3.31) satisfies $F_2(t)\in V^{\eta -2m}_{\varvec{\beta },\delta }(D)$. Applying Lemma 3.1 again (with ${\tilde{\gamma }}=m$, ${\tilde{\beta }}_j=0$, $j=1,\ldots ,d'$, ${\tilde{\delta }}_k=0$ $k=1,\ldots ,d$, $\gamma '=\eta$, $\varvec{\beta }'=\varvec{\beta }$, $\delta '=\delta$, since $\partial _{t^l}w(t)\in \mathring{H}^m(D)\subset V_{0,0}^m(D)$) gives $\partial _{t^l}w(t)\in V^{\eta }_{\varvec{\beta },\delta }(D)$ with a priori estimate

$$\begin{aligned}&\Vert \partial _{t^l}w(t)| V^{\eta }_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}F(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert +\Vert \partial _{t^{l+1}}w(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \sum _{r=0}^{l-1} \Vert \partial _{t^{l-r}}L (\partial _{t^r}w)(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert \\&\quad \lesssim \Vert \partial _{t^l}F(t)| V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \Vert \partial _{t^{l+1}}w(t)|V^{\eta -2m}_{\varvec{\beta },\delta }(D)\Vert + \sum _{r=0}^{l-1} \Vert \partial _{t^r}w(t)|V^{\eta }_{\varvec{\beta },\delta }(D)\Vert . \end{aligned}$$

Integration w.r.t. the parameter t together with our inductive assumptions and with the embedding $V^{\eta -1}_{\varvec{\beta },\delta }(D)\hookrightarrow V^{\eta -2m}_{\varvec{\beta },\delta }(D)$ yields

$$\begin{aligned}&\Vert \partial _{t^l}u| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \Vert \partial _{t^l}g| L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert + \Vert \partial _{t^l}F|L_2([0,T], V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert \\&\qquad + \Vert \partial _{t^{l+1}}u|L_2([0,T],V^{\eta -1}_{\varvec{\beta },\delta }(D))\Vert +\Vert \partial _{t^{l+1}}g|L_2([0,T],V^{\eta -2m}_{\varvec{\beta },\delta }(D))\Vert \\&\qquad +\sum _{r=0}^{l-1} \Vert \partial _{t^r}u|L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert +\sum _{r=0}^{l-1} \Vert \partial _{t^r}g|L_2([0,T],V^{\eta }_{\varvec{\beta },\delta }(D))\Vert \\&\quad \lesssim \sum _{k=0}^{l+\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{\eta -2m} (D))}\Vert + \sum _{k=0}^{l+1+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],V_{\varvec{\beta },\delta }^{{\eta }} (D))}\Vert \\&\qquad +\sum _{k=0}^{l+1+\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T],H^{(\eta -2m+l+1-k)2m}(D))}\Vert \\&\qquad +\sum _{k=0}^{l+2+\eta -2m}\Vert \partial _{t^k} g|{L_2([0,T],H^{(\eta -2m+l+2-k)2m+m}(D))}\Vert \\&\qquad + \Vert u_0|H^{(2(\eta -2m+l+1)+1)m}(D) \Vert , \end{aligned}$$

where we used $V^{\eta -2m}_{\beta ,\delta }(D)\hookrightarrow V^{\eta -1-2m}_{\beta ,\delta }(D)$. This shows the claim for arbitrary $\eta \ge 2m$ and $l\in \mathbb {N}_0$, which finishes the proof. $\square$

3.4 Regularity results in Besov spaces

In this section we study regularity in Besov spaces for the parabolic problems ($P_{\text {hom}}$) and ($P_{\text {inhom}}$) with homogeneous and inhomogeneous boundary conditions, respectively, on domains of polyhedral type. We shall rely on our previous regularity results in weighted Sobolev spaces (cf. Theorems 3.14, 3.17, 3.19, and 3.21).

3.4.1 Besov regularity for the homogeneous problem

A combination of the regularity results from Theorems 3.4 and 3.14 together with the embedding from Theorem 2.10 yields the following result concerning Besov regularity of the homogeneous parabolic problem ($P_{\text {hom}}$).

Theorem 3.23

($A_{\text {hom}}$: Besov regularity of homogeneous problem) We assume that the conditions of Theorem 3.14 hold. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, {H^{-m}})$ of problem ($P_{\text {hom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\tau }(D)), \quad \text {where}\quad r<\min \Big \{{2m(\gamma _m+1)},{3\big (2m(\gamma _m+1)-|\delta ^+|\big )}, {3m} \Big \}. \end{aligned}$$

(3.4.1)

Moreover, we have the a priori estimate

$$\begin{aligned}&\Vert u| L_2([0,T],B^r_{\tau ,\tau }(D))\Vert \lesssim \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)} (D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert , \end{aligned}$$

(3.4.2)

where the constant is independent of u and f.

Proof

By the assumptions, Theorem 3.14 provides a solution $u\in L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1)}(D))$. Using Theorem 2.10 (with $l:=2m(\gamma _m+1),\, s:=m,\, p:=2$) and the fact that $B^m_{2,2}(D)=H^m(D)$ (in sense of equivalent norms) we obtain

$$\begin{aligned} u\,&\in \, L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1)}(D))\cap H^1([0,T], \mathring{H}^m, H^{-m}) \nonumber \\&\hookrightarrow \, L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1)}(D)\cap B^m_{2,2}(D))\nonumber \\&\hookrightarrow \, L_2([0,T],B^r_{\tau ,\tau }(D)), \end{aligned}$$

(3.4.3)

where the restrictions on r in (3.4.1) immediately follow from the restrictions of Theorem 2.10. Moreover, $2m(\gamma _m+1)>\beta$ holds, since $2m(\gamma _m+1)> m\ge \beta$.

Furthermore, the a priori estimate (3.4.2) follows from (3.4.3), Theorem 3.4 and Theorem 3.14 with the following consideration,

$$\begin{aligned} \Vert u| L_2([0,T],B^r_{\tau ,\tau }(D))\Vert&\lesssim \ \Vert u| L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1)}(D))\Vert +\Vert u|H^1([0,T], \mathring{H}^m, H^{-m})\Vert \\&\lesssim \ \sum _{k=0}^{\gamma _m}\Vert \partial _{t^k} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)} (D))}\Vert +\sum _{k=0}^{\gamma _m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert . \end{aligned}$$

This completes the proof. $\square$

Remark 3.24

We consider some interesting cases of Theorem 3.23 using the results of [29, Rem. 4.6], where the underlying domain is a polyhedral domain with equal angles $\theta$ and n edges by a vertex. If we consider the heat equation with $s:=m=1$ and replace l by $2m(\gamma _m+1)=2\gamma _1+2$, from [29, Rem. 4.6] we obtain that

$$\begin{aligned} 2\gamma _1+2-|\delta ^+| < (2\gamma _1+2)(1-n)+ \frac{2n^2-2n}{n-2} . \end{aligned}$$

Hence, from (3.4.1) we deduce

$$\begin{aligned} r< \min \left\{ 2\gamma _1+2 ,\, 3\left( (2\gamma _1+2)(1-n)+\frac{2n^2-2n}{n-2} \right) ,3 \right\} . \end{aligned}$$

For a tetrahedron ($\theta <\frac{\pi }{2}$) with $n=3$ and $\gamma _1=1$, cf. Remark 3.16, this yields $r<3.$ Furthermore, for a cube ($\theta =\frac{\pi }{2}$) with $n=3$ and $\gamma _1=0$, cf. (3.3.7), we get $r< 2.$

Alternatively, we combine Theorems 2.10, 3.4, and 3.17. This leads to the following regularity result in Besov spaces for the homogeneous problem ($P_{\text {hom}}$).

Theorem 3.25

($B_{\text {hom}}$: Besov regularity of homogeneous problem) We assume that the conditions of Theorem 3.17 hold. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ of ($P_{\text {hom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\tau }(D)), \qquad \text {where}\quad r<\min \Big \{{\eta },{3(\eta -|\delta ^+|)}, {3m} \Big \}. \end{aligned}$$

(3.4.4)

In particular, we have the a priori estimate

$$\begin{aligned} \Vert u| L_2([0,T],B^r_{\tau ,\tau }(D))\Vert \lesssim \sum _{k=0}^{\eta -2m}\Vert \partial _{t^k} f|{L_2([0,T], V^{\eta -2m}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{k=0}^{\eta -2m+1}\Vert \partial _{t^k} f|{L_2(D_T)}\Vert , \end{aligned}$$

(3.4.5)

where the constant is independent of u and f.

Proof

According to Theorem 3.17 by our assumptions we know $u\in L_2([0,T],V_{\varvec{\beta },\delta }^{\eta }(D))$. Using Theorem 2.10 (now with $l:=\eta ,\, s:=m,\, p:=2$) and the fact that $B^m_{2,2}(D)=H^m(D)$ (in sense of equivalent norms) we obtain

$$\begin{aligned} u\,&\in \, L_2([0,T],V_{\varvec{\beta },\delta }^{\eta }(D))\cap H^1([0,T], \mathring{H}^m, H^{-m}) \nonumber \\&\hookrightarrow \, L_2([0,T],V_{\varvec{\beta },\delta }^{\eta }(D)\cap B^m_{2,2}(D))\nonumber \\&\hookrightarrow \, L_2([0,T],B^r_{\tau ,\tau }(D)), \end{aligned}$$

(3.4.6)

where the restrictions on r in (3.4.4) immediately follow from the restrictions of Theorem 2.10. Moreover, $\eta >\beta$ holds, since $\eta \ge 2m> m\ge \beta$. Furthermore, the a priori estimate (3.4.5) follows from (3.3.8), (3.4.6) and Theorem 3.4 with similar consideration as in the proof of Theorem 3.23. $\square$

Remark 3.26

For the same case as in Remark 3.24 replacing now l by $\eta$ we obtain with analogous arguments that

$$\begin{aligned} r<\min \left\{ \eta ,\, 3\eta (1-n)+ 6\frac{n^2-n}{n-2},\, 3 \right\} . \end{aligned}$$

Now in view of Remark 3.18 we can assume $\eta =3$ for a tetrahedron or a cube ($\theta \le \frac{\pi }{2}$) with $n=3$ (the number of the edges by a vertex) and conclude $r< 3.$

3.4.2 Besov regularity for the inhomogeneous problem

We now provide two regularity results in Besov spaces for the inhomogeneous problem. First we consider the counterpart of Theorem 3.23. The proof is analogous replacing Theorem 3.4 by Theorems 3.12 and 3.14 by Theorem 3.19.

Theorem 3.27

($A_{\text {inhom}}$: Besov regularity of inhomogeneous problem) We assume that the conditions of Theorem 3.19 hold. Then for the weak solution $u\in H^1([0,T], {H}^m, {L_2})$ of problem ($P_{\text {inhom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\tau }(D)), \qquad \text {where}\quad r<\min \Big \{{2m(\gamma _m+1)},{3\big (2m(\gamma _m+1)-|\delta ^+|\big )}, {3m} \Big \}. \end{aligned}$$

Moreover, the norm $\Vert u|L_2([0,T], B_{\tau ,\tau }^r(D))\Vert$ can be estimated from above by the right-hand side of (3.3.12).

Proof

This follows from similar considerations as in Theorem 3.23 now replacing Theorem 3.14 by Theorem 3.19, which yields

$$\begin{aligned} u\,&\in \, L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m+1)}(D))\cap H^1([0,T], {H}^m, H^{-m}) \hookrightarrow \, L_2([0,T],B^r_{\tau ,\tau }(D)). \end{aligned}$$

(3.4.7)

Furthermore, the a priori estimate follows from (3.4.7), (3.2.4), and (3.3.12). $\square$

Alternatively, we can combine Theorem 2.10 with Theorem 3.21 and obtain the following theorem.

Theorem 3.28

($B_{\text {inhom}}$: Besov regularity of inhomogeneous problem) We assume that the conditions of Theorem 3.21 hold. Then for the weak solution $u\in H^1([0,T], {H}^m, {L_2})$ of ($P_{\text {inhom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\tau }(D)),\quad \text {where}\quad r<\min \Big \{{\eta },{3(\eta -|\delta ^+|)}, {3m} \Big \}. \end{aligned}$$

Moreover, the norm $\Vert u|L_2([0,T],B^r_{\tau ,\tau }(D))\Vert$ can be estimated from above by the right-hand side of (3.3.26).

Proof

This follows by similar considerations as in Theorem 3.25 now replacing Theorem 3.17 by Theorem 3.21, which yields

$$\begin{aligned} u\,&\in \, L_2([0,T],V_{\varvec{\beta },\delta }^{\eta }(D))\cap H^1([0,T], {H}^m, H^{-m}) \hookrightarrow \, L_2([0,T],B^r_{\tau ,\tau }(D)). \end{aligned}$$

(3.4.8)

Furthermore, the a priori estimate follows from (3.3.26), (3.4.8), and (3.2.4). $\square$

3.4.3 Hölder–Besov regularity for the homogeneous problem

We observe the fact that Theorems 3.14 and 3.17 not only provide regularity properties of the solution u of problem ($P_{\text {hom}}$) but also of its partial derivatives $\partial _{t^k}u$. Following [28, Subsec. 5.4.3] in this subsection we use this fact in combination with the generalized Sobolev embedding (2.3.6) in order to obtain some mixed Hölder–Besov regularity results.

Theorem 3.29

($A_{\text {hom}}$: Hölder–Besov regularity of homogeneous problem) We assume that the conditions of Theorem 3.14 together with $\gamma \ge 4m+1$ hold. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ (with time-derivatives $\partial _{t^k}u\in H^1([0,T], \mathring{H}^m, H^{-m}) \text { for } k=1,\ldots ,\gamma _{m}+1$) of problem ($P_{\text {hom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in {\mathcal {C}}^{\gamma _m-2,\frac{1}{2}}([0,T],B^{r}_{\tau ,\tau }(D)), \quad \text {where}\quad r<\min \big \{3(4m-|\delta ^+|),3m\big \}. \end{aligned}$$

Furthermore, the norm $\Vert u| {\mathcal {C}}^{\gamma _m-2,\frac{1}{2}}([0,T],B^{r}_{\tau ,\tau }(D))\Vert$ can be estimated from above by the right-hand side of (3.3.1).

Proof

Using the fact that $H^m(D)=B^m_{2,2}(D)$ in the sense of equivalent norms, Theorems 2.14, 3.4, 3.14, 2.10 together with (2.3.5) and the generalized Sobolev’s embedding (2.3.6), show that under the given assumptions we have for $0\le k\le \gamma _m-2$ (where $\gamma _m-2\ge 0$ since $\gamma \ge 4m+1$) that

$$\begin{aligned} u\quad&\in \, \,\, H^{k+1}([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D))\cap H^{\gamma _m+1}([0,T],H^m(D))\nonumber \\&\hookrightarrow \, H^{k+1}([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D)\cap H^m(D))\nonumber \\&\hookrightarrow \, {\mathcal {C}}^{k,\frac{1}{2}}([0,T],V_{\varvec{\beta },\delta }^{\eta }(D)\cap B^m_{2,2}(D))\nonumber \\&\hookrightarrow \, {\mathcal {C}}^{k,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D)), \end{aligned}$$

(3.4.9)

where in the second step we require $\eta \le 2m(\gamma _m-k)$. Moreover, in the last step by Theorem 2.10 we get the additional restrictions $\eta >\beta$ and

$$\begin{aligned} r<\min \{\eta ,3(\eta -|\delta ^+|),3m \} < \min \{2m(\gamma _m-k),3(2m(\gamma _m-k)-|\delta ^+|),3m \}. \end{aligned}$$

Therefore, choosing $k=\gamma _m-2$ the upper bound on r reads as

$$\begin{aligned} r< \min \{4m,3(4m-|\delta ^+|),3m \}=\min \{3(4m-|\delta ^+|),3m \}, \end{aligned}$$

and for $\eta =2m(\gamma _m-k)=4m$ it holds $\eta >m\ge \beta$. Applying Theorems 3.4, 3.14, and the embedding (3.4.9) yields the a priori estimate

$$\begin{aligned} \Vert u| {\mathcal {C}}^{k,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D))\Vert&\lesssim \Vert u|H^{k+1}([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D)) \Vert \\&\quad + \Vert u|H^{\gamma _m+1}([0,T],H^m(D)) \Vert \\&\lesssim \displaystyle \sum _{i=0}^{\gamma _m}\Vert \partial _{t^i} f|{L_2([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-i)} (D))}\Vert \\&\quad +\sum _{i=0}^{\gamma _m+1}\Vert \partial _{t^i} f|{L_2(D_T)}\Vert , \end{aligned}$$

which for $k=\gamma _m-2$ shows the a priori estimate and completes the proof. $\square$

Remark 3.30

• (i) For $\gamma \ge 2m+1$ and $k=\gamma _m-1$ we obtain $r<\min \{ 2m,3(2m-|\delta ^+|)\}$ in the theorem above. For $\gamma \ge 2m$ and $k=\gamma _m$ we get $\eta =r=0$ and $\tau =2$ which for $\beta ,\,\delta _i\in [-m,0]$, $i=1,\ldots ,d,$ gives $u\in {\mathcal {C}}^{\gamma _m,\frac{1}{2}}([0,T],L_2(D))$.

• (ii) In analogy to [28, Rem. 5.4.9] (for the case of Kondratiev spaces) from the proof above one can see that the solution satisfies

  $$\begin{aligned} u\in {\mathcal {C}}^{k,\frac{1}{2}}([0,T],V_{\varvec{\beta },\delta }^{2m(\gamma _m-k)}(D)), \end{aligned}$$

  which implies that for high regularity in time, which is displayed by the parameter k, we have less spacial regularity in terms of $2m(\gamma _m-k)$.

We now consider Theorem 3.17 instead of Theorem 3.14 and obtain the following Hölder–Besov regularity result.

Theorem 3.31

($B_{\text {hom}}$: Hölder-Besov regularity of homogeneous problem) We assume that the conditions of Theorem 3.17 hold. Then for the weak solution $u\in H^1([0,T], \mathring{H}^m, H^{-m})$ (with time-derivatives $\partial _{t^k}u\in H^1([0,T], \mathring{H}^m, H^{-m})$ for all $k\in \mathbb {N}$) of ($P_{\text {hom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ and all $k\in \mathbb {N}_0$ that

$$\begin{aligned} u\in {\mathcal {C}}^{k,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D)),\quad \text {where }\quad r<\min \Big \{{\eta },{3(\eta -|\delta ^+|)}, {3m} \Big \}. \end{aligned}$$

In particular, for fixed k we have the a priori estimate

$$\begin{aligned}&\displaystyle \Vert u| {\mathcal {C}}^{k,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D))\Vert \nonumber \\&\quad \lesssim \sum _{i=0}^{k+1+\eta -2m}\Vert \partial _{t^i} f|{L_2([0,T], V^{\eta -2m}_{\varvec{\beta },\delta }(D))}\Vert +\sum _{i=0}^{k+2+\eta -2m}\Vert \partial _{t^i} f|{L_2(D_T)}\Vert , \end{aligned}$$

(3.4.10)

where the constant is independent of u and f.

Proof

Using $H^m(D)=B^m_{2,2}(D)$ in the sense of equivalent norms, Theorems 2.14, 3.4, 3.17, 2.10 together with (2.3.5) and the generalized Sobolev’s embedding (2.3.6), show that under the given assumptions we have for arbitrary $k\in \mathbb {N}_0$ that

$$\begin{aligned} u\quad&\in \, \,\, H^{k+1}([0,T],V_{\varvec{\beta },\delta }^{\eta }(D))\cap H^{k+1}([0,T],H^m(D))\nonumber \\&\hookrightarrow \, {\mathcal {C}}^{k,\frac{1}{2}}([0,T],V_{\varvec{\beta },\delta }^{\eta }(D)\cap B^m_{2,2}(D))\nonumber \\&\hookrightarrow \, {\mathcal {C}}^{k,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D)), \end{aligned}$$

(3.4.11)

where in the last step by Theorem 2.10 we get the restrictions $\eta >\beta$ (which is satisfied since $\eta >m\ge \beta$) and $r<\min \{\eta ,3(\eta -|\delta ^+|),3m \}.$ Applying Theorems 3.4, 3.17, and embedding (3.4.11) yields the a priori estimate (3.4.10) and completes the proof. $\square$

3.4.4 Hölder–Besov regularity for the inhomogeneous problem

Replacing Theorems 3.4 and 3.14 in the proof of Theorem 3.29 by their inhomogeneous counterparts Theorems 3.12 and 3.19, respectively, immediately gives the following counterpart of Theorem 3.29 for the inhomogeneous problem.

Theorem 3.32

($A_{\text {inhom}}$: Hölder–Besov regularity of inhomogeneous problem) We assume that the conditions of Theorem 3.19 together with $\gamma \ge 4m+1$ hold. Then for the weak solution $u\in H^1([0,T], {H}^m,{L_2})$ (with derivatives $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\gamma _m+1$) of problem ($P_{\text {inhom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in {\mathcal {C}}^{\gamma _m-2,\frac{1}{2}}([0,T],B^{r}_{\tau ,\tau }(D)), \qquad \text {where}\quad r<\min \big \{3(4m-|\delta ^+|),3m\big \}. \end{aligned}$$

Furthermore, the norm $\Vert u|{\mathcal {C}}^{\gamma _m-2,\frac{1}{2}}([0,T],B^{r}_{\tau ,\tau }(D))\Vert$ can be estimated from above by the right-hand side of (3.3.12).

In a similar manner as above, replacing Theorems 3.4 and 3.17 in the proof of Theorem 3.31 by Theorems 3.12 and 3.21, respectively, immediately yields the following counterpart of Theorem 3.31 for the inhomogeneous problem.

Theorem 3.33

($B_{\text {inhom}}$: Hölder–Besov regularity of inhomogeneous problem) We assume that the conditions of Theorem 3.21 hold. Then for the weak solution $u\in H^1([0,T], {H}^m, {L_2})$ (with $\partial _{t^k}u\in H^1([0,T], {H}^m, {L_2})$ for $k=1,\ldots ,\eta -2m+l+1$) of ($P_{\text {inhom}}$) we have for $\frac{1}{\tau }=\frac{r}{3}+\frac{1}{2}$ that

$$\begin{aligned} u\in {\mathcal {C}}^{l-1,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D)),\qquad \text {where}\quad r<\min \Big \{{\eta },{3(\eta -|\delta ^+|)}, {3m} \Big \}. \end{aligned}$$

Moreover, the norm $\Vert u| {\mathcal {C}}^{l-1,\frac{1}{2}}([0,T],B^r_{\tau ,\tau }(D))\Vert$ can be estimated from above by the right-hand side of (3.3.26).

Remark 3.34

Finally, we compare our regularity results in Besov and Hölder–Besov spaces obtained for parabolic PDEs (cf. Theorems 3.23, 3.25, 3.29, 3.27, 3.28, 3.32), which are based on the regularity results in weighted Sobolev spaces (the V-spaces), with the corresponding forerunners [28, Thms. 5.4.1, 5.4.5, 5.4.8].

• Since the scale of V-spaces (our weighted Sobolev spaces with mixed weights) contains the scale of Kondratiev spaces on domains of polyhedral type, cf. Remark 2.4, our results are more general and cover the results from [28] completely.

• Moreover, in Theorems 3.27, 3.28, and 3.32, we also study the inhomogeneous problem ($P_{\text {inhom}}$). Although we reduce the inhomogeneous case to the homogeneous one, for parabolic problems this transfer is technically quite involved and requires much more effort in comparison to the homogeneous case, see the proofs of Theorems 3.19 and 3.21 in this context.

• We now compare the maximal Besov regularity obtained in [28, Thm. 5.4.1] with the regularity results from Theorem 3.23. In [28, Thm. 5.4.1] for a bounded polyhedral domain with singularity set of dimension 1 (i.e., a domain with edges) it was shown that

  $$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\infty }(D))\quad \text {for all}\quad 0<r<\min \left( \gamma , 3m \right) , \end{aligned}$$

  (3.4.12)

  subject to some further restrictions on the parameters. In Theorem 3.23 we obtain

  $$\begin{aligned} u\in L_2([0,T],B^r_{\tau ,\tau }(D)) \qquad \text {for all} \quad 0<r<\min \Big \{{\gamma },{3\big (\gamma -|\delta ^+|\big )}, {3m} \Big \}. \end{aligned}$$

  (3.4.13)

  Actually, in Theorem 3.23 we stated the upper bound with $\gamma$ replaced by $2m(\gamma _m+1)$ instead of $\gamma$. However, these numbers are comparable (essentially the same). In particular, using the fact that $2m(\gamma _m+1)=2m\left( \left[ \frac{\gamma -1}{2m}\right] +1\right) \ge \gamma$ and choosing $r\le \gamma$ in (3.4.3) (which is how we argued in [28, Thm. 5.4.1]) yields (3.4.13). Alternatively, we might replace $\gamma$ by $2m(\gamma _m+1)$ in (3.4.12).

  Comparing (3.4.12) with (3.4.13) we see that the first and third restriction are the same. Since we now deal with the more general V-spaces, we have the additional restriction $3\big (\gamma -|\delta ^+|\big )$ resulting from the embedding (2.2.1), which does not appear in [28, Thm. 5.4.1] when one deals with Kondratiev spaces.

  The same phenomenon is observed when one compares [28, Thm. 5.4.5] and Theorem 3.25, which for the maximal Besov regularity yield the upper bounds $r<\min (\eta ,3m)$ and $r<\min (\eta ,3(\eta -|\delta ^+|),3m)$, respectively. Moreover in [28, Thm. 5.4.8] we have $r<3m$ compared to $r<\min (3(4m-|\delta ^+|),3m)$ in Theorem 3.29.

  In conclusion, we see that the generalization from Kondratiev to the V-spaces does not yield a better result in terms of the maximal Besov regularity. It would therefore be sufficient to work with the Kondratiev spaces in this context. However, a lot of the regularity results for parabolic PDEs on non-smooth domains are stated in terms of V-spaces, and therefore, it makes sense to use them directly. Our major contribution in this paper is that we are able to study the maximal Besov regularity of inhomogeneous parabolic problems as well, which has not been done so far.