SRMD: Sparse Random Mode Decomposition

Abstract

Signal decomposition and multiscale signal analysis provide many useful tools for time-frequency analysis. We proposed a random feature method for analyzing time-series data by constructing a sparse approximation to the spectrogram. The randomization is both in the time window locations and the frequency sampling, which lowers the overall sampling and computational cost. The sparsification of the spectrogram leads to a sharp separation between time-frequency clusters which makes it easier to identify intrinsic modes, and thus leads to a new data-driven mode decomposition. The applications include signal representation, outlier removal, and mode decomposition. On benchmark tests, we show that our approach outperforms other state-of-the-art decomposition methods.

Appendixes

As additional examples, we include more comparison results on the intersection time series signal described in Sect. 3.2 as well as the experiments on a noisy signal where the noise level has a larger amplitude than one of the modes (see Sect. 3.3) and on an overlapping and noisy signal (see Sect. 3).

1.1 Appendix A: Comparing Different Methods on the Intersecting Time Series Example

In this section, we present our reconstructed signals as well as our learned modes from the challenging intersecting time series in Sect. 3.2. Specifically, applying the DBSCAN on the extracted time-frequency pairs $\{(\tau _j,\omega _j)\}_j$ yields three clusters denoted by green triangles, orange circles, and orange squares (see Fig. 3 (right figure in the first row)). The corresponding learned modes are plotted in Fig. 8. To reduce the decomposition to two modes, we keep the mode with the largest $\ell _2$-norm and combine the two learned modes with the smallest $\ell _2$-norm to construct the second mode, which is shown in Fig. 9. Our proposed algorithm provides a reasonable extraction of modes where the errors between the learned modes and the true ones are almost zero everywhere, except on a time-shift region corresponding to the intersection of instantaneous frequencies. As seen in Fig. 10, the other approaches have difficulty obtaining the two modes, likely due to the intersecting of frequencies in the spectrogram.

Fig. 8

Example from Sect. 3.2. The three modes from SRMD associated with the clusters: orange circles, green triangles, and orange squares from Fig. 3 (left to right)

Fig. 9

Example from Sect. 3.2. Decomposition results of our proposed SRMD method into two modes. First row: noiseless ground truth signal (in black) with the learned signal (in blue) of the full signal (top) and the two learned modes. Last row from left to right: errors between noiseless ground truth and the learned representation, between the true modes and the extracted modes

Fig. 10

Example from Sect. 3.2. Comparing different methods on the intersecting time-series example. Top to bottom rows are SRMD, EMD, EEMD, CEEMDAN, EWT, and VMD. The first column displays the noiseless ground truth (in black) and the learned signal representation (in blue). The remaining two columns are the two modes, where the true IMFs are plotted in black and the learned IMFs are in blue

In Fig. 10, we compare the reconstruction and the decomposition results of our method versus those obtained from some of the state-of-the-art intrinsic mode decomposition methods (EMD, EEMD, CEEMDAN, EWT, and VMD) on the intersecting time series signal given in Sect. 3.2.

1.2 Appendix B: Comparison Results on Pure Sinusoidal Signals with Noise

In this section, we present our reconstructed signals as well as our learned modes from the challenging noisy tri-harmonic signal described in Sect. 3.3. In particular, in Fig. 11, we plot the time-frequency pairs associated with non-zero coefficients (top left), the clustering of those non-zero coefficients (top right), the reconstruction signal and the three learned modes (second row), and the corresponding errors (third row). Our method can extract the first two learned modes with high accuracy. Note that both VMD (see [11]) and our method (see Fig. 11) have difficulty in extracting the weak and high-frequency mode $y_3(t) = \frac{1}{16}\cos (576\uppi t)$. Nevertheless, our method can identify the frequencies of all three modes. More precisely, the median frequencies of the three learned clusters are 1.99, 24.03, and 288.02 Hz, which are very close to the ground truth frequencies 2, 24, and 288 Hz.

Fig. 11

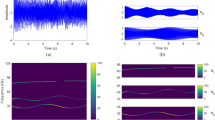
Example from Sect. 3.3. First row: the noisy input signal. Second row: magnitude of non-zero learned coefficients (left) and learned clusters (right). Third row from left to right: reconstructed signal (in blue) and the three extracted modes (in blue) versus the corresponding noiseless signal and modes (in black). Last row: error of the reconstruction and the three IMFs compared to the ground truth

1.3 Appendix C: Overlapping Time-Series with Noise

In this experiment, we investigate an example with overlap. The input signal y(t) is the summation of two modes $y_1(t) = \mathcal{F}^{-1}\{Y_1\}(t)$ and $y_2(t) = \mathcal{F}^{-1}\{Y_2\}(t)$ with overlapping frequencies and is contaminated by noise:

$$\begin{aligned} y(t) = y_{\rm true}(t) + \varepsilon = y_1(t) + y_2(t) + \varepsilon ,\quad \varepsilon \sim \mathcal {N}\left( 0, \dfrac{r \Vert y_{\rm true}\Vert _2}{\sqrt{m}}\right) . \end{aligned}$$

(C1)

Here $\mathcal{F}^{-1}\{Y_i\}$ denotes the inverse Fourier transform of $Y_i$ for $i=1,2$, where

$$\begin{aligned} \begin{aligned} Y_1(k) = m{\rm e}^{-{\rm i}\uppi k} \left({\rm e}^{-\frac{9(k-16)^2}{32}}-{\rm e}^{-\frac{9(k+16)^2}{32}}\right) , Y_2(k) = m{\rm e}^{-{\rm i}\uppi k} \left( {\rm e}^{-\frac{9(k-20)^2}{32}}-{\rm e}^{-\frac{9(k+20)^2}{32}}\right) \end{aligned} \end{aligned}$$

(C2)

for $k\in \mathbb {Z}$ and $t\in [0,1].$ Note that the modes $y_1(t)$ and $y_2(t)$ produce Gaussians in the Fourier domain centered at $k=16$ and $20\text {\,Hz}$, respectively. The leading term, $m{\rm e}^{-{\rm i}\uppi k}$, centers the wave packets to $t=0.5\text {\,s}$ where $m=160$ is the total number of samples. For the SRMD algorithm, the hyperparameters to generate the basis are set to $\omega _{\max } = 40$, $N = 20,m = 3\,200$, and $\Delta =0.2$. The hyperparameter for the DBSCAN algorithm is set to $\varepsilon = 1.5$.

Fig. 12

Example from Appendix C. Ground truth (left) and noisy input with $r=25\%$ (right)

The noiseless and noisy time series with $r=25\%$ are shown in Fig. 12. All reconstruction and decomposition results will be compared against the true signal (or modes) $y_{\rm true}(t), y_1(t),$ and $y_2(t)$. We compare our results with other methods applied to noisy signals with different noise ratios $r = 5\%, 15\%,$ and $25\%$. From the results in Fig. 13, we see that only VMD and our method properly reconstruct and decompose the noisy signal. Moreover, when the noise level r is small (5%), the VMD approach produces comparable results with our method. When r increases, our method is still able to capture the intrinsic modes and denoise the input signal. On the other hand, the VMD is able to identify some aspects of the two intrinsic modes but is polluted by noise, see Figs. 14 and 15.

The clusters of the non-zero coefficients obtained by SRMD applied to the noisy signal with the noise levels $r= 5\%, 15\%$, and $25\%$ are shown in Fig. 16. Note that the clusters surround the two Gaussian peaks ($16 \text {\,Hz}$ and $20 \text {\,Hz}$) that define the true input signal. The other features obtained by the SRMD provide slightly corrects to the overall shape to ensure the reconstruction error is below the specified upper bound. This implies one has the flexibility in choosing the width and number of random features since additional features can be used to ensure the reconstruction is reasonable.

Fig. 13

Example from Appendix C. Decomposition results with $r= 5\%$ noise using six different methods. Top to bottom rows: SRMD, EMD, EEMD, CEEMDAN, EWT, and VMD. First column: the noiseless ground truth (black) and the learned signal (blue). Middle and last columns: the first and second ground truth IMFs (black) with the learned IMFs (blue)

Fig. 14

Example from Appendix C. Decomposition results with $r= 15\%$ noise using SRMD (first row) and VMD (second row). First column: the noiseless ground truth (black) and the learned signal (blue). Middle and last columns: the first and second ground truth IMFs (black) with the learned IMFs (blue)

Fig. 15

Example from Appendix C. Decomposition results with $r= 25\%$ noise using SRMD (first row) and VMD (second row). First column: the noiseless ground truth (black) and the learned signal (blue). Middle and last columns: the first and second ground truth IMFs (black) with the learned IMFs (blue)

Fig. 16

Example from Appendix C. First column: magnitude of non-zero learned coefficients for noisy signals with $r=5\%, 15\%$ , and $25\%$. Second column: two learned clusters (green and orange)

1.4 Appendix D: Example on Parameter Tuning and Limitations

As we discuss in Sect. 3.6, the window size $\Delta$ and the clustering neighborhood scale $\varepsilon$ are sensitive tunable parameters. For example, in the discontinuous time-series example (see Sect. 3.1), if $\varepsilon = 0.06$ (instead of 0.1), the non-zero learned coefficients align with the true instantaneous frequencies. However, the learned modes are not reasonable due to wrong clusters (see Fig. 17). On the other hand, if $\varepsilon = 0.15$, although the non-zero learned coefficients still align with the true instantaneous frequencies, Algorithm 2 can not extract the mode since the clustering part is not able to cluster the set ${\widehat{S}}$.

Fig. 17

Example from Sect. 3.1with DBSCAN hyperparameter $\varepsilon = 0.05$. First row from left to right: magnitude of non-zero learned coefficients used for DBSCAN and clustering of non-zero coefficients into three modes. Second row from left to right: three extracted modes

Finally, if we choose the window size $\Delta$ too big or too small, the non-zero learned coefficients may not align well with the instantaneous frequencies or make it difficult to cluster (see Fig. 18).

Fig. 18

Example from Sect. 3.1with various window sizes $\Delta$. From left to right: clustering of non-zero coefficients (the true instantaneous frequencies are in black) for $\Delta = 0.02$ (left) and $\Delta = 0.2$