Skip to main content
SpringerLink
Log in

An Eulerian formulation of a growing rod in three dimensions with mass accretion

  • Original Paper
  • Published:
Mechanics of Soft Materials Aims and scope Submit manuscript

Abstract

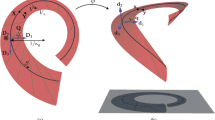
Motivated by a general thermomechanical theory of Cosserat rods, an isothermal constrained theory is developed which generalizes a three-dimensional elastica to have a growing circular cross-section and a growing centroidal length. An Eulerian formulation of constitutive equations is developed using evolution equations for elastic dilatation, elastic cross-sectional radial stretch, elastic curvature and elastic torsional twist. These evolution equations include time-dependent inelastic effects of homeostasis which cause a tendency for these elastic deformation measures to approach their homeostatic values. An important feature of the Eulerian evolution equations is that they depend only on the current state of the rod and therefore are appropriate for modeling growth. Examples of growing rods are considered. In particular, the example of a stress-free growing helical rod suggests a possible mechanical mechanism for a climbing vine which grabs an object as its radius decreases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Ambrosi, D., Ateshian, G.A., Arruda, E.M., Cowin, S., Dumais, J., Goriely, A., Holzapfel, G.A., Humphrey, J.D., Kemkemer, R., Kuhl, E., et al.: Perspectives on biological growth and remodeling. J. Mech. Phys. Solids. 59(4), 863–883 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ateshian, G., Humphrey, J.: Continuum mixture models of biological growth and remodeling: past successes and future opportunities. Ann. Rev. Biomed. Eng. 14, 97–111 (2012)

    Article  Google Scholar 

  3. Ateshian, G.A., Costa, K.D., Azeloglu, E.U., Morrison, B., Hung, C.T.: Continuum modeling of biological tissue growth by cell division, and alteration of intracellular osmolytes and extracellular fixed charge density. J. Biomech. Eng. 131(10), 101001 (2009)

    Article  Google Scholar 

  4. Bilby B, Gardner L, S. A.: Continuous distributions of dislocations and the theory of plasticity. In: Proceedings of the 9th International Congress of Applied Mechanics. vol. 9, pp.35-44. University de Brussels (1957)

  5. Bruce, D.M.: Mathematical modelling of the cellular mechanics of plants, Philosophical Transactions of the Royal Society of London. Ser. B Biol. Sci. 358(1437), 1437–1444 (2003)

    Article  Google Scholar 

  6. Chen, Y. C., Hoger, A.: Constitutive functions of elastic materials in finite growth and deformation. In: Advances in Continuum Mechanics and Thermodynamics of Material Behavior. Springer (2000)

  7. Cowin, S.C., Hegedus, D.: Bone remodeling I: theory of adaptive elasticity. J. Elast. 6(3), 313–326 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  8. Cowin, Stephen C.: Wolff’s law of trabecular architecture at remodeling equilibrium. J. Biomech. Eng. 108, 83–88 (1986)

    Article  Google Scholar 

  9. Tissue growth and remodeling: Annu. Rev. Biomed. Eng. 6, 77–107 (2004)

    Article  Google Scholar 

  10. Eckart, C.: The Thermodynamics of irreversible processes. IV, The theory of elasticity and anelasticity. Phys. Rev. 73(4), 373–382 (1948)

    Article  MathSciNet  MATH  Google Scholar 

  11. Erlich, A., Moulton, D.E., Goriely, A.: Are homeostatic states stable? dynamical stability in morphoelasticity. Bull. Math. Biol. 81(8), 3219–3244 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  12. Goriely, A.: The Mathematics and Mechanics of Biological Growth, vol. 45. Springer (2017)

  13. Goriely, A., Neukirch, S.: Mechanics of climbing and attachment in twining plants. Phys. Rev. Lett. 97(18), 184302 (2006)

    Article  Google Scholar 

  14. Goriely, A., Robertson-Tessi, M., Tabor, M., Vandiver, R.: Elastic growth models. In: Mathematical Modelling of Biosystems, pp. 1-44. Springer (2008)

  15. Green, A.E., Naghdi, P.M.: A dynamical theory of interacting continua. Int. J. Eng. Sci. 3(2), 231–241 (1965)

    Article  MathSciNet  Google Scholar 

  16. Green, A.E., Naghdi, P.M.: A theory of mixtures. Arch. Ration. Mech. Anal. 24(4), 243–263 (1967)

    Article  MathSciNet  Google Scholar 

  17. Green, A.E., Naghdi, P.M.: On thermodynamics and the nature of the second law. Proc. R. Soc. Lond. A. Math. Phys. Sci. 357(1690), 253–270 (1977)

    MathSciNet  Google Scholar 

  18. Green, A.E., Naghdi, P.M.: On thermal effects in the theory of rods. Int. J. Solids Struct. 15(11), 829–853 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  19. Green, A.E., Naghdi, P.M., Wenner, M.L.: On the theory of rods. I. derivations from the three-dimensional equations. Proc. R. Soc. Lond. A. Math. Phys. Sci. 337(1611), 451i483 (1974a)

    MathSciNet  MATH  Google Scholar 

  20. Green, A.E., Naghdi, P.M., Wenner, M.L.: On the theory of rods II. developments by direct approach. Proc. R. Soc. Lond. A. Math. Phys. Sci. 337(1611), 485i507 (1974b)

    MathSciNet  MATH  Google Scholar 

  21. Hamant, O., Traas, J.: The mechanics behind plant development. New Phytol. 185(2), 369–385 (2010)

    Article  Google Scholar 

  22. Hsu, F.-H.: The influences of mechanical loads on the form of a growing elastic body. J. Biomech. 1(4), 303–311 (1968)

    Article  Google Scholar 

  23. Humphrey, J.D., Rajagopal, K.R.: A constrained mixture model for growth and remodeling of soft tissues. Math. Model. Methods Appl. Sci. 12(03), 407–430 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kröner, E.: General continuum theory of dislocations and intrinsic stresses. Arch. Ration. Mech. Anal. 4(1), 273 (1959)

    Article  Google Scholar 

  25. Kuhl, E.: Growing matter: A review of growth in living systems. J. Mech. Behav. Biomed. Mater. 29, 529–543 (2014)

    Article  Google Scholar 

  26. Lee, E.H.: Elastic-plastic deformation at finite strains. J. Appl. Mech. 36(1), 1–6 (1969)

    Article  MATH  Google Scholar 

  27. Leonov, A.: Nonequilibrium thermodynamics and rheology of viscoelastic polymer media. Rheological Acta. 15, 85–98 (1976)

    Article  MATH  Google Scholar 

  28. Naghdi, P.M., Rubin, M.B.: Constrained theories of rods. J. Elast. 14(4), 343–361 (1984)

    Article  MATH  Google Scholar 

  29. Onat, E.: The notion of state and its implications in thermodynamics of inelastic solids. In: Irreversible Aspects of Continuum Mechanics and Transfer of Physical Characteristics in Moving Fluids, pp. 292–314. Springer (1968)

  30. Rajagopal, K. R., Tao, L.: Mechanics of mixtures, vol. 35. World scientific (1995)

  31. Rodriguez, E.K., Hoger, A., McCulloch, A.D.: Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27(4), 455–467 (1994)

    Article  Google Scholar 

  32. Ross, S., Callaghan, T., Ennos, A., Sheffield, E.: Mechanics and growth form of the mosshylocomium splendens. Ann. Bot. 82(6), 787–793 (1998)

    Article  Google Scholar 

  33. Rubin, M.B.: Hyperbolic heat conduction and the second law. Int. J. Eng. Sci. 30(11), 1665–1676 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rubin, M.B.: Plasticity theory formulated in terms of physically based microstructural variables - Part I: Theory. Int. J. Solids Struct. 31(19), 2615–2634 (1994)

    Article  MATH  Google Scholar 

  35. Rubin, M.B.: On the treatment of elastic deformation in finite elastic- viscoplastic theory. Int. J. Plast. 12(7), 951–965 (1996)

    Article  MATH  Google Scholar 

  36. Rubin, M.B.: An intrinsic formulation for nonlinear elastic rods. Int. J. Solids Struct. 34(31–32), 4191–4212 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  37. Rubin, M. B.: Cosserat Theories: Shells, Rods and Points. vol. 79 of Solid Mechanics and its Applications. Kluwer ( 2000)

  38. Rubin, M.B.: Physical reasons for abandoning plastic deformation measures in plasticity and viscoplasticity theory. Arch. Mech. 53(4–5), 519–539 (2001)

    MATH  Google Scholar 

  39. Rubin, M.B.: Removal of unphysical arbitrariness in constitutive equations for elastically anisotropic nonlinear elastic-viscoplastic solids. Int. J. Eng. Sci. 2012, 38–45 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  40. Rubin, M.B., Safadi, M.M., Jabareen, M.: A unified theoretical struc- ture for modeling interstitial growth and muscle activation in soft tissues. Int. J. Eng. Sci. 90, 1–26 (2015)

    Article  MATH  Google Scholar 

  41. Rubin, M. B.: Continuum Mechanics with Eulerian Formulations of Constitutive Equations, vol. 265. Springer Nature ( 2020)

  42. Rubin, M.B.: Invariance under superposed rigid body motions with constraints. J. Elast. 142(1), 83–88 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. Rubin, M.B.: Modeling orthotropic elastic-inelastic response of growing tissues with application to stresses in arteries. Mech. Soft Mater. 3(1), 1–27 (2021)

    Article  Google Scholar 

  44. Sassi, M., Traas, J.: When biochemistry meets mechanics: A systems view of growth control in plants. Curr. Opin. Plant Biol. 28, 137–143 (2015)

    Article  Google Scholar 

  45. Sciume, G., Shelton, S., Gray, W.G., Miller, C.T., Hussain, F., Ferrari, M., Decuzzi, P., Schrefler, B.: A multiphase model for three-dimensional tumor growth. New J. Phys. 15(1), 015005 (2013)

    Article  Google Scholar 

  46. Skalak, R.: Growth as a finite displacement field. In: Proceedings of the IUTAM symposium on finite elasticity, pp. 347-355. Springer (1981)

  47. Skalak, R., Dasgupta, G., Moss, M., Otten, E., Dullemeijer, P., Vilmann, H.: Analytical description of growth. J. Theor. Biol. 94(3), 555–577 (1982)

    Article  MathSciNet  Google Scholar 

  48. Speck, T., Rowe, N.P.: Modelling primary and secondary growth pro- cesses in plants: a summary of the methodology and new data from an early lignophyte. Phil. Trans. R. Soc. Lond. Ser. B. Biol. Sci. 358(1437), 1473–1485 (2003)

    Article  Google Scholar 

  49. Truesdell, C.: Mechanical basis of diffusion. J. Chem. Phys. 37(10), 2336–2344 (1962)

    Article  Google Scholar 

  50. Truesdell, C., Toupin, R.: The Classical Field theories. In: Principles of classical mechanics and field theory, pp. 226-858. Springer (1960)

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Technion-Israel Institute of Technology, 32000, Haifa, Israel

    MB Rubin

Authors
  1. MB Rubin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to MB Rubin.

Ethics declarations

Conflict of interest

The author declares no competing interests.

Appendix. Details of some developments

Appendix. Details of some developments

Using (3), (9), and (47) yields

$$\begin{aligned} \frac{d}{d t} \big ( \frac{{\partial } \mathbf {e}_t}{{\partial } s} \big )= & {} \frac{d}{d t} \big [ \frac{1}{\lambda } \frac{{\partial }}{{\partial } S} \big (\frac{1}{\lambda } \mathbf {d}_3 \big )\big ] =\frac{{\partial } }{{\partial } s} \big ( \frac{1}{\lambda } \mathbf {w}_3 - \frac{\dot{\lambda }}{\lambda } \mathbf {e}_t \big ) - \frac{\dot{\lambda }}{\lambda } \frac{{\partial } \mathbf {e}_t}{{\partial } s} \,, \nonumber \\= & {} \frac{1}{\lambda } \frac{{\partial } \mathbf {w}_3}{{\partial } s} - \frac{1}{\lambda } \frac{{\partial } \lambda }{{\partial } s} \mathbf {L} \mathbf {e}_t - \frac{{\partial }}{{\partial } s} \big ( \frac{\dot{\lambda }}{\lambda } \big ) \mathbf {e}_t - 2 \kappa \big (\frac{\dot{\lambda }}{\lambda } \big ) {\mathbf {e}}_n \,. \end{aligned}$$
(96)

Then, with the help of (46) and (48) it follows that

$$\begin{aligned} \dot{\kappa } = \frac{1}{\lambda } \frac{{\partial } \mathbf {w}_3}{{\partial } s} \cdot {\mathbf {e}}_n - \frac{1}{\lambda } \frac{{\partial } \lambda }{{\partial } s} ({\mathbf {e}}_n \otimes {\mathbf {e}}_t) \cdot \mathbf {L} - 2 \kappa ({\mathbf {e}}_t \otimes {\mathbf {e}}_t) \cdot \mathbf {D} \,. \end{aligned}$$
(97)

Next, using the fact that for the constrained theory \(\mathbf {d}_\alpha\) are orthogonal to \(\mathbf {d}_3\), it can be shown that

$$\begin{aligned}&\mathbf {w}_\alpha \cdot \mathbf {d}_3 + \mathbf {d}_\alpha \cdot \mathbf {w}_3 = 0 \,, \quad \mathbf {w}_3 = - \lambda (\mathbf {w}_\alpha \cdot {\mathbf {e}}_t) \mathbf {d}^\alpha + \dot{\lambda } {\mathbf {e}}_t \,. \nonumber \\&\frac{{\partial } \mathbf {w}_3}{{\partial } s} = - \lambda (\frac{{\partial } \mathbf {w}_\alpha }{{\partial } s} \cdot {\mathbf {e}}_t) \mathbf {d}^\alpha - \frac{{\partial } \lambda }{{\partial } s} (\mathbf {w}_\alpha \cdot {\mathbf {e}}_t) \mathbf {d}^\alpha - \kappa \lambda (\mathbf {w}_\alpha \cdot {\mathbf {e}}_n) \mathbf {d}^\alpha \nonumber \\&\quad \quad - \lambda (\mathbf {w}_\alpha \cdot {\mathbf {e}}_t) \frac{{\partial } \mathbf {d}^\alpha }{{\partial } s} +\frac{{\partial } \dot{\lambda }}{{\partial } s} {\mathbf {e}}_t +\dot{\lambda } \kappa {\mathbf {e}}_n \,, \nonumber \\&\frac{{\partial } \mathbf {w}_3}{{\partial } s} \cdot {\mathbf {e}}_n = - \lambda (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) ({\mathbf {e}}_t \cdot \frac{{\partial } \mathbf {w}_\alpha }{{\partial } s}) \nonumber \\&\quad \quad - \frac{{\partial } \lambda }{{\partial } s} (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) ({\mathbf {e}}_t \otimes \mathbf {d}_\alpha ) \cdot \mathbf {L} \nonumber \\&\quad \quad - \kappa \lambda (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) ({\mathbf {e}}_n \otimes \mathbf {d}_\alpha ) \cdot \mathbf {L} \nonumber \\&\quad \quad - \lambda \big (\frac{{\partial } \mathbf {d}^\alpha }{{\partial } s} \cdot {\mathbf {e}}_n \big ) ({\mathbf {e}}_t \otimes \mathbf {d}_\alpha ) \cdot \mathbf {L} + \kappa \lambda ({\mathbf {e}}_t \otimes {\mathbf {e}}_t) \cdot \mathbf {D} \,, \nonumber \\&\frac{{\partial } \mathbf {w}_3}{{\partial } s} \cdot {\mathbf {e}}_n = - \lambda (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) ({\mathbf {e}}_t \cdot \frac{{\partial } \mathbf {w}_\alpha }{{\partial } s}) \nonumber \\&\quad \quad - \frac{{\partial } \lambda }{{\partial } s} \big [({\mathbf {e}}_t \otimes (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) \mathbf {d}_\alpha \big ] \cdot \mathbf {L} \nonumber \\&\quad \quad -\lambda {\mathbf {e}}_t \cdot \mathbf {L} \big (\mathbf {d}_\alpha \otimes \frac{{\partial } \mathbf {d}^\alpha }{{\partial } s} \big ) {\mathbf {e}}_n \nonumber \\&\quad \quad - \kappa \lambda \big [({\mathbf {e}}_n \otimes (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) \mathbf {d}_\alpha \big ] \cdot \mathbf {L} + \kappa \lambda ({\mathbf {e}}_t \otimes {\mathbf {e}}_t) \cdot \mathbf {D} \,, \nonumber \\&\frac{{\partial } \mathbf {w}_3}{{\partial } s} \cdot {\mathbf {e}}_n = - \lambda (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) \, {\mathbf {e}}_t \cdot \big (\frac{{\partial } \mathbf {w}_\alpha }{{\partial } s} - \mathbf {L} \frac{{\partial } \mathbf {d}_\alpha }{{\partial } s} \big ) \nonumber \\&\quad \quad - \frac{{\partial } \lambda }{{\partial } s} ({\mathbf {e}}_t \otimes {\mathbf {e}}_n) \cdot \mathbf {L} \nonumber \\&\quad \quad - \lambda {\mathbf {e}}_t \cdot \mathbf {L} \big (\frac{{\partial } \mathbf {d}_\alpha }{{\partial } s} \otimes \mathbf {d}^\alpha +\mathbf {d}_\alpha \otimes \frac{{\partial } \mathbf {d}^\alpha }{{\partial } s} \big ) {\mathbf {e}}_n \nonumber \\&\quad \quad + \kappa \lambda ({\mathbf {e}}_t \otimes {\mathbf {e}}_t- {\mathbf {e}}_n \otimes {\mathbf {e}}_n) \cdot \mathbf {D} \,, \nonumber \\&\frac{{\partial } \mathbf {w}_3}{{\partial } s} \cdot {\mathbf {e}}_n = - \lambda (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) \, {\mathbf {e}}_t \cdot \big (\frac{{\partial } \mathbf {w}_\alpha }{{\partial } s} - \mathbf {L} \frac{{\partial } \mathbf {d}_\alpha }{{\partial } s} \big ) \nonumber \\&\quad \quad - \frac{{\partial } \lambda }{{\partial } s} ({\mathbf {e}}_t \otimes {\mathbf {e}}_n) \cdot \mathbf {L} + \kappa \lambda (2{\mathbf {e}}_t \otimes {\mathbf {e}}_t- {\mathbf {e}}_n \otimes {\mathbf {e}}_n) \cdot \mathbf {D} \,, \end{aligned}$$
(98)

where use has been made of the expressions

$$\begin{aligned}&{\mathbf {e}}_n = (\mathbf {d}^\alpha \cdot {\mathbf {e}}_n) \mathbf {d}_\alpha \,, \quad \mathbf {d}_\alpha \otimes \mathbf {d}^\alpha = \mathbf {I} - {\mathbf {e}}_t \otimes {\mathbf {e}}_t \,, \nonumber \\&\frac{{\partial } \mathbf {d}_\alpha }{{\partial } s} \otimes \mathbf {d}^\alpha +\mathbf {d}_\alpha \otimes \frac{{\partial } \mathbf {d}^\alpha }{{\partial } s} = -\kappa ({\mathbf {e}}_n \otimes {\mathbf {e}}_t + {\mathbf {e}}_t \otimes {\mathbf {e}}_n) \,. \end{aligned}$$
(99)

Finally, substituting (98) into (97) yields the evolution equation (49).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rubin, M. An Eulerian formulation of a growing rod in three dimensions with mass accretion. Mech Soft Mater 4, 9 (2022). https://doi.org/10.1007/s42558-022-00047-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42558-022-00047-0

Keywords

PACS

Search

Navigation