Modeling orthotropic elastic-inelastic response of growing tissues with application to stresses in arteries

Abstract

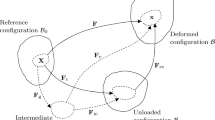
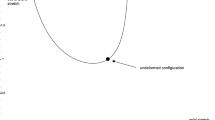
This paper generalizes previous work on physically based nonlinear orthotropic invariants for thermomechanical response of soft materials to include the inelastic process of homeostasis, which causes a biological tissue to approach its homeostatic state. This process of homeostasis can cause a homogeneous material (one with the same constitutive equations and material constants as each material point) to develop a nonuniform state. Within the context of biological tissues, this means that the tissue cannot be unloaded elastically to a zero-stress state. A simplified version of the theory is used to describe elastic response of an artery from its nonuniform homeostatic state using a Fung-type exponential orthotropic strain energy function with material constants determined for a human carotid artery. As discussed in Safadi and Rubin (Int. J. Eng. Sci. 118(40), 2017), the approach of assuming a homeostatic state at systolic pressure and limiting extrapolation of the constitutive response to the physiological pressure range reduces uncertainty in the stress distributions in the artery. The specific results here show that the circumferential stress in the physiological pressure range exhibits a strong sensitivity to residual stresses known to exist in the cut unloaded state. This approach suggests that detailed experimental data on the response of the artery in its physiological pressure range and more complete understanding of mechanobiological processes during homeostasis are essential for determining an accurate constitutive equation of an artery.

Appendix A: Details of some the mathematical expressions

1.1 A.1 Details of the functions N _i and A _i

The scalar functions N_i and A_i in Eq. 26 are defined by

$$ \begin{aligned} &\quad \quad \quad N_{1} =\frac{J_{e}}{\eta_{1}} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime}\right) \frac{\partial \eta_{1}}{\partial J_{e}} , \\ &\quad \quad \quad N_{2} =\frac{J_{e}}{\eta_{2}} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime}\right) \frac{\partial \eta_{2}}{\partial J_{e}} , \\ &\quad \quad \quad N_{3} =\frac{J_{e}}{\eta_{3}} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime}\right) \frac{\partial \eta_{3}}{\partial J_{e}} , \\ &\quad \quad \quad A_{1} =- \frac{1}{\eta_{1}} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime} \right) \frac{\partial \eta_{1}}{\partial \theta} , \\ &\quad \quad \quad A_{2} =- \frac{1}{\eta_{2}} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime} \right) \frac{\partial \eta_{2}}{\partial \theta} , \\ &\quad \quad \quad A_{3} =- \frac{1}{\eta_{3}} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime} \right) \frac{\partial \eta_{3}}{\partial \theta} . \end{aligned} $$

(101)

1.2 A.2 Details of the tensors $\mathbf {B}_{i}^{\prime \prime }$

The deviatoric tensors $\mathbf {B}_{i}^{\prime \prime }$ in Eq. 26 are defined by

$$ \begin{aligned} &\mathbf{B}_{1}^{\prime\prime} = \frac{1}{{\eta_{1}^{2}}} \mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime} - {\eta_{1}^{2}} \mathbf{m}^{1 \prime} \otimes \mathbf{m}^{1 \prime} \\ &\quad \quad - \frac{1}{3} \left( \frac{m_{11}^{\prime}}{{\eta_{1}^{2}}} - {\eta_{1}^{2}} m^{11 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{2}^{\prime\prime} = \frac{1}{{\eta_{2}^{2}}} \mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime} - {\eta_{2}^{2}} \mathbf{m}^{2 \prime} \otimes \mathbf{m}^{2 \prime} \\ &\quad \quad- \frac{1}{3} \left( \frac{m_{22}^{\prime}}{{\eta_{2}^{2}}} - {\eta_{2}^{2}} m^{22 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{3}^{\prime\prime} = \frac{1}{{\eta_{3}^{2}}} \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime} - {\eta_{3}^{2}} \mathbf{m}^{3 \prime} \otimes \mathbf{m}^{3 \prime} \\ &\quad \quad- \frac{1}{3} \left( \frac{m_{33}^{\prime}}{{\eta_{3}^{2}}} - {\eta_{3}^{2}} m^{33 \prime} \right) \mathbf{I} , \\ &\mathbf{B}_{4}^{\prime\prime} = \frac{m_{12}^{\prime}}{m_{11}^{\prime} m_{22}^{\prime}} \left[(\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{2}^{\prime}+ \mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{1}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{12}^{\prime}}{m_{11}^{\prime}} (\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime}) - \frac{m_{12}^{\prime}}{m_{22}^{\prime}} (\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime}) \right] , \\ &\mathbf{B}_{5}^{\prime\prime} = \frac{m_{13}^{\prime}}{m_{11}^{\prime} m_{33}^{\prime}} \left[(\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{3}^{\prime}+ \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{1}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{13}^{\prime}}{m_{11}^{\prime}} (\mathbf{m}_{1}^{\prime} \otimes \mathbf{m}_{1}^{\prime}) - \frac{m_{13}^{\prime}}{m_{33}^{\prime}} (\mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime}) \right] , \\ &\mathbf{B}_{6}^{\prime\prime} = \frac{m_{23}^{\prime}}{m_{22}^{\prime} m_{33}^{\prime}} \left[(\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{3}^{\prime}+ \mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{2}^{\prime})\right. \\ &\left.\quad \quad- \frac{m_{23}^{\prime}}{m_{22}^{\prime}} (\mathbf{m}_{2}^{\prime} \otimes \mathbf{m}_{2}^{\prime}) - \frac{m_{23}^{\prime}}{m_{33}^{\prime}} (\mathbf{m}_{3}^{\prime} \otimes \mathbf{m}_{3}^{\prime}) \right] . \end{aligned} $$

(102)