1 Introduction

Pakistan, the sixth largest population in the world, is one of the developing countries [1, 2] with abundant water resources yet not fully utilized [3]. Ecological deterioration has increased the extent of rainfall worldwide, thus increasing the apprehension about excessive flooding [4]. Floods are an inherent component of the hydrological cycle, and their occurrence can lead to loss of life, population displacement, and environmental devastation, significantly jeopardizing economic progress [5]. Extreme rainfall and excessive flooding are expected to traumatize the hydraulic structures [6, 7], natural and artificial reservoirs, and existing water bodies [8, 9]. The Indus flood 2010 was one of the greatest river disasters in recent history, affecting more than 14 million people in Pakistan [10, 11]. Although excessive rainfall between July and September 2010 has been cited as the major causative factor for this disaster, human interventions in the river system over the years have made this disaster a catastrophe. Geomorphic analysis suggests that the Indus River has had a very dynamic regime in the past [12, 13]. Water regulatory bodies must consider designing hydraulic structures to cope with more severe natural catastrophic challenges expected to occur [14,15,16]. Barrages and weirs are engineered structures designed to redirect water flow from rivers to serve multiple purposes such as irrigation, navigation, power generation, and supplying water for drinking and industrial use [17, 18]. The construction material of the structure, whether masonry, plain concrete, or reinforced concrete, is determined by factors such as the type of foundation [19], availability of construction materials, dewatering requirements, construction costs, and other relevant considerations [20, 21]. Barrage or weir structures typically comprise key elements, including cut-offs, flooring, piers, dividing walls, energy dissipation systems, flexible protection measures, abutments, side walls, flared walls, gates or sliding shutters, stop logs, lifting mechanisms and bridges, trestles, guiding embankments, overflow embankments, connecting embankments, main gates, sediment exclusion systems, fish passages, and road or railway bridges. However, including these components may vary depending on site-specific conditions and project needs [22,23,24]. Dividing walls within these structures is crucial in regulating water flow and distribution. Yet, the complete scope of their beneficial effects on flow dynamics within barrages is still undergoing thorough investigation [25]. Hydraulic structures (barrages, dams, and canal head regulators) are designed based on the maximum discharge capacity to stand during extreme flood events [26, 27]. Sedimentation control is another primary concern associated with Barrage designs, and several studies have been conducted to evaluate the sedimentation rate for various Barrages and their design capacities [28,29,30,31,32,33,34,35].

As global precipitation levels rise due to ecological degradation, there is a growing recognition of the importance of hydraulic structures in mitigating flooding incidents [36, 37]. Extreme rainfall events pose significant challenges to hydraulic structures, including natural and artificial reservoirs and existing water bodies [38]. This underscores the increasing necessity for water regulatory bodies to design resilient hydraulic structures that can withstand these environmental stressors. Granados and Wostecki [8] performed a detailed analysis of Niedów Barrage in South Poland, using numerical and physical modeling to evaluate its structural sustainability under extreme flood conditions. The results of their study predicted that the structure would be adequate to withstand the flood severities. They found the discharge coefficient to be the most crucial parameter for the hydraulic structure. Ezzat et al. [39] conducted 2-D modeling to study the impact of the Barrage on flow distribution and velocities. Their results revealed that the best distribution for the left and right branches was 60% and 40%, with a negligible effect on velocity. Chaudhary and Sarwar [40] conducted a similar analysis of Taunsa Barrage in Pakistan to assess the prospects and concerns. They analyzed a sub-weir to investigate its effect on the overall performance of the Barrage during the flood season and found that the sub-weir created a poor impact on the function of under-sluices. Brammer et al. [41] performed the numerical and physical modeling of Severn Barrage to study the stream behavior and evaluated the velocity magnitudes to predict the velocity pattern across the Barrage. Barrage structures not only influence the flow distribution, flow behavior, and velocity but also display a critical role in sedimentation control [42, 43].

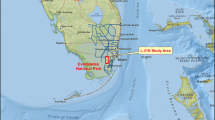
A major part of Pakistan's river basin lies in the province of Sindh, which is prone to floods. Floods pose a major environmental hazard, particularly when they overtop a few km wide river channel [44]; the natural floodplain, confined by the manmade levees (flood protective embankments/bunds) several kilometers apart, constructed on both sides of the channel, forms the riverine area (manmade flood plain) [45, 46]. The Guddu Barrage was inaugurated in 1962 on the Indus River in the Kashmore district of Sindh province, Pakistan. The Indus River flows southward from Pakistan's northern regions into the Arabian Sea [47,48,49]. The "Ghotki" and "Rainee" Canals off-taking from the Guddu Barrage are vulnerable to severe financial loss if discharge rates change. To irrigate some 412,000 acres in the Ghotki, Sukkur, and Khairpur districts of Sindh, Pakistan, the Rainee Canal off-takes from the left bank of the Guddu Barrage. It was decided that the existing division wall needed to be lengthened on the upstream side to achieve the design discharge in the Rainee Canal. The extension of the split wall, which will join the already-existing divide wall at the barrage, has begun construction on the upstream side, near the barrage. When the gap between the existing and extended divide wall was 166.7 ft, the designated capacity of the left pocket decreased due to the extension of the divide wall at this location. Similarly, construction toward the existing divide would affect the flow of the Ghotki Canal [50]. The map showing the location of Guddu Barrage on the Indus River is shown in Fig. 1.

Fig. 1
figure 1

Location map of the Guddu Barrage

Full size image

Consequently, the Ghotki Canal would not receive the full design discharge required. This underscores the necessity for a crevice in the dividing walls to facilitate the intended flow of water into the Ghotki Canal. The existing gap impedes the effectiveness of silt excluders and disrupts the flow regime. The present research study objectives are:

  • To quantify the impact of extending the divide wall and the existing divide wall gap on river and canal flows.

  • To investigate the flow parameters and the behavior of the flow under varying spaces between the dividing walls,

  • Application of a non-distorted physical model to quantify the impact of the divide wall on off-taking canal discharges.

A detailed flow analysis at Guddu Barrage will help the authorities develop better water management practices and well-informed policy decisions. Figure 2 shows the physical model layout of Guddu Barrage with cross-regulator, head regulators, and off-taking canals.

Fig. 2
figure 2

The physical model layout of Guddu Barrage (up) with cross-regulator (left) and head regulators, and off-taking canals (right)

Full size image

2 Material and methods

2.1 Site description

The construction of the Guddu Barrage on the Indus River was engineered to accommodate a maximum discharge of 1,200,000 CFS. Despite this, the barrage faced overwhelming flows during the floods of both 1976 and 2010, surpassing its designed capacity [51,52,53,54].

Spanning a length of 4,445 feet between its abutments, the barrage comprises 65 spans, with 64 measuring 60 feet wide and one serving as a navigation lock at 50 feet wide. The intricate network of canals branching from the Guddu Barrage plays a crucial role in regional irrigation. To the right, the Beghari Sindh Canal and Desert Pat Canal diverge, while the Ghotki Canal and Rainee Canal branch off to the left. Recently completed by the Water and Development Authority (WAPDA), the Rainee Canal contributes to the intricate system.

The Desert Pat Canal is of particular significance, as it channels a complete supply discharge of 13,275 CFS from the barrage's right bank into the Desert Pat Canal. Serving the irrigation needs of Sindh and Baluchistan provinces, this canal system covers approximately 176 km of canal space within Sindh, irrigating a critical command area (CCA) of about 0.38 million acres. The Desert Pat Canal system, with a total design discharge of 7391 CFS, is a monumental engineering feat, spanning 617 km through the desert terrain. Meanwhile, the Ghotki Canal, discharging at 14,000 cubic feet per second, irrigates 1.00 million acres (GCA) and 0.858 million acres (CCA) through its 1448 km of irrigation canals. At the Guddu Barrage, discharge for the four primary off-taking channels is regulated through strategically positioned dividing walls, each featuring a fish ladder. Notably, the left pocket, housing gates 62 (the lock) and 65 are smaller due to the original absence of a canal on that side. Rainee Canal was a later addition to the system [55,56,57,58,59]. Further enhancing the intricate network of water management along the Indus River.

2.2 Collected data

Data collected for use in model construction is shown in Tables 1 and 2.

Table 1 Hydraulic data of the Guddu Barrage
Full size table
Table 2 Levels of Barrage components
Full size table

2.3 Physical modeling

2.3.1 Definition of hydraulic similarities

Engineers have used a new scientific method to predict the performance of hydraulic structures [60]. From the perspective of the topic at hand, the following three sorts of hydraulic similarities are significant:

There are three types of similarity: geometric, kinetic, and dynamic.

We can only assert that the model and the prototype are geometrically similar to each other if the ratios of all the corresponding linear dimensions are identical. Equation 1 illustrates the relationship of the geometric parameters in geometric similarity.

$$ L_{r} = \frac{L}{l} = \frac{B}{b} = \frac{D}{d} $$
(1)

In Eq. 1, “L,” “B,” and “D” represent the length, width, and depth of the prototype, whereas “l,” “b,” and “d” represent the length, width, and depth of the model, respectively. Similarly, the area ratio and the volume ratio of the prototype and the model are computed by Eqs. 2 and 3, respectively.

$$ A_{r} = \left( {{ }\frac{L}{l}{ }} \right)^{2} = { }\left( {{ }\frac{B}{b}{ }} \right)^{2} = \left( {{ }\frac{D}{d}{ }} \right)^{2} $$
(2)
$$ V_{r} = { }\left( {{ }\frac{L}{l}{ }} \right)^{3} = { }\left( {{ }\frac{B}{b}{ }} \right)^{3} = \left( {{ }\frac{D}{d}{ }} \right)^{3} $$
(3)

The model and prototype are dynamically similar if their force ratios at corresponding places are equivalent. If dynamic similarity exists, Eq. 4 calculates the prototype-model force ratio.

$$ F_{r} = \frac{{F_{1} }}{{f_{1} }} = \frac{{F_{2} }}{{f_{2} }} = \frac{{F_{3} }}{{f_{3} }} $$
(4)

In Eq. 4, “F1”, “F2”, “f1”, and “f2” represent the forces acting on the prototype at points 1 and 2, and on the model at points 1 and 2, respectively.

If the ratios of the corresponding velocities at corresponding points of prototype and model are equal, then it is called kinematic similarity. In Eq. 5, “V1”, “V2”, “v1”, and “v2” represent the velocity of the fluid in the prototype at points 1 and 2, and corresponding values for the velocity of the fluid in the model at points 1 and 2, respectively. Now if the kinematic similarity exists between the prototype and the model, then the velocity ratio is

$$ V_{r} = \frac{{V_{1} }}{{v_{1} }} = \frac{{V_{2} }}{{v_{2} }} = \frac{{V_{3} }}{{v_{3} }} $$
(5)

2.3.2 Scale selection and discharge calculation for model

Models of the Ghotki Canal and the Rainee Canal Head Regulators and seven (7) barrage bays are included in the left pocket of the Guddu Barrage. To ensure the highest level of precision, it was decided to build the model at a scale of 1:85 without distorting any details. For this model, we decided to use a 40 feet long and 5.5 feet wide tray. The 1,200,000 CFS is accommodated by a discharge of 1.97 CFS. Equation 6 describes the relationship between the original structure and the constructed undistorted physical model.

$$ Q_{{\text{r}}} = {\text{ L}}_{{\text{r}}}^{5/2} $$
(6)

In Eq. 6, Qr represents the discharge ratio, and Lr represents the length-to-height ratio. Whereas Qr is further described in Eq. 7 as.

$$ Q_{r} = \frac{{Q_{p} }}{{Q_{m} }} $$
(7)

Equation 7 describes the relationship between the prototype discharge (Qp) and the model discharge (Qm), where the Froude number discharge ratio (Qr) is defined as the ratio of prototype discharge to model discharge. The fundamental factors influencing the hydraulics in this model research are inertial and gravitational forces, established using the Froude number (Fr) criterion for dynamic similitude. In undistorted models, the length-to-height ratio (Lr) is the same as the height-to-width ratio (Yr). The length ratio for this analysis was 85, and the discharge ratio was 66,611.2. This sectional model was divided into approximately seven bays to enable the study of flow behavior through partition walls. Consequently, our examination is based on calculations involving these seven bays throughout.

  • The barrage is 3,840 feet long, has 64 bays, and can discharge 1,200,000 cubic feet per second.

  • Discharge per unit length is 312.5 cubic feet per second.

  • Seven 420-foot-long bays from the prototype were chosen for modeling. According to discharge per unit length, seven 420-foot berths received 131,250 CFS. Model discharge and prototype discharge at a 1:85 scale ratio are 1.97 CFS and 131,250 CFS, respectively.

2.4 Model layout

After drawing a baseline in the model tray, all dimensions were gathered according to barrage layout plans. The division wall, head regulators of both canals (Ghotki and Rainee), and main weir were modeled in white lime [61].

Based on the collected data, a benchmark was selected, and dumpy levels were employed to integrate bed, crest, and pier top levels. The benchmark was designed with minimal cut and fill to minimize human error and reduce labor costs. The dimensions of the river reach, and all other structural components of the barrage section were scaled down with a ratio of 85 to determine the model dimensions. The derivation of the model dimensions is presented in Table 3, and the model layout is depicted in Fig. 2.

Table 3 Derivation of model dimensions
Full size table

The turbine supplied the necessary water for the model. A 1.5-foot-long, sharp-crested weir was erected at the model's entrance, and v-notches (60 degrees) were positioned at the end of both canals to measure the flow of water entering the model. The following is the formula for determining discharge against the head based on a v-notch of 60 degrees. Equation 8 of the v-notch discharge equation was utilized to quantify electrical currents.

$$ Q = k\,tan\left( {0.5{\upalpha }} \right)h^{2.5} $$
(8)

Here, “Q,” “h,” “k,” and “\({\upalpha }\)” represent the discharge, head, head correction factor, and angle of v-notch (60\(^\circ\)) respectively.

3 Results

Five tests were carried out to analyze the impact of the remodeled divide wall on the flow. For each divide wall gap, discharge and velocity measurements are made at Ghotki and Rainee Canal for river flows of 100,000, 200,000, 300,000, 400,000, and 500,000 CFS. The design discharge capacity of the Ghotki Canal is 14,000 CFS, and the Rainee Canal is 10,000 CFS. The results obtained are discussed below.

3.1 Influence of river flow on the discharge of off-taking canals

Different test scenarios with varied divide wall openings are shown in Fig. 3, discussing them one by one.

Fig. 3
figure 3

(Right) five test scenarios with different divide wall openings; (middle) modeled canal discharges against the river flows; (left) test scenarios results without divide wall opening; *green and red colors are added in water to show the flow directions

Full size image

3.1.1 Test-1

For a divide wall gap of 166.7 ft, the pond level is consistently maintained at 256 ft. Notably, in the Ghotki canal, a direct correlation is observed between increasing river flow rates and canal discharge, culminating in the attainment of 93.3% of the design capacity at 500,000 CFS. Conversely, the Rainee canal demonstrates a lower utilization, with only 53% of the design discharge capacity achieved at 100,000 CFS river inflow. However, as the river flow increases to 200,000 CFS, the discharge in the Rainee Canal escalates to 98% of the design capacity and maintains this level for higher river discharges. These insights are graphically depicted in Table 4. Also, the flow velocity in the gap varies, going from 1.21 fps at 100,000 CFS to 2.45 fps at 500,000 CFS, respectively. Illustrated in Fig. 3, scenario 1, the off-taking discharge and velocity fluctuations are visually represented as a bar chart, offering a clear view of the behavior of flows, particularly in the left pocket. Based on the findings of Test-1, it can be inferred that a 166.7 ft gap in the prototype's divide wall leads to a diversion of more river flow towards the head regulator of the Ghotki canal compared to the Rainee canal within the specified range of river flows.

Table 4 Flows and velocities recorded during Test 1
Full size table

3.1.2 Test-2

In Test-2, the divide wall gap is reduced to 127.5 ft, revealing in the Ghotki canal a direct correlation between increasing river flow rates and canal discharge, reaching a peak of 92.27% of the canal's discharge capacity at 500,000 CFS. However, the measured discharge in the Ghotki canal slightly lags behind that of Test-1 across all river flow rates, indicating a proportional reduction in flow as the gap narrows. Conversely, the Rainee canal achieves full supply discharge at 300,000 CFS, suggesting a minimal impact on discharge with a decreased divide wall gap. Flow velocity within the gap experiences a corresponding uptick with escalating river discharge, spanning from 1.27 to 2.60 ft/s. Figure 3, scenario 2 vividly delineates the altered flow patterns within the left pocket, notably intensifying flow velocity as the gap diminishes, yet maintaining a significant portion of the flow trajectory towards the head regulator of the Ghotki canal. This shift in flow behavior is notably more pronounced in Test-2 compared to prior iterations, as corroborated by the findings summarized in Table 5.

Table 5 Flows and velocities recorded during test-2
Full size table

3.1.3 Test-3

The reduction of the divide wall gap to 90.5 feet is a significant adjustment in Test-3, highlighted in Table 6, which presents data on flows and velocity. Observations reveal that higher river flows lead to increased water release from the Ghotki canal, with discharge reaching 12,728 CFS at a flow of 500,000 CFS, representing 90.91% of the design discharge. Interestingly, the modification in gap width has minimal impact on the Rainee Canal's discharge, as it consistently receives its design discharge at river flow rates of 300,000 CFS or higher. The flow velocity across this dividing wall gap varies from 1.33 feet per second to 2.81 feet per second. Figure 3 provides a visual representation of the off-taking discharge and resulting velocity variations through a bar chart, while Fig. 3, scenario 3, offers clarity on flow patterns within the left pocket. Notably, the figures illustrate a significant shift in flow dynamics as the gap narrows. Despite the heightened speed, the majority of the gap's flow continues to be directed into the Ghotki canal's head regulator. Moreover, the flow behavior undergoes more sudden changes in this test compared to the preceding ones.

Table 6 Flows and velocities recorded during Test 3
Full size table

3.1.4 Test-4

In this scenario, the gap between the walls is precisely 53.5 feet, a key parameter examined in Test-4, as delineated in Table 7 showcasing the flow and velocity data. Consistent with prior experiments, higher river flow rates lead to increased discharge from the Ghotki Canal. Specifically, at a flow of 500,000 CFS, discharge was measured at 12,562 CFS, amounting to 89.72% of the design discharge, or 10.27% below the intended capacity. Interestingly, despite the narrowing of the split wall gap, the outflow from the Rainee Canal remains unaffected. Notably, at a river flow rate of 300,000 CFS, the Rainee Canal resumed receiving its intended discharge, a trend consistent with previous testing. The total velocity range between the divide wall gap is from 1.42 to 2.87 ft/s across flow rates ranging from 100,000 CFS to 500,000 CFS. Figure 3 provides a graphical representation of the off-taking discharge outcomes and resultant velocity variations through a bar chart, while Fig. 3, scenario 4, offers a clear visualization of flow patterns within the left pocket. With a divide wall gap of 53.5 feet in the prototype, the tracer concentration reveals a diversion of more river flows towards the head regulator of the Ghotki Canal. This observation underscores that the Ghotki Canal draws more flows than the Rainee Canal within the specified range of river flows.

Table 7 Flows and velocities recorded during Test 4
Full size table

3.1.5 Test-5

In Test 5, the divide wall is fully closed, resulting in no gap present. An overview of the flow and velocity data collected for this experiment is shown in Table 8. Notably, at a river flow of 500,000 cubic feet per second (CFS), the Ghotki canal registers a discharge of 12,375 CFS, equivalent to 88.40% of the design discharge capacity, indicating the absence of a gap in the system. Initially, the discharge of the Rainee Canal rises in proportion to the river flow rate. Still, it stabilizes at 9,998 CFS once the river flow exceeds 200,000 CFS, slightly below the design discharge of 10,000 CFS. Owing to the lack of separation in the divide wall, no velocities could be determined during this experiment. Figure 3, scenario 5, illustrates the outcomes of the off-taking discharges via a bar chart while also providing a visual depiction of flow patterns within the left pocket. Despite the absence of a gap, there is no discernible effect on flow behavior, as evidenced by the consistent tracer color distribution. Notably, the Rainee Canal receives its maximum design discharge due to most water being directed towards it, while the Ghotki Canal receives less than its full supply discharge (14,000 CFS).

Table 8 Flows and velocities recorded during test 5
Full size table

3.2 Influence of gap in the divider wall

The results of the experiments elaborate the following observations:

  • The Rainee Canal consistently achieves its maximum supply discharge of 300,000 CFS, showcasing resilience to fluctuations in river flow. Analysis across the five tests, ranging from Test-1 (166.7 ft gap) to Test-5 (no gap), reveals a gradual decrease in discharge from 93 to 88% at 500,000 CFS and from 90.5 to 84.9% at 400,000 CFS. Comparably, at 300,000 CFS, the discharge drops to 83.1% from 87.3%, and at 200,000 CFS, it drops to 82.8% from 83.9%. At the lowest threshold of 100,000 CFS, the discharge ranges from 39 to 38%.

  • The narrowing gap between the walls corresponds to increased flow velocity within the gap. Velocity varies from 1.21 to 1.42 ft/s (Test-1 to Test-4) at 100,000 CFS and 1.36 ft/s to 1.54 ft/s at 200,000 CFS. The velocity difference between Test-1 and Test-4 is 0.21 feet per second at 300,000 CFS and 2.12 feet per second to 2.51 feet per second at 400,000 CFS. At the highest flow of 500,000 CFS, velocity ranges from 2.45 to 2.87 ft/s, indicating a consistent increase in speed with each test.

  • Fig. 3 illustrates the relationship between the Ghotki Canal's discharge and the gap width at various river levels. A smaller gap correlates with reduced Ghotki Canal discharge, while the canal's output aligns with river volume.

Additionally, Fig. 3 demonstrates that narrowing the gap increases discharge from the Rainee Canal. At 300,000 CFS, the Rainee Canal attains its full discharge capacity, indicating minimal impact from the divide wall gap on its discharge behavior.

4 Discussion

This research experimentally examined the effect of divide wall geometry on flow behavior. A non-distorted model was created to demonstrate how the shape of the divide wall influences flow patterns. Based on the experimental data, several important conclusions were drawn. The methodological framework employed in this study can be applied to similar hydraulic structure and flow analysis scenarios worldwide, and the physical model presented can be adapted to local conditions.

The experiments' findings provide valuable insights into the hydraulic behavior of the Rainee Canal and the influence of the divide wall gap on flow dynamics within the canal system. The results of this study contribute to a better understanding of the complex interactions between hydraulic infrastructure, river dynamics, and water resource management. By highlighting the influence of divide wall gap width on flow regimes and canal performance, this research informs decision-making processes to optimize water allocation and sustain agricultural livelihoods in Sindh Province, Pakistan. One of the notable findings is the significant impact of the divide wall gap on flow regimes within the canal system. The reduction in inflow to the Ghotki Canal due to the extended divide wall has led to a substantial gap between the original and extended segments, exacerbating the challenges this vital irrigation infrastructure faces. This disruption in flow regimes has cascading effects, particularly on critical components such as the silt excluder and left pocket capacity, highlighting the interconnectedness of various elements within the hydraulic system. The experimental approach employed in this study, utilizing a non-distorted physical model at a scale ratio of 1:85, provides valuable insights into the hydraulic behavior of the canal system under different scenarios. The study effectively captures the range of conditions that influence canal performance by varying the width of the divide wall gap and simulating different river flow rates. This comprehensive analysis enables a nuanced understanding of the factors contributing to the observed outcomes, facilitating informed decision-making in infrastructure planning and management. These findings significantly affect the region's water resource management and infrastructure planning. The observed impacts of divide wall modifications on flow dynamics highlight the need for careful assessment and design considerations to ensure the optimal performance of hydraulic structures. Furthermore, the resilience of the Rainee Canal provides valuable insights into canal system management and underscores the importance of adaptive strategies in mitigating the effects of variability in river flow. Investigating the influence of divide wall extension and gap width on water flow dynamics at Guddu Barrage provided valuable insights. Results highlighted a clear relationship between gap width and the discharge capacity of the Ghotki Canal, with wider gaps favoring increased water flow towards the head regulator. In comparison, narrower gaps promoted a more balanced distribution. Conversely, the Rainee Canal displayed consistent discharge patterns across various gap widths, exhibiting minimal sensitivity to divide wall configurations. Notably, flow velocity across the gap intensified with higher river flow rates and narrower gaps, indicating heightened flow dynamics. Conducted with a non-distorted physical model at a scale ratio of 1:85, the study ensured hydraulic similarities to real-world conditions. These findings have practical implications, emphasizing the importance of optimizing divide wall geometry for maximizing canal discharge capacities and efficient water management.

Previous research works are also discussed here to place the findings in the broader context of existing literature, highlighting the consistencies and discrepancies and providing a comprehensive perspective on how the current study’s results fit within the broader scientific discourse. A study by [61] proposed a methodology for the unmeasured offtake and flowing discharge estimation along the open-canal Canale Emiliano Romagnolo (CER), a major irrigation infrastructure in Northern Italy. The “multi-disciplinary approach” adopted refers to agronomic and hydraulic aspects, and satisfactory results were obtained using the modeling techniques. A similar study by [62] critically reviewed the judiciousness of two model studies in which feasibility consultants proposed a subsidiary weir to rehabilitate and modernize Jinnah Barrage at the Irrigation Research Institute (IRI), Pakistan. Some other research works, i.e., [63, 64], have also discussed the importance of divide walls and marginal bunds along the barrages on the Indus River. According to [65] 66, the policy recommendations include periodic monitoring and assessment of divide wall conditions to enhance flow distribution within barrages. In a study, [67] constructed a physical model in a test flume to check the Smoothed Particle Hydrodynamics (SPH) outcomes exhibiting large dispersion for instantaneous water height values. In another study, a movable bed physical model was constructed by [68] to investigate hydraulic de-siltation by flushing and lateral erosion in the Tapu reservoir, Taiwan; their results showed that the total cumulative flushed sediment volume by physical modeling was close to that of numerical simulation. In another study by [69], the construction of the cofferdams changed the hydraulic behavior of water flowing over the ogee spillway, which was investigated using a physical model and numerical simulations. These studies highlighted the significance of the results assessed by the physical modeling. Besides this, some other researchers, i.e., [70,71,72] used a hydraulic simulation model developed for steady and unsteady flow simulation in irrigation canal networks. The model used the implicit four-point Preissmann scheme to discretize the Saint–Venant equations and solved the resulting equations using the sparse matrix solution technique, emphasizing the suitability of the results obtained by the physical modeling. In short, the study, comprising the experimentation and physical modeling, underscores the pivotal role of divide walls in regulating water flow, informing strategies for sustainable agricultural practices and regional development in water-scarce regions like Sindh Province, Pakistan.

5 Conclusions

The analysis of flow velocity within the divide wall gap revealed a clear relationship between gap width and flow velocity. As the gap narrowed, flow velocity increased, indicating a concentration of flow through a smaller space. This phenomenon became more pronounced at higher river flow rates, emphasizing the sensitivity of flow dynamics to structural modifications. The consistent increase in velocity with each test underscores the importance of gap width in regulating flow dynamics and highlights the need for careful design considerations in hydraulic infrastructure projects. The model results reveal that the gap in the dividing wall disrupts flow behavior in the left pocket. The Ghotki Canal cannot draw its full capacity discharge due to a 166.7 ft gap in the dividing wall, while the Rainee Canal can. Reducing the gap width diminishes the discharge capacity of the Ghotki Canal, whereas the Rainee Canal head regulator receives full capacity. When there is no gap, the Ghotki Canal head regulator draws 88% of the specified capacity, while the Rainee Canal head regulator draws full capacity. The observed impacts of divide wall modifications on flow regimes have significant implications for water resource management and infrastructure planning in the region. Changes in gap width directly influenced water distribution between canals, highlighting the interconnectedness of hydraulic infrastructure with natural water sources. Balancing hydraulic infrastructure with environmental considerations is crucial for optimizing water allocation and sustaining agricultural livelihoods in Sindh Province. The resilience of the Rainee Canal underscores the importance of adaptive strategies in mitigating the effects of variability in river flow. To minimize the impact on river flow behavior in the left pocket and enhance the performance of silt excluders, it is advisable to eliminate the gap in the divide wall. Lowering the crest level of the Ghotki canal is suggested to accommodate the discharge deficiency in the canal. By understanding the complex interactions between hydraulic infrastructure and river dynamics, decision-makers can develop informed strategies to optimize water allocation and minimize the potential disruptions caused by structural modifications. Adaptive management approaches are essential for ensuring the long-term sustainability of water resource systems in the face of changing environmental conditions. The research was performed in the laboratory to analyze the hydraulic model. Future research may explore innovative divide wall designs to improve water resource utilization efficiency.