Influence of synthesis route on structural properties of SnFe₂O₄ spinel phase via methods of co-precipitation, sol–gel and solvothermal: morphology, phase analysis, crystallite size and lattice strain

Abstract

In this study, regarding to the wide applications of spinel ferrites in various fields such as Li ion-batteries, photocatalysts, and optoelectronics, the structural and morphological properties of tin ferrite oxide (SnFe₂O₄) nanoparticles are investigated using X-ray diffraction (XRD) analysis and field emission scanning electron microscopy (FESEM). The sol–gel, solvothermal, and co-precipitation methods were used to synthesize the SnFe₂O₄ nanoparticles, and the effect of annealing temperatures at T = 350 °C, 450 °C, and 550 °C was investigated. The XRD results confirmed the formation of tin ferrite spinel phase at an annealing temperature of 350 °C with a preferred peak (311). Crystallite size (D) and strain (ε) of SnFe₂O₄ nanoparticles was determined in region 20–45 nm and 2–4 × 10^–4, respectively, using the Scherer, Williamson–Hall, and Rietveld computational methods. The results showed that the crystallite size in the samples increased with increasing annealing temperature. This increase is attributed to the reduction of defects, imperfections and lattice strain, which leading to an increase in the lattice constants and unit cell volume in the nanocrystalline structure. The Rietveld method determine smaller crystal sizes compared to the Williamson–Hall and Scherer methods because it can correct for peak broadening by taking into account all instrumental factors. The FESEM images of the synthesized nanostructures of SnFe₂O₄ showed cubic and polyhedral grains with cluster growth and an average grain size of 50–80 nm. According to the crystal structure of tin ferrite spinel, the cubic morphology confirmed the formation of this structure. The average crystallite size and grains in the synthesized samples was determined using X-ray diffraction (XRD) and field emission scanning electron microscopy (FESEM) analysis, respectively. The formation conditions of the SnFe₂O₄ spinel phase and other phases in the synthesis process at different temperatures and dependence of structural parameters was studied by various structural models for the samples.

Article Highlights

• The structural and morphological properties of SnFe₂O₄ spinel structure were investigated.

• Influence of synthesis route and annealing temperatures at T = 350 °C, 450 °C, and 550 °C was investigated.

• The Scherer, Williamson–Hall, and Rietveld computational methods were used for structural analysis.

1 Introduction

The ferrite phase is a compound of the iron oxide and metal oxides. These oxides are both non-conductive and ferromagnetic, which means they are easily magnetized or attracted to a magnet. Magnets are classified as hard or soft based on their magnetic coercivity, with hard ferrites having high coercivity and soft ferrites having low coercivity [1]. Ferrites are also classified according to their crystal structure, with types including garnet, spinel, orthoferrite, and hexagonal ferrites. Ferrites are similar to ceramic materials in that they are hard, brittle, and poor conductors. Most ferrites have structural sites such as dodecahedral (c sites), tetrahedral, and octahedral sites. Spinel ferrites are a type of material that is inexpensive, very stable, and does not easily lose its magnetic properties. This makes them suitable for use in a wide range of applications [2]. Spinel ferrite has the general formula AB₂O₄ and a cubic structure. In this structure, 8 ions of A occupy tetrahedral sites and 16 ions of B occupy octahedral sites. Based on the distribution of cations in the sublattices, there are three normal, reversed and mixed spinel structures that affect the properties of nanomaterials [3]. Tin-doped hematite (α-Sn_xFe_2−xO₃) is of considerable interest because of its potential applications in energy storage and other areas. The structure of tin-doped hematite involves the integration of Sn⁴⁺ ions into the crystalline structure of hematite. This is achieved by substitution of octahedrally coordinated Fe³⁺ ions with significantly larger Sn⁴⁺ ions. This substitution leads to an expansion of the unit cell [4]. The doping process significantly affected the electronic properties of tin-doped hematite. The incorporation of tin into the hematite structure played a critical role in facilitating efficient ion transport and enhancing conductivity. This promotes favourable conditions for various electrochemical reactions [5]. The compound Fe_1.727Sn_0.205O₃, also known as tin-doped hematite, has been studied for its unique electrical, chemical, and optical properties and potential applications [6].

Sarkar and her team have published research papers detailing the creation and analysis of various ferrite compounds. These compounds include Y-doped cobalt ferrite [7], perovskite BiFeO₃ ferrite [8], sodium doped magnesium nanoferrite [9], zinc ferrite [10], cobalt doped bismuth ferrite [11] and nickel-doped ferrite [12]. The researchers investigated how impurities can enhance the optical, magnetic, and structural properties of ferrite nanoparticles. These studies were conducted to explore potential applications such as photoelectrochemical cells. In our previous research, tin ferrite oxide nanoparticles (Fe_1.42Sn_0.435O₃) were synthesized by the co-precipitation method [13, 14]. We investigated the structural, optical, surface morphology and electrochemical properties of these synthesized samples. The band gap of the material was found to be in the range of E_g = 1.96–2.58 eV. In the electrochemical analysis, the specific capacitance was measured in the range of SC = 477–822 F g⁻¹. These results suggest that this nanostructure could potentially be used in the anode electrode of energy storage systems.

In this study, tin ferrite oxide nanoparticles were synthesized by sol–gel, solvothermal and co-precipitation methods. Then, the samples were annealed at T = 350 °C, 450 °C, and 550 °C. The effect of the synthesis method on the formation of different phases of tin ferrite oxide nanoparticles such as SnFe₂O₄, Fe_1.42Sn_0.435O₃, and Fe_1.727Sn_0.205O₃, were investigated. The structural and morphological properties of the synthesized nanoparticles were investigated by XRD and FESEM analyses.

The aim of this research is study of the optimum temperature for annealing and to developing a simple and efficient method for the preparation of SnFe₂O₄ nanoparticles with spinel structure. These nanoparticles have unique surface morphology and structural properties that make them suitable for use in optoelectronics, photocatalysts, and lithium battery electrodes.

2 Experimental details

2.1 Materials

FeCl₃.6H₂O (98%), SnCl₂.2H₂O (99.8%), NaOH (98%), NaBH₄ (99%), Ethylene glycol (99.5%), Citric acid (99%), and Sodium acetate (99%) were bought from Merck Chemical company, and Deionized water (DW) was produced using the deionizer machine at Nab-Mell company.

2.2 Preparation of iron tin oxide nanoparticles

Three methods were used for synthesize of the tin ferrite oxide nanoparticles which have attracted the most interest from others and are described in the following sections.

2.2.1 Sol–gel method

A homogeneous solution was prepared by dissolving 4.79 g iron chloride (FeCl₃·6H₂O) and 2 g tin chloride (SnCl₂·2H₂O) in 50 ml deionized water (DW) using a magnetic stirrer. Next, 2.49 g ethylene glycol and 7.70 g citric acid were dissolved in 50 ml DW. This solution was then slowly added to the homogeneous solution. The pH of the solution is 1.74. Next, the final solution was poured into a one-hole balloon and refluxed at 120 °C for 6 h. The pH of the solution at this stage was 1.58. The solution at this stage was clear and yellow. The solution was then heated to 85 °C in an oil bath. The color of the solution changed to dark green. The gel was then dried in an oven at 120 °C for 6 h. The synthesized nanoparticles were annealed at 350 °C (SFO1), 450 °C (SFO2) and 550 °C (SFO3) to study the effect of annealing temperature.

The optimum annealing temperature for the formation of tin ferrite oxide (SnFe₂O₄) structure is T = 350 °C, therefore, in this study we investigated the temperatures of T = 350, 450 °C and 550 °C to ensure this phase. At higher temperatures (> 550 °C), the single-phase composition of tin ferrite transforms into other phases such as SnO₂ and Fe₂O₃.

2.2.2 Solvothermal method

2 g of tin chloride (SnCl₂·2H₂O) and 4.79 g of iron chloride (FeCl₃·6H₂O) were dissolved in 50 ml of ethylene glycol (EG), then 2.88 g of sodium acetate (NaAC) was slowly added to the mixture and stirred vigorously for 1 h. The pH of the solution was measured to be 1.35. The base solution was then poured into a 150 ml reflux and placed in an oil bath at 170 °C for 24 h. The solution was poured into a beaker and placed in an oven at T = 190 °C for 6 h. The resulting compounds were collected after solvent removal and drying. The synthesized nanoparticles were annealed at T = 350 °C (SFO4), 450 °C (SFO5), and 550 °C (SFO6) to study the effect of annealing temperature.

2.2.3 Co-precipitation method

In this method, two reducing agents were used.

2.2.3.1 NaOH as reducing agent

2 g of tin chloride(SnCl₂·2H₂O), together with 4.79 g of iron chloride(FeCl₃·6H₂O) were dissolved in 100 mL of alcohol and stirred for 30 min. The pH of the solution was measured to be 1.04. Then, 70 ml of 1 M sodium hydroxide solution was slowly added to the solution and the pH of the solution was measured to be 10.27. The precipitates formed were then separated by filtration. The precipitates were centrifuged to separate the salts and reaction impurities. The collected precipitate was then dried in an oven at 80 °C for 12 h. The synthesized nanoparticles were annealed at T = 350 °C (SFO7) and T = 550 °C (SFO8) to investigate the effect of annealing temperature.

2.2.3.2 NaBH₄ as the reducing agent

2 g of tin chloride (SnCl₂·2H₂O) and 4.79 g of iron chloride (FeCl₃·6H₂O) were dissolved in 50 mL of DW. The pH of the solution was measured to be 0.98. Then 70 mL of 0.4 molar sodium borohydride solution was added dropwise and the pH of the solution was measured to be 8.70. The mixture was stirred for 2 h. The solution was filtered and the precipitates obtained were washed 10 times with water and alcohol. The solution was centrifuged for 15 min to remove impurities. The collected precipitate was then dried in an oven at T = 80 °C for 12 h. The synthesized nanoparticles were annealed at T = 550 °C (SFO9) to study the effect of annealing temperature.

In Table 1 provides information on the sample name, annealing temperature, weight before and after crystallization, and relative weight loss (Δw). The weight loss of the sample is due to the release of some reactive components from the compound in the form of gas. In Fig. 1, the steps of solution preparation and extraction of precipitates prepared by different synthesis methods are briefly shown. The performance and graphical route of the synthesis of iron tin oxide nanoparticles are shown in Fig. 2.

Table 1 The name of the samples, the calcination temperature, the weight before and after recrystallization, and the relative weight loss (Δw)

Fig. 1

Steps of preparation of solutions and tin ferrite oxide nanoparticles synthesized by sol–gel, hydrothermal and co-precipitation methods

Fig. 2

Schematic diagram of the synthesis route of tin ferrite nanoparticles

3 Characterization techniques

The X-ray diffraction (XRD) patterns were recorded by Bruker D8 Advance X-Ray diffractometer with a Cu K_α anode (λ = 1.5405 Å) operating at 40 kV and 30 mA. The diffraction angular range was measured from 10° to 80° (2θ). Field-emission electron microscopy (FESEM) model: MIRA3-TESCAN was used to analyze the morphology of the nanoparticles. The qualitative elemental analysis was conducted using an Energy Dispersive X-ray (EDX) plug in a Field Emission Scanning Electron Microscope (FESEM). During this analysis, an accelerating voltage of 20 (keV) and a beam current of 10 (nA) were used. The analysis focused on a silicon crystal and a gold coating.

4 Results and discussion

4.1 Structural properties

X-ray diffraction (XRD) analysis provides important information such as crystal phases and composition, structural properties such as crystallite size, lattice parameters, distance between crystal planes, intensity of the preferred peak, and strategy for Optimum synthesis parameters including annealing temperature. To determine the crystallite size, we use the Scherrer equation [14]:

$$ D = \frac{k\lambda }{{\beta \cos \theta }} $$

(1)

In this relationship, D is the crystallite size, λ is the X-ray wavelength (λ = 1.5405 Å), K = 0.98 is the shape constant, β is the full width at half maximum (FWHM) of the peak, and θ is the diffraction angle.

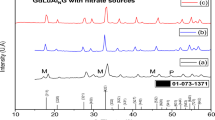
The X-ray diffraction (XRD) pattern of tin ferrite oxide nanoparticles prepared by different synthesis methods is shown in Fig. 3. In this section, we will study the different phases that are synthesized such as SnFe₂O₄, Fe_1.42Sn_0.435O₃, and Fe_1.727Sn_0.205O₃ using the sol–gel, solvothermal, and co-precipitation methods at temperatures of T = 350 °C, T = 450 °C, and T = 550 °C.

Fig. 3

The X-ray diffraction (XRD) of tin ferrite oxide nanoparticles: a SFO1, b SFO2, c SFO3, d SFO4, e SFO5, f SFO6, g SFO7, h SFO8, i SFO9, annealed at T = 350 °C, T = 450 °C and T = 550 °C, respectively, in comparison with XRD pattern related the JCPDS reference card of SnFe₂O₄ compound

4.1.1 Formation of SnFe₂O₄ phase

Based on the X-ray diffraction pattern data shown in Fig. 3a (SFO1), Fig. 3d (SFO4), and Fig. 3g (SFO7), it can be concluded that tin ferrite nanoparticles with the chemical formula SnFe₂O₄ have been formed. This compound was synthesized by sol–gel, sol-thermal, and co-precipitation methods and annealed at a temperature of T = 350 °C. According to the information in the JCSP database and the presence of the tin element in the reaction, we expect that the XRD analysis will show the composition of SnFe₂O₄. On the other hand, according to the information obtained from the XRD analysis, the peaks of the diagram correspond to the peaks of the JCSP reference card No. 00-011-0614 related to the Fe₃O₄ phase. According to studies and their declared references, the place of formation of peaks of SnFe₂O₄ composition is close to Fe₃O₄ composition with a very small deviation. To put it differently, SnFe₂O₄ is synthesized by substituting Sn²⁺ for Fe²⁺ in FeFe₂O₄ spinel lattice. The difference in the peaks is due to the fact that Sn²⁺ has a larger ionic radius (118 pm) than Fe²⁺ (70 pm) [15]. The crystal structure of SnFe₂O₄ is spinel with an Fd$\overline{3}$m space group [16].

The lattice parameters of SnFe₂O₄ are a = b = c = 8.38 Å. The unit cell volume is V = 592.7ų. The bond lengths in SnFe₂O₄ are Fe–O = 1.95 Å and Sn–O = 2.12 Å [17].

The process used to create SnFe₂O₄ goes like this [18].

$$ {\text{SnCl}}_{2} \cdot {\text{2H}}_{2} {\text{O }} + {\text{ 2 FeCl}}_{3} \cdot {\text{6H}}_{2} {\text{O }} + {\text{ 8 NaOH}} \to {\text{SnFe}}_{2} {\text{O}}_{4} + {\text{ 8 NaCl }} + {\text{ 18 H}}_{2} {\text{O}} $$

(2)

Based on the reported potentiometric titration curve [19], The regions in which the formation of the compound structure has been identified are determined by the changes in pH. The first zone corresponds to a pH range of (1.18–1.80), indicating that OH-ions are consumed by solutions of iron chloride and tin chloride. The second zone corresponds to a pH range of (1.81–2.11), indicating a high consumption of OH-ions. In this range, larger clusters called "embryos" are formed as a result of mass collisions. In the third region (pH 2.12–11.90), as the pH increases, the growth rate of the clusters decreases and fewer hydroxide ions are consumed. This means that in this particular range, embryos were observed to grow steadily and nuclei were formed. The solution is saturated in this region. The fourth zone is associated with a high pH (11.91–13.22), indicating a high consumption of OH⁻ ions. The solution is supersaturated in this range. The chemical process that took place during the formation of the compound is described as follows. The highest intensity peak occurs at 2θ = 35.55° with the Miller index (311).

$$ {\text{Sn}}^{{4} + } + {\text{Fe}}^{{2} + } + {\text{Fe}}^{{3} + } + {\text{9OH}}^- \to {\text{ Sn}}\left( {{\text{OH}}} \right)_{4} \downarrow + {\text{Fe}}\left( {{\text{OH}}} \right)_{2} \downarrow + {\text{Fe}}\left( {{\text{OH}}} \right)_{3} \downarrow $$

(3)

4.1.2 Formation of α-Fe₂O₃ and SnO₂ phases

Based on the information obtained from the X-ray diffraction (XRD) pattern shown in Fig. 3b (SFO2), and Fig. 3e (SFO5), it can be concluded that the crystal structures of Fe₂O₃ and SnO₂ metal oxide compounds have been obtained. These samples were synthesized by sol-sol and solvothermal methods and then subjected to annealing at T = 450 °C.

Based on the information obtained from the XRD analysis, the peaks observed with JCSP reference card number 00-003-1114 correspond to the SnO₂phase, while the peaks observed with JCSP reference card number 00-033-0664 correspond to the α-Fe₂O₃ phase.

This pattern illustrates that Fe and Sn have absorbed oxygen from the environment as a result of the annealing temperature, resulting in the formation of iron oxide (magnetite) and tin dioxide. On the other hand, chlorine reacts with sodium from NaOH to form NaCl, which is removed from the structure during the process of synthesis and washing of sediments. The compound α-Fe₂O₃has a rhombohedral crystal structure with a space group of (R-3C) and a space group number of 167. The angles within the crystal structure are α = β = 90° and γ = 120°, and the lattice sides have dimensions of a = b = 5.0356 Å and C = 13.7489 Å. The structure of hematite (Fe₂O₃) is determined by observing the intensity of peaks and the characteristics of specific d-values. In this case, the d-values 3.68 (D₀₁₂), 2.70 (D₁₀₄), 3.56 (D₁₁₀), 2.20 (D₁₁₃), 1.84 (D₀₂₄), 1.69 (D₁₁₆), 1.48 (D₂₁₄) and 1.45 (D₃₀₀) correspond to a rhombohedral medium crystalline structure of α-Fe₂O₃. This means that the composition of hematite can be identified based on these specific d-values and the intensity of the peaks in the structure [20]. Also, by increasing the annealing temperature between T = 450 and T = 550, the possibility of forming independent phases of tin oxide and iron oxide increases, as shown in Table 2.

Table 2 The crystallite size of tin ferrite nanoparticles from X-ray Diffraction (XRD) characterization according to Scherer's relation with a maximum relative uncertainty up to 5%

The compound SnO₂ has a tetragonal structure. In this phase, the angles between the lattice sides are all equal, with a value of 90° (α = β = γ = 90°). The lengths of the lattice sides are measured as a = 4.7455 Å, b = 4.7355 Å, and c = 3.1850 Å.

4.1.3 Formation of tin ferrite oxide phases (Fe_1.727Sn_0.205O₃ and Fe_1.420Sn_0.435O₃)

Based on the X-ray diffraction (XRD) patterns shown in Fig. 3c (SFO3), Fig. 3f (SFO6), Fig. 3h (SFO8), and Fig. 3i (SFO9), the crystal is composed of Fe_1.727Sn_0.205O₃ and Fe_1.42Sn_0.435O₃/SnO₂ structures. These samples were synthesized by sol–gel, solvothermal and co-precipitation methods and then annealed at T = 550 °C. Based on the XRD analysis data, the peaks formed are related to the SnO₂ and Fe_1.727Sn_0.205O₃ phases and correspond to the JCSP reference cards with numbers 00-003-1114 and 01-088-0434, respectively.

These patterns illustrate that as the annealing temperature is increased, the tin element present in the reaction transforms into the structure of doped hematite and tin ferrite oxide with the chemical formula Fe_1.727Sn_0.205O₃. The compound Fe_1.727Sn_0.205O₃ has a rhombohedral crystal structure with space group (R-3C) number 167. The lattice sides of this crystal structure are a = 5.0301 Å, b = 5.0301 Å and c = 13.775 Å, with angles α = β = 90° and γ = 120°. By increasing the annealing temperature, the strength of the X-ray diffraction peaks from the sample has increased and their width has decreased. This means that the higher peaks are a result of the sample becoming more crystalline. In Fig. 3c, the diffraction pattern of the sample shows that the (104) plane has the most intense peaks, indicating that the diffraction from this plane is most prominent. This is related to the presence of the iron tin oxide phase. For SFO8 compound in Fig. 3h, a specific reference map number (JCSP reference map number 01-088-0433) is associated with the Fe_1.42Sn_0.435O₃ phase. This association was determined by X-ray diffraction (XRD) analysis. This sample was synthesized by the co-precipitation method with NaOH reducing agent and then annealed at T = 550 °C. Tin ferrite oxide is a type of material that has a specific arrangement of atoms called a rhombohedral crystal structure. This structure is described by a number of measurements, including the length of the sides of the crystal lattice (a, b, and c) and the angles between them. In this case, the lattice sides are a = b = 5.0880 Å and c = 13.8420 Å, with angles of 90° between α and β, and 120° between γ and the other two sides. The space group number, which describes the symmetry of the crystal structure, is 167. The calculated density of this material is 5.74 (g/cm³), which means it is relatively dense. The unit cell volume, which is the amount of space occupied by a repeating unit of the crystal structure, is V = 310.33 (10⁶ pm³).

Figure 3i shows the X-ray diffraction (XRD) pattern of the SFO9 sample. This sample was synthesized by the co-precipitation method with Na(BH₄) as reducing agent and then annealed at T = 550 °C. The peaks in the graph correspond to the JCSP reference card number 01-088-0434, which is related to the Fe_1.727Sn_0.205O₃ phase according to the XRD analysis.

The chemical reaction that occurs after annealing to form iron tin oxide is as follows.

$$ {\text{xSn}}^{{2} + } + {\text{2xFe}}^{{3} + } + {\text{8OH}}^- \to {\text{ Sn}}_{{1} - {\text{x}}} {\text{Fe}}_{{2} - {\text{x}}} {\text{O}}_{{4} - {\text{X}}} + {\text{4H}}_{2} {\text{O }}\left( {0 \, < {\text{ x}} < { 1}} \right) $$

(4)

The different methods were used to measure the size of the crystallites in the synthesized samples. The first method was to use Scherer's equation to calculate the size of the crystallites.

4.2 Structural identification methods

4.2.1 Scherrer method

In Scherer's relation (Eq. 1), the crystallite size refers to the average of the cube root of the volume of the individual crystals.

Table 2 shows the structural parameters calculated from X-ray diffraction (XRD) data along the preferred peak of the synthesized samples. In addition, the size of the crystallites was determined using Scherer's equation and included in the Table 2.

During the synthesis steps, the size of the crystallites within them is increased with the temperature at which they were annealed. After, thermal annealing, the surface of the crystals that was originally in contact with the vapor phase is transformed by diffusion into a solid–solid interface. This transformation helps to reduce the overall surface energy of the crystals, which in turn causes the volume of the crystals to expand [21]. The increase in crystal size can be attributed to the decrease in imperfections and flaws in the crystal structure, which is a result of the increase in network parameters and the increase in the unit cell in the nanostructured crystal. Conversely, the decrease in irregularities in the crystal structure due to rapid grain growth can lead to an increase in the size of the crystal [22, 23]. Lattice strain in nanoparticles samples is the result of crystal defects and can be calculated using the following equation [23].

$$ \varepsilon \, = \frac{{\beta_{hkl} }}{4\tan \theta } $$

(5)

To calculate the lattice strain more accurately, the peak width parameter (b) should be corrected with iodine. According to sources, the full width at half maximum (FWHM) parameter can be obtained from the relationship $\beta^2 = \sqrt {{\beta_s^2 - \beta_{exp}^2 }}$ where β_s is the width of the standard sample and β_exp is the width of the measured sample.

4.2.2 Rietveld method

In Fig. 4, we can see the analysed plots of X-ray diffraction (XRD) data by Rietveld analysis performed using HighScore Plus software. In these plots, the red lines represent the observed intensity (I_o) obtained from the XRD analysis, the blue lines correspond to the calculated intensity (I_c), and the green lines show difference between the experimental and calculated data (I_o − I_c). The accuracy of the experimental data is evaluated by calculating parameters such as the “goodness of fit” i.e., χ² and the R factors (R_p = profile factor, R_B = Bragg factor, and R_F = crystallographic factor). The parameters of R_p R_B, R_F, depend on the coordinate and position of ions. When, these parameters reach their minimum value, it indicates that the best fit to the experimental diffraction data has been achieved and the crystal structure is considered satisfactory. The occupancy of cations in the tetrahedral and octahedral interstitial sites is constrained to maintain the stoichiometric composition of the materials. The proposed cation occupancies in the two interstitial sites are determined by ensuring that the sum of the cationic distributions for the A site is one and for the B site is two. The initial model and atomic coordinates are obtained from existing literature sources. The pseudo-Voigt function is used to fit the background in the data. The X-ray diffraction (XRD) patterns after refinement show that the samples are single phase. Moreover, the broad peaks observed in the XRD patterns indicate that the crystallites in the samples are of small size. In Table 3, various R factors are provided for samples SFO1, SFO4 and SFO7. In the diffraction pattern of nanocrystalline materials, the presence of diffuse scattering is more pronounced compared to bulk crystalline materials. This is due to the high ratio of surface atoms to volume atoms in nanocrystalline materials. As the size of the material decreases to the nanoscale, diffuse scattering becomes more prominent while Bragg scattering, which is characteristic of well-defined crystal structures, decreases. This decrease in Bragg scattering leads to a reduction in the crystallinity of the material and contributes to the larger R factors observed in the diffraction pattern.

Fig. 4

The plots of X-ray diffraction (XRD) data by Rietveld analysis performed using the Xpert software for a SFO1, b SFO4 and c SFO7 annealed at T = 350 °C with SnFe₂O₄ spinel phase for observed (red), calculated (blue) and I_o − I_c (difference) (green)

Table 3 Structural parameters calculated by Rietveld method for synthesized samples of SFO1, SFO4 and SFO7 at T = 350 °C with SnFe₂O₄ composition phase

In Table 4, the lattice parameters and unit cell volumes for samples SFO1, SFO4, and SFO7 are given, along with any error (∆). Despite being subjected to the same annealing conditions, these samples have different lattice constants. This discrepancy in lattice constants suggests that the samples contain different distributions of cations.

Table 4 The various information related to the crystallite size of the synthesized samples has been calculated using three different methods (Scherer, UDM, UDEDM), as well as lattice constants, cell volume, and limits by the McMaille method. Additionally, X-ray density (dx), stress values, and the SSP plot method have been used in the calculation and plotting of crystallite size and lattice strain for the samples

The size of the crystalline structures in the synthesized samples (SFO1, SFO4, SFO7) was determined using the Rietveld method. It was observed that the size of the crystallites varied even when the samples were subjected to the same annealing temperature. The size of the crystals in a material is influenced by the relationship between the initial formation of nuclei and the subsequent growth of these nuclei. This relationship is strongly influenced by the method used to produce the material, as different synthesis routes can lead to different rates of formation of the crystalline structure known as spinel ferrite. Analysis of the crystallite size values in samples SFO1, SFO4 and SFO7 shows that when they were synthesized under the same annealing temperature conditions (T = 350 °C), sample SFO1 had larger crystallite sizes compared to SFO4 and SFO7. This suggests that in the SFO1 sample, the nucleation rate (initial crystal formation) is lower while the crystal growth rate is higher, resulting in a higher level of crystallinity. This result implies that the sol–gel method using citrate precursor helps in the formation of well-developed crystals by promoting proper crystal growth.

4.2.3 Williamson–Hall analysis

The Williamson–Hall method is another way to calculate the strain lattice size of crystallites. According to Scherer's relation, the broadening of peaks in XRD diagrams is due to the size of the grains. However, studies have shown that strain in the crystal lattice can also affect peak broadening. The Williamson–Hall proposed that the broadening of peaks in XRD diagrams is caused by the size of the crystallites and the strain in the lattice. According to the Williamson–Hall theory, the width of the peak at half maximum intensity is determined by the size of the particles and the strains in the lattice, as shown in the following equation [24].

$$ \beta_{{\text{hkl}}} = \, \beta_{{\text{Strain}}} + \, \beta_{\text{D}} $$

(6)

This equation includes two variables, β_Strain and β_D, which represent the amount of peak broadening due to two different factors. β_s represents the broadening due to strain in the lattice structure of the material, while β_D represents the broadening due to the size of the individual grains within the material.

The UDM Williamson–Hall relation is expressed by the following equation [25].

$$ \beta _{{{\text{hkl}}}} {\text{Cos}}\theta {\text{ }} = \frac{{K\lambda }}{{\text{D}}}~ + {\text{ 4}}\varepsilon {\text{ Sin}}\theta $$

(7)

The given equation represents UDM Williamson–Hall plots, which are used to extract information about the size and strain of a material. We can determine the size and strain by analysing the y-intercept and slope of the plot. When performing the plot analysis, the x-axis is (4Sin(θ)) and the y-axis is (βCos (θ)). In this context, UDM assumes that the strain is uniform in all directions. Lattice strain in nanocrystals is mainly caused by the expansion or contraction of the lattice due to size confinement. This is because the atomic arrangement is slightly different in nanocrystals compared to their larger counterparts. In addition, the size confinement also leads to the creation of defects in the lattice structure, which further contributes to the lattice strain. The positive slope in the graphs for samples SFO1, SFO2, SFO3, SFO4, and SFO8 indicates that the crystalline lattice is expanding. This expansion causes a stretching force within the nanocrystals, known as tensile strain. The tensile strain values were calculated from the slope of the graph and are 0.36 $\times$ 10^–3, 0.33 $\times 10^{ - 3}$, 0.28 $\times 10^{ - 3}$, 0.23 $\times 10^{ - 3}$ and 0.43 $\times 10^{ - 3}$ for these respective samples.The negative slope in the plots of the synthesized samples SFO5, SFO6, SFO7, and SFO9 indicates that the crystal lattice is contracting. This crystal lattice contraction leads to compressive strain in the nanocrystals.

Figure 5 shows the size of the crystalline particles in the samples synthesized by the UDM method.

Fig. 5

The Williamson–Hall diagram (UDM method) of tin ferrite oxide nanoparticles using the XRD analysis: a SFO1, b SFO4 and c SFO7 at T=350ºC with SnFe₂O₄ phase

On the other hand, the Williamson–Hall equation, which is used to analyse the properties of crystals, must be adjusted for anisotropic crystals. In this case, anisotropic strain is taken into account. This modified model is called the Uniform Stress Deformation Model (USDM), where the stress caused by lattice deformation is considered to be uniform in all directions of the lattice planes, although it contains a small amount of macrostrain. Hooke's Law describes the limits of stress and strain that a material can experience. It states that the strain in a material is directly proportional to the stress applied to it, and this relationship is presented as a linear function with E_hkl as the Young's modulus (σ = ε E_hkl), where σ is the stress and ε is the strain of the crystal. Stress refers to the force applied to a material, while strain refers to the resulting deformation or change in shape of the material.In the USDM system, the x-axis and y-axis are represented by the expressions $(\frac{{4{\text{Sin}}\theta }}{{E_{hkl} }})$ and (βCos(θ)), respectively.

The USDM takes into account the broadening of the X-ray diffraction peak caused by stress and the fact that the Young's modulus ($E_{hkl}$) varies in different directions [26].

$$ \beta_{hkl} = \left( {\frac{k\lambda }{D}} \right) + \left( {\frac{4\sigma \sin \theta }{{E_{hkl} }}} \right) $$

(8)

This method determined the value of D from the y-intercept and the value of stress (σ) from the slope. Figure 6 shows the size of the crystalline particles in the samples synthesized by the USDM method.

Fig. 6

The USDM method diagram of tin ferrite oxide nanoparticles using the XRD analysis: a SFO1, b SFO4 and c SFO7 at T=350ºC with SnFe₂O₄ phase

However, in real crystals, it is not accurate to assume that they are isotropic and that there is a linear relationship between stress and strain. This is because various defects, dislocations and agglomerates create imperfections in almost all crystals. Therefore, a different model is needed to study the different microstructures of crystals. In this context, the Uniform Deformation Energy Density Model (UDEDM) is used to account for the uniform anisotropic lattice strain in all crystallographic directions. This model considers the deformation energy density as the cause of the uniform anisotropic lattice strain.

Hooke's law states that the energy density (u) is related to strain to a specific mathematical relationship.

$$ u = \left( {\frac{{\varepsilon^2 E_{hkl} }}{2}} \right) $$

(9)

Stress (σ) and strain (ε) are related through the equation $\sigma = \varepsilon .E_{hkl}$.Therefore, the intrinsic strain can be expressed as a function of energy density.

$$ \varepsilon = \sigma .\sqrt {{\frac{2u}{{E_{hkl} }}}} $$

(10)

The term “E_hkl” refers to the anisotropic Young's modulus, which is a measure of the stiffness or resistance to deformation of a material in a specific direction. Anisotropic means that the material's properties, such as its Young's modulus, vary depending on the direction of the force applied. Putting the value ε in Eq. (6) and on re-arrangement we get [27],

$$ \beta_{hkl} = \left( {\frac{k\lambda }{D} } \right) + \left( {4\sin \theta \cdot \left( {\frac{2u}{{E_{hkl} }}} \right)^\frac{1}{2} } \right) $$

(11)

In the given statement, the slope of the β cosθ graph can be used as the x-axis, and (4sinθ/(E_hkl/2)^1/2) can be used as the y-axis to measure the energy density of the crystal. Additionally, the y-intercept can be used to measure the crystallite size. The UDEDM method assumes that the crystals are homogeneous and isotropic. However, it is noted that this assumption is not always true in many cases.

The statement means that the crystallite size for the synthesized samples was determined by measuring the interception of a straight-line drawn graphs, and the slope of the line graphs and the values of energy density synthesized samples. The specific values of energy density mentioned are 26.13, 27.44, 33.19, 28.39, 23.12, 50.84, 54.42, 69.37, and 38.20 k j m⁻³.

Figure 7 displays the size of the crystalline particles in the samples that were synthesized using the UDEDM method.

Fig. 7

The UDEDM method diagram of tin ferrite oxide nanoparticles using the XRD analysis: a SFO1, b SFO4 and c SFO7 at T=350ºC with SnFe₂O₄ phase

The Williamson–Hall method examines the broadening of peaks in X-ray diffraction as a function of the diffraction angle (2θ), which is assumed to be caused by both the size and strain of the crystalline material. However, there are other models that analyse the peak profile in XRD. One such method is the Size-Strain plot (SSP), which considers the XRD peak profile as a combination of a Lorentzian function and a Gaussian function. In this method, the size-broadened XRD profile is represented by a Lorentzian function, while the strain-broadened profile is represented by a Gaussian function.

The values for the lattice constants are determined by using the following mathematical formulas.

$$ \frac{1}{{d_{hkl}^2 }} = \left( {\frac{h^2 }{{a^2 }}} \right) + (\frac{k^2 }{{b^2 }}) + \left( {\frac{l^2 }{{c^2 }}} \right) $$

(12)

The connection between the size of a crystal, the amount of strain it experiences, and the expansion of its peak can be described as follows [28].

$$ (d_{hkl} \beta_{hkl} Cos\theta )^2 = \frac{k}{D} \left( { d_{hkl}^2 \beta_{hkl } Cos\theta } \right) + \left( {\frac{\varepsilon }{2}} \right)^2 $$

(13)

In this equation, the variables represent the following: k is the shape constant, d is the distance between the Bragg planes, β is the full width at half maximum (FWHM) of the peak and θ is the diffraction angle. The SSP plot is a graph that shows the relationship between (d²_hklβ_hklCosθ) on the x-axis and (d_hklβ_hklCosθ)² on the y-axis for different peaks in the XRD range from 2θ = 10°–80°. This graph can be used to determine the particle size by looking at the slope of the graph, and the amount of strain can be found by calculating the root of the intercept on the y-axis [29].

In Fig. 8, there are graphs that show how the lattice strain size was calculated for the synthesized samples. The lattice strain and crystal size can be determined by looking at the cut and slope of the y-axis on these diagrams.

Fig. 8

The Strain diagram (SSP Plot) of tin ferrite oxide nanoparticles using the XRD analysis: a SFO1, b SFO4 and c SFO7 at T=350ºC with SnFe₂O₄ phase

4.2.4 Halder–Wagner method

In the SSP method, the XRD peak profile is assumed to be a combination of a Lorentzian function for size broadening and a Gaussian function for strain broadening. However, in reality, the XRD peak does not perfectly match either of these functions [30]. The peak region aligns well with a Gaussian function, but the tail of the peak falls off too quickly to match. On the other hand, the tails of the profile fit well with a Lorentz function, but it fails to match the XRD peak region. To address this challenge, the Halder–Wagner method is employed. This method operates under the assumption that peak broadening follows a symmetric Voigt function, which is a combination of a Lorentzian function and a Gaussian function. According to the Halder–Wagner method, the full width at half maximum of the physical profile of the Voigt function can be expressed as follows.

$$ \beta_{hkl}^2 = \beta_l \cdot \beta_{hkl} + \beta_G^2 $$

(14)

In this equation, β_L and β_G represent the full width at half maximum of the Lorentzian and Gaussian functions, respectively. This method is advantageous because it places more emphasis on the peaks at low and mid angles, where there is less overlap of the diffracting peaks. The relationship between the size of the crystallite and lattice strain according to the Halder-Wagner Method is then given by [30],

$$ \left( {\frac{{\beta_{hkl}^* }}{{d_{hkl}^* }}} \right)^2 = \frac{1}{D}.\frac{{\beta_{hkl}^* }}{{d_{hkl}^* }} + \left( {\frac{\varepsilon }{2}} \right)^2 $$

(15)

In this equation $\beta_{hkl}^* = \beta_{hkl} .\frac{\cos \theta }{\lambda } \,{\text{and}}\, d_{hkl}^* = 2d_{hkl} .\frac{\sin \theta }{\lambda }$. The graph in Fig. 9 shows the relationship between the values of $\left( {{{\beta_{hkl}^* } / {d_{hkl}^{*^2 } }}} \right)$ on the X-axis and $({{\beta_{hkl}^* } / {d_{hkl}^* }})^2$ on the Y-axis for each peak of the XRD pattern, as described by equation. The slope of a plotted straight line provides the average size of the nanoparticles, while the intercept gives the intrinsic strain of the nanoparticles. The average particle size has been calculated from the plot for the synthesized samples SFO1, SFO2, SFO3, SFO4, SFO5, SFO6, SFO7, SFO8, and SFO9, with the respective sizes being 36.12, 38.22, 41.30, 35.21, 58.23, 61.23, 71.32, 38.23, and 56.22 nm. These values match well with those obtained from the SSP model. The strain values calculated using the Halder-Wagner diagram for the synthesized samples are 5.03 × 10^–3, 4.01 × 10^–3, 5.24 × 10^–3, 1.02 × 10^–3, 3.48 × 10^–3, 3.68 × 10^–3, 3.67 × 10^–3, 2.50 × 10^–3, and 2.73 × 10^–3. The strain values calculated through the Halder-Wagner plot are higher than the SSP plot. This increase in the estimated strain value is due to the inclusion of low and mid-angle X-ray diffraction (XRD) data. Additionally, the higher calculated strain value obtained using the Halder–Wagner method may be linked to lattice dislocations, which have a notable impact on the broadening of the reflection peaks at lower angles.

Fig. 9

The Halder-Wagner method diagram of tin ferrite oxide nanoparticles using the XRD analysis: a SFO1, b SFO4 and c SFO7 at T=350ºC with SnFe₂O₄ phase

Figure 9 show the size of the crystalline and lattice strain of particles in the samples that were calculated by the Halder–Wagner method.

In addition, the volume of the unit cell of the synthesized samples can be determined using the following formula [31].

$$ V = a^2 c $$

(16)

The program McMaille is used for indexing powder patterns using a combination of Monte Carlo and grid search methods. It takes 2-theta peak positions and intensities from a peak hunting program to create a pseudo powder pattern. This pattern is then compared to calculate patterns based on cell parameters proposed by a Monte Carlo or grid systematic search. In versions 0.9–2.0 of McMaille, the calculated intensities were adjusted using a Le Bail fit, which applies three iterations of the Rietveld decomposition formula and uses Gaussian peak shapes [32]. This report utilizes the McMaille method to determine the volume of the unit cell for the synthesized samples.

The x-ray density (d_x) is determined by using the following mathematical equation [33].

$$ d_x = \frac{nM}{{NV}} $$

(17)

This equation represents the relationship between the molecular weight of a sample (M), the number of atoms in each unit cell (n), Avogadro's number (N), and the volume of the unit cell (V). Table 4 lists the different parameters related to the crystal structures of nanoparticles from samples that were synthesized using sol–gel, solvothermal, and co-precipitation methods.

4.3 Morphology of tin ferrite nanoparticle by FESEM

To obtain additional information about the internal structure and physical characteristics of the nanoparticles that were synthesized, and to understand how the surface morphology changes with different annealing temperatures, images of the nanoparticle surface were captured using a Field Emission Scanning Electron Microscope (FESEM). These images can be found in Fig. 10. On the other hand, for the investigation of the measured particle size distribution and the average grain size in the synthesized samples, the histogram corresponding to each sample (Fig. 11) was drawn. The histogram chart for analyzing grains was created using FESEM image analysis with the Digimizer software [34, 35]. This histogram shows that the size of nanoparticles for sample SFO5 is the largest and the average size of grains is about 50 nm.

Fig. 10

The FESEM electron microscope images of tin ferrite oxide nanoparticles: a, b SFO1, c, d SFO2, e, f SFO3, g, h SFO4, i, j SFO5, k, l SFO6, m, n SFO7, o, p SFO8, and q, r SFO9: annealed at T=350° C T=450° C and T=550° C, respectively

Fig. 11

The histogram of the grain size distribution from FESEM images for tin ferrite oxide nanoparticles

In the images taken from the synthesized nanoparticle sample, we can observe polyhedral nanostructures and cubic grains with cluster growth using a field-emission scanning electron microscope (FESEM). The average grain size in the SFO1 sample Fig. 10a, b is 87.21 nm, and it is related to the tin ferrite composition (SnFe₂O₄). After annealing at different temperatures, the grain size for the SFO2 sample (Fig. 10c, d) is 89.02 nm, and for the SFO3 sample (Fig. 10e, f), it is 92.71 nm. The images of the SFO1(Fig. 10a, b), SFO4 (Fig. 10g, h), and SFO7 (Fig. 10m, n) samples show that the formed grains have elongated cube shapes. The crystal structure of spinel consists of an oxygen face-centred cubic (FCC) lattice, where the cations occupy the 4-sided (Fe³⁺) and 8-sided (Sn²⁺) sites. Spinel have elongated cubic shapes in their crystal structure. Therefore, the FESEM images of these samples indicate the formation of tin ferrite (SnFe₂O₄) with a spinel structure.

In the SFO4 sample (Fig. 10g, h), the grain size is approximately 78.23 nm. After annealing the sample at higher temperatures, the grain size for SFO5 sample (Fig. 10i, j) increased to 84.14 nm, and for SFO6 (Fig. 10m, n) it increased to 126.02 nm. This indicates that the size of grains increases with increasing annealing temperature, and crystallization occurs faster [36]. In the SFO7 sample (Fig. 10m, n), the average grain size is 38.28 nm. After annealing at a T = 550 °C using two reducing agents, NaOH and Na (BH₄), the grain size of SFO8 sample (Fig. 10o, p) increased to 89.41 nm, and for SFO9 (Fig. 10q, r) it increased to 51.04 nm. In Fig. 12a–i, you can see the spectrum of the EDX analysis, as well as a table specifying the elements present in the synthesized samples. The results of the analysis show that the weight percentage (wt%) and atomic concentration (in%) of the elements (Fe, Sn, O) in the samples, matches the weight percentage calculated based on the composition of the raw materials used during the synthesis. The EDAX results show that for iron to tin [Fe/Sn] atomic ratio (%) greater than 1.1, it is possible to form tin ferrite spinel (SnFe₂O₄) structure. Also, different stoichiometric compounds (Fe_1.727Sn_0.205O₃ and Fe_1.420Sn_0.435O₃) are also possible in different proportions in the sample composition, which is mostly dependent on the annealing temperature of the samples. The independent composition of iron oxide (Fe₂O₃) and tin oxide (SnO₂) is also independent of the atomic ratio of iron to tin, which is attributed to the synthesis and annealing temperature. In Fig. 13, you can see a graphic image depicting the coordinated arrangement of iron, iron, and oxygen ions in the crystal structure of tin ferrite spinel [37].

Fig. 12

The EDX spectrum diagrams of the synthesized samples a SFO1, b SFO2, c SFO3, d SFO4, e SFO5, f SFO6, g SFO7, h SFO8, i SFO9, annealed at T = 350 °C T = 450 °C and T = 550 °C, respectively

Fig. 13

a The first part describes how the atoms of iron and tin are arranged in octahedral and tetrahedral shapes, which are types of geometrical structures and b a single unit cell of SnFe₂O₄, which is the smallest repeating unit of its crystal lattice structure. c The extended polyhedral representation of SnFe₂O₄. Colour code: Brown polyhedral: Iron; green polyhedral: Tin; and red spheres: oxygen [40]

5 Conclusion

In this study, nanoparticles of tin ferrite spinel oxide were synthesized by various methods such as sol–gel, solvothermal, and co-precipitation. The nanoparticles were annealed at different temperatures (T = 350 °C, 450 °C, and 550 °C). The XRD analysis results showed that the tin ferrite (SnFe₂O₄) spinel structure was formed at annealing temperature of 350 °C in the SFO1, SFO4, and SFO7 samples. The preferred peak (311) of this composition with a spinel structure was observed at the angle 2θ = 35.55°. With increasing the annealing temperature, a shift in the crystal structure of spinel tin ferrite occurred. This change led to a mixing up of the positions of positively charged ions (cations) and negatively charged ions (anions) within the crystal, as well as the breaking of covalent bonds between the elements making up the composition. As a result, additional phases such as SnO₂, Fe₂O₃, Fe_1.727Sn_0.205O₃, and Fe_1.42Sn_0.435O₃ appears in the structure. The results from analyzing the samples indicate that the size of the crystals increases as the annealing temperature is raised. The increase in the size of the crystal is due to the reduction of imperfections and flaws in the crystal structure. This reduction is a result of the increase in lattice parameters and the enlargement of the unit cell in the crystalline nanostructure. On the other hand, the decrease in irregularities in the crystal structure caused by rapid grain growth can also lead to an increase in the size of the crystal.

The Sol–gel method facilitates the formation of crystallites by promoting the growth of crystals. The Rietveld method present smaller crystallite sizes compared to the Williamson–Hall method, with an error margin of 1%–2%. This discrepancy is attributed to the Rietveld method's ability to correct for peak broadening by accounting for all instrumental factors. Similarly, the Williamson–Hall method yields smaller crystallite sizes than Scherrer's formula, within the same error margin. This difference is due to the inclusion of a strain correction factor in the Williamson–Hall method, which is not present in Scherrer's formula. The surface morphology of the samples was examined using FESEM, and the results indicated that the phases present in the samples were similar to those found in previous reports. Additionally, the shape of elongated cubic grains, which are associated with spinel structures, was observed in samples SFO1, SFO4, and SFO7. The EDAX results show that for iron to tin [Fe/Sn] atomic ratio (%) greater than 1.1, it is possible to form tin ferrite spinel (SnFe₂O₄) structure. Also, different stoichiometric compounds such as Fe_1.727Sn_0.205O₃, Fe_1.420Sn_0.435O₃, Fe₂O₃ and SnO₂ are also possible in different proportions in the sample composition, which is mostly dependent on the annealing temperature of the samples and reaction agents.