1 Introduction

Buckling problems of elastic columns are often encountered in many engineering areas of structural designs. Therefore, its importance has necessitated researchers to devote their efforts to finding closed or approximate forms of solutions for the modeling equations, cf. [12, 35]. The most simple one is the Euler column buckling after the pioneer work of Euler who firstly solved the buckling problem of elastic column with a constant flexural rigidity and axial compressive load, cf. [18]. As a result, the column buckles to another equilibrium state which called the secondary equilibrium path. The Euler buckling load causes a bifurcation buckling, which basically creates a branching of the secondary equilibrium paths that follow the onset of buckling, cf. [30, 31]. The buckling is also known as the structural instability, and generally it might be classified into two categories: bifurcation buckling and limit load buckling, cf. [11].

In the engineering applications, the design of structures is often based on strength and stiffness of their structural members. Strength is defined to be the ability of the structure to withstand the applied load, while stiffness is the resistance to the external deformation. Tapered members, which enjoy varying cross sections in structural components, represent now the common components in machine and civil parts. Naturally, the important variables in buckling problems are often related to a variable flexural rigidity of the member or a nonhomogeneous nature of the elastic property (resulting in the variable nature of the Young’s modulus of elasticity), cf. [4, 19]. A great deal of research work has been done to calculate the critical buckling loads of tapered shapes using various mathematical techniques in various directions of buckling applications. Some of them has been deduced compact forms of critical loads by using the closed form solution for specific buckling problems in the presence of different boundary conditions, cf. [21,22,23].

In particular, the buckling problem of tapered column under the axial compressive load and the axial weight distribution is taken as a main interest through the calculations in the engineering structural design. An idealization of this phenomenon can be modeled by a long, flexible column of varying cross-section, the base of which is clamped in the ground, so that the column is considered vertical. Hence, one naturally asked that at what length or compressive load will the column suffer the instability. In particular, for some specific cases, the solution of this question will involve the use of eigenvalue problem at most to satisfy two-point boundary conditions. But in some complex models, the governing equations sometimes have no exact solutions due to some new involved terms of modeling. Many of the previous studies have delved to finding special functions for describing the shape modes of non-uniform columns and the distributions of axial weights in order to derive some special closed-form solutions or at least their approximate forms. However, the attempt to get closed forms of solutions has a great of interest and its benefit for the investigation of stability with exact calculations in the presence of different types of distributions and supports, cf. [20, 34, 35].

The study of stability in structural engineering is an important part within the fields of structural and mechanical designs. The of elastic stability deals with the behavior of structures subjected to compressive forces besides the effect of weight distributions on their members in the space of elastic zones. The elastic stability analysis might be provided by the theoretical study or the experimental calculations to obtain the critical buckling load of the structural members. In both directions, the critical buckling load are simply considered as the force that corresponds to the equilibrium state between the external and internal forces in the structural members. In theoretical studies, most of calculations to obtain the critical force is always based on the eigenvalues as a linear analysis of buckling. Of course, it is of practical interest to know that the instability depends mainly on boundary conditions (including elastic end restraints) and bending rigidity. The effect of boundary conditions on the stability and instability has been studied and investigated for some cases of buckling in the literatures such as [1, 2, 20], and the references therein.

One of the best ways to explain the linear stability analysis of such problems is the stability charts or Ince–Strutt diagrams. The construction of stability charts of continuous or discrete-time linear systems is to show topologically the stability (instability) conditions in a complete and assembled graph among the included parameters in the system, cf. [9, 10]. The idea is based on the prediction of eigenvalue curves to represent the periodic behavior of the solution emitted from eigenvalue axis with two branches of cosines and sines solutions. So that, the domain of the chart is divided into two regions of stability and instability. The regions that are located inside the two branches of periodic solution (the cosine and the sine curves), represent the region of instability but the others represent the regions of stability. A particular interest in the study of such systematic stability charts may exist or occur in linear systems with periodic coefficients such as Mathieu equation, Ince equation and El Borhamy-Rashad-Sobhy equation, cf. [8, 16, 24]. Also, stability charts might be predicted in linear systems with aperiodic coefficients that might be possessed a nature of periodic responses such as the generalized Bessel equation, cf. [7]. The construction of stability charts for these specific equations are shown in Fig. 1. According to this displayed figure, the regions of instability are represented by the areas outlined in red.

Fig. 1
figure 1

Examples of stability charts

Full size image

Many methods of solution methodology can be suggested to treat the bucking problems. On top of these methods, the minimum residual methodology which is based on seeking the minimum of the residual functions over the problem domain with respect to the unknown generalized parameters, cf. [17]. However, the utilizing of the minimum residual Galerkin’s method to determine the critical loads and the constructing stability charts is a quite suitable semi-analytical approach for the buckling problems. Furthermore, the benefit to use this method lies in enhancing the accuracy of the approximation and demonstrating a rigorous systematic approach for solving the yielded eigenvalue problems. Anyway, many extensive literatures have developed by using such methods coupled to Galerkin’s approach for buckling problems such as in [15, 25, 26, 37] and the references therein.

In this study, it is aimed to investigate the buckling instability and dynamic responses of tapered columns using a minimum residual Galerkin-based approximation with different periodic trial shape modes. The choices are significantly related to get an approximation of the exact solutions provided that high accuracy calculations are obtained in the stability analysis as well. The method presented can be used to yield a straightforward formula for computing the least eigenvalue and hence the critical buckling load in a rigorous systematic way. So that, it could be an effective semi-analytical tool for the buckling problem with variable flexural rigidity due to the selection of an appropriate guess function of periodic behavior that satisfies the boundary conditions, cf [5, 6, 14, 36]. Normally, the boundary conditions are physically interpreted as higher-order force and moment terms affecting on the column.

After this presentation containing the scientific content of the study, the challenge now is to obtain appropriate periodic buckling shape modes to obtain the corresponding transition curves up to few terms as stopping criteria of Galerkin’s approach. Subsequently, we will construct an approximate realization of the eigenvalue matrix which is similar to Hill’s matrix obtained by the harmonic balance method, cf. [8]. The constructed matrix is used to determine the buckling loads or the eigenvalues (represented in the concentrated load (P) as a function of the involved parameters in the governing equation). Hence, the stability chart is constructed and the stability (instability) domains can be suitably obtained based on the boundary curves. The chart is drawn between the eigenvalue of the linear problem and the parameter \(\beta\) as a variable parameter for the flexural rigidity and the axial weight distribution. However, the overall objective of the research represented in this work is to quantify the elastic buckling capacity of a tapered column subjected to a compressive load, an axial weight distribution and a varying flexural rigidity. The results obtained in the present paper can be quite useful for design of stiffened beams and columns subjected to varying flexure and compression loads for the heavy tapered members in structural and mechanical engineering.

The organization of the paper is as follows:

In Sect. 2, we present the problem statement and the basic modeling of buckling problem for tapered columns explaining the linear governing equation of buckling under the concentrated and distributed loads. In Sect. 3, it is illustrated the description of the tapered columns under the gradual variation of their cross area leading to a corresponding variation of their material flexural rigidity as well as the modeling of axial load distributions. In Sect. 4, the minimum residual Galerkin’s method is presented and its employing as a method of solution for the governed boundary value problem. In Sect. 5, two examples of verification are included and discussed to compare the results with analytical solutions for known problems. In Sect. 6, the stability charts are shown as a commendable tool for visualizing and comprehending instability regions across various cross-section and weight distributions in the problem. In the last section, the conclusion is given.

2 Problem statement and modeling

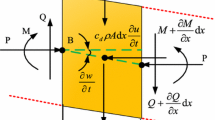
Let us model the problem by considering a flexible column of length L with a variable flexural rigidity \(\kappa (x)=EI(x)\) constructed from material with a constant Young’s modulus of elasticity E, and I(x) represents the moment of inertia of a cross-section about a diameter normal to the plane of bending. The line density along the rod is assumed to be variable and equal to W(x). Certain assumptions are made in the analysis:

  1. (i)

    The column is perfectly straight.

  2. (ii)

    The load is applied along the centroidal axis of the column.

  3. (iii)

    The material of the column is homogeneous and obeys Hooke’s law.

  4. (iv)

    The assumption of the theory of bending is applied, i.e. plane sections before deformation remain plane after deformation.

  5. (v)

    The deformation of the column is small so that, the flexural curvature is assumed to be

$$\begin{aligned} \mu (x) \approx \frac{d^2y}{dx^2}. \end{aligned}$$
(1)

This means that the term \(\left( \frac{dy}{dx}\right) ^2 \ll 1\) in the flexural curvature expression,

$$\begin{aligned} \mu (x)= \frac{\frac{d^2y}{dx^2}}{\left( 1+\left( \frac{dy}{dx}\right) ^2\right) ^{3/2}}, \end{aligned}$$
(2)

where y is the lateral deflection of the column at the cross section x.

The x-axis will be taken to be vertical and to coincide with the undistorted axis of the rod, and its origin will be located at the base of the rod.

From bending theory, the bending moment (\(\mathbb {M}\)) is given from the following relation [13],

$$\begin{aligned} \kappa (x)\frac{1}{\rho } = \mathbb {M}(x), \end{aligned}$$
(3)

where \(\rho\) is the curvature. Let us assume that, the deflection at point x on the rod is small, then

$$\begin{aligned} \tan \vartheta = \frac{dy}{dx} \approx \sin \vartheta =\vartheta . \end{aligned}$$
(4)

where \(\vartheta\) is the angle of deflection of the rod from the vertical at a point x. Hence, it represents the finite rotation suffered by the cross section at the point (x, y).

According to the modeling procedures in [19, 32] and by considering that, the material satisfies the assumptions (i–v), then the governing equation for an inextensible and unshearable finite configuration of elastic column subjected to a general continuous axial distributed load along its length (W(x)) and a compressive force (P) is given by

$$\begin{aligned} \frac{d\mathbb {M}}{dx} + [P + W(x)(L-x)] \vartheta =0. \end{aligned}$$
(5)

Let us introduce the problem by the following non-dimensional variables:

$$\begin{aligned} \xi = \frac{x}{L}, \quad \lambda = \frac{PL^2}{EI_o}, \quad \vartheta = \frac{\theta L}{EI_o}, \quad M = \frac{\mathbb {M} L}{EI_o}, \quad \quad w = \frac{WL^3}{EI_o}. \end{aligned}$$
(6)

where \(EI_o = max_{x\in [0,L]}EI(x)\), is considered the maximum value attained by \(\kappa (x)\) along the span and \(\xi \in (0,1)\).

So, it is clear to obtain the following linearized dimensionless form as follows:

$$\begin{aligned} (\kappa (\xi )\theta ')' + [\lambda + w(\xi )(1-\xi )] \theta =0, \quad \quad \theta '=\frac{d\theta }{d\xi }. \end{aligned}$$
(7)

Consequently, the linearized form of Eq. (7) leads to the following eigenvalue equation,

$$\begin{aligned} -(\kappa (\xi )\theta ')' - w(\xi )(1-\xi ) \theta =\lambda \theta . \end{aligned}$$
(8)

By using the Rayleigh quotient [3], the eigenvalue \(\lambda\) reads,

$$\begin{aligned} \lambda = \frac{-\kappa (\xi )\theta (\xi )\theta '(\xi )|_0^1 +\int _0^1 (\kappa (\xi )(\theta '(\xi ))^2 - w(\xi )(1-\xi )(\theta (\xi ))^2) d\xi }{\int _0^1 (\theta (\xi ))^2 d\xi }, \end{aligned}$$
(9)

that subjects to the clamped-clamped boundary conditions,

$$\begin{aligned} \theta (0)=\theta (1)=0. \end{aligned}$$
(10)

From Rayleigh quotient and Eq. (9), it follows that:

  1. (i)

    \(\lambda \ge 0\) if \(\kappa (\xi )\theta (\xi )\theta '(\xi )|_0^1 \le 0\) and \(w(\xi )(1-\xi ) \le 0\), for all \(\xi \in [0,1]\).

  2. (ii)

    The minimum value of the Rayleigh quotient over all continuous functions satisfying

    $$\begin{aligned} \theta (0)+ \theta '(0)=0, \quad \quad \theta (1) + \theta '(1)=0. \end{aligned}$$
    (11)

    is the smallest eigenvalue.

Anyway, by using Eqs. (7) and (10), the model can be solved by the weighted residual Galerkin’s method. This allows us to suggest perfectly a complete set of admissible periodic functions to represent the buckling shape modes subjected to the related boundary conditions.

3 Description and modeling of tapered column

In this section, we introduce the mathematical description of a tapered column subjected to an axial distributed load along its length as shown in Fig. 2 for its linear configuration of the tapering. The flexural rigidity (\(\kappa (\xi )\)) has to be function of \(\xi\) by using a varying moment of inertia at any section (\(\xi\)). Similarly, by considering that, the axial distribution of the weight has the similar variation for the simplicity of the calculations. So that, the following cases are considered with the associated flexural rigidity and the axial distributed load as follows:

  • Case (a):

    The tapered column of the class of flexural rigidity and distribution of the axial weight are given by the following power function for \(c=\{\frac{1}{2},\frac{3}{4},1\}\) and \(\beta \in [0,1]\),

    $$\begin{aligned} \kappa (\xi ) = \kappa _o(1-c\beta (1-\xi )^n)^m, \end{aligned}$$
    (12)
    $$\begin{aligned} w(\xi ) = w_o(1-c\beta (1-\xi )^n)^{m}. \end{aligned}$$
    (13)

  • Case (b):

    The tapered column of the class of flexural rigidity and distribution of the axial weight are given by the following power function for \(c=\{\frac{1}{2}, \frac{3}{4},1\}\) and \(\beta \in [0,1]\),

    $$\begin{aligned}{} & {} \kappa (\xi ) = \kappa _o(1-c\beta \xi ^n)^m, \end{aligned}$$
    (14)
    $$\begin{aligned}{} & {} w(\xi ) = w_o(1-c\beta \xi ^n)^{m}. \end{aligned}$$
    (15)

where, m and n are positive integer numbers or zeros, \(\kappa _o \in (0,\infty )\) and \(w_o \in [0,\infty )\).

Fig. 2
figure 2

Configuration of columns with linear tapering

Full size image

Note that, from the definition of the flexural rigidity functions and the representation of axial distributed load in the two cases, the attempt to obtain closed form of solutions is not easy due to the included parameters. So that, the alternatives have to be employed to get such approximate forms of solutions.

4 Minimum residual Galerkin’s Solution

For some special representations of buckling problems, there are wide ranges of literatures introduced to obtain the exact solution of Sturm–Lioville eigenvalue problem by using some special functions such as Bessel’s functions, cf. [3]. Somehow, here the attempt is not easy, so that Galerkin’s method could be become an efficient way to obtain the critical bucking loads and the buckling shape modes. Some numerical methods can be employed such as finite difference and finite element methods to discretize the system. But for the completeness of solution, some methods should be employed such as polynomial or power methods to calculate the eigenvalues, cf. [29].

Let us employ the Galerkin’s method to calculate the buckling shape modes of tapered columns with general continuously varying stiffness and weight distribution. By using the approximating solution with a finite linear combination of simple basis functions satisfying the clamped-clamped boundary conditions, then let us assume that,

$$\begin{aligned} w(x,A,B)= \sum _{j=1}^{N} W_j, \end{aligned}$$
(16)

where \(W_j\) belongs to a complete set of admissible periodic functions. Then, for the associated boundary conditions, several examples of possible sets can be introduced for instance,

$$\begin{aligned}&W_j = A_j (1-\cos 2j\pi \xi ), \end{aligned}$$
(17a)
$$\begin{aligned}&W_j = B_j \sin j\pi \xi . \end{aligned}$$
(17b)

Then, the possible set of buckling shape modes satisfying \(\Theta _j(0)=\Theta _j(1)=0\) reads

$$\begin{aligned}&\Theta _j\approx \frac{\partial W_j}{\partial A_j}= 1-\cos 2\pi j \xi ,\end{aligned}$$
(18a)
$$\begin{aligned}&\Theta _j\approx \frac{\partial W_j}{\partial B_j}= \sin \pi j \xi . \end{aligned}$$
(18b)

Typically, the basis functions are chosen so that the admissible functions satisfy the homogenous boundary conditions \(\theta (0)=\theta (1)=0\) as well. Due to the continuous variation of cross section, the admissible functions are also continuously differential functions in the interval [0, 1].

According to the Galerkin’s method, substituting Eq. (16) in Eq. (7) and by minimizing the weighted residual, it yields the following algebraic systems,

$$\begin{aligned}&[\varvec{\textsf{K}}^E - \varvec{\textsf{K}}^W - \lambda ^o \varvec{\textsf{K}}^G] \varvec{\textsf{A}}=0, \end{aligned}$$
(19a)
$$\begin{aligned}&[\varvec{\textsf{K}}^E - \varvec{\textsf{K}}^W-\lambda ^o \varvec{\textsf{K}}^G] \varvec{\textsf{B}}=0, \end{aligned}$$
(19b)

where \(\lambda ^o\) represents the approximated buckling load in the framework of \(\lambda\) ( i.e \(\lambda \approx \lambda ^o\)), and

$$\begin{aligned} K^{E}_{jk} = -\int _0^1 \Theta _j(\xi ) (\kappa (\xi )\Theta '_k(\xi ))' d\xi , \end{aligned}$$
(20)

and,

$$\begin{aligned}&K^{W}_{jk} = \int _0^1 \Theta _j(\xi ) w(\xi )(1-\xi )\Theta _k(\xi ) d\xi ,\end{aligned}$$
(21a)
$$\begin{aligned}&K^{G}_{jk} = \int _0^1 \Theta _j(\xi ) \Theta _k(\xi ) d\xi . \end{aligned}$$
(21b)

So that, it yields the nth buckling load which is the nth root of the following characteristic equation,

$$\begin{aligned} det(\varvec{\textsf{K}}^E - \varvec{\textsf{K}}^W- \lambda ^o \varvec{\textsf{K}}^G)=0. \end{aligned}$$
(22)

The associated m-eigenvector solution of

$$\begin{aligned}&[\varvec{\textsf{K}}^E-\varvec{\textsf{K}}^W - \lambda ^o \varvec{\textsf{K}}^G] \varvec{\textsf{A}}_m =0,\end{aligned}$$
(23a)
$$\begin{aligned}&[\varvec{\textsf{K}}^E-\varvec{\textsf{K}}^W - \lambda ^o \varvec{\textsf{K}}^G] \varvec{\textsf{B}}_m =0. \end{aligned}$$
(23b)

Then, the buckling shape mode defines

$$\begin{aligned} \Theta (\xi ) = \sum _{j=1}^N W_j. \end{aligned}$$
(24)

So that, if we have \(\Theta _j = 1- \cos 2\pi j\xi\) then we obtain,

$$\begin{aligned}&K^E_{jk} = 4jk \pi ^2 \int _0^1 \sin (2\pi j \xi ) \kappa (\xi ) \sin (2\pi k \xi ) d\xi ,\end{aligned}$$
(25a)
$$\begin{aligned}&K^W_{jk} = \int _0^1 (1-\cos (2\pi j \xi )) w(\xi )(1-\xi ) (1-\cos (2 \pi k \xi )) d\xi ,\end{aligned}$$
(25b)
$$\begin{aligned}&K^C_{jk}= \frac{1}{2}\delta _{jk}. \end{aligned}$$
(25c)

where \(\delta _{jk}\) is the Kronecker delta.

Also, if we have \(\Theta _j = \sin \pi j\xi\) then we obtain,

$$\begin{aligned}&K^E_{jk} = jk \pi ^2 \int _0^1 \cos (2\pi j \xi ) \kappa (\xi ) \cos (2\pi k \xi ) d\xi ,\end{aligned}$$
(26a)
$$\begin{aligned}&K^W_{jk} = \int _0^1 \sin (2\pi j \xi ) w(\xi )(1-\xi ) \sin (2 \pi k \xi ) d\xi ,\end{aligned}$$
(26b)
$$\begin{aligned}&K^C_{jk}= \frac{1}{2}\delta _{jk}, \end{aligned}$$
(26c)

becomes the nth eigenvector is defined within an arbitrary constant. The normalized eigenvector \(\Theta (\xi )\) is obtained by normalization condition with respect to geometric stiffness, namely,

$$\begin{aligned} \int _0^1 \theta _m \cdot \theta _m d\xi =1. \end{aligned}$$
(27)

This implies that eigenvectors \(\varvec{\textsf{A}}_m\) and \(\varvec{\textsf{B}}_m\) are normalized with respect to the geometric stiffness as

$$\begin{aligned} \varvec{\textsf{A}}_m^T K^G \varvec{\textsf{A}}_m =1, \quad \quad \text {and} \quad \quad \varvec{\textsf{B}}_m^T K^G \varvec{\textsf{B}}_m =1. \end{aligned}$$
(28)

Hence, the mth buckling load \(\lambda ^o_m\) can be obtained as

$$\begin{aligned}&\lambda _m^o = \varvec{\textsf{A}}_m^T [\varvec{\textsf{K}}^G-\varvec{\textsf{K}}^W] \varvec{\textsf{A}}_m,\end{aligned}$$
(29a)
$$\begin{aligned}&\lambda _m^o = \varvec{\textsf{B}}_m^T [\varvec{\textsf{K}}^G-\varvec{\textsf{K}}^W] \varvec{\textsf{B}}_m. \end{aligned}$$
(29b)

However, the Sturmian theory ascertains that [3, 19]:

  1. (i)

    The eigenvalues \(\lambda _m^o\), \(m=1,2,3,\ldots\) are simple and positive,

  2. (ii)

    \(\lim _{m \rightarrow \infty } (\lambda _m^o) \rightarrow \infty\),

  3. (iii)

    The eigenfunctions corresponding to \(\lambda _m^o\) possesses exactly m zeros in [0, 1] each simple \(\theta _m(0)=0\) and \(\theta '_m(0) \ne 0\).

5 Validation of the method

We first investigate the linearly elastic tapered column with linearly varying stiffness

$$\begin{aligned} \kappa (\xi ) = (\alpha -1)\xi +1, \quad w(\xi )=0, \end{aligned}$$
(30)

where \(\alpha \in (0,\infty )\). The case of \(\alpha =1\) corresponds to the uniform column with \(\kappa =1\) whose lower buckling load is \(\pi ^2\) under the boundary condition \(\theta '(0)=\theta '(1)=0\). Therefore, to render the results more meaningful, it is introduced the ratio of the lowest buckling loads of linear tapered column to the critical load as the uniform load

$$\begin{aligned} P_1^o = \frac{\lambda _1^o}{\pi ^2}. \end{aligned}$$
(31)

Similarly, in the general load range, we have

$$\begin{aligned} P^o_m= \frac{\lambda ^o_m}{\pi ^2}, \end{aligned}$$
(32)

in the sense that the non-dimensional number \(P^o_m\) possesses the meaning of the load multiplication with respect to buckling load of the uniform elastic column.

In the following table (Table 1) and its associated configuration in Fig. 3 which forming the values of the buckling loads according to the value of \(\alpha\) under the following suggested admissible functions for the boundary conditions \(\theta '(0)=\theta '(1)=0\),

$$\begin{aligned}{} & {} \theta (\xi ) = \sum _{j=1}^{N} A_j\cos \pi j \xi , \quad \quad \text {and} \nonumber \\{} & {} \quad \theta (\xi ) = \sum _{j=1}^{N} B_j(\xi -\frac{1}{2\pi j}\sin 2\pi j \xi ). \end{aligned}$$
(33)
Table 1 Lower buckling loads for \(\kappa (\xi )= (\alpha - 1)\xi +1\) for \(\theta '(0)=\theta '(1)=0\)
Full size table

In the shown charts in Fig. 3, the relation between the eigenvalue (\(\lambda ^o\)) and \(\alpha\) is exposed, so it used the admissible cosine functions to yield the solid lines and the sine functions to yield the dot lines in the related chart.

Fig. 3
figure 3

Stability charts for \(\kappa (\xi ) = (\alpha -1)\xi +1\) and \(w(\xi )=0\)

Full size image

This agree with the solution of the differential equation

$$\begin{aligned}{} & {} (a+bx) y_{xx} + c y_{x} + \delta ^2 y=0, \end{aligned}$$
(34)
$$\begin{aligned}{} & {} y(z) = z^{\frac{c}{b}-1}\left( c_1 J_{\frac{c}{b}-1}\left( \frac{2\delta }{b}z \right) + c_2 Y_{\frac{c}{b}-1}\left( \frac{2\delta }{b}z \right) \right) , \nonumber \\{} & {} \quad z^2 = a+bx.. \end{aligned}$$
(35)

By comparing with

$$\begin{aligned} (1+(\alpha -1)\xi )\theta '' + \alpha \theta ' + \lambda \theta =0, \end{aligned}$$
(36)

we obtain

$$\begin{aligned} a=1, \quad b= \alpha -1, \quad c=\alpha -1, \quad \lambda = \delta ^2, \end{aligned}$$
(37)

then,

$$\begin{aligned}{} & {} \theta (z) = c_1 J_0\left( \frac{2\sqrt{\lambda }}{\alpha -1}z \right) + c_2Y_0\left( \frac{2\sqrt{\lambda }}{\alpha -1}z \right) , \nonumber \\{} & {} \quad z^2 = 1+(\alpha -1)\xi . \end{aligned}$$
(38)

Applying the boundary conditions \(\theta (0)=\theta (1)=0\), then one obtains the following approximated value of the critical load

$$\begin{aligned} J_0\left( \frac{2\sqrt{\lambda }}{\alpha -1}\right) Y_0\left( \frac{2\sqrt{\lambda \alpha }}{\alpha -1}\right) - J_0\left( \frac{2\sqrt{\lambda \alpha }}{\alpha -1}\right) Y_0\left( \frac{2\sqrt{\lambda }}{\alpha -1}\right) =0. \end{aligned}$$
(39)

Also, applying the boundary conditions \(\theta '(0)=\theta '(1)=0\), then one obtains the following approximated value of the critical load

$$\begin{aligned} J_1\left( \frac{2\sqrt{\lambda }}{\alpha -1}\right) Y_1\left( \frac{2\sqrt{\lambda \alpha }}{\alpha -1}\right) - J_1\left( \frac{2\sqrt{\lambda \alpha }}{\alpha -1}\right) Y_1\left( \frac{2\sqrt{\lambda }}{\alpha -1}\right) =0. \end{aligned}$$
(40)

Hence, the relation between \(\lambda\) and \(\alpha\) is easily constructed as shown in Fig. 3 for both cases, cf. [7].

6 Buckling instability via stability charts

The purpose now is to present the buckling instability characteristics through the stability chart (Ince–Strutt diagram) between the two parameters \(\lambda ^o\) and \(\beta\) via the algorithm of minimum residual Galerkin’s method. The yielded equation (Eq. (22)) represents the buckling characteristic equation to describe the approximated buckling loads of the generalized tapered column modeled by polynomials for the flexural rigidity and axial weight distribution as presented in section 3.

However, the algorithm of solution is employed to obtain the critical loads as a function of the parameter \(\beta\) involving the powers m and n. Hence, by Eq. (22) with \(\beta = 0\), it is clearly that the entire positive \(\lambda ^o\) axis must be within the stable region of solution. The transition curves, which separate the stable and unstable regions, are mostly associated with the type of the periodic solutions. If the curve represented by the eigenvalue \(\lambda ^o\) as a function of the parameter \(\beta\) in the stability chart by solid lines, it is for the even trigonometric solutions, and by dashed lines, it is for the odd trigonometric solutions. So that, this configuration is quite similar to the characteristics for systems of periodic coefficients by using the harmonic balance method, cf.

[9, 10]. Hence, in our treatment, the results of this series of calculations are shown in the attached figures of stability charts where the regions of instability is presented as a function of parameters (\(\beta\),m,n) by red lines regions.

The general periodic solution is typically obtained by using the eigenfunction in Eq. (24). Then, after some manipulation, the relations among the parameters are obtained by making the coefficients of the determinant of buckling characteristic equation is identically equal to zero. The yielded algebraic equations may be solved for \(\lambda ^o\) as a function of \(\beta\) such as by employing the method of successive approximations. Although the methods are tedious if it applied in a manual way. Actually, it used a Maple program to do some symbolic calculations which can not printed here due to their long symbolic forms. However, several methods can be used to handle the symbolic relations between \(\beta\) and \(\lambda ^o\) as described in [27, 28, 33].

However, on approximately carrying out the calculation using Galerkin’s method, approximate and simple slow flows for each case of the stability charts can be obtained by drawing the deduced relation between \(\lambda ^o\) and \(\beta\) for the stopping parameter \(N=31\). Some comparisons at specific values with the theoretical methods are fit well to show that these approximate slow flow curves are somewhat accurate, cf. [12].

During the various trials on the cross sections of the column and the axial weight distributions represented by the parameter m, the attempt was made whether or not to determine the instability regions. Then, some of the involved parameters has to be carefully chosen. The chosen values for the calculations are \(\kappa _o=w_o=1\), \(n=11\), for two values \(m=5\) and \(m=9\) respectively. Typically, these regions might topologically changed from one to another due to the variation of that parameters. However, after some trials, the instability regions are appeared and increased according to the specific mentioned values of the parameter m.

For the stability chart represented by Fig. 4: The column has a constant cross section or a constant flexural rigidity in the presence of no axial weight distribution, it has no instability regions and the critical load is coincided to the theoretical values of \(\lambda ^o=4\pi ^2\approx =40\). Since there is no parameter \(\beta\) to vary with the load as vividly shown.

Fig. 4
figure 4

Stability chart at the constant flexural rigidity (\(\kappa (\xi )=1\)) and \(w_o=0\)

Full size image

For the stability chart represented by Fig. 5: The result is amazing which has a curved variation of \(\beta\) with the eigenvalue \(\lambda ^o\) and there is no existence for the instability domains at \(m=5\) and \(m=9\). It noted that the values of critical loads are decreased with the increase of power m according to the reference value \(\lambda ^o=4\pi ^2\) in Fig. 4.

For the stability chart represented by Fig. 6: Further delving into possible corrective actions for the existence of instability, it is noticed that, c parameter is strongly associated to determine how the instability regions existed. It clearly shown from the figure that, the increase of the instability region is strongly associated with the increase of the parameter c and the power m in the flexural rigidity and the weight distribution.

For the stability chart represented by Fig. 7: Another further delving for the instability domains which occur with the parameter \(\beta\). Also, in this case, it is enjoyed with the increasing of instability regions than the two previous cases. Since, it is easily to deduce that, the power m has a big significance to increasing the instability domains.

For the stability charts represented by the tapered column in case (b), similar stability diagrams are obtained with case (a). Since, the difference only is the configuration of the tapered column is reversed. So that, the boundary curves have the same directions and values in all cases. Additionally, these results are used to validate the method.

Typically, as a result of the stability charts, the increasing of the ranges of the parameters c, m and n has a big influence by using the forms of associated flexural rigidity and the weight distribution on the existence of instability. Of course, the nature of buckling instability is changed due to the values of the parameter \(\beta\) but the related figures associated to these cases explain how big the change in instability regions done according to their variations.

Fig. 5
figure 5

Stability charts at \(c=\frac{1}{2}\) and \(n=11\)

Full size image
Fig. 6
figure 6

Stability charts at \(c=\frac{3}{4}\) and \(n=11\)

Full size image
Fig. 7
figure 7

Stability charts at \(c=1\) and \(n=11\)

Full size image

7 Conclusion

In this work, the minimum residual Galerkin’s method as a rigorous and systematic approach in the family of minimum residual methods is applied to solving buckling problem of general tapered columns. The method was designed for optimality with regard to the construction of bucking stability and instability domains via stability charts. The obtained results investigate its superiority over standard methods in the creation of simple relations among the problem parameters in cases of static buckling problems.

The resulted stability charts can describe effectively the characteristics of buckling to obtain its instability regions which might be better than the calculated results due to the exposition of the whole picture of (in)stability. Since, the chart yields the stability characteristics directly, and it furnishes a more desirable way to stability problems than the analytical or numerical approximated calculations definitely in cases of the complex buckling problems. In the studied problem, through the shown stability graphs, the variation of the flexural rigidity and weight distribution have a highly precise effect on increasing or decreasing the instability regions and also on the existence of stability boundaries.

According to the results presented in the work, the introduced treatment offers a visual information which could delve a deeper into the practical implications of instability regions. Therefore, the importance of the work lies in the discussion how these findings that might have an impact on the design and analysis of real-world structures. In general, these results might be taken as a guidance to expect the better choices to identify the optimal design of beams and columns than the previous calculations in the related literatures. Therefore, the extension of the work has become a future request for problems that have a practical nature in structural engineering design.