1 Introduction

With the rapid development of manufacturing and electronic industry, the function and precision requirements of rotating machinery are increasingly improved, and the structure is more and more complex. In this sense, the safety, reliability and fault diagnosis requirements of rotating machinery are improved seriously. According to relevant data analysis, 40% of rotating machinery failures are caused by the failure of rolling bearings [1]. Once the failure of rolling bearings occurred, all kinds of losses is immeasurable, it is of great significance to carry out state-based detection and fault diagnosis of rotating machinery [2]. The acquisition and processing of fault signals is one of the important steps to realize the fault monitoring and diagnosis of rotating machinery. The collected bearing fault signal is a particularly sensitive random signal. Generally, the processing of bearing fault signal includes fault diagnosis, residual life estimation and reliability analysis [3]. Among the three preventive measures of faults, the most important is the early diagnosis of bearing faults, which can be divided into three steps, as shown in Fig. 1.

Fig. 1
figure 1

Bearing fault diagnosis process

Full size image

As the most critical part of bearing fault diagnosis, the acquisition signal-based fault signal feature extraction method has attracted a lot of attention, such as Kalman filter [4], collections, empirical mode decomposition and combined fault feature extraction of band entropy [5], the kurtosis optimization variational mode decomposition of fault feature extraction [6], smooth cycle analysis [7], etc..

However, most of the aforementioned methods focused on the purpose of noise elimination. There are some problems to be overcome, such as poor accuracy, uncertain parameters, and difficulty in extracting early weak faults with strong interference components. Different from other denoising methods, Benzi et al. [8] proposed a stochastic resonance model, in which the noise signal was adopted to extract fault signal features. In addition, Professor Hu Niaoqing introduced normalized scale transform into stochastic resonance model to deal with early fault detection of rotating machinery [9]. Furthermore, stochastic resonance has a variety of steady-state models, such as monostable, bistable, trustable and multi-stable. In [10], Woods-Saxon potential function was combined with stochastic resonance to optimize the bistable stochastic resonance model. Thus, as bistable system can be widely applied to multi-steady state, matched steady state and more complex systems, the research on bistable system became a hot spot.

While, restricted by the adiabatic approximation hypothesis, stochastic resonance is only applicable to feature extraction of small signals with input signal amplitude and noise intensity less than 1. Fortunately, Leng Yonggang proposed the quadratic sampling stochastic resonance technology in 2002, which extracted the weak signals from strong noises under the condition of large parameters of adiabatic approximation theory [11]. In addition, Li et al. proposed a new frequent-shifted multi-scale SR method for weak signal detection of wind turbines, which can realize weak signal detection at any frequency [12]. Through frequency translation and scaling, Tan Jiyong proposed the frequency shift rescaling stochastic resonance (FRSR) method by alleviating the contradiction between sampling frequency and number of sampling points [13].

To be honest, during the process of SR model solving, different model parameters result in various and suboptimal solution. Then, the adaptive stochastic resonance model is proposed, which is a multi-dimensional and multi-parameter continuous optimization problem. In 2013, Zhu Weina et al. used artificial fish swarm algorithm to adjust the stochastic resonance system parameters of the bistable system, so as to achieve the generation of stochastic resonance effect and the enhancement of characteristic signals [14]. In 2014, Li Yibo used quantum particle swarm optimization algorithm to optimize system parameters and transformed the adaptive stochastic resonance problem into a multi-parameter parallel optimization problem in [15]. In 2018, Chi Kuo carried out a research on the application of Cuckoo Search (CS) algorithm to stochastic resonance parameter optimization. Cuckoo Search algorithm has brought many applicable effects in medical, measurement, electronic information, aerospace and other fields [16].

Among the optimal algorithm mentioned above, how to avoid falling into local optimal solution is always the main concern. Focusing on this issue, Seyedali Mirjalili proposed the Gray Wolf Optimization (GWO) algorithm in 2014 [17]. Recently, Pan Chengsheng proposed a K-means text clustering method by developing GWO [18]. Furthermore, GWO has demonstrated to gain a strong global search ability characteristic than above mentioned methods [19].

Aiming at the problems of adaptive stochastic resonance parameter uncertainty, poor calculation accuracy, multi-dimensional and multi-parameter continuous optimization in realistic industrial rolling bearing fault signal feature extraction, we propose a rolling bearing fault feature extraction method based on GWO-optimized adaptive stochastic resonance signal processing method. Compared with previous research, the proposed method gains the advantages of higher computational speed and global optimal solution during optimization, and then a higher signal-to-noise ratio in rolling bearing fault signal feature extraction. In Sect. 2, the bistable SR is introduced, and then the SR of large parameter signal is realized by normalized scale transformation. In Sect. 3, the SNR fitness function is established to evaluate stochastic resonance output effect. And also, the theory of GWO algorithm, the calculation diagram and the technical flow of the proposed method are described. In Sect. 4, we introduced an inner race fault data set to verify the performance of the proposed method. Meanwhile, CS-based stochastic resonance signal processing method was adopted in inner race fault signal feature extraction for comparison. Finally, in Sect. 5, we drawn the conclusions from the proposed bearing fault feature extraction method.

2 Stochastic resonance theory and scale transformation

Stochastic resonance has monostable, bistable, tri-stable, multi-stable and other steady-state models. Classical bistable stochastic resonance model is the most studied and most in-depth nonlinear system model. Bistable system can be widely applied to multi-stable, matched steady state and more complex systems. Therefore, we chooses classical bistable model for study and analysis.

2.1 Basic principle of stochastic resonance

The bistable system subjected to random uncertain signals and external disturbances can be expressed by the Langevin equation [9]:

$$\dot{x}\left( t \right) = - \dot{U}(x) + S\left( t \right) + N\left( t \right)$$
(1)

here, \(x\left( t \right)\) is the output of the bistable stochastic resonance system, \(U\left( x \right)\) is nonlinear bistable situation function, \(S\left( t \right) = Af\left( {2\pi f_{{\text{d}}} t + \psi } \right)\), is the analog deterministic signal, \(f\left( {2\pi f_{{\text{d}}} t + \psi } \right)\) is the deterministic sine of frequency \(f_{{\text{d}}}\) and amplitude \(A\) of 1, \(\psi\) is the phase of the signal. Let \(N\left( t \right) = \sqrt {2D} \varepsilon \left( t \right)\) represents the Gaussian white noise, where the noise intensity is denoted by \(D\), and \(\varepsilon \left( t \right)\) is the standard Gaussian white noise.

Nonlinear bistable situation function \(U\left( x \right)\) is as follows:

$$U\left( x \right) = - \frac{a}{2}x^{2} + \frac{b}{4}x^{4} \cdots a > 0,b > 0$$
(2)

The output state of the bistable system is similar to the motion of a particle between bistable potential Wells (Fig. 2). When \(x = \pm \sqrt{\frac{a}{b}}\), \(U\left( x \right)\) obtains the minimum barrier height \(- \Delta U\), and \(\Delta U = \frac{{a^{2} }}{4b}\). It can be deduced from Eq. (1) that:

$$\dot{x}\left( t \right) = ax - bx^{3} + A(2\pi f_{{\text{d}}} + \psi ) + \sqrt {2D} \varepsilon \left( t \right)$$
(3)
Fig. 2
figure 2

Potential function of nonlinear bistable system

Full size image

If the intensity of the applied noise is appropriate and the particle achieves good coordination with the periodic driving force according to the Kramers transition rate \(r_{{\text{k}}}\) transition between the two barriers, the random transition motion between the two potential Wells become an ordered transition motion consistent with the frequency of the periodic modulated signal, and the stochastic resonance occurs.

2.2 Normalized scale transformation

Limited by the adiabatic approximation hypothesis, stochastic resonance is only applicable to feature extraction of small signals with input signal amplitude and noise intensity less than 1. In practice, when bearings fail, the output signals are large signals with amplitude and noise intensity greater than 1. In order to transfer the collected fault signals into the stochastic resonance model for effective extraction, the normalized scale transformation is introduced [9]. The normalized scale transformation is detailed in the following content.

When \(a > 0,b > 0\) and \(a,b\) are real numbers, assuming \(z = x\sqrt{\frac{a}{b}} ,\tau = at\), Eq. (3) can be transformed to Eq. (4):

$$\dot{z}\left( \tau \right) = z - z^{3} + \sqrt {\frac{b}{{a^{3} }}} \left[ {Af\left( {\frac{{2\pi f_{{\text{d}}} }}{a}\tau } \right) + N\left( {\frac{\tau }{a}} \right)} \right]$$
(4)

By assuming the scaling coefficient \(K = \sqrt {\frac{b}{{a^{3} }}}\), the step size \(H = {\raise0.7ex\hbox{$a$} \!\mathord{\left/ {\vphantom {a {f_{{\text{s}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${f_{{\text{s}}} }$}}\), where \(f_{{\text{s}}}\) is the sampling frequency, \(z\) is the stochastic resonance output and \(z\left( 1 \right) = 0\), then Eq. (4) can be solved by fifth-order Runge–Kutta algorithm with a high precision 0.

2.3 Adaptive stochastic resonance parameter optimization based on Gray Wolf algorithm

In order to extract characteristic signals effectively, the collected bearing fault signals are input into the stochastic resonance model for normalized scale transformation. Since the transformation coefficient \(K\) and step size \(H\) affect the stochastic resonance output \(z\) significantly, we applied GWO algorithm in the process of normalized scaling to obtain a higher SNR of output signal z. When the optimized parameters, noise intensity and nonlinear system are coordinated, the stochastic resonance output is effective, the characteristic frequency pulse is prominent, thus the fault characteristic signal can be effectively extracted.

Since the larger the signal-to-noise ratio is, the better the output of stochastic resonance is, then SNR is adopted as the objective function of stochastic resonance output. The SNR is expressed as follows:

$$SNR = 10\log \left( {\frac{{A_{{\text{d}}} }}{{A_{{\text{u}}} }}} \right)$$
(5)

In Eq. (5), \(A_{{\text{d}}}\) is the amplitude of periodic signal, and \(A_{{\text{u}}}\) is the amplitude of noise signal.

3 Grey Wolf Optimization algorithm

\(H\) and \(K\) parameters mentioned in Eq. (4) are very sensitive to the results of differential equations and directly affect the output of stochastic resonance. Particle swarm optimization, Genetic algorithm, Firefly algorithm, Ant colony algorithm and other algorithms are commonly used to solve the problem, but the above methods have long computing time, low computing accuracy, easy to fall into local optimal and other problems. Literature [16] compares these optimization algorithms with CS algorithm on parameter optimization, but the cuckoo algorithm still suffers from shortcomings such as optimization ability, convergence accuracy and calculation speed that need to be improved. In view of the good performance of the GWO algorithm, which can address the above problems properly, we adopts the GWO algorithm to optimize the parameters \(H\) and \(K\) in solving Eq. (4), in which Eq. (5) was taken as the object function in GWO.

3.1 Calculation principle of Gray Wolf algorithm

Gray wolves are at the top of the food chain, living in packs of 5 to 12 on average, and have a strict pyramid hierarchy. The gray wolf pyramid ranks \(\alpha ,\beta ,\delta ,\omega\) from top to bottom. Wolves search, surround and hunt prey by the first wolf \(\alpha\), the second and third wolves of the pyramid, and the bottom wolf \(\omega\) assists in hunting [17].

The predation process of gray wolves was transformed into a functional optimal solution to solve the problem. The distance between the individual wolf and its prey when the wolf is searching for prey is indicated as follows:

$$R = \left| {CX_{p} \left( t \right) - X\left( t \right)} \right|$$
(6)
$${\mathbf{X}}\left( {t + 1} \right) = {\mathbf{X}}_{p} \left( t \right) - {\mathbf{AR}}$$
(7)

The prey position vector is represented by \({\mathbf{X}}_{p} \left( t \right)\), the gray wolf position vector is \({\mathbf{X}}\left( t \right)\), the distance between the individual gray wolf and the prey is indicated by \(R\), and \(t\) is the number of iterations. The synergy coefficient of vector are represented by \(A\) and \(C\), respectively. Then, we have

$$A = 2ar_{1} - a$$
(8)
$$C = 2r_{2}$$
(9)

In the process of hunting, the value of convergence factor \(a\) decreases linearly from 2 to 0, and the value range of random vector \({\mathbf{r}}_{1}\) and \({\mathbf{r}}_{2}\) is [0, 1].

When the prey is surrounded, the position of the prey is determined according to the position of the wolves in the first three layers of the pyramid. And the distance between wolf \(\omega\) and the optimal wolf \(\alpha ,\beta ,\delta\) is estimated respectively to update its position. The distance between \(\omega\) and the optimal ones is as follows:

$$\left\{ \begin{gathered} R_{\alpha } = \left| {C_{1} X_{\alpha } - X} \right| \hfill \\ R_{\beta } = \left| {C_{2} X_{\beta } - X} \right| \hfill \\ R_{\delta } = \left| {C_{3} X_{\delta } - X} \right| \hfill \\ \end{gathered} \right.$$
(10)

After the distance between \(\omega\) wolves and optimal ones is obtained, the individual positions of gray wolves are updated:

$$\left\{ \begin{gathered} X_{1} = X_{\alpha } - A_{1} R_{\alpha } \hfill \\ X_{2} = X_{\beta } - A_{2} R_{\beta } \hfill \\ X_{3} = X_{\delta } - A_{3} R_{\delta } \hfill \\ \end{gathered} \right.$$
(11)
$${\mathbf{X}}(t + 1) = \frac{1}{3}\left( {{\mathbf{X}}_{1} + {\mathbf{X}}_{2} + {\mathbf{X}}_{3} } \right)$$
(12)

The process of gray wolf attacking prey was simulated by the random variable \(A\) decreasing linearly from 2 to 0 during the iteration. When \(A \le 1\), gray wolves begin to attack prey, and the optimal solution is obtained through convergence [17].

3.2 Parameter optimization of Gray Wolf algorithm

There are mutual effects among parameters such as step size and scale transformation factor. In this paper, the parameters of stochastic resonance are adjusted to achieve coordination with the system and noise intensity, so as to achieve the best effect of stochastic resonance output. In this paper, GWO was used to optimize the stochastic resonance parameter step size and scale transformation factor. Therefore, we can find the best matching value of the two parameters, improve the output SNR, and facilitate the extraction of stochastic resonance output characteristic frequency. Parameter setting of GWO: population number is 20, the number of population is 2.

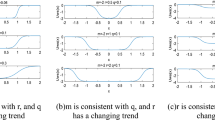
As can be seen from Fig. 3, as the value of \(H\) and \(K\) decreases, the output SNR becomes larger. Furthermore, the continuous adjustment and optimization of parameters \(H\) and \(K\) are conducive to the synergistic effect among the parameters of the nonlinear system, the intensity of noise and the nonlinear system, which demonstrates the stochastic resonance phenomenon.

Fig. 3
figure 3

Influence of GWO on output SNR after optimization of parameters H and K

Full size image

The calculation steps and technical flowchart of rolling bearing fault feature extraction based on GWO algorithm adaptive stochastic resonance are as follows (Seen from Fig. 4).

  1. (1)

    GWO is initialized to determine the number of iterations, the number of gray wolf population, the dimension of variables and the optimization range of parameters \(H\) and \(K\).

  2. (2)

    Initialization of the optimal fitness value. According to Eq. (7), the fitness values corresponding to wolf individuals are calculated. The SNR of the largest gray wolf individual is calculated as the global optimal fitness value, and the top three wolves with the best fitness are preserved.

  3. (3)

    Update the optimal fitness value. According to Eq. (12), update the current gray wolf position, update the convergence factor and cooperation coefficient vector, and recalculate the fitness value of the individual gray wolf. If the fitness value of the current individual gray wolf is better than that of the previous generation, then the updated current individual gray wolf is the global optimal fitness value.

  4. (4)

    Obtain the final optimal search results of parameters \(H\) and \(K\) according to the gray wolf individuals corresponding to the global optimal fitness value of the final output, and input the optimal search results of parameters into the stochastic resonance model for feature extraction of the collected signals.

Fig. 4
figure 4

Flowchart of GMO-SR algorithm

Full size image

4 Example verification results and discussion

In order to verify the feasibility and effectiveness of the method proposed in this paper, common bearing inner race wear faults (as shown in Fig. 5) are introduced, and CS and GWO are respectively used for comparative analysis.

Fig. 5
figure 5

Bearing inner race wear failure

Full size image

Experimental data were collected from the bearing failure data set collected in 2012 by Dr. Eric Bechhoefer, chief engineer of NRG system, on behalf of MFPT [20]. Bearing data and bearing working conditions are shown in Table 1.

4.1 Bearing fault signal calculation analysis and parameter optimization comparative analysis

Different from other noise elimination feature extraction methods stochastic resonance model is a feature extraction method of fault signal based on noise. Noise intensity is one of the factors that directly affect the output of stochastic resonance model. Since the original signal of bearing fault collected contains a lot of background noise, in order to make better use of noise intensity and make the output of the stochastic resonance model more conducive to fault feature extraction, the signal is pre-processed and filtered before the bearing fault signal is input into the stochastic resonance model. Multipoint Optimal Minimum Entroy Deconvolution Adjusted (MOMEDA) [21, 22] was used for the pre-processed method. The characteristics and advantages of the noise reduction effect of this method have been analyzed in [22]. MOMEDA is a method proposed by McDond [21] in 2017 to solve the deconvolution problem and solve the optimal filter by obtaining an infinite pulse sequence as the target. Filter length and test period are the parameters of MOMEDA. In [22], they obtained the parameter optimal filter length setting and the best value of test period through calculation and analysis. The parameters are set as follows: Filter length L = 1000, test period T = 70.

Fig. 6 show signal waveform and spectrum after MOMEDA preprocessing and filtering, respectively. As shown in spectrum diagram, there are many harmonics near the high frequency in the frequency band of 0–300 Hz, and the fault signal is submerged in the harmonic signal and cannot be extracted. The signal needs to be processed in the next step, and the filtered signal is input into the stochastic resonance model for fault feature signal processing.

Fig. 6
figure 6

Vibration signal pre-processing calculation and analysis of noise reduction diagram

Full size image

In addition to noise intensity, the transformation coefficient \(K\) and the step size \(H\) are also one of the factors affecting the feature extraction of the stochastic resonance model. In [16], CS algorithm was used to optimize the stochastic resonance parameters \(H\) and \(K\). Based on this study, GWO algorithm was applied in this paper to optimize the stochastic resonance parameters \(H\) and \(K\).

After MOMEDA noise reduction filtering, the signal is transformed into the bistable SR model, and the maximum SNR is searched by CS and GWO, respectively. Considering the influence of the parameters, maximum iteration time and cycle of the two algorithms, we set the maximum iteration cycle was the same in both optimization algorithm during the calculation and analysis. The maximum iteration time was set as 100, the population dimension was set as 2, and the number of the population was set as 20. CS and GWO optimization parameter settings are shown in Table 2.

Then, the iteration of the two above mentioned algorithms was analyzed and compared. The fitness convergence curves of the two optimization algorithms under the same conditions are shown in Fig. 7. It can be seen from the CS iteration curve in Fig. 7A that, at the beginning of optimization, it is linear and straight. When the number of iterations was 2, it fell into a local optimum, then converged when the number of iterations is 25. While in Fig. 7B, at the beginning of optimization, the curve varies linearly and then converged at 20. By comparative analysis, we know that the convergence curve of GWO is steep and the convergence speed is fast. Compared with CS algorithm, GWO algorithm achieves better performance in searching the optimal global solution.

Fig. 7
figure 7

Iterative curves of CS and GWO search algorithms [20]

Full size image

As shown in Table 3, The multipoint peak Kurtosis is represented by Mkurt. \(SNR_{{{\text{in}}}}\) and \(SNR_{{{\text{out}}}}\) represent the input SNR and the output SNR respectively. Within the same maximum number of iterations, the calculation time of GWO is 15 s, which is faster than that of CS optimization. The SNR of CS algorithm is 70.87%, while 72.01% for GWO. There is an obvious improvement in convergence speed. In a word, compared with CS algorithm, GWO gains higher computational speed, better performance in searching the optimal global solution, and also higher signal-to-noise ratio (Tables 2, 3).

Table 1 Bearing data and bearing working conditions
Full size table
Table 2 CS and GWO optimization parameter settings
Full size table
Table 3 Optimization results and related parameters of CS and GWO algorithms
Full size table

4.2 Feature extraction of bearing fault signals

In order to verify the advantages of GWO algorithm in parameter optimization and the practicability of the proposed method in feature extraction of fault signals, we uses the CS-optimizer and GWO-optimizer algorithms to calculate and analyze the optimal solution of stochastic resonance parameters \(H\) and \(K\) in coordination with nonlinear system and noise intensity to extract bearing fault signal.

GWO and CS parameter optimization algorithms were respectively used for comparative analysis of characteristic signal processing calculation of bearing inner race.

Figure 8 shows waveform diagram and spectrum diagram calculated by SR, and compared with Fig. 6 after noise reduction of vibration signal. Both optimization methods reduce noise and enhance the characteristic frequency of characteristic signal. Waveform diagram and spectrum diagram after CS-SR model processing are shown in Fig. 8A. It can be found that CS-SR model suppressed noise and highlighted fault signal characteristic frequency, but there were many harmonics, and there were many pulses with similar amplitude to characteristic frequency in harmonics, which easily affected the extraction effect of characteristic frequency.

Fig. 8
figure 8

Spectrum diagram of CS-SR and GWO-SR signal output

Full size image

Figure 8B demonstrates the GMO-SR signal processing diagram, in which the characteristic frequencies are highlighted and the low-frequency signals are few, and the characteristic signals are amplified. Thus, the superiority and practicability of the proposed methos is verified.

5 Conclusion

In this paper, we proposed a Grey Wolf Optimizer based adaptive stochastic resonance signal processing algorithm for rolling bearing weak fault feature extraction problem. The main advantage of the proposed method are high computational speed, signal-to-noise ratio and global optimal solution. To our best knowledge, these properties are essential for industrial applications, especially for large amplitude and noise intensity in rolling bearing fault signals or defect detection vibration signals.

While, whether the method can be applied to other noisy environments or composite fault detection is out of the scope of this work, which are the issues to be explored in future. In another opinion, machine learning method, such as Support Vector Machine (SVM) and Gaussian Process Regression (GPR), may carry out a more satisfying result as the good performance demonstrated in [23, 24]. In addition, the possible scheme for the compound fault sceneries, we could process the fault signals independently.