1 Introduction

A BLDC motor is controlled by electronic phase change, with simple structure, high power output and high efficiency. It is widely used in national defense, aerospace, robotics, industrial control processes, precision machine tools, automotive electronics, and household appliances [1]. At present, many studies on the control technology of BLDC motors. From the control method, the current research hotspot is the BLDC motor speed and torque ripple suppression method, which belongs to the application of advanced control strategy in order to improve the servo accuracy and expand the application range [2, 3].

The BLDC, motor control system, is a typical nonlinear, multivariable coupling system [4], and it is difficult for the traditional PI control algorithm to achieve high precision operation of the motor. Therefore, many researchers have made efforts to improve the control effect of the system and further expand the application scope of PI controller to achieve a speed control system with a wide speed regulation range, slight static difference, and superior following and anti-disturbance performance.

PI controllers produce hysteresis effects and create uncertainty problems in some practical situations of BLDC motor. To avoid these problems, fuzzy logic controllers (FLC) are developed. In [5], the fuzzy PI control algorithm is proposed to solve the problem of PI control with large overshoot and long setting time when switching speed. In [6], it was verified that the fuzzy controller system has a better response than the PI control. In [7], the parameters of the adaptive fuzzy PI controller are optimized using the genetic algorithm optimization toolbox. In [8], fuzzy system rules and PI parameters are adjusted online to minimize the fitness function. The fuzzy adaptive PI control system is designed to avoid lengthy fuzzy systems in [9]. In [10], the application of PI, FLC, PI + AW controllers in speed control is compared. In [11], the velocity characteristics of fuzzy proportional integral (FPI) controllers based on trigonometric membership functions (trimf) were evaluated.

From [5,6,7,8,9,10,11], all approaches support fuzzy logic-based controllers, although the performance of FLCs depends on the scaling factors of the FLC inputs and outputs, which can also affect the control system’s performance. To overcome these problems, nature-inspired algorithms such as the particle swarm optimized (PSO) algorithm are used to tuning the scaling factors of PID and FLCs to optimize the parameters in the control system.

In the past few years, various PSO algorithms have been proposed. Particle motion trajectory analysis and parameter selection have also been thoroughly explored two major research topics. Tang et al. [12] presented to optimize the control parameters of the controller using the PSO to obtain the optimal response error. Feng et al. [13] proposed optimizing the PID controller coefficients using an improved PSO algorithm to obtain the optimal trajectory tracking accuracy. Daraz et al. [14] applied the fitness-related optimization algorithms, integral time absolute error (ITAE), integral time square error (ITSE), integral square error (ISE), and integral absolute error (IAE) to optimize the controller. Ye and Li [15] presented an adaptive control strategy based on PSO algorithm and it was used to achieve approximate global optimization. Zhang and Yang [16] showed PSO’s new incremental PID control search strategy. Xiang et al. [17] presented updated particles using their past momentum and current orientation to speed up the convergence and adjust the search direction to get rid of the local optimum. Chiou and Li [18] studied the hybrid algorithm structure of PSO-EP to generate new parameters of the fuzzy PID controller. Cui et al. [19] focused on the relationship between PSO–PID parameters using stability theory. Bouallegue et al. [20] proposed a constrained PSO algorithm for solving the scale factor optimization problem of PID-type fuzzy structures. Ghoulemallah et al. [21] improved the speed control performance using the fuzzy-PSO technique. Chang and Shih [22] presented an improved PSO algorithm for find the optimal PID controller gain. Wang and Pu [23] tuned control of complex nonlinear systems using PSO–PID. Gani et al. [24] studied the application of PID controller based on particle swarm algorithm and Z–N algorithm.

To sum up, above, the FLC is an advanced control method capable of overcoming uncertainties and nonlinear parameters [25]. Nevertheless, FLC still has no adaptive capability and no learning mechanism, so difficulties arise in redesigning and adapting when new rules are applied. PSO algorithm is a technique for finding optimal solutions through the interaction between individuals in a population. Many studies have shown that PSO algorithms can overcome getting trapped in local optima.

Initially, many conventional speed controllers and other machine learning models available, but based on their use and application, these controllers had several limitations. After that, there was always a need to use the latest techniques to further improve and perform BLDC motors with better speed control and enable the motors to be widely used. Therefore, the aim of this paper is to develop a new PF-PI based speed controller for effective control of BLDC motor.

The remaining section of this paper is structured as follows: the mathematical modeling of the BLDC motor is provided in Sect. 2. Section 3 details the controller optimization method. Section 4 selects the appropriate performance indicator as the fitness function. In the end, summarizing the simulation results and analysis.

2 Mathematical modeling

2.1 BLDC motor modeling

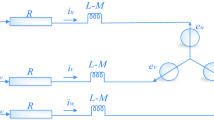
The original voltage equation for the armature voltage of a brushless DC (BLDC) motor is derived as follows:

$$ \begin{gathered} U_{a} = R \cdot I_{a} + \frac{d}{{dt}}(L_{a} \cdot I_{a} + M_{{ab}} \cdot I_{b} + M_{{ac}} \cdot I_{c} ) + e_{a} , \hfill \\ U_{b} = R \cdot I_{b} + \frac{d}{{dt}}(L_{b} \cdot I_{b} + M_{{ba}} \cdot I_{a} + M_{{bc}} \cdot I_{c} ) + e_{b} , \hfill \\ U_{c} = R \cdot I_{c} + \frac{d}{{dt}}(L_{c} \cdot I_{c} + M_{{ca}} \cdot I_{a} + M_{{cb}} \cdot I_{b} ) + e_{c} , \hfill \\ \end{gathered} $$
(1)

where \(L\) is the armature self-inductance, \(M\) is the armature mutual inductance, \(R\) is the armature resistance of the stator phase windings, \(V_a\), \(V_b\), \(V_c\) are the terminal phase voltages, \(I_a\), \(I_b\), \(I_c\) are the input currents of the motor, and \(e_a\), \(e_b\), \(e_c\) are the trapezoidal counter-electromotive forces of the corresponding phases.

Since the three-phase current satisfies the condition by

$$ I_a + I_b + I_c = 0. $$
(2)

Equation (1) can be further simplified so that the matrix form of the phase voltage equation for BLDC motors can be expressed as

$$ \left[ \begin{gathered} U_a \hfill \\ U_b \hfill \\ U_c \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} R & 0 & 0 \\ 0 & R & 0 \\ 0 & 0 & R \\ \end{array} } \right]\left[ \begin{gathered} I_a \hfill \\ I_b \hfill \\ I_c \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} {L - M} & 0 & 0 \\ 0 & {L - M} & 0 \\ 0 & 0 & {L - M} \\ \end{array} } \right]\frac{d}{dt}\left[ \begin{gathered} I_a \hfill \\ I_b \hfill \\ I_c \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} e_a \hfill \\ e_b \hfill \\ e_c \hfill \\ \end{gathered} \right]. $$
(3)

In order to form a complete mathematical model of an electromechanical system, it is also necessary to introduce the motor equations of motion.

$$ T_e - T_L = J\frac{d\Omega }{{dt}} + B \cdot \Omega , $$
(4)

where \(J\) is inertia, \(B\) is friction coefficient and \(T_L\) is load torque.

2.2 PI controller design

The structure of a conventional PI controller is shown in Fig. 1. The parallel structure of a PI controller is expressed in Eq. 5 as

$$ PI = K_p + \frac{K_I}{S}. $$
(5)
Fig. 1
figure 1

Structure of conventional PI controller

Full size image

The controller processes the error signal directly. In the design phase, the controller parameters Kp, KI depend on the closed-loop feedback system, and its regulation usually relies on three ways according to the actual situation, namely critical proportionality method (Z–N), decay curve method and empirical adjustment method [26].

It is practically impossible to achieve an ideal PI controller. Therefore, by using advanced control methods and optimization algorithms, a response closer to the ideal state can be achieved.

3 The scheme of optimization

3.1 Fuzzy logic controller design

FLC design technology broadly consists of three parts: fuzzification, fuzzy rules (knowledge base and fuzzy inference), and defuzzification [27]. The fuzzy control technology has the characteristics of broad applicability and robustness to time-varying loads.

The fuzzy control has two inputs and two outputs. The two inputs are the error \(e\) and the error rate of change \(ec\). The two outputs are \(Kp\) and \(Ki\) parameters. The size of the scaling factor \(\Delta Kp\) and \(\Delta Ki\) has a great impact on the FLC control performance, which can fundamentally change the output characteristics of the system. Fuzzy logic-PI (F-PI) controller structure is shown in Fig. 2.

Fig. 2
figure 2

Structure of F-PI controller

Full size image

The \(e\) and \(ec\) can be taken as seven linguistic variables (NL, NM, NS, ZE, PS, PM, PL) corresponding to negative large, negative medium, negative small, zero, positive small, positive medium, positive large.

Fuzzy rules are derived from expert knowledge, experience, etc. It is essentially a rule lookup table in the form of “if … and … then …”, and given \(e\), \(ec\) yields 49 different outputs \(Kp\), \(Ki\). The fuzzy rule list is given in Tables 1 and 2.

Table 1 Fuzzy rule list for \(Kp\) and \(e\), \(ec\)
Full size table
Table 2 Fuzzy rule list for \(Ki\) and \(e\), \(ec\)
Full size table

The minimum operation (Mamdani), which takes the minimal value of the membership function (MF). The Mamdani method is used for fuzzy inference, and the center of gravity method is used for defuzzification. The MF using trimf, the output of \(Kp\) and \(Ki\) in NL adopts zmf, PL adopts smf. The theoretical domain of \(e\), \(ec\) can be determined as \(e \in ( - 6,\;6)\), \(ec \in ( - 6,\;6)\). The theoretical domain of \(Kp\), \(Ki\) can be set as \(Kp \in (1,\;6)\), \(Ki \in (0,\;1)\). The MF and domain of each variable are shown in Fig. 3. The surface viewer of the input and output relationship rules is shown in Fig. 4.

Fig. 3
figure 3

Setup FLC of a \(e\), \(ec\) MFs and domains, and b \(Kp\), and c \(Ki\) MFs and domains

Full size image
Fig. 4
figure 4

Surface viewer of rules a relationship of \(e\), \(ec\) and \(Kp\) and b relationship of \(e\), \(ec\) and \(Ki\)

Full size image

3.2 Particle swarm optimization technology

The PSO algorithm is a flock iterative search algorithm, proposed by Kennedy and Eberhart [28]. The PSO algorithm has the characteristics of a simple algorithm, easy to implement, and not too many parameters to be adjusted.

In the process of finding the optimal values of \(\Delta Kp\) and \(\Delta Ki\), the update rate and position solution of each particle are given by

$$ v_k + 1 = w \times v_k + c1 \times (pbest_k - x_k) + c2 \times (gbest_k - x_k), $$
(6)
$$ x_k + 1 = x_k + v_k + 1, $$
(7)

where \(v_k\) is the velocity vector of the particle, \(x_k\) is the position of the particle, \(pbest_k\) is the optimal solution position found by the particle itself, and \(gbest_k\) is the optimal solution position currently found by the whole population. \(w\) is the inertia weight. \(c1\) and \(c2\) are two learning factors. These two factors are used to adjust the strength of \(pbes_tk\) and \(gbest_k\) on particle attraction. \(c1\) and \(c2\) are in the range of [0, 2]. \(v_k\), \(pbest_k - x_k\) and \(gbest_k - x_k\) are used as the sum of vectors, which is denoted by \(v_k + 1\). The maximum value of particle velocity in each dimension is less than \(v_max\).

Due to the PSO algorithm has fallen into a local optimal solution. Shi [29] introduced the inertia weight formula

$$ w = {\text{w}}_{{{\text{max}}}} - ({\text{w}}_{{{\text{max}}}} - {\text{w}}_{{{\text{min}}}})g/G,$$
(8)

where \(g\) generation index represents the current number of evolutionary generations, and \(G\) is predefined maximum number of generations. Here max and min are set to 1 and 100 respectively.

In this paper, the PF-PI controller with proposed method is shown in Fig. 5. PF-PI controller of BLDC motor algorithm flow chart is shown in Fig. 6. The implementation parameters of PSO are given in Table 3.

Fig. 5
figure 5

PF-PI controller with proposed method

Full size image
Fig. 6
figure 6

PF-PI controller of BLDC motor algorithm flow chart

Full size image
Table 3 Implementation parameters of PSO
Full size table

The steps of the proposed PF-PI Algorithm are as follows:

  1. Step 1.

    Initiate the parameters such as particle swarm size, parameters range, iterations, dimensions and factors \(w\), \(c1\) and \(c2\).

  2. Step 2.

    Initially, start with the random position of particles. Determine the fitness function.

  3. Step 3.

    Estimate each particles fitness value using @PSO_PI.

  4. Step 4.

    Update the position and speed of particle.

  5. Step 5.

    Repeat step (2) in the new position and speed.

  6. Step 6.

    If the required solution is obtained, go to the outcome, else return the first step.

  7. Step 7.

    Achieve the best optimal solution.

4 Simulation and discussions

4.1 BLDC motor modeling based on PF-PI structure controller

BLDC motor system simulation control scheme based on PF-PI structure controller is as follows.

The design of BLDC motor controller needs to consider the working environment, load characteristics, position detection method, etc. The goal is to achieve a control system with a wide speed regulation range, slight static difference, superior following and anti-disturbance performance.

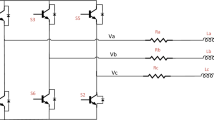
The modeling is done using the dynamic system modeling toolbox in Simulink, which is completed by assembling according to the module connection relationship of each component. According to the motor circuit connection and motion relationship, the necessary modules of the system are: PWM module of HPWM-LON modulation mode, three-phase inverter, BLDC motor, signal acquisition, Hall sensor, feedback current calculation, powergui. Hall sensor is mainly applicable to 120° energized control, and every 60° to obtain a signal.

The system is built-in discrete time frame. Simulation time is set to 1 s, discrete sampling time 5e−06 s. The start-up method is load start, initial load torque is 1 N m, given speed 1500 rpm, 0.35 s increase load torque 4 N m, speed increase to 3000 rpm at 0.5 s.

The working principle of conventional control of BLDC motor is explained as follows:

First, the difference between the reference speed and the feedback speed is the speed error supplied to the speed controller. This module uses a classical PI controller, which processes the speed error and gives a loss based on the reference torque (\(Te\)), then the DC power is chopped into a PWM wave by a PWM chopper. Then a drive signal is given to the inverter based on the logical relationship between the state of the switching tubes and the presence of Hall signals. Thus, the average value of the voltage applied to both ends of the armature is changed to regulate the speed of the motor. The PWM control power switching tube modulation is used in the HPWM-LON modulation mode.

The BLDC motor simulation model of PF-PI structure controller is shown in Fig. 7. The logical relationship between the switching tube state and Hall signal is given in Table 4. Implementation parameters of the BLDC motor is given in Table 5.

Fig. 7
figure 7

BLDC motor simulation model of PF-PI structure controller

Full size image
Table 4 Logical relationship between switching tube state and Hall signal
Full size table
Table 5 Implementation parameters of BLDC motor
Full size table

4.2 Selection of performance indicators

The PI controller and F-PI controller are optimized using the PSO algorithm. The optimization factor is the scale factor, and the fitness function performance indicators are used to evaluate the model by ITAE, ITSE, and ISE. The ITAE performance indicator is finally selected.

$$ ITAE = \int_{0}^{\infty } {t \cdot \left| {e(t)} \right|dt} , $$
(9)
$$ ITSE = \int_{0}^{\infty } {t \cdot e(t)^{2} dt} , $$
(10)
$$ ISE = \int_{0}^{\infty } {e(t)^{2} dt} . $$
(11)

Three performance metrics, ITAE, ITSE, and ISE, are used to verify the feasibility of PSO. These metrics are allowed to optimize the PF-PI controller for 50 generations, respectively. The PI optimization curves and the associated fitness function values are obtained. This is used to select the best performance indicator fitness function. Optimization of scale factors for PF-PI controller using ITAE, ITSE, and ISE, respectively, shown in Figs. 8 and 9. Optimization of the three performance indicators under the velocity response curve is shown in Fig. 10.

Fig. 8
figure 8

Optimization of scale factors for PF-PI controller using a ITAE, b ITSE, and c ISE

Full size image
Fig. 9
figure 9

Optimization of fitness values for PF-PI controller using a ITAE, b ITSE, and c ISE

Full size image
Fig. 10
figure 10

Optimized enlargement of the three performance indicators under the velocity response curve

Full size image

According to the following figures, the scale factor and fitness values are iteratively stabilized at 2, 27, and 33 generations when using ITAE, ITSE, and ISE metrics, respectively, and the speed response curve performance. It can be known that using ITAE as the performance indicator of PSO algorithm is the best in this model.

4.3 Analysis of experimental results with 100 iterations of the model using ITAE

After selecting ITAE as the best fitness function for this model, the P-PI controller is compared with the F-PI controller. The optimization results are shown in Figs. 11 and 12. From the results in the figure, it can be seen that the P-PI controller model has the best \(Kp = 1.76745,\) \(Ki = 0.371068,\) and the fitness value is 14.2071; the PF-PI controller model has the best \(Kp = 0.578728,\) \(Ki = 2.6598,\) and the fitness value is 7.73426.

Fig. 11
figure 11

P-PI controller optimal a scale factor and b fitness value

Full size image
Fig. 12
figure 12

PF-PI controller optimal a scale factor and b fitness value

Full size image

4.4 Analysis of experimental results

The simulation results were verified for the case of variable speed with load. The speed response curve under different conditions with load is shown in Fig. 13. The torque ripple curve under different conditions with load is shown in Fig. 14.

Fig. 13
figure 13

Speed response curves of variable speed sudden addition disturbance load start under different conditions

Full size image
Fig. 14
figure 14

Torque response curves of variable speed sudden addition disturbance load start under different conditions

Full size image

According to the torque ripple Eq. (12), the torque ripple under the P-PI controller and PF-PI controller can be known. The speed performance comparison under different schemes is given in Table 6. The torque ripple ranges under different schemes are given in Table 7. Torque ripple equation is given by

$$ {\text{Torque}}\;{\text{ripple}}\;(\% ) = \frac{{T_{\max } - T_{\min } }}{{T_{avg} }} \times 100. $$
(12)
Table 6 The speed performance of different schemes
Full size table
Table 7 The torque ripple ranges under different schemes
Full size table

From the speed response curve, it can be learned that the PF-PI controller model has the best speed characteristics compared to PI, P-PI, and F-PI controllers. It can be clearly seen that the overshoot, rise time and settling time of the control system under the PF-PI controller are better than the classical PI controller.

4.5 Controller performance testing and analysis

In order to verify the effect of the controller on medium and high range operation, the servo responses from stand still to 1500 rpm and from stand still to 3000 rpm were tested respectively. It is also necessary to analyze and experimentally verify the controller's operation with load and no-load conditions. Meanwhile, to demonstrate that the PF-PI controller can satisfy 4-quadrant operation, the speed and torque reverse curves of variable speed with sudden disturbance load start are given in Fig. 15. The speed response curves of sudden addition disturbance load start under different conditions are shown in Figs. 16 and 17. The torque ripple curves of no-load start under different conditions are shown in Figs. 18 and 19.

Fig. 15
figure 15

Reverse operation curves of variable speed sudden addition disturbance load start a speed and b torque

Full size image
Fig. 16
figure 16

Speed response curves of sudden addition disturbance load start under different conditions a 0–1500 rpm and b 0–3000 rpm

Full size image
Fig. 17
figure 17

Speed response curves of no-load start under different conditions a 0–1500 rpm and b 0–3000 rpm

Full size image
Fig. 18
figure 18

Torque ripple curves of sudden addition disturbance load start under different conditions a 0–1500 rpm and b 0–3000 rpm

Full size image
Fig. 19
figure 19

Torque ripple curves of no-load start under different conditions a 0–1500 rpm and b 0–3000 rpm

Full size image

In Fig. 15, it can be seen that the PF-PI controller has symmetrical speed response and torque ripple under reverse operation. Therefore, the PF-PI controller satisfies the control conditions for 4-quadrant operation.

In Fig. 16, under sudden addition disturbance load start, the speed response curve shows that the PF-PI controller has the fastest speed response and is able to quickly stabilize to the specified speed command at 0.5 s. In Fig. 17, under no-load start, the speed response curve shows that the PF-PI controller has higher relative overshoot for medium speed 0–1500 rpm range operation, but has the best performance with no overshoot for 0–3000 rpm range operation. In general, no-load start has higher overshoot compared to load start in the medium speed 0–1500 rpm range operation.

In Figs. 18 and 19, it can be seen that the PF-PI controller has less torque ripple under no-load start and sudden addition disturbance load start conditions. The robustness of the PF-PI torque is better when subjected to sudden load addition at 0.5 s.

5 Conclusion

In this paper, the optimal PF-PI controller is proposed for the BLDC motor to achieve speed control effectively. PSO is used for scaling factor adjustment of the PF-PI controller. The presented controller is evaluated on MATLAB/Simulink platform, and the fitness function performance indicators are analyzed. From the results, it is seen that the motor is settled down faster and lower vibration. The stability analysis performance indicators viz ITAE, ITSE, ISE values are improved in this proposed method. Finally, the superiority of the proposed PF-PI controller is demonstrated. It is suitable for obtaining a smooth speed response over a wide speed range while reducing torque ripple. Also, the proposed method may give a new dimension towards the controller design field for a BLDC motor drive system.