1 Introduction

Groundwater models serve as support tools to assess water resources, evaluate management strategies, design remediation systems and optimize monitoring networks [1,2,3,4]. As such, results of numerical groundwater models guide decision makers on practical issues of public concern [5]. Therefore, the correct development of groundwater models and their ability to simulate the functioning of real groundwater systems are important beyond the realm of particular engineering or environmental projects. As a minimum, it is expected that models are able to reproduce observed data and that their results can be used as reasonably approximations to evaluate future or hypothetical scenarios for groundwater systems. This requires the integration of observations and models through calibration [6,7,8,9]. Furthermore, it is generally also important to quantify the uncertainty of the model results in order to include it into the risk associated to decisions supported by them [10, 11].

The increase in computational power and availability of new software have made possible the development of complex mathematical models to simulate groundwater systems [11,12,13,14,15,16]. Until recently, such models were developed, calibrated and analyzed in ad hoc ways, e.g. using trial and error for calibration and the manual variation of selected parameters for sensitivity analysis. However, the level of complexity and the number of parameters included in new models have made necessary the use of more systematic approaches [11, 13, 17, 18]. Methodological frameworks for these purposes have become available during the past decades; some were brought to groundwater modelling from other fields, such as the oil industry or climate science [10, 19, 20]. However, the correct application of a systematic approach to develop, calibrate and analyze the results of such mathematical models is challenging, because it requires understanding and applying concepts that are far beyond traditional groundwater hydrology from disciplines such as linear algebra, calculus, and geostatistics. There are books, technical documents and detailed review articles about the subject [7,8,9,10,11, 13, 17, 20,21,22]. However, there is still much need for a brief, simple and practitioner oriented introductory discussion that explains with the use of only a few equations the functioning of sophisticated software tools that modelers apply nowadays.

Previous articles [16, 23] used simple groundwater models to discuss problems that may arise when trying to calibrate them and assess the uncertainty of their results. Freyberg [23] reported on the results of an exercise performed by graduate students who used trial and error (manual calibration) to calibrate a synthetic groundwater model using only a set of observed piezometric head values. The main findings of that exercise were that groups of students used very different strategies to accomplish the calibration and that their results were in some cases quite different. Moreover, the quality of the forecasts performed with the calibrated models, assuming slightly different boundary conditions to the ones considered for calibration, was wide-ranging and, surprisingly, it did not correlated well with the quality of the calibration. Calibrated models that had low residuals between simulated and observed piezometric heads did not provide better forecasts than calibrated models that had larger residuals. The group of students that reported the worst prediction used different values of hydraulic conductivity for each cell of the model. Moreover, the quality of the forecasts did not directly correlate with the ability of the modelers to find the correct values of the hydraulic conductivity used in the synthetic model adopted as virtual reality. Freyberg [23] explained some of the results of the exercise based on the theoretical understanding about parameter estimation for groundwater models available at the time. The solution of the inverse problem to estimate parameters of groundwater models, even discounting differences in their conceptualization, admits multiple solutions [7]. The non-uniqueness of the solution can be due to a larger number of parameters than available observations or to correlation between parameters [16]. For example, the problem reported by [23] considered 1389 unknown values of hydraulic conductivity (parameters), but only 22 piezometric head measurements. The findings of [23] established reservations with respect to the end result of the calibration of groundwater models and its usefulness to reduce the uncertainty of forecasts.

Recently, [16] revisited the original problem presented by [23], this time applying the latest available automatic parameter estimation and uncertainty analysis techniques, including mathematical regularization techniques based on subspace methods to decrease the effective number of parameters included in the inverse problem [10, 13]. Their main findings were that automatic calibration of even highly parameterized models could be constrained, i.e. the potential large number of multiple solutions could be reduced to a much lower number, by including a single groundwater flow estimation as additional information to the available piezometric heads. [16] found that the use of automatic frameworks for parameter estimation resulted in better-calibrated models that produced improved forecasts when compared to the original results presented by [23], which demonstrated the potential usefulness of using recently developed methods. Then, contrary to one of the conclusions of [23], highly parameterized models with many parameters performed better than simple models with fewer parameters. The solution of the inverse problem for highly parameterized models, which demands a large number of model runs, is well suited for increasingly available parallel platforms. Thus, the calibration of this type of models is becoming more accessible in practical applications. On the other hand, [16] also concluded that good calibration does not necessarily imply good forecasts assuming slightly different forcing terms, e.g. boundary conditions, to the scenario considered for calibration.

The main objective of this article is to explain, using an example, the main concepts required to calibrate a physically based mathematical model to simulate a groundwater system, assess its sensitivity and estimate the uncertainty of its results. We explain the main steps that are required and comment on some of the main pitfalls that can arise. We use as example a simplified model of a real natural setting previously studied as part of a long-term environmental study [24, 25]. To promote the use of simple analytical calculations to gain understanding that can be useful to interpret the results of more complex numerical models and to overcome some numerical challenges for obtaining reliable numerical solutions for this particular setting, we use an analytical model instead of a numerical groundwater model [26]. Therefore, this article aims to address the needs of modelers interested in applying methods for parameter estimation and uncertainty analysis. It also attempts to be useful for decision makers who base their decisions on the results of groundwater models and need to understand their potential and limitations. Finally, since this article provides a practitioner-oriented introduction to the topic, it can also serve as material for an advanced graduate level groundwater modeling course.

This article is structured in four main sections, including this introduction. In the next section we describe the Example problem that we use throughout the article. Next, we present a mathematical analysis of the application of parameter estimation and uncertainty analysis for the Example problem. Finally, we provide some concluding remarks based on the results presented in the other sections.

2 Example description

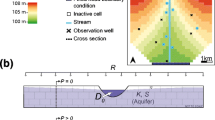
We will consider as example the estimation of the position of the phreatic surface (water table) for an aquifer located between two rivers as shown in Fig. 1. Both rivers are separated by a distance \(L\) [L], the aquifer receives a constant recharge rate \(R\) [L/T], and we assume that there is only one observed value of the piezometric head \(h\) [L], \(h_{w}\), at the position of an existing well \(x_{w}\) [L]. This example corresponds to an idealization of a real groundwater system previously analyzed as part of an environmental study [24, 25] and, hence, it provides a realistic case problem. The numerical solution for this problem is challenging because it requires simulating the position of the water table, which for this case is very sensitive to the grid resolution due to the potential occurrence of high hydraulic gradients as result of the combination of recharge and low hydraulic conductivity. See the Supplementary Material for details about the difficulties to obtain reliable numerical solutions for this example.

Fig. 1
figure 1

Schematic of conceptual problem: Water table position for a phreatic aquifer located between two rivers that are connected to the groundwater system, so that they act as prescribed piezometric head boundary conditions

Full size image

This example provides a reasonable case of study of practical interest that is similar to many other cases (i.e. unconfined aquifer with recharge) that occur often in practice, while it includes only a limited number of parameters. Thus, the detailed explanation of the application of the methods for parameter estimation and uncertainty analysis can be kept brief. The development of a mathematical model to simulate a groundwater system similar to this example includes three main parts:

  1. (a)

    Conceptual model We consider only the part of the subsurface that is completely saturated and that the aquifer behaves as unconfined, so that all recharge \(R\) enters directly and immediately to the aquifer. Furthermore, the two rivers are connected to the aquifer and can be modeled as prescribed head boundary conditions, \(h_{1}\) and \(h_{2}\). The water elevation in both rivers and the recharge rate are relatively stable, so that we can model the system as steady-state. Given the different magnitude of the flow discharge in both rivers, it is likely that the shallow aquifer contains at least two materials of different grain size with an interface located at position \(x_{K}\) [L]. Based on experience and comparison with similar sites, it is estimated that the values of \(K_{1} \in k_{1} \left[ {0.1,10} \right]\) [L/T] and that \(K_{2} \in k_{2} \left[ {0.1,10} \right]\) [L/T], where \(k_{1}\) and \(k_{2}\) represent a scale of the magnitude of \(K\) for both materials. Therefore, the range of variability of \(K\) for each hydrogeological unit is two orders of magnitude, which for hydraulic conductivity is a reasonable estimate without additional information [27]. We use dimensionless variables to define parameters that have the same units: \(f_{K} = k_{2} /k_{1}\), \(f_{R} = R/K_{1}\) and \(f_{h} = \left( {h_{2} - h_{1} } \right)/L\). The parameters are set such that recharge is never higher than hydraulic conductivity.

  2. (b)

    Mathematical model Darcy Law describes the saturated flow system, which combined with the mass balance equation results in a partial differential equation. We assume that the Dupuit approximation is valid, i.e. flow is preferentially horizontal, so that vertical piezometric gradients and velocity component are negligible [28]. Furthermore, the thickness of the saturated aquifer is equal to the piezometric head or water table elevation, so that the datum level considered for computing the energy of the flow coincides with the horizontal bottom of the aquifer.

  3. (c)

    Evaluating solution Given these assumptions, the piezometric head as a function of the position measured from River 1, \(x\), can be calculated from

    $$h^{2} \left( x \right) = \left\{ {\begin{array}{*{20}l} {a_{1} x^{2} + b_{1} x + c_{1} ,} \hfill & {x \le x_{K} } \hfill \\ {a_{2} \left( {x - x_{K} } \right)^{2} + b_{2} \left( {x - x_{K} } \right) + c_{2} } \hfill & {x > x_{K} } \hfill \\ \end{array} } \right.$$
    (1)

The analytical solution depends upon the hydraulic conductivity \(K\) and piezometric head \(h\). The constant coefficients of both polynomials can be evaluated from both boundary conditions, \(h\left( {x = 0} \right) = h_{1}\) and \(h\left( {x = L} \right) = h_{2}\), and imposing continuity of the water table and flow through the interface, i.e. \(h\left( {x_{K}^{ - } } \right) = h\left( {x_{K}^{ + } } \right)\), and \(- K_{1} \left[ {h\frac{\partial h}{{\partial x}}} \right]_{{x_{K}^{ - } }} = - K_{2} \left[ {h\frac{\partial h}{{\partial x}}} \right]_{{x_{K}^{ + } }}\).

The model can be written most concisely as \(h\left( x \right) = h\left( {\left\{ {K_{1} ,K_{2} } \right\};\left\{ {h_{1} ,h_{2} ,R} \right\}, x} \right)\), where we can identify the following sets of output variables \({\varvec{o}} = \left\{ h \right\}\), input parameters to be estimated \({\varvec{e}} = \left\{ {K_{1} ,K_{2} } \right\}\), and forcing input variables \({\varvec{f}} = \left\{ {h_{1} ,h_{2} ,R} \right\}\). We have left \(R\) as a forcing parameter for reasons that will become clear later.

Although we perform this analysis based on an analytical solution, the same type of reasoning applies to a numerical model that solves similar partial differential equations, since the numerical solution should converge to the analytical solution. The comparison between the analytical and numerical solutions presented in the Supplementary Material, demonstrates that despite the presence of vertical gradients in this case, the analytical solution based on the Dupuit approximation provides an adequate approximation. For this example, the solution (analytical or numerical) for the position of the water table at a given location in the aquifer can be highly non-linear with respect to the input parameters (\(K_{1}\) and \(K_{2}\)) depending on the settings of the problem as shown in the Supplementary Material. The non-linear behavior of the solution can represent additional challenges for the application of automatic techniques to estimate parameters and for assessing the uncertainty of the model results.

3 Mathematical analysis

3.1 Water table

Considering a homogeneous aquifer with a single material, i.e. single \(K\) value, the mathematical solution reduces to

$$h^{2} \left( x \right) = ax^{2} + bx + c$$
(2)

where \(a = - R/K\), \(b = \left( {h_{2}^{2} - h_{1}^{2} - aL^{2} } \right)\)/L and \(c = h_{1}^{2}\). Thus, different values of recharge \(R\) and hydraulic conductivity \(K\) that result in the same ratio \(R/K\) produce the exact same value of \(h\left( x \right)\), i.e. \(K\) and \(R\) are strongly correlated. We can only estimate either \(K\) or \(R\), or the combination of both \(R/K,\) which sometimes can be used as a surrogate or modified parameter for calibration. Therefore, we excluded \(R\) from the set of parameters that must be estimated. It is also direct from (2) that piezometric head depends in a non-linear fashion with the input parameters of the problem, \(K\) and \(R\).

Figure 2 shows simulated water table elevations for the homogeneous case (\(f_{K} = 1.00)\). The water table has a parabolic shape that is the result of the difference between the prescribed head values at both boundaries and recharge that produces the mounding of the water table between both rivers. For this case, the magnitude of the maximum mounding due to recharge is proportional to \(R/K\) [26]. For \(f_{R} = 1 \times 10^{ - 3}\) mounding is limited and all recharged water exits the model domain through the boundary with lower prescribed head on the left side, while water also enters the domain through the right boundary with higher \(h\). Increasing the recharge rate, while keeping the values of hydraulic conductivity, i.e. larger \(f_{R}\), would result in larger mounding.

Fig. 2
figure 2

Water table as a function of position between both rivers for two ratios of hydraulic conductivity, \(f_{K} = K_{2} /K_{1}\). a Homogeneous and b heterogeneous aquifer. Dashed red line shows position of interface between materials \(x_{K}\)

Full size image

Figure 2 also shows the solution for heterogeneous case (\(f_{K} = 0.01\)). Since we assume that \(K_{2}\) is a couple of orders of magnitude smaller than \(K_{1}\), we observe that the mounding effect within material 2 is significantly larger than in material 1, and a flow divide occurs within material 2. Then, the only water that enters and exits the domain comes from recharge, i.e. the total flow is \(Q = R L\) [L2/T], which exits through the right and left boundaries.

3.2 Sensitivity analysis: Jacobian matrix

We numerically compute the Jacobian, \({\mathbf{J}}\), or sensitivity matrix to quantify the local sensitivity of the model, i.e. the magnitude of the changes of the results due to changes in the input parameters. The element of \({\mathbf{J}}\) that corresponds to the result \(r\) and input parameter \(p\), is defined as

$$J_{rp} = \frac{\partial r}{{\partial p}}$$
(3)

Then, \({\mathbf{J}}\) can be evaluated using a first-order forward finite-difference approximation, to obtain

$${\mathbf{J}}\left( {\left\{ {K_{1} ,K_{2} } \right\}{|}{\mathbf{f}},{\text{x}}} \right) = \left[ {\frac{{{\Delta }h}}{{{\Delta }K_{1} }},\frac{{{\Delta }h}}{{{\Delta }K_{2} }}} \right]$$
(4)

Figure 3 shows normalized values of the components of the sensitivity matrix as function of position along the model domain. The fact that the components of \({\mathbf{J}}\) are equal to 0 at both boundaries indicates that the results of the model do not change at those positions independently of the values of the parameters, as it would be expected when applying prescribed head values at both boundaries. Two interesting results derive from this. First, values of head near the boundaries are less sensitive to changes in parameters than values located toward the center of the domain. Second, observations of wells located near both extremes are less relevant or provide less meaningful information for the calibration of \(K\) than observations collected near the position of the interface between both materials, since the simulated head at those positions does depend upon the values of the parameters [10, 17, 20]. This last conclusion has importance for real-world models that consider observations measured at tens or hundreds of different locations within a model domain. Moreover, if we had to decide where we should collect data or drill a new borehole to measure piezometric levels, we would select a location near the center between both rivers, since the variability of the results is greatest at that location.

Fig. 3
figure 3

First component of sensitivity matrix or Jacobian (\({\mathbf{J}}\), defined in Eq. 3) as function of the position of the observation well. a Homogeneous and b heterogeneous aquifer. Dashed red line shows position of interface between materials \(x_{K}\) and blue line shows position of well with measured head \(x_{w}\)

Full size image

It is important to notice the drastic change in the shape of \(J_{12}\) between the homogeneous and heterogeneous cases. In the latter, the simulated water table within material 1 is almost completely independent of the value of \(K_{2}\). Hence, any measurement of piezometric levels taken from a borehole located within material 1 would provide no relevant information for the estimation of \(K_{2}\). This result can vary between both extremes presented here, homogeneous and heterogeneous case, depending upon the specific value of \(f_{K}\).

The fact that the components of the sensitivity matrix, \({\mathbf{J}}\), change with \(x\) and with the ratio between both values of \(K\) in a non-linear fashion, confirms that it only provides a measure of the local-sensitivity of the model around a given set of input parameters. This information may not be enough to evaluate the overall performance of complex models that include non-linear relations between parameters and results and many parameters for other material distributions or locations.

3.3 Calibration: inverse problem

We use the single measurement of \(h\) that is available to constrain or condition the values of \(K_{1}\) and \(K_{2}\), i.e. to calibrate the parameters of the model. Once we have evaluated the Jacobian of the model at the position of the well with observed piezometric head \(h_{w}\), we can write a first-order Taylor series approximation to get

$$h_{w} \left( {\left\{ {K_{1} + {\Delta }K_{1} ,K_{2} + {\Delta }K_{2} } \right\}{|}{\mathbf{f}},x_{w} } \right) - h_{w} \left( {\left\{ {K_{1} ,K_{2} } \right\}{|}{\mathbf{f}},x_{w} } \right) = {\mathbf{J}} \cdot {\Delta }{\mathbf{K}} + \epsilon$$
(5)

where \({\Delta }{\mathbf{K}} = \left[ {{\Delta }K_{1} ,{\Delta }K_{2} } \right]\) and \(\epsilon\) corresponds to errors of the approximation that can be neglected. The last expression corresponds to Newton's method. Assuming that \(h_{w}^{i}\) represents the solution of the model for an initial set of variables \(\left\{ {K_{1} ,K_{2} } \right\}\) and \(h_{w}^{o}\) corresponds to the observed value at the well, we can write

$$h_{w}^{0} - h_{w}^{i} = {\mathbf{J}} \cdot {\Delta }{\mathbf{K}}$$
(6)

The solution of the linear system provides an expression to compute the magnitude of the variation of parameters \(K_{i}\) that required so that the results of the model are similar to the observed data. From linear algebra, we know that \({\mathbf{J}}\) has an inverse only if it is square and no singular, i.e. \(det\left( {\mathbf{J}} \right) \ne 0\). For the general case of rectangular matrices with more rows than columns, as happens when there are more observations than independent parameters, the solution of (6) can be found by using methods to solve over-determined linear systems, e.g. least squares [29]. When there are more parameters than observations, there is only a reduced number of parameter combinations that can be estimated [10, 13]. The combination of parameters that cannot be uniquely estimated, because they do not have effect on the output of the model, correspond to the null-space of \({\mathbf{J}}\) [30], i.e. all vectors \({\mathbf{x}}\) such that \({\mathbf{J}} \cdot {\mathbf{x}} = 0\) [29].

To understand what happens when there are more parameters than observations, as in this example and in most real world applications, we can rewrite (6) as a system of algebraic equations, which for this case contains only one equation,

$${\Delta }h_{w} = J_{11} {\Delta }K_{1} + J_{12} {\Delta }K_{2}$$
(7)

where \({\Delta }h_{w} = h_{w}^{0} - h_{w}^{i}\). Then, given an arbitrary variation of \(K_{1}\), we can compute the corresponding variation of \(K_{2}\) needed to obtain a model that reproduces the observed data, as

$${\Delta }K_{2} = \frac{{{\Delta }h_{w} - J_{11} {\Delta }K_{1} }}{{J_{22} }}$$
(8)

Therefore, for this case we can find infinite solutions to the inverse problem by selecting an arbitrary variation of \(K_{1}\) and computing the corresponding variation of \(K_{2}\) from the last equation. In summary, this example with 2 parameters and 1 single observation is equivalent to an algebraic system with 2 unknown variables and a single equation, which admits an infinite number of solutions. This is a simple and intuitive demonstration of the non-uniqueness of the solution for the parameter estimation problem when there are more parameters than observations, as it happens often for groundwater models due to the heterogeneity of the parameters that they include, e.g. hydraulic conductivity, recharge rates, etc.

An important step after computing the solution of the linear system, is to verify that the linear approximation is valid by evaluating the model using the estimated set of parameters and comparing the result with the observed measurements. In most cases, models are non-linear, so that differences between observations and the results provided by the calibrated model based on the linear approximation are expected. Moreover, in real cases, measurement errors affect observations; while simplifications in model structure and parameter distribution, referred to as structural errors, influence the results of simulations [10]. For simplicity, we consider that such errors do not affect our synthetic example.

The set of parameters that fit the observation, i.e. \({\mathbf{e}}^{*} = \left\{ {K_{1} ,K_{2} } \right\}\), found by solving (8) or by directly applying (6) is computed through an iterative process, since they are based on the local linear approximation (5), which is only valid for a small region around the set of parameters that are used to evaluate it. We opted to use (8), since it is straightforward to implement according to the following steps:

  1. 1.

    Select an initial set \(\left\{ {K_{1}^{0} ,K_{2}^{0} } \right\}\).

  2. 2.

    Evaluate model to compute initial result, \(h_{w}^{i}\) and check if \({\Delta }h_{w} > {\text{TOL}}\), where \({\text{TOL}}\) is a prescribed tolerance to stop iterations, which should be chosen such that it is compatible with the potential magnitude of measurement errors and the overall precision level of the model. If the last condition is true, continue to next step, else stop iterations.

  3. 3.

    Evaluate components of the Jacobian around the initial parameter set. For this model with two parameters, it requires evaluating the model two additional times.

  4. 4.

    Define a change in \(K_{1}\), \({\Delta }K_{1}\), and apply (8) to calculate a corresponding \({\Delta }K_{2}\). For example, \({\Delta K}_{1}\) can be specified as a fixed percentage of the current value of \(K_{1}\).

  5. 5.

    Calculate new values \(K_{1} = K_{1}^{i} + {\Delta }K_{1}\) and \(K_{2} = K_{2}^{i} + {\Delta }K_{2}\).

  6. 6.

    Check if new values are within ranges defined during the conceptual model stage. If they are not, stop iterating and report failure to find a satisfactory solution. Then, only a limited number of initial parameters may result in a satisfactory solution. In practice, this can result in a large computational overhead due to attempting to solve many cases that end up in failure.

  7. 7.

    Evaluate model for \(K_{1}\) and \(K_{2}\) to compute \(h_{w}\) and check residual versus tolerance. If residual is still too big, set last parameter values as initial set and go back to Step 1.

We applied the previous algorithm to estimate combinations of \(K_{1}\) and \(K_{2}\) that fits the observed head \(h_{w}\). The true or target value \({\mathbf{e}}^{*}\) for this synthetic example is known, since we use it to generate the observed head \(h_{w}\). We used as initial guesses random combinations of both variables generated assuming a uniform distribution of \(\ln \left( K \right)\) within the specified ranges of \(K\) for each material. Figure 4 shows the initial and estimated combinations of parameters for the homogeneous and heterogeneous cases. While the initial sets cover the full range of each parameter, the ones that result in satisfactory combination of parameters define a much smaller region that coincides with an almost straight line defined by (8), which passes through the target or true parameter set. For the heterogeneous case, the estimated parameters define an almost vertical rectangular region in the plane \(K_{1} - K_{2}\), which indicates that the simulated piezometric head at the well is much less sensitive to the value of \(K_{2}\) than to the value of \(K_{1}\). This is a consequence of: (1) the location of the well with observed data within material 1, and (2) the ratio between \(f_{K}\) considered for the heterogeneous case (lower \(K_{2}\)). It also agrees with the estimation of the local sensitivity of the model shown in Fig. 3. Figure 4 also shows the initial sets of parameters for which the iterative process finished with a solution that satisfied the convergence criteria fixed at \(1.5\)% of the observed head \(h_{w}\). Note that for the heterogeneous case only 130 out of 500 initial sets of parameters resulted in satisfactory results.

Fig. 4
figure 4

Combinations of \(K_{1}\) and \(K_{2}\) assuming two different ratios, \(f_{K}\) = 1.00, 0.01; for randomly selected values within specified range (blue dots) and after parameter estimation (red squares). Green dots show initial parameter values (seed) for the cases for which convergence criteria was satisfied. a Homogeneous and b heterogeneous aquifer

Full size image

As for most iterative algorithms, the convergence rate and the estimated solution depend on: (1) the initial set of parameters, (2) the tolerance or threshold value defined as criterion to stop the iterative process, \({\text{TOL}}\); and (3) the size of the potential range defined for each parameter during the conceptual model stage, since larger ranges would potentially result in more iterations. Therefore, finding acceptable solutions for the parameter estimation problem by using this type of algorithms involves a trade-off between the tolerance criteria that is set and the amount of computational effort considered acceptable. More relaxed criteria result in more parameter combinations that fit the observed data, but at the cost of larger residuals. This trade-off is important to consider for reducing the uncertainty of the calibrated model results, as we will show next.

Figure 5 shows normalized residuals of piezometric head for the observation well versus normalized randomly generated values of \(K_{1}\) and \(K_{2}\). For the homogeneous case, there is a wide range of values of \(K_{1}\) and \(K_{2}\) (from the minimum value to almost 60% of the maximum value) that can result in simulated head at the well that is similar to the observed or target value (indicated by a red cross). However, for the heterogeneous case (\(f_{K} = 0.01\)) the range of potential values of \(K_{1}\) that result in a simulated value similar to the observed one is much reduced, while the range for \(K_{2}\) covers the full potential range of values considered as part of the conceptual model. For the heterogeneous case, the relation between residuals and \(K_{1}\) is well represented by a single decreasing line from low to high values of \(K_{1}\).

Fig. 5
figure 5

Normalized residual (i.e. difference between simulated and observed head) at position of observation well versus normalized values of hydraulic conductivity for randomly generated parameter sets. Red cross indicates values for the adopted virtual reality site. a Homogeneous and b heterogeneous aquifer

Full size image

Previous studies have found that introducing a few estimates of groundwater flows as additional observations can reduce the number of solutions for the inverse problem [16]. Figure 6 shows computed left and right outflows from the model considering only calibrated parameter sets for \(f_{K} = 0.01\). For a large number of estimated parameter sets, the water table includes a water divide within material 2 as shown in Fig. 2, so that water can flow to the left or the right depending on the location. Thus, the sum of both outflows (right and left) is equal to the total recharge. For other cases, when the total flow is larger than the total recharge, water can also enter the domain through the right boundary, thus it can only flow from right to left at any given location of the domain. This means that groundwater flow at some locations can even have different direction between calibrated models. Figure 6 shows that all calibrated parameter sets result in outflows through the left boundary that vary between ± 20% of the total recharge. This means that for this particular example, any flow estimation that could be useful to discriminate between different calibrated parameter sets should have a level of confidence higher than 20% of the total flow, which is seldom achievable in real world projects. This could be a major limitation for the use of flow estimations to constrain the solution of the inverse problem for highly parameterized models, since groundwater flows cannot be measured except in very few cases and only with large margins of error.

Fig. 6
figure 6

Outflows through left and right boundaries divided by total recharge for calibrated parameter sets for the heterogeneous aquifer, \(f_{k} = 0.01\)

Full size image

Note that for this simple problem, the algorithm requires up to five iterations to find an acceptable solution, and that each iteration requires evaluating the sensitivity matrix, which means running the model \(N_{e} + 1\) times. In addition, only \(25\)% of the initial guesses provided solutions that were considered acceptable according to the set tolerance, which was relatively relaxed for this demonstration. Then, many iterations and computations did not produce a satisfactory solution. The method that we used is very basic and it does not incorporate some relatively easy improvements that have demonstrated to accelerate convergence, such as using transformed variables or using a modified Newton method by including an acceleration factor as in the Levenberg–Marquardt method implemented in software platforms for parameter estimation [13, 20]. However, these findings point to the importance of using good initial guesses, and that the computational cost of applying this type of algorithms can grow very quickly with the number of parameters and the number of initial sets considered.

Sometimes the problem of finding suitable parameter values expressed in (5) is recast into an optimization problem that aims to reduce the value of an objective function to assess the goodness of fit between observed and simulated variables. This is, in most cases, equivalent to making the residuals in the left side of (5) close to zero [10]. The main advantages of this formulation is that using an objective function allows assigning different weights for the residuals of observed variables at different locations and, also, introducing additional penalty terms to further force the calibrated model. For example, penalty terms can be included to enforce estimated flow discharges, or to force the calibrated parameters to be close to preferred values assigned during the conceptual model stage. Nevertheless, the problems discussed previously such as non-uniqueness of the solution and dependency on the convergence criteria still apply.

3.4 Uncertainty analysis

There are three main sources of uncertainty that can affect model results, which we review next.

  1. a.

    Uncertainty due to parameter distribution

    We use the model to evaluate the water table for different random combinations of \(K_{1}\) and \(K_{2}\) that are within the ranges defined as part of the conceptual model, which is a form of global sensitivity analysis. Figure 7 shows simulated water table for 500 different combinations of \(K_{1}\) and \(K_{2}\) generated using a uniform distribution of \(\ln \left( K \right)\) within the specified ranges.

    For the homogeneous aquifer case (\(f_{K} = 1.00\)), the simulated water table differs from the true solution by up to \(15\)% of the prescribed head at the left boundary, \(h_{1}\); however the difference increases up to more than 100% for \(f_{K} = 0.01\) (heterogeneous aquifer). Those few cases represent extreme situations that are the result of less likely combination of parameters, however, since all values of \(K\) are within the specified ranges, it is not possible to discard any of them without additional information. Furthermore, the variability between the different realizations is higher at the center of the simulated domain for the homogeneous case, while it is maximum at around the middle point of the area occupied by material 2 (lowest \(K\)) in the heterogeneous case. The magnitude of the variability of the simulated water table provides an indication of the prior uncertainty of the model results, which is only constrained by soft-knowledge before calibration. Despite the advantages and the valuable information that this type of analysis provides, it is seldom performed in practice, because it may still be excessively time consuming for models with hundreds or thousands of parameters, which require several hours or days to complete [31].

  2. b.

    Uncertainty due to parameter estimation

    By including additional information about observed measurements, we can decrease the uncertainty of the model results at least at the locations where data is available. Since we created a synthetic base scenario or virtual reality by evaluating the model for a given set of parameters to generate the observed value of head at \(x_{W} ,\) we can also compare the results of the model at other locations between both rivers. Figure 8 shows the simulated water table considering only sets of calibrated parameters, i.e. the ones that result in a simulated \(h_{w}\) similar to the observed value. A small tolerance criteria or threshold limit, \({\text{TOL}}\), set during the parameter estimation stage, results in a better match between simulated and observed \(h_{w}\), while adopting a larger limit for the tolerance results in the opposite: larger differences between simulated and observed \(h_{w}\), together with more combinations of parameters that satisfy the converge criteria. Therefore, the tolerance threshold must be selected with care considering a trade-off between the need for reducing uncertainty of the model results and the computational cost.

    Figure 8 shows that the selection of the convergence criteria must also consider the possibility that for some problems, even restrictive convergence criteria used to evaluate the difference between simulated and observed values at a few locations (e.g. at the well in this case) may not imply a significant reduction of the uncertainty of the model results at other locations. It is also immediate from Fig. 8 that all simulations satisfy the convergence criteria imposed at the well, but that depending on the ratio between the hydraulic conductivity of both materials \(f_{K}\), the difference between the results of the model and the adopted virtual reality case can be quite large at other locations. Figure 8 also shows in a simple way that the non-uniqueness of the parameter estimation problem is equivalent to having a large number of alternative parameter sets that reproduce the observed data with similar precision and thus, are equally likely to be correct. A consequence of this is that, ideally, every calibrated model should be reported with at least a few sets of parameters that are equally likeable in the sense that they reproduce observations. A null-space Monte Carlo approach, which reuses some of the results computed as part of the solution of the inverse problem, can be an economical and practical way to produce multiple alternative sets of parameters that explain observations [10].

    To quantify uncertainty, it is customary to identify the range of possible outcomes and the probability associated to intervals of those ranges. Histograms as the ones shown in Figs. 9 and 10 summarize well this type of information. Figures 9 and 10 show results for the heterogeneous aquifer (\(f_{k} = 0.01\)), while similar results for the homogeneous aquifer are included in the Supplementary Material. Figure 9 shows the probability of simulated heads at the well \(h_{w}\) versus the normalized simulated value \(h/h_{0}\). We used 5000 initial different parameter sets to obtain reasonable accurate estimations of the probabilities of the simulated heads, which allows quantifying the inherent uncertainty of the model result without conditioning them to observed data. In a Bayesian framework, the resulting simulated heads would represent the prior probability distribution of the variable [10]. This particular set of initial guesses resulted in only 1216 sets of estimated parameters that matched the observed \(h_{w}\). The piezometric head values simulated considering only the estimated parameter sets describe the posterior probability distribution. Additional analysis considering different sets of randomly generated initial parameter sets demonstrated that this number of realizations provided probabilities that are significant and are consistent between different groups of random parameter sets.

    When randomly generated sets of parameters are used to compute the probabilities, the range of potential outcomes of the model is relatively large (about 20% of the true value), but most of the simulations produce values that are close to the true value, i.e. values of \(h/h_{0}\) near 1 have highest probability. The shape of the probability distribution depends on the model features (see computed probabilities for the homogenous aquifer included in Supplemental Material), but also on the sampling strategy used to define the input parameter sets. For this example, the true parameter set, i.e. the one that defines the adopted virtual reality, was selected as centered within the ranges, hence the probability is higher for values of \(h\) similar to the true values. If we consider only calibrated sets, then the range of potential outcomes of the model for \(h_{w}\) decreases to less than 4%. Even though the estimated set of parameters results in a reduction of the uncertainty of the model results around the single location with information, \(x_{w}\), the uncertainty of the results for other locations may not be much reduced. For example, Fig. 10 shows the probability of the simulated head at approximately the middle point of the area occupied by material 2 (\(x_{2} = 0.8L)\). The range of potential values of \(h\) computed for \(x_{2}\) is similar for the random and estimated parameter sets, however the probability of each interval is slightly different.

  3. c.

    Uncertainty due to forcing variables

    The standard procedure to quantify this uncertainty is similar to the one used to quantify the uncertainty of the model due to estimated parameters: generate many equally likeable or probable series of forcing parameters, e.g. recharge series for this example, and use them to run the model and collect its results to generate probability distributions of the possible outcomes. Then, this analysis also requires defining possible ranges for forcing variables and selecting mathematical models to generate plausible time series. The rest of the analysis is similar to the one described previously (Figs. 9, 10). Some forcing variables, e.g. boundary conditions, can sometimes be considered as part of the model parameters as part of the uncertainty analysis. However, it is better to keep them separate from the real parameters of the model that must be estimated, because, in general, the uncertainty related to their values have different origin and magnitude.

Fig. 7
figure 7

Water table for different combinations of randomly generated values of \(K_{1}\) and \(K_{2}\). Thick black line shows the water table for the combination of parameters that represents the virtual reality site. Dashed red line shows position of interface between materials \(x_{K}\) and blue line shows position of well with measured head \(x_{w}\). a Homogeneous and b heterogeneous aquifer. Note: \(f_{K}\) corresponds to ratio between both scales \(k_{1}\) and \(k_{2}\), thus for \(f_{K} = 1.0\), \(K_{1} /K_{2}\) ranges between \(\left[ {0.01, 100.0} \right]\)

Full size image
Fig. 8
figure 8

Simulated piezometric head \(h^{*}\) using estimated parameters \({\mathbf{K}}^{*}\) for different tolerance threshold (TOL). Thick black line shows the water table for the combination of parameters that represents the virtual reality site. Dashed red line shows position of interface between materials \(x_{K}\) and blue line shows position of well with measured head \(x_{w}\). Note: \(f_{K}\) corresponds to ratio between both scales of hydraulic conductivity, \(k_{1}\) and \(k_{2}\), thus for \(f_{K} = 1.0\), \(K_{1} /K_{2}\) ranges between \(\left[ {0.01, 100.0} \right]\)

Full size image
Fig. 9
figure 9

Uncertainty of predicted piezometric head at the well position \(x_{w}\) using a randomly generated sets of parameters \(K_{1}\) and \(K_{2}\) and b after parameter estimation. Normalized simulated head expressed as function of the head value assigned to right boundary

Full size image
Fig. 10
figure 10

Uncertainty of predicted piezometric head at position \(x_{2} = 0.8 L\) using a randomly generated sets of parameters \(K_{1}\) and \(K_{2}\) and b after parameter estimation. Normalized simulated head expressed as function of the head value assigned to right boundary

Full size image

4 Conclusions

The fact that for practical applications, models always include more parameters than available observations, leads to an inverse problem that has multiple solutions. Automatic parameter estimation methods make explicit the existence of these multiple solutions and facilitate to find them. Thereby, they help to explore the potential variability of the model results that is coherent or supported by collected observations. We demonstrated through a synthetic example inspired by a real-world setting, that adding estimates of groundwater flow as previously proposed [16] to reduce the number of potential solutions for the inverse problem, may be rather difficult and/or ineffective. Hence, it may be a better strategy to accept that the calibration of numerical models that include a large number of parameters will always lead to a large number of multiple solutions.

It is likely that the full quantification of the uncertainty associated to groundwater models will remain reserved for limited applications for some time due to the computational effort needed. The computational effort for models that include hundreds or even thousands of parameters may be prohibitively expensive even with the computational resources available today. Meanwhile, calibrated models used to make forecasts should at least include a sensitivity analysis that attempts to bound its potential results and help identifying the parameters that have greatest importance. Although this may be simple for linear models with few parameters, it may still be rather difficult for non-linear models that depend on multiple parameters with wide ranges of potential values, as it is the case of most groundwater models. Alternatively, linear uncertainty quantification, which requires little additional computational effort, can provide results that are informative for ranges of parameters for which models behave quasi-linearly, but must be analyzed considering their limitations [10, 11].